0 引言
图像角点检测是图像分析和计算机视觉领域的一个关键的预处理步骤,常用于图像配准[1]、目标识别[2]和场景分析[3]等领域。现有的角点检测算法大致可分为3类:基于模型的方法、基于灰度的方法和基于轮廓的方法[4]。其中基于轮廓的角点检测算法具有定位误差小的优点[5]。
基于轮廓的角点检测算法的关键是构建高效的角点响应函数。Mokhtarian等[6]提出基于曲率尺度空间(curvature scale space,CSS)的角点检测算法,是该领域的标志性算法。随后,多种基于CSS的角点检测算法被提出。Zhong等[7]提出直接曲率尺度空间(direct curvature scale space,DCSS)算法,作为CSS的一种衍生技术,该算法降低了计算复杂度;Zhang等[8]通过分析多尺度空间曲率行为,提出了一种鲁棒的多尺度曲率积(multi-scale curvature product,MSCP)检测算法。基于CSS技术的角点检测算法通常面临2个问题:①对曲线的局部变化和噪声敏感,导致检测性能不佳;②如何选择合适的高斯平滑参数,这是一项艰巨的工作。
针对上述问题,研究者们提出了各种解决方案。Awrangjeb等[9]提出了弦点距离累积(chord-to-point distance accumulation,CPDA)算法,该算法定位误差较小,但计算量较大,且其支持域[10]半径较大,可能会融合强度较弱的角点;Teng等[11]利用三角形理论(chord to triangular arms ratio,CTAR)计算曲率并检测角点,该方法使用单弦代替CPDA算法多弦计算,检测速度更快。
本文提出一种基于平行四边形对角线之比的角点检测算法,该算法用商之比作为曲率估计函数,既大大减少了计算量,又增强了对尺度变换的鲁棒性。
1 CTAR算法
Teng等[11]提出的CTAR角点检测算法使用简单三角形理论来估计曲率,其算法过程如图1所示。P1,P2,…,PN为曲线上的N个点,Pi为要确定的曲率值的角点。首先,将Pi分别向前、向后遍历t个点到Pi+t、Pi-t。如果Pi-t、Pi和Pi+t三点共线,线段Pi-tPi+t与PiPi-t和PiPi+t的长度之和的比值为1;反之,若Pi-t、Pi和Pi+t三点不共线,则构成三角形PiPi-tPi+t,弦Pi-tPi+t的长度与三角形2条边长PiPi-t和PiPi+t之和的比值小于1;且∠Pi越小,该比值越小,即∠Pi越尖锐。曲线在点Pi的曲率为
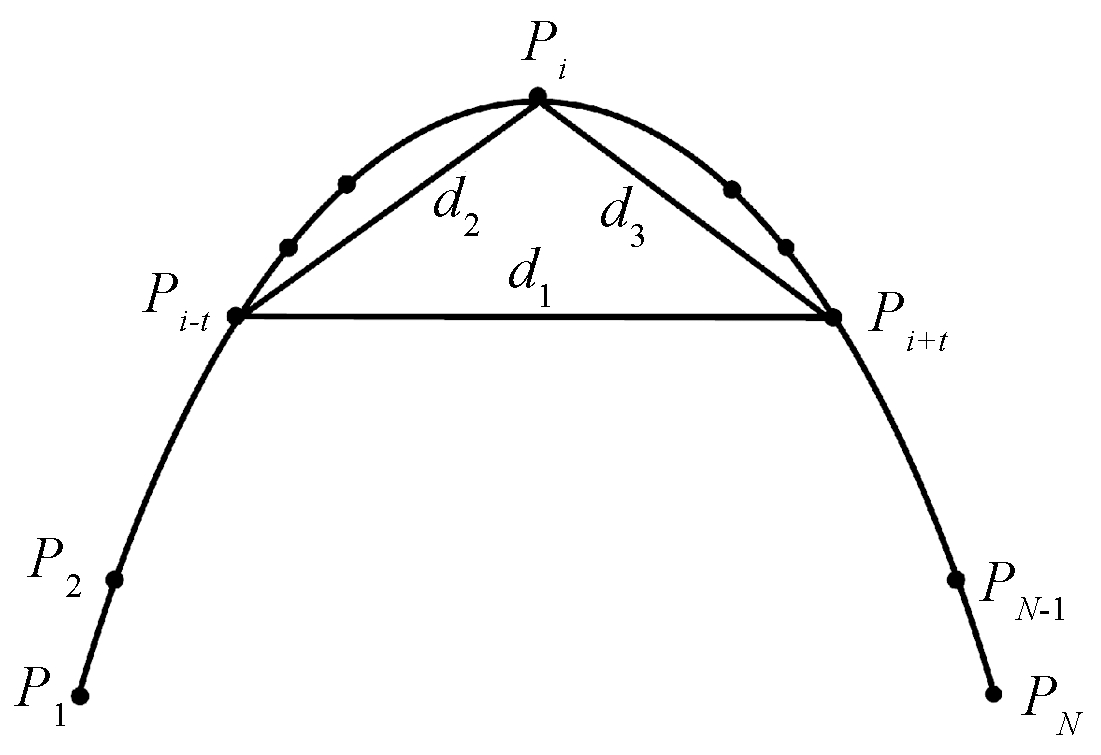
图1 基于弦的CTAR曲率估计
Figure 1 Estimation of curvature using CTAR with chord
(1)
式中:![]()
当R(i)小于设定的阈值[11]Th=0.989 6时,R(i)为极大值,则将Pi视为角点。与CPDA算法[9]相比,CTAR算法计算效率更高,鲁棒性更好[12]。
2 FRPD算法
CTAR计算角点响应函数使用了三次平方根运算,计算量较大。针对此问题,本文提出了一种不涉及平方根运算的FRPD算法。
FRPD算法利用平行四边形对角线之比估计曲率值。首先,将曲线段对应的弦作为三角形的1条边,弦的两端点和曲线段的中点连线,形成1个三角形;其次,过弦的两端点对三角形另外2条边作平行线,使其相交于一点,形成1个平行四边形。则沿着曲线移动的这条弦是平行四边形的1条对角线,绘制另外1条对角线,计算弦与该对角线的长度之比,比值为曲线上中点的离散曲率值。
图2为直角坐标系中1个对角线相互垂直的平行四边形,设该平行四边形1条边为r,则对角线之比为
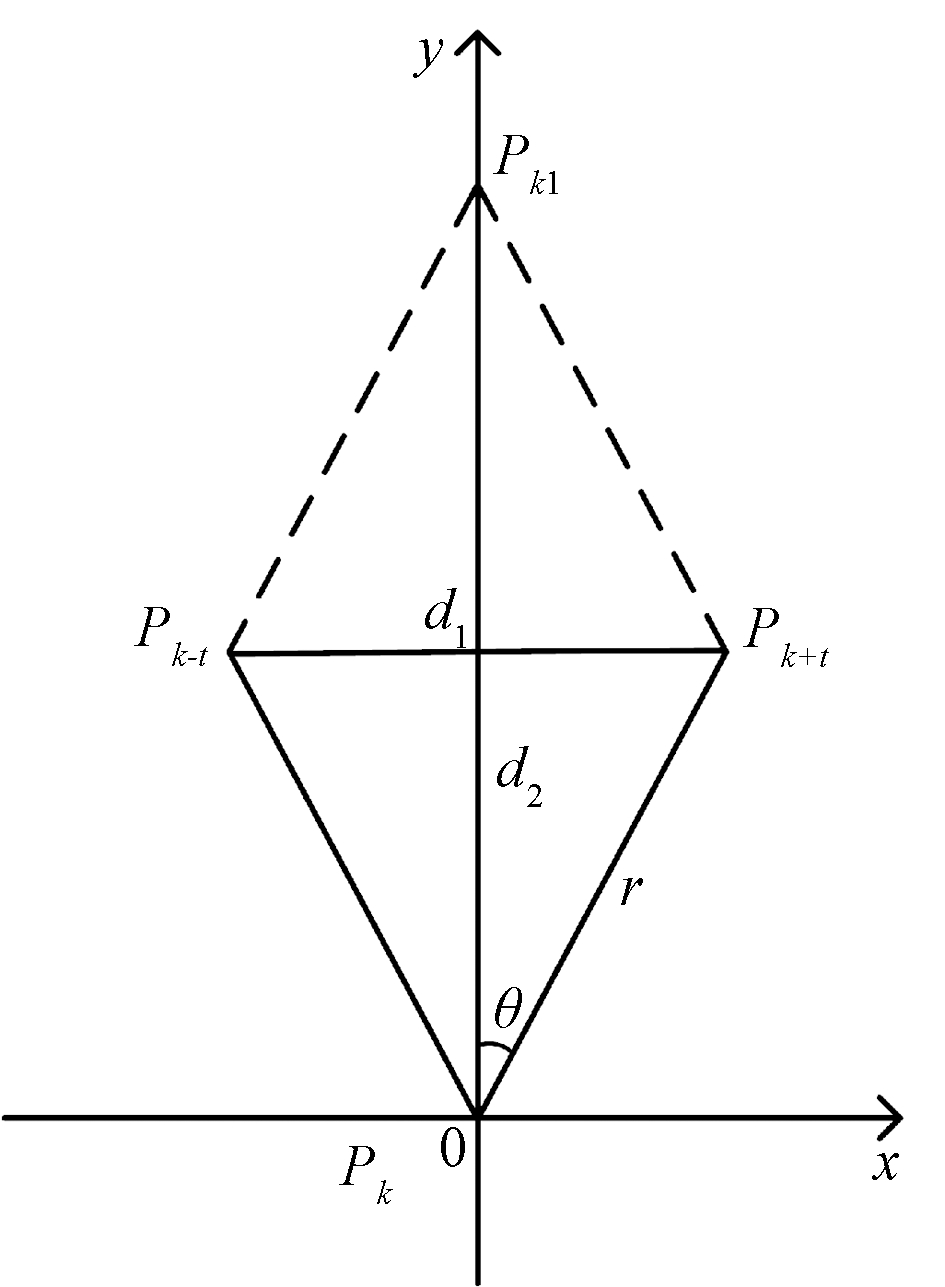
图2 平行四边形对角线曲率估计理论示意图
Figure 2 Schematic diagram of diagonal curvature estimation theory of parallelogram
(2)
式中:d1=2rsin θ;d2=2rcos θ。代入式(2)可得
(3)
从式(3)可以看出,FRPD曲率估计值与cot θ成正比,d2/d1可以准确反映离散曲率的行为。FRPD算法过程如图3所示。设曲线上的N个点为P1,P2,…,PN,令Pk向前、向后分别遍历t个像素点到Pk+t、Pk-t;然后,作线段PkPk+t和线段PkPk-t的平行线,使其相交于一点Pk1,此时,如果4个点Pk-t、Pk、Pk+t和Pk1共线,即像素点Pk和Pk1重合,d2/d1的值等于0,反之,d2/d1的值大于0。因此曲线在点Pk的曲率为
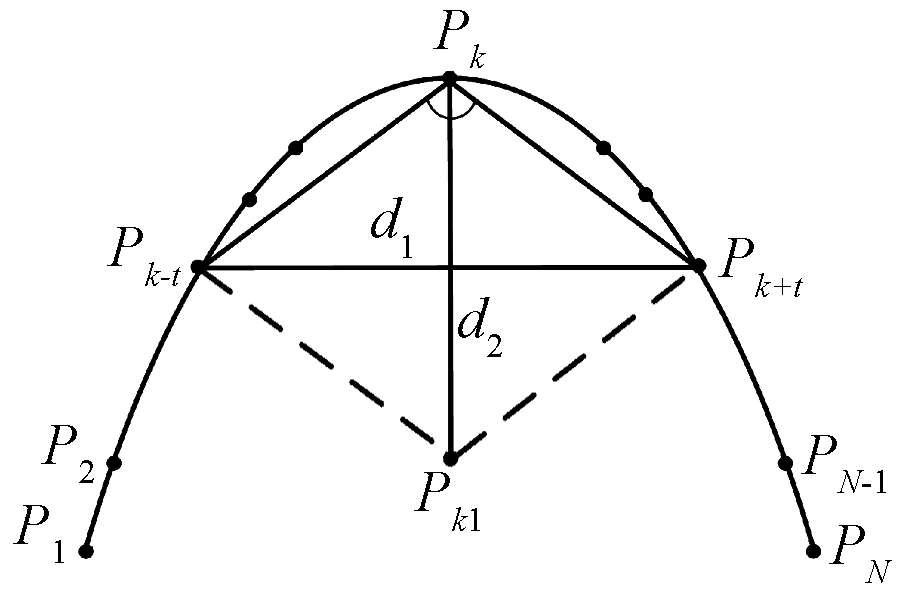
图3 基于FRPD曲率估计
Figure 3 Curvature estimation using FRPD
(4)
式中:![]()
去掉d1和d2的平方根,可以保证算法性能,且减少计算量。因此式(4)可变换为
(5)
如图4所示,图4(a)叶子图像4个角点的曲率值对应图4(b)中4个峰值,可以看出,角越尖锐所对应的曲线的曲率值越高。
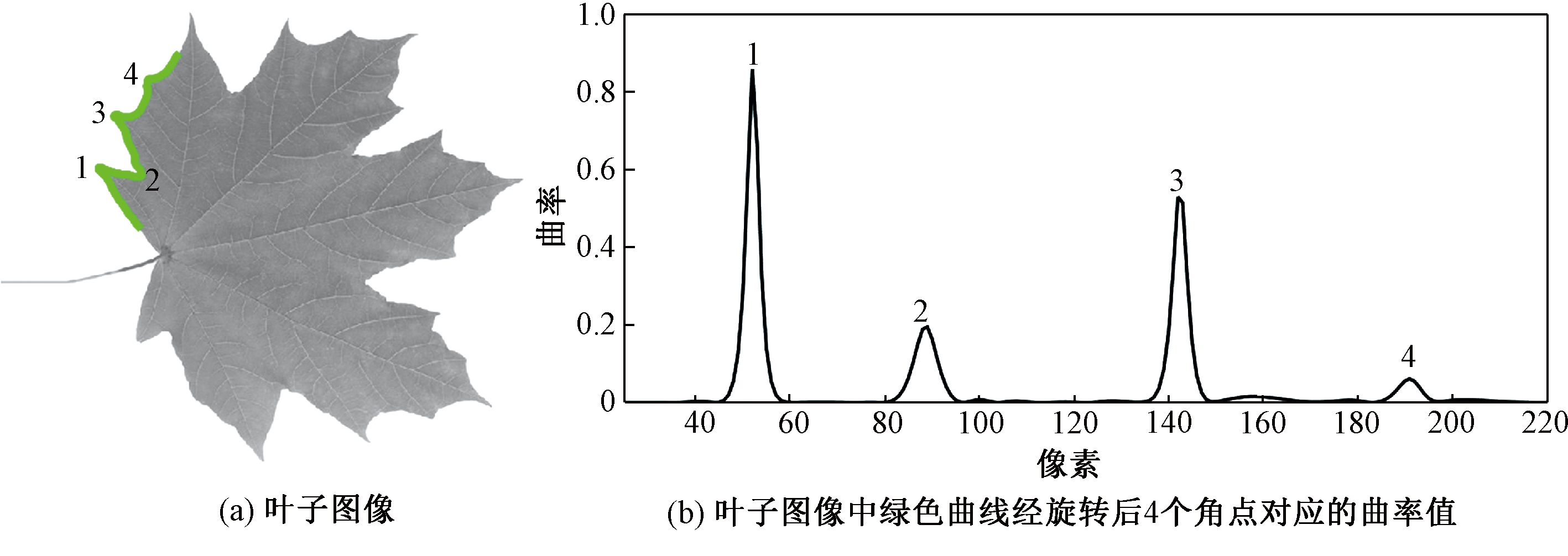
图4 叶子图像中4个角点的FRPD曲率响应值
Figure 4 FRPD curvature response value of four corners points in the leaf image
根据上文分析,FRPD算法主要步骤如下。
Step 1 使用Canny算子[13]从原始图像中提取边缘和轮廓,并将其标记为直线轮廓或封闭轮廓。
Step 2 找到T型结点并将其标记为角点。
Step 3 使用均值为0、方差为σ的高斯函数对提取的轮廓进行平滑以去除量化噪声和局部细节。
Step 4 根据式(5)计算平滑后曲线的角点响应函数值。
Step 5 进行非极大值抑制,将角点响应值大于设定阈值的点作为角点。
3 图像数据集和评价准则
3.1 图像数据集
使用GCM图像数据集[14]和CPDA图像数据集[15]来评估角点检测算法的性能,如表1所示。从数据集中选取的每幅图像均通过5种不同类型的变换来获得测试图像集。
表1 GCM数据集和CPDA数据集的图像转换
Table 1 Image transformation applied on GCM dataset and CPDA dataset based images

转换类型影响因子图片数量GCM数据集CPDA数据集旋转在[-90°,90°]内间隔为10°进行旋转变换380437一致尺度在[0.5,2]内间隔为0.1的缩放变换范围,其中x轴和y轴缩放范围相等,并且不包括1.0300345非一致尺度x轴缩放变换范围为[0.7,1.5],y轴缩放变换范围为[0.5,1.8],间隔为0.125202898旋转-缩放同时进行以下变换:旋转范围以10°为间隔在[-30°,30°]转换,x、y轴分别以0.1为间隔在[0.8,1.2]进行缩放变换 35004025高斯噪声零均值高斯白噪声在[0.005,0.05]内以0.005为间隔加入原始图像200230
3.2 评价准则
本文使用平均重复率和定位误差2个标准[16]来评估角点检测算法的鲁棒性。
平均重复率Ravg表示原始图像和测试图像之间被检测角点的匹配率,表达式为
(6)
式中:No和Nt分别表示原始图像和测试图像角点的个数;Nr是重复角点的数量。Ravg的最大值为1,数值越大表示算法的重复率越高,鲁棒性越强。
定位误差Le是对重复角点的像素偏差量的一种度量[16],表达式为
(7)
式中:(xoi,yoi)和(xti,yti)分别是原始图像和测试图像中第i个重复角点位置。允许均方根误差值RMSE最大为3个像素查找重复。
4 结果分析
本文算法的仿真实验平台为i7-4790处理器,主频为3.60 GHz,内存为8 GB,64位操作系统,在MATLAB 2014b上实现。
4.1 参数选择
为了使提出的角点检测算法的角点检测性能更好,首先将Canny边缘检测的阈值设置为[0.2,0.7],然后进行参数选择实验,采用一次只调整1个参数同时保持另外2个参数不变的方法。3个参数值分别设置为:①高斯平滑尺度因子,即高斯标准差σ=3.5;②支持域RoS=3;③GCM图像集曲率阈值Th=0.015,CPDA图像集曲率阈值Th=0.013。为保证公平,另外5个对比算法的参数值均按照本文参数选取方式调整获得最优值,同时所有算法均采用相同的Canny边缘检测算法提取轮廓。
4.2 性能评价
这一节中,主要对FRPD角点检测算法与其他5种基于轮廓的角点检测算法CTAR[11]、GCM[14]、CPDA[9]、F-CPDA (fast corner detector based on the chord-to-point distance accumulation)[17]和SODC (second-order difference of contour)[18]进行平均重复率和定位误差性能比较、角点匹配对比实验和算法运行速度的比较。
4.2.1 平均重复率和定位误差
平均重复率用来评估检测算法对仿射变换的稳定性,而定位误差用来评估角点定位的精准性。如图5所示,对于带有不同高斯噪声的图像,随着高斯标准差的增大,所有方法的平均重复率逐渐降低,定位误差逐渐增大。造成该现象的原因:测试图像受噪声污染的越多,对检测算法性能的影响越大。从图5(a)和5(b)可以发现,在GCM和CPDA数据集中,FRPD检测算法的平均重复率下降速度趋势明显比其他检测算法缓慢,其平均重复率最高,证明FRPD算法对噪声具有稳健性;F-CPDA检测算法随噪声方差的增大下降最快,其平均重复率最低,证明F-CPDA对噪声的干预非常敏感。从图5(c)和5(d)可以看出,在GCM和CPDA数据集中,CPDA定位误差最低,FRPD定位误差居中。
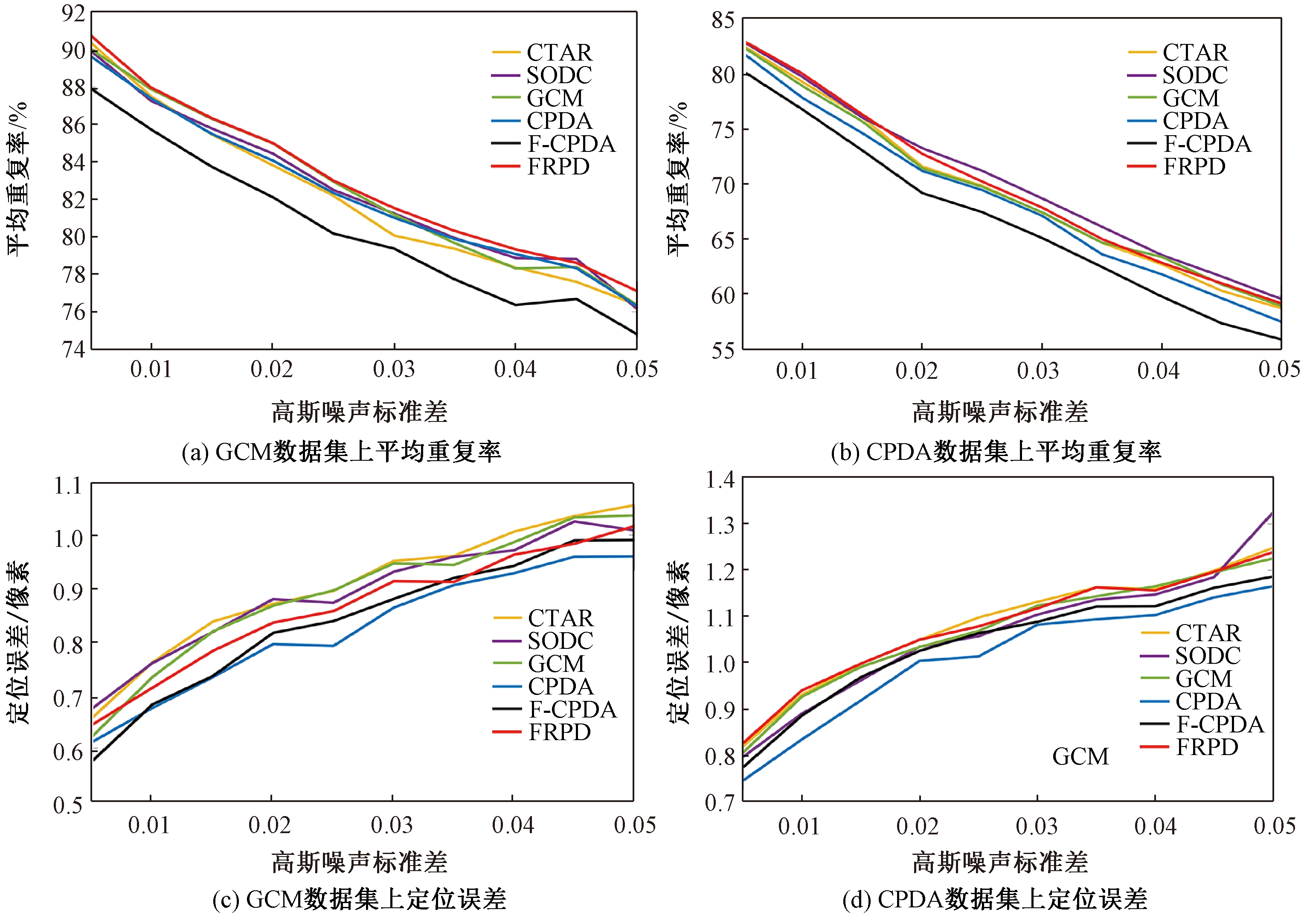
图5 带有不同高斯噪声的图像重复率和定位误差
Figure 5 Repeatability and localization error under Gaussian noise image transformations
对于旋转变换,如图6所示,当旋转角度接近π/4和-π/4时,所有检测算法的性能均较差,造成这种现象的主要原因是对应检测轮廓的质量很差,直接影响角点检测算法的性能。与其他5个检测算法相比,FRPD检测算法有最高的平均重复率以及良好的定位误差。
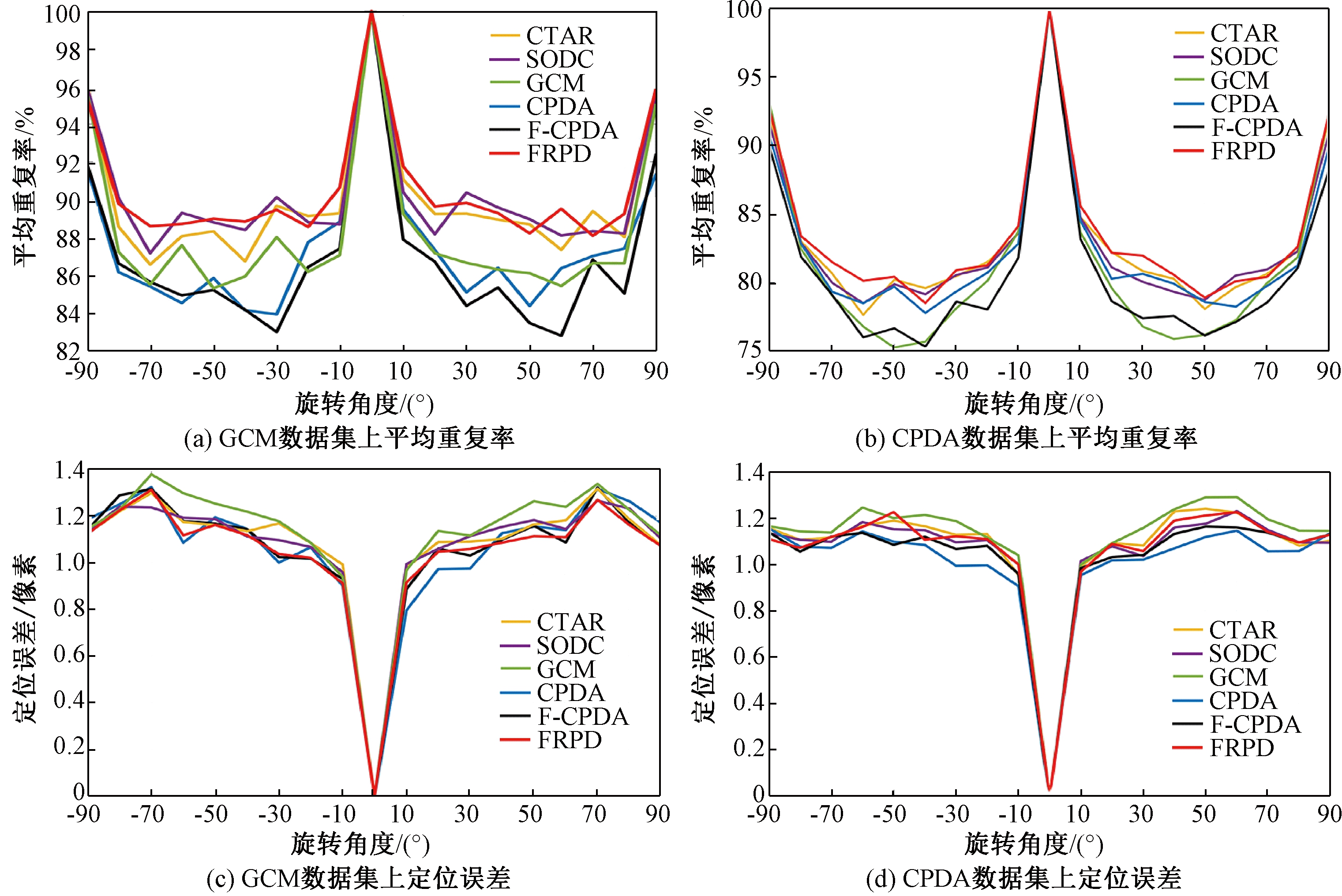
图6 旋转变换下重复率和定位误差
Figure 6 Repeatability and localization error under rotation transformations
对于一致尺度变换,当尺度因子小于1.0时,平均重复率随着尺度因子的增大而增大,如图7(a)和7(b)所示;定位误差随着尺度因子的增大而减小,如图7(c)和7(d)所示。当尺度因子大于1.0时,结论相反。与另外5种算法相比,FRPD检测算法在GCM数据集上有最高的平均重复率和最低的定位误差;在CPDA数据集上,平均重复率最高,定位性能和SODC相似。
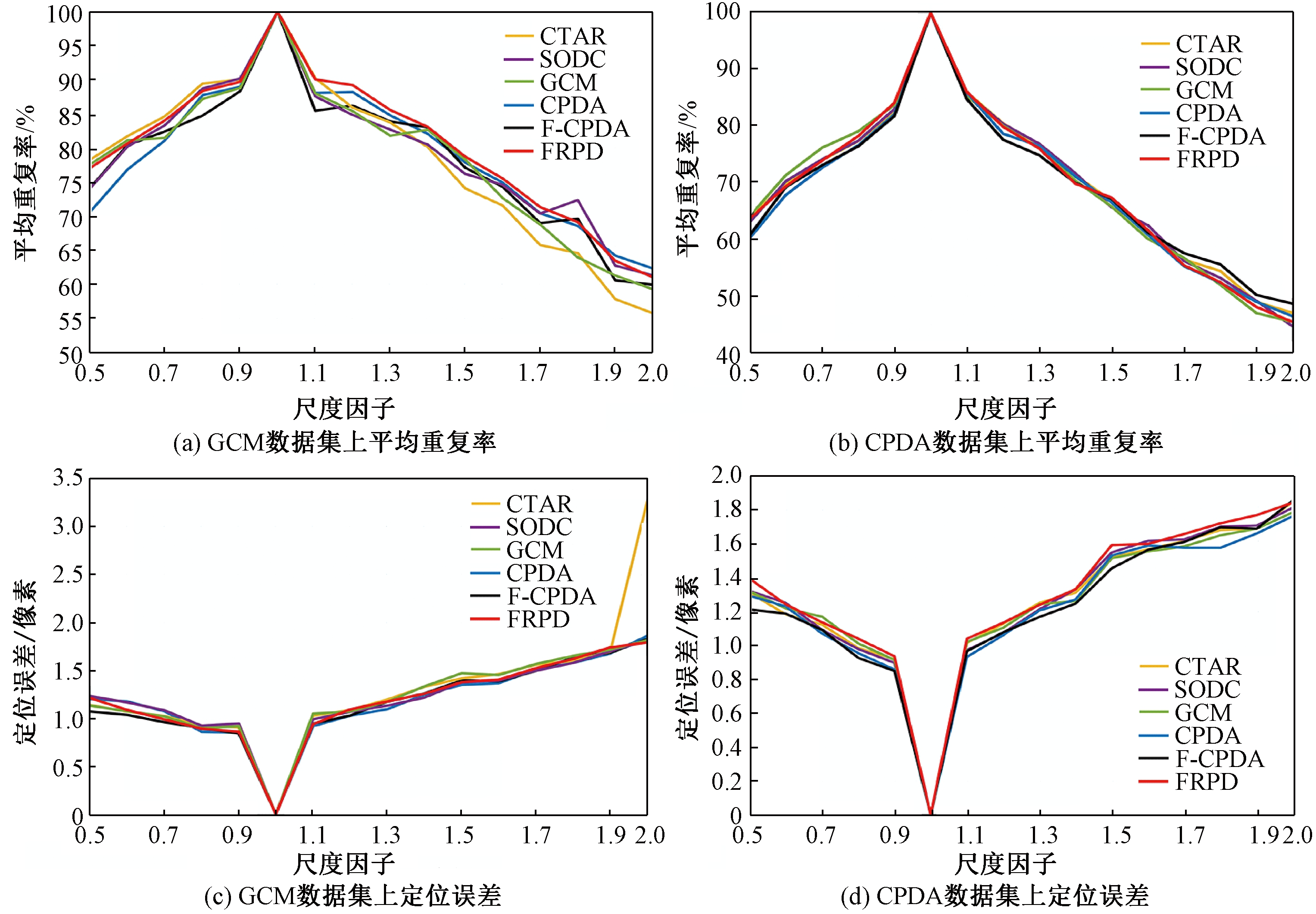
图7 一致尺度变换下重复率和定位误差
Figure 7 Repeatability and localization error under uniform scale transformations
如图8所示,对于非一致尺度和旋转-尺度变换,FRPD算法在6个角点检测算法中平均重复率最高。如图9所示,在GCM数据集中,FRPD算法在两种变换下均获得了最低的定位误差。在CPDA数据集中,FRPD算法非一致尺度变换的定位误差与SODC相似,旋转-尺度变换中FRPD算法的定位误差与CTAR相似。因此,从5种变换的检测结果得出,FRPD算法具有较好的检测性能。
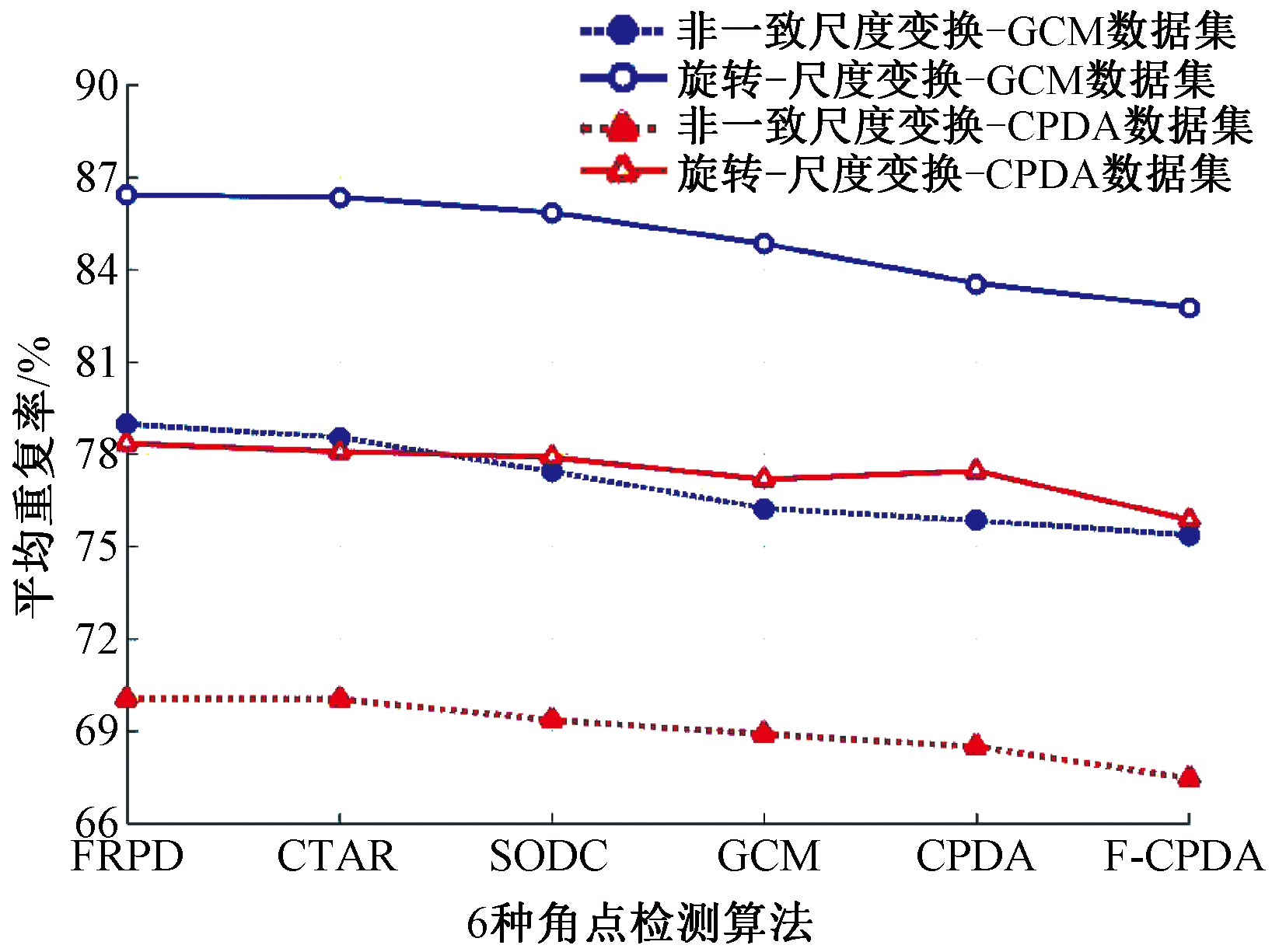
图8 非一致尺度和旋转-尺度变换下重复率
Figure 8 Repeatability under non-uniform scale and rotation-scale transformations
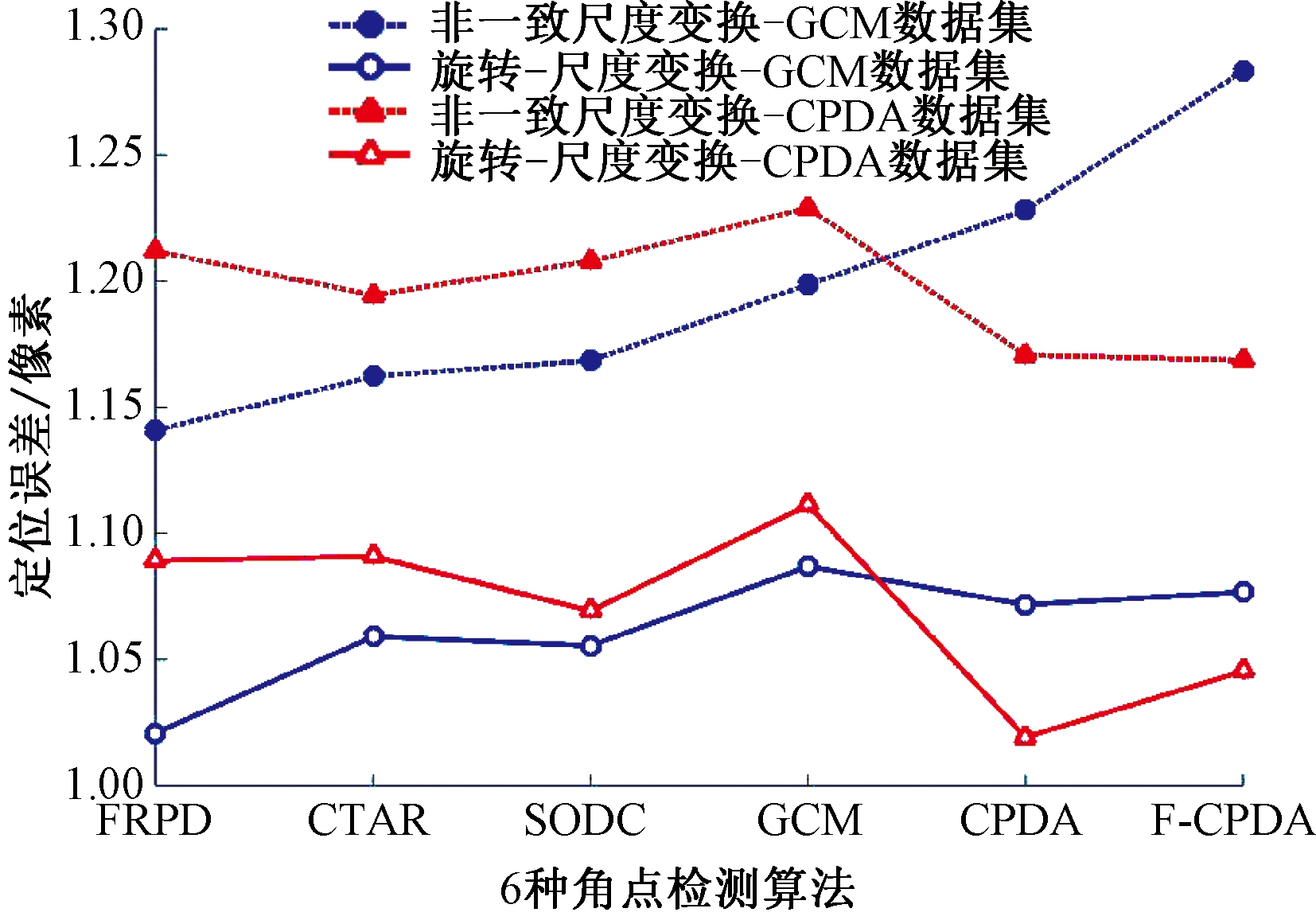
图9 非一致尺度和旋转-尺度变换下定位误差
Figure 9 Localization error under non-uniform scale and Rot.-scale transformations
为了验证FRPD算法对图像角点的正确响应,分别使用不同算法对Lena图像进行角点检测,Lena的真实角点可以参考文献[19]。对比结果如图10所示,FRPD算法不仅准确地检测出所有真实角点,而且未引入任何伪角点或丢失真角点,GCM引入了一些伪角点,SODC、CPDA和F-CPDA不仅检测到伪角点,还丢失了部分的真角点。
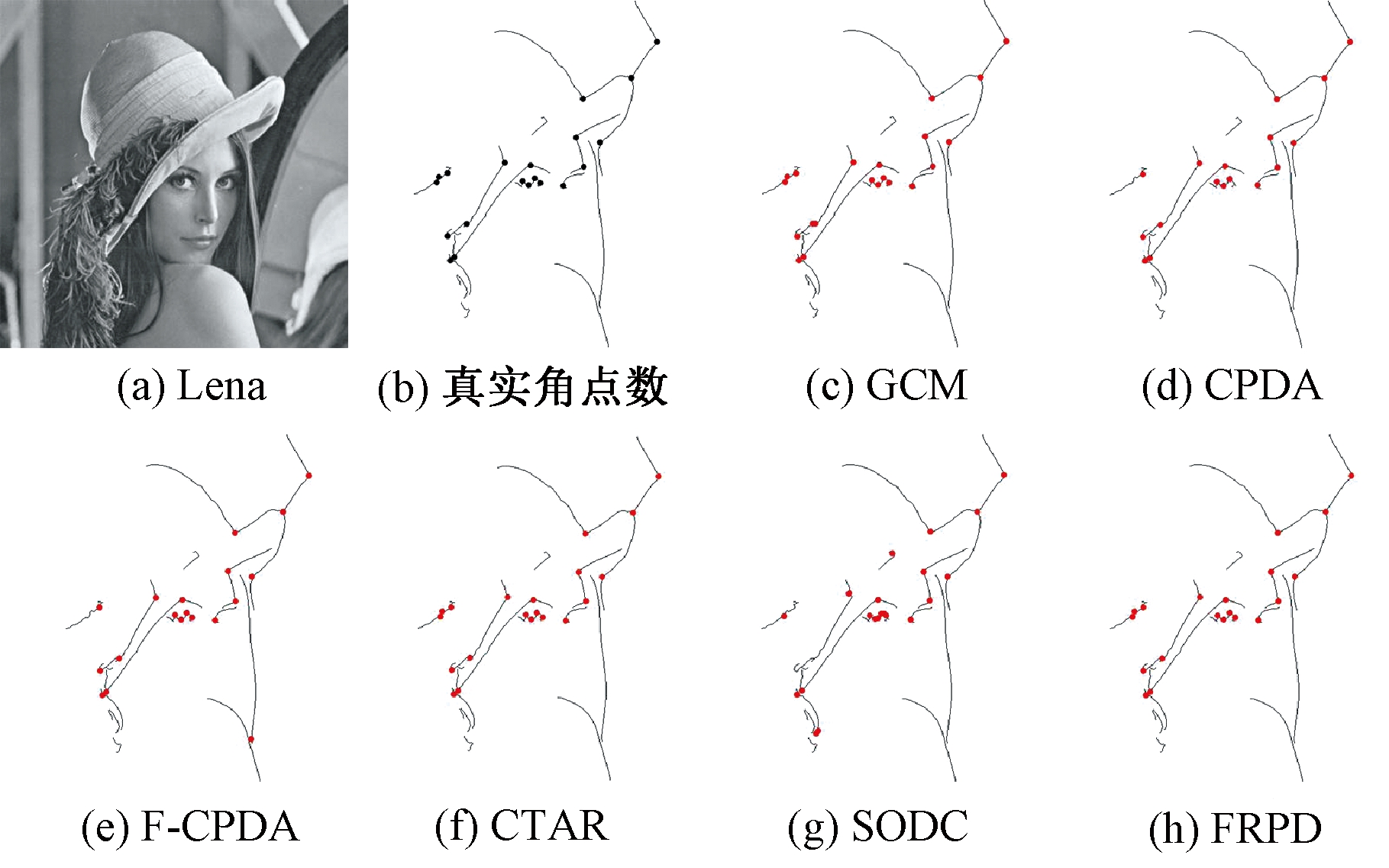
图10 6种基于轮廓的角点检测算法检测到的Lena的角点
Figure 10 Corner of Lena detected by six contour-based detection algorithms
4.2.2 算法效率评价
对于具有n个点的轮廓,CPDA检测算法需要54n平方根运算,而F-CPDA则需要(n+54np)平方根运算,其np是候选点的数目,CTAR和SODC都需要3n平方根运算[18]。相比之下,FRPD算法利用平行四边形对角线之比计算角点响应函数不需要平方根运算,计算复杂度为n。表2是对比算法检测角点的总时长(100次随机实验平均结果)。从表2可以看出,FRPD算法检测角点时间最少,约是CTAR的1/3,证明了FRPD算法的高效性。因此,FRPD算法在仿射变换、角点检测和时间复杂度方面具有优异的性能。
表2 算法检测角点时间效率对比
Table 2 Comparison of time efficiency
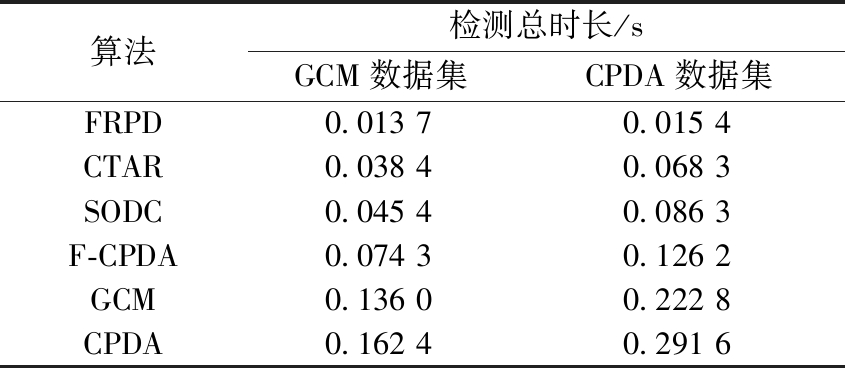
算法检测总时长/sGCM数据集CPDA数据集FRPD0.01370.0154CTAR0.03840.0683SODC0.04540.0863F-CPDA0.07430.1262GCM0.13600.2228CPDA0.16240.2916
5 结论
提出了一种响应函数构造简单且检测效率高的平行四边形对角线之比算法。实验结果表明,所提出的角点检测算法时间复杂度低,计算效率高,鲁棒性优异。从对比实验中可以看出,作为典型的基于轮廓的检测器,FRPD高度依赖边缘提取,这种技术会导致角点处的边缘出现漏检或错检。此外,只利用固定数目的邻域轮廓点来计算角点响应函数,这可能导致检测算法对某些情况比较敏感。
[1] 刘妍,余淮,杨文,等.利用SAR-FAST角点检测的合成孔径雷达图像配准方法[J].电子与信息学报,2017,39(2):430-436.
[2] 张青建,韩建平.一种基于RGB-D的人体关节点定位方法[J].郑州大学学报(工学版),2018,39(5):33-38.
[3] 逯鹏,梁玉,陈树伟.基于角点动能的视频群体异常行为检测[J].郑州大学学报(工学版),2015,36(3):20-24.
[4] 李云红,何亚瑞,章为川,等.利用点弦距离递归的图像角点检测算法[J].中国图象图形学报,2019,24(7):1148-1159.
[5] LIN X Y,ZHU C,LIU Y P,et al.Robust corner detection using altitude to chord ratio accumulation[J].Multimedia tools and applications,2019,78(1):177-195.
[6] MOKHTARIAN F,SUOMELA R.Robust image corner detection through curvature scale space[J].IEEE transactions on pattern analysis and machine intelligence,1998,20(12):1376-1381.
[7] ZHONG B J,LIAO W H.Direct curvature scale space:theory and corner detection[J].IEEE transactions on pattern analysis and machine intelligence,2007,29(3):508-512.
[8] ZHANG X H,LEI M,YANG D,et al.Multi-scale curvature product for robust image corner detection in curvature scale space[J].Pattern recognition letters,2007,28(5):545-554.
[9] AWRANGJEB M,LU G J.Robust image corner detection based on the chord-to-point distance accumulation technique[J].IEEE transactions on multimedia,2008,10(6):1059-1072.
[10] ROSENFELD A,JOHNSTON E.Angle detection on digital curves[J].IEEE transactions on computers,1973,22(9):875-878.
[11] TENG S W,SADAT R M N,LU G J.Effective and efficient contour-based corner detectors[J].Pattern recognition,2015,48(7):2185-2197.
[12] AWRANGJEB M,LU G J.A performance review of recent corner detectors[C]//2013 International Conference on Digital Image Computing:Techniques and Applications (DICTA).Piscataway:IEEE,2013:1-8.
[13] CANNY J.A computational approach to edge detection[J].IEEE transactions on pattern analysis and machine intelligence,1986,8(6):679-698.
[14] ZHANG X H,WANG H X,SMITH A W B,et al.Corner detection based on gradient correlation matrices of planar curves[J].Pattern recognition,2010,43(4):1207-1223.
[15] AWRANGJEB M.Data set [EB/OL].(2015-05-25)[2020-06-10].http://users.monash.edu.au/~mawrangj/corner.html.
[16] AWRANGJEB M,LU G J,MURSHEDM.An affine resilient curvature scale-space corner detector[C]//2007 IEEE International Conference on Acoustics,Speech and Signal Processing-ICASSP ′07.Piscataway:IEEE,2007:1233-1236.
[17] AWRANGJEB M,LU G J,FRASER C S,et al.A fast corner detector based on the chord-to-point distance accumulation technique[C]//2009 Digital Image Computing:Techniques and Applications.Piscataway:IEEE,2009:519-525.
[18] LIN X Y,ZHU C,ZHANG Q,et al.Efficient and robust corner detectors based on second-order difference of contour[J].IEEE signal processing letters,2017,24(9):1393-1397.
[19] ZHANG S Z,HUANG S,ZHANG Z F,et al.Corner detection based on tangent-to-point distance accumulation technique[J].Multimedia tools and applications,2019,78(18):25685-25706.