0 引言
过去几十年,随着集成电路技术的发展,晶体管的制造成本不断降低。但是,单个晶体管的测试成本并未随着工艺进步而降低。随着集成在芯片中的晶体管数量不断增加,测试成本在集成电路总成本中所占的比例越来越大。因此,迫切需要降低芯片制造中的测试成本。
在传统的VLSI测试中,所有芯片均采用相同的测试项目。为降低测试成本,减少不必要的测试项目,适应性测试方法被广泛提及[1-2]。适应性测试方法是根据测试数据和统计数据分析来改变测试条件、测试流程、测试内容和测试限值的方法[3]。通常,适应性测试主要从测试排序和测试选择着手。
在测试排序中,依据不同测试项目对缺陷检测的有效性进行排序[4-5],使得在测试流程中尽早检测到缺陷。对于测试选择,最终选择的是可以最有效地检测到缺陷的原始测试集的子集[6-15]。但是以上方法普遍存在一些不足,由于不同批次间工艺变化的影响,芯片的缺陷机制可能会不同[4]。任何比晶圆级更细粒度的测试方法都需要对ATE体系结构进行修改,这通常是十分困难的。
针对以上问题,本文提出一种新的适应性测试方法,同时进行了测试排序与测试选择。该方法利用能检测到的故障芯片的测试项目和具体数值,针对不同批次的芯片快速完成建模,从而对芯片质量进行预测;还可以删除某些测试项目,在减少测试时间的同时,保持较高的预测准确率。
1 随机森林预测模型
1.1 随机森林算法
与单一的弱分类器不同,随机森林算法是一种基于决策树的集成学习算法[16],比单一决策树算法表现更好。样本和特征的随机选择使得生成的决策树之间具有差异,能够提高算法的泛化能力和抗噪声能力,性能更加稳定。基于Bagging集成算法,随机森林算法各个决策树之间互不影响,极大提高了整体模型的运行速度。
芯片质量预测的测试项目通常较多,且不同晶圆或批次间会有工艺偏差,而利用随进森林算法可以有效地消除这些非理想因素,以保证良好的分类效果。与SVM算法相比,随机森林算法在面对维度较高或样本量较大的数据时速度更快,且时间复杂度较低,可快速完成芯片质量预测。其次,使用树模型可以十分直观地看出每个特征的重要性,即每个测试项目对芯片质量预测的贡献程度。在此基础上,可以对部分测试项目进行删减,从而缩短测试时间。
1.2 特征重要性
本文方法采用随机森林的特征重要性评分来对特征进行评估,得到测试组的重要性信息,从而对部分测试组进行删除以减少测试时间。计算特征重要性的基本思想:计算每个特征在随机森林中每棵树的贡献值后取平均值,对该值进行比较、排序。特征对每棵树的贡献通常可以用基尼指数来衡量。基尼指数GIn为
(1)
式中:k表示有k个类别;pnk表示节点n中类别k所占的比例,即任意从节点n中随机抽取2个样本,其类别标记不一致的概率。
假设有n个特征x1,x2,…,xn,计算每个特征的基尼指数评分,即第i个特征在随机森林所有决策树中节点分裂不纯度的平均改变量。特征xi在节点n的重要性,即节点n分枝前后的基尼指数变化量为
VIMin=GIn-GIl-GIr。
(2)
式中:VIMin为特征重要性评分;GIl和GIr分别表示分枝后左右2个新节点的基尼指数。
最后,把重要性评分归一化处理:
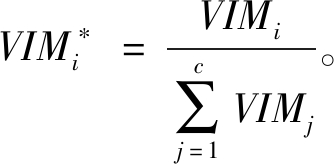
(3)
式中:![]() 是所有特征的增益之和。
是所有特征的增益之和。
2 适应性测试
2.1 本文方法
本文提出的芯片质量预测方法流程如图1所示。给定一批芯片测试数据,先将数据划分为训练集与测试集。除了训练模型,训练集还可以统计失败信息,即统计训练集芯片中每个测试项目所能测试到的故障芯片数量。以此为依据,对测试项目重新排序,将能测出故障芯片最多的项目排在测试顺序的最前列。测试芯片时,以重排顺序进行测试,可以更快测试出故障芯片,从而减少测试时间。为保证本文方法的适用性,使用的数据是从芯片测试开始到首次失败为止所收集到的数据。
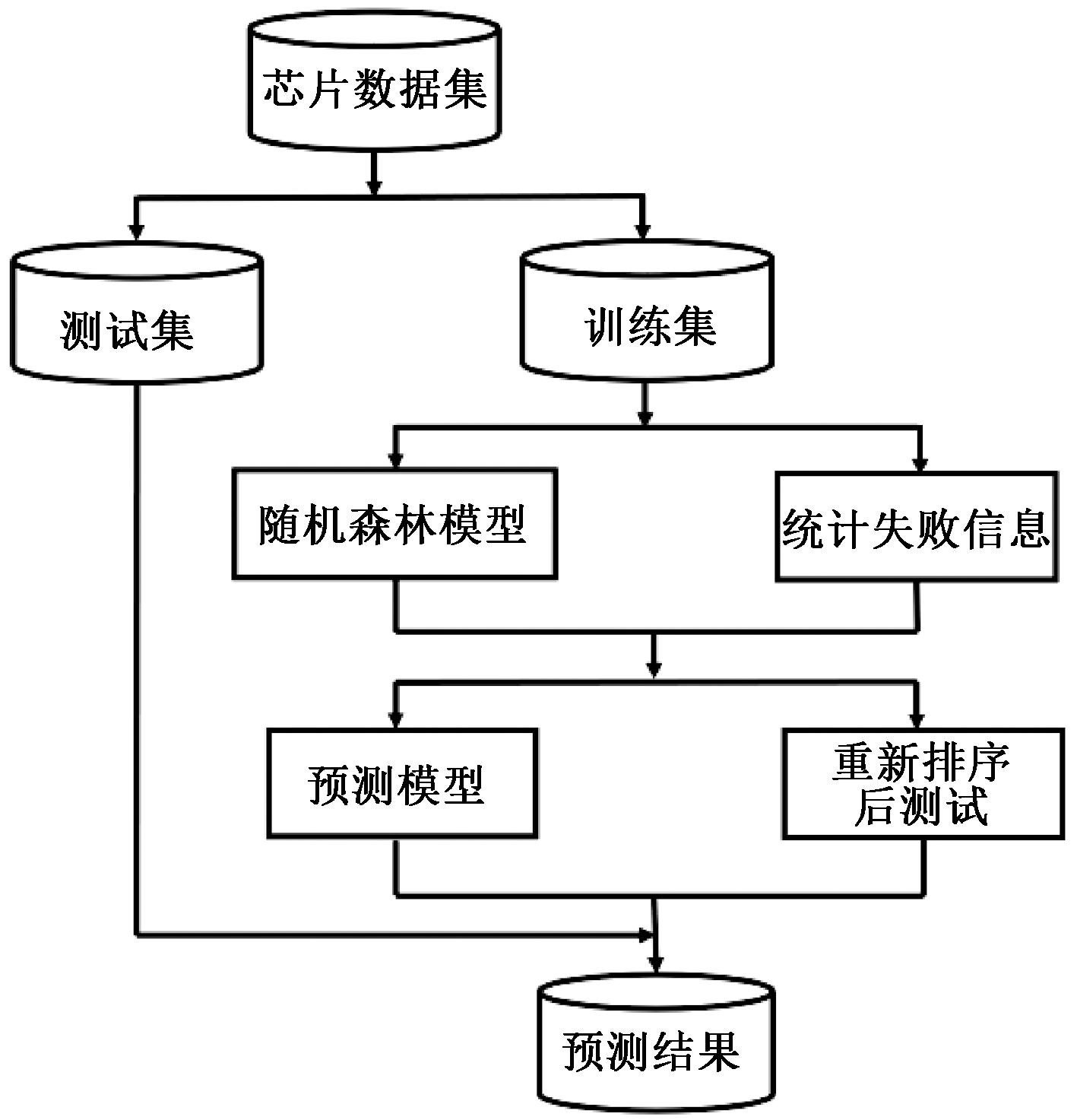
图1 芯片质量预测方法流程
Figure 1 Process of chip quality prediction method
相比于在单个测试项级别中进行重新排序,本文的操作对象是测试组。测试组是指在相同的测试配置上依次执行的由各个测试项所组成的组。当测试设置不同时,测试组间切换耗时较长,研究跳过或执行单个测试项的意义不大。而本文方法中每个测试组的测试设置相同,各测试组之间切换耗时较短,因此,有必要对跳过或执行测试组进行研究。
模型训练完成后,根据各测试组对质量预测的重要程度,计算测试组的特征重要性。再按照重新排序的测试顺序对测试集芯片进行测试,删除重要性较低的测试组,以缩短测试时间。
2.2 芯片质量预测
使用随机森林算法实现芯片质量预测的主要步骤如下。
Step 1 数据预处理。根据芯片质量预测,获得测试项名称、测试项值、测试失败项、失败项所在的测试组、测试时间和测试结果。其中无法测出的部分用无故障芯片测试数据的平均值代替。
Step 2 特征提取。对Step 1中经过预处理的芯片测试数据进行分析并提取特征。
Step 3 利用Step 2中提取的特征建立基于随机森林算法的芯片质量预测模型。
Step 4 优化模型的各超参数,以保证模型的预测效果。
Step 5 实时预测。将无标签的芯片测试数据代入建立的预测模型对芯片质量进行判断。
3 实验部分
3.1 实验配置
实验环境为Windows 10系统,4 GB内存,IntelCore-i54210 2.6 GHz 处理器。实验使用的芯片测试数据来自一款混合信号芯片的晶圆测试结果。实验测试了6片晶圆,共计57 117个裸片。其中无故障芯片为47 630个,故障芯片为9 487个。所有无故障芯片标签相同,有故障芯片因测试失败的项不同而有不同的标签,所有标签共计47类。实验完整的测试包括16个测试组,共计72个测试项目。
实验采用Python3.7软件,选取总数据的20%作为测试集,此时测试集包含11 424个裸片。使用随机森林算法,决策树的数量为100,随机数种子为0。共进行2组实验,2组实验的测试集不完全相同:第1组实验中无故障芯片数为9 523个,故障芯片数为1 901个;第2组实验中无故障芯片数为9 544个,故障芯片数为1 880个。
3.2 特征重要性
图2给出了16个测试组的特征重要性排序,2次实验结果相同。其中重要性最高的为第16测试组,最低的为第10测试组。后续实验中对测试组的删除按照重要性从低到高进行,即第1次删除第10测试组,第2次删除第10和第9测试组,以此类推。
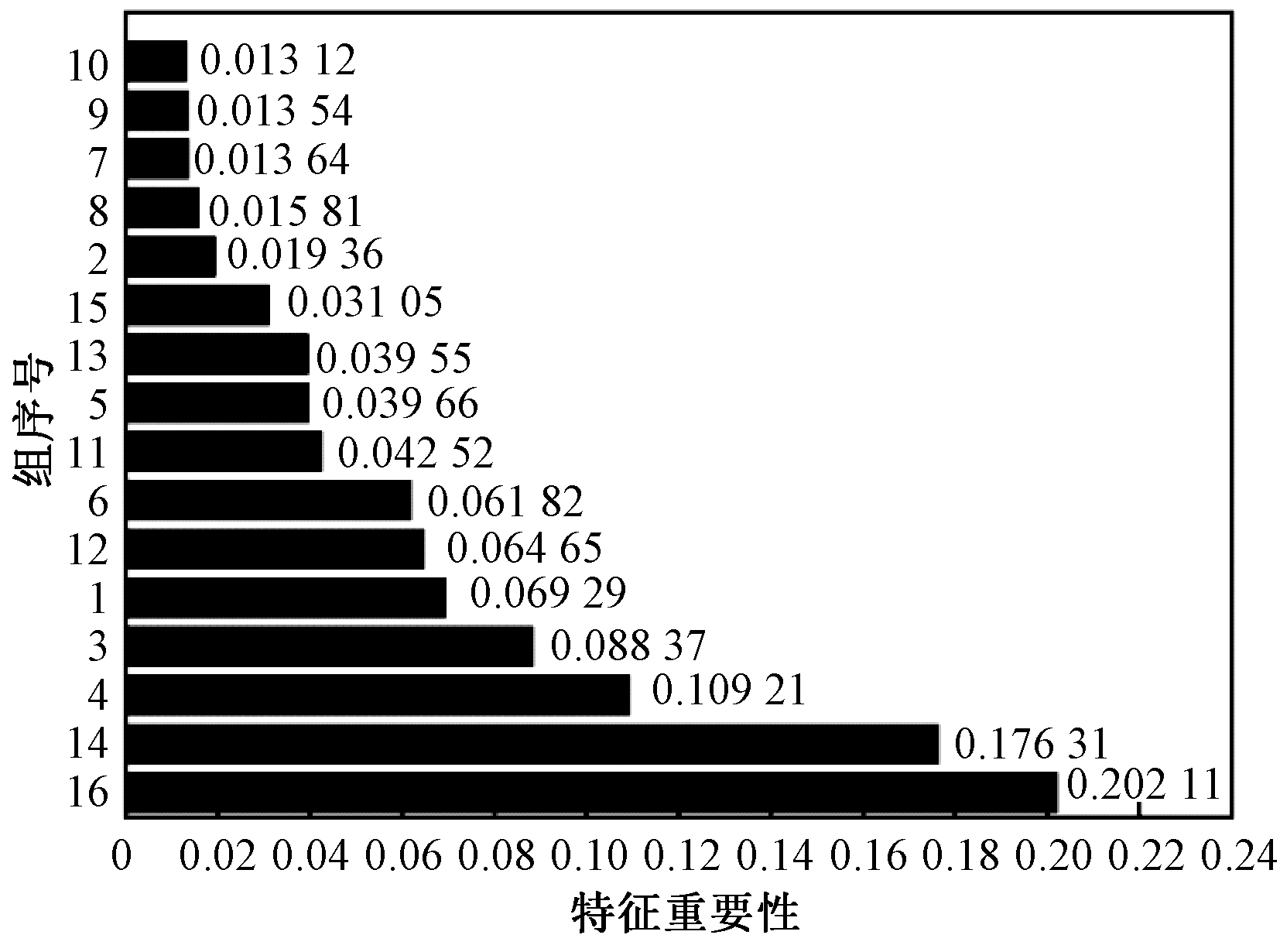
图2 测试组特征重要性排序
Figure 2 Order of test groups importance
3.3 预测准确率
在分类问题中准确率Accuracy为
(4)
式中:TP为预测为正的正样本;FP预测为正的负样本;FN预测为负的正样本;TN预测为负的负样本。
具体来说,准确率综合考虑了模型对有故障和无故障芯片的预测能力。依据测试组的重要性从低到高对测试组进行删除,每次在前1次的基础上多删除1组。2组实验预测准确率如表1所示。
表1 预测准确率
Table 1 Prediction accuracy
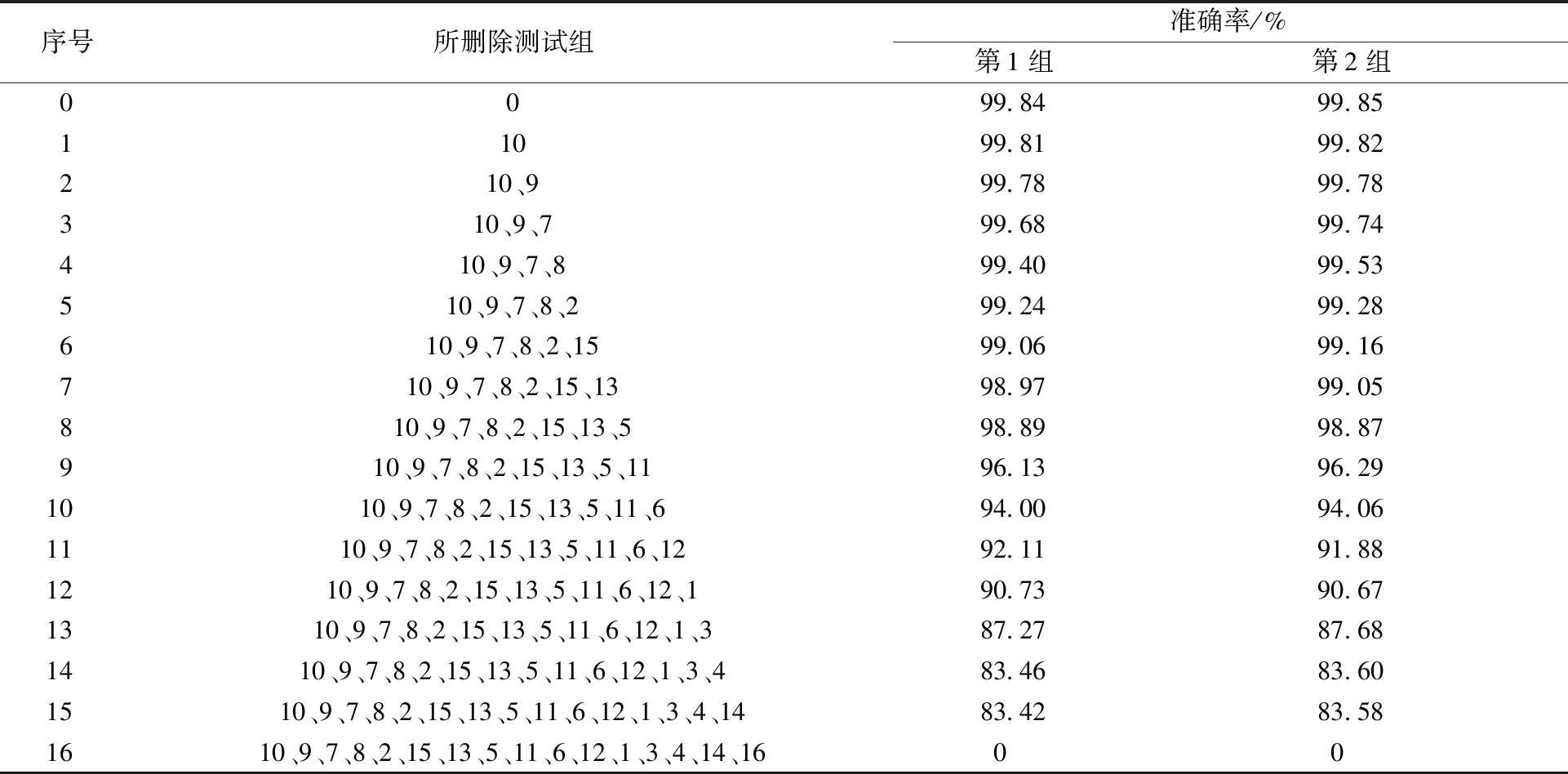
序号所删除测试组准确率/%第1组第2组0099.8499.8511099.8199.82210、999.7899.78310、9、799.6899.74410、9、7、899.4099.53510、9、7、8、299.2499.28610、9、7、8、2、1599.0699.16710、9、7、8、2、15、1398.9799.05810、9、7、8、2、15、13、598.8998.87910、9、7、8、2、15、13、5、1196.1396.291010、9、7、8、2、15、13、5、11、694.0094.061110、9、7、8、2、15、13、5、11、6、1292.1191.881210、9、7、8、2、15、13、5、11、6、12、190.7390.671310、9、7、8、2、15、13、5、11、6、12、1、387.2787.681410、9、7、8、2、15、13、5、11、6、12、1、3、483.4683.601510、9、7、8、2、15、13、5、11、6、12、1、3、4、1483.4283.581610、9、7、8、2、15、13、5、11、6、12、1、3、4、14、1600
从表1可以看出,没有删除测试组时,随机森林预测模型的预测准确率最高,此时,芯片拥有完整的测试信息,随机森林模型更易判断芯片质量的好坏。随着删除测试组数量的增加,预测准确率逐渐降低,直到删除所有测试组后准确率降为0。这是因为对故障芯片而言,测试失败的测试项目各不相同,故有多种失败芯片标签。而表1中,随着所删除测试组的增加,一些重要测试内容被删去,随机森林预测模型无法准确判断该失败芯片具体应属于哪类标签,因此,对故障芯片的分类能力逐渐降低,从而导致整个模型的预测准确率下降。
3.4 测试逃逸和时间减少情况
删除部分测试组必然会造成测试逃逸,即有故障的芯片仍然通过了测试。在模型中表现为故障芯片被分类到了无故障芯片中。表2为2组实验中删除不同测试组后的测试逃逸情况。
表2 测试逃逸情况
Table 2 Results of test escapes
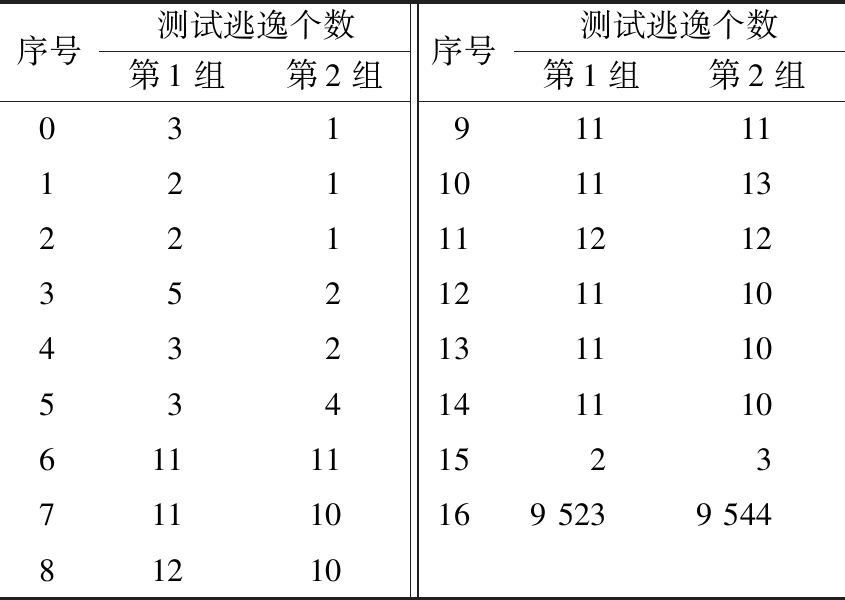
序号测试逃逸个数第1组第2组序号测试逃逸个数第1组第2组0319111112110111322111121235212111043213111053414111061111152371110169523954481210
从表2可以看出,对于序号0~5的情况,序号5所代表删除的测试组为10、9、7、8、2,即删除的测试组数目少于6个时,测试逃逸维持在一个较低水平;当删除的测试组大于等于6个时,测试逃逸数变大。从表1和表2可以看出,当删除的测试组数目少于6个时,模型预测的准确率在99%以上且测试逃逸水平较低。综上分析知,在本批次的芯片中,所删除测试组少于6个时是较理想情况。
表3为本文方法和使用传统测试方法相比的时间减少情况。在芯片测试过程中对部分测试组进行了删除,与传统测试方法相比,本文方法可以减少测试时间。2组实验的测试时间减少的变化趋势相同。删除1个测试组后时间减少可达约12%,时间减少与删除测试组的数目成正相关。
表3 测试时间减少情况
Table 3 Results of test time reduction %
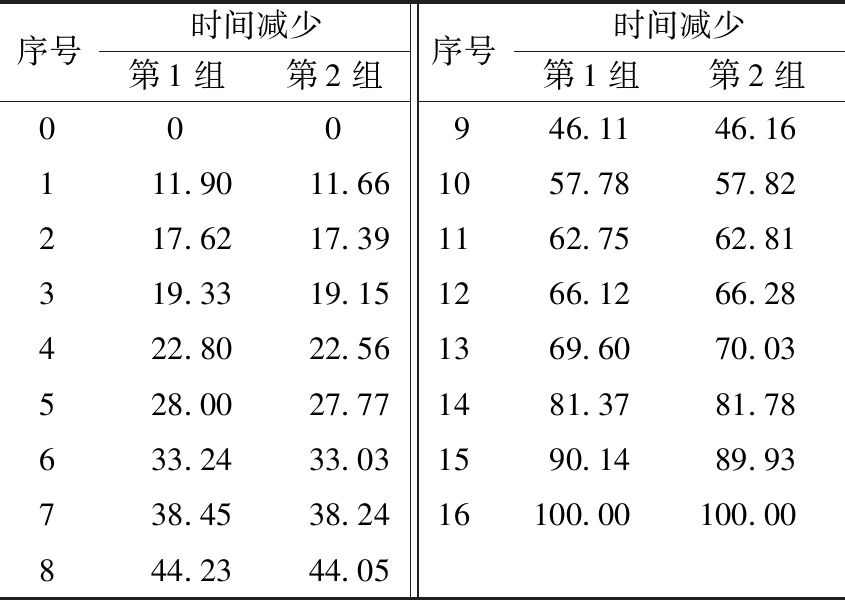
序号时间减少第1组第2组序号时间减少第1组第2组000946.1146.16111.9011.661057.7857.82217.6217.391162.7562.81319.3319.151266.1266.28422.8022.561369.6070.03528.0027.771481.3781.78633.2433.031590.1489.93738.4538.2416100.00100.00844.2344.05
结合表2可知,测试时间减少意味着测试逃逸相对增加。当保持较低测试逃逸水平时(删除1~5个测试组),测试时间减少约28%,此时为较理想情况,可以在保证测试质量的前提下大幅减少测试时间。
3.5 模型比较
为验证随机森林预测模型的预测准确率,实验采用第1组数据,和KNN、逻辑回归算法进行对比。当删除测试组个数低于6时,这3种算法的预测准确率如表4所示。
表4 3种算法预测准确率
Table 4 Prediction accuracy of the three algorithms
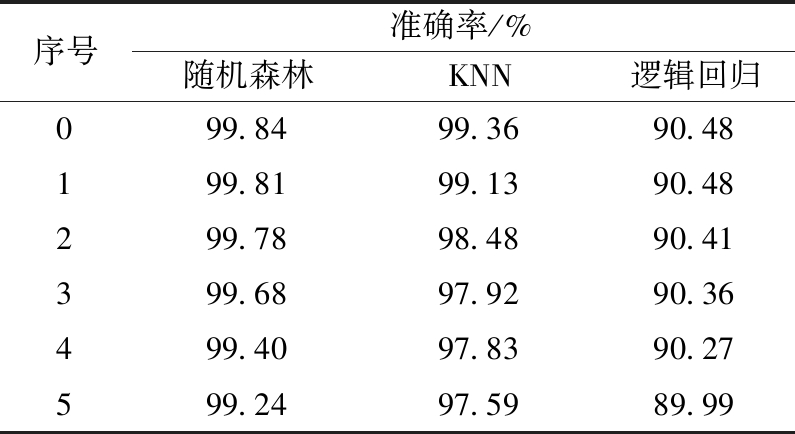
序号准确率/%随机森林KNN逻辑回归099.8499.3690.48199.8199.1390.48299.7898.4890.41399.6897.9290.36499.4097.8390.27599.2497.5989.99
从表4可以看出,3种算法的预测准确率都随着删减测试组数量的增加而降低。KNN的预测准确率略低于随机森林,逻辑回归效果最差。
图3为3种算法中删除部分测试组后测试逃逸个数的情况。为表明3种测试逃逸情况,从左往右3条纵坐标分别代表随机森林、KNN和逻辑回归的测试逃逸个数。KNN的测试逃逸个数为[6,10],逻辑回归为[1021,1 073],而随机森林仅为[2,5],测试逃逸数量最少。
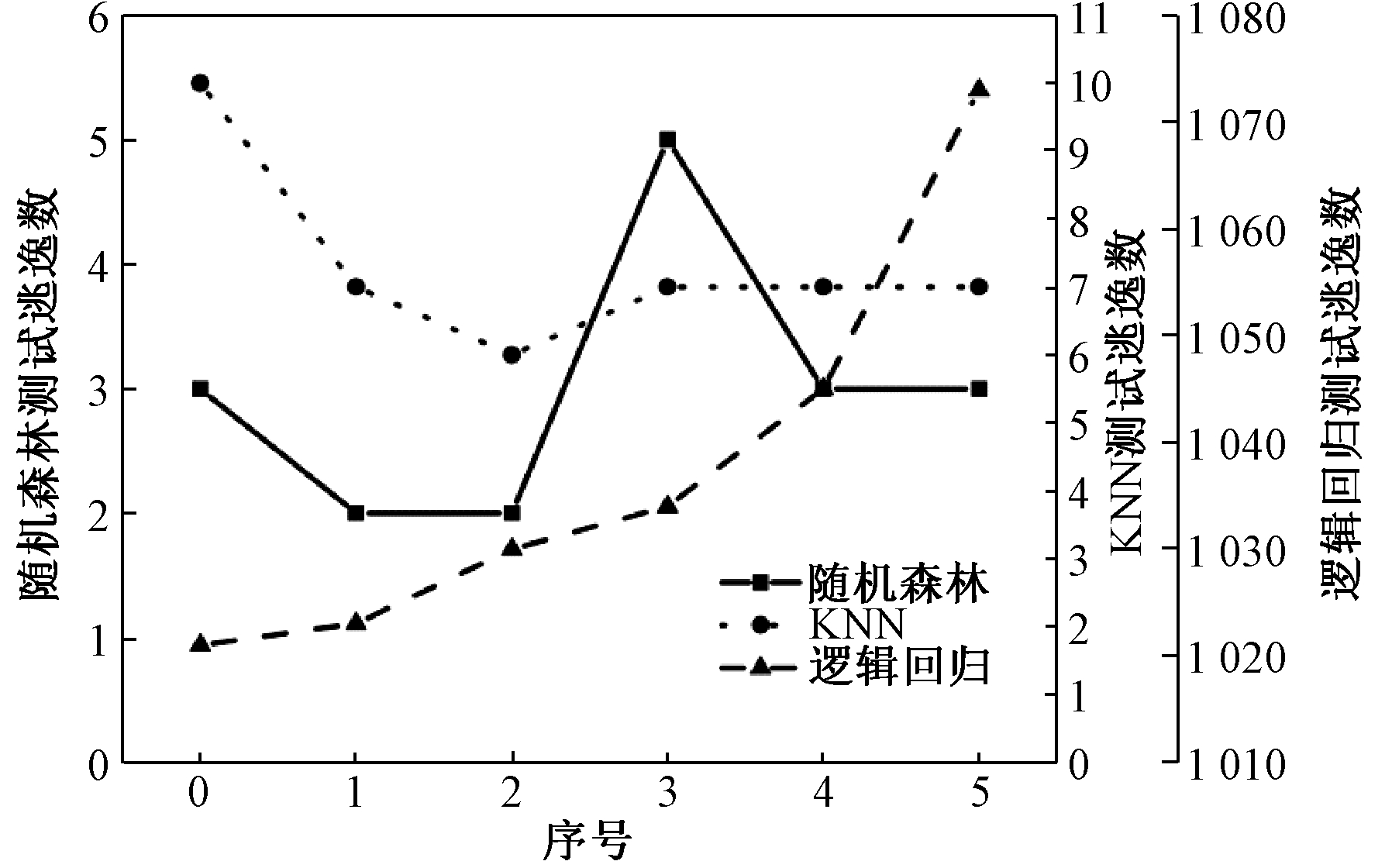
图3 3种算法测试逃逸情况
Figure 3 Test escapes of three algorithms
表5为使用3种算法对芯片进行1次质量预测时的CPU平均运行时间。从表5中可以看出,当运用不同的算法建模对芯片质量作出预测时,随机森林所用时间最短,仅为14 s,远低于KNN和逻辑回归。
表5 3种模型平均运行时间
Table 5 Average running time of three models

算法CPU平均运行时间/s随机森林14KNN215逻辑回归460
综合考虑准确率、测试逃逸数和运行时间3个度量指标,随机森林的表现最优,说明该模型在芯片质量预测方面有一定的应用空间。
3.6 方案对比
图4是使用本文方法、文献[6]方法和文献[15]方法在删除不同比率的测试项目后的测试时间减少情况。文献[6]方法选择最有效地检测故障芯片的测试子集合,文献[15]方法使用贝叶斯统计来选择测试项。3种实验方案所用的测试项目挑选和排序方法各不相同。从图4中可以看出,在保持相同的测试项删除率(删除的测试项目数/总测试项目数)的情况下,本文所能达到的测试时间减少始终高于另外2种方案。
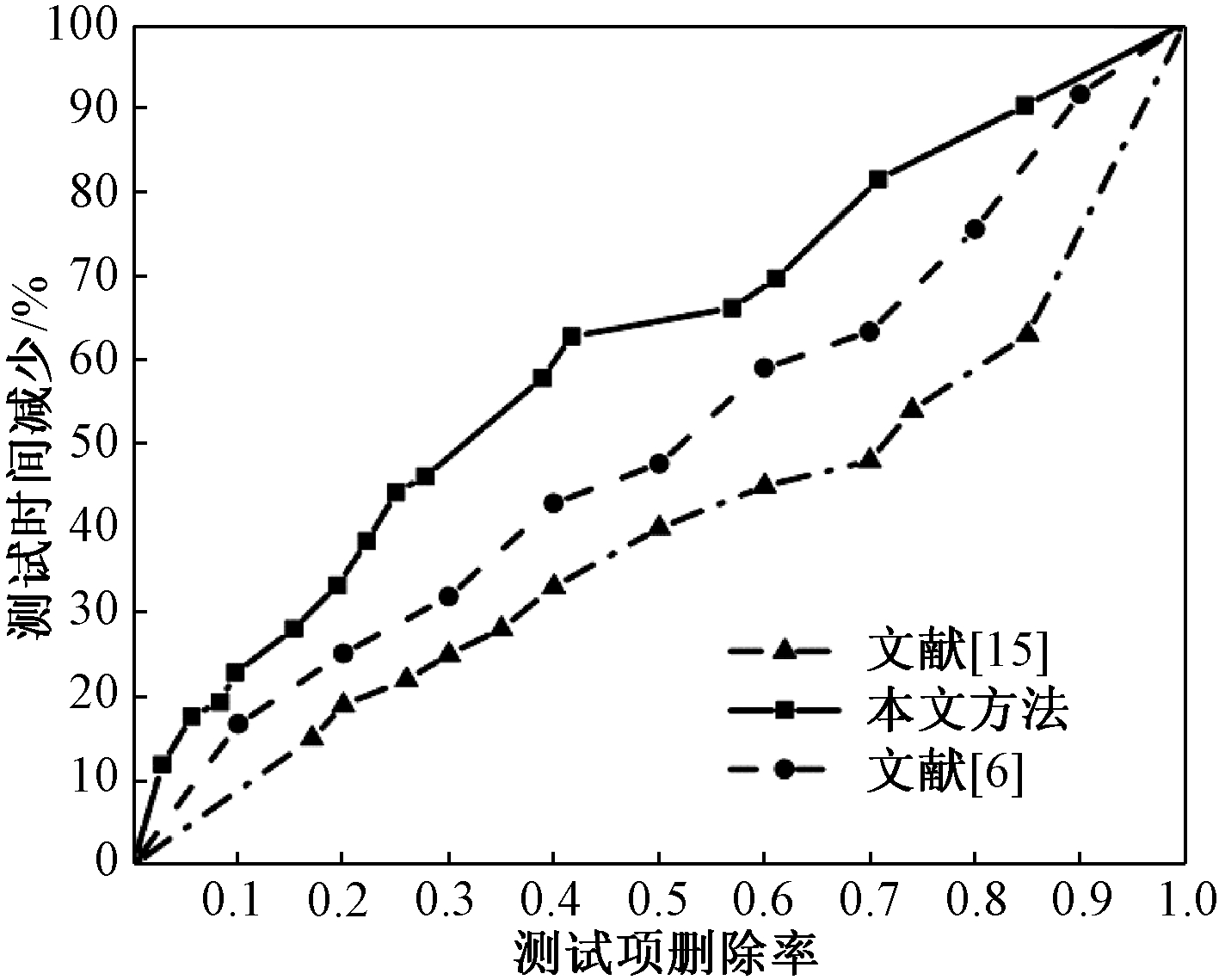
图4 3种方案测试时间减少情况
Figure 4 Test time reduction in three methods
4 结论
提出了一种使用随机森林的适应性测试方法。利用该模型中的特征重要性指标可以对测试组作出重要性评估,保留对模型重要的测试组,删除传统的静态测试流中的部分测试项,从而减少测试时间。根据测试结果预测芯片质量,在节省测试时间和模型预测准确率之间折中选择。
与传统测试方法相比,本文方法可以大幅减少测试时间。与KNN和逻辑回归算法相比,随机森林算法各项指标均为最优,且本文方法能节省更多测试时间。
[1] YILMAZ E,OZEV S,SINANOGLU O,et al.Adaptive testing:conquering process variations[C]//2012 17th IEEE European Test Symposium (ETS).Piscataway:IEEE,2012:1-6.
[2] STRATIGOPOULOS H G,STREITWIESERC.Adaptive test flow for mixed-signal ICs[C]//2017 IEEE 35th VLSI Test Symposium (VTS).Piscataway:IEEE,2017:1-6.
[3] MARINISSEN E J,SINGH A,GLOTTER D,et al.Adapting to adaptive testing[C]//2010 Design,Automation&Test in Europe Conference &Exhibition (DATE 2010).Piscataway:IEEE,2010:556-561.
[4] CHEN M J,ORAILOGLU A.Test cost minimization through adaptive test development[C]//Proceedings of the IEEE International Conference on Computer Design.Piscataway:IEEE,2008:234-239.
[5] AKKOUCHE N,MIR S,SIMEU E,et al.Analog/RF test ordering in the early stages of production testing[C]//2012 IEEE 30th VLSI Test Symposium (VTS).Piscataway:IEEE,2012:25-30.
[6] XUE C,SHAWN R D.A one-pass test-selection method for maximizing test coverage[C]//2015 33rd IEEE International Conference on Computer Design (ICCD).Piscataway:IEEE,2015:621-628.
[7] GONÇALVES H,LI X,CORREIA M,et al.A fast spatial variation modeling algorithm for efficient test cost reduction of analog/RF circuits[C]//2015 Design,Automation &Test in Europe Conference &Exhibition (DATE).Piscataway:IEEE,2015:1042-1047.
[8] AHMADI A,NAHAR A,ORR B,et al.Wafer-level process variation-driven probe-test flow selection for test cost reduction in analog/RF ICs[C]//2016 IEEE 34th VLSI Test Symposium (VTS).Piscataway:IEEE,2016:1-6.
[9] WANG K L,LIN B Y,WU C W,et al.Test cost reduction methodology for InFO wafer-level chip-scale package[J].IEEE design &test,2017,34(3):50-58.
[10] GRADY M,PEPPER B,PATCH J,et al.Adaptive testing-cost reduction through test pattern sampling[C]//2013 IEEE International Test Conference (ITC).Piscataway:IEEE,2013:1-8.
[11] LIU M Y,PAN R J,YE F M,et al.Fine-grained adaptive testing based on quality prediction[C]//2018 IEEE International Test Conference (ITC).Piscataway:IEEE,2018:1-10.
[12] AGRAWAL M,CHAKRABARTYK.Test-cost modeling and optimal test-flow selection of 3-D-stacked ICs[J].IEEE transactions on computer-aided design of integrated circuits and systems,2015,34(9):1523-1536.
[13] HSU C K,SARSON P,SCHATZBERGER G,et al.Variation and failure characterization through pattern classification of test data from multiple test stages[C]//2016 IEEE International Test Conference (ITC).Piscataway:IEEE,2016:1-10.
[14] AHMADI A,XANTHOPOULOS C,NAHAR A,et al.Harnessing process variations for optimizing wafer-level probe-test flow[C]//2016 IEEE International Test Conference (ITC).Piscataway:IEEE,2016:1-8.
[15] GOTKHINDIKAR K R,DAASCH W R,BUTLER K M,et al.Die-level adaptive test:real-time test reordering and elimination[C]//2011 IEEE International Test Conference.Piscataway:IEEE,2011:1-10.
[16] 李燕燕,杨昊天,曾玙璠.基于随机森林MOPSO的城市最优资本结构分析[J].郑州大学学报(工学版),2019,40(4):80-85.