0 引言
在大多数农村地区,出行需求密度偏低且分布分散,导致常规公交运营效率低下。针对常规公交模式在农村地区运营的局限性,研究者提出在农村地区推行需求响应公交模式(demand responsive transit,DRT),需求响应公交模式可以动态地改变出行路线和时间表,更灵活地为农村居民提供精准出行服务。
近年来,对于DRT的研究正在逐步深入。Daganzo[1]首次提出了可变线路公交(需求响应)系统;Amirgholy等[2]建立了分析模型,用来近似求解DRT系统运行的动态需求成本和总的广义成本。Diana等[3]通过对比分析发现需求响应式系统在低需求水平地区表现最佳。Dantzig等[4]最早提出车辆路径问题,采用线性规划可得到近似最优解。Sánchez-oro等[5]提出一种求解多目标开放车辆路径问题的广义变邻域搜索方法。Gu等[6]研究了一种考虑时间效率的多车辆段车辆路径规划问题,并利用改进人工蜂群算法求解。人工蜂群算法(artificial bee colony algorithm,ABC算法)是由Karaboga等[7]提出的一种基于蜂群智能行为的优化算法。毛声等[8]提出了一种双重进化人工蜂群算法,提高了搜索效率且不易陷入局部最优解。自适应大邻域搜索算法在车辆路径问题的研究中,最早由Ropke等[9]用于解决带有时间窗和预定线路的同时接送问题。此外,魏占阳等[10]通过自适应大邻域搜索算法对车辆路径问题模型进行了改进和优化。
目前的DRT模式研究[11-12]并未考虑农村客运出行需求的特殊运行规律和同时接送模式。本文基于农村地区客运出行的实地调查结果,构建了考虑同时接送农村乘客的DRT问题模型,并用实例验证了模型和算法的可行性。
1 模型构建
1.1 问题描述
本文对某地进行了为期2个月的出行情况调查,共3 013份问卷,其中有效问卷为2 301份。结果显示,在某地农村地区出行需求量很小,人均出行率为0.97次/d,远低于中心城区平均出行率。在出行方式结构上,公共交通总占比仅为0.48%。相对于中心城区,农村地区需求密度偏低,且需求比较分散。另外,公共交通在出行方式中占比很小,表明了常规公交在这类地区面临的运营困境。
调查显示,某地村级范围的出行是农村居民最重要的出行路径,频率高达71.6%。此外,农村居民的出行特征具有往返的性质。出行频率最高为6次/d,频率为2次/d的出行占比最大,为60%。显然,农村居民的出行频率以偶次出行居多。因此,在本文模型构建中,参照物流研究中的同时取送货方式和需求响应公交在低需求密度地区的研究[13-14]提出需求响应公交模型的同时接送模式,如图1所示。
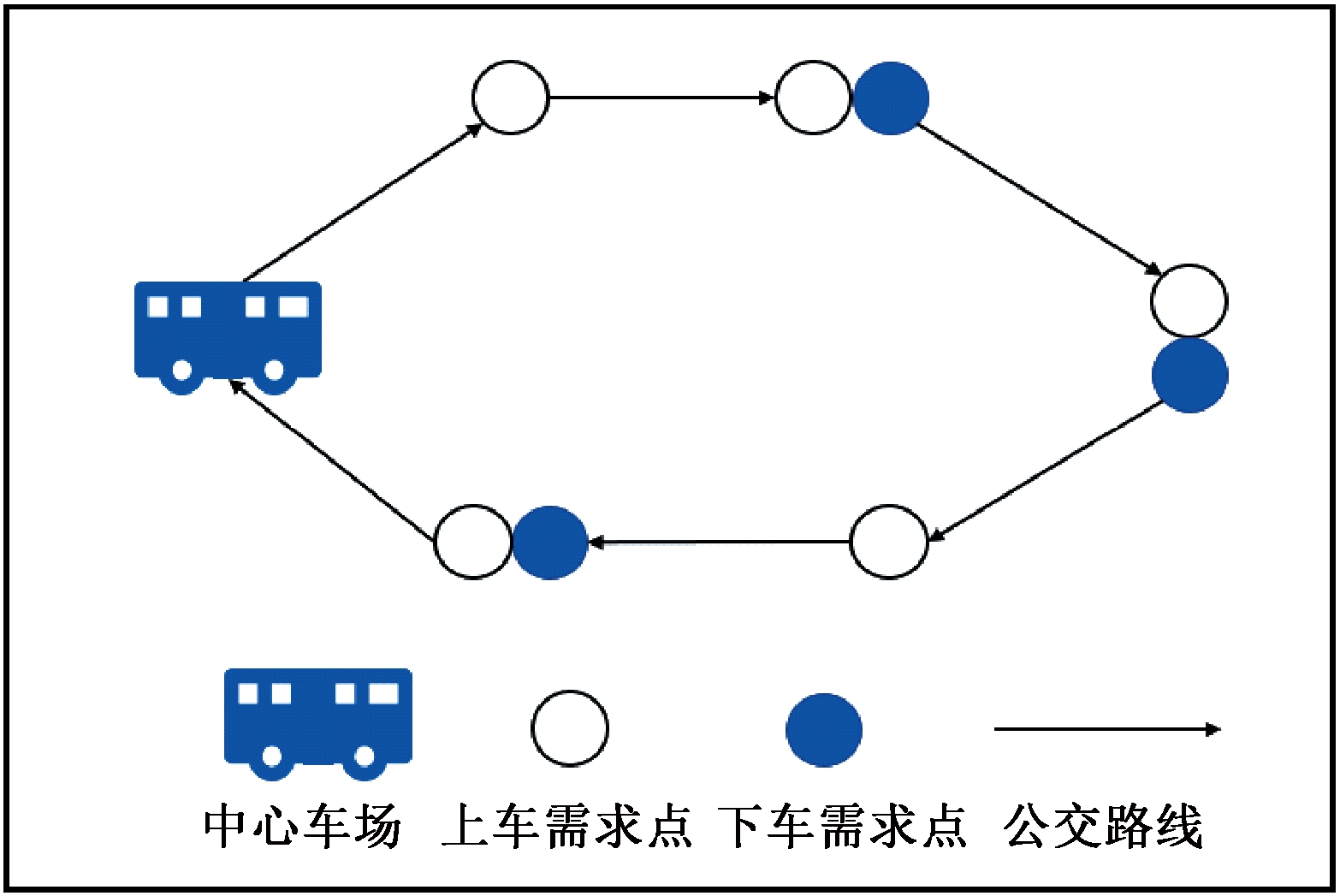
图1 需求响应同时接送模式
Figure 1 Demand response simultaneous pick-up and delivery mode
研究场景设置如下:在农村地区,通过网上预约获得居民的出行需求,然后实时规划农村居民的需求响应公交线路。需求响应公交线路规划包含一个中心车场,以及从车场中衍生的连接到不同的需求点的不同路线。车辆线路的起讫点均为中心车场。
普通需求响应模型一般只考虑单一的接乘客或送乘客,然而,在实际情况中,由于农村居民出行具有往返的特性,不能将农村DRT模式简单地当作普通需求响应模型处理。在规划需求响应线路时应考虑实现同时接送农村居民,因此,本文提出了一种需求响应公交同时接送模式。需求响应同时接送模式,是指需求响应公交车辆在一次完整的运输过程中,包含接收乘客和送达乘客,即车辆在同一地点同时服务上车需求点和下车需求点。
对于此类农村地区需求响应式公交模式问题,可以用一个实时的包含同时接送条件的车辆路径问题模型来解决。
1.2 模型构建
该农村地区DRT的同时接送车辆路径问题模型(the simultaneous pick-up and delivery vehicle routing problem,SPDVRP)包含的基本参数如表1所示。
表1 SPDVRP模型相关参数
Table 1 Related parameter of SPDVRP model

参数数学定义单位H{i|i=1,…,N}表示有N个不同的需求点,H为需求点集合,且i=0表示中心车场V{k|k=1,…,K}表示全部运输工具(车辆)合集,其中车辆的上限数量为KCij表示从需求点i到另一需求点j的单位距离运输成本元T(t)表示时间窗惩罚成本函数qPj表示需要到达某一需求响应点的乘客数,也可以表述为车辆送往j点的乘客数pPj表示需要从某一需求响应点上车的乘客数,也可以表述为车辆在j点接取的乘客数QRPk表示车辆k在离开中心车场时车内的起始乘客数量gPjk表示车辆k在离开需求点j时车辆内乘客剩余数量QPk表示车辆k的最大乘客数容量限制dij表示从需求点i到需求点j的运输距离mCk表示车辆k的固定成本元ai表示车辆到达需求点i的时间窗上限minsi表示车辆到达需求点i的准确时间minbi表示车辆到达需求点i的时间窗下限minαi表示车辆在需求点i停留的时间惩罚成本元βi表示车辆延迟到达需求点i的时间惩罚成本元tij表示车辆从需求点i开往需求点j的行驶时间minfi表示车辆在需求点i停留的时间minXk0~1整数限制变量,表示车辆是否被使用Xijk0~1整数限制变量,表示i、j点之间是否有车辆通过
模型中运输总成本包含:车辆固定成本、可变运输成本和时间窗惩罚成本,其中时间窗惩罚成本包含停留惩罚成本和延迟到达惩罚成本。模型表达式为
(1)
(2)
s.t.:
(3)
(4)
(5)
(6)
(7)
QRPk≤QPk;
(8)
gPjk=QRPk-qPj+pPj;
(9)
gPjk=gPik-qPj+pPj;
(10)
gPjk≤QPk;
(11)
max{qPj,pPj}≤QPk;
(12)
si+fi+tij-M(1-Xijk)≤sj;
(13)
Xijk=0,1;
(14)
Xk=0,1。
(15)
式中:∀i=0;∀j∈H;∀P∈H;∀k∈V。其中,式(1)是模型的目标函数,T(t)表示其时间窗惩罚成本函数;式(2)是函数T(t)的具体表达式,其包含停留惩罚成本和延迟到达惩罚成本两部分;式(3)表示每一条车辆路径起点和终点均为中心车场;式(4)表示车辆路径的连续性,进出某一需求响应点的车辆必须为同一车辆;式(5)、(6)表示每一个需求响应点只被一辆车服务;式(7)表示某一车辆k在离开车站时的需要送达目的地的乘客数QRPk的计算;式(8)表示对于某一车辆k在离开车站时,车辆内乘坐的乘客数不能超过该车辆k的最大乘客数限制;式(9)、(10)表示某一车辆k在离开某一个需求响应点j时的车内剩余乘客数量;式(11)表示对于某一车辆k在离开某一个需求响应点j时的乘客数限制,不能超过该车辆k的最大乘客数限制;式(12)表示任一需求响应点的接送乘客的数量均要满足车辆的最大乘客数限制;式(13)确保在规划路径中满足车辆行驶、需求响应点服务耗时的时间窗约束;式(14)、(15)为0~1整数限制。
2 自适应大邻域人工蜂群求解算法设计
自适应大邻域人工蜂群算法采用两阶段嵌套算法模型。针对人工蜂群算法中由于同类蜜蜂缺乏交流而导致的易陷入局部最优解的缺陷,在算法的雇佣蜂阶段,嵌套采用ALNS算法进行邻域搜索,在搜索大邻域过程中尽可能多地探索解空间。
2.1 编码方式
首先假设例子中需求点的数量为N(由1~N之间的N个整数,表示各需求点),可行解中路径数量为M,那么就有长度为N+M+1的向量表示其中的一个解[15]。其次,有M+1个0来表示每条路径的起讫点,即中心车场。
如图2所示,图中2个0之间的字符表示车辆到达不同需求点的路径顺序。在这个解中,N=7,M=3。第1条路径0—4—1—0表示车辆从中心车场出发,依次经过需求点4、1,最后回到中心车场。同理,该解中第2、3条路径具备相似的路径过程。
图2 编码示意图
Figure 2 Coding diagram
2.2 人工蜂群算法算子
人工蜂群算法通过连续派出雇佣蜂、跟随蜂和侦察蜂来寻找最优解。
雇佣蜂搜索开发食物源,食物源的个数(N)和雇佣蜂逐一对应。用xi=(xi1,xi2,…,xiD)表示第i个食物源(i=1,2,…,N),其中D表示搜索空间的维数[16-17]。雇佣蜂搜索对应的食物源后记录食物源优劣程度,回到巢穴后把这些信息共享给跟随蜂。雇佣蜂搜索时在食物源的邻域生成一个候选食物源为
vij=xij+rij(xij-xkj)。
(16)
式中:j∈{1,2,…,D};k∈{1,2,…,N},且k≠i;rij是[-1,1]上均匀分布的随机数。
跟随蜂根据食物源的适应值确定更优的食物源进一步开采[16-17]。其适应值表示为
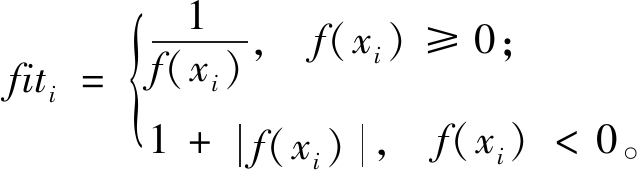
(17)
跟随蜂以轮盘赌的方式选择相应的食物源进行进一步的开采。食物源选择的概率为
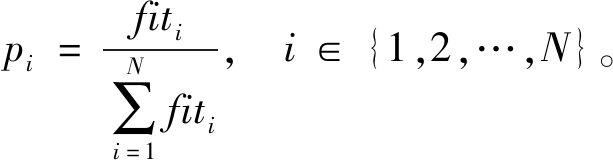
(18)
当在某个食物源附近搜索多次都找不到更好的食物源(达到最大食物源连续搜索次数Lmax),则转化产生新的侦察蜂寻找新的食物源代替该食物源[18]。食物源生成规律为
(19)
式中:![]() 表示新的食物源;rand(0,1)为(0,1)的随机数;
表示新的食物源;rand(0,1)为(0,1)的随机数;![]() 分别为第j维变量的最大值和最小值。
分别为第j维变量的最大值和最小值。
2.3 ALNS算法算子
ALNS算法给每个移除和重建算子赋予一个权重,权重决定算子被选择的概率,且在搜索过程中可以根据解的优劣自适应地调整[19-20]。
ALNS算法在搜索过程中可以有多个移除和重建方式。根据求解情况反馈,动态地选择其中的一种移除或重建方式来操作[21]。
Step 1 移除算子,从当前解中删除部分食物源节点,得到破坏解[22]。移除算子1:随机删除,随机选择一个食物源节点进行删除。移除算子2:邻近删除,选择距离候选食物源最近的一个食物源节点进行删除。
Step 2 重建算子,将未搜索过的食物源节点以及删除的食物源节点插入破坏解中,得到新解[22]。重建算子1:随机插入,随机选择任务池中的食物源节点进行插入,产生新的解。重建算子2:最优贪婪插入,每次都选择任务池中适应值最高的食物源节点插入破坏解,从而得到更优的新解。
2.4 改进的自适应大邻域人工蜂群算法流程
Step 1 初始化阶段,随机生成一组初始解。
Step 2 雇佣蜂阶段,计算每个食物源的适应值fiti,之后内部采用ALNS算法进行邻域搜索:①初始化权重,并在权重的基础上随机生成移除算子和重建算子;②ALNS移除操作;③ALNS重建操作。
Step 3 跟随蜂阶段,跟随蜂通过轮盘赌的方式,按食物源概率pi选择相应的食物源开采。
Step 4 侦察蜂阶段,当达到最大食物源连续搜索次数Lmax时,按式(19)寻找新的食物源。
Step 5 记录当前最优食物源,并令迭代次数C=C+1。
Step 6 判断C是否大于等于Cmax,若是,则输出最优解;否则,转到Step 2重新开始循环。
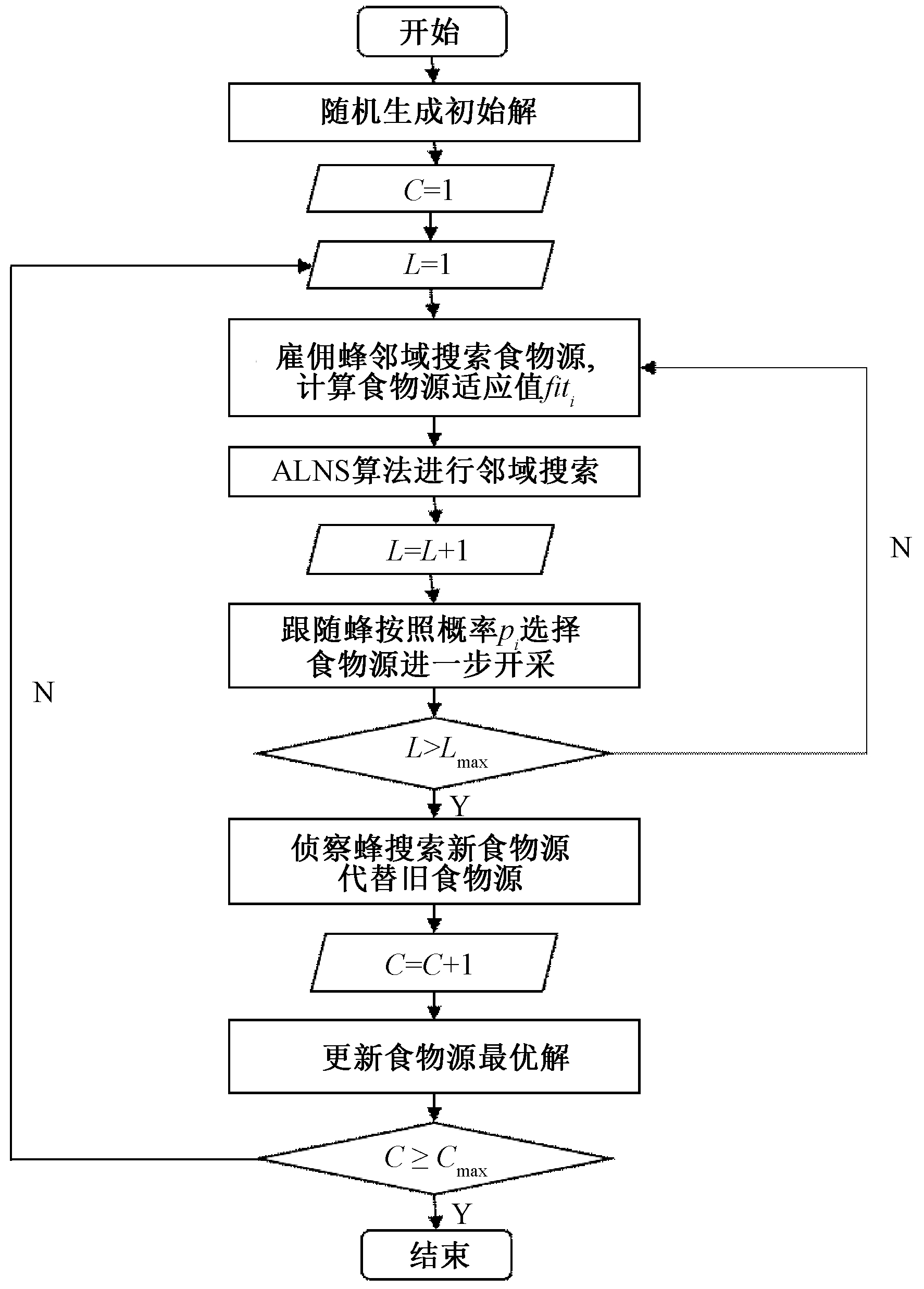
图3 算法流程图
Figure 3 Algorithm flow chart
3 算例分析
某地全县17个乡镇、280个行政村,居民调查显示农村居民对于公交的需求在提升,同时对于需求响应公交的接受度也比较高。
算例选择在某地东部农村地区设置了7个需求响应点(包括5个行政村需求点、1个客运站需求点和1个学校需求点),设置1个中心车场。车辆平均时速为40 km/h,单位运输成本为1元/km,最大运输距离为300 km,每次运输均有相应的时间窗限制。车辆装载人数限制为15人,车辆的固定成本为50元/d。其中,中心车场信息和需求响应点信息如表2所示,为了满足公交实际运营与数据计算的直观性,根据经纬度坐标和实际距离的欧几里德度量建立相应坐标系,表2中的坐标位置信息是换算后的信息。中心车场为厚埔停保场。
表2 中心车场和需求响应点信息
Table 2 The information of central depot and demand response point
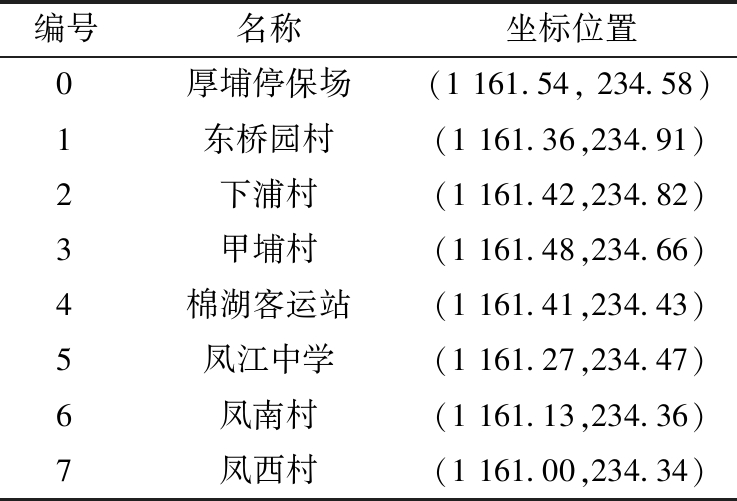
编号名称坐标位置0厚埔停保场(1161.54,234.58)1东桥园村(1161.36,234.91)2下浦村(1161.42,234.82)3甲埔村(1161.48,234.66)4棉湖客运站(1161.41,234.43)5凤江中学(1161.27,234.47)6凤南村(1161.13,234.36)7凤西村(1161.00,234.34)
需要代入SPDVRP模型中的需求响应点的详细参数信息如表3所示。
表3 需求响应点的参数信息
Table 3 Parameter information of demand response point
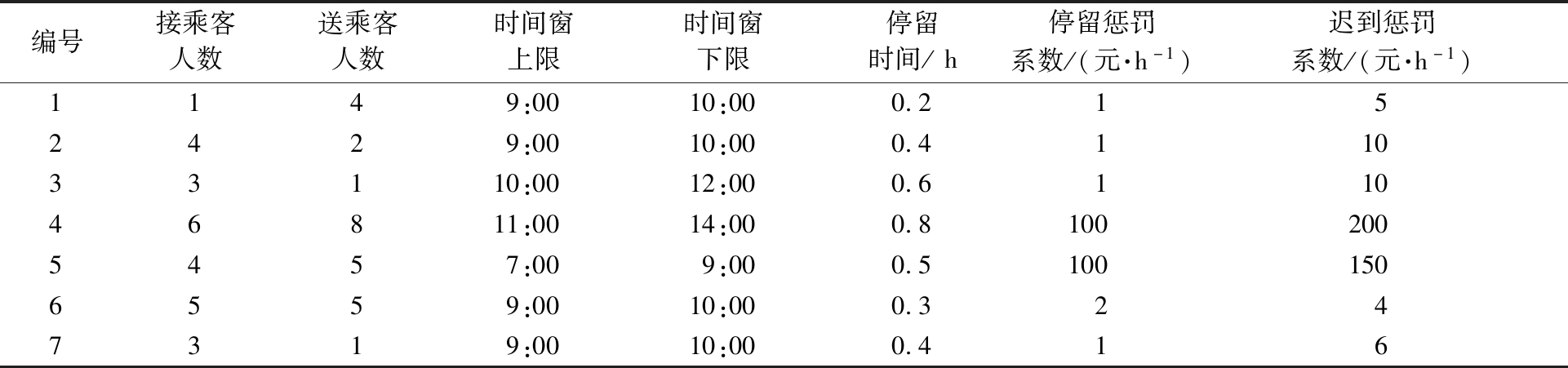
编号接乘客人数送乘客人数时间窗上限时间窗下限停留时间/h停留惩罚系数/(元·h-1)迟到惩罚系数/(元·h-1)1149:0010:000.2152429:0010:000.411033110:0012:000.611046811:0014:000.81002005457:009:000.51001506559:0010:000.3247319:0010:000.416
人工蜂群算法预设蜂群规模为400,其中雇佣蜂规模为200,观察蜂规模为200。侦查蜂侦查阈值为30,自适应大邻域人工蜂群算法的终止条件迭代次数为1 000次。
从图4求解迭代的情况可以看出,自适应大邻域人工蜂群算法在第50次左右开始快速收敛。在迅速收敛后,从第50~100次陆续出现明显的跳跃式进化过程,这是自适应大邻域人工蜂群算法在雇佣蜂阶段进行新的自适应邻域搜索。
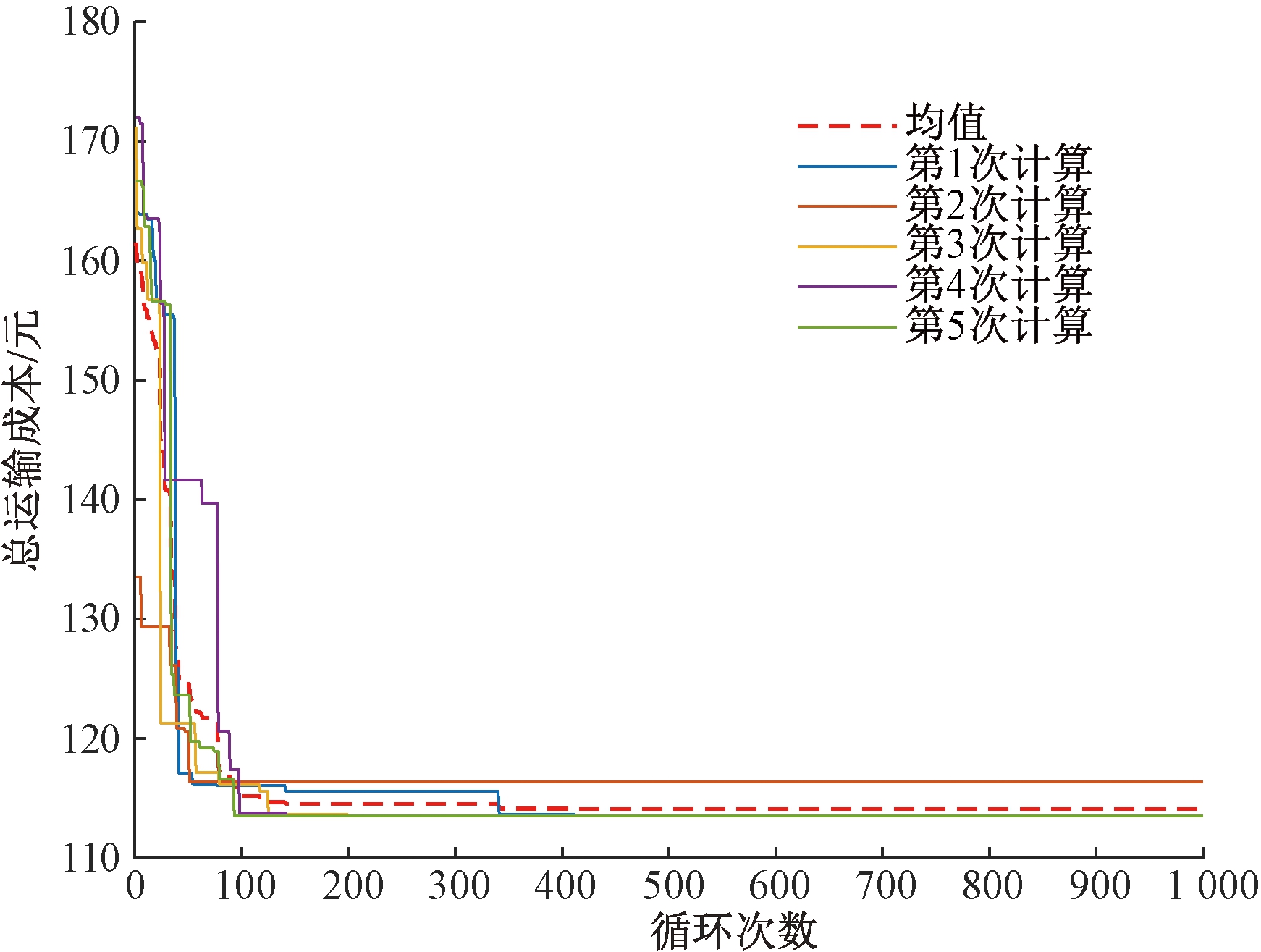
图4 自适应大邻域人工蜂群算法求解迭代情况
Figure 4 Iteration of adaptive large neighborhood search artificial bee colony algorithm
最终的模型求解结果为:需求响应公交车辆调度共安排2条需求响应线路,分别是0—3—7—4—0和0—5—1—2—6—0,运行轨迹如图5所示。
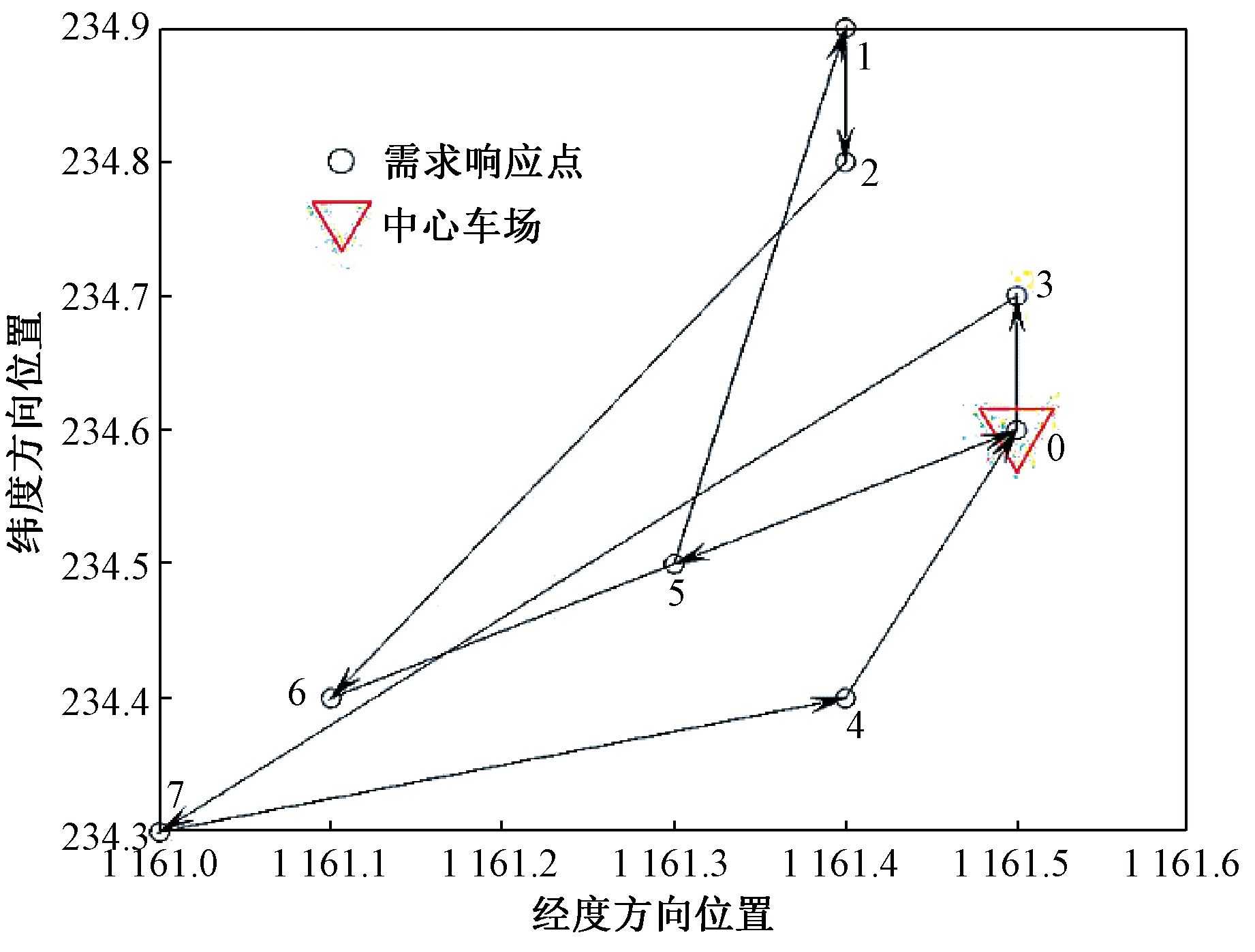
图5 自适应大邻域人工蜂群算法求解结果的运行轨迹
Figure 5 Adaptive large neighborhood search artificial bee colony algorithm solution result trajectory
为了深入分析计算结果的优劣程度,利用MATLAB编程工具分别采用遗传算法和ALNS算法对同一算例模型进行求解,求解迭代结果分别如图6、7所示。
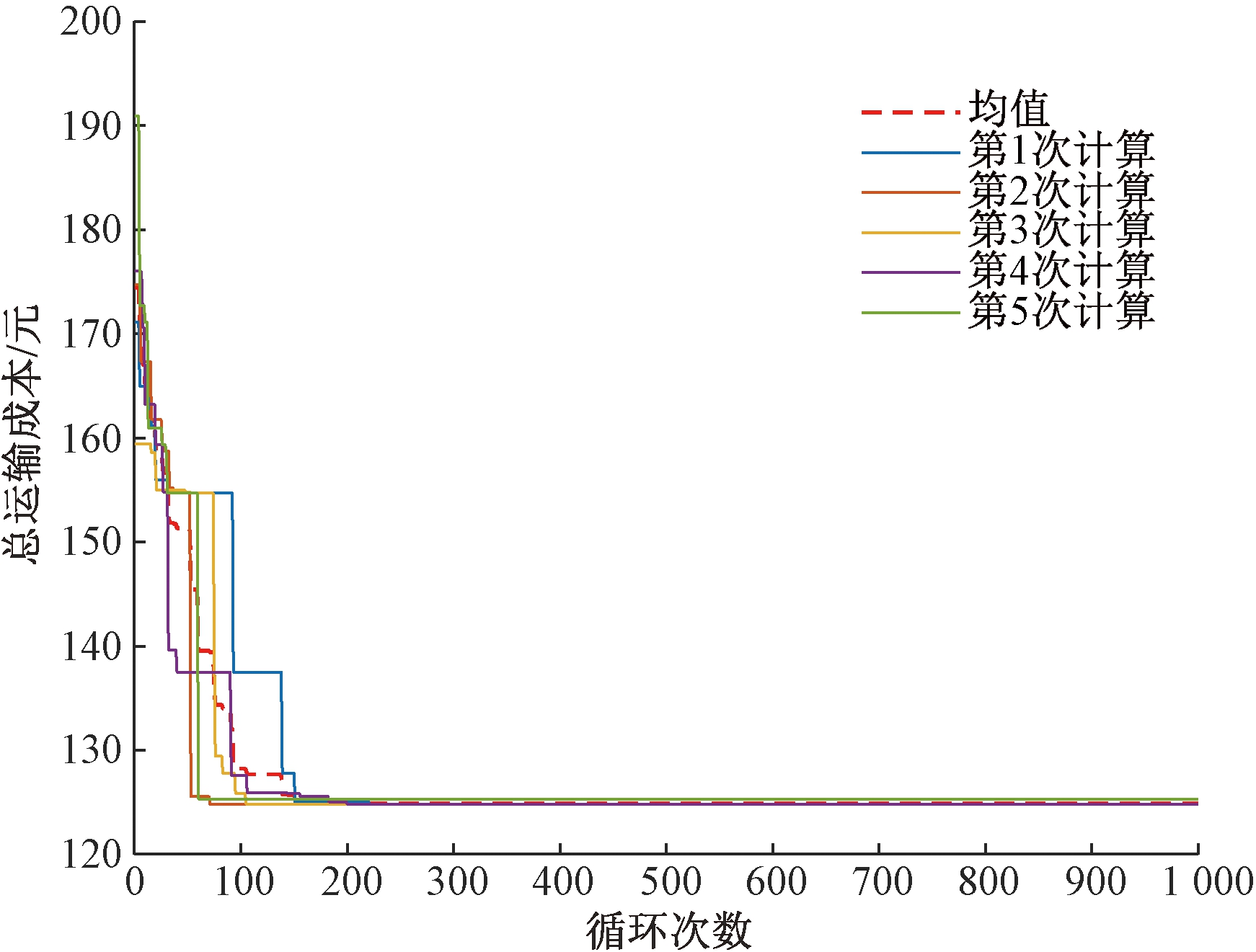
图6 遗传算法求解迭代情况
Figure 6 Iteration of genetic algorithm
从图4、6、7所示算法的求解迭代情况来看,自适应大邻域人工蜂群算法的收敛速度最快,其次是遗传算法。ALNS算法在第50~100次开始逐步收敛,但在第100次之后收敛速度减缓,出现波动,导致迭代的收敛速度和计算精度下降。
从表4的求解结果对比情况来看,自适应大邻域人工蜂群算法比其他2种算法在成本均值、迭代计算的标准差上效果更优。在优化效果上,自适应大邻域人工蜂群算法具有较大的优势,最优成本均值仅为114.946元,比遗传算法结果低9%,比ALNS算法低3%。总体而言,自适应大邻域人工蜂群算法在解决这类农村地区需求响应公交问题时有更好的优化效果。在迭代计算的精度方面,自适应大邻域人工蜂群算法迭代计算的标准差为0.942,比遗传算法低22%。在求解速度上,自适应大邻域人工蜂群算法也具有明显优势,计算耗时仅268.601 s。
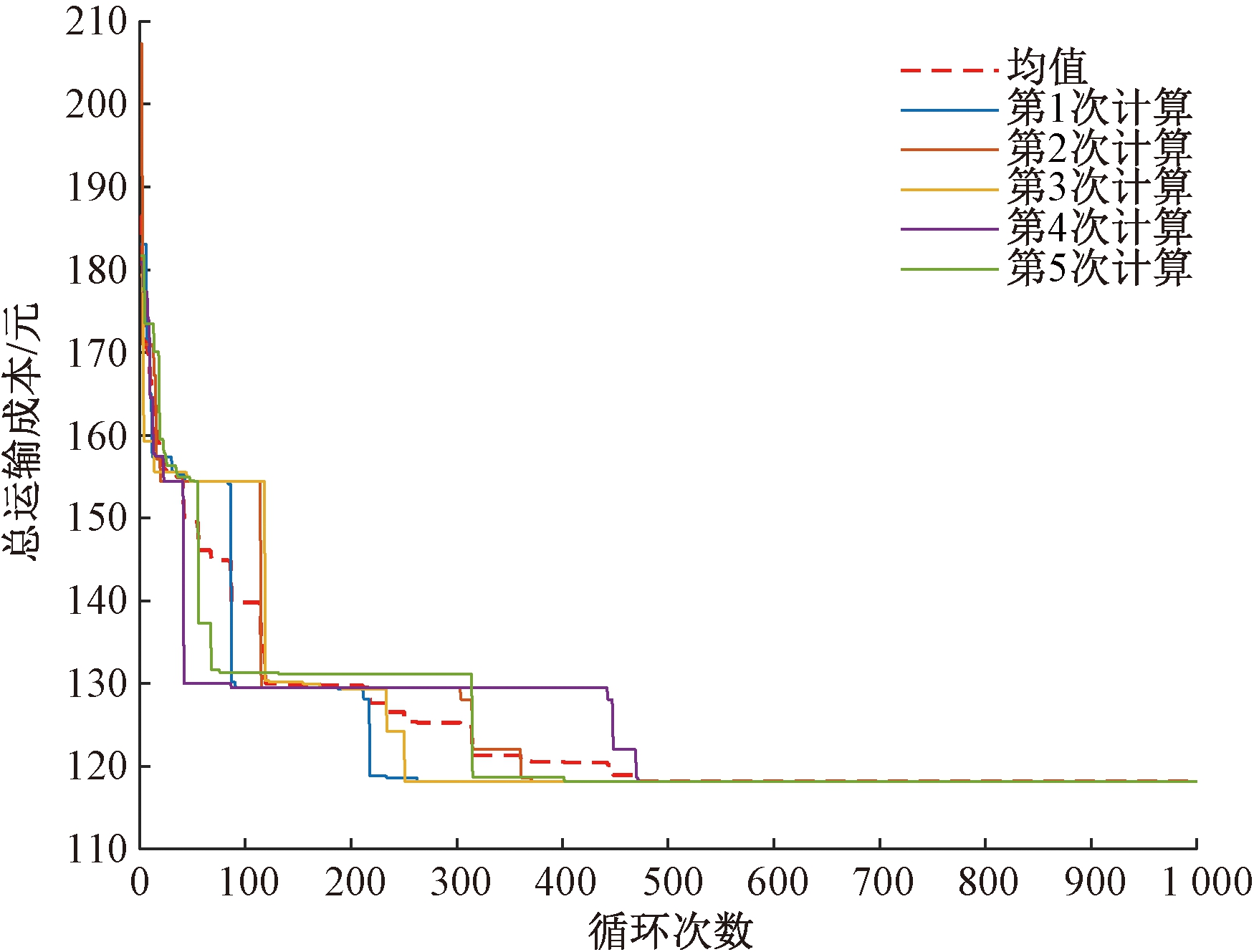
图7 ALNS算法求解迭代情况
Figure 7 Iteration of adaptive large neighborhood search algorithm
表4 不同算法结果对比
Table 4 Comparative of the results of different algorithms
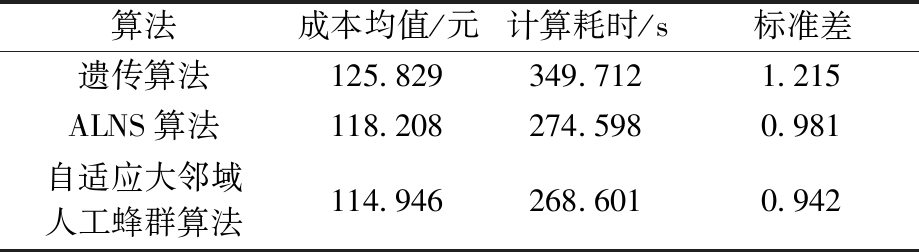
算法成本均值/元计算耗时/s标准差遗传算法125.829349.7121.215ALNS算法118.208274.5980.981自适应大邻域人工蜂群算法114.946268.6010.942
4 结论
算例分析结果显示,在农村低需求密度的环境下,农村DRT同时接送模型更具实用性与现实意义。采用这一模型既能精准满足农村居民出行需求,又能有效控制运输成本、提高路径优化效果。自适应大邻域人工蜂群算法具有收敛速度快、计算精度高的特点。与遗传算法相比,自适应大邻域人工蜂群算法在解决农村DRT问题时有更好的表现。与ALNS算法相比,自适应大邻域人工蜂群算法在继承了ALNS算法优点的同时,在算法收敛速度和结果的优劣性上更有优势。本文模型为需求响应公交模式在农村地区的应用与探索提供了一种思路,关于本文算法在其他领域的应用还有待进一步拓展。
[1] DAGANZO C F.Checkpoint dial-a-ride systems[J].Transportation research part B:methodological,1984,18(4/5):315-327.
[2] AMIRGHOLY M,GONZALES E J.Demand responsive transit systems with time-dependent demand:userequilibrium,systemoptimum,and management strategy[J].Transportation research part B:methodological,2016,92:234-252.
[3] DIANA M,QUADRIFOGLIO L,PRONELLO C.A methodology for comparing distances traveled by performance-equivalent fixed-route and demand responsive transit services[J].Transportation planning and technology,2009,32(4):377-399.
[4] DANTZIG G B,RAMSER J H.The truck dispatching problem[J].Management science,1959,6(1):80-91.
[5] S NCHEZ-ORO J,L
NCHEZ-ORO J,L PEZ-S
PEZ-S NCHEZ A D,COLMENAR J M.A general variable neighborhood search for solving the multi-objective open vehicle routing problem[J].Journal of heuristics,2020,26(3):423-452.
NCHEZ A D,COLMENAR J M.A general variable neighborhood search for solving the multi-objective open vehicle routing problem[J].Journal of heuristics,2020,26(3):423-452.
[6] GU Z Q,ZHU Y,WANG Y X,et al.Applying artificial bee colony algorithm to the multidepot vehicle routing problem[J].Software:practice and experience,2020:1-16.
[7] KARABOGA D,BASTURK B.A powerful and efficient algorithm for numerical function optimization:artificial bee colony (ABC)algorithm[J].Journal of globaloptimization,2007,39(3):459-471.
[8] 毛声,谢文俊,张建业,等.车辆路径问题的双重进化蜂群算法求解研究[J].计算机工程与应用,2016,52(7):35-42,78.
[9] ROPKE S,PISINGER D.Anadaptive large neighborhood search heuristic for the pickup and delivery problem with time windows[J].Transportation science,2006,40(4):455-472.
[10] 魏占阳,邬炼,张佳伟,等.基于自适应大规模邻域搜索算法的两级车辆路径问题[J].物流科技,2015,38(8):4-7.
[11] HUANG D,GU Y,WANG S A,et al.A two-phase optimization model for the demand-responsive customized bus network design[J].Transportation research part C:emerging technologies,2020,111:1-21.
[12] DAGANZO C F,OUYANG Y F.A general model of demand-responsive transportation services:from taxi to ridesharing to dial-a-ride[J].Transportation research part B:methodological,2019,126:213-224.
[13] PAPANIKOLAOU A,BASBAS S.Analytical models for comparing demand responsive transport with bus services in low demand interurban areas[J].Transportation letters,2020:1-8.
[14] GOREV A,POPOVA O,SOLODKIJ A.Demand-responsive transit systems in areas with low transport demand of “smart city”[J].Transportation research procedia,2020,50:160-166.
[15] 林镇泽.求解双层车辆路径问题的改进人工蜂群算法[D].广州:华南理工大学,2014.
[16] 王志刚,夏慧明.求解车辆路径问题的人工蜂群算法[J].计算机工程与科学,2014,36(6):1088-1094.
[17] 金叶,孙越泓,王加翠,等.基于单纯形的改进精英人工蜂群算法[J].郑州大学学报(工学版),2018,39(6):36-42.
[18] 朱子轩,靳文舟,巫威眺,等.考虑驾驶员需求的定位运输线路安排问题[J].广西大学学报(自然科学版),2020,45(1):229-238.
[19] ALINAGHIAN M,SHOKOUHI N.Multi-depot multi-compartment vehicle routing problem,solved by a hybrid adaptive large neighborhood search[J].Omega,2018,76:85-99.
[20] SARASOLA B,DOERNER K F.Adaptive large neighborhood search for the vehicle routing problem with synchronization constraints at the delivery location[J].Networks,2020,75(1):64-85.
[21] 苗国强,于岚,胡娟娟,等.基于自适应大规模邻域搜索算法的带时间窗的车辆路径问题[J].物流技术,2015,34(11):156-158,173.
[22] GU W J,CATTARUZZA D,OGIER M,et al.Adaptivelarge neighborhood search for the commodity constrained split delivery VRP[J].Computers &operations research,2019,112:104761.