0 引言
我国已经成功冶炼出600 MPa级钢筋,但由于目前对该钢筋的研究尚处于起步阶段,缺乏充足的理论依据而未被编入设计规范。混凝土和钢筋能共同工作的前提是钢筋和混凝土之间具有良好的黏结性能。因此,探明600 MPa级钢筋与混凝土的黏结性能及黏结-滑移关系是该钢筋应用于混凝土结构的基础。
近年来,国内外学者对高强钢筋与混凝土的黏结性能进行了研究[1-9]。郝彤等[5]和姚瑞[6]对HRB500钢筋与混凝土的黏结锚固性能进行试验,研究两者黏结性能的影响因素及黏结-滑移关系,提出了计算黏结强度的表达式及合理锚固长度。张建伟等[7]的研究表明:HRB600钢筋与高强混凝土的黏结强度与普通混凝土的变化规律类似,都随混凝土强度、保护层厚度、配箍率的提高而提高,极限黏结强度随着钢纤维掺量的增多而提高。秦程程[8]研究得出,HRB600钢筋与活性粉末混凝土的黏结强度随黏结长度增大而降低,随钢筋直径和强度的增大而增大,且黏结-滑移曲线存在二次上升段。牛旭宁[9]认为HRB600钢筋与混凝土的黏结强度随混凝土强度、相对保护层厚度、配箍率的提高而提高,随锚固长度增加而降低。
尽管一些学者对600 MPa级钢筋与高强混凝土的黏结性能进行了初步研究,但相关的力学参数一直未明确规定,因此有必要对其进行继续研究。本文设计制作了42个600 MPa级钢筋与高强混凝土的黏结锚固试件,通过中心拉拔试验来研究混凝土强度、锚固长度、保护层厚度对黏结锚固性能的影响,分析其黏结-滑移关系,为600 MPa级钢筋在高强混凝土结构的应用提供理论依据。
1 黏结-滑移关系模型研究现状
国内外学者针对钢筋混凝土τ-s关系模型进行了系列研究,其中包括Houde本构模型[10]、欧洲规范本构模型[11]、狄林生本构模型[12]、徐有邻本构模型[13]、《混凝土结构设计规范》本构模型[14]等数十种本构关系模型。其中,《混凝土结构设计规范》建议采用式(1)来计算钢筋与混凝土的黏结-滑移本构关系:
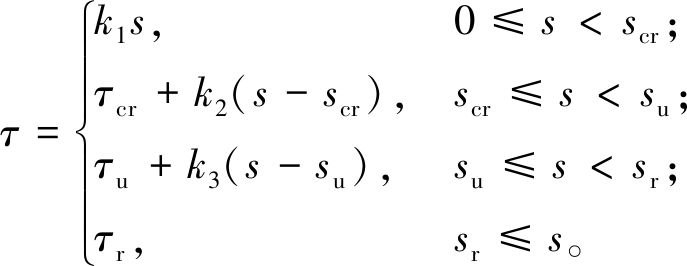
(1)
式中:τ为黏结应力;s为滑移量;τcr、τu、τr分别为劈裂强度、极限强度和残余强度;scr、su、sr为各点对应的特征滑移值。
2 试验部分
2.1 试验方案
本文通过中心拉拔试验来探讨混凝土强度、锚固长度及保护层厚度对600 MPa级钢筋与高强混凝土黏结锚固性能的影响。试验共设计4组42个试件,详细参数见表1。试件设计如图1所示。所有拉拔试件的钢筋均在该截面的中心处,试件截面尺寸为150 mm×150 mm。在试件的两端都设置长度为5d(d为钢筋直径,mm)的PVC套管作为非黏结段,防止黏结锚固试件的端部因应力集中发生局部破坏。
表1 黏结锚固试验设计方案
Table 1 Design scheme of bond anchorage test
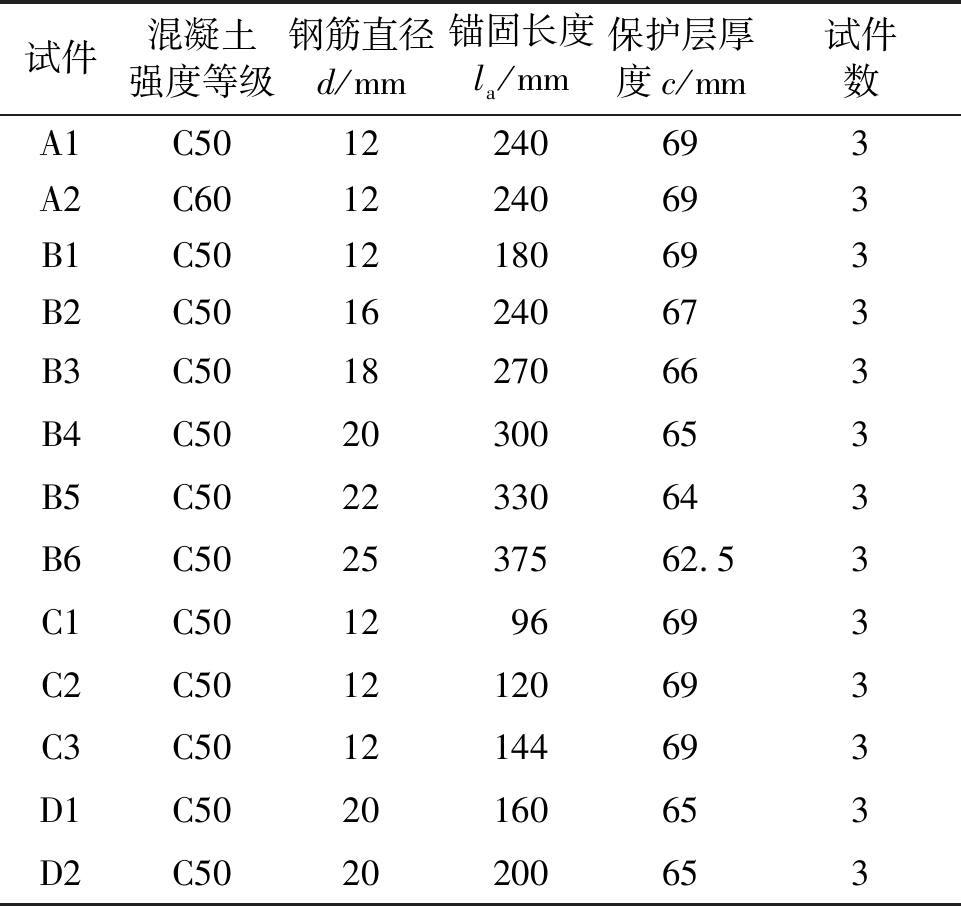
试件混凝土强度等级钢筋直径d/mm锚固长度la/mm保护层厚度c/mm试件数A1C5012240693A2C6012240693B1C5012180693B2C5016240673B3C5018270663B4C5020300653B5C5022330643B6C502537562.53C1C501296693C2C5012120693C3C5012144693D1C5020160653D2C5020200653
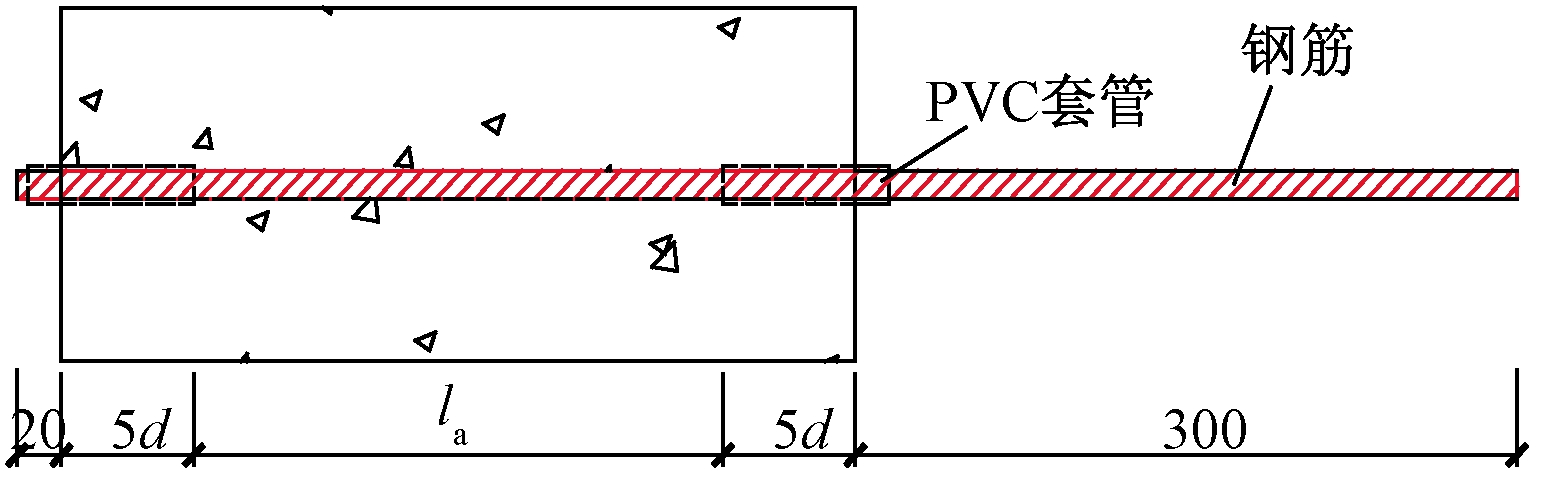
图1 拉拔试件示意图
Figure 1 Schematic of pull-out specimens
2.2 试验装置及加载方案
采用50 t一体式锚杆拉拔仪进行手动加载,加载端采用与钢筋直径对应的专用钢筋锚具加持。试验装置如图2所示。为确保在拉拔过程中黏结试块的底部表面和钢垫板平整均匀接触,在加载之前先进行预拉。当试验过程中发生如下现象时停止加载:①600 MPa钢筋断裂或被拔出;②高强混凝土试件破坏。试验测量的内容包括:①位移计第1次测量到数据时对应的荷载值Fs;②各级荷载及各级荷载下位移计测量值;③拉拔力达到最大时对应的荷载Fu。
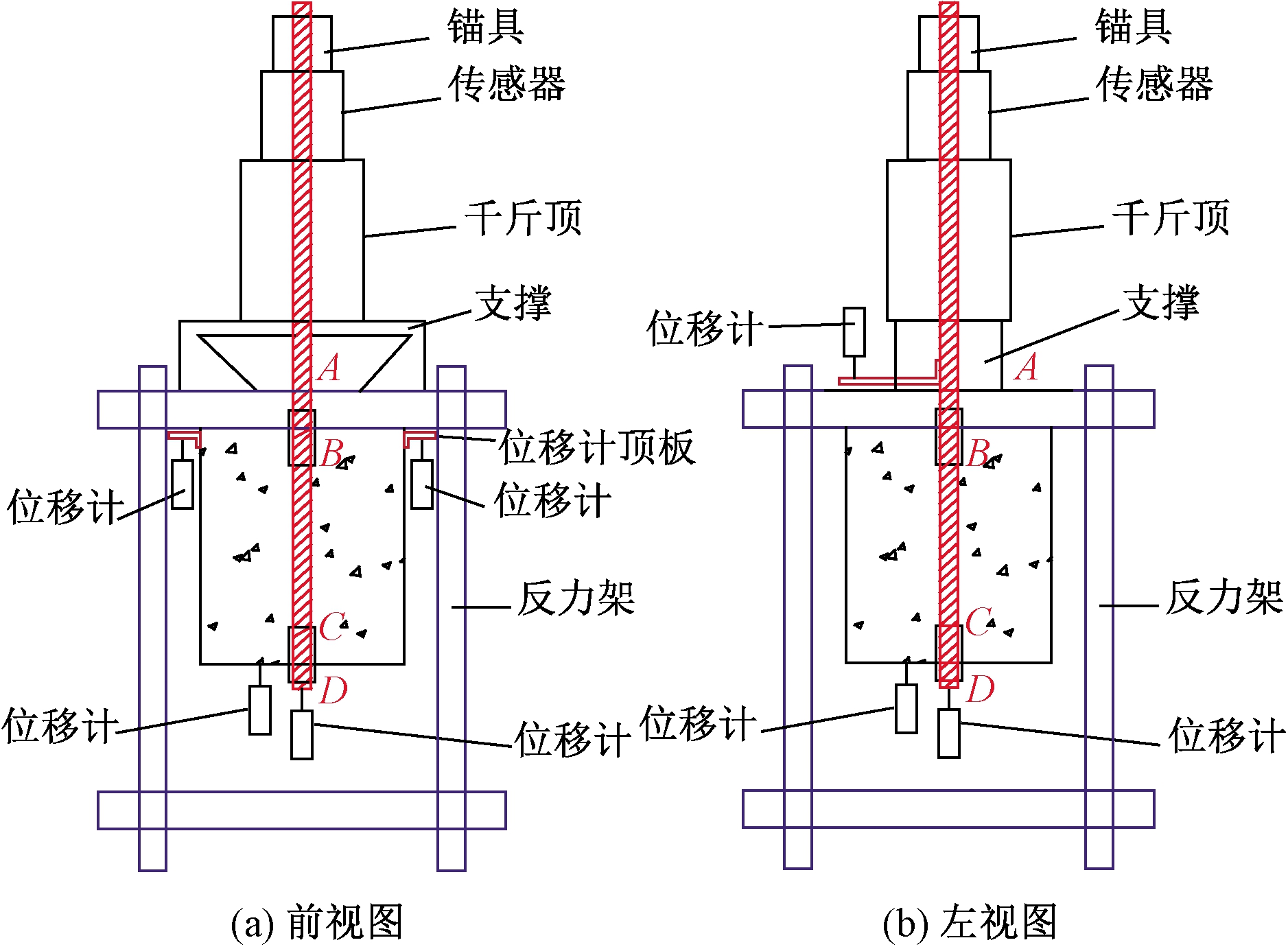
图2 拉拔试件加载装置及测点布置图
Figure 2 Test set-up and measuring points of specimens
由图2可以看出,BC段为600 MPa级钢筋与混凝土的实际锚固长度。CD段为自由端的非黏结段,试验过程中几乎不受力,因此可以用D点的滑移值代替C点的滑移值,即D点2个位移计的差值为试件自由端的滑移值。对于加载端的滑移值,由于AB段较长且受力较大,钢筋的变形对加载端滑移值的影响不可忽略,因此,在用A点的钢筋与混凝土相对滑移表示加载端的滑移值时应去除AB段的钢筋变形sAB。
sAB=FlAB/(E主体A主体)。
(2)
式中:F为试验拉拔荷载;lAB为AB段长度;E主体、A主体分别为钢筋的弹性模量和实测截面面积。加载端的相对滑移值sL为:
sL=sA-sAB。
(3)
式中:sA为A点的滑移值。拉拔试件黏结长度内平均相对滑移量s为:
s=(sL+sD)/2。
(4)
2.3 试验结果
表2列出了各拉拔试件的拉拔试验的混凝土抗拉强度ft、平均黏结强度τu、极限拉拔荷载Fu和破坏情况。其中,平均黏结应力τ为:
τ=F/(πdla)。
(5)
由表2可以看出,当钢筋直径不变时,600 MPa级钢筋与混凝土之间的极限拉拔荷载随着混凝土强度或锚固长度的增大而增大。但是,当锚固长度达到界限值后,再增大锚固长度,将全部发生钢筋屈服破坏,使得极限拉拔荷载不再继续增加。对于钢筋拔出破坏的试件,极限拉拔荷载与锚固长度有关,随着锚固长度的增加,极限拉拔荷载增加。对于发生混凝土劈裂破坏的试件,破坏原因是:在试件相对保护层厚度较小的情况下未配置箍筋,极限拉拔荷载与钢筋直径和锚固长度有关,随着钢筋直径和锚固长度的增大,极限拉拔荷载增加。当相对保护层厚度较大、锚固长度较长时,试件将发生钢筋屈服破坏,极限拉拔荷载仅与钢筋直径有关,随着钢筋直径增大,极限拉拔荷载增加。
表2 600 MPa级钢筋拉拔试验结果
Table 2 Pull-out test results of 600 MPa grade steel bars
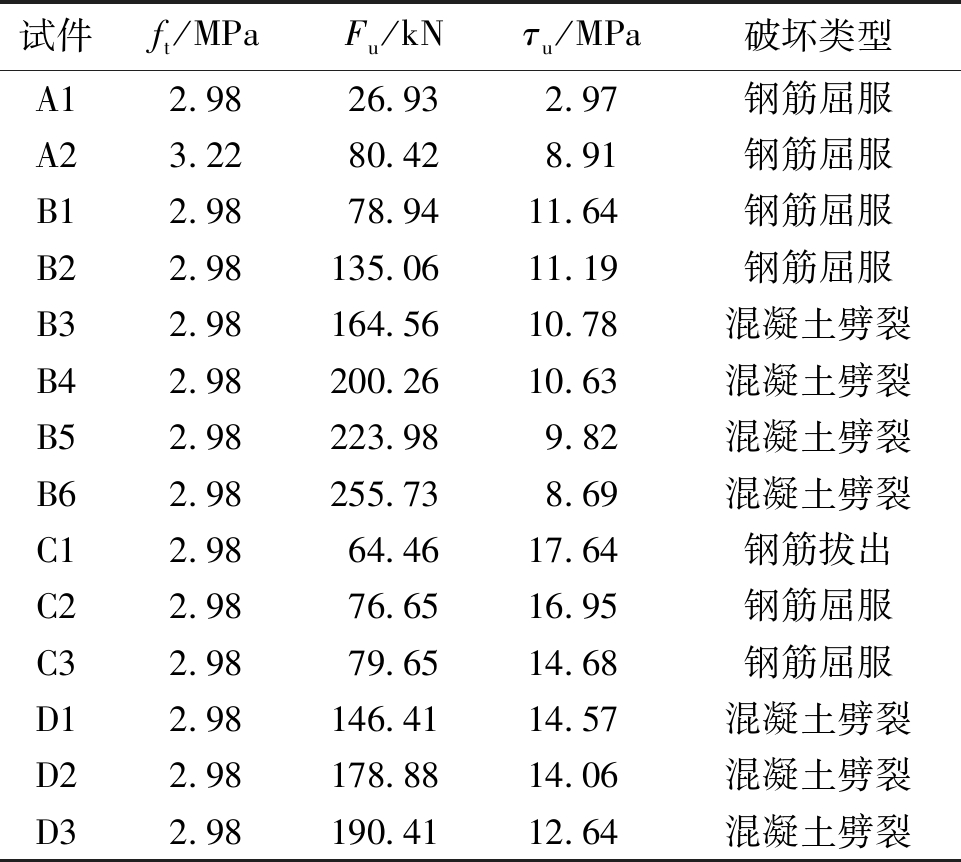
试件ft /MPaFu/kNτu/MPa破坏类型A12.9826.932.97钢筋屈服A23.2280.428.91钢筋屈服B12.9878.9411.64钢筋屈服B22.98135.0611.19钢筋屈服B32.98164.5610.78混凝土劈裂B42.98200.2610.63混凝土劈裂B52.98223.989.82混凝土劈裂B62.98255.738.69混凝土劈裂C12.9864.4617.64钢筋拔出C22.9876.6516.95钢筋屈服C32.9879.6514.68钢筋屈服D12.98146.4114.57混凝土劈裂D22.98178.8814.06混凝土劈裂D32.98190.4112.64混凝土劈裂
3 600 MPa级钢筋与高强混凝土黏结-滑移关系模型
3.1 黏结破坏特征分析
对42个黏结锚固试件进行中心拉拔试验,试件的破坏类型可分为3类,分别为钢筋拔出破坏、混凝土劈裂破坏和钢筋屈服破坏,如图3所示。

图3 试件破坏模式
Figure 3 Failure modes of specimens
(1)钢筋拔出破坏:加载初期,加载端的滑移随着荷载增加而增加,随着荷载的继续增大,自由端开始出现滑移。当荷载达到极限荷载之后,荷载开始下降,并产生较大滑移,最后荷载几乎维持在一个恒定值。当试件破坏时,试件的表面依然保持完整。
(2)混凝土劈裂破坏:加载初期,试件表面无明显现象,加载端的滑移随着荷载的增加而增加,但自由端几乎无滑移。当荷载达到极限荷载时,混凝土突然发生劈裂破坏,试件变为多瓣,并伴随巨大响声。
(3)钢筋屈服破坏:在加载过程中,试件表面无明显现象,加载端的滑移随着荷载的增大而增大,在钢筋达到屈服后,加载端的滑移主要由钢筋的伸长引起,自由端基本无滑移。发生钢筋屈服破坏后,试件仍保持完整。
3.2 黏结-滑移曲线特征分析
根据试验结果得出的平均黏结应力-滑移曲线有3种形式:①发生钢筋拔出破坏的黏结应力-滑移曲线,包括上升段、下降段和残余段;②发生混凝土劈裂破坏的试件的黏结应力-滑移曲线,只包括上升段;③发生钢筋屈服破坏的黏结应力-滑移曲线,包括上升段和水平段。
3.2.1 钢筋拔出破坏的黏结应力-滑移曲线分析
图4为钢筋拔出破坏试件(C1)典型黏结-滑移全曲线,包括5个阶段:微滑移段、滑移段、劈裂段、下降段、残余段。
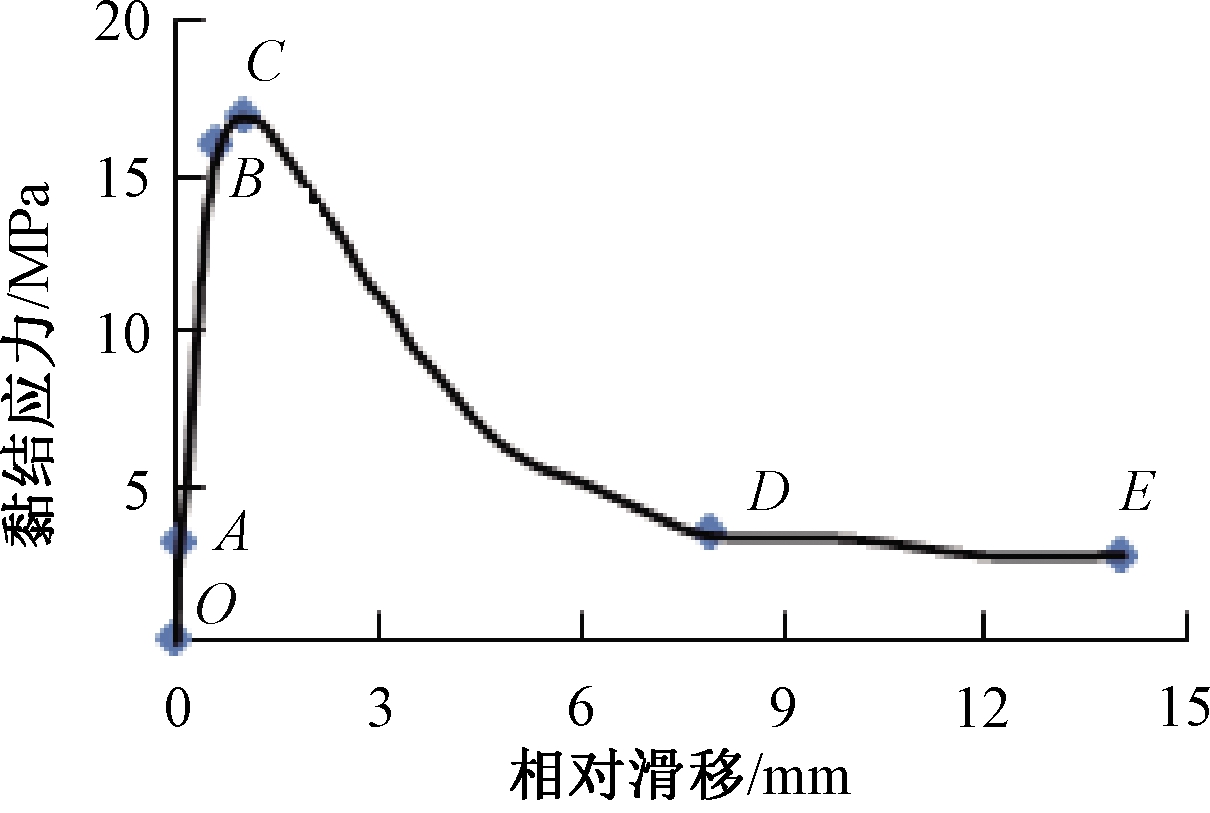
图4 C1试件的黏结应力-滑移曲线
Figure 4 Bond stress-slip curves of specimen C1
(1)微滑移段(OA段):在试件加载初期,加载端的滑移微小,自由端未滑移,此时钢筋与混凝土之间的黏结主要是化学胶结力,随着荷载增大,化学胶结力逐渐消失,加载端附近开始产生黏脱现象,并从加载端慢慢往自由端传递。
(2)滑移段(AB段):当荷载达到极限拉拔荷载的20%左右时,自由端开始发生滑移。随着荷载不断增大,加载端和自由端的滑移均不断增大,荷载滑移进入较为稳定的增长阶段,曲线表现为线性。这个阶段钢筋与混凝土之间的黏结主要由钢筋与混凝土之间的机械咬合力和摩擦阻力承担。
(3)劈裂段(BC段):当荷载达到极限拉拔荷载的80%~90%时,黏结应力进入了非线性增长阶段。此时稍微增加荷载,钢筋与混凝土之间的相对滑移便会发生较大增长,曲线表现为明显的非线性。
(4)下降段(CD段):当荷载达到极限拉拔荷载之后,钢筋与混凝土间的咬合齿被破坏,钢筋肋前的混凝土被压碎,机械咬合力和摩擦阻力迅速减小,荷载会因钢筋与混凝土之间的约束不足而下降,钢筋也会大幅增长。
(5)残余段(DE段):当荷载下降至极限拉拔荷载的20%~30%时,荷载下降十分缓慢,甚至不再降低,滑移仍在继续增大,直至钢筋被拔出。在此阶段,残余荷载仅由钢筋与混凝土之间的摩擦阻力提供。
3.2.2 混凝土劈裂破坏的黏结应力-滑移曲线分析
图5为根据混凝土劈裂破坏试件(B4)得出的典型黏结应力-滑移全曲线,包括3个阶段:微滑移段、滑移段、劈裂段。
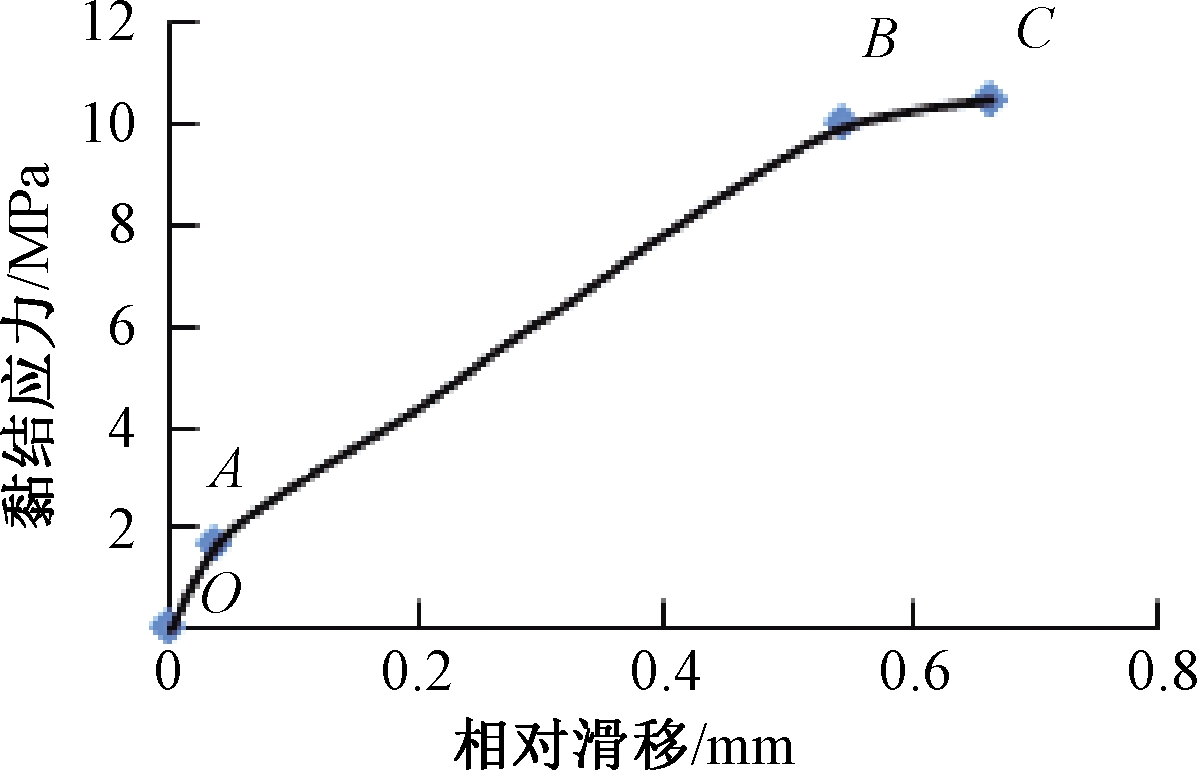
图5 B4试件的黏结应力-滑移曲线
Figure 5 Bond stress-slip curve of specimen B4
(1)微滑移段(OA段):在试件加载初期,加载端滑移微小,自由端未滑移,此时钢筋与混凝土之间的黏结主要是化学胶结力。随着荷载增大,化学胶结力逐渐消失,加载端附近开始产生黏脱现象,并从加载端慢慢往自由端传递,这个阶段与拔出破坏的黏结滑移曲线微滑移段规律一致。
(2)滑移段(AB段):当荷载达到极限拉拔荷载的20%左右时,钢筋与混凝土之间开始发生明显的相对滑移。随着荷载增大,相对滑移不断增大,曲线进入一段较为稳定的线性增长阶段,但是滑移量明显小于钢筋拔出破坏时的值;达到B点时,对应的拉拔力约是极限拉拔荷载的90%。
(3)劈裂段(BC段):由于相对保护层厚度较小,稍增加拉拔力,试件突然发生瞬间劈裂破坏,并传出巨大响声,试件变为多瓣。因钢筋与混凝土分离,无法继续加载,故曲线没有下降段;最大相对滑移值亦远小于钢筋拔出破坏时的值。
3.2.3 钢筋屈服破坏的黏结应力-滑移曲线分析
图6为根据钢筋屈服破坏试件(A2)得出的典型黏结应力-滑移曲线,包括3个阶段:微滑移段、滑移段、屈服段。
(1)微滑移段(OA段):在试件加载初期,加载端的滑移很小,自由端未发生滑移,这个阶段与拔出破坏的黏结-滑移曲线微滑移段规律一致。
(2)滑移段(AB段):当荷载达到极限拉拔荷载的20%左右时,自由端开始发生滑移,此时钢筋与混凝土之间的化学胶结力消耗殆尽。而随着荷载的不断增大,加载端和自由端的滑移开始增大,滑移进入较为稳定的线性增长阶段;和钢筋拔出破坏及劈裂破坏相比,该段的滑移量非常小。
(3)屈服段(BC段):由于锚固长度很大,在钢筋和混凝土未发生较大滑移时,钢筋已达到屈服,此时荷载不再增大,仅是钢筋屈服后的应变伸长。
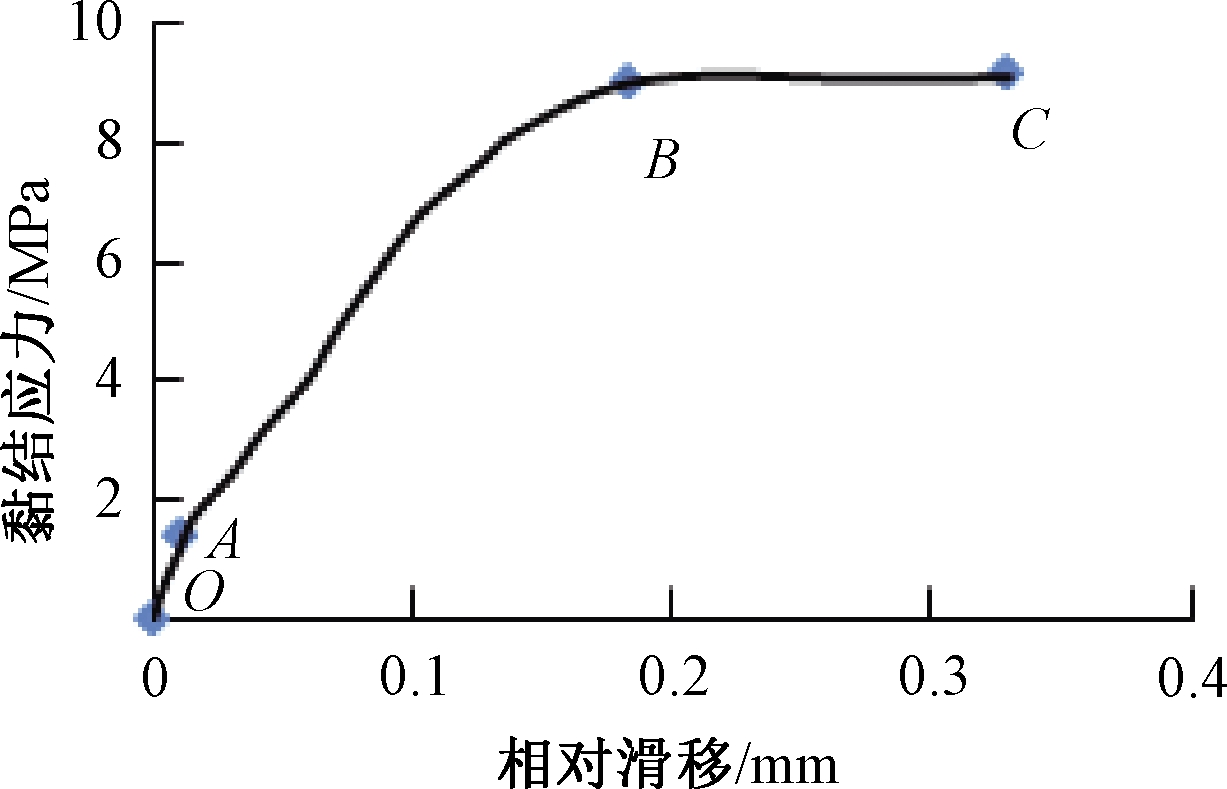
图6 A2试件的黏结应力-滑移曲线
Figure 6 Bond stress-slip curve of specimen A2
3.3 600 MPa级钢筋与高强混凝土黏结-滑移劈裂模型
3.3.1 劈裂破坏的黏结-滑移关系特征点分析
根据本文试验结果绘制600 MPa级钢筋和高强混凝土之间发生劈裂黏结破坏的黏结应力-滑移关系曲线,可将该曲线分为3个明显阶段,每个阶段可以通过3个特征点来描述其劈裂破坏下的黏结-滑移关系特点。各特征点定义如下:①微滑移点,钢筋与混凝土完全丧失化学胶结力,自由端开始发生滑移时的微滑移强度τs,对应的微滑移量ss;②劈裂点,试件滑移段的拐点,曲线发生明显转折时的劈裂强度τcr,对应的劈裂滑移量为scr;③极限点,试件发生劈裂破坏,达到极限荷载,此时曲线的峰值点为极限强度τu,对应的极限滑移量为su。
3.3.2 劈裂破坏的黏结-滑移关系曲线模型
综上分析,600 MPa级钢筋和高强混凝土劈裂破坏的黏结应力-滑移曲线可按3个阶段分析,即微滑移段、滑移段和劈裂破坏段,且每段接近直线。整个曲线在各个特征点连续,但斜率发生改变,见图7。各段表达式如下。
微滑移段(OA段):
τ=k1s,0≤s≤ss;
(6)
k1=τs/ss。
(7)
滑移段(AB段):
τ=τs+k2(s-ss),ss≤s≤scr;
(8)
k2=(τcr-τs)/(scr-ss)。
(9)
劈裂段(BC段):
τ=τcr+k3(s-scr),scr≤s≤su;
(10)
k3=(τu-τcr)/(su-scr)。
(11)
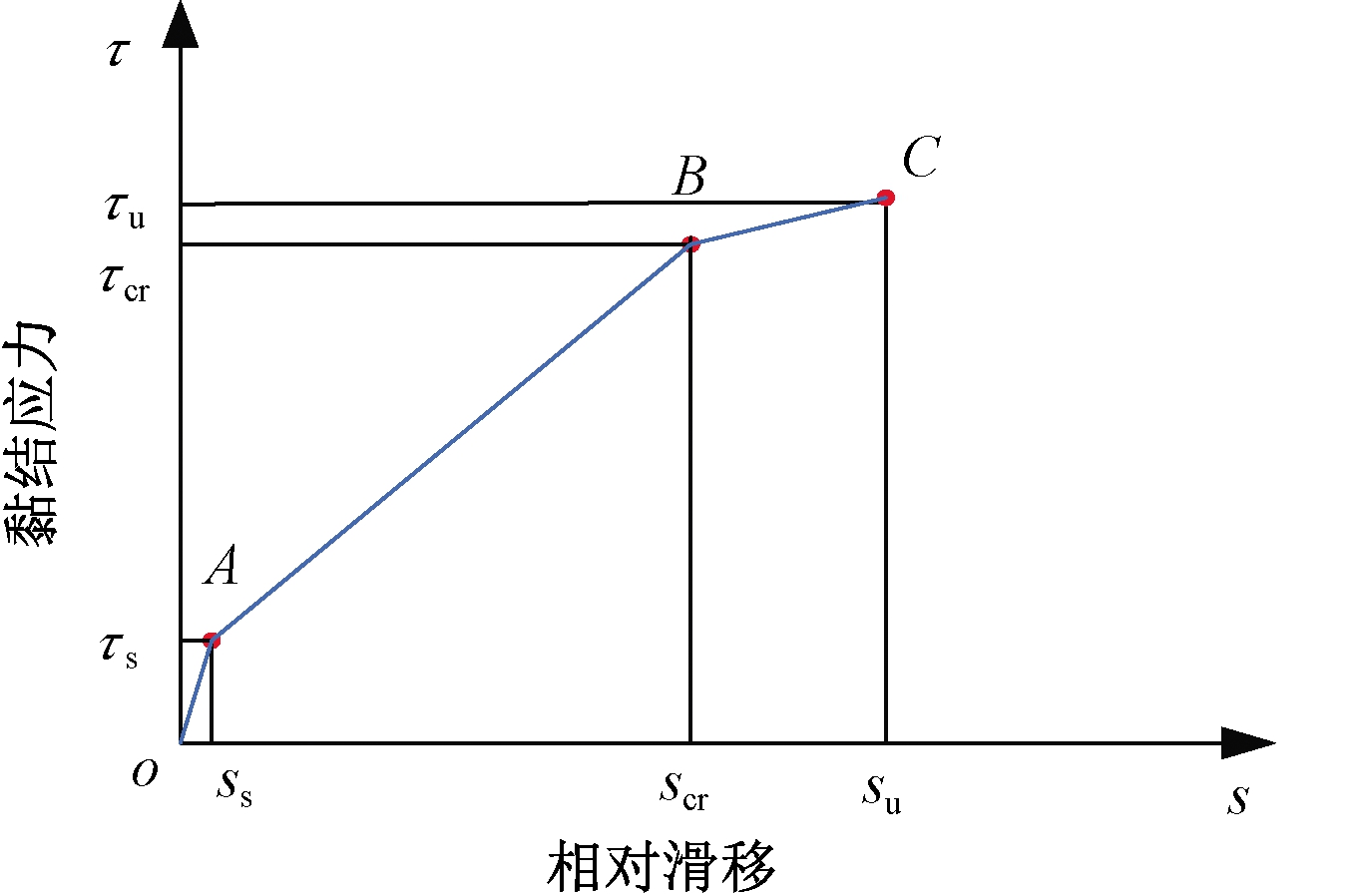
图7 劈裂破坏下黏结-滑移关系模型曲线
Figure 7 Bond-slip model curve under splitting failure
3.3.3 模型参数分析
针对混凝土强度、相对保护层厚度、锚固长度3个影响因素,基于试验结果,分析劈裂破坏时黏结-滑移模型参数与各影响因素的关系。
(1)各特征点的黏结强度。分析试验结果可知,各特征点的黏结强度与相对锚固长度、相对保护层厚度、混凝土强度均相关。拟合试验结果,得到微滑移点黏结强度τs、劈裂黏结强度τcr、极限劈裂黏结强度τu的表达式:
τs=(0.37+0.84 d/la)(0.94+0.16c/d)ft;
(12)
τcr=(0.54+7.19 d/la)(0.93+0.66c/d)ft;
(13)
τu=(0.57+7.59 d/la)(0.98+0.69c/d)ft。
(14)
(2)各特征点的滑移量。分析试验结果可知,各特征点的滑移量与相对锚固长度、钢筋直径均相关。拟合试验结果,得到微滑移点滑移量ss、劈裂点滑移量scr、极限点滑移量su的表达式:
ss=(0.086 7+0.049 6 d)(0.026 2+
0.000 7la/d);
(15)
scr=(0.742 8+0.106 7 d)(0.155 3+
0.001 6la/d);
(16)
su=(0.694 2+0.119 0 d)(0.194 7+
0.002 5la/d)。
(17)
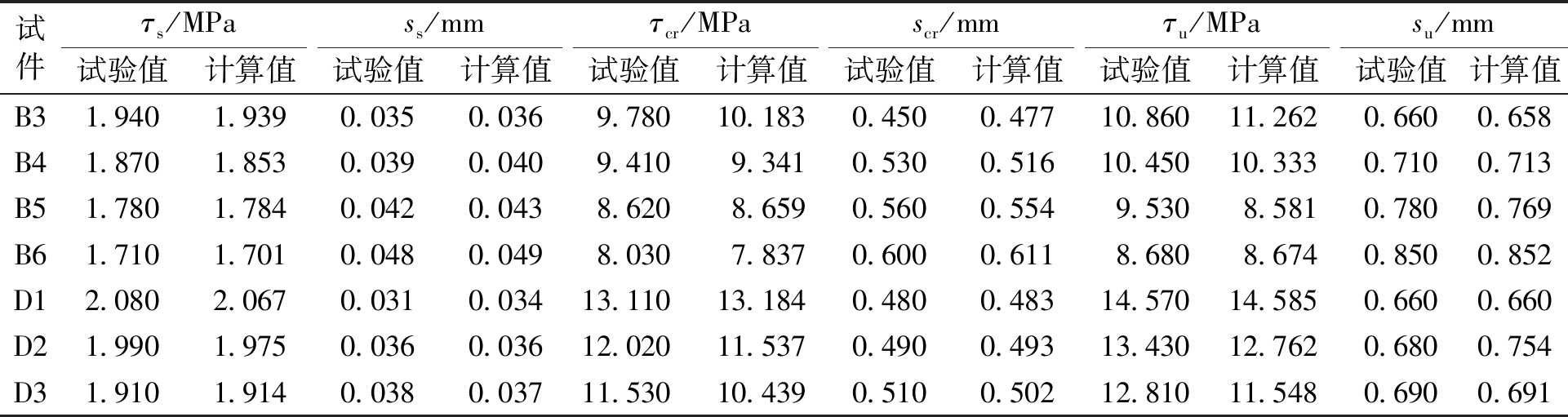
将各模型参数的试验值和计算值列于表3。由表3可知,拟合得出的劈裂破坏情况下黏结-滑移模型各参数计算值与试验值吻合良好。
4 模型验证
为了验证劈裂破坏情况下黏结-滑移模型及模型参数表达式的准确性,将该模型与本文试验数据对比,如图8所示,计算值与试验曲线吻合良好,且计算所得极限黏结强度与试验峰值黏结应力较为接近。故该模型及模型参数表达式能较好反映600 MPa级钢筋与混凝土发生劈裂破坏时的黏结-滑移关系。
表3 劈裂破坏黏结-滑移模型参数的试验值与计算值
Table 3 Experimental and calculated values of bond-slip model parameters under splitting failure
试件τs/MPass/mmτcr/MPascr/mmτu/MPasu/mm试验值计算值试验值计算值试验值计算值试验值计算值试验值计算值试验值计算值B31.9401.9390.0350.0369.78010.1830.4500.47710.86011.2620.6600.658B41.8701.8530.0390.0409.4109.3410.5300.51610.45010.3330.7100.713B51.7801.7840.0420.0438.6208.6590.5600.5549.5308.5810.7800.769B61.7101.7010.0480.0498.0307.8370.6000.6118.6808.6740.8500.852D12.0802.0670.0310.03413.11013.1840.4800.48314.57014.5850.6600.660D21.9901.9750.0360.03612.02011.5370.4900.49313.43012.7620.6800.754D31.9101.9140.0380.03711.53010.4390.5100.50212.81011.5480.6900.691
为进一步验证本文提出的黏结-滑移模型的准确性,采用文献[9]的试验结果进行验证。文献[9]中的混凝土试件抗拉强度为2.90 MPa,钢筋直径为18 mm,锚固长度为10d,相对保护层厚度为3.67d,破坏类型为劈裂破坏。黏结-滑移关系曲线对比如图8(h)所示,可以看出,按本文黏结-滑移模型的计算曲线与试验曲线吻合良好,验证了所提模型及模型参数表达式的准确性。
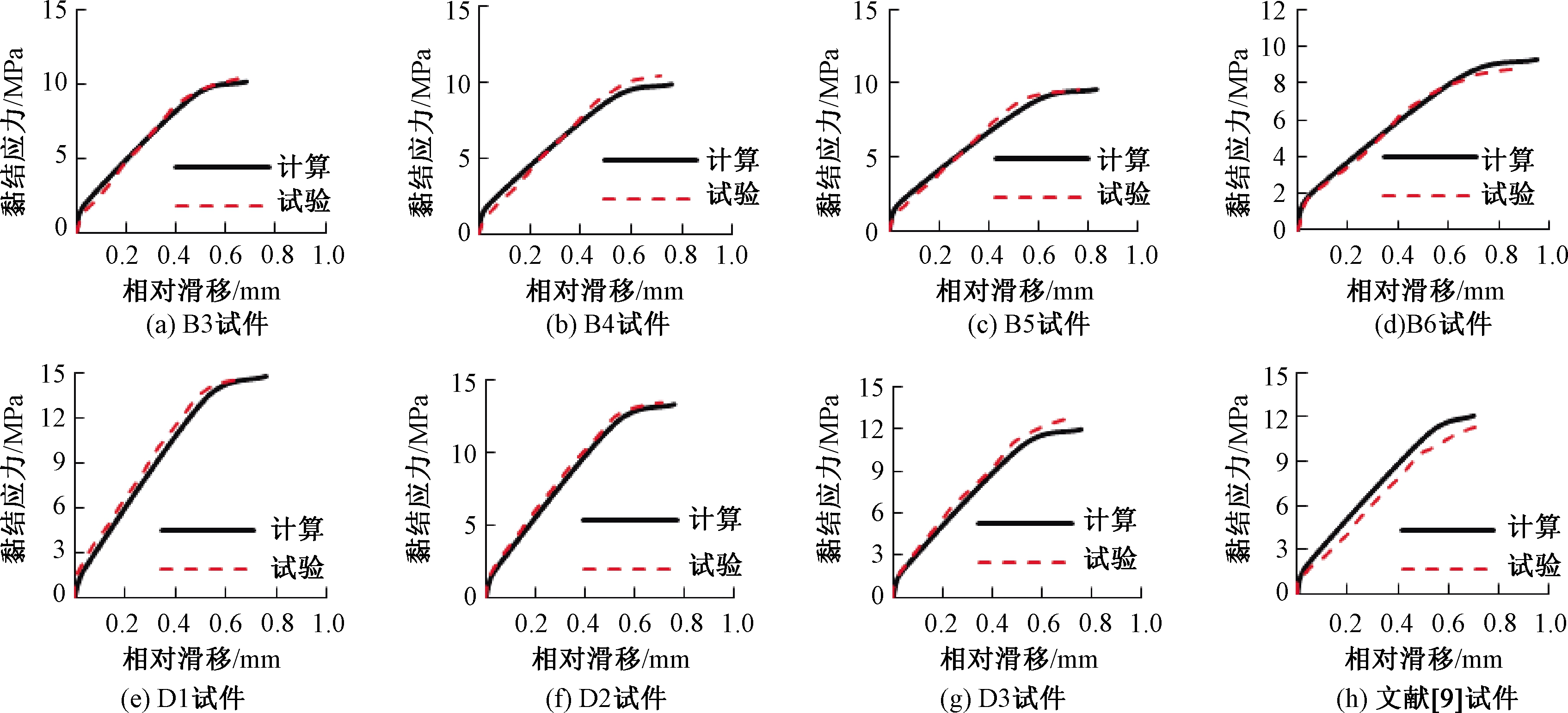
图8 本文及文献[9]试验曲线与黏结-滑移模型对比
Figure 8 Comparison between the test curves of this paper and literature [9] and the bond-slip model
5 结论
(1)在未发生钢筋屈服破坏的情况下,600 MPa级钢筋的极限拉拔荷载随混凝土强度、锚固长度、钢筋直径的增大而增大。
(2)600 MPa级钢筋在高强混凝土中的拉拔破坏模式包括:钢筋拔出破坏、混凝土劈裂破坏、钢筋屈服破坏。钢筋拔出破坏的黏结-滑移曲线包含上升段(包括微滑移段、滑移段、劈裂段)、下降段和残余段;混凝土劈裂破坏的黏结-滑移曲线,只包含上升段(包括微滑移段、滑移段、劈裂段);钢筋屈服破坏的黏结-滑移曲线,包含上升段(包括微滑移段、滑移段)和水平段。
(3)提出了劈裂破坏情况下600 MPa级钢筋与高强混凝土的黏结-滑移模型及各特征点表达式。所提的黏结-滑移模型与试验结果吻合良好,验证了该模型的准确性。
[1] YOO D Y,PARK J J,KIM S W,et al.Influence of reinforcing bar type on autogenous shrinkage stress and bond behavior of ultra high performance fiber reinforced concrete[J].Cement and concrete composites,2014,48:150-161.
[2] GUDONIS E,KACIANAUSKAS R,GRIBNIAK V,et al.Mechanical properties of the bond between GFRP reinforcing bars and concrete[J].Mechanics of composite materials,2014,50(4):457-466.
[3] GUERRA M,CEIA F,De BRITO J,et al.Anchorage of steel rebars to recycled aggregates concrete[J].Construction and building materials,2014,72:113-123.
[4] PRINCE M J R,SINGH B.Investigation of bond behaviour between recycled aggregate concrete and deformed steel bars[J].Structural concrete,2014,15(2):154-168.
[5] 郝彤,刘斌,于秋波,等.全轻混凝土的钢筋黏结锚固性能试验研究[J].建筑科学,2018,34(3):69-75.
[6] 姚瑞.高强陶粒混凝土与高强钢筋的黏结锚固性能试验研究[D].郑州:郑州大学,2017.
[7] 张建伟,李晨,冯曹杰,等.HRB600级钢筋与高强混凝土的黏结性能试验研究[J].北京工业大学学报,2019,45(6):566-574.
[8] 秦程程.高强钢筋与活性粉末混凝土间黏结性能研究[D].吉林:东北电力大学,2018.
[9] 牛旭宁.600 MPa级热轧带肋钢筋黏结锚固性能试验研究[D].天津:河北工业大学,2015.
[10] MIRZA S M,HOUDE J.Study of bond stress-slip relationships in reinforced concrete[J]. Journal proceedings,1979,76(1):19-46.
[11] Comite euro-international du beton. CEB-FIP model code 2010, completed draft[S]. Switzerland:Thomas Telford Services Ltd, 2010.
[12] 狄生林.钢筋混凝土握裹力-滑移关系的试验研究[D].南京:东南大学, 1981.
[13] 徐有邻.钢筋混凝土黏结锚固性能的试验研究[J]. 建筑结构学报,1994,15(3): 26-37.
[14] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB/T 50010—2010[S]. 北京:中国建筑工业出版社,2010.