0 引言
随着城市的快速发展,地下轨道交通和地下管线系统越来越多,这使得城市地下空间规模不断增大[1]。中国地处环太平洋地震带上,地震活动非常频繁,是世界上最大的一个大陆浅源强震活动区。与大量的地面结构震害相比,地下结构震害资料相对较少,导致一段时间以来,人们普遍认为地下结构具有较好的抗震性能,未对地下结构抗震研究给予足够重视[2-3]。随着地下空间开发和地下结构建设规模的不断加大,地下结构的抗震设计及其安全性评价的重要性、迫切性愈来愈明显。
目前国内学者对于复杂场地条件下地下结构抗震性能研究不够深入。黄润秋等[4]针对软弱夹层对地震波强度的影响进行了研究,结果表明,软弱夹层对地震波的放大作用主要与地震波波速有关;陈国兴等[5]利用SHAKE91程序,在3种不同场地条件下,构造不同的土层截面进行数值分析,研究了软弱土层的埋深、厚度对深厚软弱场地中的地表加速度峰值和加速度放大系数的影响;王子辉[6]假定结构侧边土体为单一均匀土层,对饱和土和单相土互层场地条件下地铁车站的地震响应进行了研究。因此深入研究含软弱夹层场地中地下结构的地震响应规律具有重要意义。
本文根据某单层双跨地铁车站结构建立二维土-地下结构相互作用整体模型,研究软弱夹层位置、厚度等因素对地下结构地震响应的影响。
1 土-地下结构整体动力时程分析法
本文采用杜修力等[7]提出的基于等效线性化的土-地下结构整体动力时程分析方法进行计算。本方法充分利用一维等效线性化方法能够快速求得土层等效剪切模量和阻尼比的优势,运用等效线性化迭代的参数确定动力时程分析方法中土体的材料参数,最终实现土-地下结构整体模型的动力时程分析。
1.1 一维场地等效线性化方法
一维场地等效线性化分析方法假定场地为水平成层的均匀介质场地,且地震波为垂直入射的P波。常用的计算程序有EERA[8]和SHAKE91[9]等。
在真实地震作用下,由于土层受不规则的荷载作用,土体内部各节点应力应变呈现无规律变化。等效线性化分析方法主旨思想就是运用1条稳态回线来近似表示所有回线的平均关系,从而将非线性问题转化为线性问题。这条等效的稳态回线的应变振幅称之为等效应变振幅。
等效应变振幅![]() 计算式为
计算式为
(1)
式中:γn,max为第n层中点剪应变最大值。
等效动剪切模量![]() 和等效滞回阻尼
和等效滞回阻尼![]() 可以表示为
可以表示为
(2)
(3)
1.2 阻尼处理方法
基于等效线性化的整体动力时程分析方法本质是运用线性模型来描述土体材料的非线性。在此过程中的一个关键问题是如何正确反映阻尼的作用。在实际分析中,人们通常采用Rayleigh阻尼假定。所以解决该问题的关键转化为如何运用等效线性化求得的阻尼来确定Rayleigh阻尼系数。
对于任意阶阵型阻尼比ξn,可由式(4)得出
(4)
式(4)表明时域计算中的阻尼比与频率相关。运用等效线性化方法可以得出不同土层的等效阻尼比![]() 假定
假定![]() 所以式(4)变形为
所以式(4)变形为
(5)
式中:ωi为场地1阶自振频率,rad/s;ωj为地震卓越频率,rad/s。由此可通过等效线性化方法求得的土体各层等效阻尼比![]() 来确定Rayleigh阻尼系数,实现运用线性模型来描述土体材料的非线性关系。
来确定Rayleigh阻尼系数,实现运用线性模型来描述土体材料的非线性关系。
2 工况设计与模型建立
2.1 工况设计
本文主要讨论软弱夹层对地下结构地震响应的影响,分析软弱夹层位置、厚度不同时地下结构的地震响应规律。为排除土层性质不同对地下结构地震响应造成的影响,本模型中除软弱夹层外,其余为均质土体,软土层、均质层均为粉质黏土,由于缺少真实土体动力参数,本文采用典型黏土[10]的剪切模量比与剪应变幅的试验曲线进行模拟,见图1。土体密度为1 900 kg/m3,泊松比为0.3,均质层的土体剪切波速为200 m/s,软弱土层剪切波速取均质层剪切波速的一半,为100 m/s。车站结构整体采用C35强度等级混凝土,泊松比为0.2,弹性模量为30 GPa,密度为2 500 kg/m3。土层物理性质见表1。
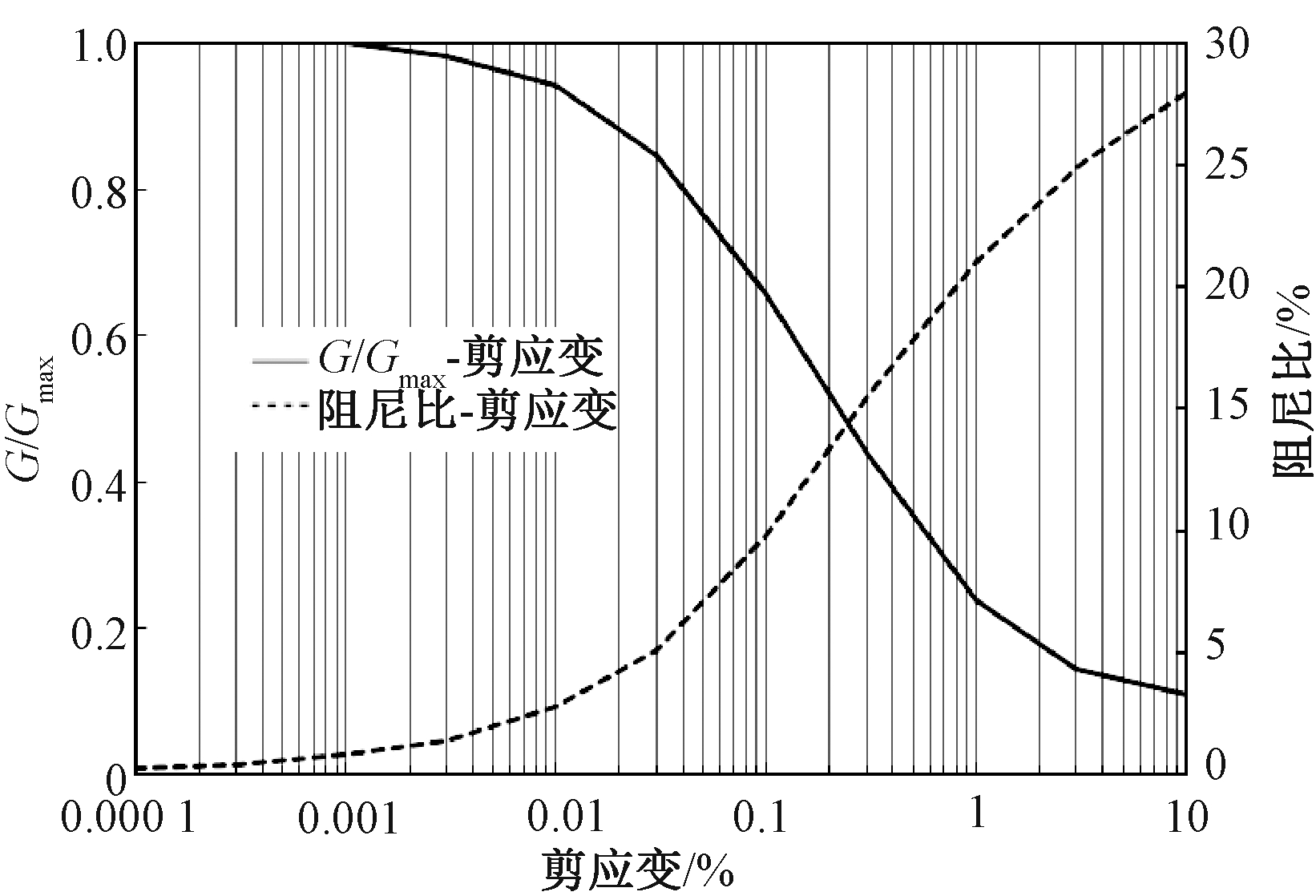
图1 黏土本构曲线
Figure 1 Constitutive curves of clay
表1 土层物理性质表
Table 1 Physical properties of soils

土层土质密度/(kg·m-3)剪切波速/(m·s-1)泊松比软弱夹层黏土19001000.3非软弱层黏土19002000.3
整体计算模型为1栋建在含软弱夹层场地中的矩形单层双跨地铁车站结构。地铁车站埋深为4 m,整体尺寸为12 m×6 m,中柱位于车站正中,车站侧墙及顶底板厚为0.7 m,中柱截面尺寸为0.6 m×1 m,各中柱纵向间距为5 m。计算简图如图2所示。
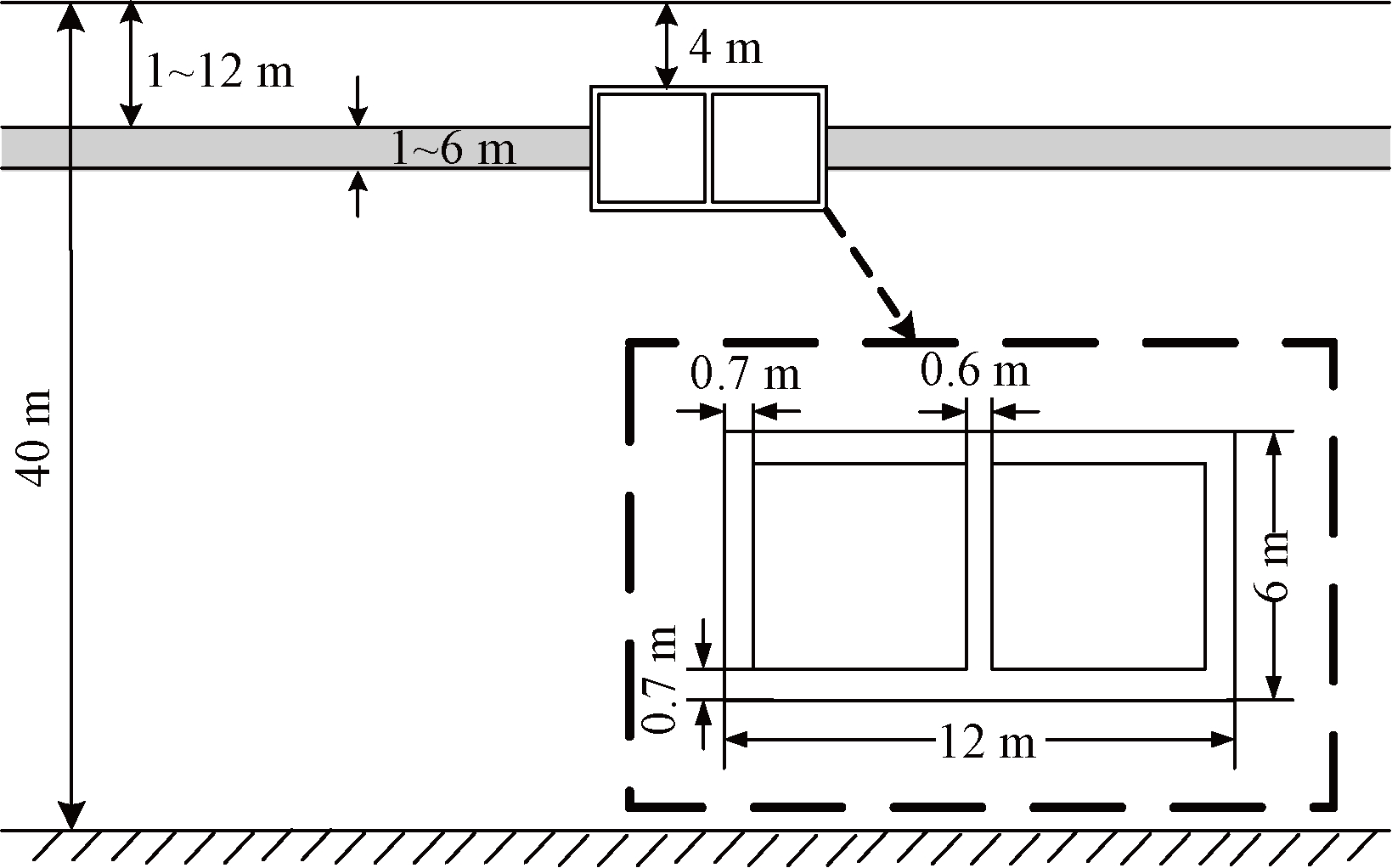
图2 土-地下结构分析模型简图
Figure 2 Schematic diagram of soil-underground structure analysis model
为反映软弱夹层位置变化对地下结构地震响应影响,设计了夹层与地下结构相对位置不同的5种工况,并设置一个无软弱夹层工况作为基准工况进行对比。为反映软弱夹层厚度变化对地下结构地震响应影响,假定软弱夹层位于结构中部时,夹层厚度由1 m递增至6 m的6种工况。各工况参数如表2所示。
表2 各工况参数表
Table 2 List of operating conditions
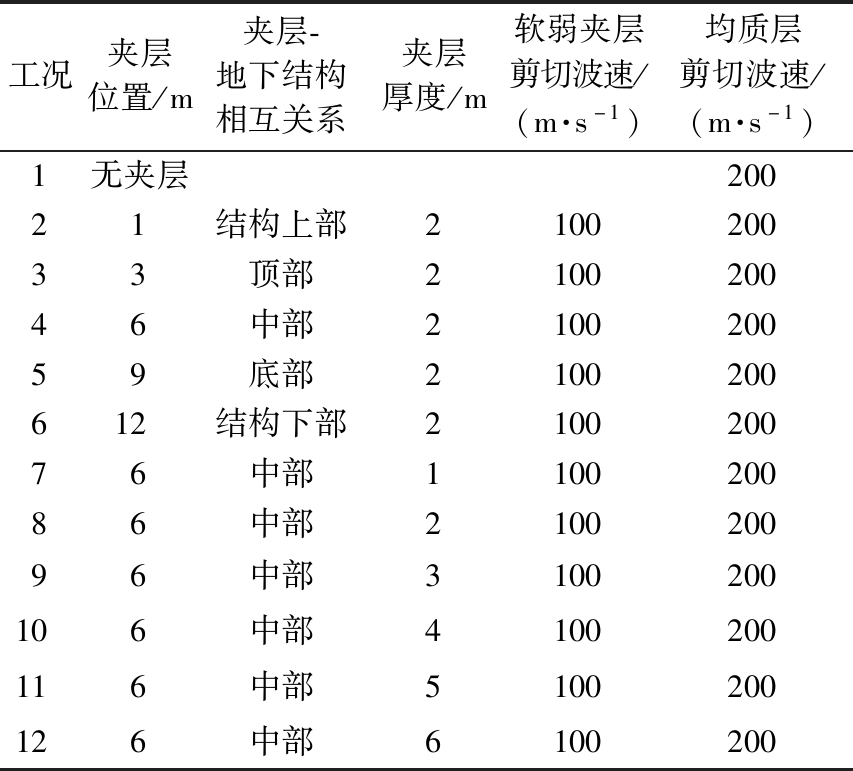
工况夹层位置/m夹层-地下结构相互关系夹层厚度/m软弱夹层剪切波速/(m·s-1)均质层剪切波速/(m·s-1)1无夹层20021结构上部210020033顶部210020046中部210020059底部2100200612结构下部210020076中部110020086中部210020096中部3100200106中部4100200116中部5100200126中部6100200
不同场地条件下的场地1、2阶自振频率如表3所示。由表3可知,随着软弱夹层位置加深,场地自振频率逐渐减小;随着软弱夹层厚度增大,场地自振频率逐渐减小。此现象表明软弱夹层的存在有助于减弱场地自振频率。
表3 场地自振频率表
Table 3 The natural vibration of field

场地自振频率工况1工况2工况3工况4工况5工况6工况7工况8工况9工况10工况11工况121阶频率1.021.031.021.021.000.971.011.021.001.001.000.992阶频率3.213.193.092.822.582.493.022.822.642.482.342.23
2.2 模型建立
本文运用通用有限元软件ABAQUS建立土-地下结构二维模型进行整体动力时程分析,其中土体采用4节点平面应变单元,车站结构(包括梁、板、柱)采用梁单元,并在出平面方向结构尺寸设为1,平面内方向取各部件真实尺寸。模型采用自由场反应的振动输入方法进行地震动输入,整体采用线弹性本构模型,外部荷载仅考虑水平地震作用,不考虑重力(若考虑重力仅需进行线弹性范围内的叠加计算,此时结构中柱轴压比为0)。梁单元与平面单元采用绑定连接,即梁单元与平面应变单元在相同位置处的节点运动完全一致,本文暂未考虑两者间的相对滑移。
车站中柱截面尺寸为0.6 m×1 m,柱间距为5 m。由于本文建立的是二维模型,车站结构采用梁单元建模,且各构件的出平面方向均设置为单位长度,因此,需先将中柱等效为纵向连续的一面纵墙,后取单位长度进行建模分析。在此过程中,考虑到中柱等效前后截面抗弯、抗剪、抗压刚度及截面质量均应不变,需将中柱弹性模量及密度折减为原模量和密度的1/5[11]。结构原顶底板、侧墙弹性模量为30 GPa,密度为2 500 kg/m3。等效后中柱弹性模量为6 GPa,密度为500 kg/m3。
由于地下结构处于半无限性质的土体之中,无法对全部土体进行建模计算,通常仅取结构周围部分土体作为研究对象,设置人工边界,以此来模拟半无限土体。根据楼梦麟等[12]的研究成果,当土体结构有限元模型宽度是结构宽度的5倍及以上时,基本可以忽略两侧人工边界对结构动力反应的影响。故本文建模宽度取5倍结构宽度60 m,计算深度由地表直至基岩,共计40 m,模型底部采用固定约束,侧边人工边界采用捆绑边界。捆绑边界是利用ABAQUS中的MPC节点自由度耦合约束功能,将土体有限元模型同高度处的边界节点捆绑在一起作一致运动,该边界条件能够模拟自由场运动,不考虑能量逸散效应[13]。李洋[13]的研究结果表明,采用捆绑边界的自由场模型能够在保证较高计算效率的前提下获得精确的自由场反应。
单元网格尺寸的大小和形状对结构动力分析的模拟计算结果的精确度和收敛性有十分重要的影响,本文采用密集网格对整体模型进行划分。车站结构统一按0.5 m宽度进行划分,确保结构受力计算的精度。土体模型采用2种划分方式:在3倍车站宽度范围内的土体,按0.5 m×0.5 m的网格尺寸进行划分;3倍车站宽度范围外的土体,网格高度取0.5 m,网格宽度由0.5 m逐步递增至2 m,递增划分法能够在保证计算精度的前提下减少计算量。具体网格划分如图3所示。
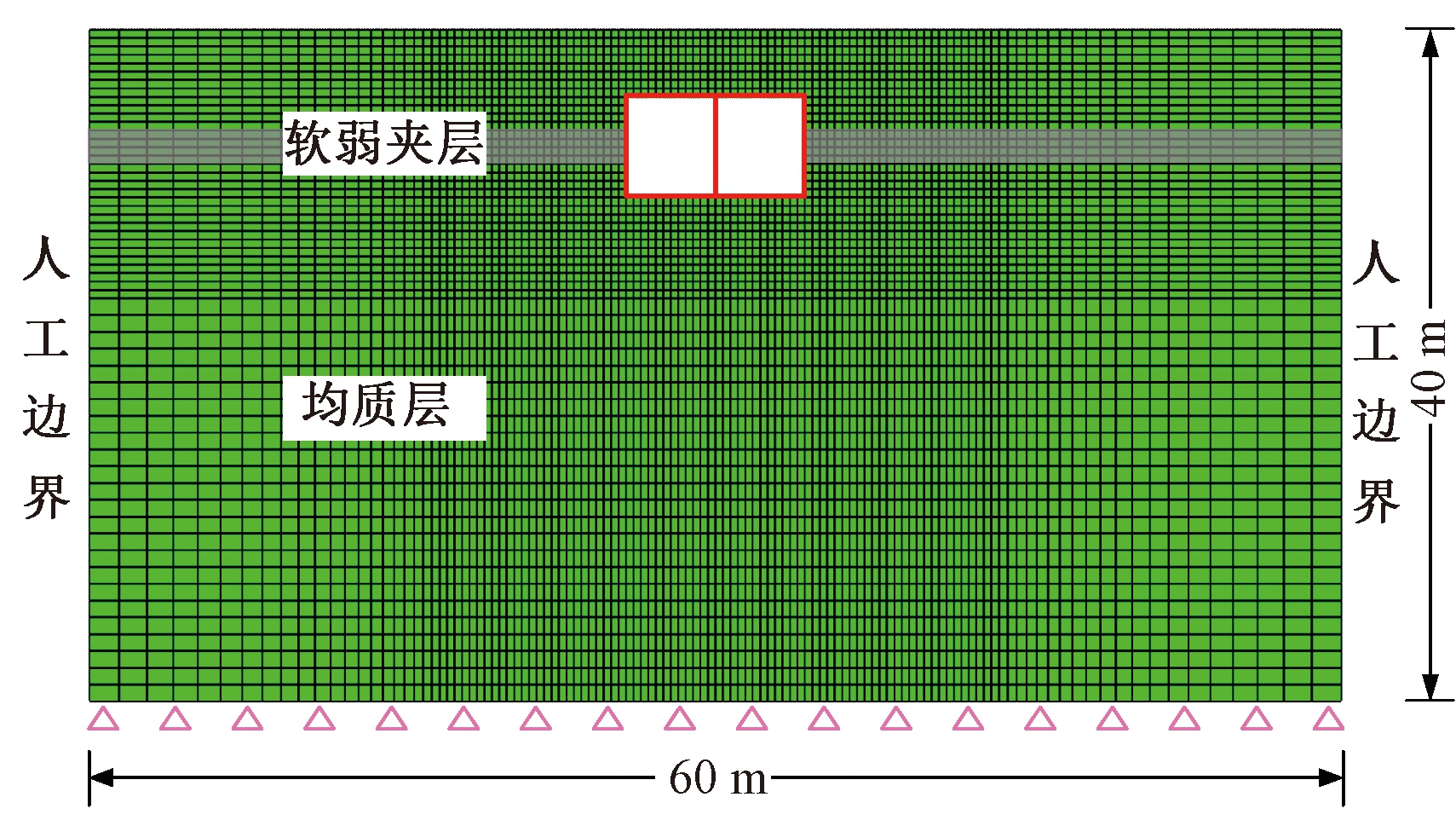
图3 有限元分析模型
Figure 3 Finite element model of metro station
2.3 地震波输入
假定基岩输入地震波为竖直向上传播,入射地震波振动平面与地铁车站横断面重合。为避免单一频谱特性地震波造成计算结果的特殊性,本文选择了3条频谱特性不同的Chichi波、Duzce波和Manjil波分别进行建模计算,峰值加速度均为0.1g。加速度时程与频谱曲线如图4所示。
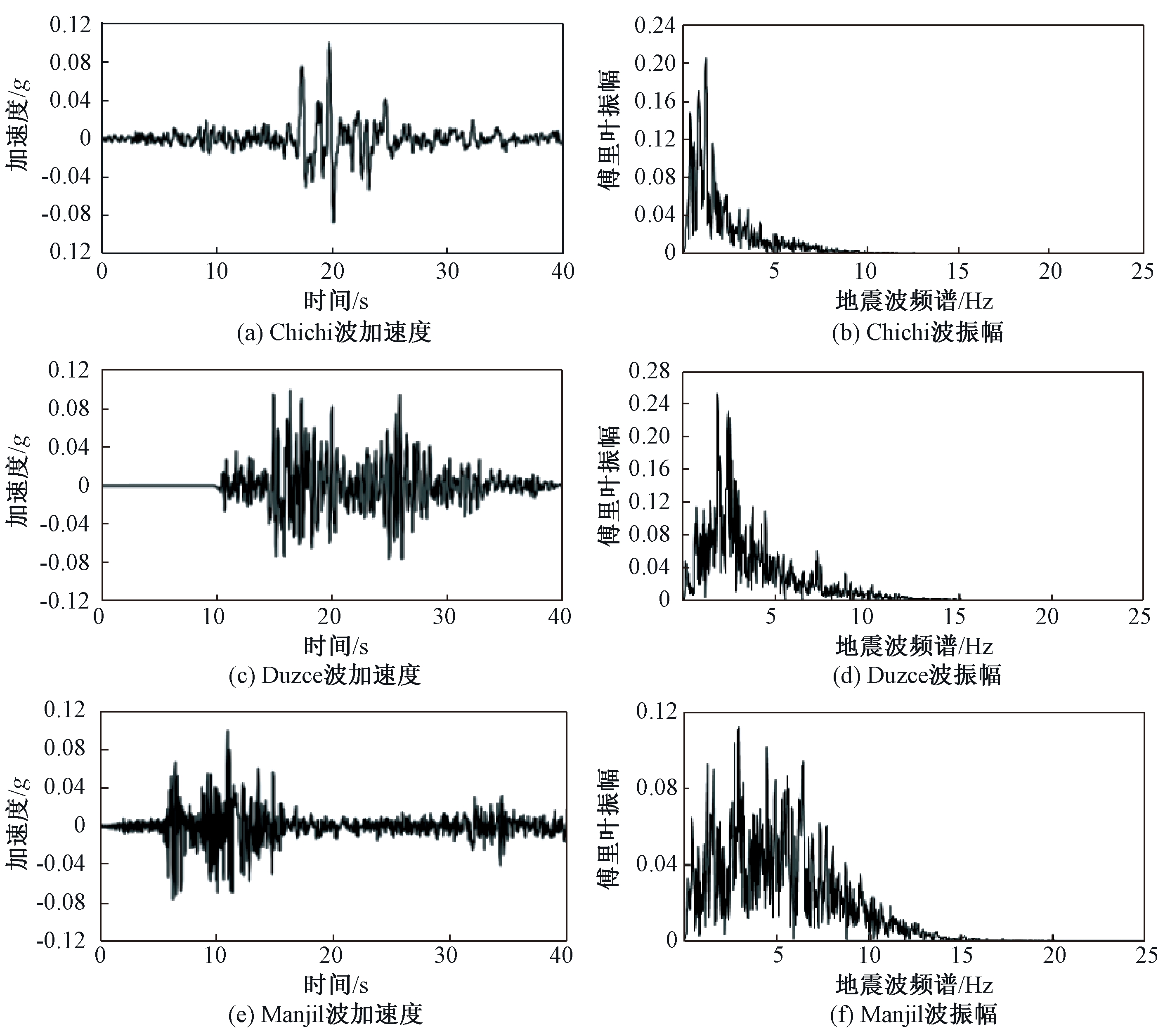
图4 地震波加速度时程与频谱
Figure 4 Acceleration time history curves and frequency spectrum
3 软弱夹层的影响
3.1 软弱夹层位置对地下结构地震响应的影响
假定软弱夹层厚2 m,当夹层距地表1、3、6、9、12 m时,软弱夹层分别位于车站结构的上部、顶部、中部、底部、下部,通过对5种工况进行建模计算,探究夹层位于车站不同位置时,结构内力及顶底相对位移的变化规律。同时设1个无夹层工况作为基准工况,用来对比分析有无软弱夹层对地下结构造成的影响。
真实震害表明,中柱作为地铁车站支撑结构的重要组成部分,由于其横截面及抗侧刚度远小于侧墙,在水平地震作用下,常先于结构侧墙破坏,是抗震分析中的关键构件。故本文选取具有代表性的地下结构顶底相对位移及中柱弯矩作为判断指标,分析软弱夹层对地下结构地震响应的影响。不同工况下地下结构顶底相对位移见图5。
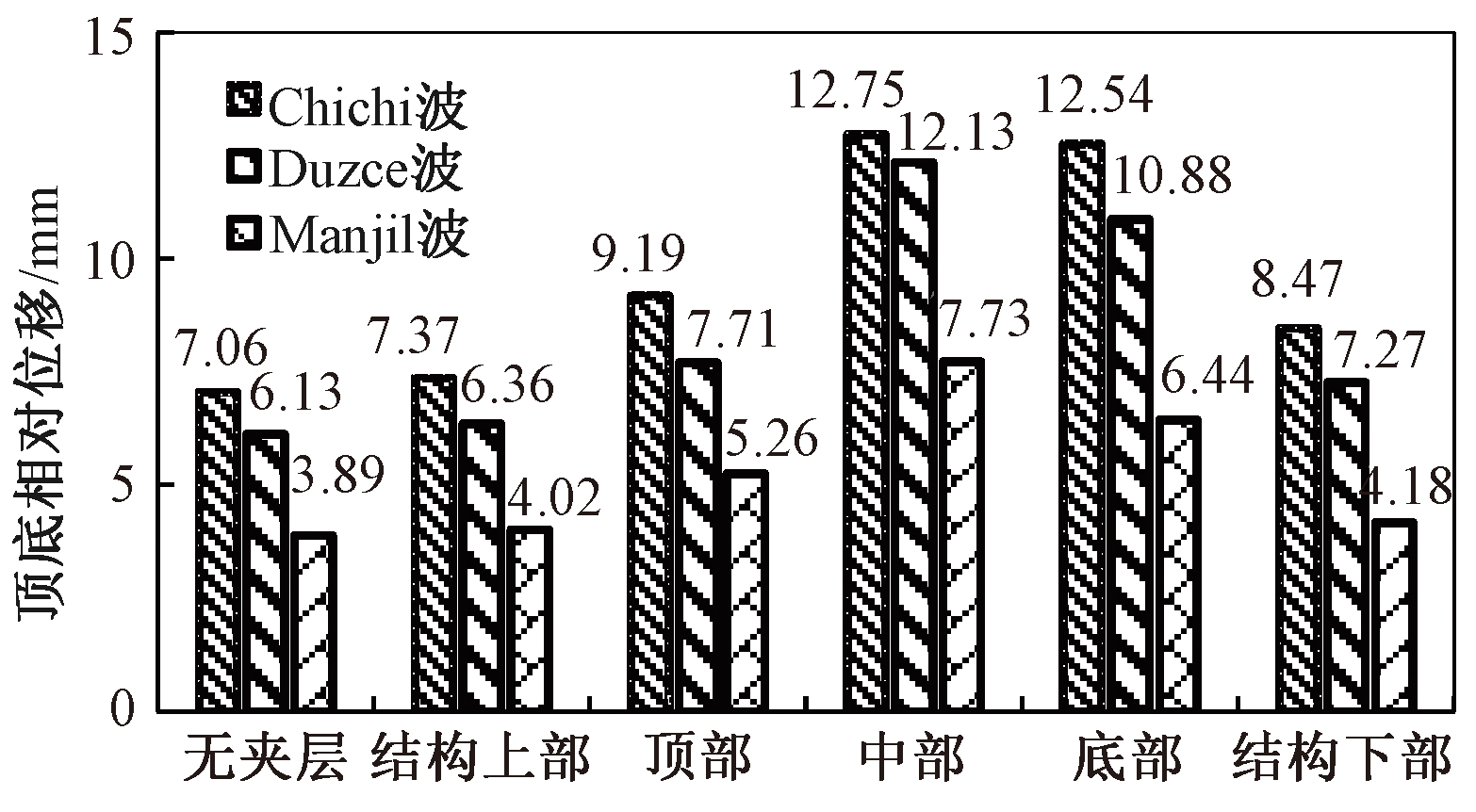
图5 不同位置时地下结构顶底相对位移
Figure 5 Relative displacement of top and bottom at different positions
由于篇幅所限,此处展示工况1、4在Chichi波作用下中柱底部弯矩及主应力时程曲线,如图6所示,不同工况条件下结构中柱弯矩见图7。
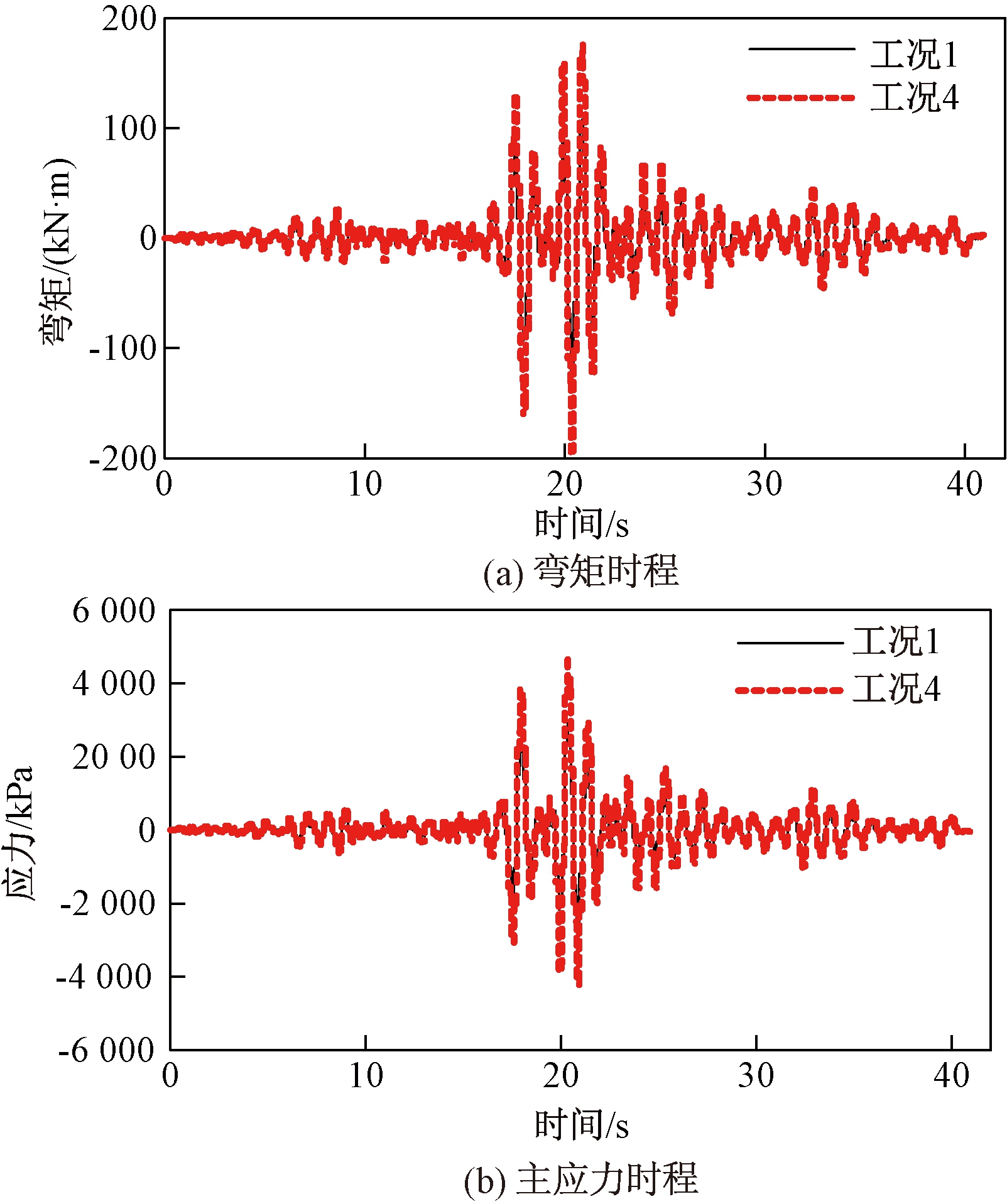
图6 工况1、4下中柱底部弯矩、主应力时程曲线
Figure 6 Time history curves of bending moment and principal stress of the central column in case 1 and 4
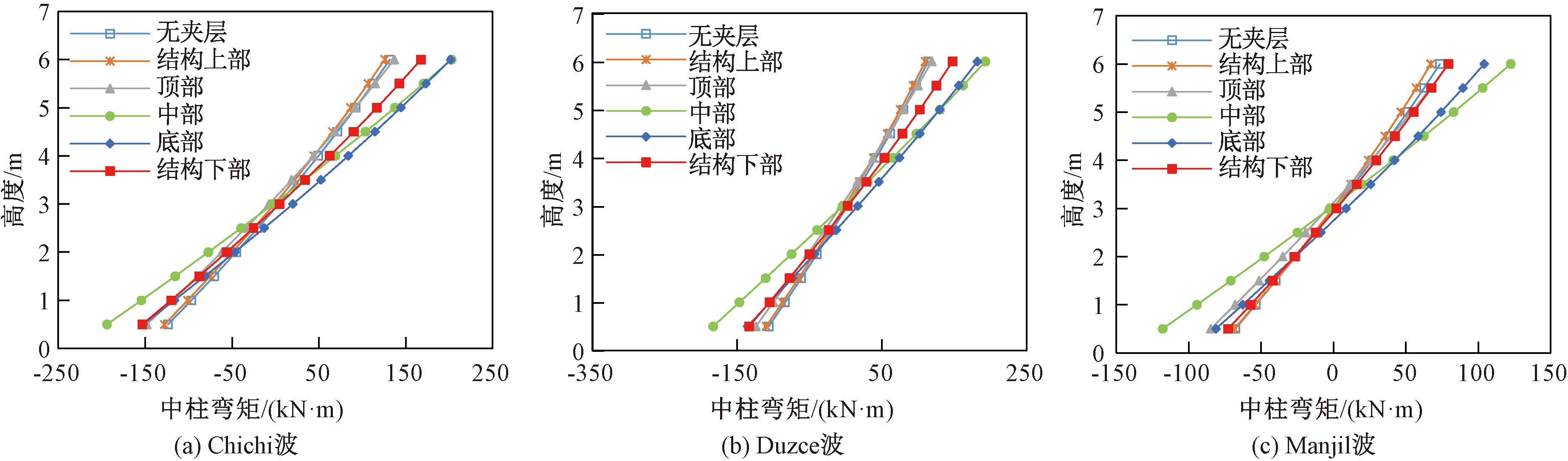
图7 位置不同时各工况下中柱弯矩
Figure 7 Bending moment of central column under different working conditions with different positions
从图5、7可以看出,在3条地震波作用下,无夹层工况较软弱夹层工况顶底相对位移、中柱弯矩均小,表明软弱夹层对地下结构受力存在不利影响。
当软弱夹层位于结构中部时,在不同地震波作用下,结构顶底相对位移分别为12.75、12.13、7.73 mm,约是无夹层工况条件下(7.06、6.13、3.89 mm)的2倍,为最不利工况。夹层位于结构中部时,在3条地震波作用下层间位移角分别为1/475、1/495、1/776,均满足GB 50909—2014《城市轨道交通结构抗震设计规范》[14]中层间位移角小于1/250的要求。由于在同一地震波作用下,软弱夹层相对于同厚度的均质土层更易发生变形,且因土与地下结构间的相互作用,当软土层位于结构中部时,软土层在地震作用下产生的较大变形会完全施加在地下结构之上,对地下结构产生不利影响。
当软弱夹层位于地下结构中部时,地震作用对地下结构的影响最大;当软弱夹层位于地下结构底部时,影响较大;当软弱夹层位于地下结构上部、下部及地下结构顶部时,3种情况对地下结构的影响均较小,与无夹层工况的影响接近,可近似忽略。软弱夹层的存在将场地土分隔为上、下两部分,当软弱夹层位于地下结构上部(或地下结构下部)时,地下结构整体处于场地下部分(或上部分),不与软土夹层相接触。在地震作用下,软土夹层产生的较大形变不直接施加在结构上,对地下结构受力影响较小,可忽略。当软弱夹层处于地下结构顶部、底部时,此时软弱夹层仅一半厚度与地下结构相接触,地震作用下软弱夹层产生的较大变形不完全施加在地下结构上,故地下结构所受不利影响小于夹层处于地下结构中部时的情况。
3.2 软弱夹层厚度对地下结构地震响应的影响
假定软弱夹层位于地下结构中部,当夹层厚度由1 m逐渐递增至6 m时,在3条不同频谱特性地震动的作用下,通过对6种工况的建模计算及数据分析,分析地下结构内力及地下结构顶底相对位移在软弱夹层厚度改变时的变化规律。不同工况下结构顶底相对位移、中柱弯矩分别如图8、9所示。
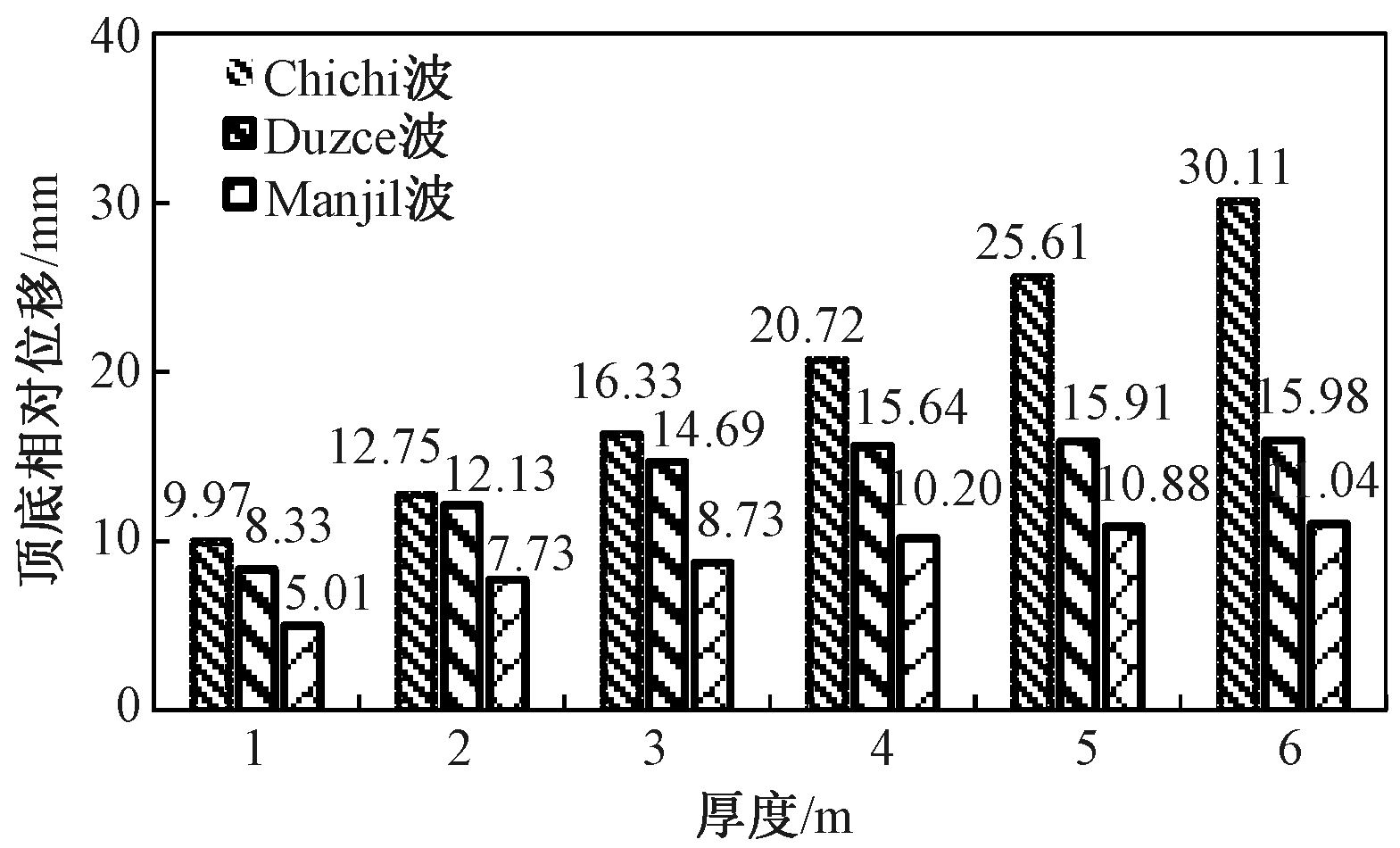
图8 不同厚度时地下结构顶底相对位移
Figure 8 Relative displacement of top and bottom with different thickness
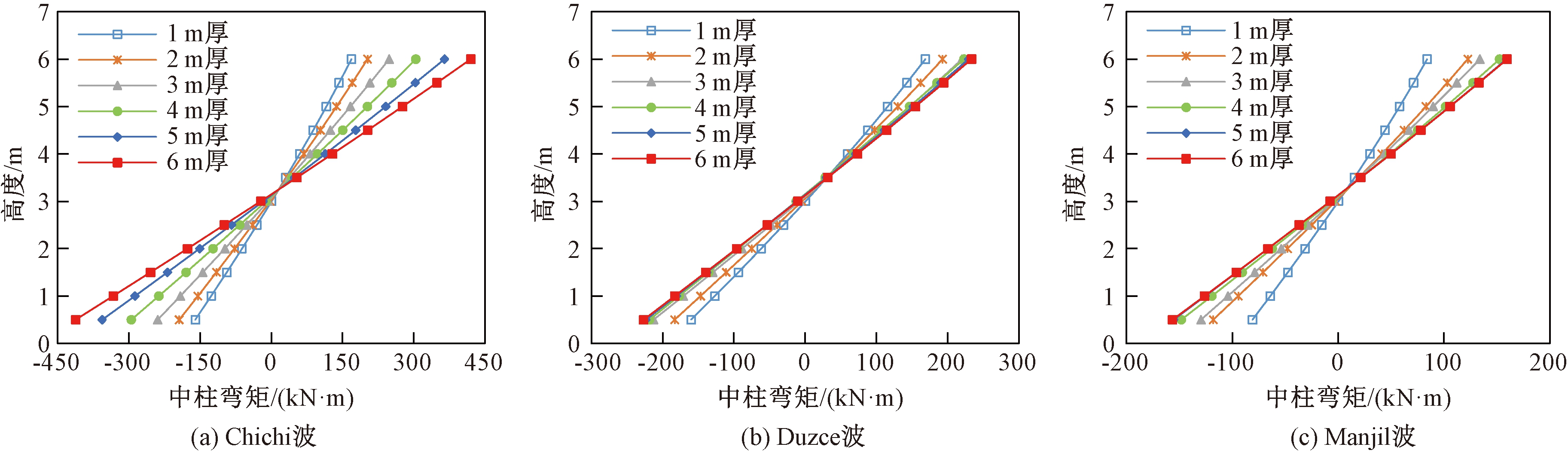
图9 厚度不同时各工况下中柱弯矩
Figure 9 Bending moment of central column under different working conditions with different thickness
从计算结果可以看出:①在不同地震波作用下,随着软弱夹层厚度不断增加,结构顶底相对位移、中柱弯矩也随之不断增大。因为在夹层厚度增加,夹层弹性模量近似不变的情况下,地震作用会使软弱夹层顶底相对位移增大,且因土-地下结构为一个整体,具有协同作用,结构变形也会随之增大。②随着软弱夹层厚度的不断增加,夹层厚度对结构顶底相对位移的影响程度逐渐减弱。
4 结论
(1)软弱夹层位于地下结构中部时最为不利,此时地下结构顶底侧向位移约为无夹层情况下的2倍;软弱夹层位于结构底部时较为不利;夹层位于结构上部、下部及顶部时,3种情况对地下结构的影响均较小,与无夹层的情况相接近,可近似忽略。
(2)随着软弱夹层厚度不断增加,地下结构顶底相对位移、中柱弯矩及剪力也随之增大,呈正相关。但随着厚度不断增加,厚度对地下结构动力响应的影响程度逐渐减弱。
软弱夹层对地下结构动力响应的影响是复杂的、多方面的,本文仅考虑了夹层位置、厚度两种因素对地下结构动力响应产生的影响,其他因素的影响有待进一步研究论证。
[1] 陈国兴,陈苏,杜修力,等.城市地下结构抗震研究进展[J].防灾减灾工程学报,2016,36(1):1-23.
[2] 孙超,薄景山,齐文浩,等.地下结构抗震研究现状及展望[J].世界地震工程,2009,25(2):94-99.
[3] 周奎,潘梦阳,林杰.一种新型组合框架滞回性能及地震反应分析[J].郑州大学学报(工学版),2015,36(5):63-67.
[4] 黄润秋,余嘉顺.软弱夹层特性对地震波强度影响的模拟研究[J].工程地质学报,2003,11(3):312-317.
[5] 陈国兴,陈继华.软弱土层的厚度及埋深对深厚软弱场地地震效应的影响[J].世界地震工程,2004,20(3):66-73.
[6] 王子辉.饱和两相与单相土互层场地中地铁车站地震反应分析[D].北京:北京交通大学,2008.
[7] 杜修力,许紫刚,许成顺,等.基于等效线性化的土-地下结构整体动力时程分析方法研究[J].岩土工程学报,2018,40(12):2155-2163.
[8] BARDET J P,ICHII K,LIN C H.EERA:a computer program for equivalent-linear earthquake site response analyses of layered soil deposits[EB/OL].(2020-08-20)[2020-10-12].http://www.ce.memphis.edu/7137/PDFs/EERA2/EERAManual.pdf.
[9] I.M IDRISS,JOSEPH I.SUN.User′s manual for shake91:a computer program for conducting equivalent linear seismic response analyses of horizontally layered soil deposits[EB/OL].(1992-08-15)[2020-10-12].https://max.book118.com/html/2018/0430/163852466.shtm.
[10] 庄海洋.土-地下结构非线性动力相互作用及其大型振动台试验研究[D].南京:南京工业大学,2006.
[11] XU Z G,DU X L,XU C S,et al.Simplified equivalent static methods for seismic analysis of shallow buried rectangular underground structures[J].Soil dynamics and earthquake engineering,2019,121:1-11.
[12] 楼梦麟,王文剑,朱彤,等.土-结构体系振动台模型试验中土层边界影响问题[J].地震工程与工程振动,2000,20(4):30-36.
[13] 李洋.浅埋地下框架结构地震破坏机理研究[D].北京:北京工业大学,2018.
[14] 中华人民共和国住房和城乡建设部.城市轨道交通结构抗震设计规范:GB 50909—2014[S].北京:中国标准出版社,2014.