0 引言
建筑物在全寿命周期服役期间,可能遭受各种意外荷载(火灾、爆炸、撞击等),引起竖向承重构件失效,导致发生与初始破坏不成比例的大规模破坏,造成严重人员伤亡和经济损失。近些年,国内外学者主要采用抽柱法[1-2]、数值模拟[3-4]和理论分析[5-6]等方法展开建筑结构的抗连续倒塌试验研究。研究对象主要以RC结构和钢结构为主,主要分析失效柱上部梁构件的破坏机理,将提高梁构件的梁机制和悬链线机制承载力作为主要设防目标,而关于非结构构件对结构的抗倒塌影响研究相对较少,如填充墙和柱间支撑等。
填充墙作为一种非结构构件,对建筑物起到分隔和围护的作用。已有研究结果表明:建筑结构在抗连续倒塌中填充墙与框架之间存在着相互作用的关系[7]。Li等[8]进行了RC裸框架和填充墙框架的倒塌试验,结果表明:填充墙能有效提高框架的初始刚度和抵抗能力,但降低了框架的延性。Qian等[9]进行了RC框架的抗连续倒塌试验,若忽略填充墙的影响,将会导致框架的强度、刚度和破坏模式预测的严重误差。喻君等[10]使用OpenSEES软件建立了填充墙的等效宏观斜撑模型,得出全填充墙框架的荷载主要通过填充墙对角传递,且填充墙与周围框架形成桁架机制。Eren等[11]研究了RC框架抗连续倒塌中填充墙对框架损伤程度的影响,提出了一种填充墙宏观模拟方法。Xavier等[12]进行了带填充墙的钢框架的准静态倒塌试验,得出填充墙与钢框架发生不协调的破坏的结论。Shan等[13]分析了填充墙对钢结构抗连续倒塌机理的影响,结果表明:填充墙能显著提高钢框架的抗力和初始刚度,但降低了框架的延性,改变了框架的破坏模式。
现有关于填充墙对框架结构的倒塌影响分析主要以RC结构为主,考虑填充墙影响的钢管混凝土框架抗连续倒塌研究鲜有报道。因此,本文对钢管混凝土框架-全填充墙结构中柱失效工况下的抗连续倒塌机理展开研究,通过计算抗倒塌承载力、破坏模式和应力变化规律来分析填充墙在抗连续倒塌过程中对钢管混凝土组合框架的影响机理,为该类结构的抗连续倒塌设计提供参考。
1 有限元模型
1.1 计算模型的选取
使用PKPM软件设计了一栋15层钢管混凝土组合框架,选取2层2跨平面框架作为研究对象。平面框架位置选取如图1所示,对全尺度框架进行1/4比例缩尺,钢管截面尺寸为150 mm×3 mm,核心混凝土截面尺寸为144 mm×144 mm,钢梁截面尺寸为150 mm×75 mm×4 mm×6 mm,边柱高为2 130 mm,失效柱高为1 550 mm,楼板宽度为630 mm,厚度为60 mm,栓钉尺寸为M13×40,填充墙的砌块尺寸分别为150 mm×75 mm×75 mm和75 mm×75 mm×75 mm。根据GB 50936—2014《钢管混凝土结构技术规范》[14]设计外环板。全填充墙框架的设计细节如图2所示。
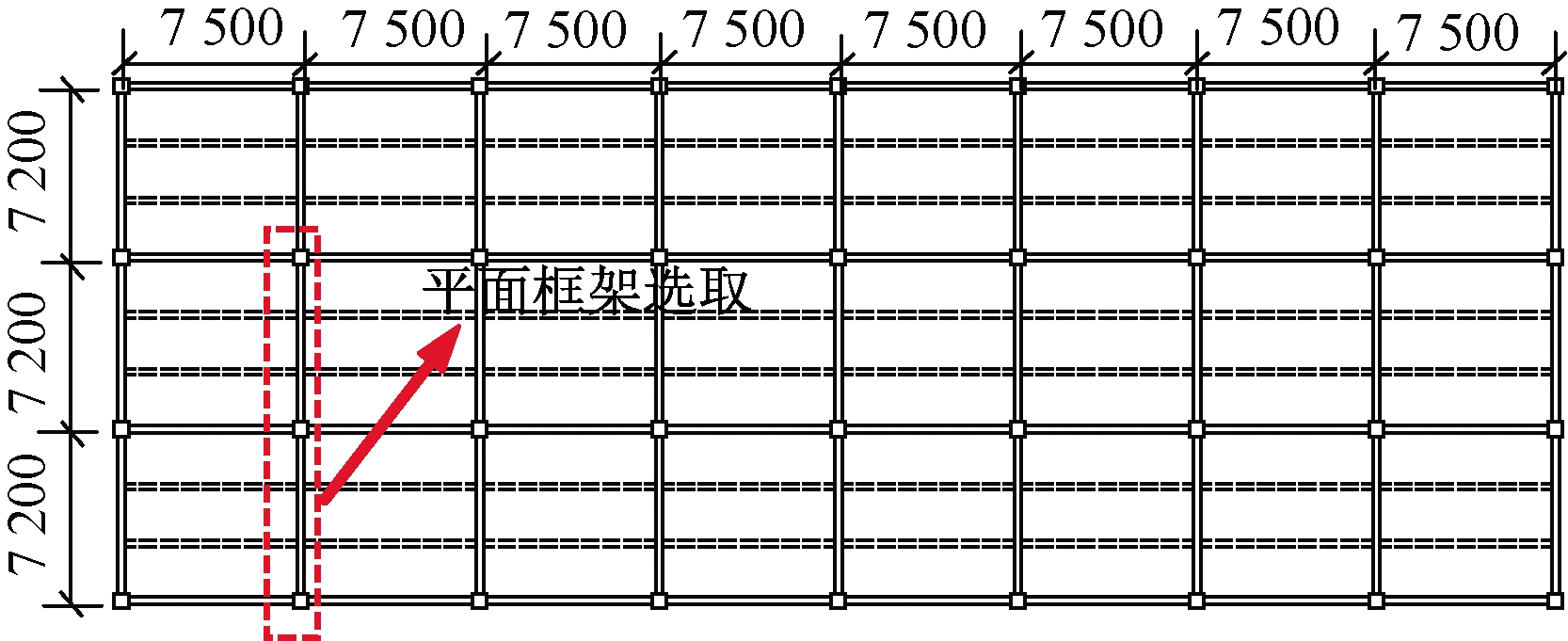
图1 平面框架位置选取(mm)
Figure 1 Plane layout of frame(mm)
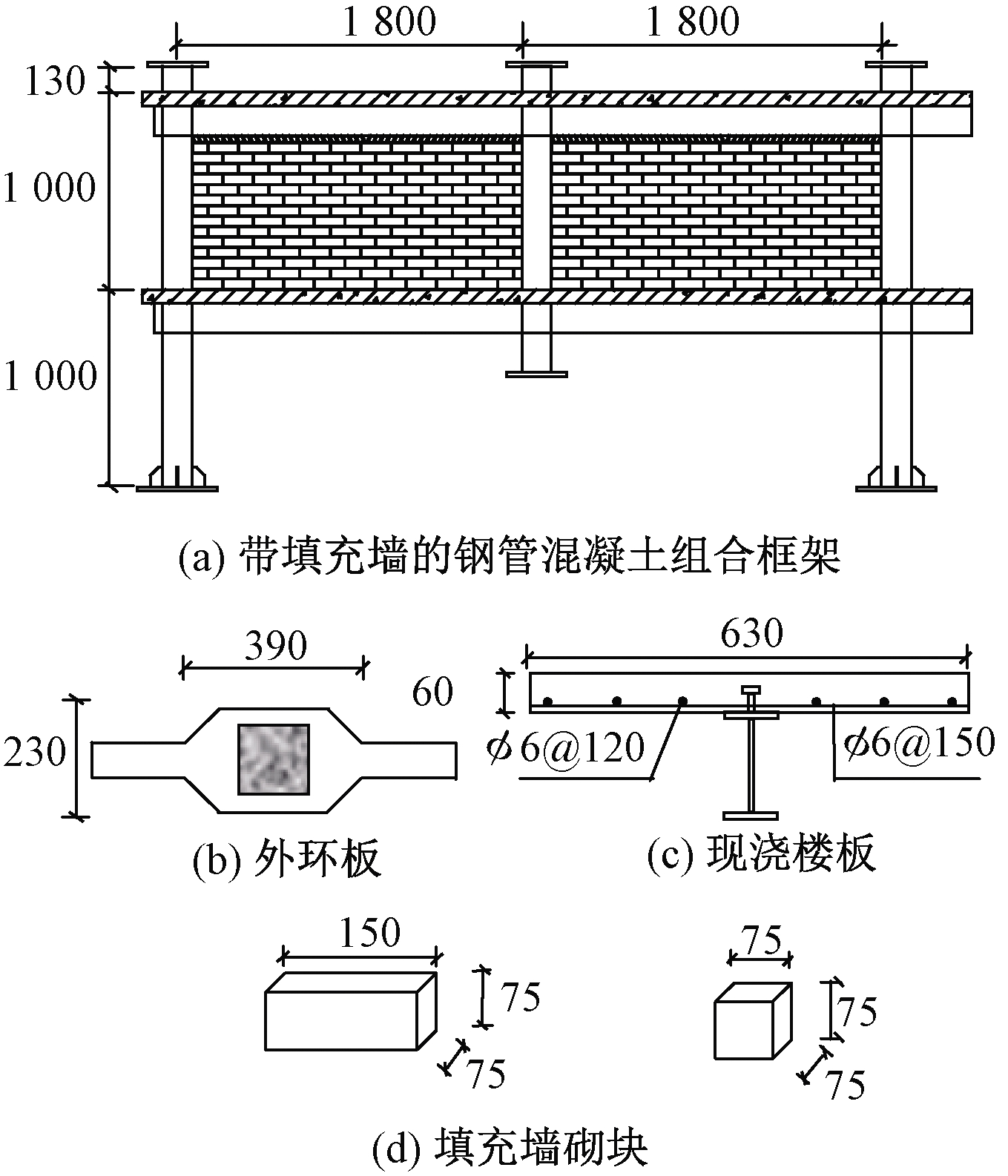
图2 全填充墙框架设计(mm)
Figure 2 Design of frame with solid infill walls specimen(mm)
1.2 建模方法
采用ABAQUS/Explicit对试件进行模拟,模型中钢筋采用桁架单元,其余部件均采用实体单元。砌块采用实体单元建模,不同砌块之间插入0厚度的内聚力单元(cohesive element),以模拟实际工程中砌块之间的砂浆作用。钢管与核心混凝土之间采用面-面接触(surface to surface),设置切向摩擦系数为0.25,法向接触为硬接触;环板与钢管壁接触的局部区域、环板与H型钢梁之间、钢管混凝土柱的上下两端和加载板之间均采用Tie接触;栓钉布置于钢梁上,通过Tie绑定连接;栓钉和钢筋网内置于楼板的混凝土中;填充墙与框架采用面-面接触;另外设置通用接触,自动识别钢管混凝土组合框架中除设置接触关系之外相互接触的区域。
1.3 网格划分和边界条件
实体单元采用8节点六面体线性缩减积分单元C3D8R,钢筋采用2节点桁架单元T3D2,内聚力单元采用8节点三维内聚力单元COH3D8。梁端的边界条件为一侧自由,另一侧梁端边界考虑周围未失效构件的水平连续拉结作用。失效柱顶部采用位移控制加载,根据GSA(2016)[15]的倒塌失效判定准则,钢梁的转角为0.20 rad即认为发生倒塌,所以失效柱向下位移加载为360 mm。边柱底部进行固结,边柱顶部施加柱顶轴力,轴压比为0.3。组合框架有限元模型如图3所示。
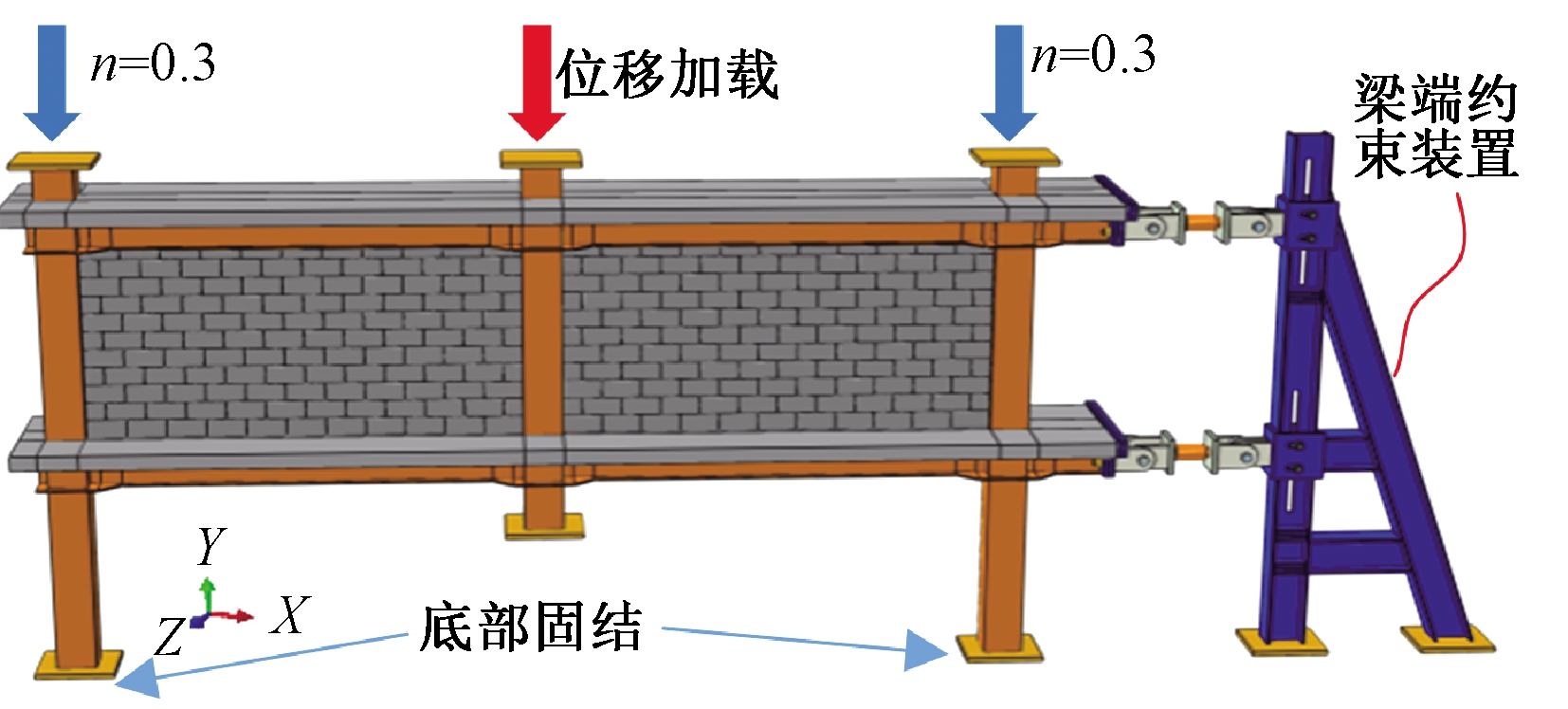
图3 组合框架有限元模型
Figure 3 Finite element model of composite frame
1.4 材料本构关系
钢管柱、钢梁和环板均采用Q235B钢材,屈服强度为235 MPa,弹性模量为206 000 MPa,泊松比为0.3;栓钉为4.8级,弹性模量为206 000 MPa,泊松比为0.3,强度设计值为300 MPa;钢筋采用HPB300钢筋;钢管柱内核心混凝土采用C40,楼板混凝土为C30;砌块采用MU20混凝土砌块,砂浆的抗压强度等级为1.08 MPa。
1.4.1 钢材本构关系
钢材的本构关系采用Esmaeily等[16]提出的考虑下降段的本构模型,可以很好地反映钢材的软化特征。通过定义钢材发生断裂时所对应的应变作为失效依据,失效应变定为0.26,本构关系为:
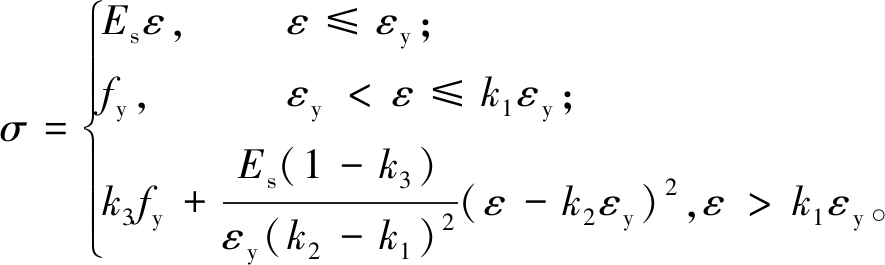
(1)
式中:Es为钢材的弹性模量;εy和fy分别为钢材的屈服应变和屈服强度;k1为钢材强化段起点应变与屈服应变的比值;k2为钢材峰值应变与屈服应变的比值;k3为钢材峰值应力与屈服强度的比值。钢材材性的应力-应变关系曲线如图4所示。
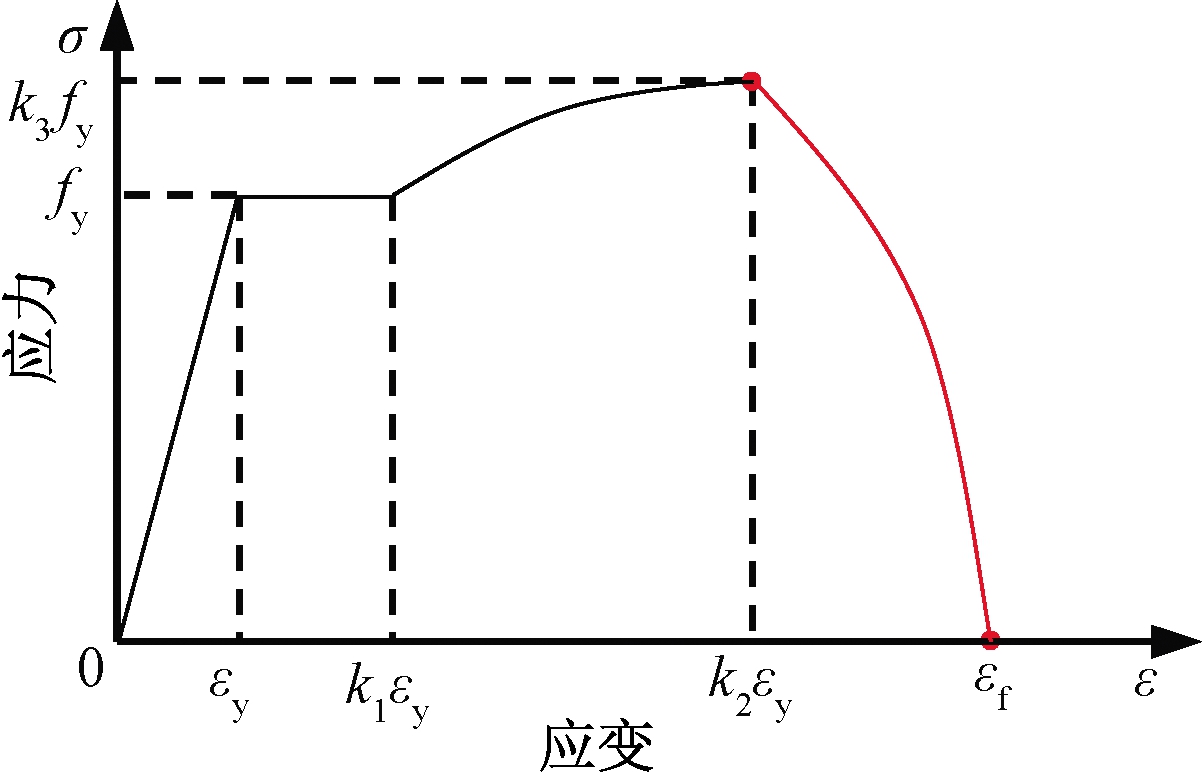
图4 钢材材性的应力-应变曲线
Figure 4 Stress-strain curve of steel
1.4.2 钢筋和栓钉本构模型
钢筋和栓钉采用线性强化模型,应力-应变曲线采用韩林海[17]提出的本构模型,如图5所示。
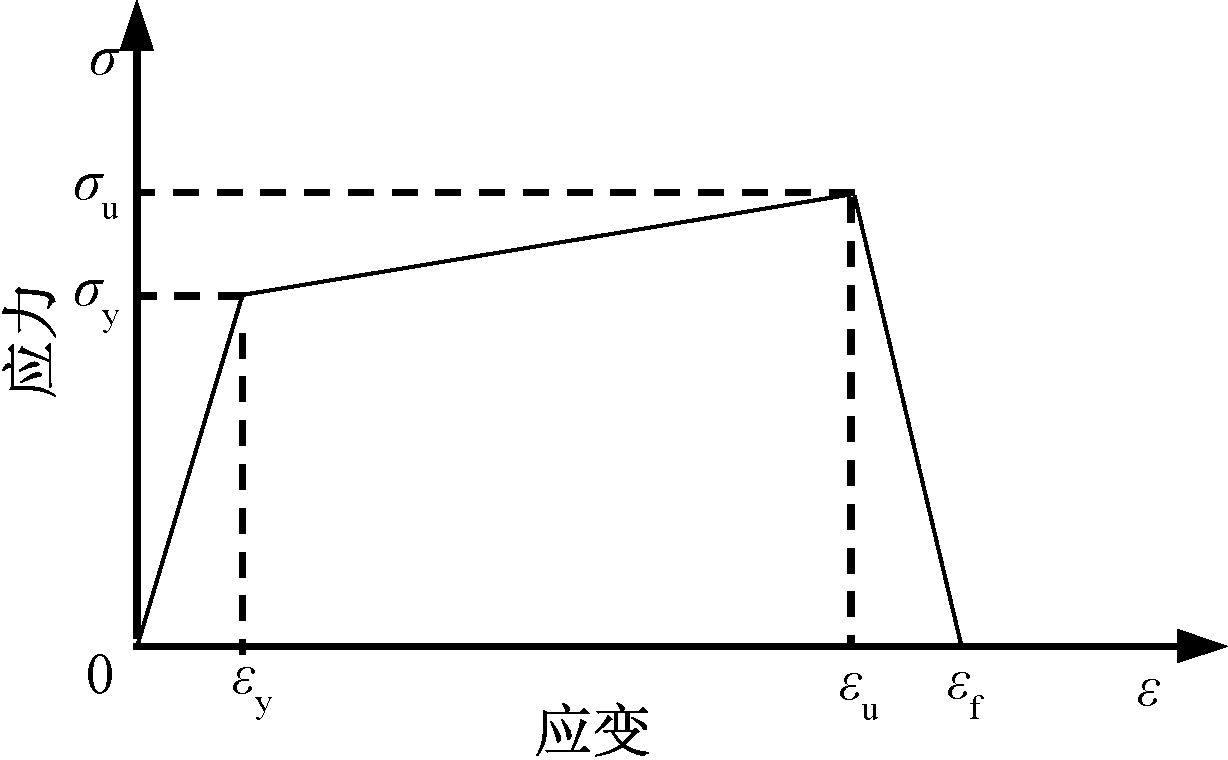
图5 钢筋的应力-应变曲线
Figure 5 Stress-strain curve of rebar
1.4.3 混凝土本构模型
钢管柱内核心混凝土需要考虑钢管对混凝土的约束效应,因此采用韩林海[17]提出的考虑约束作用的本构关系模型,其表达式为:
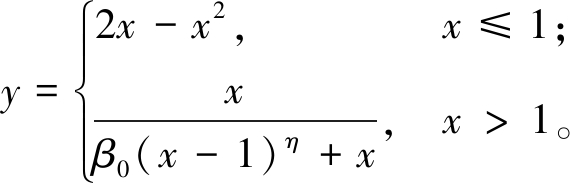
(2)
式中:![]() 为混凝土的应变,ε0为混凝土的峰值应变;
为混凝土的应变,ε0为混凝土的峰值应变;![]() 为混凝土的应力,σ0为混凝土的峰值应力。
为混凝土的应力,σ0为混凝土的峰值应力。
楼板中混凝土采用普通混凝土本构模型,采用GB 50010—2010《混凝土设计规范》[18]给出的应力-应变关系,表达式为:
σ=(1-dc)Ecε。
(3)
式中: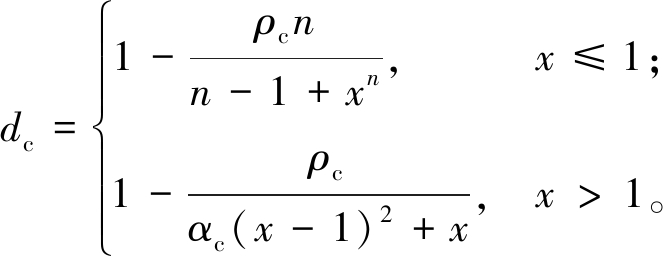
1.4.4 填充墙砌块本构模型
砌块的本构模型采用ABAQUS软件中的混凝土塑性损伤模型。单轴受压砌体本构关系采用文献[19]的表达式:
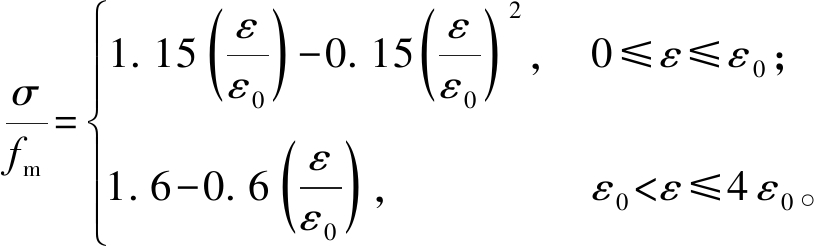
(4)
式中:fm为砌体抗压强度平均值;ε为砌块应变;ε0取0.002;σ为砌块的应力。
1.4.5 牵引-分离本构模型
砂浆内聚力单元(cohesive element)采用文献[20]中的双线性本构模型,该本构模型中应力-应变模型认为这种黏性行为在损伤起始和演化之前,单元初始为线弹性行为,之后产生损伤和演化。如图6所示,纵坐标t为界面上的牵引力,横坐标δ为牵引力对应的相对分离应变,具体参数见文献[20]。
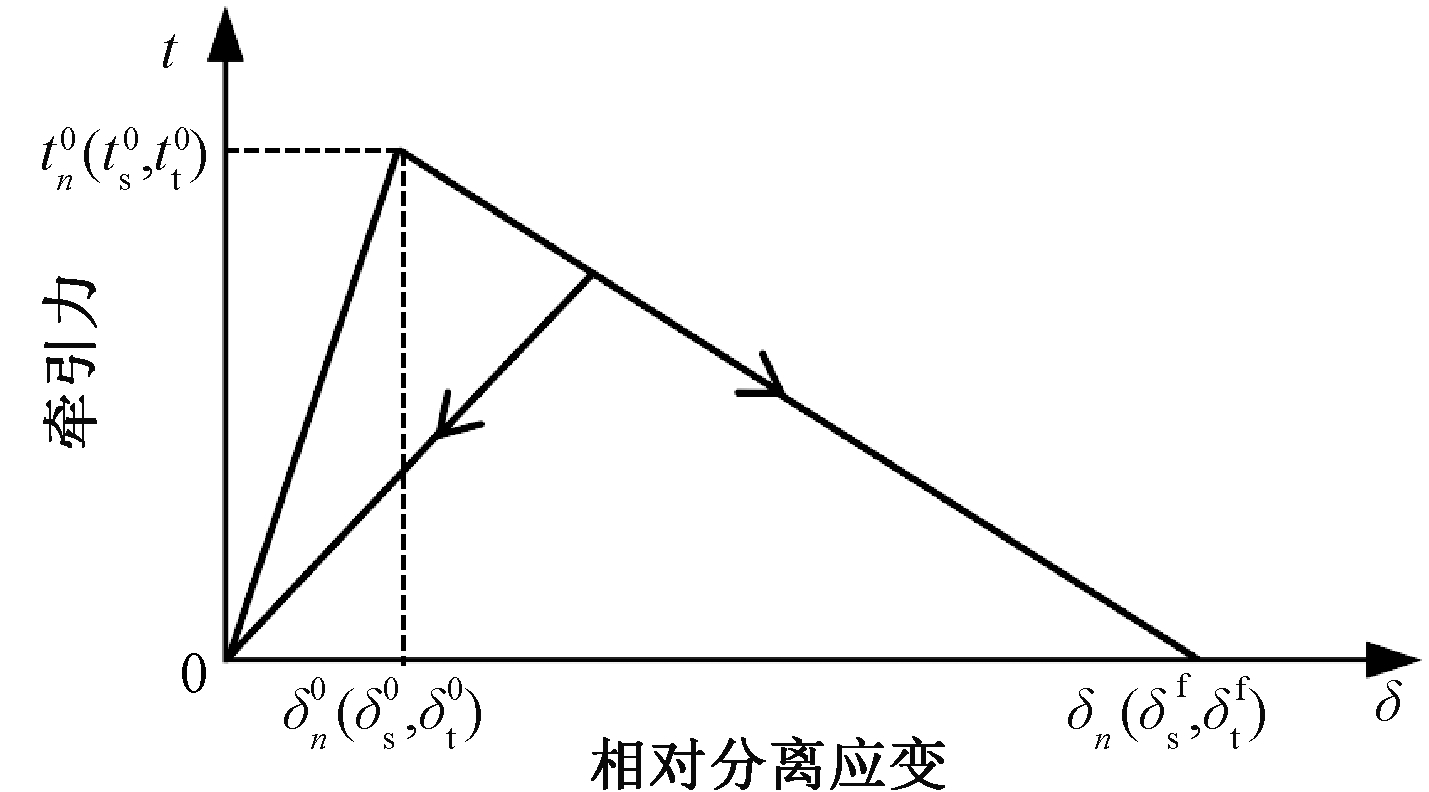
图6 内聚力单元本构关系
Figure 6 Constitutive relationship of cohesive element
2 算例验证
为了验证本文数值模拟方法的合理性,选取文献[8]中关于填充墙对钢筋混凝土框架抗连续倒塌性能的影响模型进行数值模拟验证。模型中1层和2层层高分别为1.4 m和1.1 m,梁的计算跨径为1.7 m,柱截面尺寸为200 mm×200 mm,梁的截面尺寸为100 mm×150 mm。另外模拟一榀除填充墙外其他条件相同的裸框架作为对比试件。详细试件尺寸信息见文献[8]。
图7和图8分别给出了框架的最终破坏形态和荷载-位移曲线。试验和有限元的最终破坏模式基本一致,荷载-位移曲线的峰值和趋势基本一致,裸框架试验曲线的后期出现陡降,之后曲线上升,而本文的数值模拟中并未出现下降段,可能是由于试验中混凝土开裂所致,但曲线基本吻合良好,验证了本文建模方法和材性选取的合理性。

图7 框架破坏对比
Figure 7 Comparisonof frame failure
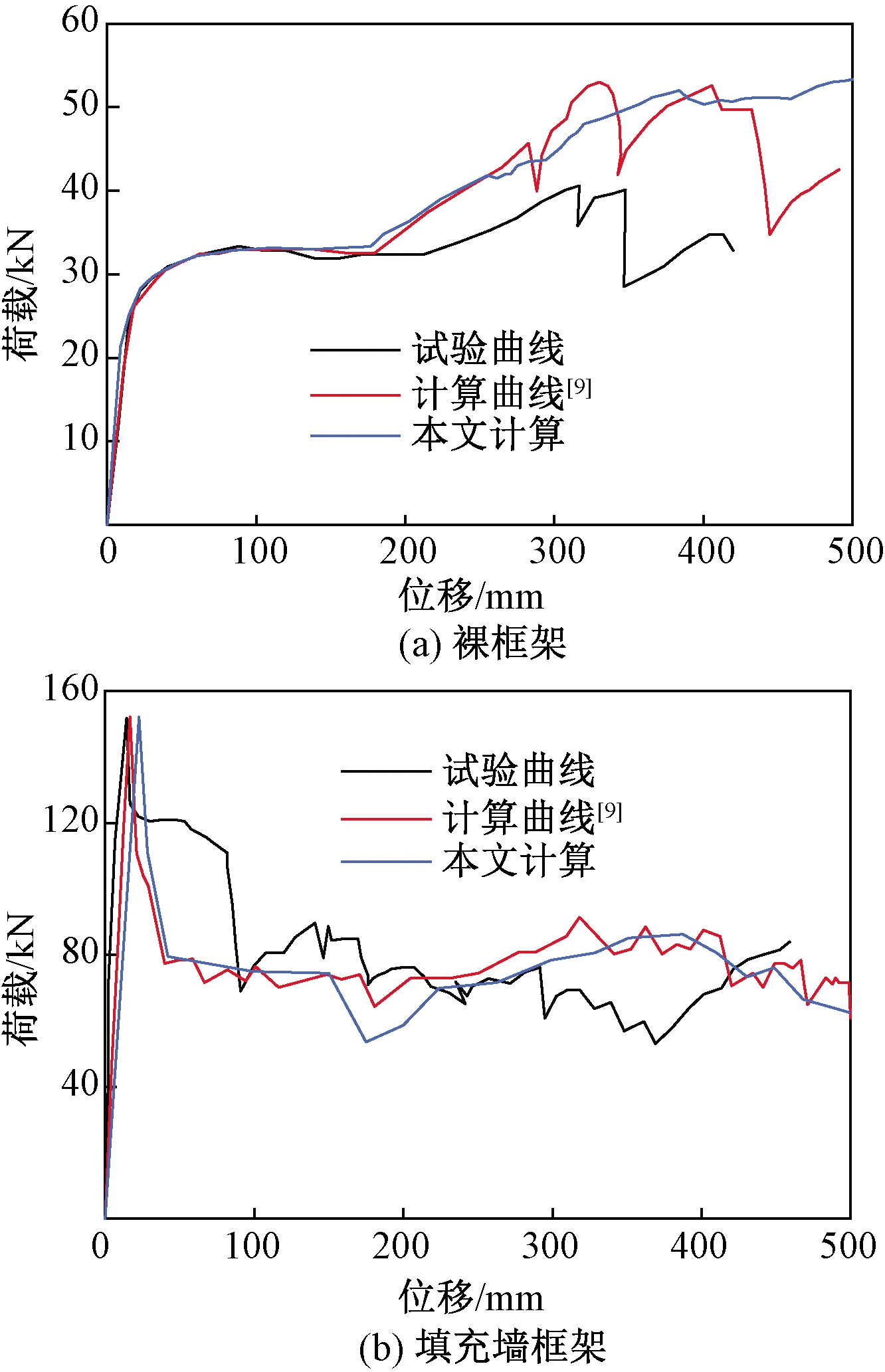
图8 试验曲线和计算曲线对比
Figure 8 Comparing the calculated curve with the test curve

图9 试件的荷载-位移关系曲线
Figure 9 Load-displacement curves of specimens
3 抗连续倒塌机理分析
3.1 失效柱上部荷载-位移关系曲线
全填充墙钢管混凝土组合框架和裸框架试件的荷载-位移曲线如图9所示,其中纵坐标为倒塌承载力,横坐标为失效柱的竖向位移。试件的抗连续倒塌破坏过程分为3个阶段,即梁机制阶段、悬链线机制阶段和破坏阶段。梁机制阶段(OA段,竖向位移为0~80 mm),由于填充墙的影响效应,框架初始刚度增大,承载力明显高于无填充墙框架。在梁机制阶段,裸框架的最大抗力为499 kN,填充墙框架的最大抗力为814.5 kN。此阶段,填充墙的受力主要发生在角部位置,压杆效应开始形成。在悬链线机制阶段(AB段,竖向位移为80~160 mm),承载力开始下降,主要是由于填充墙开始开裂,此阶段框架的承载力主要由组合梁的抗拉能力提供。在破坏阶段(BC段,竖向位移为160~352 mm),该阶段填充墙框架的最大承载力为620 kN,无填充墙框架的承载力为321 kN,相较于梁机制阶段,此阶段填充墙框架与无填充墙框架抗力最大值的比值减小,此阶段填充墙对组合框架在抗连续倒塌中的贡献减小。
3.2 失效模式分析
裸框架和带填充墙框架的最终破坏模态如图10所示。两榀框架的最终破坏模态不同,裸框架的初始破坏位置为失效柱节点核心区域,下翼缘首先出现裂缝,随后钢梁破坏。带填充墙框架中,填充墙的砌块之间发生较大的开裂,且开裂方向沿框架的对角方向,但两跨填充墙的破坏现象有所不同,右跨填充墙的开裂程度较大,主要是由于平面框架左右梁端边界条件不同所致。填充墙开裂后,底层钢梁受力明显开始增大。分析可知,无填充墙作用的裸框架破坏由钢梁裂断直接导致,而带填充墙作用的框架受力初期,填充墙受力明显,延缓了钢梁过早开裂,保护了主要受力构件。
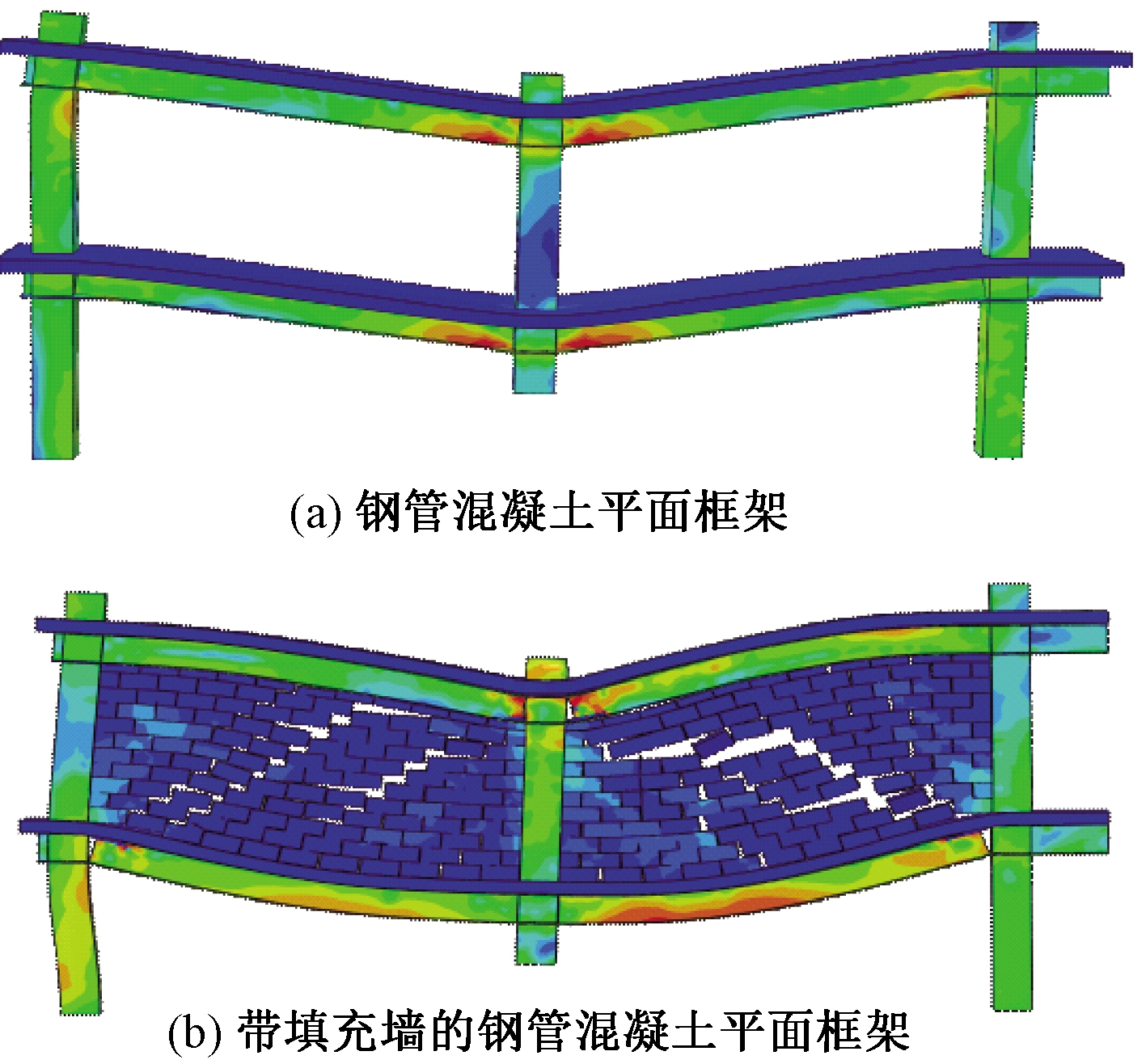
图10 框架的失效模式
Figure 10 Failure mode of frame
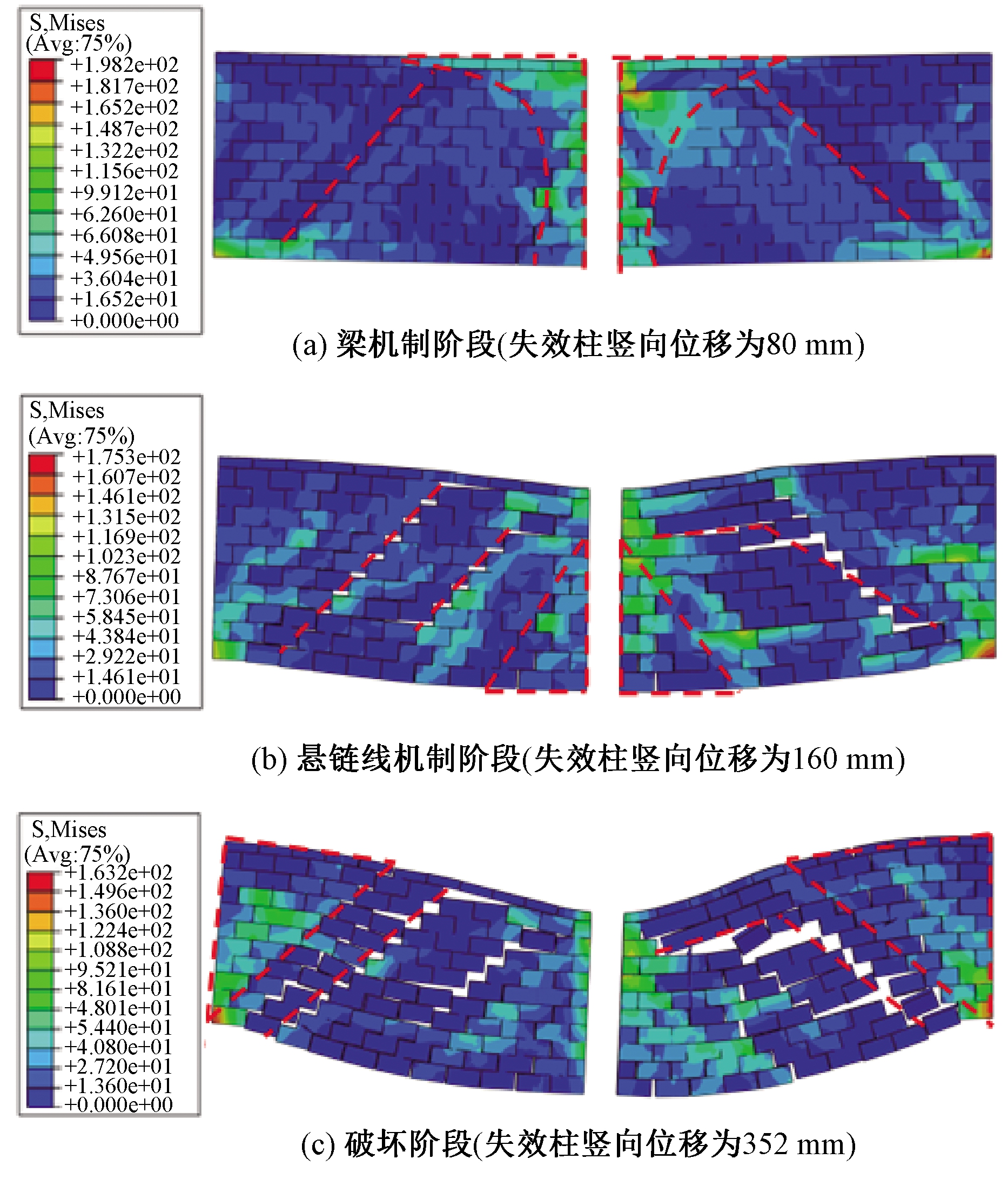
图11 不同阶段填充墙的Mises图
Figure 11 Mises diagram of in-filled walls
3.3 填充墙局部破坏分析
图11为填充墙在抗连续倒塌不同阶段Mises应力图。图11(a)为梁机制阶段,填充墙靠近失效柱两侧的区域(图中标注部分)最先开始受压,填充墙沿对角线方向有开裂迹象,说明斜压杆作用开始形成。图11(b)为悬链线机制阶段,左侧的填充墙沿对角线方向发生了开裂,2条裂缝方向大致平行,右侧的填充墙沿对角线方向也发生开裂,但有一小段平行于砌块的裂缝。填充墙的砌块之间主要沿对角方向发生开裂,这说明填充墙对框架抗连续倒塌产生了支撑作用,靠近失效柱两侧的填充墙下部三角区域开始受拉。图11(c)所示为破坏阶段,随着裂缝继续扩大和延伸,填充墙中的三角区域(图中标注区域)处于受压状态,其余区域的填充墙均完全丧失了承载力,此阶段由于填充墙的大多数砌块之间发生开裂,填充墙对框架的抗连续倒塌承载力积极贡献减小。可见,由于框架梁端左右边界条件不相同,左右填充墙发生的破坏并不对称,右跨填充墙砌块之间产生的裂缝较大。
4 结论
(1)竖向荷载作用下,钢管混凝土框架-填充墙结构主要经历了3个阶段:梁机制阶段,填充墙的斜向压杆效应开始产生;悬链线机制阶段,填充墙开始产生裂缝,支撑作用开始形成;破坏阶段,填充墙由于裂缝较大,对组合框架的积极贡献减小。
(2)填充墙能显著提高钢管混凝土组合框架的承载力,这种效应在梁机制阶段更加明显。填充墙的受力主要通过沿对角方向产生斜压杆支撑作用形成。
(3)组合框架左右梁端边界条件不对称,导致左右两侧框架和填充墙最终破坏状态不一致,靠近有梁端约束一侧的填充墙在抗连续倒塌中破坏较严重。
[1] 孟宝,钟炜辉,郝际平.基于节点刚度的钢框架梁柱子结构抗倒塌性能试验研究[J].工程力学,2018,35(6):88-96.
[2] 杜轲,滕楠,燕登,等.楼板对RC空间框架结构抗连续倒塌性能影响试验研究[J].土木工程学报,2019,52(6):14-23.
[3] 周云,陈太平,胡翔,等.考虑周边结构约束影响的RC框架结构防连续倒塌性能研究[J].工程力学,2019,36(1):216-226,237.
[4] 王景玄,王文达,李华伟.钢管混凝土平面框架子结构抗连续倒塌精细有限元分析[J]. 工程力学,2018,36(6):105-114.
[5] LI G Q,ZHANG J Z,JIANG J.Analytical modeling on collapse resistance of steel beam-concrete slab composite substructures subjected to side column loss[J].Engineering structures,2018,169:238-255.
[6] WANG S,KANG S B.Analytical investigation on catenary action in axially-restrained reinforced concrete beams[J].Engineering structures,2019,192:145-155.
[7] BAGHI H,OLIVEIRA A,VALENÇA J,et al.Behavior of reinforced concrete frame with masonry infill wall subjected to vertical load[J].Engineering structures,2018,171:476-487.
[8] LI S,SHAN S D,ZHAI C H,et al.Experimental and numerical study on progressive collapse process of RC frames with full-height infill walls[J].Engineering failure analysis,2016,59:57-68.
[9] QIAN K,LI B.Effects of masonry infill wall on the performance of RC frames to resist progressive collapse[J].Journal of structural engineering,2017,143(9):04017118.
[10] 喻君,甘艺平,李爽.考虑全填充墙作用的钢筋混凝土框架抗连续倒塌性能分析[J]. 建筑结构学报,2019,40(11):112-121.
[11] EREN N,BRUNESI E,NASCIMBENE R.Influence of masonry infills on the progressive collapse resistance of reinforced concrete framed buildings[J].Engineering structures,2019,178:375-394.
[12] XAVIER F B,MACORINI L,IZZUDDIN B A,et al.Pushdown tests on masonry infilled frames for assessment of building robustness[J].Journal of structural engineering,2017,143(9):04017088.
[13] SHAN S D,LI S,WANG S H.Effect of infill walls on mechanisms of steel frames against progressive collapse[J].Journal of constructional steel research,2019,162:105720.
[14] 中华人民共和国住房和城乡建设部.钢管混凝土结构技术规范:GB 50936—2014[S].北京:中国建筑工业出版社,2014.
[15] General services administration. Alternative path analysis and design guidelines for progressive collapse resistance[S]. Washington, D.C.: Office of Chief Architects,2016.
[16] ESMAEILY A, XIAO Y. Behavior of reinforced concrete columns under variable axial loads: analysis[J]. ACI structure journal, 2005, 102(5): 736-744.
[17] 韩林海.钢管混凝土结构:理论与实践[M].3版.北京:科学出版社,2016.
[18] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010[S].北京:中国建筑工业出版社,2011.
[19] 刘桂秋.砌体结构基本受力性能的研究[D].长沙:湖南大学,2005.
[20] CAMANHO P P,DAVILA C G,DE MOURA M F.Numerical simulation of mixed-mode progressive delamination in composite materials[J].Journal of composite materials,2003,37(16):1415-1438.