0 引言
测试是保证软件安全性的重要手段[1],测试一般分为4个阶段:单元测试、集成测试、系统测试及验收测试。集成测试是将不同模块按一定顺序组成系统并对其进行测试的过程,用于验证该系统是否满足设计要求[2]。测试序列生成的主要目的是使测试能够更高效。然而由于工程实际应用状况复杂,现存方法还有诸多问题。
测试序列生成通常会经历以下几个步骤。首先对工程进行分析并划分模块获得模块间依赖关系;然后在获取依赖关系后为防止测试陷入死循环,通过将环路中某些模块使用桩模块替换的方式对其进行破环;最后采用适当的集成策略遍历无环的依赖关系生成测试序列。常见的集成策略根据被测系统的规模可以分为2类:①随着测试的不断进行,模块依次被集成,被测部分逐渐增长的增量集成策略,例如自顶向下集成、自底向上集成等;②测试时被测部分规模不随测试进行而增长的非增量集成策略,例如大爆炸集成、成对集成及邻居集成等。
通过桩模块消除模块间环路的方法较复杂且可能引入新故障,因此如何精确地衡量桩模块构造成本,并在此基础上生成合适的测试序列是测试序列生成面临的主要问题[3]。早期的破环方法是以最小化构造桩模块的数量为目标[4-5]。随着技术发展,研究人员发现每个桩模块的构造成本并不相同,因此更多学者开始以最小化总体桩构造复杂度为目标[6-11],但仍不能彻底解决桩模块带来的相关问题[12]。
除此以外,现存方法易发生故障影响测试进度。现存的测试序列生成方法均为静态方法,不会随着测试过程中桩模块的变化动态调整后续的测试。如测试中发现某一模块存在故障,按静态方法依原测试序列继续测试可能导致后续测试结果不可信。
在对故障模块进行修改排障后应进行回归测试以验证其效果,而目前的测试序列生成方法并没有针对此类情况进行专门优化。
结合多种测试方法及策略,扬长避短实现高效的集成测试。在对整个工程进行精细建模并获得无环模块间依赖关系基础上,利用成对集成对被测工程快速进行首轮测试,之后靠增量集成策略继续测试模块整体配合情况;提出动态的测试序列优化方法以应对发生故障的情况;针对有目标的回归测试场景进行专门优化。系统框架如图1所示。
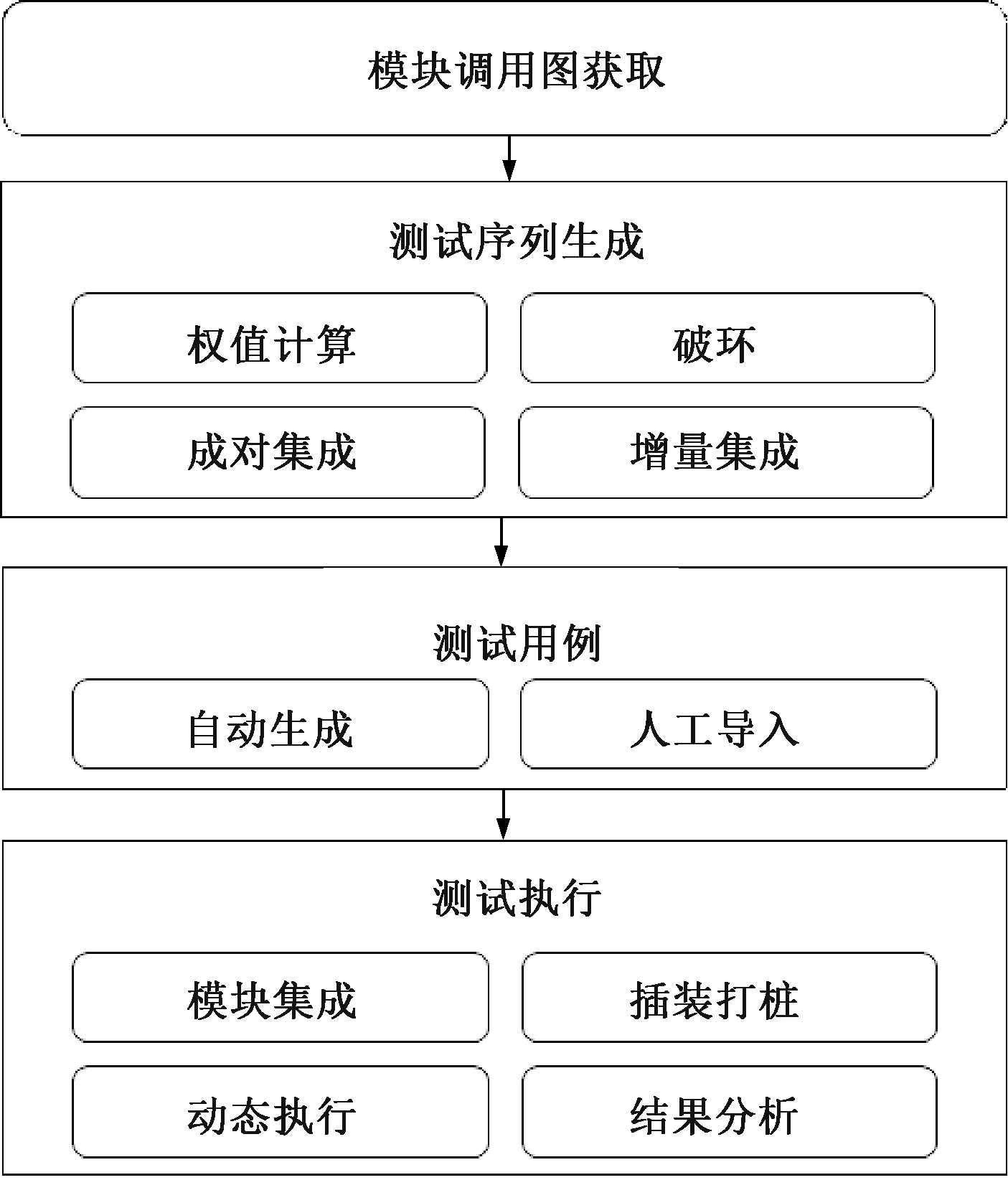
图1 集成测试基本框架
Figure 1 Basic frame work of integration testing
1 测试工程建模
在生成测试序列前首先需要对测试工程进行建模,其中模块的权值是其测试必要性的定量描述。测试必要性可以用程序中的操作符和操作数目定义,也可以用控制流或数据流方式进行定义,也可以综合上述元素共同定义[13]。
1.1 基于代码属性度量的模块权值计算方法
合理地设计模块权值的计算方法,使其能够尽量真实地表达每一模块的测试必要性是十分重要的。模块的测试必要性表现为:模块本身的规模、模块的结构复杂度、模块的传播性等[13-14]。
1.1.1 与模块结构和规模相关的度量元
(1)代码行数(CL):模块中实际有效的行数,是将注释和空白行排除之后的行数。该度量元反映了模块规模的大小,模块越大,可理解性、可维护性都会相应降低,模块的测试必要性则会随之升高。
(2)参数个数(AN):模块的参数越多,也就表示需要从外部接收更多的信息,会使模块易受外部变化影响,从而影响测试工作。
(3)局部变量个数(LV):在模块体内部定义的变量的数量。模块中局部变量越多,代码越复杂,越会影响对模块的理解。
(4)最大循环深度(LDmax):指在模块中最多有几个循环嵌套在一起。比如1个模块中有2个循环结构,若1个循环在另1个循环之中,则最大循环深度为2,若是一先一后出现在模块中,则最大循环深度为1。
(5)圈复杂度(CC):用来衡量一个模块判定结构的复杂程度,数量上表现为线性无关的路径条数,即合理地预防错误所需测试的最少路径条数。圈复杂度大说明程序代码可能质量低且难以测试和维护。
1.1.2 与模块在工程中的耦合性相关的度量元
(1)模块的出度(O):表示在模块体中调用其他模块的数量,对同一模块的多次调用计为一次。该值过大,会使模块易于受外部(其他部分的代码)变化的影响,从而增加维护的工作量,也会增加阅读程序的人在理解程序上的困难。
(2)模块的入度(I):表示该模块被其他模块调用的数量,同一调用者对被调用模块的多次调用计为一次。该值过大,会使模块的变化易于对外部(其他部分的代码)产生影响,从而增加维护的工作量。该度量元直接反映为函数调用图中节点的入度。
(3)模块所处循环的数量(l):该变量反映模块节点在调用图中所处循环的数量,与圈复杂度不同,圈复杂度主要反映的是图中分支结构的数量。如图2所示,1、4号节点处在两个循环之中,2、3号节点只处在1个循环中。模块若处在多个循环之中,说明该模块很有可能是多个递归环节中共用的部分,该值越大影响力也越大。
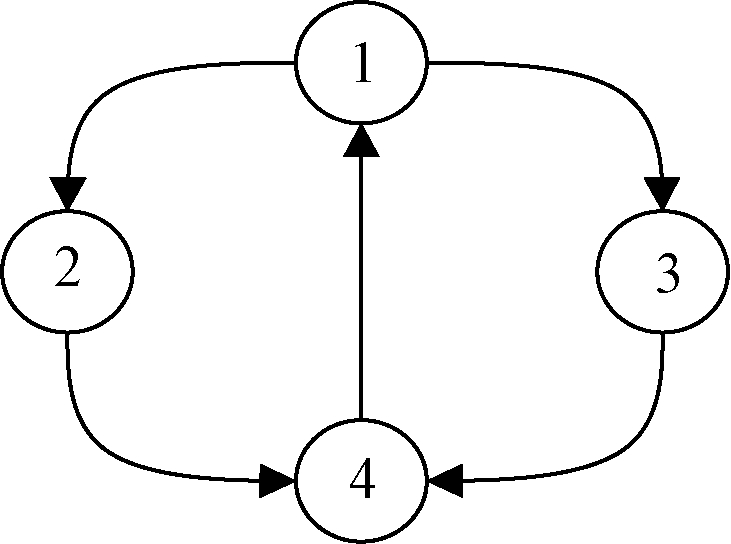
图2 双重循环
Figure 2 Double cycle
在设计模块权值的计算方式的过程中,由于不同度量元的数据量级不同,若直接在计算过程中将这些度量元的数据相加,很有可能出现某些度量元的影响过大的情况,比如代码行数在通常情况下肯定会比其他参数大很多,会削弱其他参数在计算过程中的影响。为了避免这样的情况发生,在计算过程中需要选择适当的方式将不同的参数进行组合。
虽然可以通过规范化方法消除量级带来的影响,但规范化方法需要对整个工程的数据进行汇总计算后才能得到规范化后的数据。若在测试过程中修改一个模块,其他模块权值也有可能发生变化。由于模块的权值是生成测试序列的重要依据,若要生成最佳的序列,需要重新计算所有模块的权值,测试的成本会大幅增加,因此,采用规范化方法不合适。
另一种方式是通过将所有度量元的值相乘来计算模块的权重,这种方式也能够正确反映不同模块间相对的重要性高低。但此方法需要注意某些度量元取值为0时的情况,在这种情况下不论其他度量元的值是多少,整个模块的权值都会是0,显然与事实不符。为避免发生此类情况,需要进行平滑处理。本文选取加一平滑(拉普拉斯平滑)计算模块的权值。通过这种方式计算模块的权值,不需要考虑工程中其他模块的影响,每一模块的权值可单独计算,又能体现出每一模块的测试必要性,具体计算方式如下。
模块规模复杂度C:
C=CL·(AN+1)·(LV+1)·(LDmax+1)·CC。
(1)
式中:CL为该模块的代码行数;AN为该模块参数个数;LV为该模块局部变量个数;LDmax为该模块最大循环深度;CC为该模块圈复杂度。上述度量元中模块参数个数、局部变量个数以及最大循环深度可能为0,所以对上述度量元进行了加一平滑。
模块传播复杂度W:
W=(α·I+β·O)·(l+1)。
(2)
式中:α+β=1;I为该模块在调用图中的入度;O为出度;l为该模块所处循环的数量。由于l可能为0,需要加一平滑。因为出度和入度同等重要,所以α取0.5,β取0.5。
模块的权值X:
X=α·C+β·W。
(3)
式中:α+β=1;C为模块的规模复杂度;W为模块的传播复杂度。由于规模复杂度的数值一般会比传播复杂度大很多,所以为了平衡两者在计算模块权值时的比重,α取0.05,β取0.95。
1.2 模块间接口调用的重要性权值
模块间接口是一个模块所实现的功能及所需参数的声明,然而在测试序列生成的过程中,模块所实现的功能的重要性很难去衡量,并且若要统计某一接口在整个工程中被其他哪些模块调用,需要分析整个工程。若要统计所有接口的被调用次数,所需时间成本较高,且在集成测试过程中,并不是一个模块被集成进来以后,所有对该模块的调用同时进行测试,而是依次进行测试的。若同时进行测试,故障难以定位。因此,在设计模块间接口调用的重要性权值计算函数时,以该接口的实际调用者及实现者组成的二元组为计算对象。
假设节点i、j为被测工程中的2个模块,其中j为i的后继模块。模块间接口调用权值函数为
Yi,j=α·Xi+β·Xj。
(4)
式中:α+β=1;Xi为实际调用者模块的权值;Xj为实现者模块的权值。本文认为2个模块同等重要,所以α取0.5,β取0.5。
1.3 算法复杂度分析
由于与模块结构和规模相关的度量元可以直接沿用单元测试获得的参数直接计算,在此不予讨论获取此类度量元的时间复杂度。
在获取与模块在工程中的耦合性相关的度量元时,首先依据抽象语法树生成工程的函数模块调用关系图,保存每个模块的前驱与后继信息以及出度和入度,此过程时间复杂度为O(n+e),n为调用图的模块数,e为边数。然后,使用Tarjan算法遍历全图获取图中的循环信息以及每个模块的l值,此过程时间复杂度为O(n+e)。最后,计算所有模块和接口的权值。因所有参数皆已获得,此过程只需访问调用图中的每个模块和边一次,时间复杂度为O(n+e)。
2 测试序列生成方法
2.1 基本单元的选取
在本方法中将模块间接口的实际调用模块和实现模块所组成的二元组作为测试序列的基本单元,对应函数模块调用图中的边。其优势有两点:①重要性权值容易计算。对于一个抽象定义的接口而言,其实现方式可能随外界原因发生变化,或同时存在多个实现方式,导致权值难以估计。②方便增量集成操作。在增量集成时可以直接将实际调用模块中对相应接口桩模块的调用改为对实际接口实现模块的调用。若使用模块作为测试序列的基本单元,在每次增量集成时都需要将所有对该模块对应桩模块的调用转化为实际模块,操作复杂且故障难以定位。
2.2 测试序列生成策略
对于成对集成来说,只需要获得整个工程的结构就可按照多种方式生成测试序列。例如直接将所有的模块间接口按权值降序排列,或者将每个模块的出边按权值排列后,采用广度优先遍历(BFS),即可获得测试序列。在最坏情况下,时间复杂度为O(elg e),平均情况为O(n+e),其中n为调用图的模块数,e为边数。
在增量集成生成测试序列前,首先需获得工程的有向无环图。通过递归删除循环中权值最小的边,即可获得整个工程的有向无环图。然后结合相应的集成策略,如深度优先的自顶向下遍历(DFS),即可获得测试序列。在最坏情况下,时间复杂度为O(elg e),平均情况为O(n+e),其中n为调用图的模块数,e为边数。
2.3 测试序列动态优化调整
发生故障时,如果整个工程的测试任务因为排除模块的故障而导致停滞是不合适的,若继续测试,与故障相关的模块测试信息又是不可信的。所以,故障排除与其他无关模块的测试应同时进行以提高效率。
首先,确定与故障相关的部分。在自顶向下测试过程中,故障模块的前驱模块一般是先于故障模块进行测试的,其测试数据仍有参考价值,因此优化测试序列时不需要对这一部分进行调整。并且在整个调用图中将某一非根模块的子树删去,剩余的部分仍是一个可遍历的有向图,因此将故障模块及其所有后继模块作为故障相关部分,从整个函数模块调用图中精简,该过程时间复杂度为O(n+e),其中n为后继模块的数量,e为后继模块间边的数量。然后,按照选定的集成策略对精简后的调用图进行测试序列生成,如图3所示。在自顶向下集成过程中,假设原先以调用图中的边为单位生成集成序列,如表1所示。
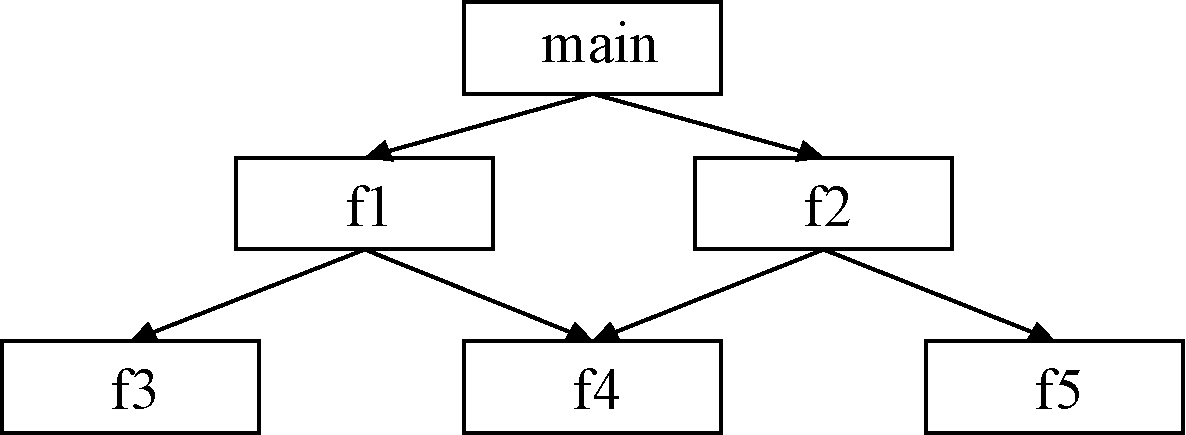
图3 模块调用图
Figure 3 Module calling graph
表1 BFS集成测试序列
Table 1 BFS integration test sequence

序号被测接口1main→f12main→f23f1→f34f1→f45f2→f46f2→f5
假设集成测试在一开始就发生故障,经分析故障位于f1中,则此时需要将与f1无关的模块继续集成,为了保证集成测试的整体结构完整,此处将故障模块及其所有后继模块定义为相关模块,其余模块定义为无关模块。如图4所示,被圈出的模块为相关模块,相关模块间的调用及对故障模块的直接调用都视为故障相关调用,将推迟测试。具体的测试序列变动如表2所示,待f1修改完毕,进行回归测试。
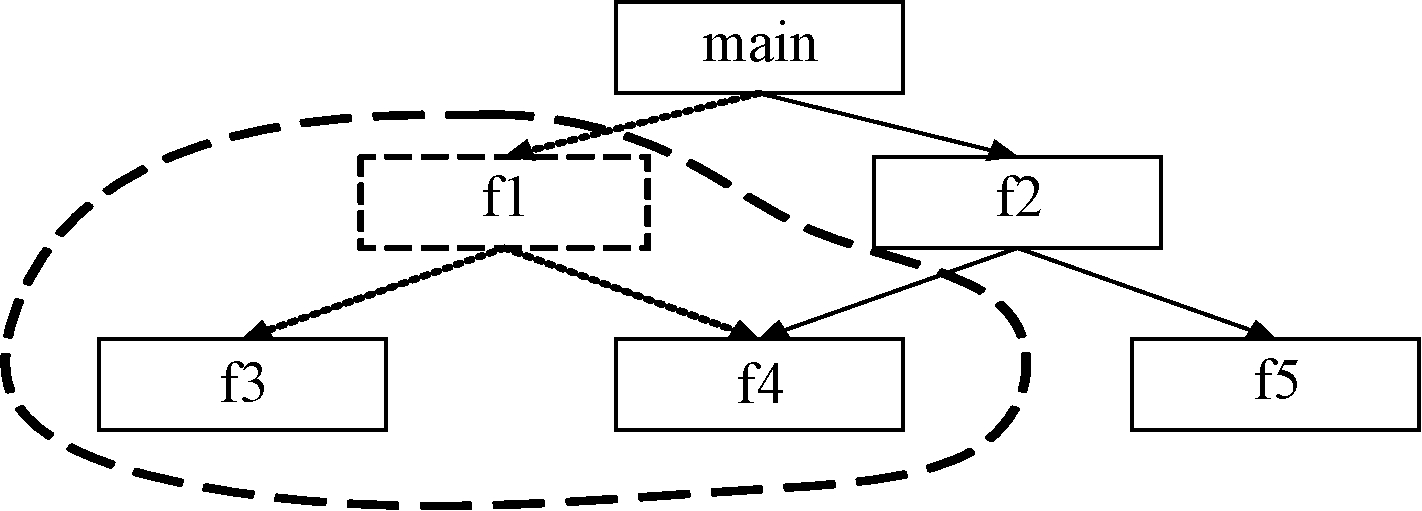
图4 优化模块调用子图
Figure 4 Adjusted module calling subgraph
表2 无关模块BFS集成测试序列
Table 2 Irrelevant node BFS test sequence

序号被测接口1main→f22f2→f43f2→f5
2.4 回归测试序列生成
在集成测试过程中,在发现故障后需对相应模块做出修改,修改完成后需进行回归测试以确定被修改模块是否引入新的故障,以及是否完成设计的功能要求。在成对集成过程中,若对模块或接口进行修改,影响范围较小,可用于测试的只有与被修改位置距离为1的模块,只要重新测试这些模块与接口即可。在增量集成过程中,因测试复杂,为提高效率需尽早测试被修改的部分。通过分析被修改点的所有前驱模块和所有后继模块,即可得到与被修改点相关的子图。该过程时间复杂度为O(N+E),其中N为前驱及后继模块的数量,E为前驱及后继模块间边的数量。结合相应的集成策略对该子图生成测试序列,再将其他的无关模块集成进来。
用上一节的例子进行说明。若在测试时对f1进行修改,则提取与f1相关的子图,如图5中圈出部分,生成回归测试序列如表3所示。
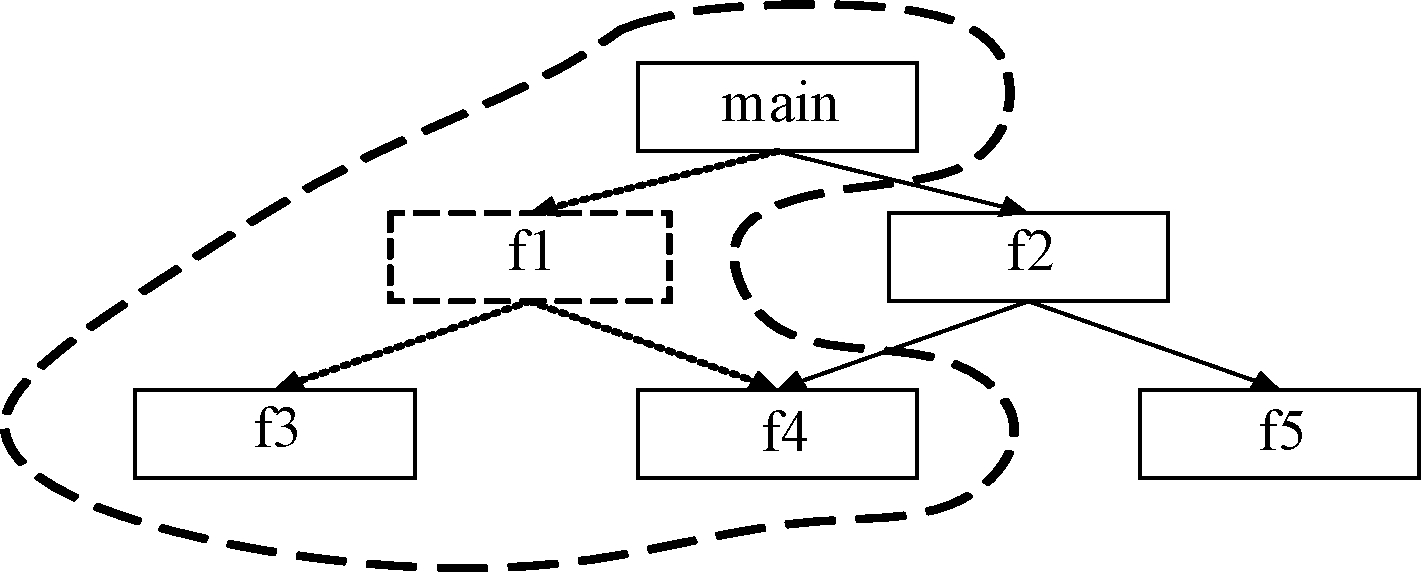
图5 回归模块调用子图
Figure 5 Regression module calling subgraph
表3 回归测试BFS集成测试序列
Table 3 BFS test sequence of regression test

序号被测接口1main→f12f1→f33f1→f44main→f25f2→f46f2→f5
3 软件集成测试工具
软件集成测试工具(integration test system,ITS)是一款由本实验室自主研发的主要用于模块间接口集成测试的集成测试工具,该工具框架结构如图6所示。该工具自动化程度高,使用简单,具体操作流程包括新建工程、模块划分、测试序列生成、测试用例生成、执行测试和测试结果分析6个环节。
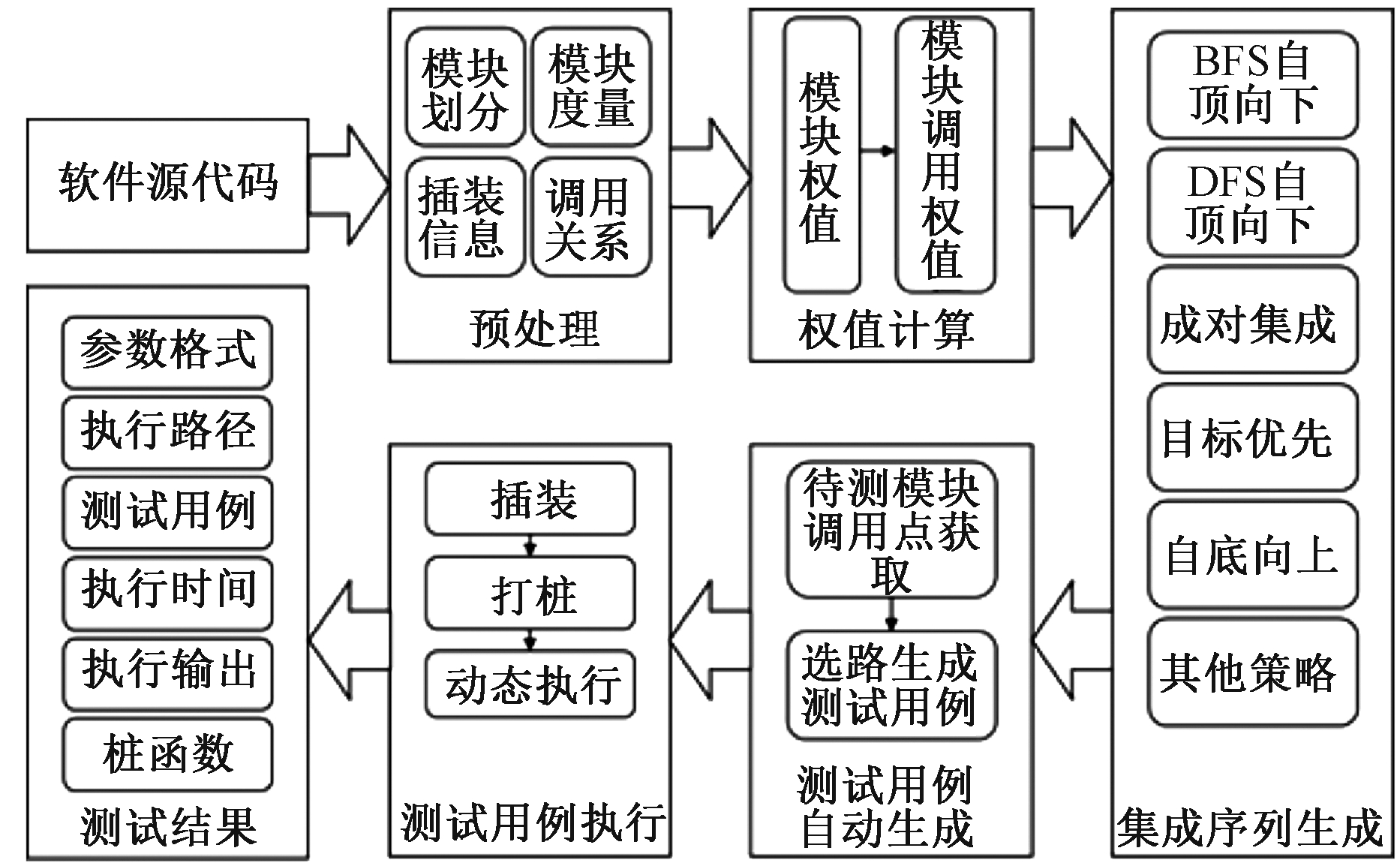
图6 ITS结构图
Figure 6 ITS structure diagram
4 实验部分
4.1 实验环境
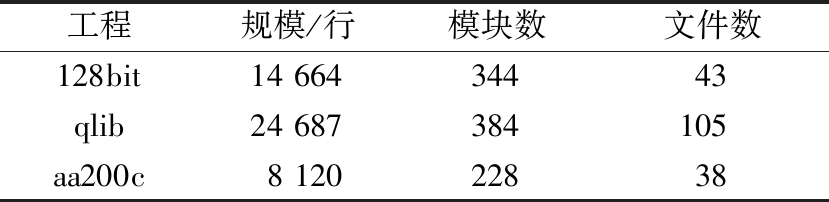
本实验是在ITS 1.0的基础上进行的,实现了测试序列生成、测试用例生成以及故障定位等功能。实验的操作系统为ubuntu12.04.1 LTS,JDK版本为JDK 1.6.0_41,JVM版本为OpenJDK Server VM,开发工具为Eclipse Luna SR2 (4.4.2),实验对象为C语言代码。实验选取了128bit、qlib以及aa200c 3个工程作为被测代码进行测试,其详细信息如表4所示。
表4 被测工程
Table 4 Project under test
工程规模/行模块数文件数128bit1466434443qlib24687384105aa200c812022838
4.2 测试序列生成时间测试
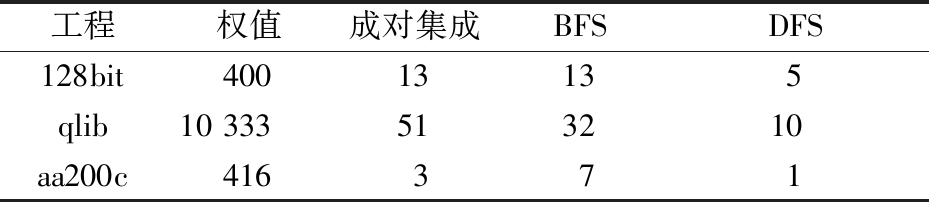
各测试序列基本单元的权值以及生成序列所耗时间基本上随着被测工程规模增大而增长。在生成成对集成测试序列时,采用了复杂度为O(elg e)的排序算法,随工程规模增大,耗时增长明显。在使用BFS和DFS生成测试序列时由于时间复杂度为O(N+E),耗时增长略缓。详细耗时情况如表5所示。
表5 权值计算及序列生成耗时
Table 5 Time of weight and sequence generation ms
工程权值成对集成BFSDFS128bit40013135qlib10333513210aa200c416371
4.3 测试序列优化及回归测试序列生成
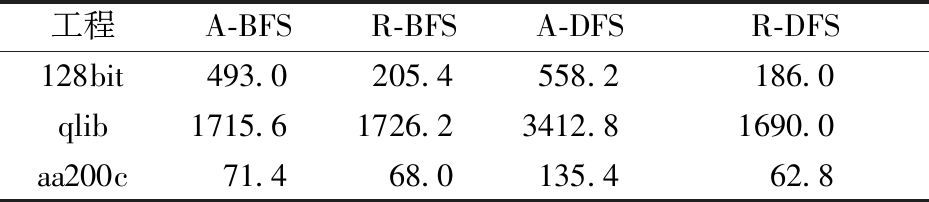
通过每次在被测工程中随机选取1个模块作为故障位置来模拟实际情况,每个工程模拟5次。由于测试序列优化及回归测试序列生成是在现有测试序列基础上进行的,耗时显著缩短,具体平均耗时如表6所示。
表6 优化序列与回归序列时长
Table 6 Time of adjusted sequence and regression sequence μs
工程A-BFSR-BFSA-DFSR-DFS128bit493.0205.4558.2186.0qlib1715.61726.23412.81690.0aa200c71.468.0135.462.8
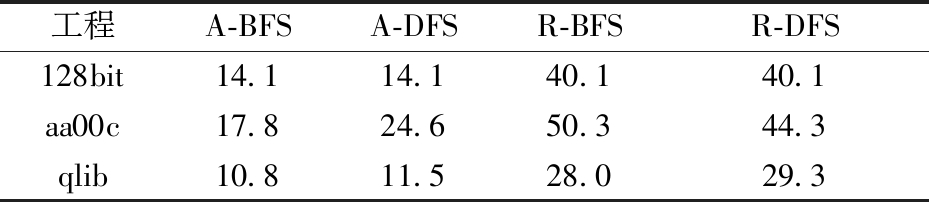
实验通过统计与故障模块相关的调用出现的位置来衡量优化后的测试序列和回归测试序列的提升效果。通过获取每次实验故障相关调用在序列中首次和最终出现位置较原序列的后移量,将二者取平均后除以整个序列的长度作为优化序列的提升百分比;通过获取每次实验故障相关调用在序列中首次和最终出现位置较原序列的前移量,将二者取平均后除以整个序列的长度作为回归序列的提升百分比。表7为每个工程中5次实验的提升效果均值。
表7 优化测试序列及回归测试序列效果
Table 7 Effect of adjusted sequence and regression sequence %
工程A-BFSA-DFSR-BFSR-DFS128bit14.114.140.140.1aa00c17.824.650.344.3qlib10.811.528.029.3
5 结论
在现有的测试序列生成策略基础上,结合实际测试过程,实现了多个集成测试序列自动生成技术、降低故障影响的测试序列自动优化技术及回归测试序列的优化技术。利用自动化程序分析技术,降低了设计实现阶段和执行评估阶段的测试成本,提高了测试效率。
基于本文在集成测试方面所做的工作,还有很多相关研究内容可以进一步优化。今后可以在提高模块间依赖关系分析的准确性和进一步结合测试用例自动生成技术方面继续进行深入研究。
[1] 吴超,杨冕,王秉.科学层面的安全定义及其内涵、外延与推论[J].郑州大学学报(工学版),2018,39(3):1-4,28.
[2] 宫云战.软件测试[M].北京:国防工业出版社,2006.
[3] 毛澄映,卢炎生.构件软件测试技术研究进展[J].计算机研究与发展,2006,43(8):1375-1382.
[4] KUNG D C,GAO J,HSIA P,et al.Class firewall,test order,and regression testing of object-oriented programs[J].JOOP-journal of object-oriented programming,1995,8(2):51-65.
[5] MAO C Y,LU Y S.AICTO:an improved algorithm for planning inter-class test order[C]//The Fifth International Conference on Computer and Information Technology (CIT′05).Piscataway:IEEE,2005:927-931.
[6] ABDURAZIK A,OFFUTT J.Using coupling-based weights for the class integration and test order problem[J].The computer journal,2009,52(5):557-570.
[7] 王莹,于海,朱志良.基于软件节点重要性的集成测试序列生成方法[J].计算机研究与发展,2016,53(3):517-530.
[8] 赵玉丽,王莹,于海,等.基于复杂网络的类间集成测试序列生成方法[J].东北大学学报(自然科学版),2015,36(12):1696-1700.
[9] 姜淑娟,张艳梅,李海洋,等.一种基于耦合度量的类间集成测试序的确定方法[J].计算机学报,2011,34(6):1062-1074.
[10] 刘坤.一种基于ORG的破除环路改进算法[J].计算机与信息技术,2008(8):58-61.
[11] ZHANG Y M,JIANG S J,WANG X Y,et al.An optimization algorithm applied to the class integration and test order problem[J].Soft computing,2019,23(12):4239-4253.
[12] 李兵,王浩,李增扬,等.基于复杂网络的软件复杂性度量研究[J].电子学报,2006,34(增刊1):2371-2375.
[13] 孙志安,裴晓黎,宋昕.软件可靠性工程[M].北京:北京航空航天大学出版社,2009.
[14] 林连进,谢怀民.软件测试技术[M].北京:北京理工大学出版社,2018.