0 引言
近年来随着无人机与高清相机的广泛应用,基于图像的大规模三维场景重建技术得到了广泛关注,其主要运用多视图几何原理,通过不同视点所拍摄的图像计算出相机姿态和场景三维结构。从运动中恢复结构(structure from motion,SfM)是基于图像的三维重建中一个关键环节,主要完成相机位姿的估计和稀疏点云的重建,其中增量式(incremental)SfM是目前最普遍、最稳定的SfM方法。增量式SfM首先需要选取一对图像作为起点进行两视图重建,最开始选取的这一对图像被称为初始图像对(initial image pair,InitIP),它对三维重建的最终效果影响巨大,整个初始图像对选取过程如图1所示。
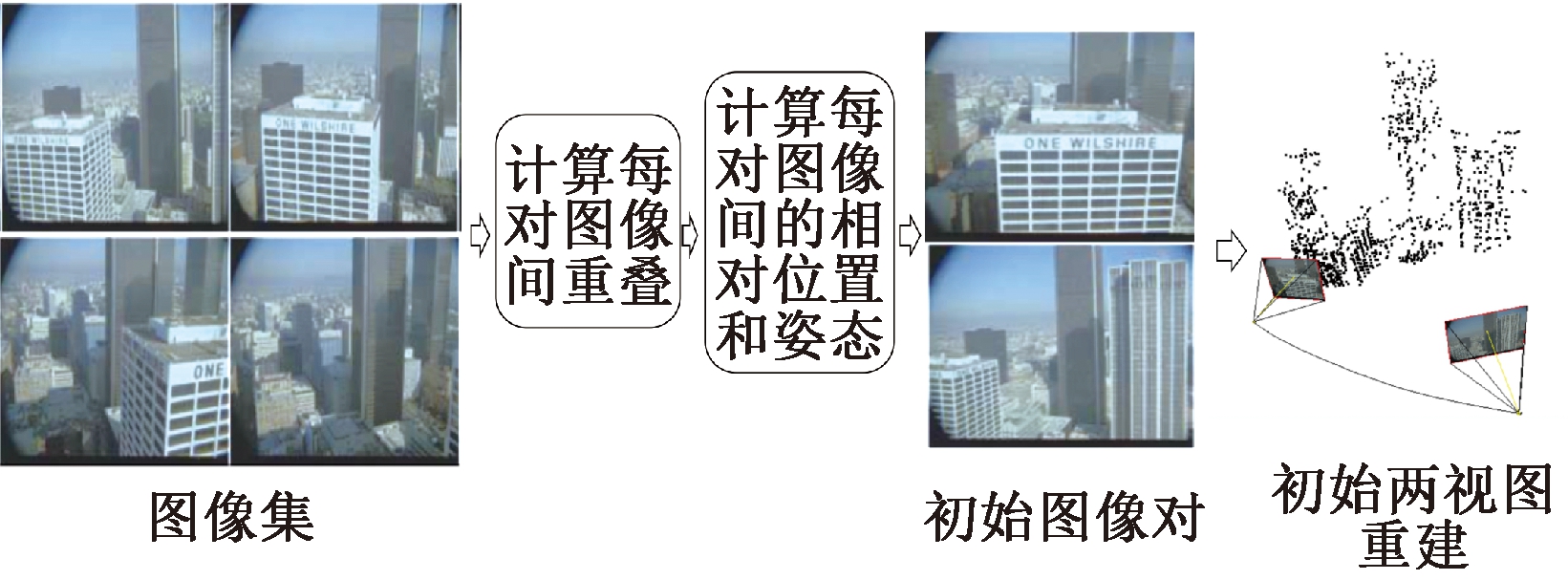
图1 初始图像对选取流程图
Figure 1 Flow chart of initial image pair selection
2006年,Beder等[1]通过计算三维点所处空间区域的圆度,来衡量InitIP对于场景重建的稳定性,首次给出了增量式SfM中初始图像对的评价方法。之后,Haner等[2]通过最小化每个相机到InitIP的距离来减小累积误差,该方法首次将InitIP与整个图像集之间的关系考虑到该选取过程之中。近年来,一些三维重建开源系统例如Colmap、Alicevision则使用Schonberger等[3]和Moulon等[4]提出的利用多尺度网格划分图像来计算特征点得分的方法,将匹配点的分布进行量化,一定程度上提高了InitIP的鲁棒性。但缺点在于面对大规模数据时,计算每幅图像多个尺度的特征分数也会额外增加计算开销。综上,现有的InitIP选取方法主要遵循两大原则:第一,足够多的匹配点;第二,两幅图像要具有足够的相对运动以保证不退化为单应模型。以上方法均需要进行大量的特征匹配导致效率较低,另一方面,特征点检测与匹配中的误差也会导致相机相对位置的估计不准确。
InitIP的选取需要建立大量图像间的连接关系,传统的做法是特征点提取与匹配[5]。同时,选取InitIP还涉及两幅图像相对空间位置的计算,因此它是一个包含多任务、多输出的问题。近年来,多任务学习[6]作为深度学习中的一个分支,能够高效地在多个相关联任务中进行学习训练、共享特征,从而得到广泛应用。因此,本文借鉴多任务学习的思想,提出基于多任务学习的初始图像对选取网络,以提高选取InitIP的效率。为了避免InitIP位于场景的稀疏区域而导致重建场景不完整的问题,进一步提出了一种结合场景连接图的选取策略,以提高重建稳定性与完整性。
1 初始图像对选取网络
多任务学习针对不同但具有相关性的任务,同时对两个或两个以上任务进行学习,在一定程度上共享学习到的知识,以提升各自的性能。因此本文提出使用多任务学习网络同时预测图像相似性和相机的位置姿态,进而加速在大规模场景下选取InitIP的整个过程。
1.1 多任务网络框架
首先选定两个特定的网络对应两个子任务,整个多任务网络框架如图2所示。上方蓝色分支为PoseNet,用来预测图像间的相对位移与旋转,下方红色分支为MatchNet,输出每一对图像间的相似度,然后联合相似度、相对位移与旋转进行图像对的整体评分,从而选出得分最高的InitIP。
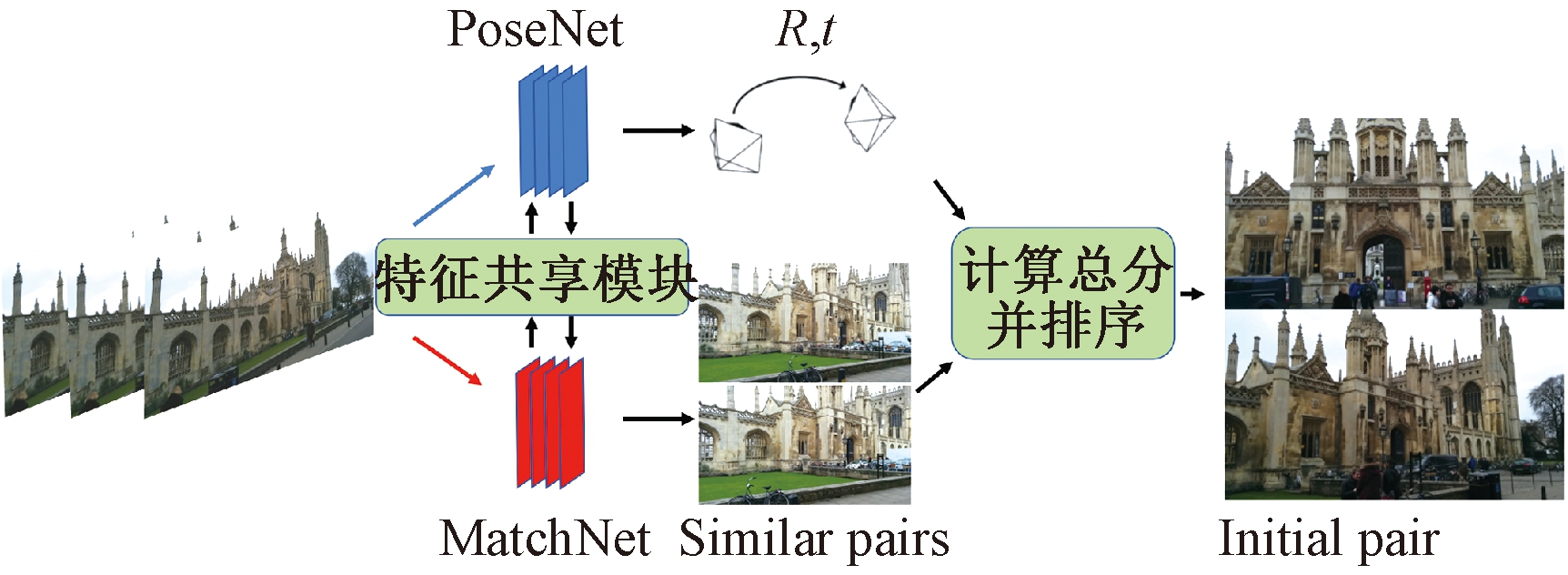
图2 多任务初始对选取网络图
Figure 2 Multi-task initial pair selection network
其中,MatchNet采用Shen等[7]提出的图像检索网络作为主体结构,如图3所示,训练时网络的一组输入为3幅图像:参考图像、正例图像、负例图像。正例图像即与参考图像相似的图像,负例图像也就是与参考图像无关的图像。
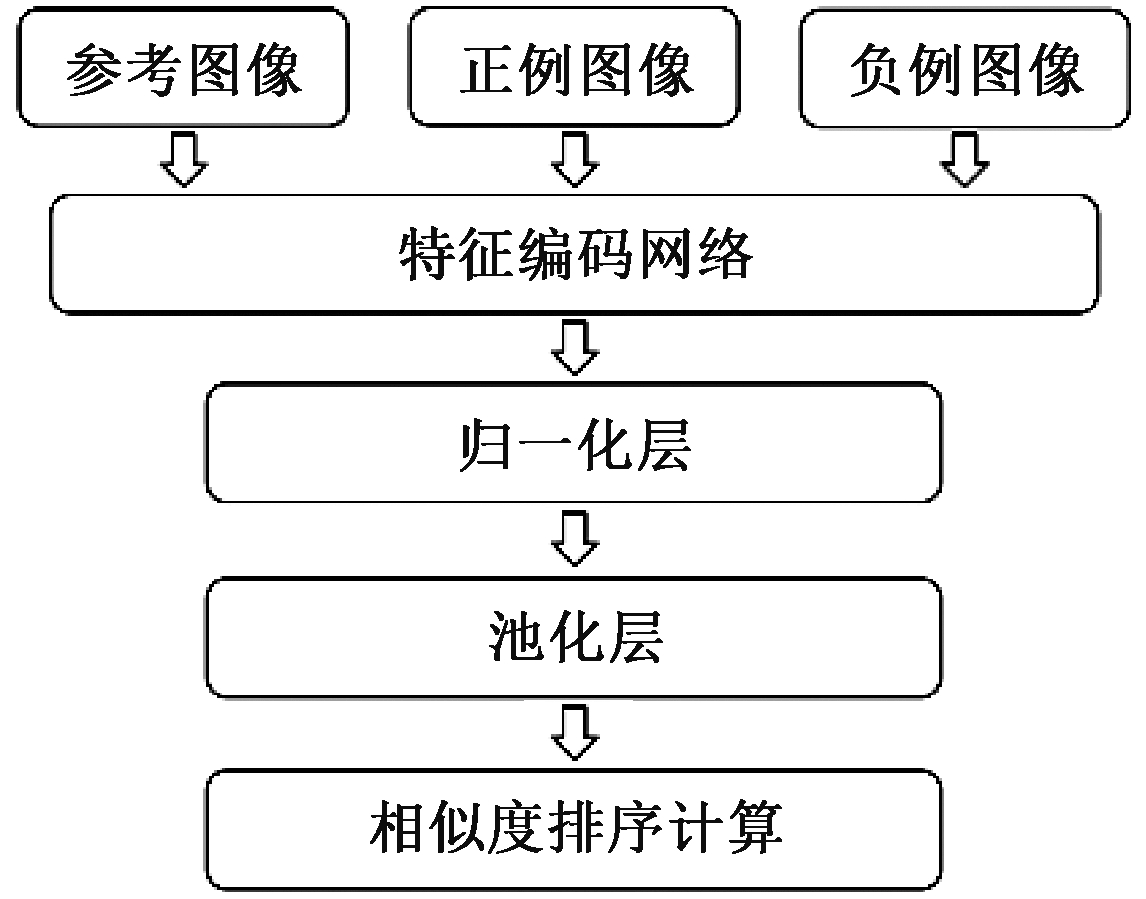
图3 图像相似性检测网络结构图
Figure 3 Structure of image similarity detection network
特征编码网络使用被广泛采用的卷积网络作为基础网络。该网络将卷积神经网络作为特征编码器,将输入图像编码成一个高维空间中的特征向量,使得包含相似场景或物体的图片经过编码后形成的向量在高维空间中尽可能接近,不包含相似场景的图像尽可能远离。因此,本文用归一化后的特征向量之间的L2距离来度量相似度,如式(1)所示:
(1)
式中: f(·)为深度神经网络;Ii、Ij为需要进行相似度量的两幅图像。
另一个分支则为相机位置姿态估计网络PoseNet,使用Kendall等[8]提出的PoseNet对输入的图像进行六自由度的位置和姿态估计。该网络以GoogLeNet[9]作为基础,将原有的3个softmax分类器修改为输出两个向量的仿射变换回归器,如图4红色标注框所示,t=(x,y,z)表示位置的三维向量,R=(w,a,b,c)表示相机旋转的四元数。图4整体为一个修改后的卷积模块。
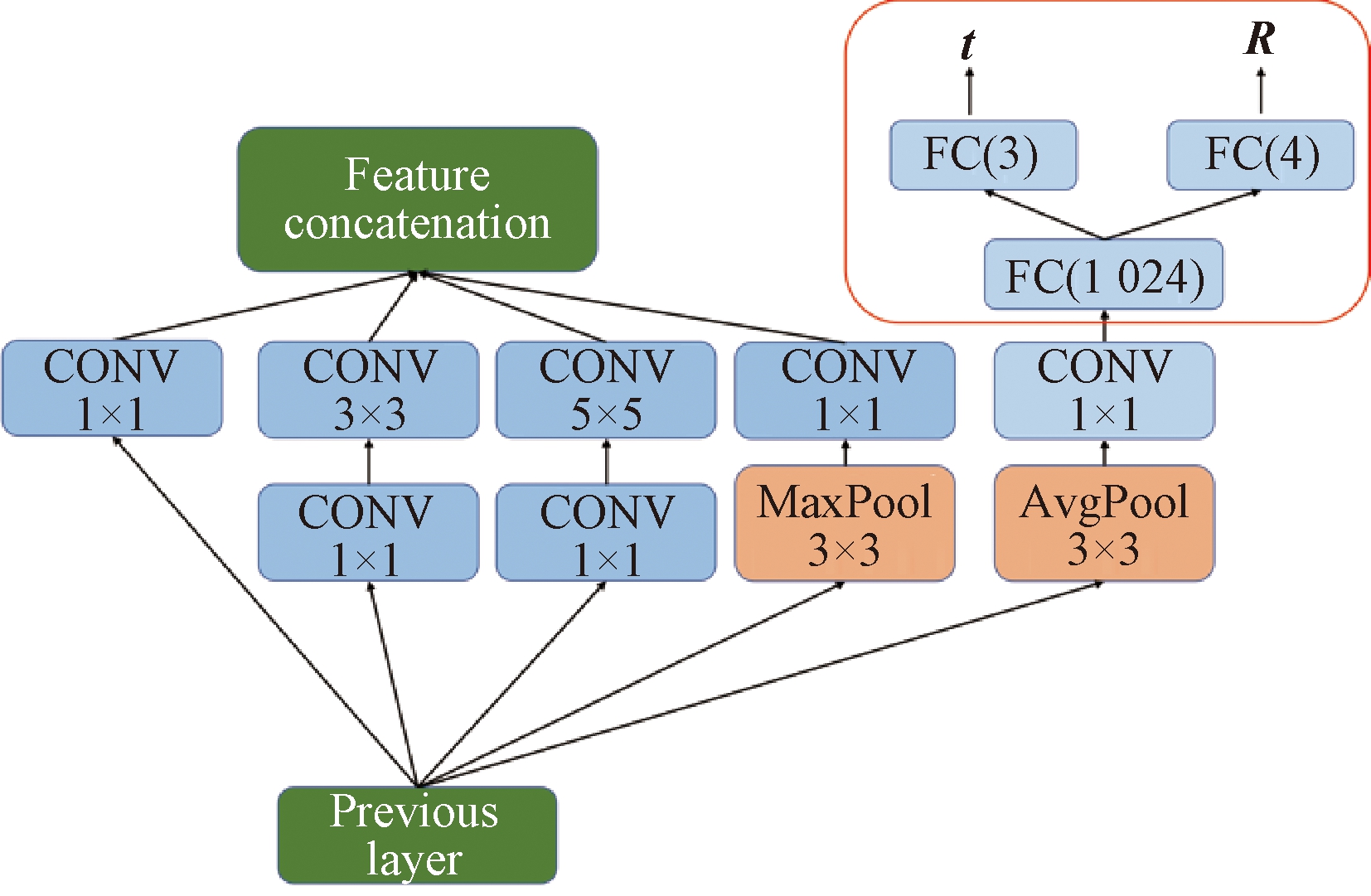
图4 PoseNet的相机位置姿态回归模块
Figure 4 Camera position attitude regression module of PoseNet
卷积层输出的特征图经过平均池化层改变尺寸,接着经过1×1的卷积层改变通道数,然后进入仿射变换回归器。在回归器中,特征向量先通过1 024维的全连接层,再分别经过维度为3和4的全连接层回归代表位置和旋转的两个向量,因此可以通过这个分支预测得到图像的位置和姿态,进而计算相对位移Trel、相对旋转Rrel。通过文献[10]中所提方法,最终由四元数R转换为相对欧拉角度Rrel。
至此,通过网络的两个分支分别得到了图像之间的特征向量距离和相对位移与旋转,然后,通过设计的评分公式(2)进行评分和排序,从而选取最终的InitIP。
Score=Trel/d2(Rrel<45°)。
(2)
式中: Score表示InitIP的最终评分;d表示式(1)中所计算的特征向量之间的距离,根据航拍三维重建中采集图像的重叠度至少为60%,相机相对夹角小于45°的原则[11],将3个轴上相对旋转的阈值设定为45°。
1.2 交叉连接网络
在确定了多任务网络框架后,就需要确定多任务网络中特征共享的方式。本文采用Fukuda等[12]所提出的交叉连接单元将PoseNet与MatchNet进行连接,实现不同任务之间特征的共享,交叉单元如图5所示。
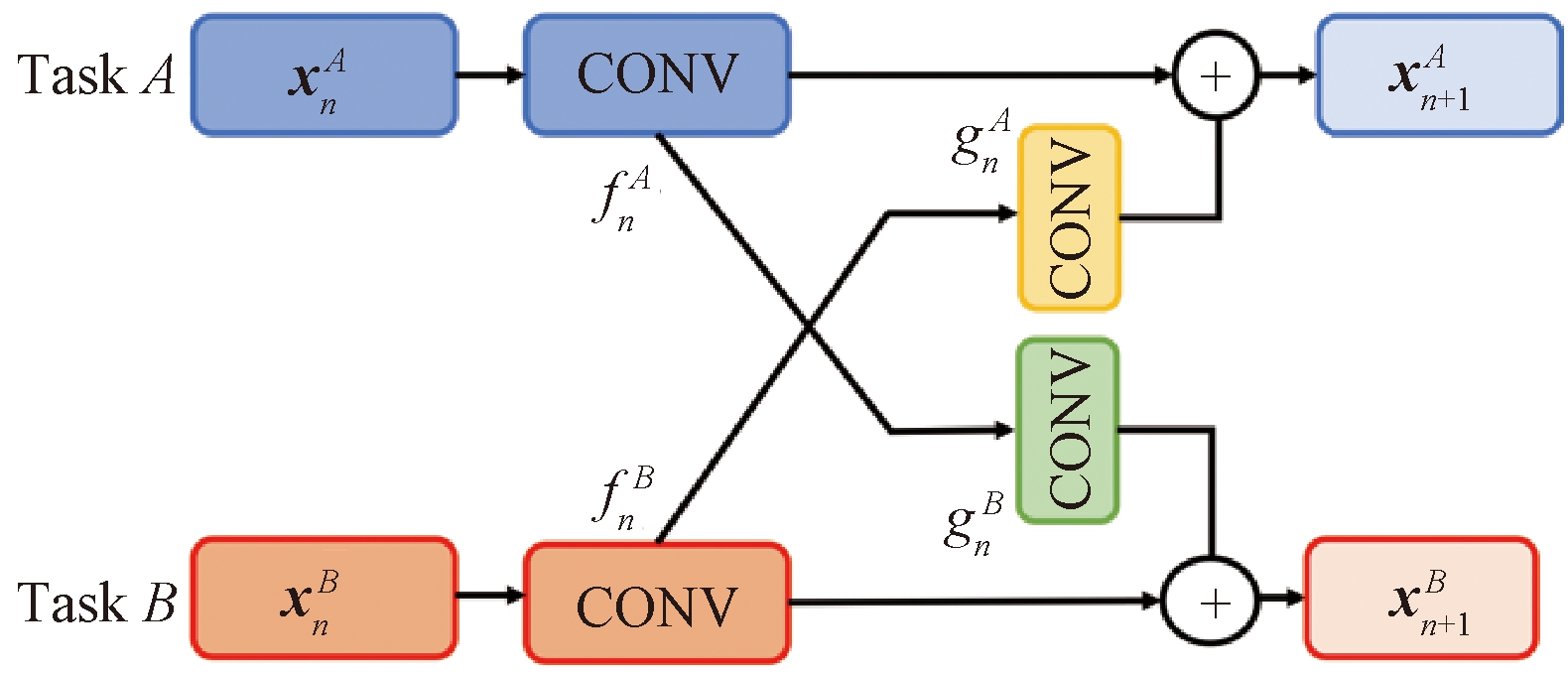
图5 交叉连接结构示意图[12]
Figure 5 Schematic diagram of cross-
connection structure[12]
网络第n层的输入表示为![]() 和
和![]() 将原任务中的卷积层表示为
将原任务中的卷积层表示为![]() 和
和![]() 假设交叉连接中的卷积层学习到变换
假设交叉连接中的卷积层学习到变换![]() 和
和![]() 则两个任务经过交叉连接的输出
则两个任务经过交叉连接的输出![]() 和
和![]() 由式(3)计算得出[12]:
由式(3)计算得出[12]:
(3)
上面两个等式右边的第二项![]() 和
和![]() 表示另一个任务中有用的信息。如果将PoseNet与MatchNet所有卷积层都进行交叉连接会增加大量的参数量和计算时间,并且两个网络在基本结构上存在许多差异,所以并不适合把两个网络进行全部交叉连接。因此,本文采用了浅层交叉连接和深层交叉连接的两种思路,构建两种网络分别进行实验,以探索性能更好的交叉连接方式。如图6所示,矩形框标注区域为建立交叉连接的层级,其余层级为两个任务各自特征提取层,不参与特征的共享。
表示另一个任务中有用的信息。如果将PoseNet与MatchNet所有卷积层都进行交叉连接会增加大量的参数量和计算时间,并且两个网络在基本结构上存在许多差异,所以并不适合把两个网络进行全部交叉连接。因此,本文采用了浅层交叉连接和深层交叉连接的两种思路,构建两种网络分别进行实验,以探索性能更好的交叉连接方式。如图6所示,矩形框标注区域为建立交叉连接的层级,其余层级为两个任务各自特征提取层,不参与特征的共享。
图6(a)中MatchNet的主干网络Resnet50的第2、3个残差块中的卷积层与PoseNet中Inception3中的卷积层进行交叉连接,输出的特征图尺寸分别为56×56、28×28。图6(b)中MatchNet的第4、5个残差块与PoseNet中的Inception4、Inception5层中的卷积层之间构建交叉连接模块,输出特征图的尺寸分别为14×14和7×7。
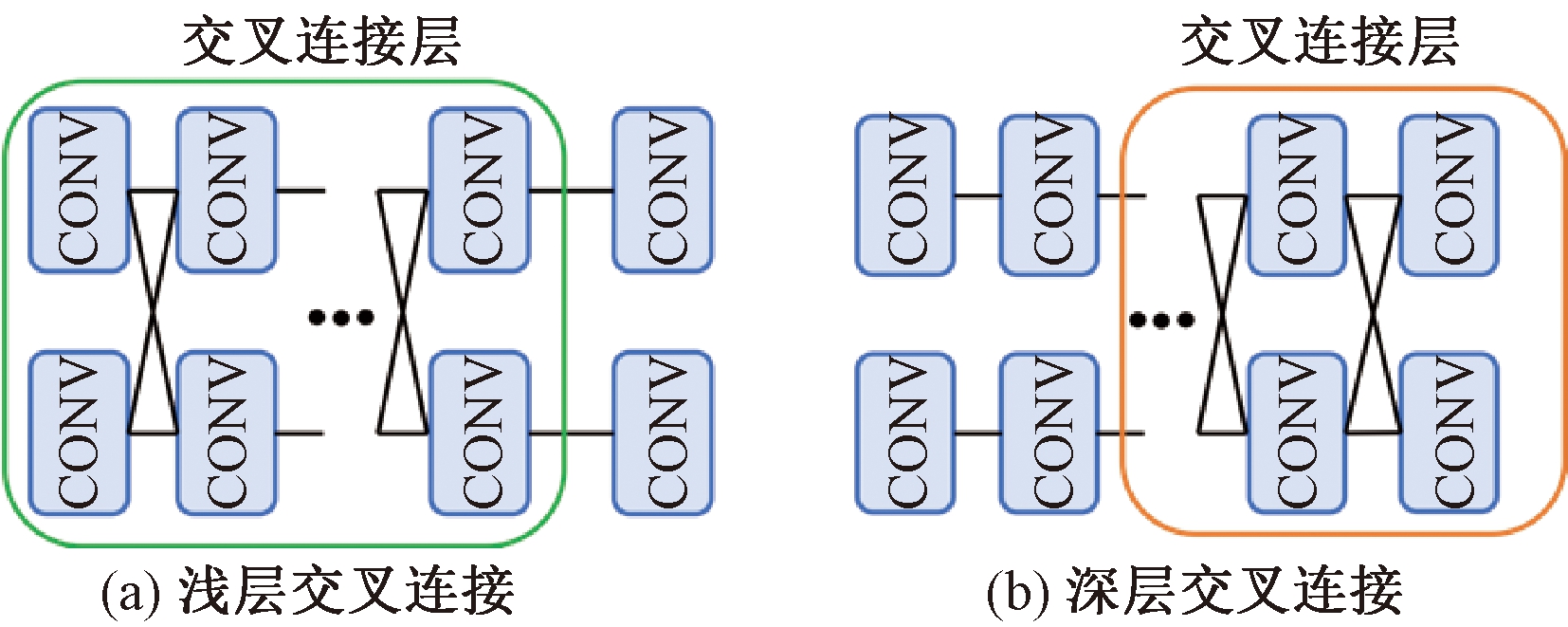
图6 两种交叉连接示意图
Figure 6 Diagram of two kinds of cross connection
1.3 联合损失函数
对整个网络框架的损失函数进行设计时,首先需要确定两个子网络各自的损失函数。对于相似性检测网络采用如下三元损失函数[7]:
L(a,p,n)=[d+-min(d-,d-′)+α]+。
(4)
式中:a,p,n分别代表参考图像、正例图像、负例图像;d+=d(f(a),f(p)),d-=d(f(a),f(n)),d-′=d(f(n),f(p)),d为式(1)所述的两幅图像之间的距离;α为一个设定的边界参数使得两个距离的计算保持一定的界限。式(4)中[σ]+=max(σ,0),即当正例距离远大于负例距离时,该组数据的损失值是需要被抑制的。
对于另一个分支的PoseNet,Kendall[8]提出的整体损失函数如式(5)所示:
(5)
式中: x与q为通过传统SfM得到的位置姿态的参考值;![]() 与
与![]() 为位置和姿态的预测值;β为用来保持位置和方向误差的期望值近似相等的尺度因子。
为位置和姿态的预测值;β为用来保持位置和方向误差的期望值近似相等的尺度因子。
训练多任务网络时,可能出现梯度主导[13]问题,导致无法收敛。主要原因是由于各任务输入数据的不平衡,以及反向传播中梯度数值相差过大。因此,本文采用一种为多个损失函数动态赋予权重的方法[14]设计联合损失函数,如式(6)所示:
Lfinal=W1·Lsimilar+W2·Lpose。
(6)
式中:Lsimilar为式(4)所表示的相似性检测网络中的三元损失函数;Lpose为式(5)表示的位置姿态回归损失函数;权重W1、W2分别为![]() 通过噪声参数σ1、σ2动态调整两个损失函数之间的平衡[13]。
通过噪声参数σ1、σ2动态调整两个损失函数之间的平衡[13]。
2 结合场景连接图的选取策略
传统的InitIP选取框架都是通过图像的外观特征和几何关系来进行筛选。然而,在某些实际场景中,这些方法选择的InitIP会出现与整个场景关联度较低,或者处于场景边缘的情况,导致场景重建不完整的问题。因此,利用多任务网络的中间输出建立一个场景连接图,在该连接图中选取处于场景稠密区域的InitIP。
2.1 场景图构建方法
首先,给出所使用符号的定义,I={Ii}代表图像集合,多任务网络的中间输出为图像特征向量间的距离集合D、相对位移集合T、相对旋转集合R。定义图像相似度集合为S,任意两幅图像Ii和Ij相似度为sij∈S,sij由式(7)计算得到:
(7)
式中: dij∈D,为式(1)所求两特征向量间的距离。
类似地,定义两幅图像的相对位移tij∈T和相对旋转Rij∈R,其中tij、Rij分别对应1.1节中的Trel、Rrel。然后,定义场景连接图为节点和边缘的集合G=(N,E),其中N代表连接图中节点集合,任意ni∈N对应I中一幅图像Ii,E则代表边缘的集合,初始时为空。当两图像之间的相似度、相对位移、相对旋转均处于所设定的取值范围时,则为两个节点ni与nj连接一条边缘eij∈E,边缘的权重被设置为相似度与相对位移的乘积,如式(8)所示:
wij=sij·tij。
(8)
该权重可以综合度量两图像的特征相似程度和几何关系,因此边缘的数据结构可表示为eij=(ni,nj,wij)。建立场景连接图的完整算法具体步骤如下。
Step 0 初始化连接图。设定图像集合I,图像间的相似度集合S,图像间的相对姿态集合R、T,为I中的每一幅图像Ii生成一个节点ni,组成节点集合N,生成一个空的边缘集合E。设置相似度阈值s0、相对位移阈值t0,相对旋转阈值R0;
Step 1 访问N中任一未被访问的节点ni,在S、 T、 R中查询ni所对应图像Ii与其余图像Ij的相似度sij、相对位移tij与相对旋转Rij;
Step 2 当sij≥s0,且tij≤t0、Rij≤R0时,为节点ni与图像Ij所对应的节点nj之间连接一条边缘eij,边缘权重为wij,然后将边缘eij=(ni,nj,wij)存储到集合E中;
Step 3 当N中所有节点都被访问,输出最终场景连接图G=(N,E),否则返回Step 1。
2.2 基于场景图的选取方法
通过2.1节方法建立了场景连接图后,本节提出基于场景连接图的初始图像对评分方法,首先计算每个节的度deg,然后通过两幅图像度之和(degi+degj)来衡量候选InitIP与剩余图像的关联程度,判断该图像对是否位于场景稠密区域。但是,在将度的数量纳入参考指标时,可能出现InitIP中一幅图像的度较大,而另一幅图像的度很小的情况,这样仍有可能导致重建结果精度不高,甚至无法重建出完整场景的问题。因此,本文将两幅图像度之间差的绝对值的指数函数e|degi-degj|定义为度平衡因子bij,以衡量两幅图像度的平衡程度,两幅图像度的差值越小,则平衡因子越小,最后计算的总评分也越高。
计算ni,nj两个节点所代表的图像的最终评分,令这两个节点的度的和为mij,度平衡因子为bij,则有式(9)、(10):
mij=degi+degj;
(9)
bij=e|degi-degj|。
(10)
评分的总体公式如式(11)所示:
(11)
式中: Gscoreij代表基于场景连接图方法的评分;wij由式(8)计算得出。
整个场景连接图的初始对选取算法具体步骤如下。
Step 0 初始化:以2.1节中建立的场景连接图、图像集合I为输入,遍历连接图G的节点集合N中每一个节点ni,计算每个节点的度degi并存储;
Step 1 访问E中任一未被访问的边缘eij,读取eij所连接的两个节点ni和nj,根据式(9)、式(10)计算两节点间的度的和mij与度平衡因子bij;
Step 2 读取eij中的wij,结合bij与mij,根据式(11)计算该对节点的Gscoreij;
Step 3 当E中所有边缘eij都被访问,对Gscoreij排序,取得分最高的节点对(ni,nj)所对应的图像对(Ii,Ij)组成初始图像对Ipair=(Ii,Ij)(InitIP)并输出,否则返回Step 1。
总体来说,本方法更倾向于选择靠近场景中心的InitIP,旨在解决特殊场景中传统方法与多任务方法所选的InitIP容易陷入局部最优,而导致的重建精度低、不完整等问题,相较于传统方法提升了计算效率的同时对特殊场景的鲁棒性更好,适用范围更广。
3 实验与结果分析
3.1 实验环境及数据
本文所有实验均在配备Intel i76700 K处理器和单个NVIDIA GTX 1080 Ti图形显卡的实验机上进行。采用的深度学习框架为TensorFlow,学习率的更新策略为每迭代10 000步,将学习率调整为当前学习率的0.9倍直至完成训练。稀疏重建对比的传统方法为Alicevision[6]。
实验中采用由香港科技大学的计算机科学与工程系建立的公开数据集GL3D[7]作为训练数据集。其中包含了90 630张涉及378个不同场景的高分辨率图像。在测试时,采用Cambridge Landmarks Dataset室外数据集[15],这是一个大型的城市数据集,包含来自剑桥大学周围的多个不同建筑场景。
3.2 多任务网络的实验
在测试数据集的5个场景的数据集上进行InitIP选取实验,图7为一个场景的InitIP示意图,图7(a)为Alicevision所选取的;图7(b)、图7(c)分别为浅层交叉网络与深层交叉网络的选取结果。从外观上看,交叉连接的两个网络所选择的InitIP也基本符合特征相似与空间位移的原则。

图7 3种方法所选InitIP对比图
Figure 7 Comparison of InitIP selected by three methods
进一步定量对比传统方法与多任务方法所选InitIP作为起点进行稀疏重建时的表现,如表1所示。定量结果显示,两种交叉连接方式相较于Alicevision速度上都有较大提升,对比选取时间,所提出的多任务方法在多种不同场景中的选取速度提升5倍以上。在相同的测试场景下,深层交叉连接网络因为在更深的层级中嵌入了通道数更多的卷积层,导致模型参数量上升,从而使得整体的推理时间略长于浅层连接。但深层交叉连接的网络的实验结果,在5个重建场景中的最终误差都最低,其中2、3场景中的重投影误差有明显降低。综合来看,深层交叉网络性能要高于浅层交叉。
表1 稀疏重建结果定量对比表
Table 1 Quantitative comparison of sparse reconstruction results
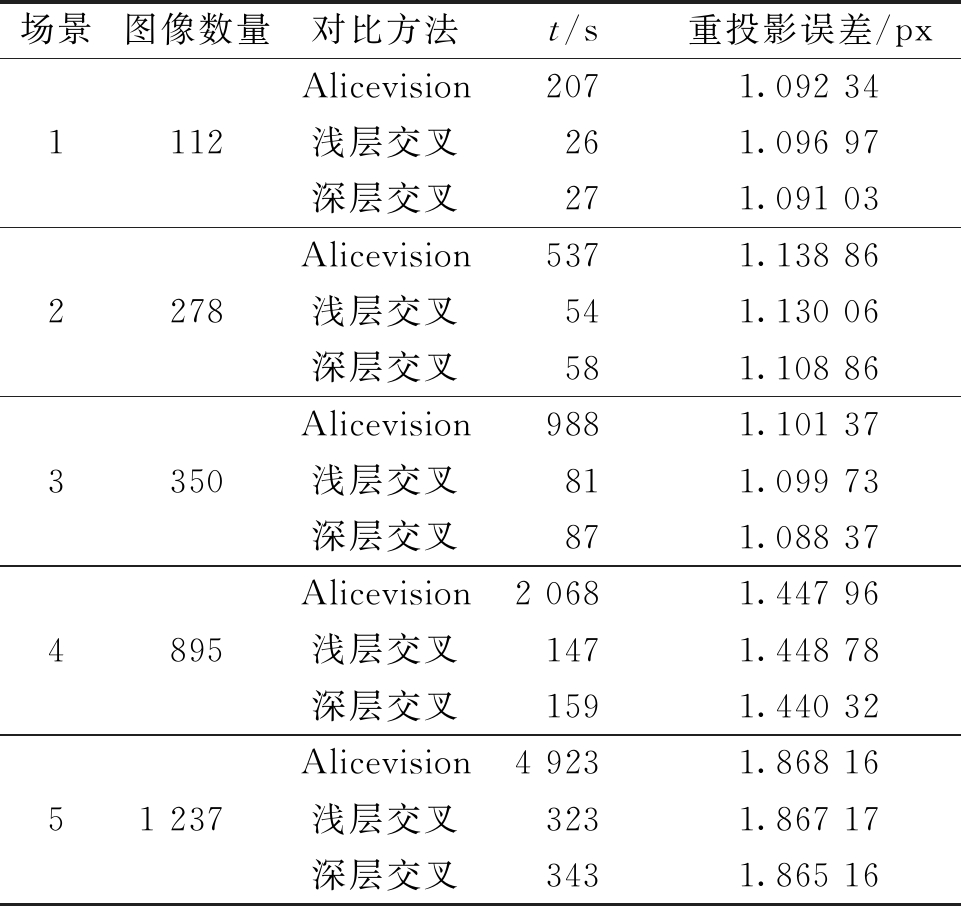
场景图像数量对比方法t/s重投影误差/px111222783350489551 237Alicevision2071.092 34浅层交叉261.096 97深层交叉271.091 03Alicevision5371.138 86浅层交叉541.130 06深层交叉581.108 86Alicevision9881.101 37浅层交叉811.099 73深层交叉871.088 37Alicevision2 0681.447 96浅层交叉1471.448 78深层交叉1591.440 32Alicevision4 9231.868 16浅层交叉3231.867 17深层交叉3431.865 16
3.3 场景图方法的实验
进一步对IVRTC比赛中无人机采集的、更大范围的场景数据[16]进行基于场景图方法的实验,该数据集包含498张分辨率为5 472×3 648像素的航拍图像,多任务网络采用精度更高的深层交叉网络,所建立场景连接图如图8所示。
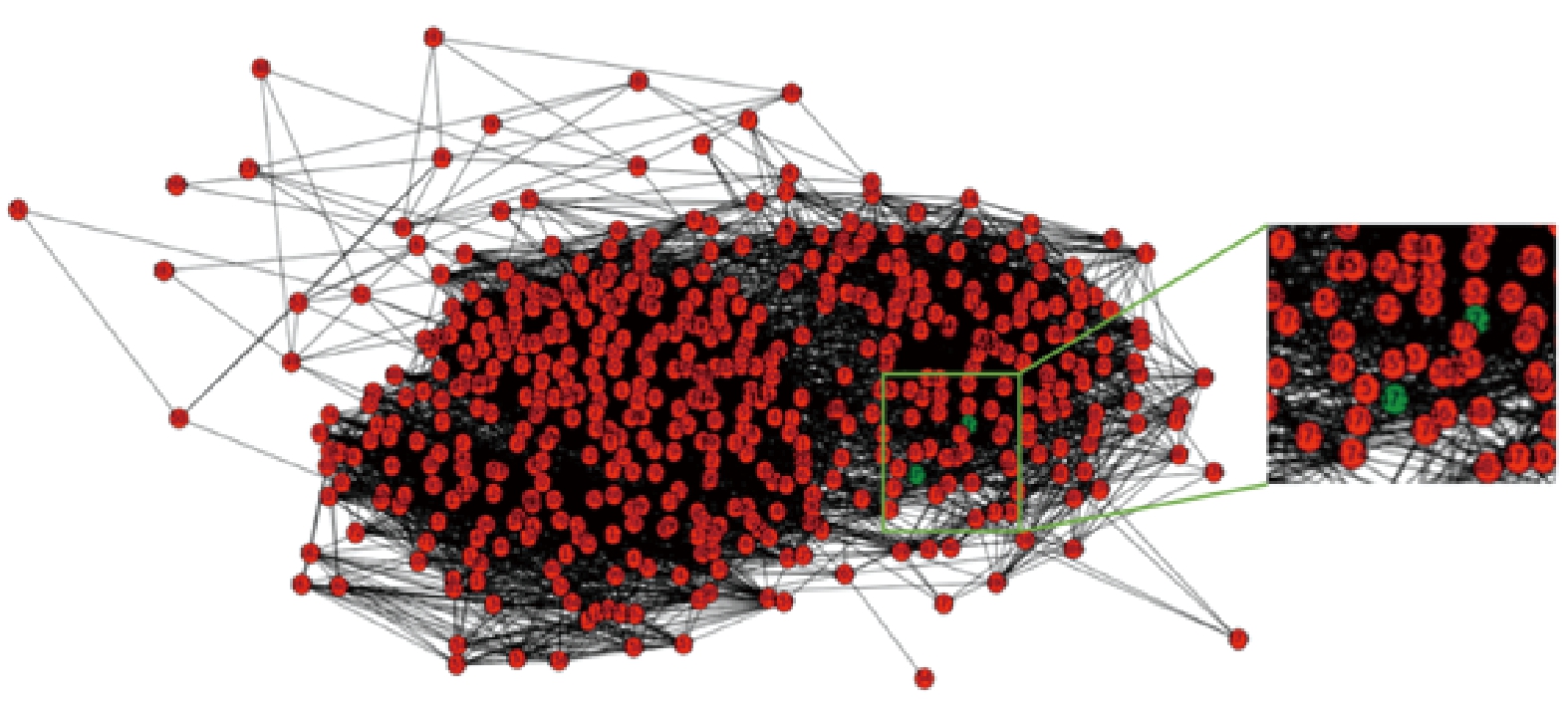
图8 利用交叉网络中间输出建立的场景连接图
Figure 8 Scene connection graph established using the intermediate output of the cross-network
所选择的InitIP在场景连接图中使用绿色节点标注,可以看出其处于场景稠密区域,与Alicevision所选的InitIP,以及交叉网络直接选取的InitIP对比如图9所示。

图9 无人机场景InitIP对比图
Figure 9 Comparison of InitIP in aerial scenes
使用以上3组图像作为稀疏重建的起始点进行增量式SfM,重建结果如图10所示,图中粉色方锥形代表的相机表示两幅初始图像。图10(a)中Alicevision所选的InitIP仅引导重建出整个场景外围的一部分,只完成了少量图像的注册。图10(b)为交叉网络+场景图方法所重建的场景,可见该方法所选InitIP(由图中红色矩形框标出)能引导出完整的重建场景,其位置也更靠近场景中心,达到了所提方法的预期。图10(c)中交叉网络直接选取的重建结果相对完整,但是InitIP(由红色矩形框标出)距离场景稠密区域还有一定距离。进一步对比图10(b)中的稀疏点云,该组实验结果仅重建出靠近InitIP中心区域的稀疏点云,在外侧树木部分还存在大量点云缺失的情况。
进一步定量地对比稀疏重建的结果,如表2所示,方法A、B、C分别为Alicevision、交叉网络+场景图方法、交叉网络直接选取。
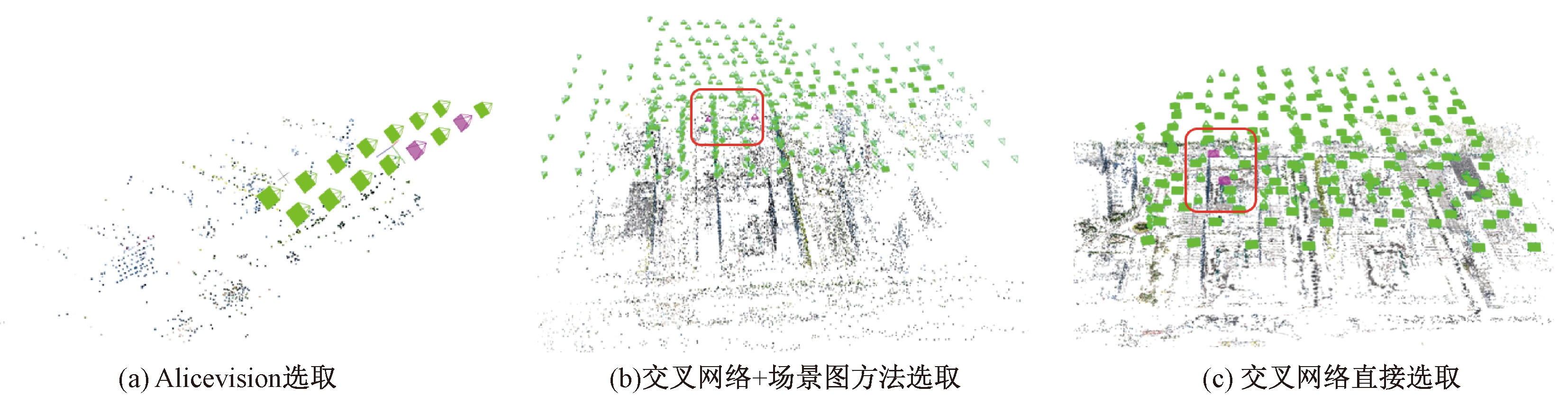
图10 无人机场景稀疏重建对比图
Figure 10 Comparison of sparse reconstruction of aerial scenes
表2 稀疏场景重建数据对比表
Table 2 Comparison of sparse reconstruction results
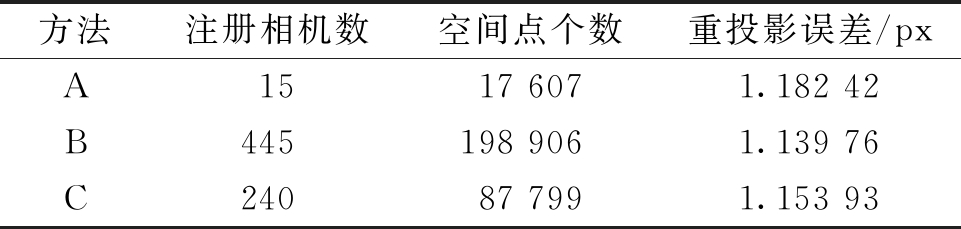
方法注册相机数空间点个数重投影误差/pxA1517 6071.182 42B445198 9061.139 76C24087 7991.153 93
可以看出,多任务方法与Alicevision对比,场景完整度均大幅提升,结合场景图的方法所选的InitIP则能够引导重建出最完整的稀疏场景,拥有最多的注册相机数、空间点数目,重建的空间点数量增加约10倍,重投影误差下降了约0.05 px。综上所述,多任务学习结合场景连接图的选取策略能够高效地选取处于场景稠密区域的InitIP,从而引导重建出更完整、精度更高的稀疏点云。
4 结论
根据初始图像对选取问题的特点,通过整合相似性检测和相机姿态回归两个子网络实现了一种基于多任务学习的InitIP选取网络,以提高增量式SfM中初始对选取过程的效率,并针对特殊重建场景提出结合场景连接图的选取策略,以提高重建的鲁棒性。实验结果证明所提方法在提高了效率的同时,能够很好地保证特殊场景重建的完整性和稳定性。
[1] BEDER C, STEFFEN R. Determining an initial image pair for fixing the scale of a 3d reconstruction from an image sequence[C]//Joint Pattern Recognition Symposium. Berlin: Springer, 2006: 657-666.
[2] HANER S, HEYDEN A. Covariance propagation and next best view planning for 3D reconstruction[C]//European Conference on Computer Vision. Berlin: Springer, 2012:545-556.
[3] SCHONBERGER J L, FRAHM J M. Structure-from-motion revisited[C]//Proceedings of the IEEE Confe-rence on Computer Vision and Pattern Recognition. New York: IEEE, 2016: 4104-4113.
[4] MOULON P, MONASSE P, MARLET R. Adaptive structure from motion with a contrario model estimation[C]//Asian Conference on Computer Vision. Berlin: Springer, 2012:257-270.
[5] 张艺琨,唐雁,陈强. 基于多特征融合的三维模型检索[J].郑州大学学报(工学版), 2019, 40(1):1-6.
[6] RUDER S. An overview of multi-task learning in deep neural networks[EB/OL]. (2017-06-15)[2020-07-25].https://arxiv.org/abs/1706.05098.
[7] SHEN T W, LUO Z W, ZHOU L, et al. Matchable image retrieval by learning from surface reconstruction[C]//Asian Conference on Computer Vision. Berlin: Springer, 2018:415-431.
[8] KENDALL A, GRIMES M, CIPOLLA R. Posenet: a convolutional network for real-time 6-DOF camera relocalization[C]//Proceedings of the IEEE International Conference on Computer Vision. New York: IEEE, 2015:2938-2946.
[9] SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York:IEEE, 2015:1-9.
[10] AKENINE-MOLLER T, HAINES E, HOFFMAN N. Real-time rendering[M]. 3rd ed. New York: A K Peters/CRC Press, 2019.
[11] 姜三. 无人机倾斜影像高效SfM重建关键技术研究[D]. 武汉:武汉大学, 2018.
[12] FUKUDA S, YOSHIHASHI R, KAWAKAMI R, et al. Cross-connected networks for multi-task learning of detection and segmentation[EB/OL]. (2018-05-15)[2020-07-25]. https://arxiv.org/abs/1805.05569.
[13] ZHANG Y, YANG Q. An overview of multi-task learning[J]. National science review, 2018, 5(1): 30-43.
[14] KENDALL A, GAL Y, CIPOLLA R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2018:7482-7491.
[15] KENDALL A, CIPOLLA R. Modelling uncertainty in deep learning for camera relocalization[C]//2016 IEEE International Conference on Robotics and Automation (ICRA). New York: IEEE, 2016:4762-4769.
[16] IVRTC dataset[EB/OL].(2019-10-31)[2020-07-25].http://www.ivrtc.org/?page_id=660.