0 引言
随着新能源战略的大力推进，风力发电开发力度不断加大，且拥有广阔的发展前景。海上风电几乎不占用土地资源且设备利用率高，因此许多临海国家正在积极探索海上风电发展之路。海上风电系统中至关重要的一环便是电力输送，目前常用的输电技术为高压交流输电(HVAC)和高压直流输电(HVDC)以及分频输电技术(fractional frequency transmission system，FFTS)。HVAC因电缆电容充电电流限制距离，仅适用于小规模近距离海上风电场。HVDC中直流断路器无法应用成熟的灭弧技术，且需要海上换流站。而FFTS可采用传统交流断路器，并使用更低的频率来提高输电能力[1]，成为大规模远距离海上风电场的更佳选择。FFTS的核心在于变频装置，继模块化多电平换流器(modular multilevel converter，MMC)应用于交-交变频系统[2-3]后，模块化多电平矩阵变换器(modular multilevel matrix converter，MMMC)采用级联式结构，在低频大容量场合更具优势[4]，且在子模块发生故障时具有更好的容错性能[5]。因其具有谐波含量低且无须额外的充电电路的优点，目前国内外对MMMC的应用主要集中在输配电系统的电压质量优化以及电动汽车充电领域[6-7]。
由于MMMC桥臂电流为输入电流分量和输出电流分量以及内部环流分量的叠加，成分较为复杂，因此桥臂电流的控制较为困难。MMMC桥臂电流的常用控制方法为直接控制法，文献[8-10]采用桥臂电流直接控制法对MMMC进行控制，事实上桥臂电流直接控制可等效为比例控制，但需忽略交流电源电压和子模块电容电压在开关周期内的变化。比例谐振控制(proportional resonant，PR)可设定不同的谐振频率来并联多个PR控制器，从而对桥臂电流中不同频率的分量分别进行调控[11]，故本文针对FFTS系统内部电气量的特性设计PR控制策略来控制MMMC桥臂电流。为了解决理想PR存在的抗扰动能力较差的问题，本文采用准比例谐振(quasi-proportional resonant，QPR)控制策略。
本文首先分析了MMMC的内部结构和工作原理，对其建立了数学模型，搭建了基于MMMC的FFTS系统，并给出了系统的控制框图，对主要电气量提出相应的控制策略。最后，搭建了仿真模型并对比直接控制和QPR控制策略的仿真结果，验证了QPR控制策略的可行性与优越性。
1 MMMC数学模型
MMMC的拓扑结构如图1所示，共由9个桥臂组成，每个桥臂由1个电感L(内阻较小，可忽略不计)和n个全桥子模块(sub-module，SM)串联组成，分别连接2个三相交流系统。系统输入侧为工频侧，定义三相输入侧电压为ua，ub，uc，三相输入侧电流为ia，ib，ic,频率为fs；系统输出侧为低频侧，定义三相输出侧电压为uu，uv，uw，三相输出侧电流为iu，iv，iw, 频率为fr。定义桥臂电压为uxy，桥臂电流为ixy，其中x取a、b、c，y取u、v、w。
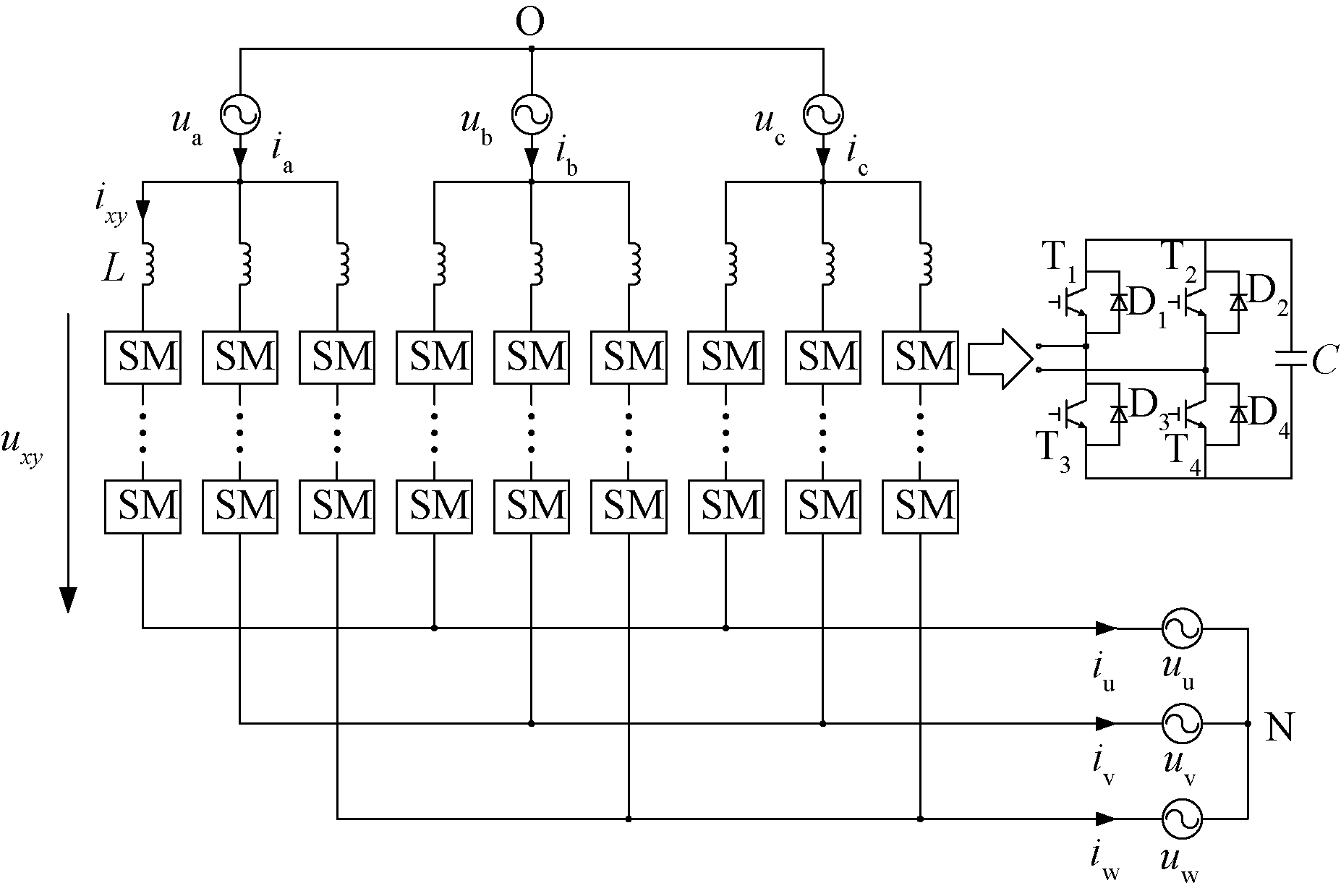
图1 MMMC内部结构示意图
Figure 1 Schematic diagram of MMMC inner structure
假设系统正常运行，此时MMMC处于三相对称工作状态，输入侧和输出侧电压、电流为三相对称的正弦波，则可定义电压、电流表达式如下：
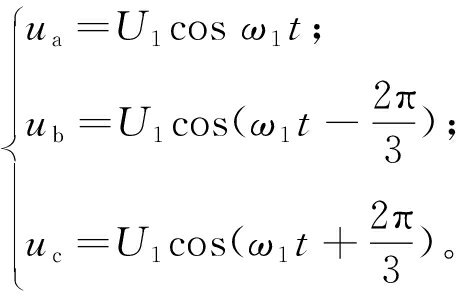
(1)
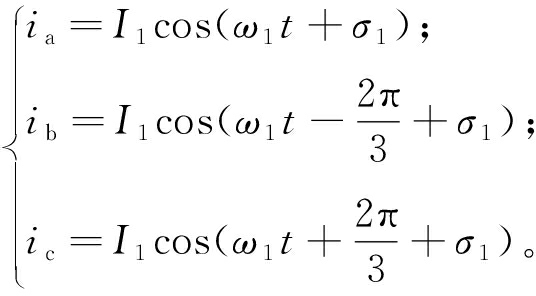
(2)
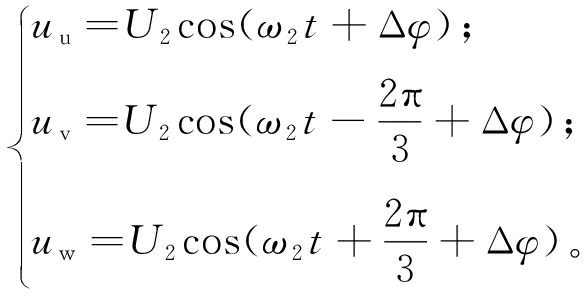
(3)
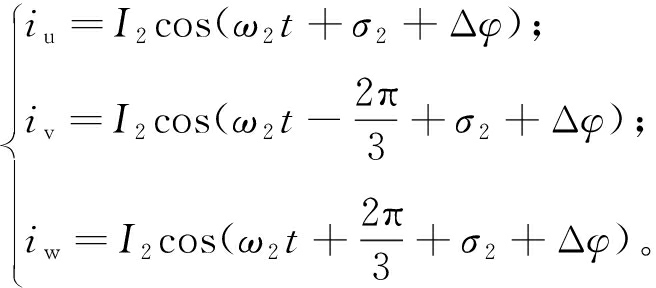
(4)
式中：U1、U2、I1、I2分别代表输入、输出侧的电压与电流幅值；ω1、ω2分别代表输入、输出侧的角频率；σ1、σ2分别代表输入、输出侧的功率因数角；Δφ为输入侧与输出侧的相位差。
根据Kirchhoff定律，MMMC桥臂电流满足：
(5)
桥臂电压满足：
(6)
式中：uNO为输入侧与输出侧的中性点电压差。
当系统稳定运行时，通过控制桥臂电流，使得MMMC导通或关断特定的子模块来改变桥臂电压，从而得到期望的输出值。因此，为便于分析，可将各桥臂支路的n个子模块等效为受控电压源，如图2所示。
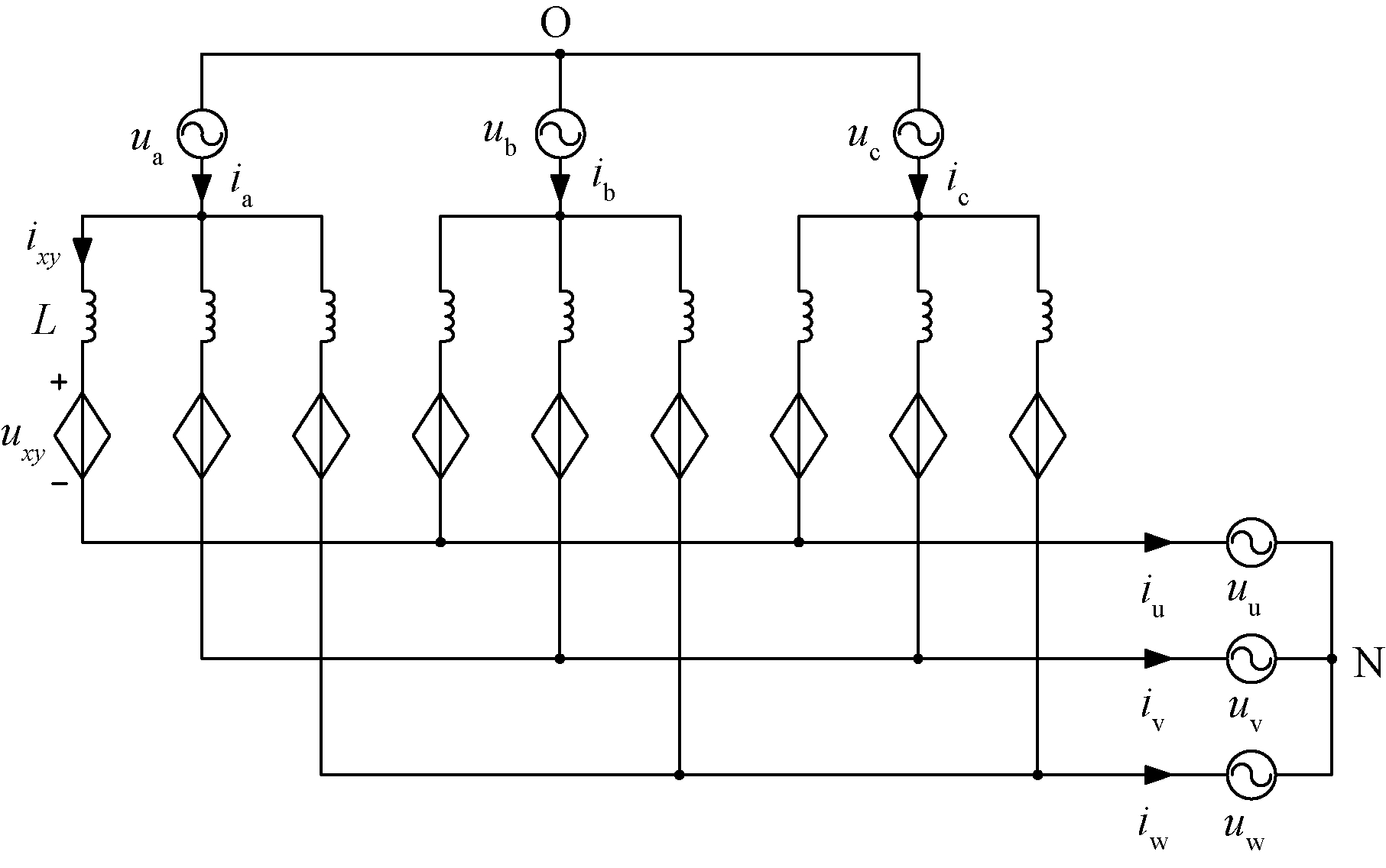
图2 MMMC等效电路模型
Figure 2 Equivalent circuit model of MMMC
由式(5)、(6)可知，各桥臂的电压和电流均由输入侧频率和输出侧频率的分量构成，为对输入侧和输出侧电气量进行解耦，需对式(6)进行双Clarke变换与Park变换[12]，因篇幅限制，此处不再详细推导。
2 MMMC控制策略
2.1 电流环控制
MMMC的桥臂电流成分较为复杂，环流路径不仅存在于各个桥臂之间，并且存在于相与相之间。桥臂电流直接控制需忽略交流电源电压和子模块电容电压在开关周期内的变化，故本文采用比例谐振控制对MMMC的桥臂电流进行控制。PR控制稳态与瞬态性能良好，可通过设定不同的谐振频率来并联多个控制器，从而实现对系统中不同频率的分量进行分别控制。
理想PR控制器传递函数为
(7)
式中：Kp为比例增益；Kr为谐振增益；ωr为谐振频率。
理想PR控制器的频率响应如图3所示。由图可知，理想PR控制器虽然能够实现无稳态误差控制，但只对单一的频率起作用。在实际应用中，电网频率往往无法恒定为额定值，此时理想PR控制器抗扰动能力较差的缺点就会凸显。
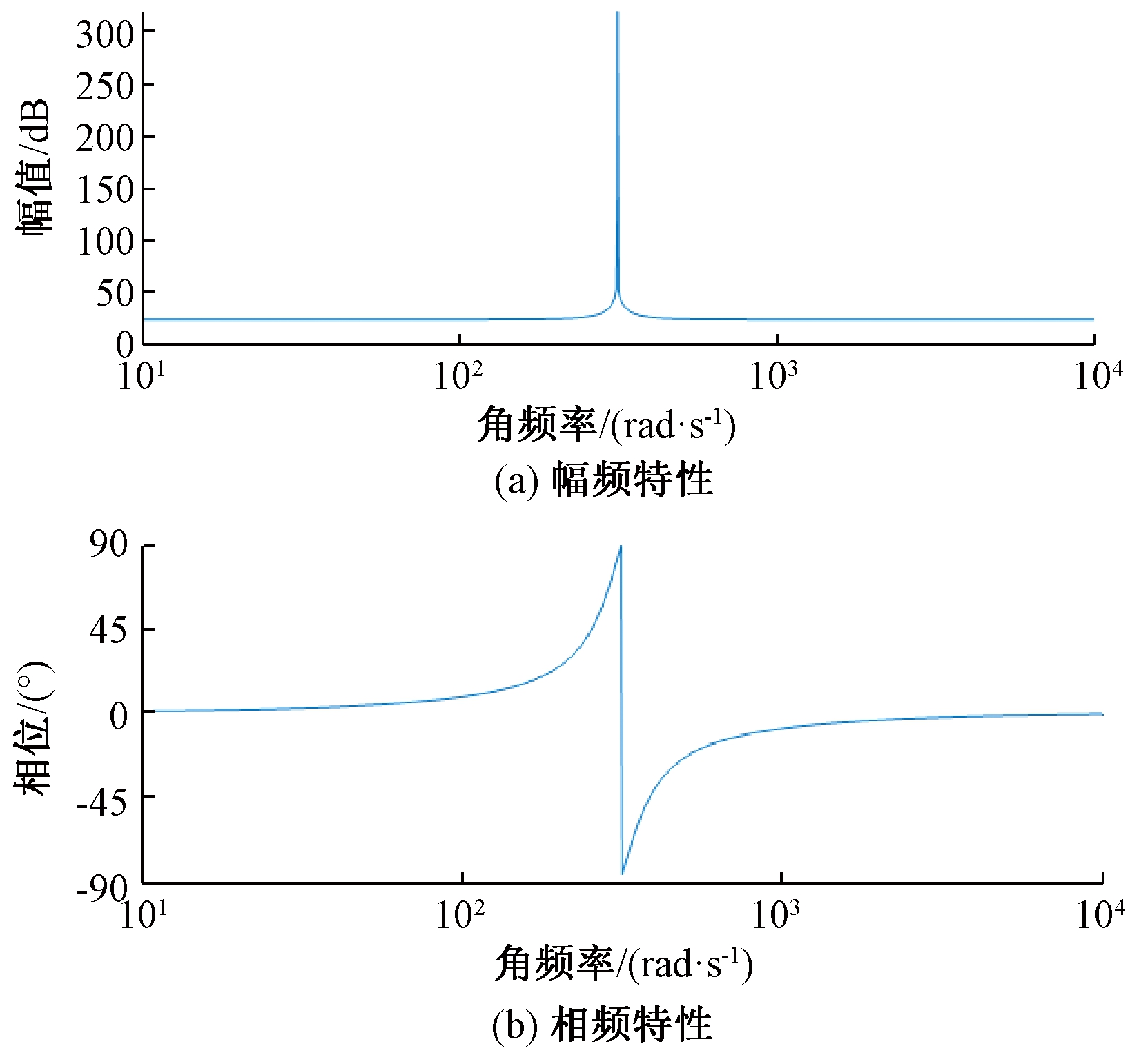
图3 理想PR控制器频率响应
Figure 3 Frequency response of ideal PR controller
准比例谐振(QPR)控制器可以解决理想PR控制器存在的问题，其传递函数为
(8)
式中：ωco为控制器的截止频率。
QPR控制器的频率响应如图4所示。由图可知，与理想PR控制器相比，QPR控制器减小了谐振频率处的增益，但在谐振频率附近形成较大增益的频率带宽，减小了频率偏移带来的影响。MMMC桥臂电流包含输入频率和输出频率分量，可共用1个比例增益Kp，谐振增益Kri、Kro可以不同，其QPR控制器如图5所示。
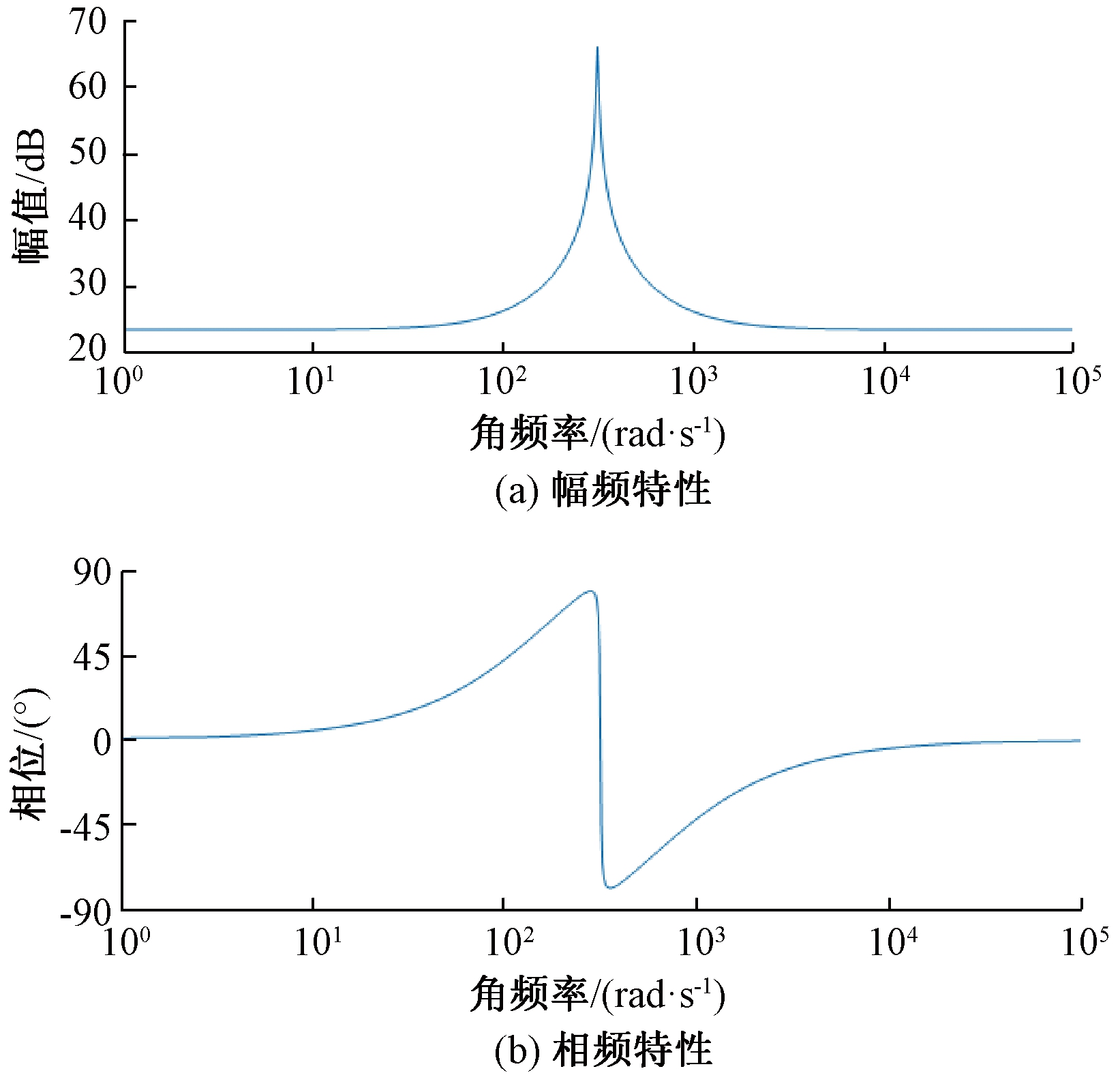
图4 QPR控制器频率响应
Figure 4 Frequency response of QPR controller
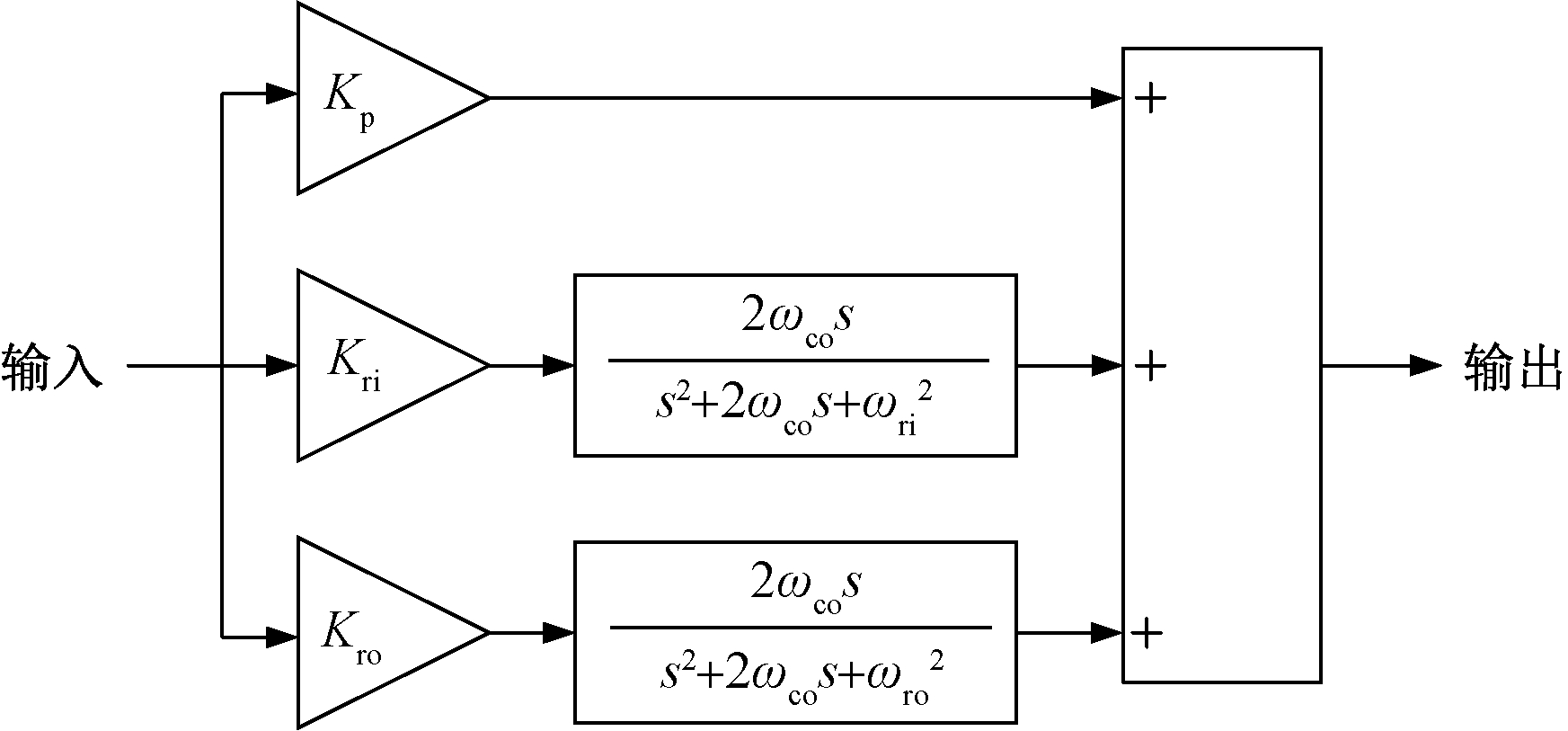
图5 QPR控制器内部结构
Figure 5 Inner structure of QPR controller
2.2 电压环控制
类似基于MMC的HVDC系统控制，MMMC外环电压输出是内环电流输入的参考值。根据相应电气量的性质，可将MMMC外环电压控制方法分为2种类型：①定有功功率控制、定交流电压频率控制、定直流电容电压控制等有功类的控制方法；②定无功功率控制、定交流电压幅值控制等无功类的控制方法[13-14]。为确保系统稳定安全运行，输入侧与输出侧应各选择一个有功类和一个无功类控制量。同时，为了保证总体电容电压均衡，必须有一侧包含定直流电容电压控制。本文外环控制方法如下。
输入侧定有功功率控制：
(9)
输入侧定交流电压幅值控制：
(10)
输出侧定无功功率控制：
(11)
输出侧定直流电容电压控制：
(12)
式中：
和
分别为输入侧相电流经过Park变换后的d、q分量；
和
分别为输出侧相电流经过Park变换后的d、q分量；Ps和
分别为输入侧系统有功功率的实际值和参考值；Us和
分别为输入侧母线电压幅值的实际值和参考值；Qr和
分别为输出侧系统无功功率的实际值和参考值；UC和
分别为所有直流电容电压平均值的实际值和参考值。
2.3 电容电压平衡控制
当工频侧与低频侧之间的有功功率不均衡时，会引起子模块电容电压波动，往往会导致系统无法处于最佳工作状态，严重时甚至导致系统不能正常工作[15-16]。实际工程中各子模块电容参数不可能完全相同，桥臂功率无法达到完全平衡，电容电压也就不能稳定在参考值处，需进行电容电压均衡。桥臂功率和电容电压间的关系为
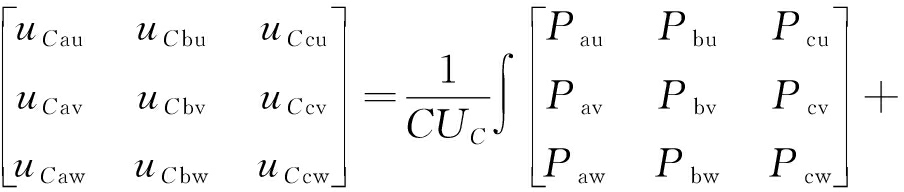
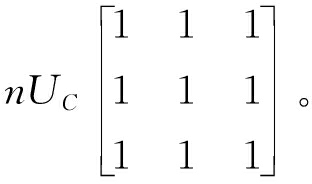
(13)
对式(13)进行双Clarke变换有
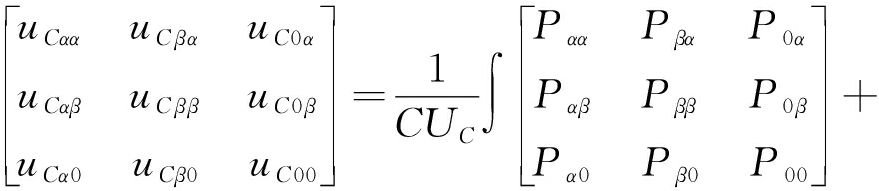
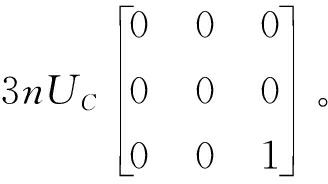
(14)
式中：uCxy为桥臂xy子模块电压之和；uCα0、uCβ0，uC0α、uC0β为相间电容电压的不均衡；uCαα、uCβα，uCαβ、uCββ为相内桥臂间电容电压的不均衡；uC00与系统总有功功率有关；Pα0、Pβ0、P0α、P0β为相间功率流动；Pαα、Pβα、Pαβ、Pββ为相内桥臂间功率流动；P00为对总电容电压均衡的控制，在输入、输出侧有功功率平衡时为0。
MMMC通过注入环流产生功率，改变相间和桥臂间的功率流动，实现功率平衡。为简化控制，忽略共模电压，仅控制注入环流实现电容电压均衡控制。通过计算αβ0坐标系下桥臂功率的参考值，再根据αβ0坐标系下桥臂瞬时功率的表达式，可得到注入环流分量的参考值
则通过PI控制得出αβ0坐标系下桥臂功率的参考值：
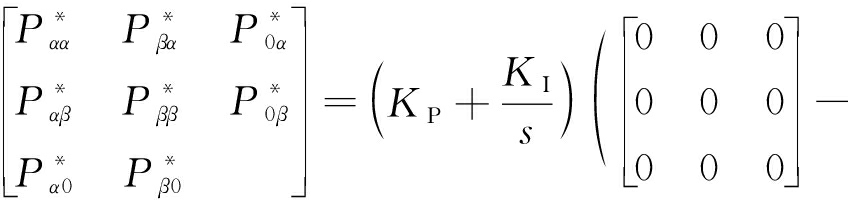
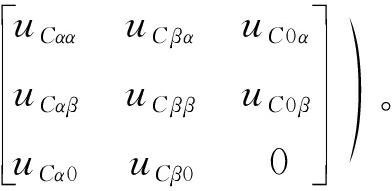
(15)
对电压环和桥臂电容电压均衡的输出进行Clarke/Park反变换，可得到直角坐标系下的桥臂电流参考值
经过QPR控制器得到调制信号。整个MMMC系统总体控制框图如图6所示。
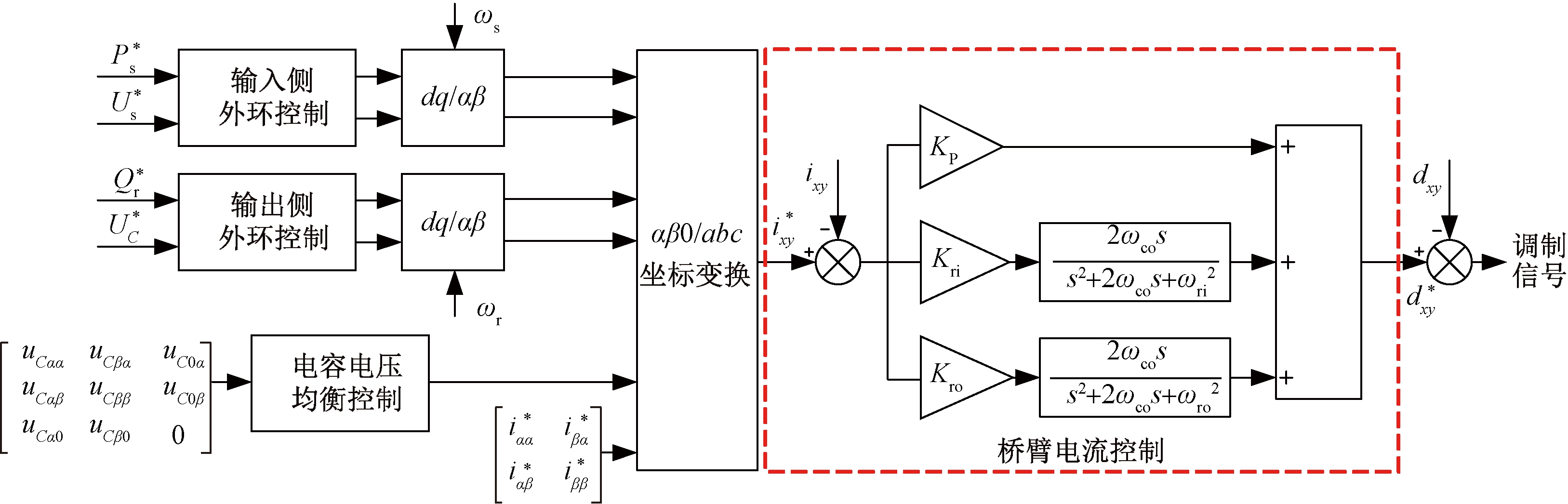
图6 MMMC系统总体控制框图
Figure 6 Diagram of overall control of MMMC system
3 仿真分析
为验证本文控制策略的可行性和优越性，搭建MMMC仿真模型进行仿真，系统参数如表1所示。
表1 仿真系统参数
Table 1 Parameters of simulation system
系统传输功率/MW输入侧电压有效值/kV输入侧电压频率/Hz子模块电容/F桥臂电感/H输出侧电压有效值/kV输出侧电压频率/Hz各桥臂子模块数目子模块电容电压/kV200110500.0050.0211050/32010
系统采用QPR控制器，传输功率初始设定为200 MW，为同时验证系统的稳态性能和动态性能，在t=1 s时，将设定的系统传输功率由200 MW降到100 MW，仿真结果如图7和图8所示。
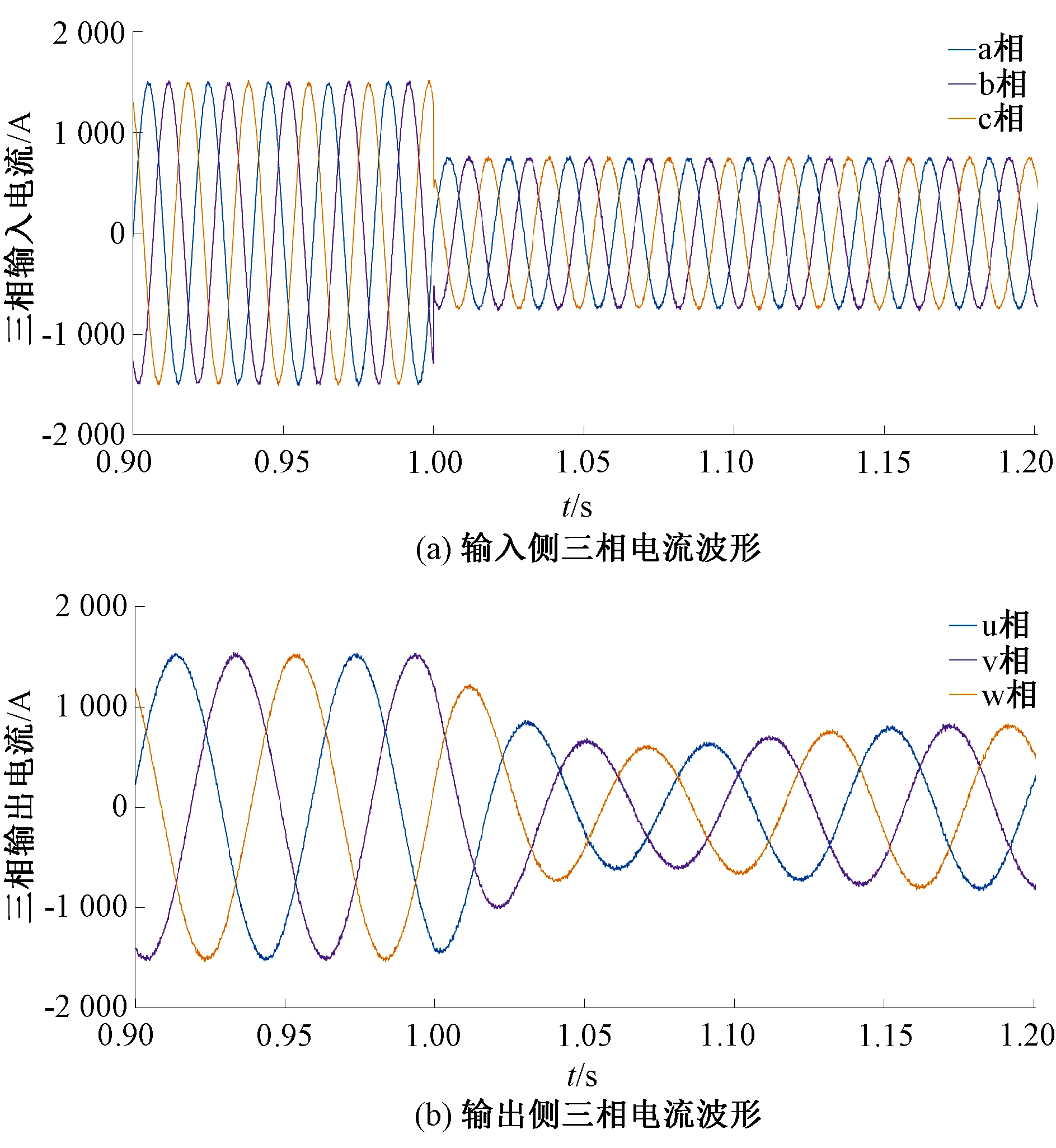
图7 系统三相电流波形
Figure 7 Three-phase current waveform of system
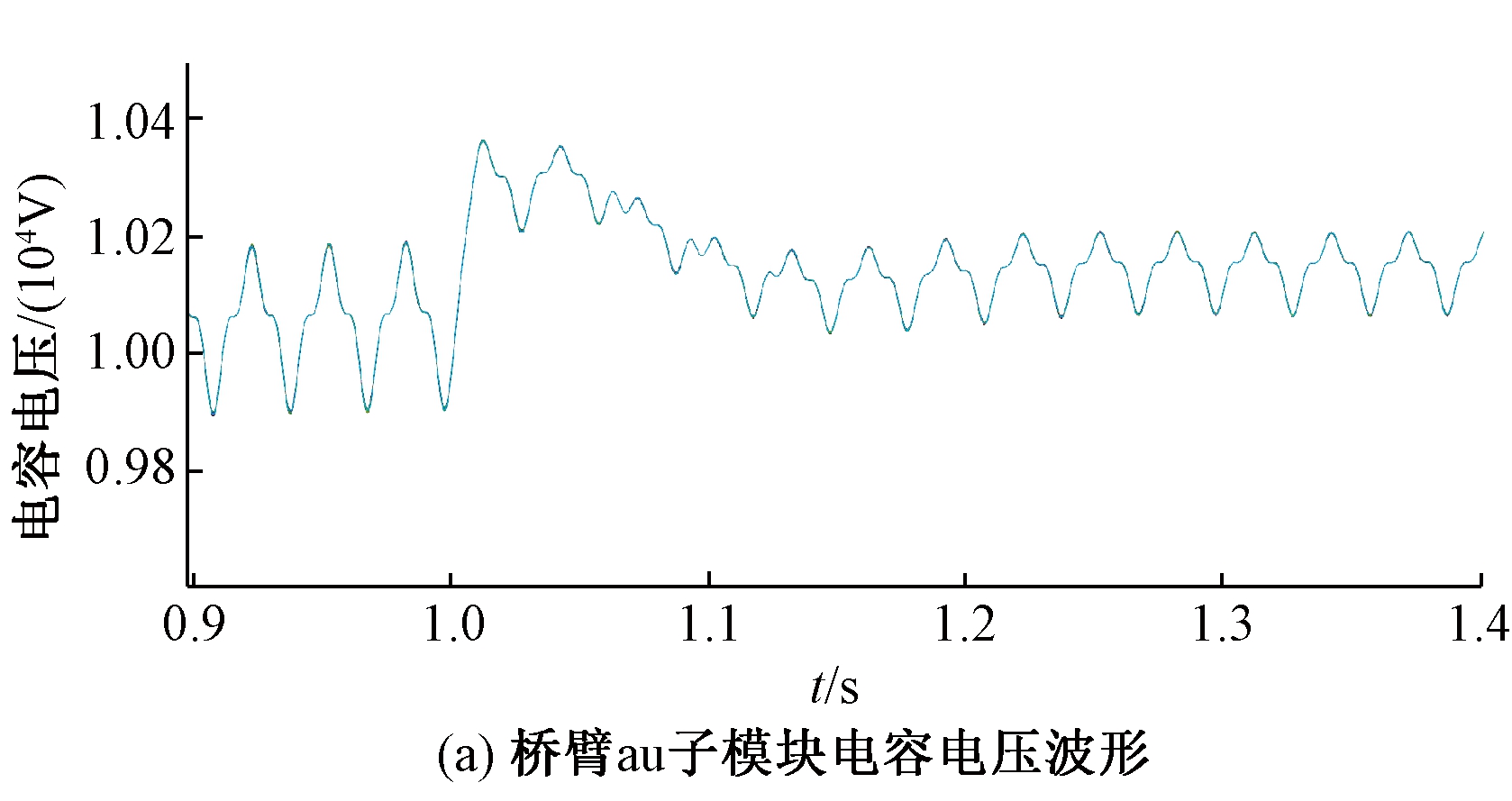
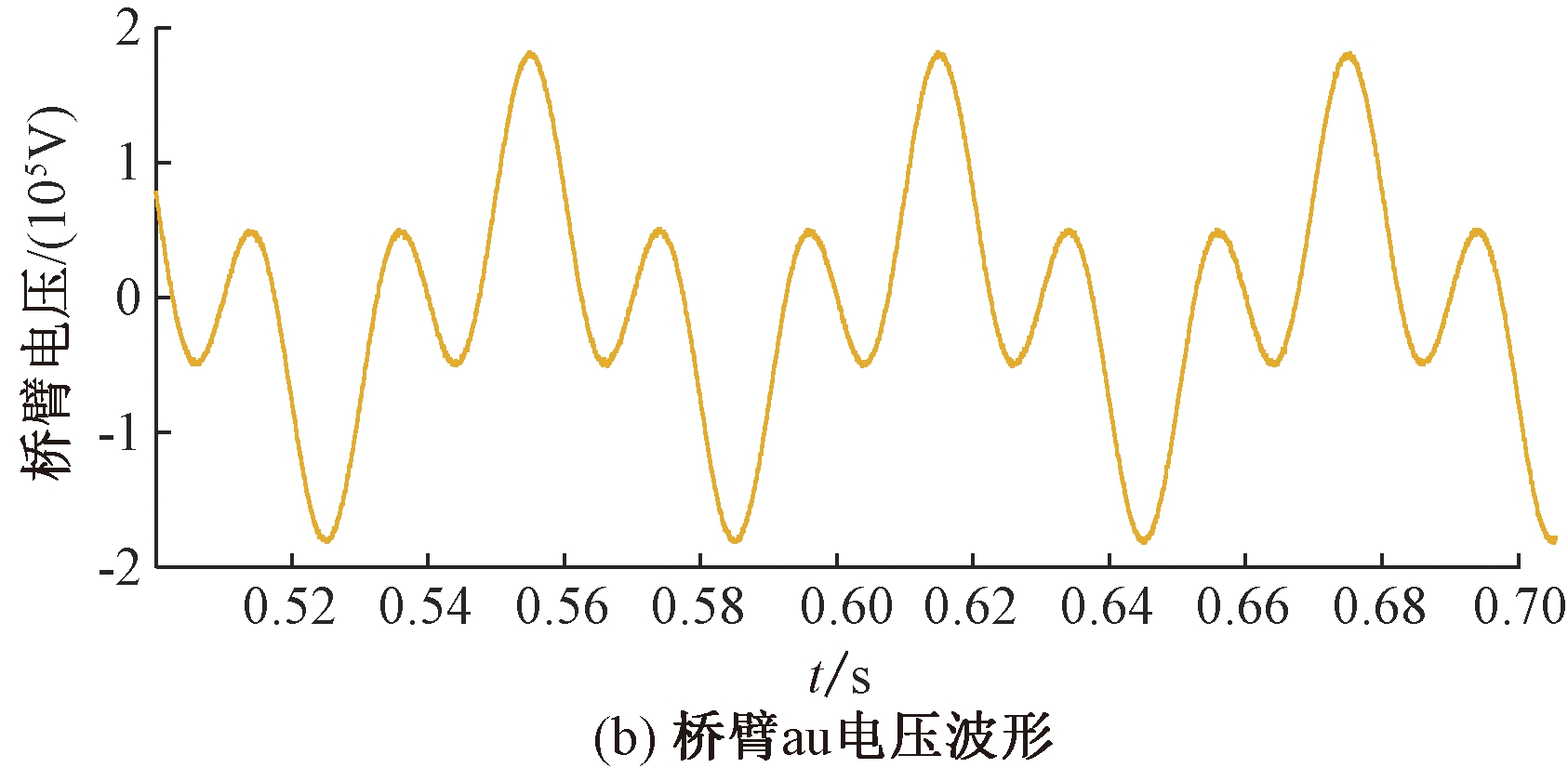
图8 MMMC桥臂电压波形
Figure 8 Arm voltage waveform of MMMC
由图7、8可以看出，稳态阶段系统运行正常，输入和输出电流波形良好，电容电压稳定在10 kV左右；当t=1 s，输入电流和输出电流在短暂的波动后重新进入稳态，电容电压小幅度波动，经过约0.12 s后重新进入稳态。该仿真结果验证了QPR控制的可行性。
同时，为验证QPR控制的优越性，分别给出了直接控制和QPR控制下桥臂电流实际值和参考值之差的波形，即两种控制方法下桥臂电流的稳态误差，仿真波形如图9所示。
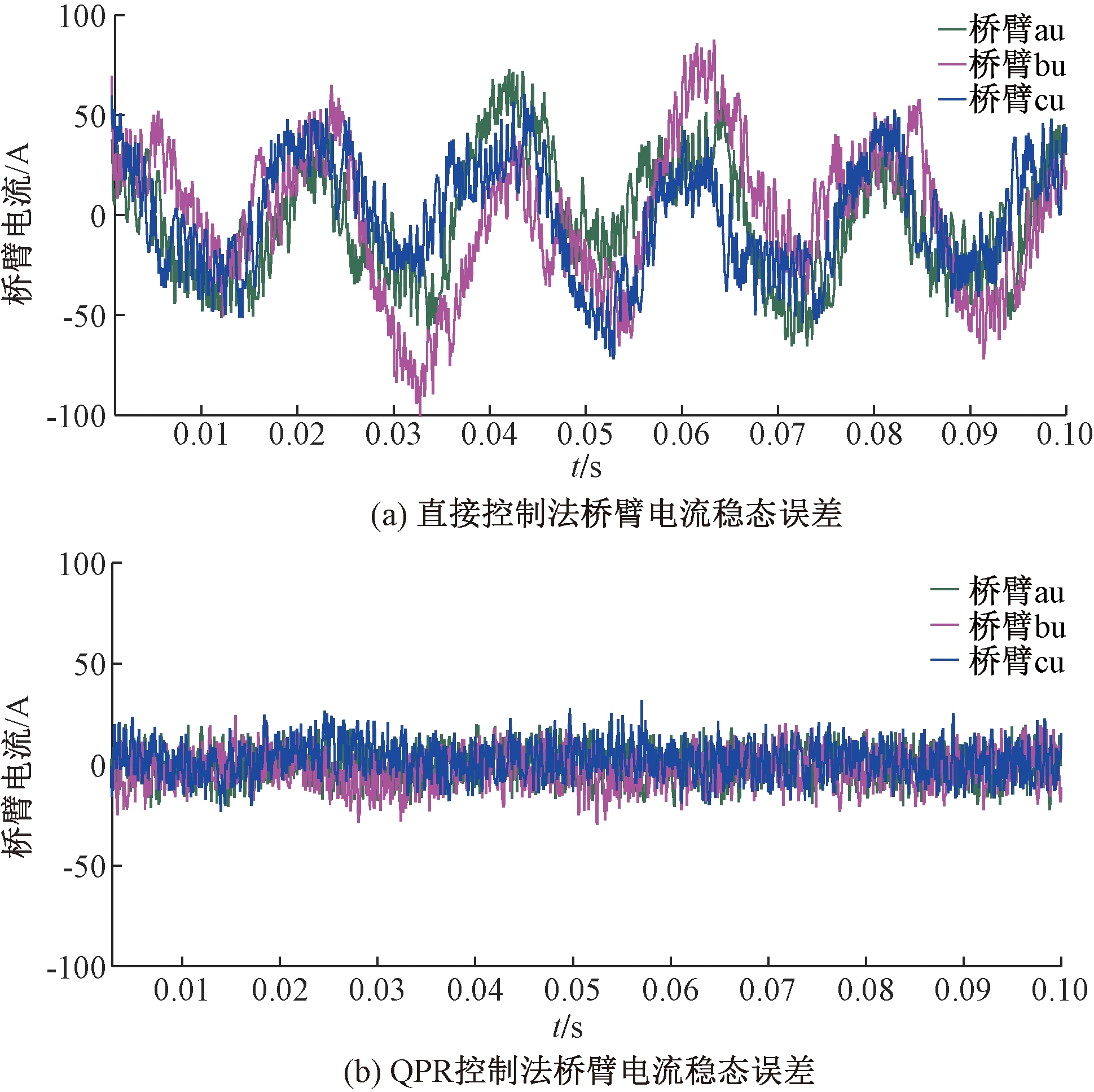
图9 两种控制方法对比
Figure 9 Comparison of two control methods
由图9可以看出，直接控制法的桥臂电流稳态误差超过了50 A，而QPR控制下的桥臂电流稳态误差仅为20 A左右，实际值与参考值更接近，稳态误差明显减小，跟踪更准确，验证了QPR控制的优越性。
4 结论
本文首先分析MMMC的内部结构，建立了其数学模型，根据分频输电系统的特性，设计了基于QPR控制器的桥臂电流控制方案；然后根据有功和无功控制要求给出了外环控制方案，并推导了桥臂电容电压和有功功率的关系，给出了电容电压平衡策略。最后在仿真平台上搭建了基于MMMC的海上风电系统模型，验证了控制系统良好的稳态和暂态性能，并通过对比直接控制法和QPR控制法的参考值跟踪仿真结果，验证了本文设计的QPR控制方法的可行性和优越性。
后期的研究可考虑在三相不对称情况下本文MMMC控制策略的实施与改进方法，亦可对子模块发生故障情况下的故障诊断和冗余子模块设置做进一步研究。
[1] 王锡凡,王秀丽.分频输电系统的可行性研究[J].电力系统自动化,1995,19(4):5-13.
[2] 张清枝,李志辉.具备直流故障隔离能力的新型MMC拓扑研究[J].郑州大学学报(工学版),2017,38(6):74-78.
[3] LIU S Q,WANG X F,WANG B Y,et al.Comparison between back-to-back MMC and M3C as high power AC/AC converters[C]//2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC).Piscataway:IEEE,2016:671-676.
[4] 李峰,王广柱,刘汝峰.模块化多电平矩阵变换器低频控制方法[J].电力系统自动化,2016,40(2):127-133.
[5] FAN B R,WANG K,ZHENG Z D,et al.Optimized branch current control of modular multilevel matrix converters under branch fault conditions[J].IEEE transactions on power electronics,2018,33(6):4578-4583.
[6] XU Q M,MA F J,LUO A,et al.Analysis and control of M3C-based UPQC for power quality improvement in medium/high-voltage power grid[J].IEEE transactions on power electronics,2016,31(12):8182-8194.
[7] 程振兴,王广柱,银泽一.基于MMMC插电式混合电动汽车变换系统及充电控制策略[J].电力系统自动化,2019,43(21):148-154.
[8] 欧朱建.模块化多电平矩阵变换器用于输电系统的关键技术研究[D].济南:山东大学,2018.
[9] 李峰.模块化多电平矩阵变换器关键技术研究[D].济南:山东大学,2016.
[10] 商秀娟.模块化多电平矩阵变换器控制策略研究[D].济南:山东大学,2016.
[11] 王文杰,杨益平,杭丽君,等.应用于交-交变换的M3C矩阵变换器系统控制策略[J].电力系统自动化,2020,44(12):186-192.
[12] 孟永庆,王健,李磊,等.基于双dq坐标变换的M3C变换器的数学模型及控制策略研究[J].中国电机工程学报,2016,36(17):4702-4712.
[13] SHARMA R,WU Q W,CHA S T,et al.Fault ride-through capability enhancement of VSC-HVDC-connected offshore wind power plants[J].电力系统自动化,2015,39(3):14-22.
[14] LI H F,LIU C R,LI G Y,et al.An enhanced DC voltage droop-control for the VSC:HVDC grid[J].IEEE transactions on power systems,2017,32(2):1520-1527.
[15] ZENG R,XU L,YAO L Z,et al.Analysis and control of modular multilevel converters under asymmetric arm impedance conditions[J].IEEE transactions on industrial electronics,2016,63(1):71-81.
[16] 李遥,许烈,李永东.单级模块化多电平矩阵变换器支路间电容电压平衡[J].清华大学学报(自然科学版),2017,57(11):1220-1227.