0 引言
图像拼接技术一般包括图像采集、图像预处理、图像配准和图像融合。其中图像配准是该流程的一个关键步骤。图像配准方法主要分为3大类：基于灰度的配准方法、基于变换域的配准方法和基于特征的配准方法。
基于特征的配准方法是最为常用的方法。以Brown等[1]的研究成果为里程碑，形成了一套相对成熟的解决方案，该方法也被称为全局单应变换方法。首先在图像对间的重叠区域内进行特征点检测匹配，生成全局单应矩阵，然后利用光束平差法修正相机参数，再将图像对投影变换至同一平面，最后利用图像融合算法生成一幅拼接结果图。此方法应用十分广泛，笔者也提供了开源的软件供下载使用，并且OpenCV计算机视觉库也封装了该方法，同时提供了多种参数选择，包括特征点检测方法、投影变换方法和图像融合方法等。但是此方法受到相机共光心和拍摄图像共平面条件的约束，而实际场景中一般很难满足该约束条件。后续的算法多是针对该问题进行改进。
针对图像配准阶段，2011年，Gao等[2]提出了一个新方法：既然仅仅使用全局单应矩阵无法解决视差所带来的深度问题，那么将场景划分为前后景分别计算单应矩阵，使用两个单应矩阵来对齐，做到无缝拼接大部分现实场景。2014年Zaragoza等[3]通过将图像划分为多个密集网格，然后每一个网格里进行特征关系查找，来计算局部单应关系，并给出了一套高效的计算方案(moving DLT)，在局部特征对齐的效果优良。2016年，Chen等[4]通过添加一个更强的全局相似性系数约束，保证了图像对之间的全局相似性变换。Misra等[5]通过利用深度学习去尝试进行特征点的检测、方向分配和描述子计算工作及端到端训练。
针对图像融合阶段，2013年，Gao等[6]提出用seam-cut指导来估计最佳几何变换，在图像融合阶段加入缝合线检测流程，以构造更为合理的拼接。2014年，Zhang等[7]借鉴经典视频去抖方法(content-preserving warps，CPW)的优化项和缝合线检测方法，提高了大视差场景的拼接性能。2016年，Lin等[8]在文献[6]的基础上，改进了缝合线估计方法，同时在配准阶段加入了曲线和直线保护项，提升了图像的拼接效果。
现阶段图像拼接技术中，仍然存在着以下几个问题：① 图像对重叠区域中深度不一致；② 图像的特征种类单一；③ 图像的特征数目相对较少；④ 图像的特征分布存在局限性。
这些问题导致目前的图像拼接算法对于大视差多焦段的图像匹配效果较差，在重叠区域易出现较为严重的伪影现象。本文对这些问题进行了研究，提出了针对伪影改善的拼接方案。
1 基于网格优化的图像配准方法
本文采用了一套基于网格优化的图像配准方法来保证对图像实施更好地对齐。首先使用点特征和线特征的特征检测方法，提高特征的数目和质量；随后利用基于先验的RANSAC方法获得最佳变换模型，并提高了模型的计算速度；紧接着使用APAP方法对图像进行网格变形；再使用多项图像对齐约束来获取到最佳的特征匹配对和变换参数，提升图像的拼接效果；最后利用柱面变换模型将一幅图像投影到同一平面之上。
1.1 结合点特征和线段特征的特征检测方法
首先使用SIFT[9](scale-invariant feature transform)特征检测算法检测图像特征点，然后使用LSD[10](line segment detector)算法来检测图像中的线段特征信息。LSD算法检测出的直线段有宽度和长度两大信息，可以根据宽度和长度对线段检测结果进行筛选，仅保留大于宽度阈值和长度阈值的有效线段，剔除对后续匹配不起作用或起干扰作用的过细或过短的冗余线段，得到优化的线段特征集合。通过足量的重复性实验选定上述长度和宽度阈值，对线段检测结果集合进行筛选。图1和图2所示是使用SIFT特征检测算法和LSD检测算法的检测结果。
1.2 基于先验的RANSAC筛选方法
1.2.1 经典的RANSAC筛选方法
在经典的RANSAC流程中，目标函数C被看作：在第k次迭代过程中，在当前变换参数H作用下，数据集U中满足变换参数的点的个数，也就是在当前变换条件下局内点(inliers)的个数，而RANSAC就是最大化C的过程。而判断当前点是否为局内点需要一个阈值t。
由此可知，RANSAC方法主要存在效率和精度的局限性。
(1)效率：与随机子集大小、局内点比例w、迭代次数k以及数据集U大小有关，因此在某些场景中效率较低。
(2)精度：经典方法计算参数时选取最小子集是从效率考虑的，往往得到的是非最佳参数，在应用之前需要做细化处理。
图1 点特征检测结果
Figure 1 Point feature detection result
图2 线段特征检测结果
Figure 2 Line feature detection result
1.2.2 基于先验的RANSAC筛选方法
由于RANSAC方法在每次初始化时会随机选取子集，而该子集与后续得到的单应矩阵的准确度存在着密切的联系，并且也会影响RANSAC方法的迭代速度。一般情况下，数据的情况是未知的，若在开始就知道特征点对的分布特点，就可以更快速地获得最佳采样集，构建最佳模型。因此，本文提出了基于先验的RANSAC筛选方法。
在初始化时提前确定好选取的子集，即构造先验集。将先验集构造的匹配结果局内点数目作为排序的依据，然后在后续每次采样时根据匹配结果进行由高到低的得分排序。这样在已知数据集的分布关系情况下，便有可能较早地确定好模型，同时提高模型的计算速度。图3是将二维样本作为输入，使用经典RANSAC方法和基于先验的RANSAC方法针对模型的计算时间做了对比验证，可以看出，本文方法在计算效率上有明显的优势。
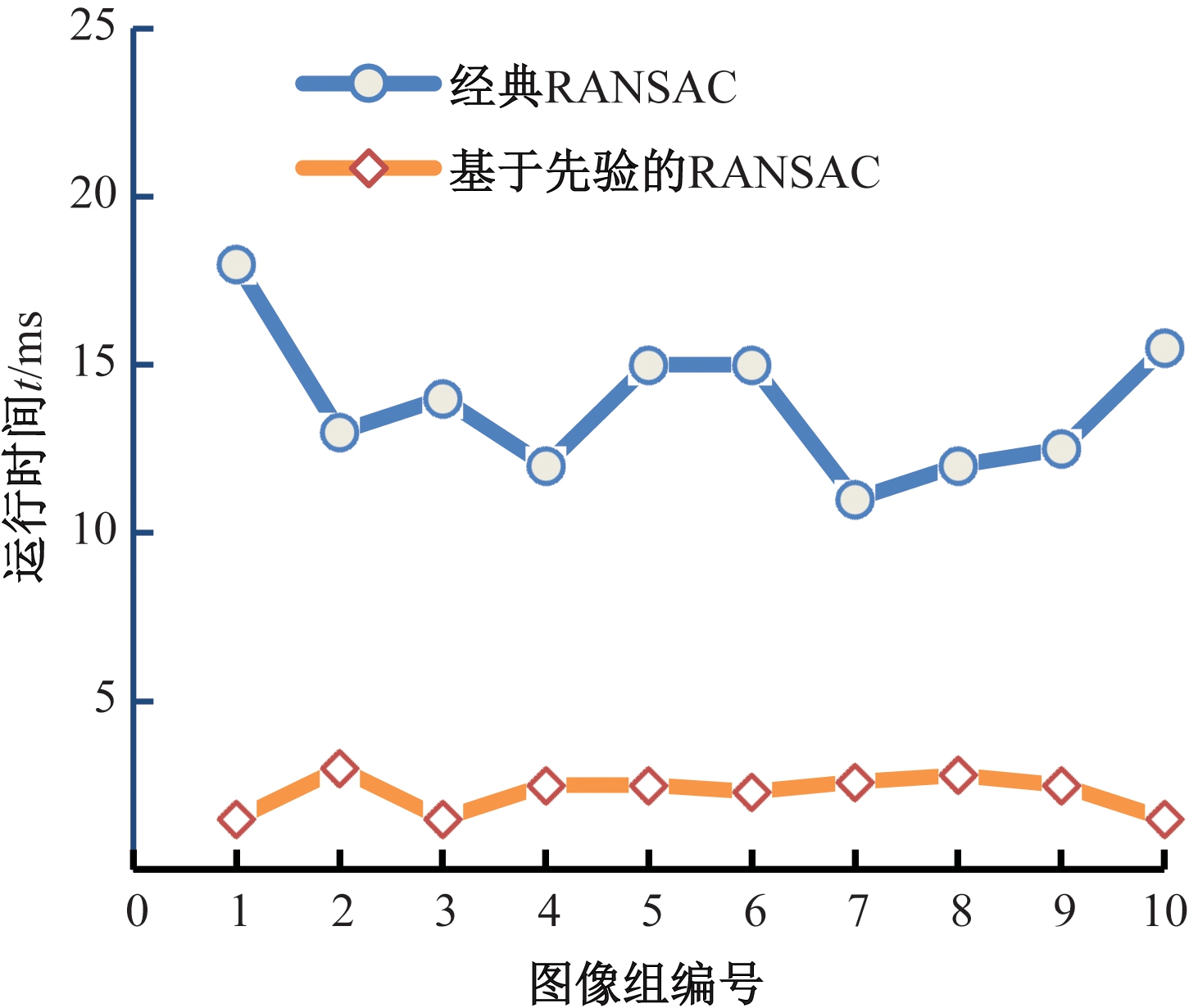
图3 基于先验的RANSAC方法与经典RANSAC
方法处理时间的比较
Figure 3 Comparison of the processing time between the results of the prior-based RANSAC method and the classic RANSAC method
1.3 网格变形
对于给定的多幅图像，分别将其划分成N1×N2=10×10个大小为GridSize的网格[11]。首先采集每个网格的顶点集合信息
(第m幅图像上的第i个顶点信息)，然后根据图像对的顶点集合信息在对应的网格内寻找单应变换关系，保证每个网格都能够对齐。对各个网格使用双线性插值方法，有效地加快计算过程。因为各个网格内是保持同一个变换关系的，所以可以利用插值计算得到的点信息来进行匹配计算；此外，每个对应网格的单应变换关系的计算是相对独立的，因此可以利用多线程技术并行计算，进一步加速算法的计算过程。
通过网格变形得到对应的匹配点信息，同时该特征匹配对在图像的重叠区域内分布也更加均匀及广泛，一定程度上避免了因低纹理场景而导致的特征分布过于局限的问题。后面的对齐约束计算会利用到该匹配对信息。
1.4 图像对齐
图像对齐是在图像中确定像素点之间的对应关系[12]。对同一场景不同视角下的图像拼接场景进行对齐时，需要解决待拼接图像对之间的刚性变化和非刚性变化的问题。本文提出了多种对齐优化方法，约束点线特征和网格四边的变形过程，最终明显改善了拼接效果。
1.4.1 点特征对约束
建立局部对齐约束时，先建立插值后的中心点对的约束关系，再最小化该关系式来修正对齐效果。假设图片Is上的点p和图片It上的点p′是一对匹配点，
是网格4个顶点的插值系数。点p是由其所在网格的4个顶点
进行插值化得到的,则可以构建得到式(1)中的匹配点对约束来最小化对齐误差。
(1)
式中：N为特征点对的数目；
为特征点对集合的第i个匹配点对。
1.4.2 线特征对约束
假定图片Is中的直线段L=[a,b]和图片It中的直线段L′=[a′,b′]是一对匹配的直线段。a、b、a′、b′分别为对应直线段的首末端点。为了最小化对齐误差，在线段L上进行采样，然后最小化采样点与匹配的直线段L′之间的距离。假设目标图像上的直线段L′的表达式为kx+b-y=0，那么可以构建线段匹配对系数约束：
(2)
式中：km、bm分别为第m个匹配线段对中目标直线段的斜率和常数；
分别为第m个匹配线段对中源直线段上第n个源匹配点的x、y值信息。
1.4.3 形状一致性约束
形状一致性约束是为了使图像中变形的网格四边形维持一个相似的变换过程，不要造成太大的扭曲变形，以保证重叠区域的局部变形效果。首先将网格划分为2个三角形，并应用局部相似性变形方法使得网格四边形维持一个相似的变换过程[13]。
设定
为第i个图像匹配对的第j个网格的4个顶点，其中
和
分别为网格四边形中的2个三角形顶点。假定三角形
中的顶点
可以被另外的2个顶点
利用相关系数m、n所表示：
(3)
则m、n系数可以通过上式计算得出。为约束每个网格维持一个相似的变换，应当保证变形后的三角形顶点
也满足
可由
经同样的系数m、n表示。可以得出以下的约束关系式：
(4)
式中：Nt为网格集合中所拥有的所有三角形数目。
1.4.4 能量函数确定
在建立以上的约束之后，通过统一这些约束来构建一个能量函数，使用该能量函数来优化点线及网格相关变量信息，并最小化该能量函数，得到精确的网格顶点数据集和点、线特征集，从而最大化精确图像的对齐效果。能量函数定义如式(5)所示：
Eshape(V)=Epoint(V)+Eline(V)+Eshape(V)。
(5)
当顶点集合中的顶点距离小于等于一个像素点时，能量函数的最优化过程便趋于收敛，最后得到一个优化的特征匹配对集合，从而得到相关的变换参数(包括单应矩阵特征匹配对数目和相机内外参数等信息)。
1.5 图像投影变换
由于图像采集设备一般会在不同角度下进行拍摄，图像对一般不会出现在同一个投影平面上。为了保证图像拼接结果的一致性观感，需要对图像进行投影变换，采用适当的投影变换模型，让图像对投影后处于同一个平面上。
平面投影是最为简单的一种投影方式，但是面对带有视差的场景图像集时，会出现较大的拉升效果，视觉效果不理想。
柱面投影是进行宽视野的类环形拼接应用时最佳的投影选择。柱面投影以相机为圆柱中心点，相机的焦距为半径，构造的一个柱面作为投影面。
2 基于最佳缝合线的图像融合
2.1 基于图像对重叠区域细节增强的缝合线检测算法
在针对多目多焦段场景时，需要利用各个图像的优势，结合短焦图像的大视角和长焦图像丰富的细节，使得图像对的重叠区域占满长焦的图像，得到一幅宽视野的高分辨率图像。为此，本文提出了基于图像对重叠区域细节增强的缝合线查找算法。针对给定的输入图像对Ii、Ij，首先需要计算出重叠区域图像的相关信息，包括长宽及左上角顶点坐标信息。利用该信息便可计算该重叠区域图像在各个图像中的位置，从而可以对图像掩码矩阵进行赋值。
图像掩码矩阵同一行/列(重叠区域宽大于高/宽小于高)值的突变便是缝合线的取值点，通过缝合线来控制重叠区域中对于图像对Ii、Ij的取值。长焦镜头的画面相较短焦镜头而言，细节更为丰富，因此可以通过操作图像掩码矩阵使得重叠区域都取图像Ij中的像素值，这样就可以达到丰富重叠区域内图像细节的效果。图4是图像输入，图5是采用本节缝合线检测算法的拼接结果。
从图5中可以看出，长焦镜头丰富了短焦镜头的画面内容，并补足了重叠区域的细节，如红框内车牌区域。
2.2 渐入渐出融合
对于上一步得到的缝合线，若是仅仅根据缝合线对于重叠区域的划分来界定图像对，那么在重叠区域中会出现很明显的接缝线，视觉上在缝合线处的过渡会出现不连贯。为此，需要对缝合线两侧的不同图像进行融合处理，本文使用了渐入渐出融合方法来实施图像融合。
图4 图像输入
Figure 4 Input images
图5 基于图像对重叠区域细节增强的缝合线检测算法的拼接结果
Figure 5 The stitching result of the stitch line detection algorithm based on the image enhancement of the overlapping area details
渐入渐出融合是通过对缝合线边界进行平滑虚化，通过渐入渐出的方法来达成相对自然的平滑效果。其平滑公式如下：
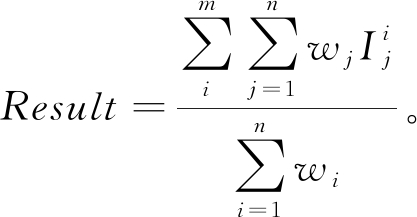
(6)
式中：Result为图像对经由渐入渐出融合后得到的结果图像；
为图像i中的像素j；wi、wj分别为对应像素点所占的权重，其与该像素和缝合线之间的距离相关。通过加权平均法，便可以得到一幅宽视野的拼接图。
3 实验与分析
3.1 实验环境
本文在i7-7700k、16 G内存的Windows10主机设备上使用了Visual Studio2017工具进行实验。
3.2 实验方法及结果分析
本文使用华为Mate20X设备进行数据拍摄，镜头能够进行3倍光学变焦，并且将现有的几个主流解决方案(APAP[3]，NIS[4]和AANAP[14])与本文的方法进行了对比实验。
场景1、2、3(图6～8所示)为大视差且焦距有较大变化的场景，若是没有恰当地处理好视差问题，在重叠区域会出现严重的伪影情况。
图9～11为本文方法和APAP、AANAP和NIS的结果对比图，图12、13为场景1、2的细节放大对比图。可以看出，在拼接结果的重叠区域内，APAP、AANAP和NIS在结果中都出现了严重的伪影和扭曲变形。相较于其他方法，本文提出的点特征与线特征结合的特征检测方法以及各项图像对齐约束有效地提升了图像配准的准确度，最后在图像融合阶段结合了基于重叠区域细节增强的缝合线检测算法来有效地处理不同尺度图像之间的融合问题。通过使用本文的方法来进行实验，重叠区域能够实现很好地对齐，并且能极大程度上避免伪影情况的产生。
图6 场景1的图像输入
Figure 6 Input images of scene 1
图7 场景2的图像输入
Figure 7 Input images of scene 2
图8 场景3的图像输入
Figure 8 Input images of scene 3
本文将原始图像与拼接结果图像使用PSNR(峰值信噪比)标准进行测试。根据PSNR的度量标准，PSNR值越高，代表图像结果的质量越好，与原始图像越相像。当度量结果为30～40 dB时，说明图像结果的质量一般，失真程度不大；当度量结果为20～30 dB时，说明图像结果的质量较差；当度量结果小于20 dB时，表明结果不可以接受，质量极差。如图14所示，可以看出，本文方法的结果是最优的，在3个场景下验证的结果数值都维持在35～40 dB内，而其余的方法则在20～32 dB内波动，表明在PNSR标准下，本文方法的拼接结果失真是最小的，并且与原始图像的重叠区域存在高度相似，很好地保留了原始图像的信息，其余方法的拼接结果均存在一定程度的失真。
图9 场景1 的结果对比图
Figure 9 Comparison of the results of scene 1
图10 场景2的结果对比图
Figure 10 Comparison of the results of scene 2
图11 场景3的结果对比图
Figure 11 Comparison of the results of scene 3
图12 场景1结果重叠区域放大图
Figure 12 The enlarged view of the overlapping area of the result of scene 1
图13 场景2结果重叠区域放大图
Figure 13 The enlarged view of the overlapping area of the result of scene 2
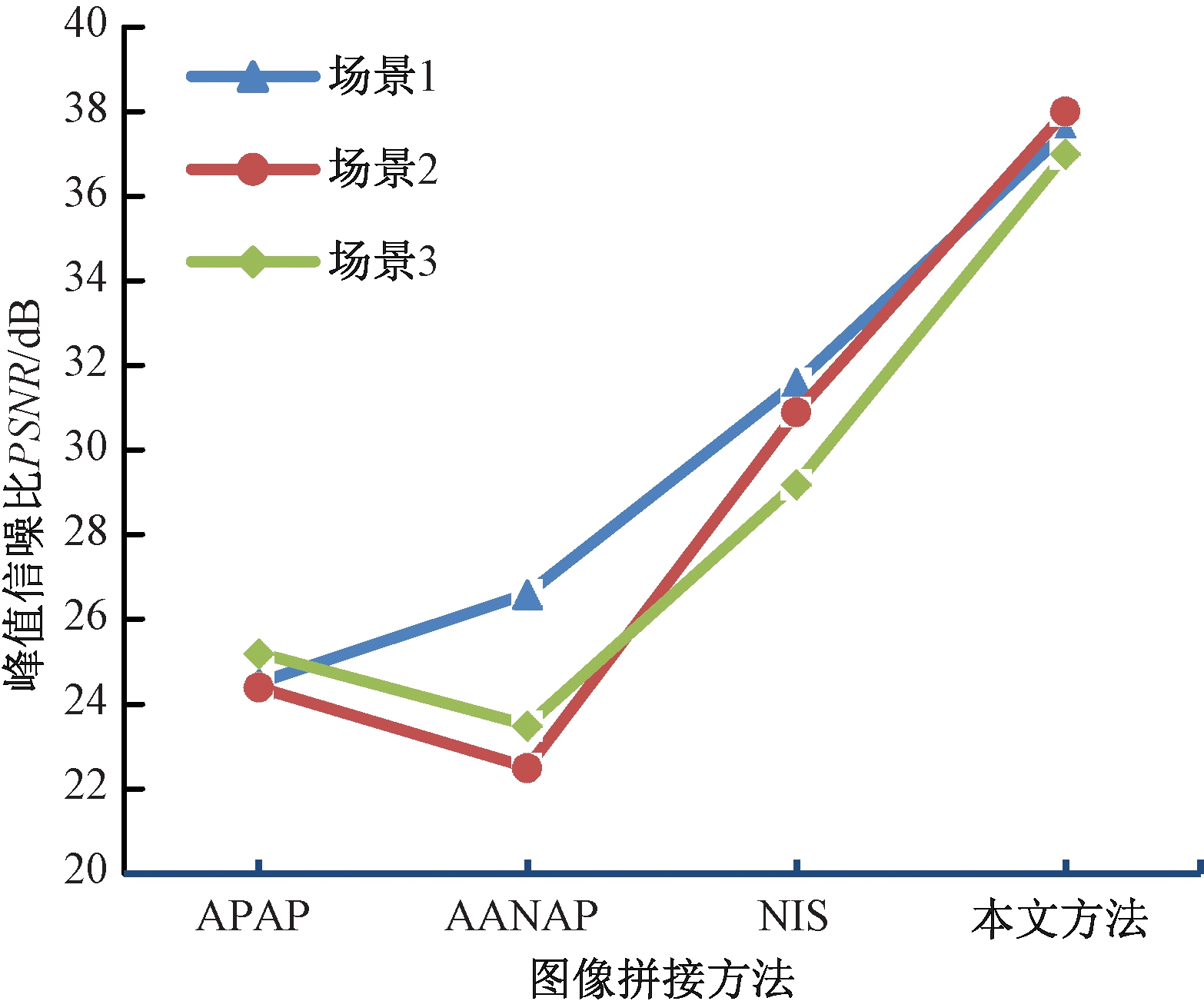
图14 PSNR对比折线图
Figure 14 PSNR line charts
4 结论
针对图像拼接中出现的各类问题提出了一整套解决方案。在图像配准阶段，提出了一种结合点特征和线段特征的特征检测方法，提升了特征的数量和质量，并提出了基于先验的RANSAC特征点对筛选方法，通过拟定先验集，更快速地获得最佳采样集；在图像融合阶段，使用了最佳缝合线的图像融合算法，保证了图像的对齐效果，并且极大程度上避免了重叠区域的伪影，通过在实验数据集上的对比验证，本文的算法在多个场景上的PSNR数值都维持在35～40 dB内，失真度较低，且图像拼接的质量也更优。但是针对图像对之间存在曝光差异的情况，本文算法未做考虑，后续可尝试用曝光补偿等方法优化曝光差异问题。
[1] BROWN M, LOWE D G. Automatic panoramic image stitching using invariant features[J]. International journal of computer vision, 2007, 74(1):59-73.
[2] GAO J, KIM S J, BROWN M S. Constructing image panoramas using dual-homography warping[C]// Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2011: 49-56.
[3] ZARAGOZA J, CHIN T J, Tran Q H, et al. As-projective-as-possible image stitching with moving DLT[J]. IEEE transactions on pattern analysis and machine intelligence, 2014, (36)7:1285-1298.
[4] CHEN Y S,CHUANG Y Y.Natural image stitching with the global similarity prior[C]//European Conference on Computer Vision. Amsterdam, The Netherlands: ECCV, 2016: 186-201.
[5] MISRA I, SHRIVASTAVA A, GUPTA A, et al. Cross-stitch networks for multi-task learning[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). New York: IEEE, 2016: 3994-4003.
[6] GAO J, LI Y, CHIN T J, et al. Seam-driven image stitching [C]//European Association for Computer Graphics. Geneva, Switzerland: Eurographics, 2013: 45-48.
[7] ZHANG F, LIU F. Parallax-tolerant image stitching[C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). New York:IEEE, 2014: 3262-3269.
[8] LIN K M,JIANG N J,CHEONG L F,et al. Seagull: seam-guided local alignment for parallax-tolerant image stitching[C]// European Conference on Computer Vision. Berlin:Springer,2016: 370-385.
[9] LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International journal of computer vision, 2004, 60(2): 91-110.
[10] VON GIOI R G,JAKUBOWICZ J,MOREL J M,et al.LSD:a line segment detector[J].Image processing on line,2012,2:35-55.
[11] 齐向明,王佳琦.网格形变细分的大视差图像拼接算法[J].计算机工程,2020,46(1):236-242.
[12] LIN K, JIANG N J, LIU S C. Direct photometric alignment by mesh deformation[C]// IEEE Conference on Computer Vision and Pattern Recognition. New York:IEEE, 2017: 2701-2709.
[13] ZHANG Y, LAI Y K, ZHANG F L. Stereoscopic image stitching with rectangular boundaries[J]. The visual computer, 2019, 35(6/7/8): 823-835.
[14] Lin C C, PANKANTI S U, RAMAMURTHY K N, et al. Adaptive as-natural-as-possible image stitching[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2015: 1155-1163.