0 引言
近年来,国内外学者针对交通事故严重程度影响因素进行了许多研究,主要集中在高速公路多车事故。如张吉光等[1]从车辆追尾机理分析为切入点,研究高速公路多车连环追尾事故影响因素,但其只研究多车碰撞的特殊碰撞,而且没有对影响因素进行定量分析;尹若愚[2]运用以随机森林模型为基础的参数敏感性分析方法,对多车碰撞事故痕迹进行仿真,发现成员损伤部位与车速、碰撞角度等因素关联性大,但其只研究了成员损伤部位与参数之间的关联性,没有对参数进行灵敏度分析;王佳丽[3]通过对雾天高速公路连环追尾事故风险产生机理进行研究,将追尾事故风险划分为高、中、低3个等级以进行评估,并建立了大雾天气下的追尾事故风险传播模型。
在研究方法上,现阶段国内外学者对事故影响和伤害程度的分析更多使用的是传统计量经济学模型,主要是有序Logit模型、多项Logit模型、巢式Logit模型等。有序Logit模型假设变量等比例,限制了解释变量的影响[4]。多项Logit模型没有有序Logit模型的限定,但是它有无关独立性(IIA)假设的内在缺陷[5]。上述模型在求解过程中,对变量的系数值均预先给出固定值的假定,也就是对任何观测样本,自变量均有着相同的效用。而随机参数模型假设自变量的参数是服从某种分布的随机参数,能够考虑事故个体差异对事故产生的效果,从而能够更加合理地刻画事故伤害特征。
综上所述,对车辆群的事故伤害程度研究目前还较少,并且是以追尾以及高速公路的多车碰撞为主,没有专门针对公路车辆群碰撞事故的研究。相对于高速公路,普通公路路况复杂,接入点较多,道路条件较差,在普通公路上发生的车辆群事故受诸多因素影响,有必要对公路车辆群碰撞事故伤害程度影响因素进行深入研究。本文拟以2016年美国得克萨斯州公路车辆碰撞数据为样本,构建考虑异质性的随机参数模型,以期为国内公路车辆群事故伤害分析提供借鉴和指导。
1 数据处理
1.1 车辆群事故数据来源
本文选用美国得克萨斯州交通厅碰撞事故信息系统(crash records information system, CRIS),选取2016年全年的公路车辆群碰撞事故,主要字段信息包括:年龄、性别、是否被甩出车外、是否酒驾、碰撞涉及车辆数、车身样式、碰撞的时间地点、天气、路面是否潮湿、路段限速等。车辆群碰撞事故定义为发生在道路上、正在运动中、涉及3辆或以上的机动车碰撞事故。选取车辆群碰撞事故共有约5.0万起,随机抽样2.5万起事故用于建模,剩余的事故用以评价模型的预测精度。沿用美国标准的事故伤害程度分类,将得克萨斯州碰撞事故伤害程度分为5级:无伤害、可能受伤、非失能性伤害、失能性伤害、死亡。文中选取发生碰撞事故中所有涉事人员中最严重的伤害程度进行建模。
1.2 车辆群事故特征分析
从驾驶员方面看,发生车辆群事故的以年龄小于等于19岁(青年)或大于等于55岁(老年)的驾驶员居多,占事故总数的46.11%,且35.58%的老年驾驶员更容易发生严重性事故。在得克萨斯州全年单车碰撞事故中,青年驾驶员和老年驾驶员的占比仅为23.07%。
从事故形态看,造成车辆群事故的主要原因是车辆追尾以及路面侧滑。而碰撞固定物及冲出道路是发生车辆单车事故的主要原因[6]。
从事故造成的损失来看,虽然车辆群事故发生的概率要比单车事故小,但是车辆群事故涉及多车辆碰撞,对车辆和道路结构的损坏更为严重,且容易造成群死群伤[7]。
综上所述,车辆群事故主要特点为:①车辆群事故涉事驾驶员主要为青年驾驶员和老年驾驶员;②车辆群事故主要是由车辆连环追尾及路面侧滑导致的;③车辆群事故造成的后果严重,容易造成群死群伤。
结合样本特征分析及前人研究的经验,从4个方面(道路特性、驾驶员特性、车辆特征、环境因素)选取21个潜在影响变量类别对公路车辆群碰撞事故进行分析。变量中有二元变量和多分类变量,二元变量可以直接代入模型拟合,而多分类变量处理需要引入虚拟变量。当多分类变量有M(M>2)个类别时,将引入(M-1)个虚拟变量,虚拟变量皆为0~1变量,详细变量描述统计如表1所示。
表1 变量定义及描述性统计
Table 1 Definition of independent variables and descriptive statistics
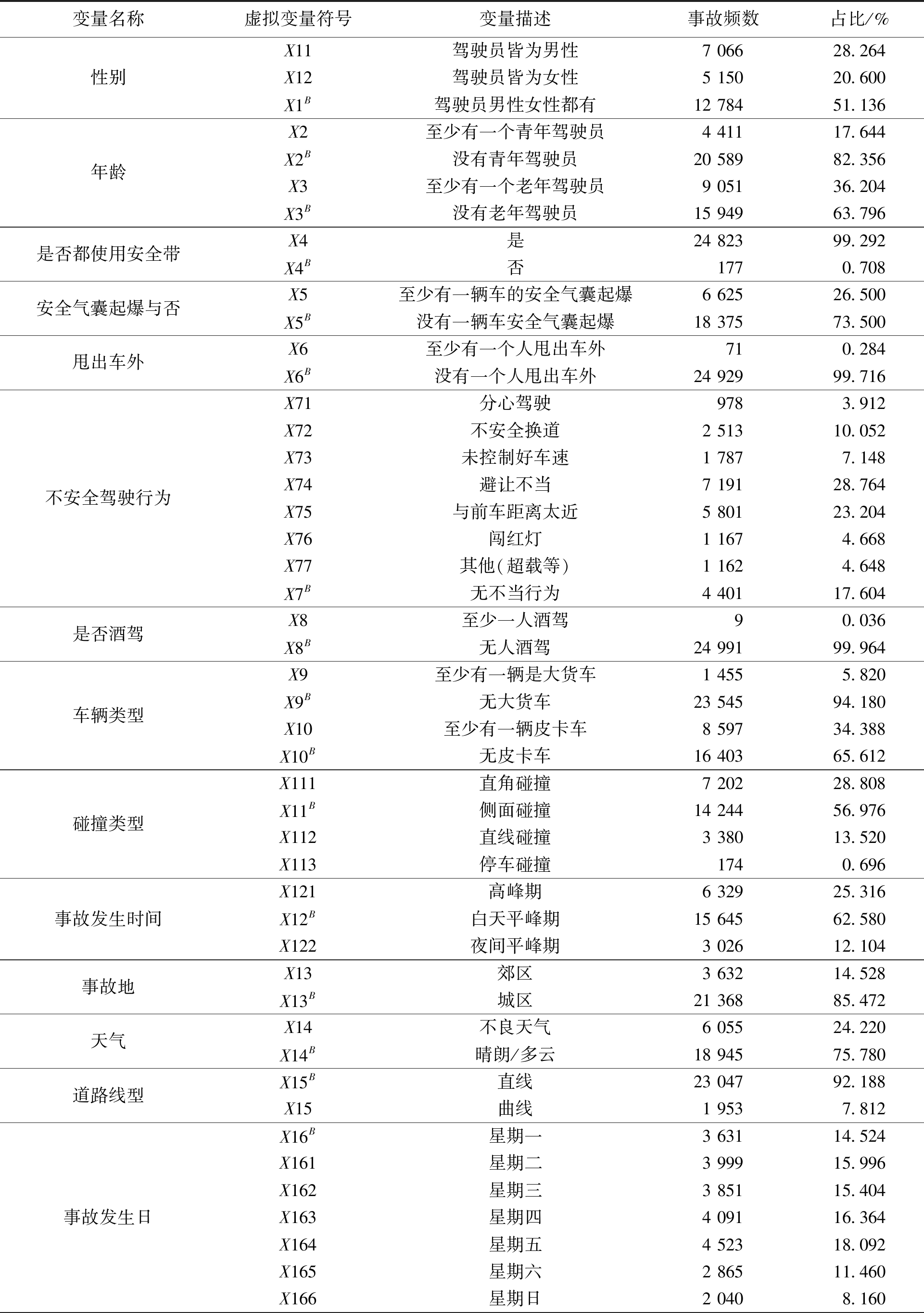
变量名称虚拟变量符号变量描述事故频数占比/%性别年龄是否都使用安全带安全气囊起爆与否甩出车外不安全驾驶行为是否酒驾车辆类型碰撞类型事故发生时间事故地天气道路线型事故发生日X11驾驶员皆为男性7 06628.264X12驾驶员皆为女性5 15020.600X1B驾驶员男性女性都有12 78451.136X2至少有一个青年驾驶员4 41117.644X2B没有青年驾驶员20 58982.356X3至少有一个老年驾驶员9 05136.204X3B没有老年驾驶员15 94963.796X4是24 82399.292X4B否1770.708X5至少有一辆车的安全气囊起爆6 62526.500X5B没有一辆车安全气囊起爆18 37573.500X6至少有一个人甩出车外710.284X6B没有一个人甩出车外24 92999.716X71分心驾驶9783.912X72不安全换道2 51310.052X73未控制好车速1 7877.148X74避让不当7 19128.764X75与前车距离太近5 80123.204X76闯红灯1 1674.668X77其他(超载等)1 1624.648X7B无不当行为4 40117.604X8至少一人酒驾90.036X8B无人酒驾24 99199.964X9至少有一辆是大货车1 4555.820X9B无大货车23 54594.180X10至少有一辆皮卡车8 59734.388X10B无皮卡车16 40365.612X111直角碰撞7 20228.808X11B侧面碰撞14 24456.976X112直线碰撞3 38013.520X113停车碰撞1740.696X121高峰期6 32925.316X12B白天平峰期15 64562.580X122夜间平峰期3 02612.104X13郊区3 63214.528X13B城区21 36885.472X14不良天气6 05524.220X14B晴朗/多云18 94575.780X15B直线23 04792.188X15曲线1 9537.812X16B星期一3 63114.524X161星期二3 99915.996X162星期三3 85115.404X163星期四4 09116.364X164星期五4 52318.092X165星期六2 86511.460X166星期日2 0408.160
2 模型建立
根据效用最大化理论,标准的多项式Logit模型可以表示为
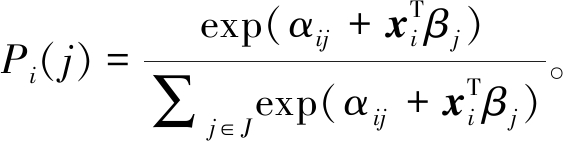
(1)
式中:Pi(j)为第i起事故伤害程度为j的概率;J为事故伤害程度的类别集合。
在多项式Logit模型中,假定βj为不变的参数值。而随机参数Logit模型没有将系数![]() 假设为固定值,而是将其假定为随机的,服从某种分布的值,也就是
假设为固定值,而是将其假定为随机的,服从某种分布的值,也就是![]() 它的密度函数用相应分布的参数集合φs来描述,将
它的密度函数用相应分布的参数集合φs来描述,将![]() 替换式(1)中的βj即可推导出随机参数Logit模型:
替换式(1)中的βj即可推导出随机参数Logit模型:
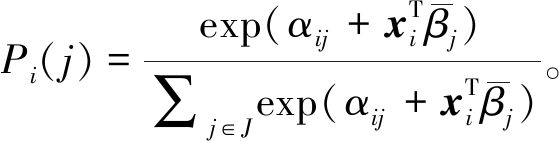
(2)
![]() 在模型中的分布形式是多样的,因而随机参数Logit模型也是具有非闭合型的概率函数,无法直接进行积分求解,需要使用计算机模拟仿真。本研究对随机参数模型的求解采用蒙特卡罗方法。
在模型中的分布形式是多样的,因而随机参数Logit模型也是具有非闭合型的概率函数,无法直接进行积分求解,需要使用计算机模拟仿真。本研究对随机参数模型的求解采用蒙特卡罗方法。
在随机参数Logit模型中,估计的参数仅能够对碰撞伤害程度受各因素影响的趋势予以反映,而无法对碰撞伤害程度受各因素的影响大小作准确衡量,因而在对模型参数进行估计后,对相关显著变量仍需进行边际效应值的测算。本文采用汤左淦[8]提出的边际效应计算方法。
3 参数标定及模型结果分析
3.1 参数标定
本文随机参数模型的参数估计结果采用Nlogit 5.0软件完成,基于蒙特卡罗方法在显著性水平分别为0.1、0.05、0.01时求解。本次拟合McFadden R2取值为0.493 6,说明模型具有较高整体拟合效果,求解过程说明如下:
(1)在求解过程中,运用Halton抽样法对参数进行标定(在抽样次数相同的前提下,Halton抽样的抽样时间仅为随机抽样的1/10,且不会影响到结果的精度[9]),通过验证抽样次数(50、250、500、750、1 000、1 250)对模型结果的稳定性进行检测,最终发现模型在抽样次数为1 000时具有较好的拟合优度,因而抽样次数选定为1 000。
(2)待估参数在最初均作随机参数的假定,并对各参数分别服从对数正态分布、正态分布、均匀分布进行模拟仿真。最终结果显示:对应于无伤害的“道路限速值>100 km/h”变量和对应于非失能性伤害的“安全气囊起爆与否”变量为随机参数,其余变量的参数均为固定参数,而且显著水平高,如表2所示。
续表1
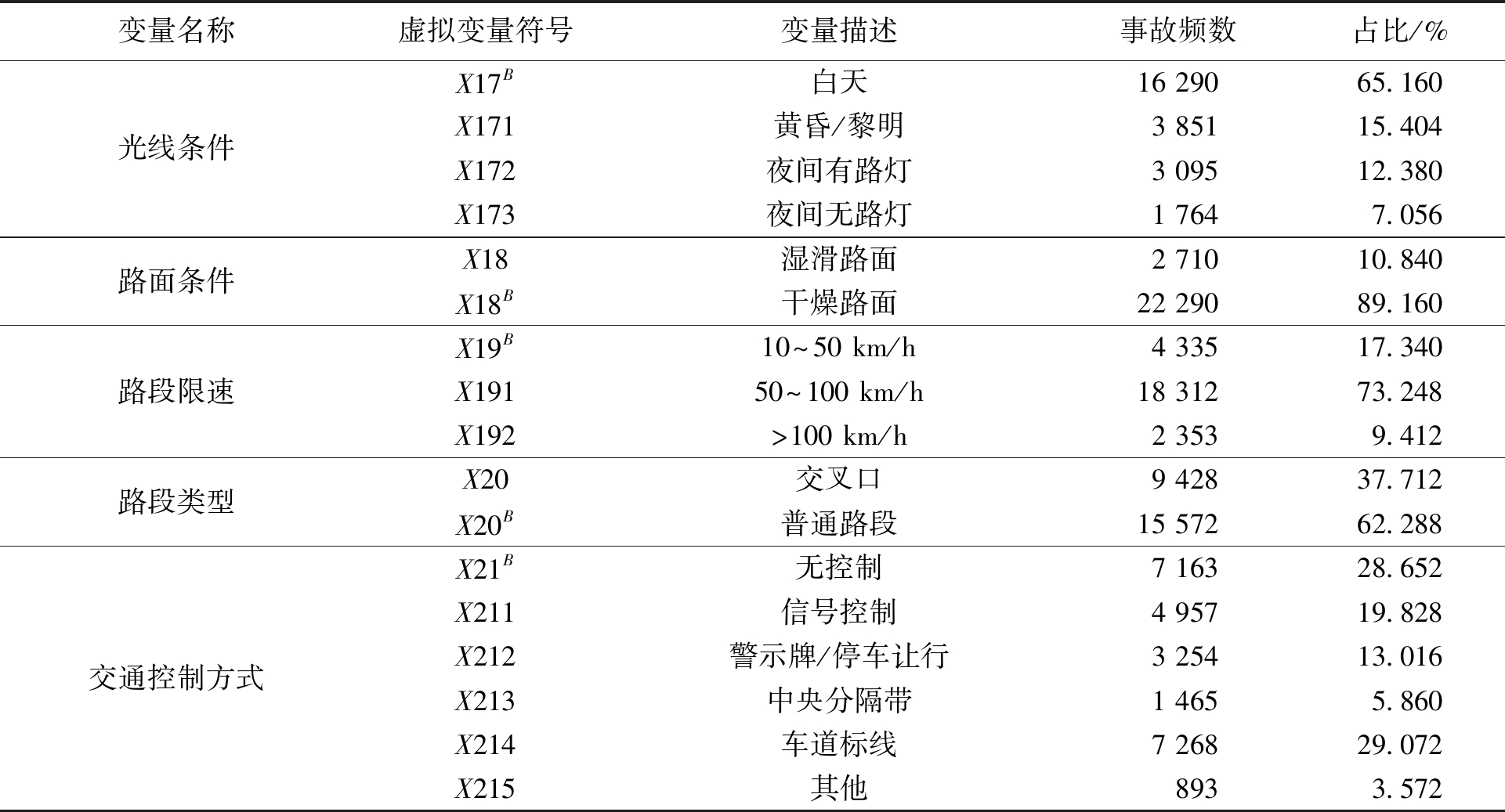
变量名称虚拟变量符号变量描述事故频数占比/%光线条件路面条件路段限速路段类型交通控制方式X17B白天16 29065.160X171黄昏/黎明3 85115.404X172夜间有路灯3 09512.380X173夜间无路灯1 7647.056X18湿滑路面2 71010.840X18B干燥路面22 29089.160X19B10~50 km/h4 33517.340X19150~100 km/h18 31273.248X192>100 km/h2 3539.412X20交叉口9 42837.712X20B普通路段15 57262.288X21B无控制7 16328.652X211信号控制4 95719.828X212警示牌/停车让行3 25413.016X213中央分隔带1 4655.860X214车道标线7 26829.072X215其他8933.572
注:“XiB,i=1,2,…,21”为固定的参考类别,此类别不纳入模型拟合。
表2 随机参数估计结果
Table 2 Random parameter estimation results

变量条件对应事故等级均值估计值标准差估计值边际效应值限速值>100 km/hNI-0.205∗∗1.222∗∗-0.005 1安全气囊起爆与否NII1.329∗∗2.004∗∗0.069 5
注:上标*、**、***分别表示显著性水平为0.1、0.05、0.01;表格中字母表示变量显著影响的伤害程度:死亡(FI)、失能性伤害(II)、非失能性伤害(NII)、可能受伤(PI)、无伤害(NI)。
(3)随机参数模型能够合理地解释各潜在变量对严重程度的影响。在最终的模型中,共有15个单因素、4个耦合因素显著,如表3所示。
表3 固定参数及耦合参数估计结果
Table 3 Fixed and coupled parameter estimation results
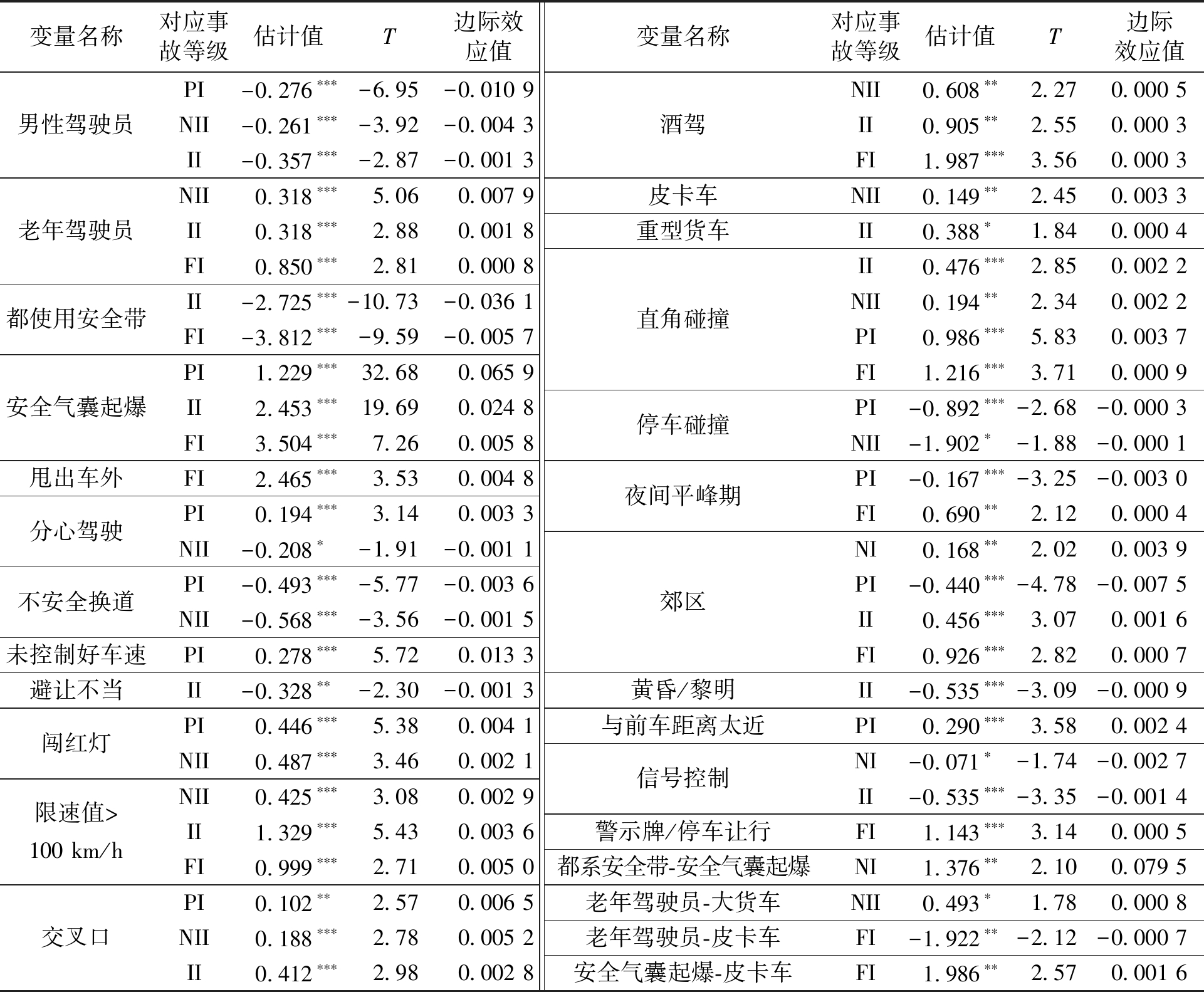
变量名称对应事故等级估计值T边际效应值变量名称对应事故等级估计值T边际效应值男性驾驶员老年驾驶员都使用安全带安全气囊起爆甩出车外分心驾驶不安全换道未控制好车速避让不当闯红灯限速值>100 km/h交叉口PI-0.276∗∗∗-6.95-0.010 9NII-0.261∗∗∗-3.92-0.004 3II-0.357∗∗∗-2.87-0.001 3NII0.318∗∗∗5.060.007 9II0.318∗∗∗2.880.001 8FI0.850∗∗∗2.810.000 8II-2.725∗∗∗-10.73-0.036 1FI-3.812∗∗∗-9.59-0.005 7PI1.229∗∗∗32.680.065 9II2.453∗∗∗19.690.024 8FI3.504∗∗∗7.260.005 8FI2.465∗∗∗3.530.004 8PI0.194∗∗∗3.140.003 3NII-0.208∗-1.91-0.001 1PI-0.493∗∗∗-5.77-0.003 6NII-0.568∗∗∗-3.56-0.001 5PI0.278∗∗∗5.720.013 3II-0.328∗∗-2.30-0.001 3PI0.446∗∗∗5.380.004 1NII0.487∗∗∗3.460.002 1NII0.425∗∗∗3.080.002 9II1.329∗∗∗5.430.003 6FI0.999∗∗∗2.710.005 0PI0.102∗∗2.570.006 5NII0.188∗∗∗2.780.005 2II0.412∗∗∗2.980.002 8酒驾皮卡车重型货车直角碰撞停车碰撞夜间平峰期郊区黄昏/黎明与前车距离太近信号控制警示牌/停车让行都系安全带-安全气囊起爆老年驾驶员-大货车老年驾驶员-皮卡车安全气囊起爆-皮卡车NII0.608∗∗2.270.000 5II0.905∗∗2.550.000 3FI1.987∗∗∗3.560.000 3NII0.149∗∗2.450.003 3II0.388∗1.840.000 4II0.476∗∗∗2.850.002 2NII0.194∗∗2.340.002 2PI0.986∗∗∗5.830.003 7FI1.216∗∗∗3.710.000 9PI-0.892∗∗∗-2.68-0.000 3NII-1.902∗-1.88-0.000 1PI-0.167∗∗∗-3.25-0.003 0FI0.690∗∗2.120.000 4NI0.168∗∗2.020.003 9PI-0.440∗∗∗-4.78-0.007 5II0.456∗∗∗3.070.001 6FI0.926∗∗∗2.820.000 7II-0.535∗∗∗-3.09-0.000 9PI0.290∗∗∗3.580.002 4NI-0.071∗-1.74-0.002 7II-0.535∗∗∗-3.35-0.001 4FI1.143∗∗∗3.140.000 5NI1.376∗∗2.100.079 5NII0.493∗1.780.000 8FI-1.922∗∗-2.12-0.000 7FI1.986∗∗2.570.001 6
注:上标*、**、***分别表示显著性水平为0.1、0.05、0.01;表格中字母表示变量显著影响的伤害程度:死亡(FI)、失能性伤害(II)、非失能性伤害(NII)、可能受伤(PI)、无伤害(NI)。
3.2 异质性结果分析
对应于无伤害的“道路限速值>100 km/h”参数估计服从均匀分布U(-2.12,1.71)。图1所示的累计概率结果表明,相比于其他限速值的道路,在高限速值(道路限速值>100 km/h)道路上,44.65%的事故为无伤害的概率更高,有55.35%的事故为无伤害的概率更低,这是因为在高限速值的道路上驾驶员会倾向于用较快的速度进行行驶,更容易发生伤害严重的车祸。
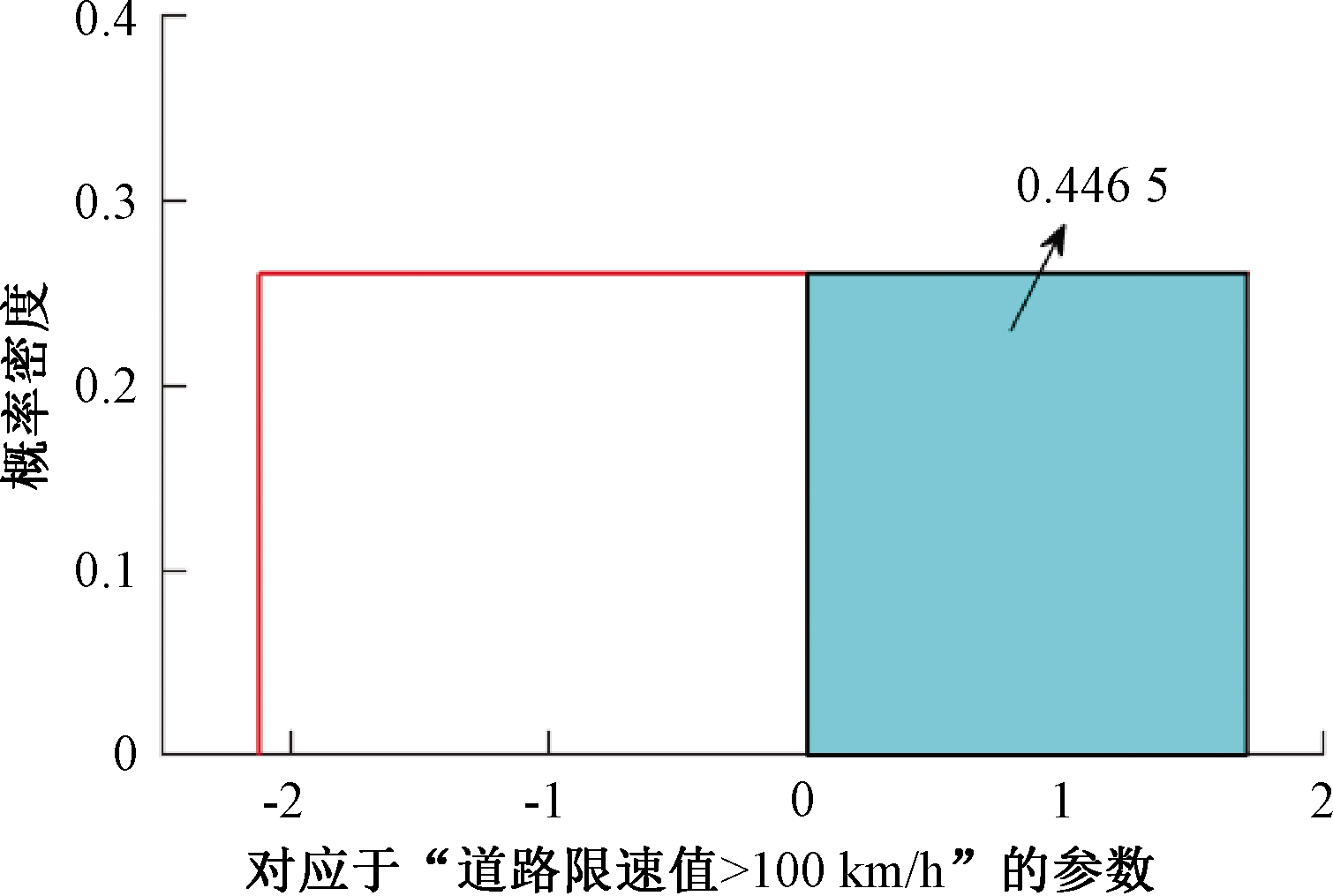
图1 “道路限速值>100 km/h”参数概率分布图
Figure 1 "Road speed limited value >100 km/h" parameter probability distribution
对应于非失能性伤害的“安全气囊起爆与否”参数估计服从正态分布N(1.329,2.0042),如图2所示。正态分布累计概率计算结果显示,相比于安全气囊没有起爆,74.64%安全气囊起爆的车辆群碰撞事故发生非失能性伤害的概率更高;而25.36%的安全气囊起爆的车辆群事故发生非失能性伤害的概率更低。根据以往学者的研究经验,安全气囊能够降低汽车碰撞的伤害严重程度[10],但是安全气囊起爆是由高级别的碰撞引起的。另外,车辆群碰撞是由多辆汽车碰撞造成的,因此给事故中人员造成更严重的伤害。
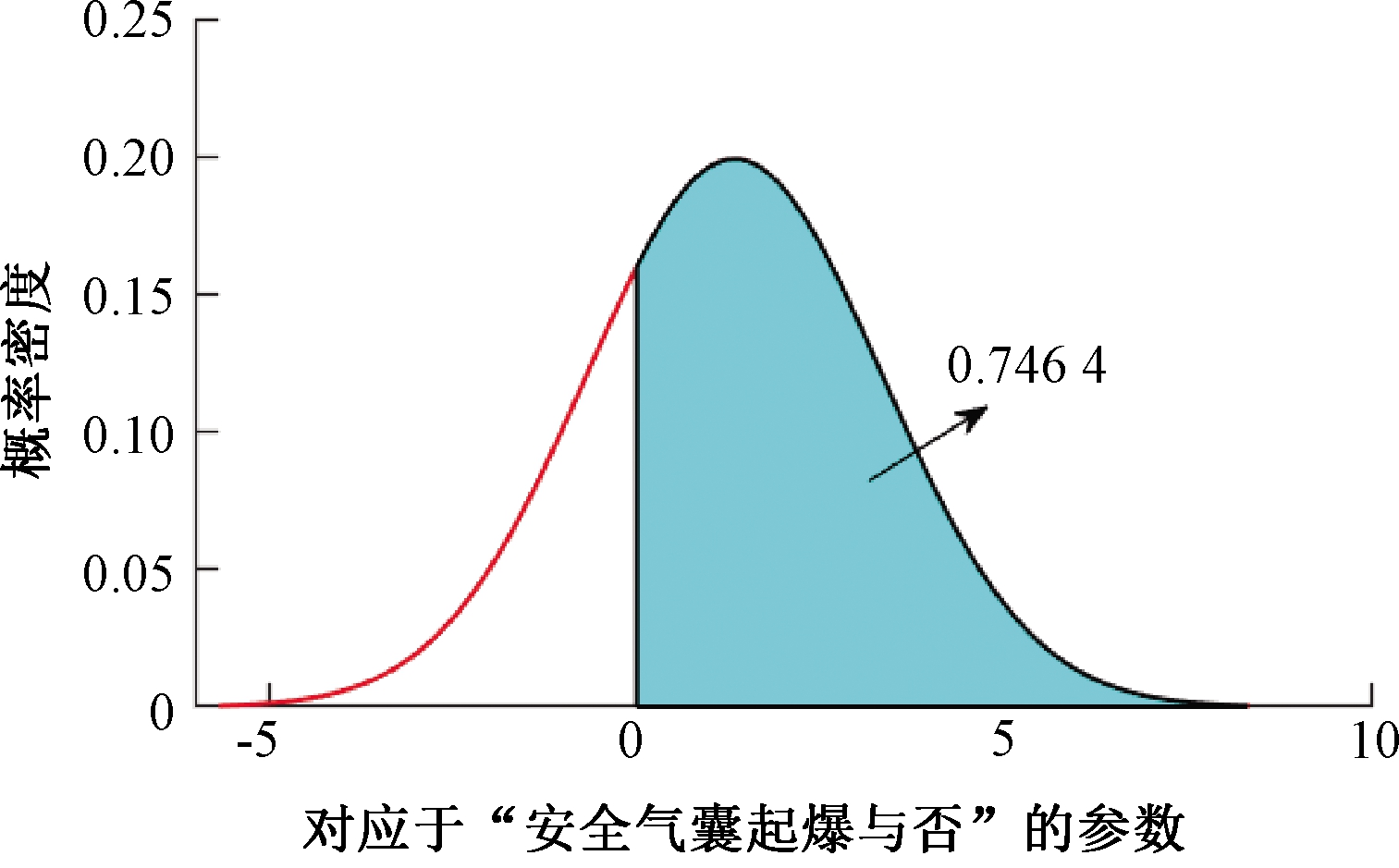
图2 “安全气囊起爆与否”参数概率分布图
Figure 2 "Airbag explosion" parameters probability distribution
3.3 模型预测精度分析
将抽样剩下的25 727起公路车辆群事故(样本2)放入混合Logit模型中进行预测,如表4所示。事故占比中,无伤害占52.70%,表示在25 727起事故中,发生无伤害事故占其中的52.70%。总体上讲,模型预测精度较高,结果可靠。
表4 随机参数Logit模型预测精度
Table 4 Random parameter Logit model prediction accuracy
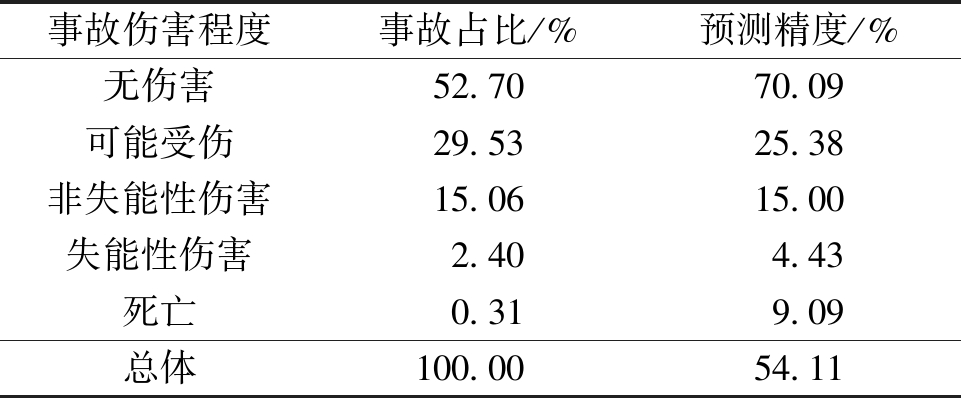
事故伤害程度事故占比/%预测精度/%无伤害52.7070.09可能受伤29.5325.38非失能性伤害15.0615.00失能性伤害2.404.43死亡0.319.09总体100.0054.11
3.4 模型结果定量分析
(1)驾驶员特性。男性驾驶员在可能受伤、非失能性伤害和失能性伤害的事故参数估计结果为负,说明上述伤害程度不易在男性驾驶员上发生,男性驾驶员降低了可能受伤事故(1.09%)、非失能伤害事故(0.43%)以及失能伤害事故(0.13%)的发生概率。
相较于其他年龄层,青年驾驶员更不容易受伤(-0.55%),可能是由于青少年的驾驶员的身体柔韧性减少了受严重车祸伤害的可能性[11];老年驾驶员发生非失能伤害和失能性伤害事故的概率分别增加了0.79%、0.18%,但老年驾驶员不太容易发生死亡伤害事故,这主要是因为老年驾驶员的驾驶经验更为丰富,且更不容易鲁莽驾驶。老年驾驶员驾驶大货车发生非失能性伤害事故的概率增加了0.08%。而老年驾驶员驾驶皮卡车发生死亡伤害事故的概率降低了0.07%,主要是因为老年驾驶员由于身体机能弱化,如视力下降、行动迟缓等,不适合操纵笨重的大型车辆。
使用安全带能够减轻事故伤害的严重程度,安全气囊起爆、驾驶员被甩出车外以及驾驶车辆避让不当会导致发生严重性事故。安全气囊起爆增加了事故伤害的严重程度,但在系安全带情况
下安全气囊起爆能够增加发生无伤害事故的概率(7.95%),说明安全带和安全气囊配合使用能够显著地降低严重事故的概率。
分心驾驶使发生可能受伤事故的概率增加了0.33%,发生非失能性伤害事故概率减少了0.11%,即分心驾驶增加了发生严重性事故的概率,其他不安全驾驶行为也有此特性。
(2)车辆特征。相较于其他碰撞车型,在非失能性伤害事故中,皮卡车发生事故的概率增加了0.33%;而在失能性伤害事故中,重型货车发生事故的概率增加了0.04%。可能原因之一是货车司机疲劳驾驶现象普遍,且重型货车行驶惯性较大,一旦发生意外,反应制动时间长,会增加发生严重性事故伤害的概率。皮卡车发生安全气囊起爆事故增加了0.16%死亡性伤害事故的概率,这很大程度上是由于皮卡车底盘高、车身坚硬,若发生安全气囊起爆事故往往是高等级碰撞事故。
(3)环境因素。夜间平峰期(晚上22:00-次日早上06:00)相较于其他驾驶时间,发生可能受伤事故的概率降低了0.3%,发生死亡伤害事故的概率增加了0.04%,说明在夜间平峰期会增加发生车辆群碰撞严重事故的概率。与城区相比较,在郊区公路上发生失能性伤害事故和死亡性伤害事故的概率分别增加了0.16%和0.07%。郊区交通监管较少,很多路段没有信号控制,以至于驾驶员在郊区驾车时速度过快,故增加了发生严重事故的概率[12]。
(4)道路特性。公路限速值与事故严重程度显著相关,当道路限速值为50~100 km/h时,发生失能性伤害事故、非失能性伤害事故、可能受伤事故的概率分别增加0.7%、1.29%、1.39%,当道路限速值>100 km/h时,更容易发生严重事故,发生失能性伤害事故、非失能性伤害事故、死亡事故的概率分别增加了0.36%、0.29%、0.5%。相比普通路段,当事故发生在交叉口时,发生失能性伤害事故、非失能性伤害事故、可能受伤事故的概率分别增加0.28%、0.52%、0.65%,原因是在交叉口,车流比较复杂,冲突点较多,容易发生碰撞。
当事故发生在交通控制方式为“信号控制”时,发生无伤害和失能性伤害的概率分别减少0.27%和0.14%。信号控制一般为城市交叉口,车辆行驶谨慎,速度缓慢,不易发生严重性事故。在交通控制方式为“警示牌/停车让行”时,更容易发生严重性事故。
3.5 预防事故建议
(1)加强交通安全教育培训。建议在驾驶员培训时,需对学员(尤其是女性)进行心态锻炼,提升其应急反应;通过平时的教育宣传、安全讲座等措施,加强驾驶员对不系安全带、酒驾、分心驾驶等不安全驾驶行为的危害的认识;倡导“一座一带”,要求车内每一位乘员都系安全带,以减少事故发生的严重程度;尽量减少私家车的出行次数,鼓励人们选择公共交通出行,特别对于老年人,鼓励采用安全的公共交通出行方式。对于年龄较大的货车驾驶员,要缩短驾驶技能考核间隔,以评估驾驶员是否还能继续驾驶重型货车。
(2)制定相关标准。通过制定较为严格的考核标准,提高重型货车驾照的考取难度,从准入门槛上减少因驾车技术水平不足而引发的车辆群事故;对于长途货运车辆,要配备两名司机才能上路,每名司机驾驶超过4 h必须休息20 min,如有可能,在车内安装疲劳驾驶监测器,当监测出疲劳驾驶现象时,可自动减速并报警。
(3)加强立法监管。由于夜间易发生严重伤害事故,可由交通管理部门立法,规定夜间行车必须打开车灯,以改善驾驶员夜间行车视距,同时严令禁止疲劳驾驶;在郊区,可根据道路实际情况设置减速带和信号控制,尽可能减少交叉口车流冲突,以保障行车安全;可采用LED显示屏提醒驾驶员低速行驶,谨慎驾驶,可根据道路等级条件适当地限制速度,使驾驶员保持警惕。
4 结论
(1)建立了随机参数Logit模型以分析多因素耦合下的公路车辆群事故严重程度的影响因子。结果显示,与多项Logit模型相比,对未能观测的异质性和影响因素之间的交互作用,随机参数Logit模型能够刻画出来,是对事故严重程度进行分析的一种有效方法。
(2)模型拟合结果表明:是否都使用安全带、驾驶员性别、是否甩出车外、年龄、安全气囊起爆与否、不安全驾驶行为、是否酒驾、车辆类型、碰撞类型、事故发生时间、事故地、光线条件、路段限速、路段类型以及交通控制方式等15个单因素及都系安全带-安全气囊起爆、老年驾驶员-大货车、老年驾驶员-皮卡车、安全气囊起爆-皮卡车4个耦合因素和公路车辆群事故伤害程度显著相关。
(3)服从均匀分布的“道路限速值>100 km/h”参数与服从正态分布的“安全气囊起爆与否”参数分析表明:2个参数对不同事故伤害程度具有差异性。
[1] 张吉光,邵维.高速公路多车连环追尾事故影响因素分析[J].长沙大学学报,2015,29(5):63-64.
[2] 尹若愚.车-车碰撞事故深度调查技术研究[D].长沙: 长沙理工大学,2017.
[3] 王佳丽.雾天高速公路连环追尾事故风险产生机理研究[D].北京: 北京交通大学,2018.
[4] MANNERING F L, BHAT C R. Analytic methods in accident research: methodological frontier and future directions[J]. Analytic methods in accident research,2014,1:1-22.
[5] HU W, DONNELL E T. Median barrier crash severity: some new insights[J].Accident analysis & prevention,2010,42(6):1697-1704.
[6] MORRIS C, YANG J J J. Understanding multi-vehicle collision patterns on freeways:a machine learning approach[J]. Infrastructures, 2020, 5(8):62.
[7] HONG J, TAMAKLOE R, PAKE D. A comprehensive analysis of multi-vehicle crashes on expressways: a double hurdle approach[J]. Sustainability, 2019,11(10):2782.
[8] 汤左淦.考虑异质性效应的翻车事故伤害程度模型对比研究[D].广州: 华南理工大学,2019.
[9] HOLDRIDGE J M, SHANKAR V N, ULFARSSON G F. The crash severity impacts of fixed roadside objects[J]. Journal of safety research,2005,36(2):139-147.
[10] 王灿,王德,朱玮,等.离散选择模型研究进展[J].地理科学进展, 2015, 34(10): 1275-1287.
[11] WALLIS A L, GREAVES I. Injuries associated with airbag deployment[J]. Emergency medicine journal,2002, 19(6):490-493.
[12] PALETI R, ELURU N, BHAT C R. Examining the influence of aggressive driving behavior on driver injury severity in traffic crashes[J]. Accident analysis and prevention,2010,42(6):1839-1854.