0 引言
椭圆拟合在许多领域有着广泛的应用,如模式识别与计算机视觉[1]、生物细胞分割[2]、农业[3]等。作为应用,有关椭圆拟合的算法很多,但通常分为3类:最小二乘法、霍夫变换法和边缘轮廓追踪法。基于几何误差最小方法[4]可以精确拟合椭圆,并有相应的算法[5],但是这类方法也存在不足,如对噪声非常敏感。霍夫变换也是检测椭圆中非常著名的方法之一[6],在此基础上有许多改进的方法[7-8],不足之处是这些方法易受图像中的噪声影响。边缘追踪法研究连续的边缘像素来检测椭圆[9-10],这类方法主要策略是检测弧,然后将它们分组归类,当然弧轮廓上的噪点也会影响弧的检测与分类的正确性。为了提高水下目标辨识的准确性,Prasad等[11]采用侧扫声纳方法实现对图像的分割,分割之前要能有效地去除噪声,还要能有效地保留边缘特征等有意义的细节,这样才能保证分割简单和准确。Huo等[12]采用活动轮廓模型(active contour model,ACM)对光学或医学图像中的目标进行目标检测,但大的噪声会严重影响和干扰采用合成孔径雷达(synthetic aperture radar,SAR)图像的处理效果。Sridar等[13]同样采用活动轮廓模型用于红外图像的处理,因为该方法对于噪声具有一定的鲁棒性。采用激光斑点切向干涉法检测表面内缺陷、通过斑点图像进行高精度绝对位移的测量以及测量晶元直径等,都涉及斑点轮廓噪声问题[14-16]。
以上方法在不同的场合取得了很好的应用效果,但在实际情况下,由于被测表面存在缺陷等原因,CCD获取的斑点图像经图像处理后会存在轮廓噪点,拟合的斑点图像的中心位置会出现偏移,将影响深度信息的测量精度。针对轮廓噪点对斑点中心的影响,本文提出了基于统计学原理的一种轮廓去噪方法,并通过理想数据和实际图像数据验证了所提方法和算法的可行性,保证成像斑点中心坐标值的鲁棒性。
1 深度测量原理与成像斑点噪点
1.1 单目视觉与激光点复合的测量原理
运用单目视觉与激光点复合进行测量,激光点作为主动标记点,照射在被测表面上,通过标记点在CCD上斑点图像的位置获取深度信息,如图1所示。
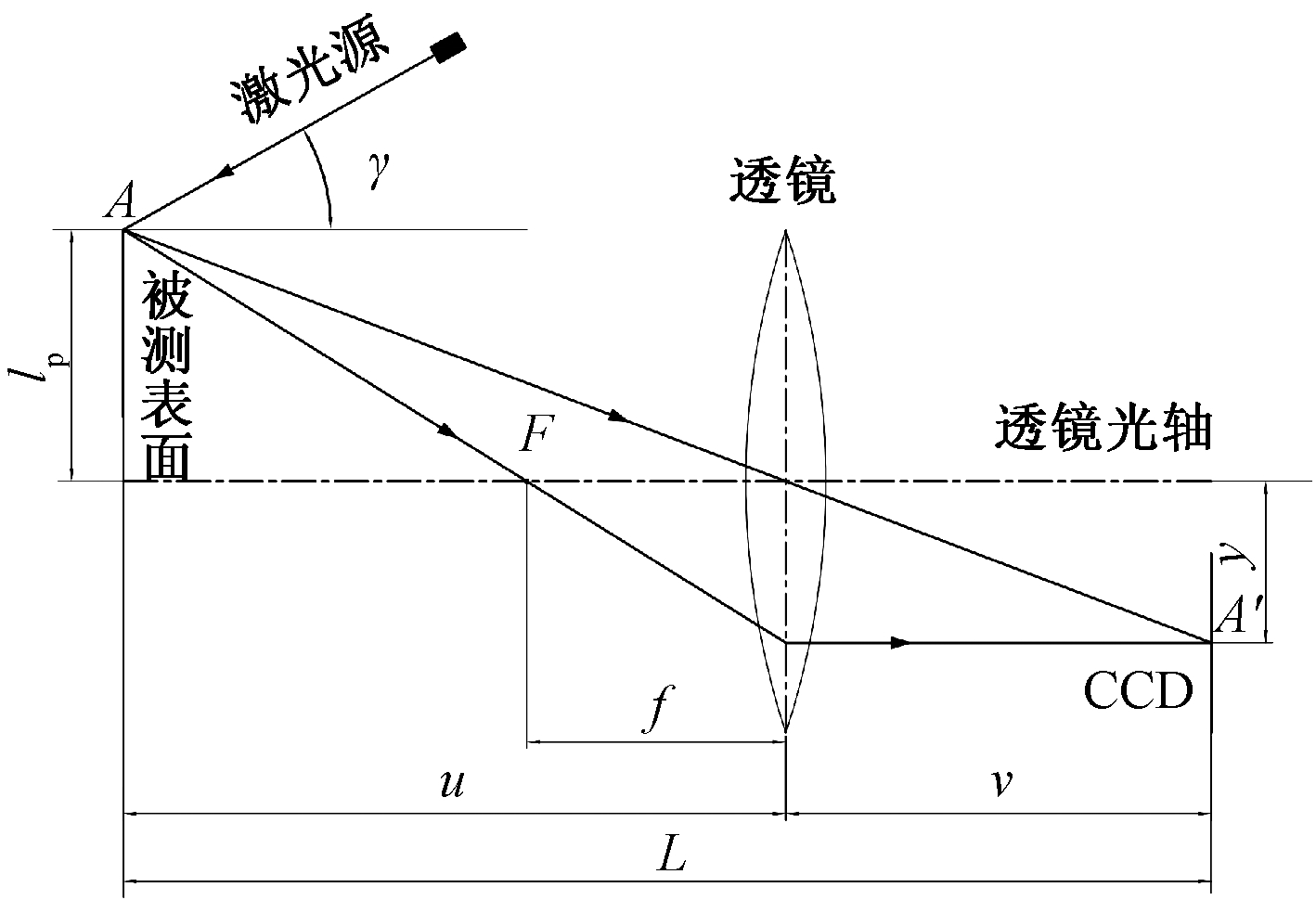
图1 透镜成像模型
Figure 1 Lens imaging model
图1中,L为被测表面与CCD面之间的距离;lp为激光点中心与透镜光轴之间的距离;y为成像面上光斑点中心的y坐标值;u、v分别表示物距和像距;f为透镜焦距,γ为激光源轴线与光轴的夹角。
在图1中,单目视觉CCD面与激光源对称偏置于在透镜光轴的两侧,且使激光源轴线、透镜光轴及CCD面的y轴线位于同一平面内,这样配置的目的:当被测物体发生移动时,成像斑点中心坐标值在CCD面上只有y坐标值发生变化,而x坐标值保持不变。
假设测量系统在初始位置,记L0为测量表面与CCD表面之间的距离,lp0为激光点中心在初始位置与光轴之间的偏置距离,y0为成像斑点的中心坐标,由透镜成像公式,可得
(1)
若被测物体相对初始位置移动ΔL,调节透镜位置,使成像斑点再次服从透镜成像规律,则有
(2)
激光点在被测表面移动后的偏置距离lp与初始位置偏置距离lp0之间的关系如式(3)所示:
lp=lp0-ΔLtan γ。
(3)
由式(2)-式(1)整理得
(4)
式中:![]()
由式(4)可知,当测量系统安装完成后,深度信息L仅与成像斑点中心坐标值y有关,如果成像斑点中心坐标值存在扰动,将直接影响深度信息的测量精度。
1.2 噪点产生的原因
由于激光照射到物体表面时,因表面粗糙度影响会产生散射,在成像斑点轮廓周围会产生一些散射的不规则光斑。由于灯光、日光、反光物等影响,也会产生背景噪点,如图2所示。

图2 表面有背景噪点的激光斑点图像
Figure 2 Laser speckle image with background noise
这样经过图像处理,获取的轮廓边缘,利用轮廓数据获取斑点中心时,中心坐标值将受噪点影响而产生扰动,影响测量精度。
2 斑点轮廓去噪方法及收敛性证明
2.1 斑点轮廓去噪方法
由以上分析可知,深度信息与斑点图像的中心坐标值有关,去噪的具体过程如图3所示。由于成像斑点呈椭圆状,其斑点轮廓离散点服从椭圆分布,如图3(a)所示。
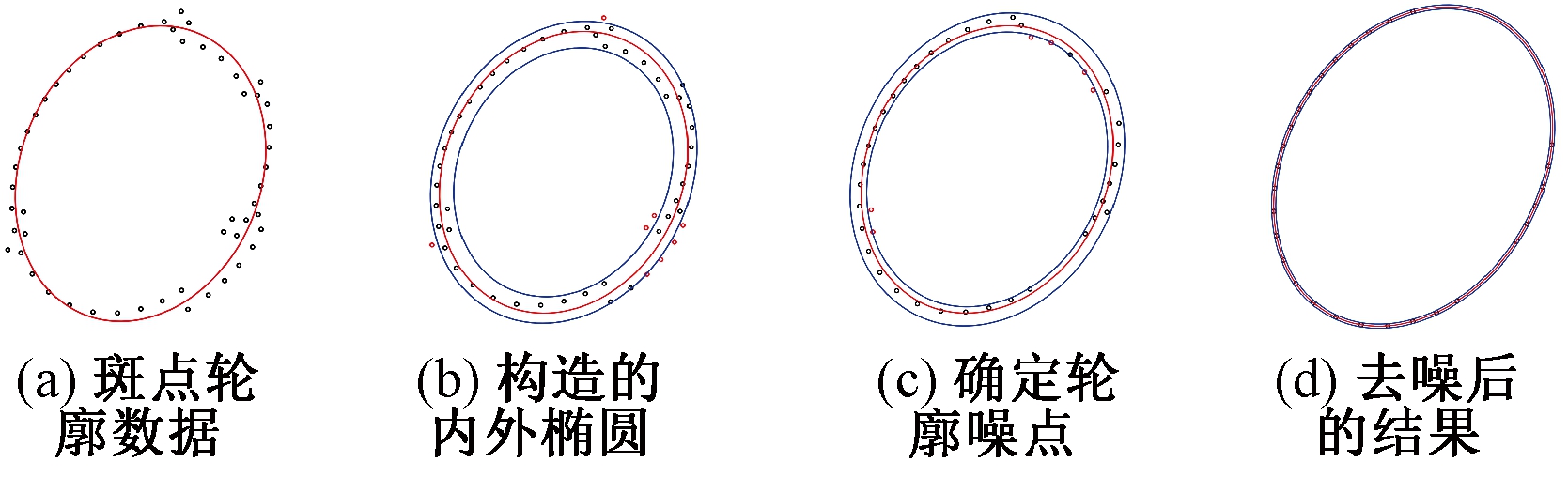
图3 去噪过程
Figure 3 Denoising process
采用最小二乘椭圆法进行椭圆拟合,记拟合椭圆为C,其中心坐标为(x0,y0),长短轴为a、b,倾角为θ,轮廓离散点集为Ai(xi,yi),i=1,2,…,n。则椭圆C:
(5)
式中:xt=(x-x0)cos θ+(y-y0)sin θ;yt=-(x-x0)sin θ+(y-y0)cos θ。
记δ为轮廓离散点集A偏离拟合椭圆C的误差δi的点集,即
(6)
式中:xt,i=(xi-x0)cos θ+(yi-y0)sin θ;yt,i=-(xi-x0)sin θ+(yi-y0)cos θ。
根据统计学原理,考虑轮廓点误差点集δ,其均值为
(7)
均方差为
(8)
由式(7)、(8)得![]() 的置信度为1-α时的置信度区间为
的置信度为1-α时的置信度区间为
(9)
式中:取t0.5α(n-1)=0.66。令![]() 可得斑点轮廓去噪方法如下。
可得斑点轮廓去噪方法如下。
在拟合椭圆长、短轴a、b的基础上,设外扩椭圆的长短轴分别为(1+S2)a和(1+S2)b,构造的外扩椭圆方程Ce为
(10)
设内敛椭圆的长短轴分别为(1-S1)a和(1-S1)b,构造的内敛椭圆方程Ci为
(11)
则构造的内外椭圆如图3(b)所示。
同样,记轮廓离散点集A偏离外扩椭圆Ce和内敛椭圆Ci的误差分别为δei和δii,则由式(10)、(11)得
(12)
式中:若δei>0,则Ai(xi,yi)在Ce之外,定义为轮廓噪点,如图3(c)红点所示;若δei≤0,则Ai(xi,yi)在Ce之内或Ce上,定义为轮廓点。
(13)
式中:若δii<0,则Ai(xi,yi)在Ci之内,定义为轮廓噪点,如图3(b)红点所示;若δii≥0,则Ai(xi,yi)在Ci之内或Ci上,定义为轮廓点。
通过以上方法,每一轮中将轮廓噪点剔除,然后再利用去噪后的轮廓数据进行椭圆拟合,如图3(c)所示。当置信区间S1→0,且S2→0,从而实现轮廓噪点的剔除,如图3(d)所示。
2.2 收敛性证明
由S1→0,S2→0,则由式(9)得
![]() 即:
即:![]()
(14)
(15)
由式(15)-式(14)得
(16)
由式(16)可知,![]() 即
即![]() 式(16)说明了经过去噪后,斑点轮廓数据偏离拟合椭圆的误差均值将趋于0,证明了每一个斑点轮廓数据将分布在拟合椭圆邻域内。
式(16)说明了经过去噪后,斑点轮廓数据偏离拟合椭圆的误差均值将趋于0,证明了每一个斑点轮廓数据将分布在拟合椭圆邻域内。
3 轮廓噪点剔除算法及验证
3.1 算法设计
根据以上提出的剔除方法,算法流程图如图4所示。在图4中,Num1为斑点轮廓的总点数;Ai为轮廓点集,S1、S2为置信区间端点,p、q为置信区间放大系数,r、s为置信区间压缩系数,p1x[count1]、p2x[count2]、p1y[count1]、p2y[count2]为临时存放轮廓点数据的数组;con1为位于外扩椭圆Ce外部的轮廓噪点数目;count1为位于外扩椭圆Ce边界和内部的轮廓点数目;δei为点集Ai与外扩椭圆Ce的偏差;δii为点集Ai与内敛椭圆Ci的偏差;con2为位于内敛椭圆Ci内部的轮廓噪点数目;count2为位于内敛椭圆Ci边界和外部的轮廓点数目;εe为外扩椭圆偏差变量;εi为内敛椭圆偏差变量。
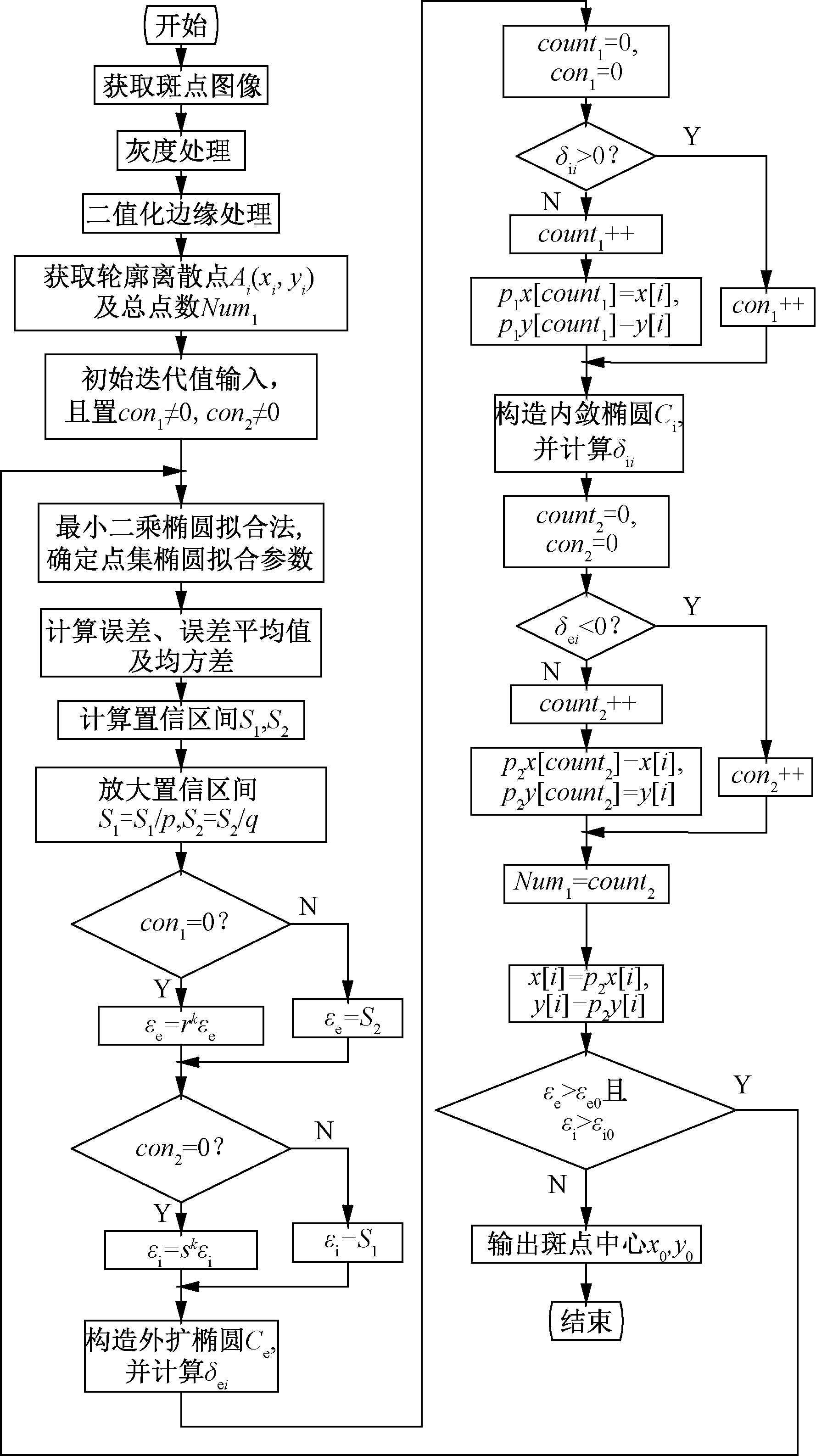
图4 算法流程图
Figure 4 Algorithm flow chart
3.2 搜索策略
(1)在上述流程图中,考虑到实际斑点轮廓点集Ai(xi,yi)是离散的像素坐标,为了避免斑点轮廓点在最初去噪中的损失,因此最初确定内外椭圆边界时,将S1和S2适当放大,其中内敛椭圆边界S1=S1/p,外扩椭圆边界S2=S2/q,且p+q=1。
由于位于内敛椭圆Ci内的轮廓噪点出现的可能性较小,所以p取值较小,在本算例中,p=0.382,即放大后的边界为S1=2.618S1,S2=1.618S2。
(2)由于放大的边界经过一轮搜索后,可能不存在噪点,所以在第二轮搜索时,引入了边界压缩系数r、s,且r+s=1,其中S1=rkS1,S2=skS2。这样将外扩椭圆边界向内压缩,把内敛椭圆边界向外推移,如果仍然没有噪点产生,继续按上述压缩系数做进一步边界压缩,直至出现轮廓噪点,其中k表示第k次压缩,r、s取值为0.5。
(3)当有轮廓噪点出现后,剔除出现的轮廓噪点,重置轮廓点数和轮廓点集Ai(xi,yi),本算例中,count2即为剔除轮廓噪点后的轮廓点数目,p2x[count2]和p2y[count2]为剔除轮廓噪点的点集,然后对外偏差变量εe和内偏差变量εi与给定的误差允许值εe0和εi0进行比较判别,如果不满足条件,则进入新一轮搜索,新一轮搜索重复上一轮搜索的过程,不同之处是轮廓点数和轮廓点集皆采用剔除噪点后的数据;如果满足条件,则停止搜索,输出斑点中心坐标值(x0,y0)。本实例中,考虑到实际图像轮廓为离散整数值,故εe0和εi0分别取0.05个像素,而非理论值0。
3.3 理想数据仿真验证
所提算法验证采用理想数据验证和实验数据验证。理想数据主要验证算法的收敛性,即中心坐标值的稳定性和鲁棒性。采用的方法是制作一个已知椭圆中心坐标,长短轴及倾角的椭圆斑点图像,如图5中红色椭圆斑点,然后加入噪点,包括边缘噪点和背景噪点。本文中噪点采用一段外圆弧,模拟测量面上的凸缘,如图5中绿色所示;一段内圆弧,模拟凹坑,如图5中青色所示;还有一个离椭圆斑点之外的圆形斑点,模拟背景灯光噪点,如图5中粉红色所示。椭圆的中心坐标值为(10 mm,10 mm),经组合形成7种带噪点的图像,加上一种无噪点的图像,总共8种理想斑点与噪点组合的图像,如图5所示。
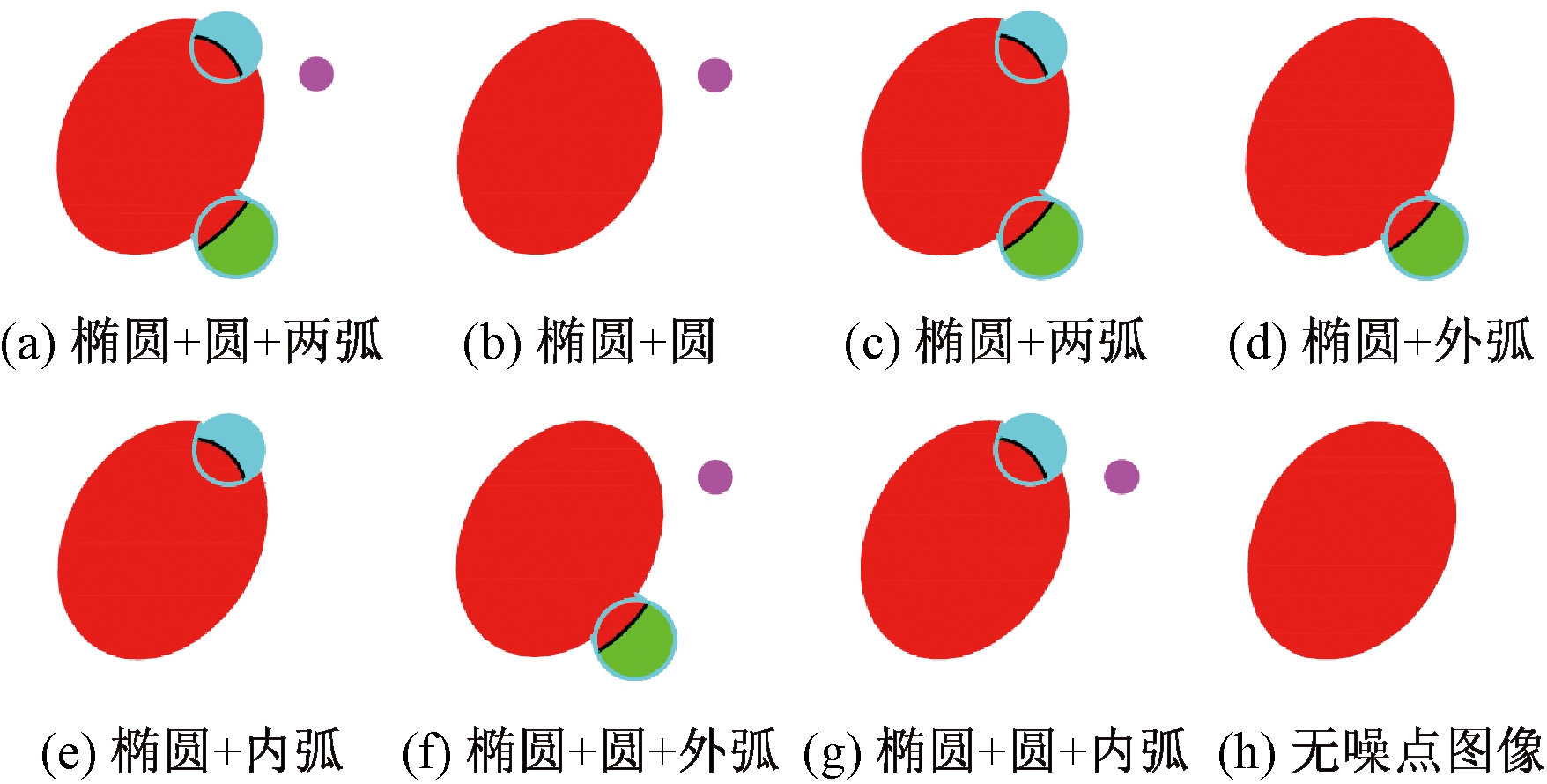
图5 理想斑点与噪点组合图像
Figure 5 Image combination of ideal speckle and noise
采用图像处理,得到灰度图像,经二值化后,按一定规律提取轮廓离散点,如图6所示。
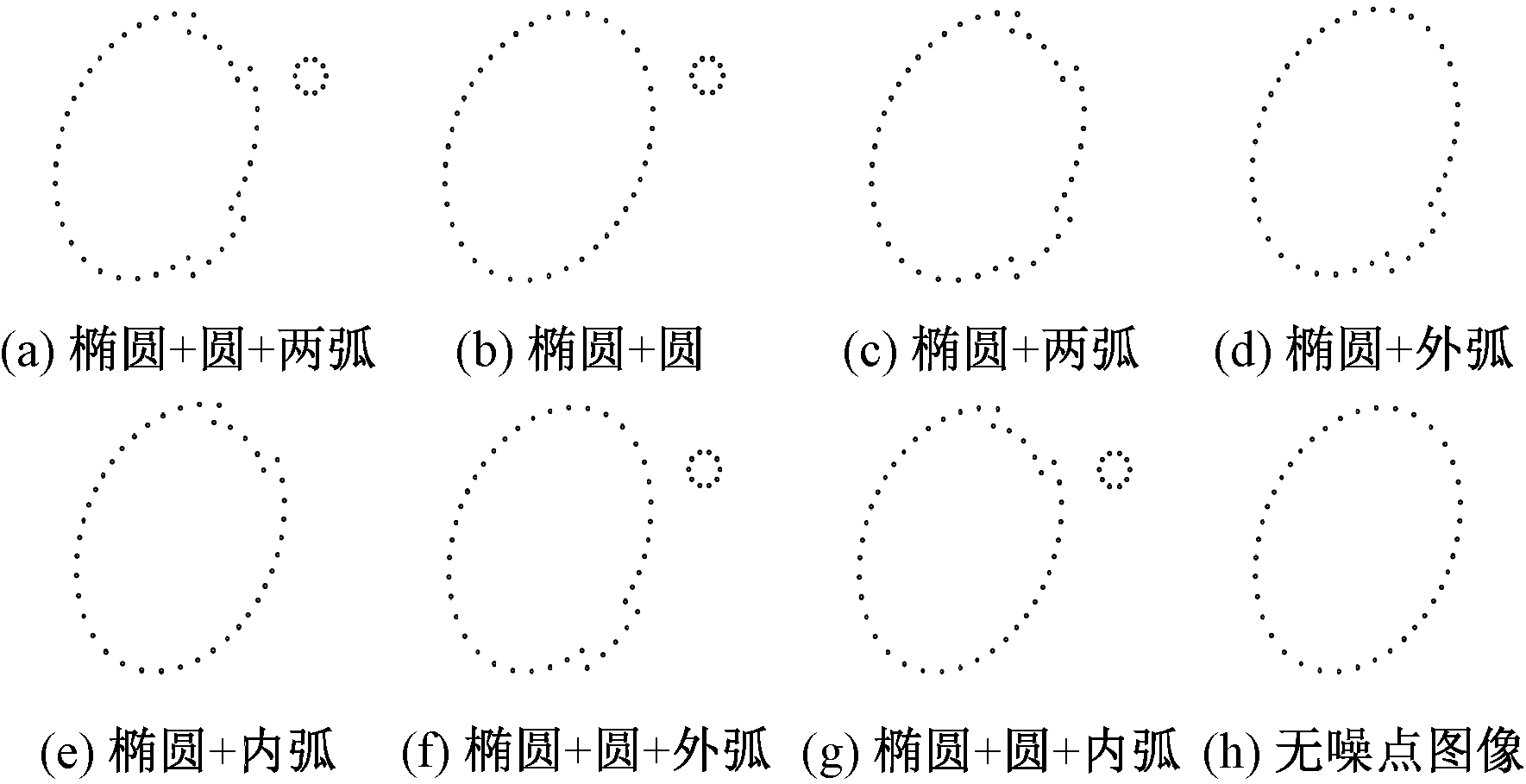
图6 提取的轮廓图像
Figure 6 Extracted contour image
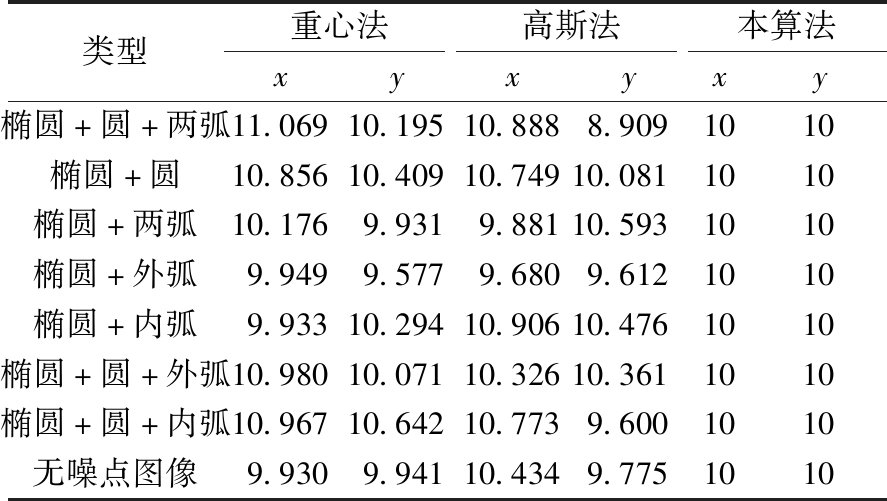
分别采用重心法、高斯法[17]及本文算法,得到椭圆斑点图像的中心坐标值如表1所示。从表1中数据可以看出:高斯法,重心法所得到的中心坐标与理想中心坐标都有不同程度的误差。采用本文提出的算法,在8种情况下,通过去除噪点能够很好地收敛到理想中心坐标位置,说明本算法具有很好的鲁棒性和稳定性。
表1 椭圆斑点中心坐标值
Table 1 Center coordinates of elliptical spots mm
类型重心法高斯法本算法xyxyxy椭圆+圆+两弧11.06910.19510.8888.9091010椭圆+圆10.85610.40910.74910.0811010椭圆+两弧10.1769.9319.88110.5931010椭圆+外弧9.9499.5779.6809.6121010椭圆+内弧9.93310.29410.90610.4761010椭圆+圆+外弧10.98010.07110.32610.3611010椭圆+圆+内弧10.96710.64210.7739.6001010无噪点图像9.9309.94110.4349.7751010
3.4 实验验证
上述验证是在已知图像中心坐标情况下,验证了算法能否收敛到所期望的椭圆中心坐标,但是实际情况下,由于椭圆斑点中心无法通过测量准确获取,通过算法获取的中心坐标是否就是椭圆斑点中心坐标值无法验证,为此本文设计了一种间接验证本算法获取的中心坐标值是否反映实际椭圆图像中心的方法,即通过被测表面移动距离的测量值与实际检测值对比,验证去噪算法的可行性。由于测量方法在物距接近两倍焦距的邻域内测量精度高以及透镜调整直线电机行程的限制,确定被测表面移动距离在1 mm的范围内。
首先构成了测量系统,该系统由相机、光纤激光器、透镜等组成。相机采用BaumerTXG50c,分辨率为2 480像素×1 920像素,像素尺寸为3.45 μm×3.45 μm,透镜焦距为25 mm。采用VS2 010开发环境和OpenCV开发工具,实验系统如图7所示。

图7 实验系统
Figure 7 Experimental system
3.4.1 标定数学模型
调节好测量系统位置(物距、像距),使CCD成像清晰,采用千分表记录被测物体表面的位移ΔL,通过实验平台获得激光斑点的图像,如图8(a)所示;经图像处理获得其灰度图像,如图8(b)所示;然后通过轮廓提取方法并去噪得到轮廓边缘,如图8(c)所示。

图8 斑点图像处理
Figure 8 Speckle image processing
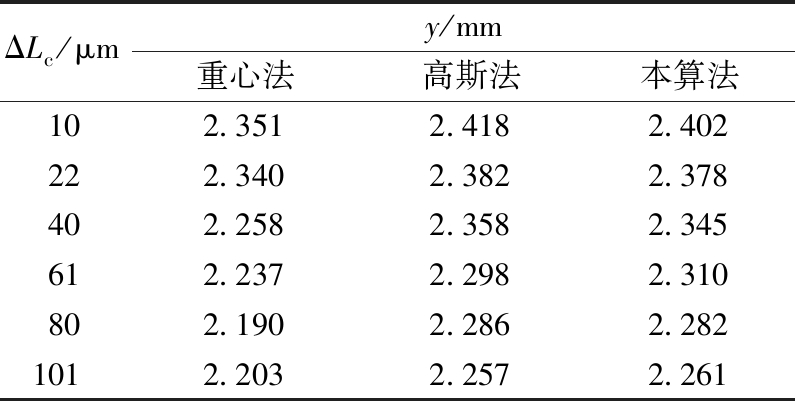
采用重心法,高斯法和本文提出的算法,移动测量表面ΔLc,ΔLc为实际测量值,处理椭圆斑点图像依次获取斑点中心坐标值y,具体数据如表2所示。
表2 斑点中心坐标值y Table 2 Spot center coordinate value y
ΔLc/μmy/mm重心法高斯法本算法102.3512.4182.402222.3402.3822.378402.2582.3582.345612.2372.2982.310802.1902.2862.2821012.2032.2572.261
根据表2的数据,可用两种拟合函数。第一种是本文所推导出的式(4),第二种采用直线法进行拟合[17]。
(1)采用本文所提出的函数拟合,即
(17)
得到拟合的数学模型的系数,如表3所示。
表3 拟合的数学模型中的系数
Table 3 Coefficients in the fitted mathematical model mm

算法k1k2k3/10-6k4k5k6k7重心法2.52760.0609-139.04 1.29108.75522.7008-1.6191高斯法0.02170.00043.4500-0.00371.00680.4539-0.2787本算法0.02050.00114.4850-0.0025-0.12520.06790.0458
(2)采用直线拟合,即ΔL=c1+c2y,得到拟合的数学模型中的系数如表4所示。
表4 拟合的数学模型中的系数
Table 4 Coefficients in the fitted mathematical model mm

算法c1/10-3c2/10-6重心法4.1762-6.2100高斯法4.9366-6.9000本算法5.5600-7.9350
3.4.2 实验验证
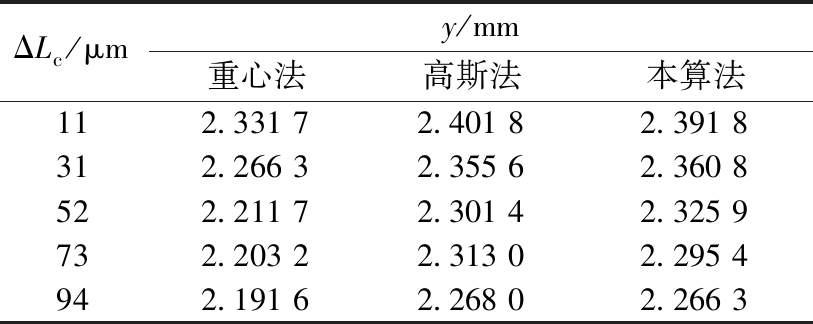
以上通过标定,获取了几种方法的拟合数学模型,下面通过实测验证模型是否能真实反映斑点轮廓的中心。移动被测物体表面至不同位置,获取斑点轮廓中心坐标值y,如表5所示。
表5 实测斑点中心坐标值y
Table 5 Measured spot center coordinate value y
ΔLc/μmy/mm重心法高斯法本算法112.33172.40182.3918312.26632.35562.3608522.21172.30142.3259732.20322.31302.2954942.19162.26802.2663
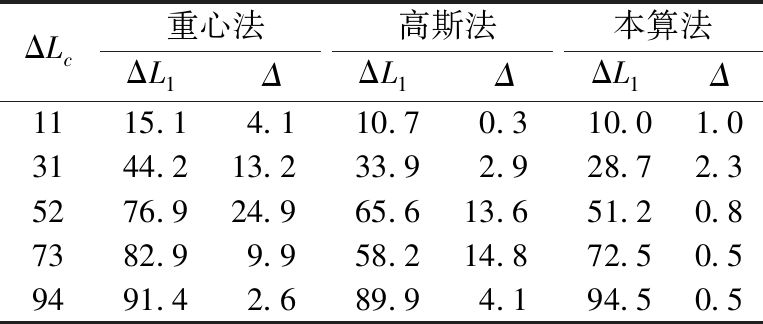
根据拟合模型,计算被测物体的位移值ΔL1,与实际测量值ΔLc比较得到绝对误差Δ,即Δ=|ΔLc-ΔL1|,具体数据如表6所示。
表6 实测值与计算值比较
Table 6 Comparison of measured and calculated values μm
ΔLc重心法高斯法本算法ΔL1ΔΔL1ΔΔL1Δ1115.14.110.70.310.01.03144.213.233.92.928.72.35276.924.965.613.651.20.87382.99.958.214.872.50.59491.42.689.94.194.50.5
从表6中看出,按本文导出的函数拟合,重心法最大误差为24.9 μm,高斯法最大误差为14.8 μm,而本文所提算法最大误差为2.3 μm。
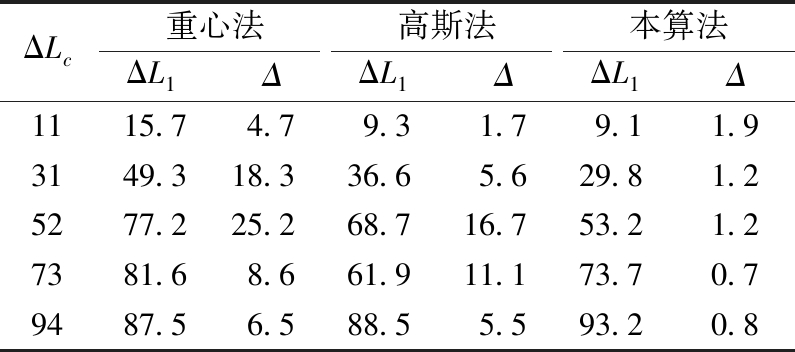
根据直线标定模型,计算被测物体的位移值,并与实际测量值比较得到绝对误差,如表7所示。
从表7中看出,按直线拟合,重心法的最大误差为25.2 μm,高斯法的最大误差为16.7 μm,而本文所提算法的最大误差为1.9 μm。由表6、7可以看出,无论是采用直线拟合,还是以本文推导的函数拟合,尽管实验中高斯法个别点的误差优于本文算法,但本文算法的误差总体上都是最好的。
表7 实测值与计算值比较
Table 7 Comparison of measured and calculated values μm
ΔLc重心法高斯法本算法ΔL1ΔΔL1ΔΔL1Δ1115.74.79.31.79.11.93149.318.336.65.629.81.25277.225.268.716.753.21.27381.68.661.911.173.70.79487.56.588.55.593.20.8
通过上述比较,间接验证了本文算法获取的椭圆中心坐标更加接近实际目标的中心坐标,所以该算法对实际图像边缘噪点的剔除是可行的。
4 结论
在采用透镜成像模型的单目视觉深度信息测量系统中,激光斑点成像中心位置对测量精度有着重要的影响。本文提出一种基于统计学原理确定内敛外扩椭圆边界去除噪点的方法,即根据内敛外扩椭圆边界确定轮廓噪点,如果存在轮廓噪点,则进行剔除,然后利用剔除噪点后的轮廓数据再重新确定内敛外扩椭圆边界,直至满足收敛条件;如果不存在轮廓噪点,则通过不断压缩内敛外扩椭圆边界,直至出现轮廓噪点,然后剔除这些噪点,再重新确定内敛外扩椭圆边界,直至满足收敛条件。通过理想数据的仿真和实际图像的实验验证,该方法能够剔除轮廓噪点,使斑点中心坐标值在有限轮次后趋于收敛并稳定,对单目视觉和激光点复合进行深度信息测量的准确性具有一定的意义。
[1] LIU Z Y,QIAO H.Multiple ellipses detection in noisy environments:a hierarchical approach[J].Pattern recognition,2009,42(11):2421-2433.
[2] BAI X Z,SUN C M,ZHOU F G.Splitting touching cells based on concave points and ellipse fitting[J].Pattern recognition,2009,42(11):2434-2446.
[3] KASHIHA M A,BAHR C,OTT S,et al.Automatic monitoring of pig locomotion using image analysis[J].Livestock science,2014,159:141-148.
[4] CHAUDHURI D.A simple least squares method for fitting of ellipses and circles depends on border points of a two-tone image and their 3-D extensions[J].Pattern recognition letters,2010,31(9):818-829.
[5] CHOJNACKI W,BROOKS M J,Van DEN HENGEL A,et al.On the fitting of surfaces to data with covariances[J].IEEE transactions on pattern analysis and machine intelligence,2000,22(11):1294-1303.
[6] DUDA R O,HART P E.Use of the Hough transformation to detect lines and curves in pictures[J].Communications of the acm,1972,15(1):11-15.
[7] NAIR P S,SAUNDERS A T.Hough transform based ellipse detection algorithm[J].Pattern recognition letters,1996,17(7):777-784.
[8] YUEN H K,ILLINGWORTH J,KITTLER J.Detecting partially occluded ellipses using the Hough transform[J].Image and vision computing,1989,7(1):31-37.
[9] JAI JAGANATH BABU J,SUDHA G F.Non-subsampled contourlet transform based image denoising in ultrasound thyroid images using adaptive binary morphological operations[J].IET computer vision,2014,8(6):718-728.
[10] MAI F,HUNG Y S,ZHONG H,et al.A hierarchical approach for fast and robust ellipse extraction[J].Pattern recognition,2008,41(8):2512-2524.
[11] PRASAD D K,LEUNG M K H,CHO S Y.Edge curvature and convexity based ellipse detection method[J].Pattern recognition,2012,45(9):3204-3221.
[12] HUO G Y,YANG S X,LI Q W,et al.A robust and fast method for sidescan sonar image segmentation using nonlocal despeckling and active contour model[J].IEEE transactions on cybernetics,2017,47(4):855-872.
[13] SRIDAR P,KUMAR A,LI C Y,et al.Automatic measurement of thalamic diameter in 2-D fetal ultrasound brain images using shape prior constrained regularized level sets[J].IEEE journal of biomedical and health informatics,2017,21(4):1069-1078.
[14] VILLAR S A,De PAULA M,SOLARI F J,et al.A framework for acoustic segmentation using order statistic-constant false alarm rate in two dimensions from sidescan sonar data[J].IEEE journal of oceanic engineering,2018,43(3):735-748.
![]() R,GRAHOVAC D,SCITOVSKI R.A method for solving the multiple ellipses detection problem[J].Pattern recognition,2016,60:824-834.
R,GRAHOVAC D,SCITOVSKI R.A method for solving the multiple ellipses detection problem[J].Pattern recognition,2016,60:824-834.
[16] PENG Y H,LIU G X,QUAN Y M,et al.The depth measurement of internal defect based on laser speckle shearing interference[J].Optics &laser technology,2017,92:69-73.
[17] 王丽丽,胡中文,季杭馨.基于高斯拟合的激光光斑中心定位算法[J].应用光学,2012,33(5):985-990.