0 引言
目前,脑影像学技术是研究大脑的重要手段。脑影像技术的成像方式主要包括结构成像和功能成像。结构成像能清晰地反映器官的结构形态,但无法提供器官的功能信息,而功能成像可以准确地提供器官的新陈代谢信息和实时活动,但无法显示大脑的结构形态细节,因此,单个模态的成像往往难以反映研究对象的完整信息。相比之下,多模态信息融合研究主要有以下优点:①通过联合不同模态数据,可以最大限度地挖掘隐藏的信息[1-2];②不同模态的数据可以进行交叉验证,提高结果可靠性[3-4];③综合不同模态特征信息,对噪声更为敏感,结果也更好。
现有的多模态磁共振成像融合策略主要分为模型驱动和数据驱动[5-6]。模型驱动往往无法发现未在假设中体现的关键信息。相比之下,数据驱动是基于数据本身得出的信息,所得到的结果也更加具有客观性、全面性。根据是否加入先验知识,多模态融合策略又可分为无监督融合方法和有监督融合方法。在有监督的融合方法中,可能因先验知识的限制而错过多模态之间更深层次的关系,且很多脑类疾病无法提供参考信息或先验知识。目前,基于数据驱动的、无监督的多模态融合方法主要包括:联合独立成分分析(joint independent component analysis,jICA)、连接独立成分分析(Linked ICA)、多模态典型相关分析(multimodal canonical correlation analysis,MCCA)、稀疏典型相关分析(sparse CCA,SCCA)、MCCA+jICA等。其中,jICA和Linked ICA分解源成分时在保持成分独立性上表现较好,但这2种方法设计的不同模态混合矩阵相同,无法保证不同模态之间的对应性;MCCA和SCCA可以使多种模态间混合矩阵协变最大,但其在分解源成分时,结果的独立性表现较差;MCCA+jICA结合了MCCA和jICA的长处,既能保留不同模态之间的对应关系,又能保证分解后的源成分之间的独立性,但其在检测不同模态共变关系时,只能挖掘出较为直接的相关关系。综上所述,基于数据驱动的、无监督的策略在多模态信息融合中具有明显优势,然而现存的方法都存在一定的局限性和缺陷。为此,本研究在MCCA+jICA的基础上进行改进,提出多模态多层次典型相关分析+联合独立成分分析(multilevel MCCA+jICA,MMCCA+jICA)的融合方法,一方面保留无监督、数据驱动方法的优势,另一方面克服其检测不全面的缺点。
1 方法
MMCCA+jICA的步骤主要包括:数据预处理、低层次特征提取、高层次特征计算、多层次特征结合并通过空间独立成分分析融合分解,最终得到大脑不同模态脑区的共变网络模式,其技术路线如图1所示。在以上步骤中,采用基础的特征提取方法[7-9]即可完成低层次特征提取,在此不详述。
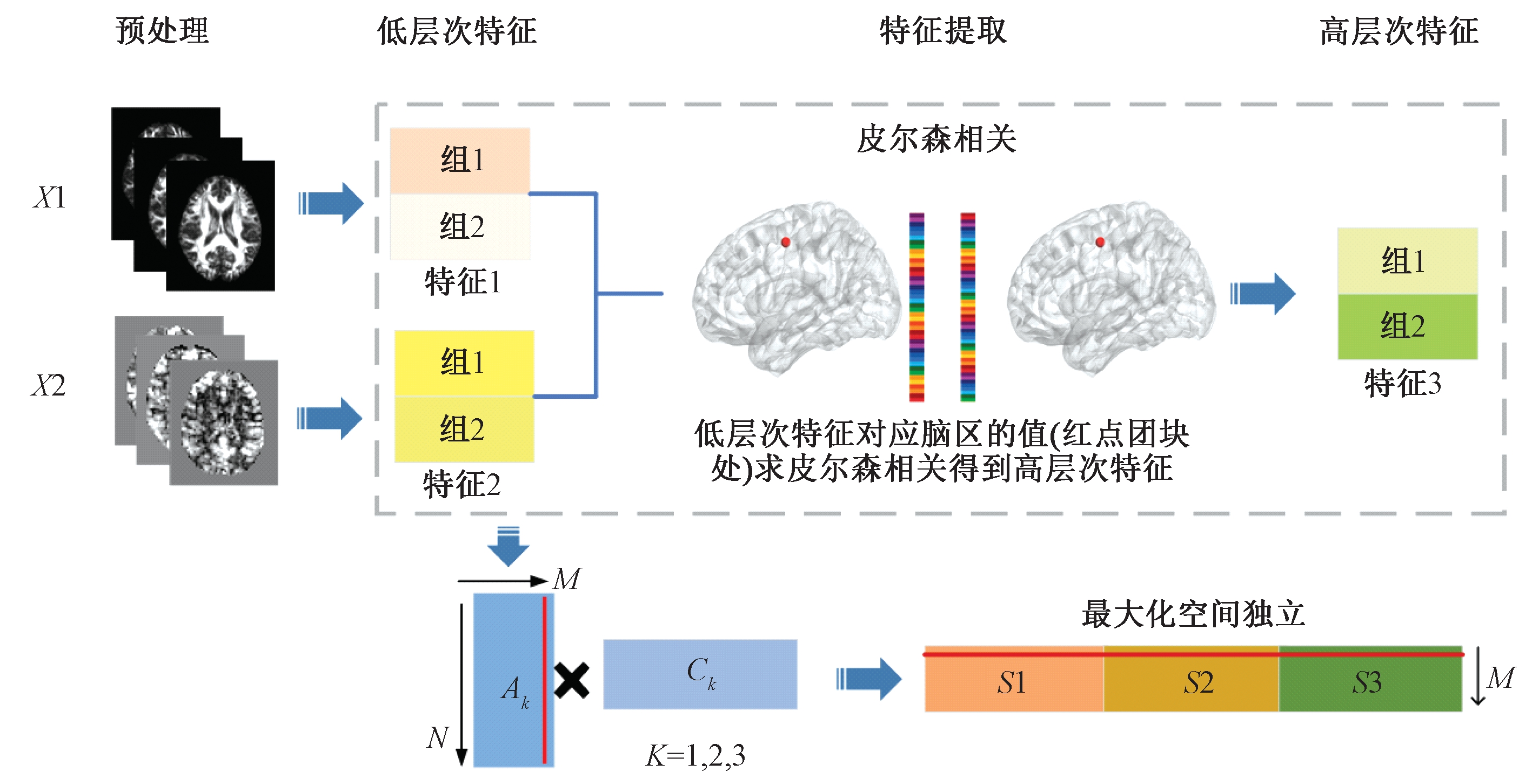
图1 MMCCA+jICA技术路线图
Figure 1 Technology road map for MMCCA+jICA
1.1 高层次特征计算
目前,磁共振脑影像学特征(低层次特征)提取主要分为:形态学特征、弥散特征及功能特征。现有的基于脑影像学的大部分多模态信息研究都是将这些低层次特征单独或者将其结合起来用于后续影像学分析,已取得了一定的成果。但此种分析只是得到不同模态之间的直接关系,无法获取不同模态之间深层次的共变信息。研究表明,与大脑相关的疾病所造成的病理学变化一般都不仅仅在某一独立区域或某一模态,而是在不同模态全脑范围内有着跨区域、高水平连接的脑网络层次上[10-12]。那么,同时应用大脑影像学多种模态的低层次和高层次特征,可以更全面地找出与疾病相关的大脑信息。因此,本文提出一种基于脑磁共振不同模态数据的高层次特征计算方法,将高层次特征与低层次特征结合,形成脑成像数据的多层次分析技术。
高层次特征提取步骤如下。
步骤1 设定团块。针对坐标为(x,y,z)的体素,可以建立一个以自身坐标为中心的团块。该团块共包含27个体素,体素x轴坐标范围从x-1到x+1;y轴坐标范围从y-1到y+1;z轴坐标范围从z-1到z+1。
步骤2 确定低层次特征向量。针对坐标为(x,y,z)的体素,提取其团块内所有体素的低层次特征值,按三维坐标顺序排列构成向量。
步骤3 计算高层次特征。针对坐标为(x,y,z)的体素,令Q表示第i个模态的低层次特征向量,令P表示第j个模态的低层次特征向量,i=1,2,…,n,j=1,2,…,n,i≠j,则以上2种模态在坐标为(x,y,z)体素处的耦合值被称为高层次特征值,记为H:
(1)
1.2 多模态多层次信息融合算法
不同模态的数据在经过预处理、低层次特征提取、高层次特征计算后,将多层次特征进行融合分析。一般来讲,单个模态的脑影像学特征数据X,是由独立信号C通过混合矩阵A混合而成,可以表示为X=AC。对于n个模态的特征数据Xk(k=1,2,…,n),假设每个模态的数据都是由M个独立成分线性混合而产生,则:
Xk=AkCk, k=1,2,…,n。
(2)
式中:Xk大小为N×L(受试者数目×体素数目);Ak大小为N×M(受试者数目×成分数目)。一般来讲,体素数目L≫M。假如有N个受试者,那么多模态多层次信息融合算法的主要步骤如下。
步骤1 多层次特征提取及降维。在获得N个被试的n个模态数据后,首先对数据进行预处理;其次,对预处理后的数据进行低层次特征提取;最后,根据式(1)计算高层次特征H,得到多层次的输入特征集Xk并对其进行降维。本文选择的降维方式是奇异值分解(singular value decomposition,SVD):
Yk=XkEk。
(3)
式中:Ek是对应于较大特征值的特征向量,大小为L×M,则Yk的大小为N×M(受试者数目×成分数目)。
步骤2 在Yk上执行多变量典型相关分析(MCCA)。MCCA是在典型相关分析(CCA)的基础上得到的,根据优化典型变量相关矩阵所选择的函数不同,又可分为SUMCOR、MAXVAR、SSQCOR、MINCOR、GENVAR等5种方法[13],本文所选函数为SSQCOR,如式(4)所示。主要通过不断迭代,使得典型变量Ak对应列之间的相关值平方和达到最大来确定最终的Ak,如式(4)~(6)。
(4)
式中:corr表示列数据之间的相关性;Ak=Ykwk。在此期间,Ak可被分解为M个成分,典型系数向量wk经过t个阶段更新得到式(5)、(6)。
阶段1:
(5)
阶段i,i=2,3,…,t:
(6)
限制条件为
其中,wki是典型稀疏矩阵wk的第i列。
步骤3 基于已求得的Xk和Ak,根据式(2)得到关联成分Ck。
步骤4 独立成分优化。由于上述步骤得到的Ck通常是一组不完全独立的成分,因此引入jICA[14]对Ck进行进一步优化。具体操作为:将步骤3得到的关联成分Ck串联到一起,形成一个级联成分[C1,C2,…,Cn]。然后在级联成分上执行jICA,得到对应混合矩阵的逆矩阵B和独立性优化后的成分Sk:
[S1,S2,…,Sn]=B·[C1,C2,…,Cn]。
(7)
此时得到的Sk就是反映不同模态之间存在共变关系的目标成分。
多模态多层次信息融合算法就是在保留MCCA方法和jICA方法优点的情况下,融合不同模态多层次特征,以便能够获取潜在的深层次多模态共变关系。
2 脑影像学数据模拟及评估方法
2.1 脑影像学数据模拟
功能磁共振成像(functional magnetic resonance imaging,fMRI)和弥散磁共振成像(diffusion magnetic resonance imaging,dMRI)是常见的2种脑影像学数据。本实验通过模拟200名受试者的fMRI和dMRI数据进行研究来检验和评估本文所提出的MMCCA+jICA方法的有效性和鲁棒性。模拟过程详情如下。
步骤1 确定不同模态数据的目标模板。fMRI模态由常用的AAL(anatomical automatic labeling)模板[15]生成,模板大小为61×73×61。AAL模板共116个区域,除去小脑区域(因小脑和大脑属于不同的系统,在此不作研究),剩余为90个大脑脑区。本研究从中随机选择8个大脑脑区作为研究目标,这8个大脑区所包含的体素值设置为1,其他区域值设置为0,构成fMRI掩膜(mask)。dMRI模态使用JHU(Johns hopkins university)白质图谱[16]生成,模板大小为61×73×61。JHU模板共68个大脑白质区域,本研究从中随机选择8个典型纤维束作为研究目标。同理,这8个纤维束所包含的体素值设置为1,其他区域值设置为0,构成dMRI掩膜(mask)。
步骤2 构建混合矩阵Ak。若仿真出200位受试者的8个fMRI目标成分及8个dMRI目标成分,根据上文可知,fMRI和dMRI的混合矩阵A1、A2对应的矩阵大小均为200×8。初始情况下,A1和A2中包含的元素在0~1之间随机生成。因为随机生成的数据是没有任何规律的,具有很大的不确定性,为了验证本文所提方法,本研究将混合矩阵A1的第5列和A2的第3列设置为具有相关关系的数据。
步骤3 基于mask,分别构建出fMRI和dMRI完全独立的目标成分S1和S2。根据前两步,S1和S2大小均为8×体素的个数(体素个数是根据mask得到,本文所选mask体素的数量为61×73×61=271 633)。
步骤4 生成200名被试的fMRI和dMRI图像数据。根据式(2)可知,当混合矩阵和独立成分确定时,可以求出Xk。因此,Xk(k=1或2,代表2种模态)即为200×271 633的矩阵,200对应的是被试人数,271 633对应的是整个图像体素的个数。此时,可获得采用一定规则模拟出的200名被试fMRI和dMRI的图像。在模拟数据中,2种模态具有共变成分的体素个数总共为535个。
步骤5 加入噪声。因真实数据易受到机器及其他人为噪声影响,故仿真过程中还需要加噪声来逼近真实数据,从而验证新方法的鲁棒性和抗噪能力。给数据加入一定噪声后,即可表示为Xk=AkSk+Nnoise,k=1,2。峰值信噪比PSNR是评价图像质量的客观标准,如式(8)所示。PSNR值越大,代表失真越少,图像质量越好。其值低于20 dB时图像质量不被接受,高于20 dB低于30 dB表示图像质量差,高于30 dB低于40 dB说明图像质量有一些失真但可以接受,高于40 dB表明图像已经近似原始图像。因此,本研究添加的模拟数据均在PSNR小于等于30 dB的情况下进行(本研究将随机选择多个PSNR进行验证)。
(8)
式中:![]() 和K是2个r×f大小的单色图像,分别代表无噪声(干净)图像和噪声图像;Omax为图像数据中的最大像素值,在本实验中为255。
和K是2个r×f大小的单色图像,分别代表无噪声(干净)图像和噪声图像;Omax为图像数据中的最大像素值,在本实验中为255。
因篇幅所限,图2仅展示了在PSNR=15情况下2种脑磁共振模拟数据。在模拟数据中,fMRI模态中的标注5和dMRI模态中的标注3存在直接的共变关系,而图2(c)中的彩色区域表示模态间存在深层次的共变关系。
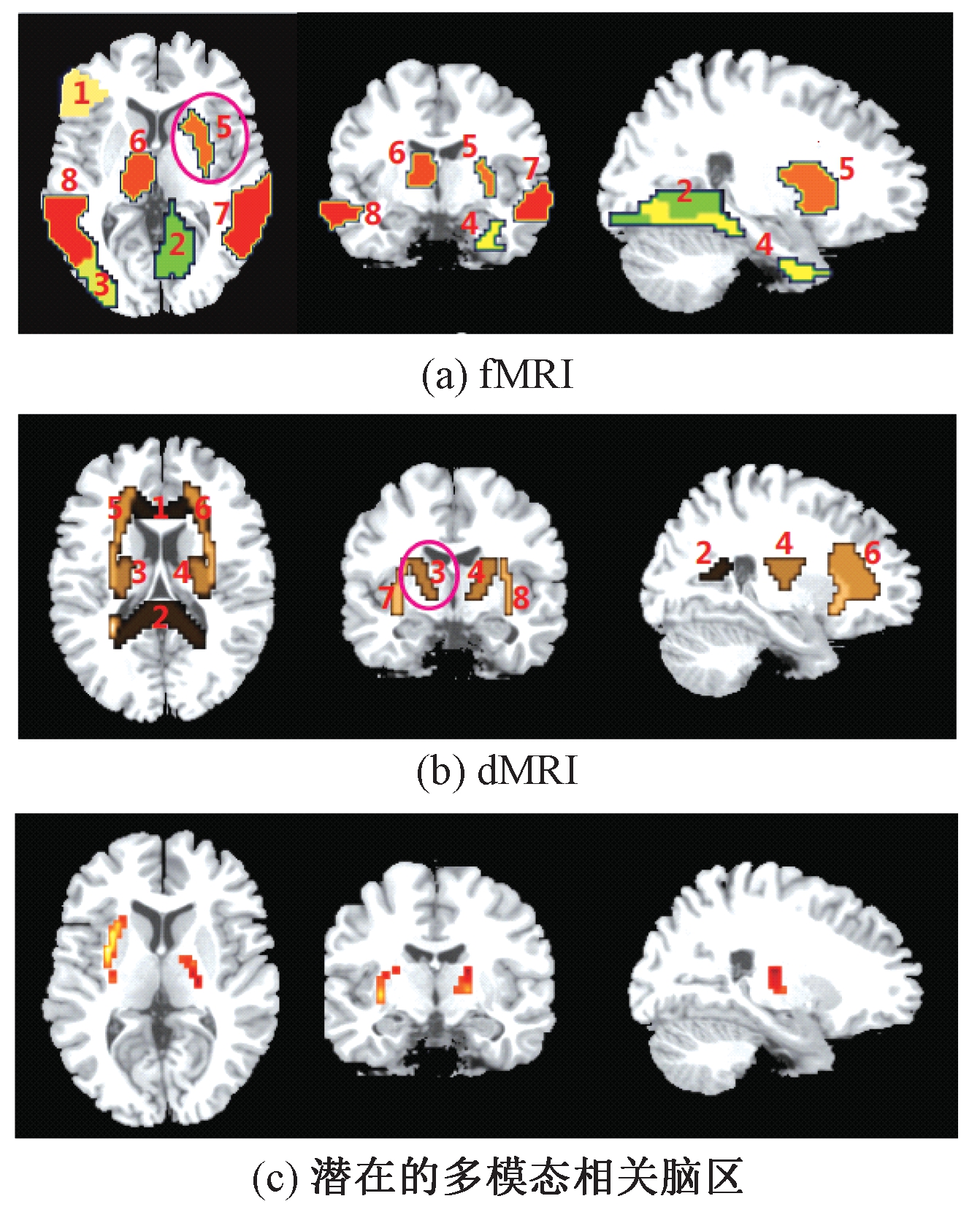
图2 脑图像模拟
Figure 2 Simulated brain images
2.2 评估方法
本研究将此方法与当前流行的、有较多优势的MCCA+jICA和MCCAR+jICA进行对比,以验证所提出方法的精确性、有效性、鲁棒性。
(1)目标成分的检测。检测跨模态间的关系目标成分是多模态信息融合方法的主要功能之一,因此对目标成分的检测准确性是衡量融合方法好坏最重要的指标。
第1种方法是通过真实目标成分与估计目标成分之间的相关性进行检测:
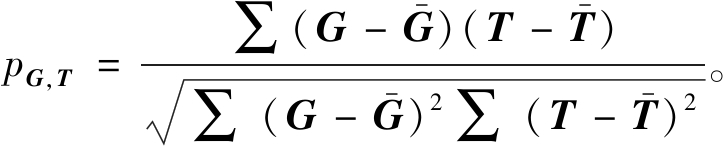
(9)
式中:G为通过MCCA+jICA、MCCAR+jICA和MMCCA+jICA 3种方法计算得到的估计目标成分;T为真实目标成分。
第2种方法是通过检测目标成分识别率进行评价:
(10)
式中:Nvoxel表示通过融合方法获得的具有共变关系的体素数目;Tvoxel表示存在共变关系的实际体素数目;D表示对存在共变关系体素的检测率。
(2)混合矩阵相关性评估。混合矩阵的相关性是不同模态数据间联系的彰显。换句话说,不同模态数据混合矩阵的相关度在一定程度上可以反映出不同模态之间对应目标成分的关系:
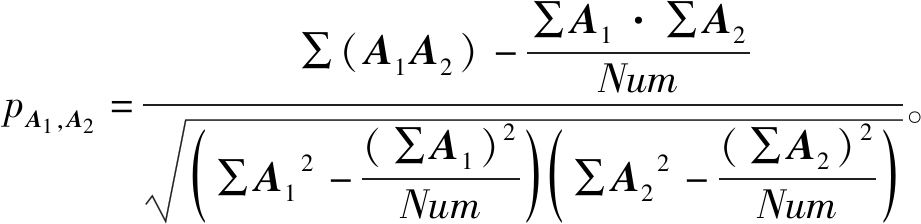
(11)
式中:A1是fMRI模态的混合矩阵;A2是dMRI模态的混合矩阵;Num表示矩阵的大小。
3 结果分析及讨论
3.1 目标成分的检测
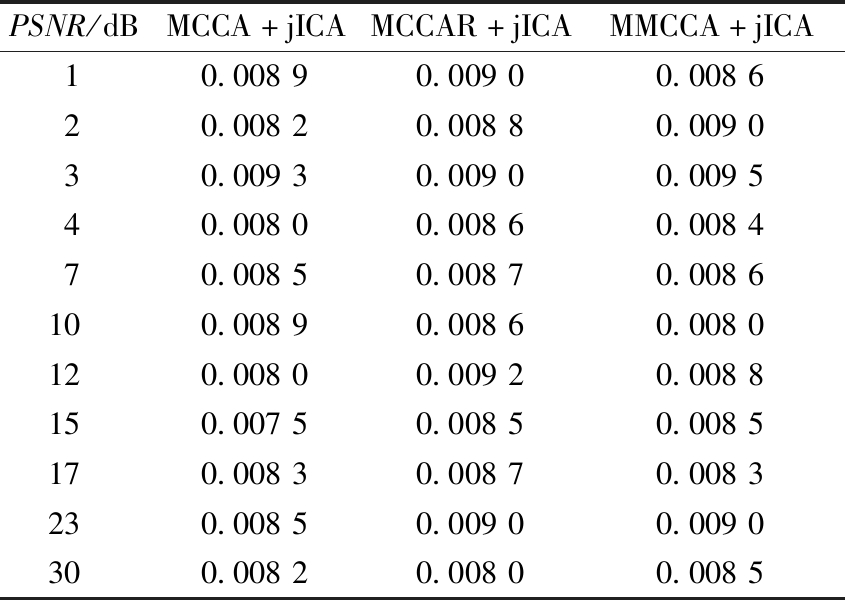
图3展示出11个峰值信噪比下通过MCCA+jICA、MCCAR+jICA和MMCCA+jICA 3种方法得到的真实成分S真和估计成分S估之间的相关性(绝对性)。相关值的大小直接说明了多模态融合方法的可靠性,相关值越大,说明得到的估计目标成分越准确。表1中展示了3种方法相关性分析的可信度及显著性意义情况。由表1可知,不同噪声级别下真实目标成分与估计成分之间均具有统计学意义的显著相关性(p<0.05)。由图3可以看出,随着信噪比的改变,MCCA+jICA、MCCAR+jICA、MMCCA+jICA 3种方法的S真和S估之间的关系值都达到了中高度相关状态,整体均值表现从好到坏依次为MMCCA+jICA(0.890 6)、MCCA+jICA(0.855 7)、MCCAR+jICA(0.699 9)。由以上可知,在11个不同级别的噪声水平下,与MCCA+jICA和MCCAR+jICA相比,本文提出的MMCCA+jICA方法相关性最高、整体结果最好。
表1 图3中相关结果的统计显著性p值
Table 1 The statistical p values of the relevant results in Figure 3
PSNR/dBMCCA+jICAMCCAR+jICAMMCCA+jICA10.00890.00900.008620.00820.00880.009030.00930.00900.009540.00800.00860.008470.00850.00870.0086100.00890.00860.0080120.00800.00920.0088150.00750.00850.0085170.00830.00870.0083230.00850.00900.0090300.00820.00800.0085
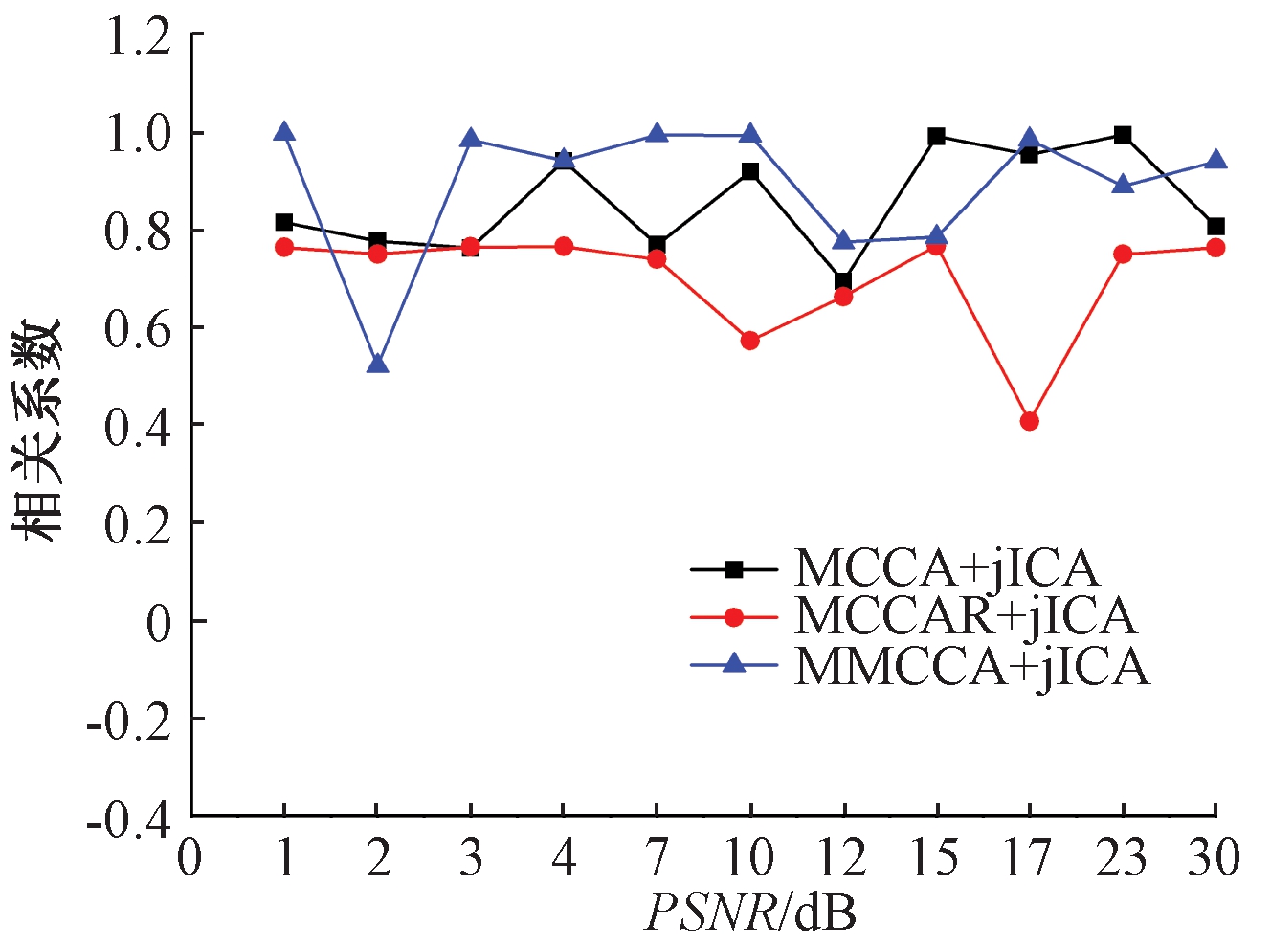
图3 在11个噪声级别下真实成分和估计成分的相关性
Figure 3 Correlation between real components and estimated components under 11 noise levels
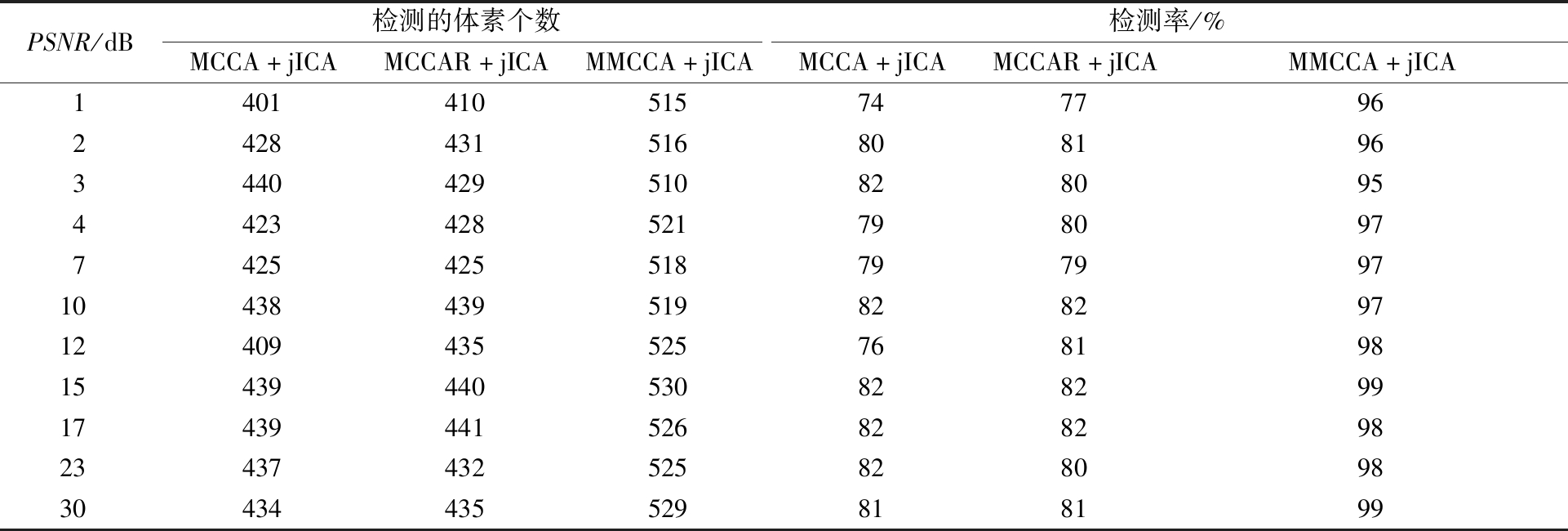
表2是在不同级别的噪声水平下,MCCA+ jICA、MCCAR+jICA和MMCCA+jICA 3种方法对2种模态具有共变关系的体素检测情况。从表2中数据计算得出,3种融合方法的检测率均值从高到低依次为:MMCCA+jICA(97.27%)、MCCAR+jICA(80.45%)、MCCA+jICA(79.91%),而且随着信噪比的改变,检测率标准差从低到高依次为:MMCCA+jICA(0.012 1)、MCCAR+jICA(0.014 4)、MCCA+jICA(0.026 1)。由以上分析可知,相比于其他2种方法,本文所提方法对共变成分的检测率最高、稳定性最强。
表2 不同方法对共变成分的检测率
Table 2 Detection of covariant components by different methods
PSNR/dB检测的体素个数检测率/%MCCA+jICAMCCAR+jICAMMCCA+jICAMCCA+jICAMCCAR+jICAMMCCA+jICA14014105157477962428431516808196344042951082809544234285217980977425425518797997104384395198282971240943552576819815439440530828299174394415268282982343743252582809830434435529818199
因篇幅所限,图4仅展示了在PSNR=15 dB这一噪声水平下,3种融合方法获得的估计成分示意图。图4中彩色区域是不同模态之间存在关系的大脑区域。由图4可知,与其他2种方法相比,本文方法不仅发现多模态间存在直接关系的成分,还检测出多模态间更深层次的耦合成分。
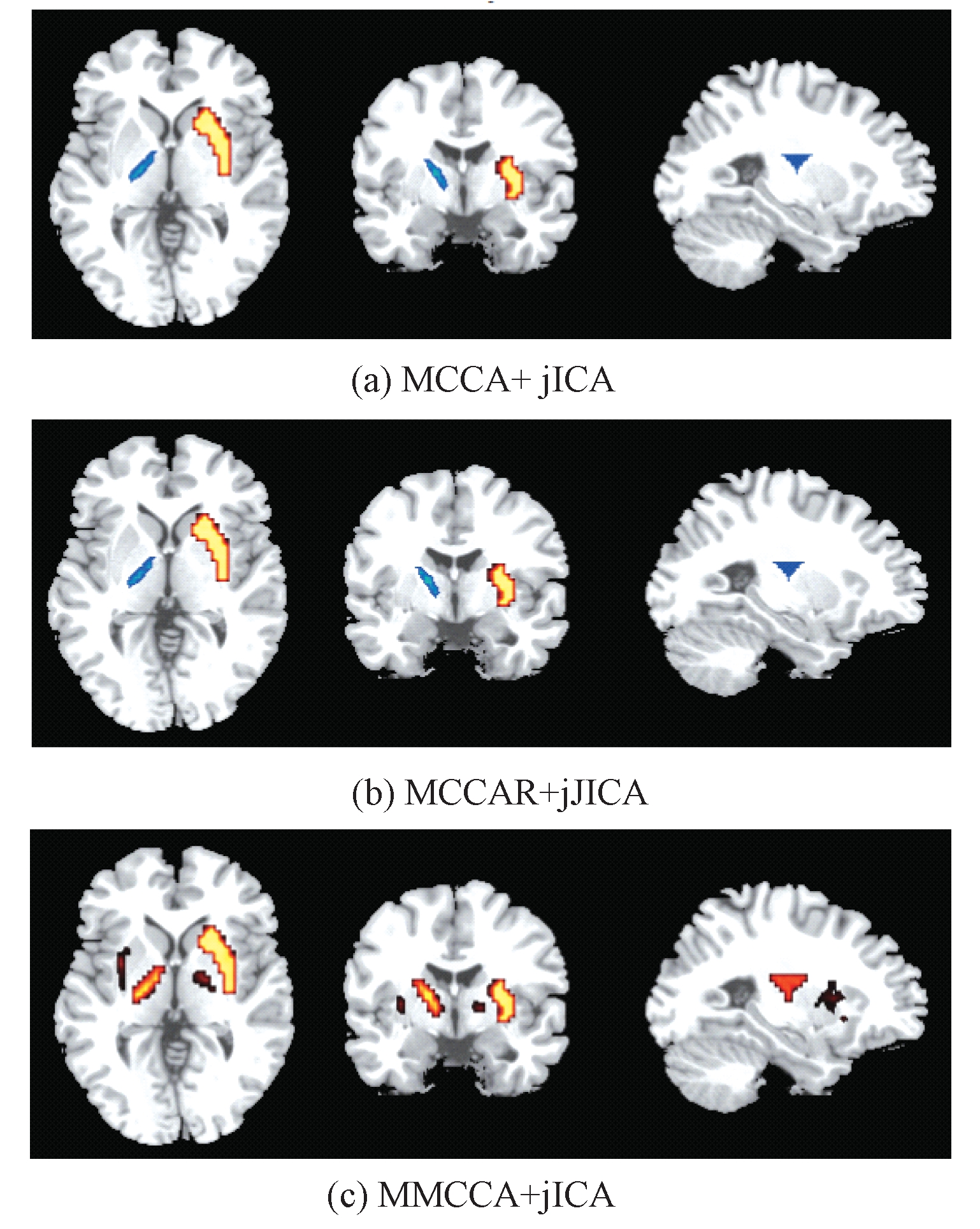
图4 估计成分示意图
Figure 4 Diagrams of estimated components
3.2 混合矩阵的相关性
图5是在11个峰值信噪比下MCCA+jICA、MCCAR+jICA和MMCCA+jICA 3种方法得到的混合矩阵之间相关性结果。由图5可知,随着信噪比的增加,3种方法获得的相关值波动从大到小依次为:MCCA+jICA(标准差为0.289 6)、MCCAR+jICA(标准差为0.138 4)、MMCCA+jICA(标准差为0.105 5)。随着信噪比的变化,其值越稳定,性能越好。因此,与MCCA+jICA和MCCAR+jICA相比,本文提出的MMCCA+jICA方法稳定性更高,抗干扰能力更强。
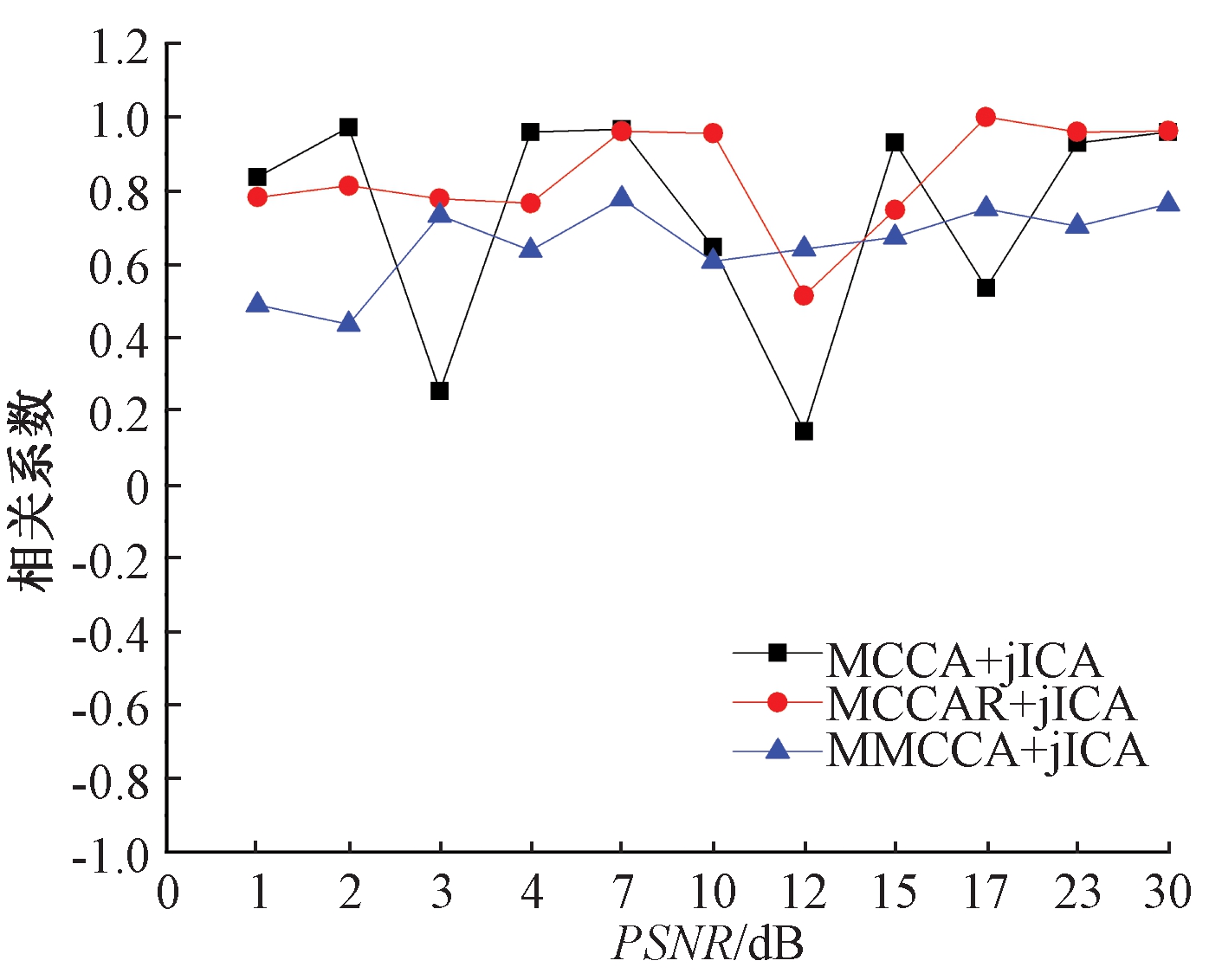
图5 在11个噪声级别下不同模态混合矩阵的相关性
Figure 5 Correlation between mixed matrices for different models under 11 level noises
4 结论
本文提出了一种基于数据驱动的、无监督的多层次多模态脑磁共振成像融合方法。通过仿真数据验证可知,本文所提出的MMCCA+jICA方法无需先验知识就能通过多层次特征信息探索模态间隐藏的潜在共变信息,而这些信息有可能在判别人类脑疾病方面发挥重要作用。与传统的MCCA+jICA和MCCAR+jICA方法相比,本文所提方法在不同噪声级别下获取的估计成分与真实成分之间相关性最高(整体均值达到0.890 6),对目标成分的检测率表现最稳定且检测率最高(检测率均值±标准差=0.972 7±0.012 1),抗干扰能力最好(混合矩阵相关性标准差结果最小,为0.105 5)。因此,MMCCA+jICA方法在探索不同模态间的目标信息上具有高检测率、高稳定性、高鲁棒性。
不同模态数据能从不同角度反映大脑信息,模态数量越多获得的结果也更全面。当前,尽可能全面、准确地探索多模态影像学数据中潜在的耦合信息对研究脑相关疾病十分重要。
[1] MENG X,JIANG R T,LIN D D,et al.Predicting individualized clinical measures by a generalized prediction framework and multimodal fusion of MRI data [J].Neuroimage,2017,145:218-229.
[2] SUI J,HUSTER R,YU Q B,et al.Function-structure associations of the brain:evidence from multimodal connectivity and covariance studies [J].Neuroimage,2014,102(1):11-23.
[3] CALHOUN V D,LEMIEUX L.Neuroimage:special issue on multimodal data fusion [J].Neuroimage,2014,102(1):1-2.
[4] LIU M X,ZHANG J,YAP P T,et al.View-aligned hypergraph learning for Alzheimer′s disease diagnosis with incomplete multi-modality data [J].Medical image analysis,2017,36:123-134.
[5] QI S L,CALHOUN V D,Van ERP T G M,et al.Multimodal fusion with reference:searching for joint neuromarkers of working memory deficits in schizophrenia [J].IEEE transactions on medical imaging,2018,37(1):93-105.
[6] SUI J,QI S,Van ERP T G M,et al.Multimodal neuromarkers in schizophrenia via cognition-guided MRI fusion[EB/OL].(2018-08-02)[2020-12-08].https://doi.org/10.1038/s41467-018-05432-w.
[7] DING C,PENG H.Minimum redundancy feature selection from microarray gene expression data [J].Bioinformatics computational biology,2005,3(2):185-206.
[8] KRAMER M A.Nonlinear principal component analysis using autoassociative neural networks [J].Aiche journal,1991,37(2):233-243.
[9] ABDI H,WILLIAMS L J.Principal component analysis [J].Wiley interdisciplinary reviews computational statistics,2010,2(4):433-459.
[10] HE Y,CHEN Z,EVANS A.Structural insights into aberrant topological patterns of large-scale cortical networks in Alzheimer′s disease [J].The journal of neuroscience,2008,28(18):4756-4766.
[11] STAM C J,De HAAN W,DAFFERTSHOFER A,et al.Graph theoretical analysis of magnetoencephalographic functional connectivity in Alzheimer′s disease [J].Brain,2009,132(1):213-224.
[12] 尚志刚,沈晓阳,李蒙蒙,等.基于格兰杰因果的效应性连接分析方法综述 [J].郑州大学学报(工学版),2020,41(3):1-7,13.
[13] KETTENRING J R.Canonical analysis of several sets of variables [J].Biometrika,1971,58(3):433-451.
[14] CALHOUN V D,ADALI T,GIULIANI N R,et al.Method for multimodal analysis of independent source differences in schizophrenia:combining gray matter structural and auditory oddball functional data [J].Human brain mapping,2006,27(1):47-62.
[15] TZOURIO-MAZOYER N,LANDEAU B,PAPATHANASSIOU D,et al.Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain [J].Neuroimage,2002,15(1):273-289.
[16] MORI S,OISHI K,JIANG H Y,et al.Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template [J].Neuroimage,2008,40(2):570-582.