在现实工程中,许多优化问题需要同时满足多个目标,并且这些目标往往相互冲突,这类问题称为多目标优化问题(multi-objective optimization problem,MOP)[1]。在过去的研究中,人们提出了各种多目标进化算法(multi-objective evolutionary algorithm,MOEA)[2]。这些算法通常可以很好地在目标空间搜索到完整且分布均匀的Pareto前沿面,为决策者提供更合适的选择。但在实际优化问题中通常会出现这样的情况:两个或多个不同的Pareto最优解对应同一Pareto前沿位置,这类问题被称为多模态多目标优化问题(multimodal multi-objective optimization problem,MMOP)[3]。虽然找到Pareto前沿面就可以满足优化要求,但是获得更多PS(Pareto最优解集)可以为决策者提供更多的备选方案[4]。现实中的出行计划就是一个很好的例子[5],如图1所示。图1中的方案1和方案4分别代表火车和长途汽车出行,方案2和方案3同为飞机出行,但这两个方案中转站不同。根据图1右侧PF(Pareto 前沿)可以看出,方案1与方案4,方案2与方案3分别具有相同的时间和成本。很明显,对于需要更短时间到达目的地的乘客,有方案2和方案3这两个选择。当某一方案的中转站受到天气等因素影响时,乘客完全可以选择备用方案;在相对成本较低的情况下,乘客可能不想换乘而选择长途汽车,或者乘客在途中有工作需要处理,在火车上工作会更方便一些。如果最终结果只能给每种乘客提供一个PS,则不能满足不同乘客的需求。因此,研究如何同时获得更多的PS从而为决策者提供更多的选择具有很重要的现实意义[5]。
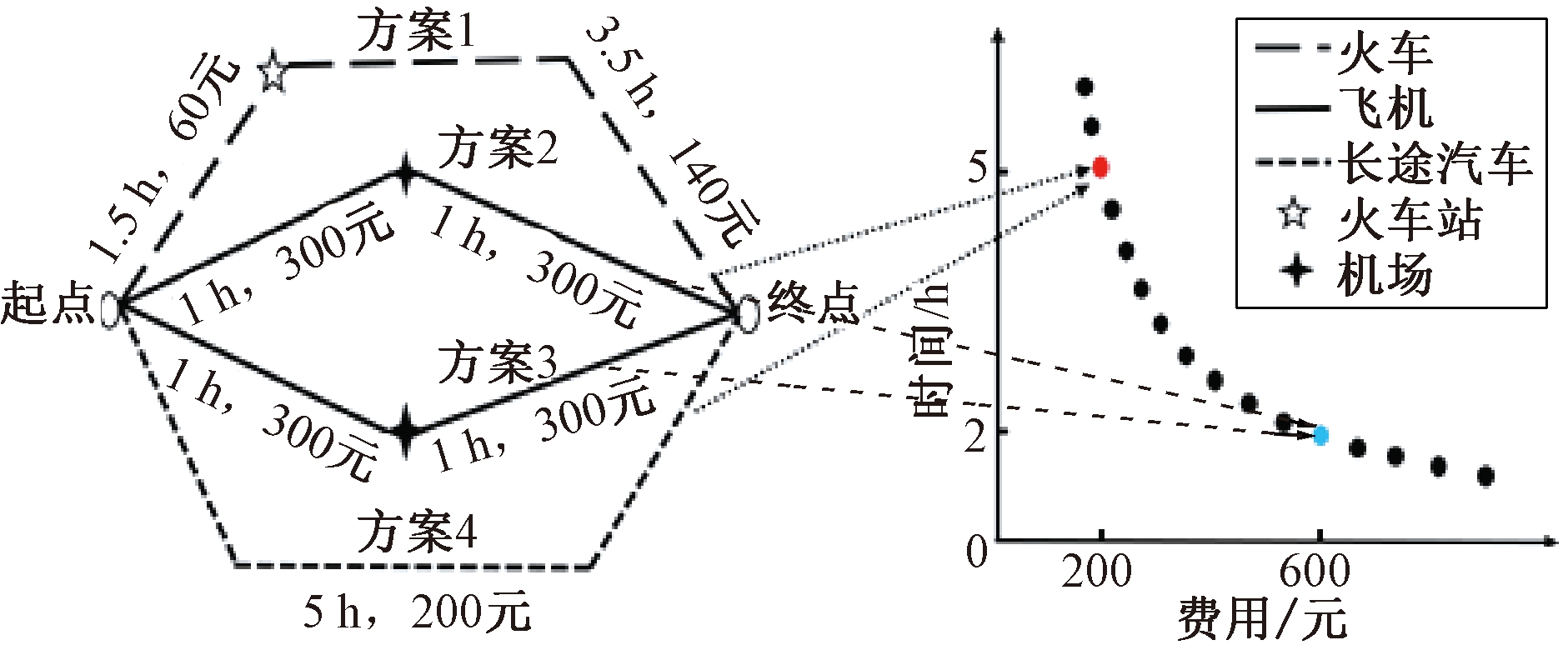
图1 出行方案及其所需时间和费用
Figure 1 Travel plan with needing time and cost
近年来,研究者们提出了大量多模态多目标进化算法(multimodal multi-objective evolutionary algorithms,MMEA)来求解多模态多目标优化问题。根据其算法特征,大致可分为以下几类:①基于拥挤距离和非支配排序的MMEA算法,这类算法引入决策空间的拥挤距离用于非支配排序,如Omni-optimizer[6]和DN-NSGAII[7]等;在多目标优化问题中可以有效搜索到更多的解,但在处理PS形状较为复杂的问题时表现并不理想。②基于小生境技术的MMEA算法,其核心思想是将种群个体分为多类,通过竞争选出适应度高的个体来维持种群的多样性,如DNEA[8]、Niching-CMA[9]等。这类算法可以有效地保持种群的多样性,但由于环境选择压力较大,随着种群的进化,种群的多样性不可避免地会恶化[10]。③基于新型进化范例的MMEA算法,采用性能优越的MOEA来求解MMOP,如SS-MOPSO[11]、MMODE[4]等。这些算法运行效率高,易于理解,并且在提高种群多样性的同时可以更好地保护解在目标空间的分布。④基于不同策略的MMEA集成算法,这类算法将MMEA中不同策略优势互补集成到一起,进一步提高算法的性能,如MO_Ring_PSO_SCD[3]、MMOCLRPSO[12]、MMOPIO[13]等。目前,这类集成算法是研究者们关注的重点,并且在处理多模态多目标问题时取得了很好的效果。
针对多模态多目标优化问题,本文提出了一种两阶段搜索的多模态多目标差分进化算法(multimodal multi-objective differential evolution algorithm based on two-stage search, TS-MMODE)。将算法的进化过程分为精英搜索和分区搜索两个阶段,使用不同的变异策略求解。该算法还引入了文献[3]中基于决策空间的非支配排序策略来提高解在决策空间的多样性。
1.1.1 特殊拥挤距离
Yue等[3]提出同时考虑决策空间和目标空间计算每个个体的特殊拥挤距离,其描述见式(1):
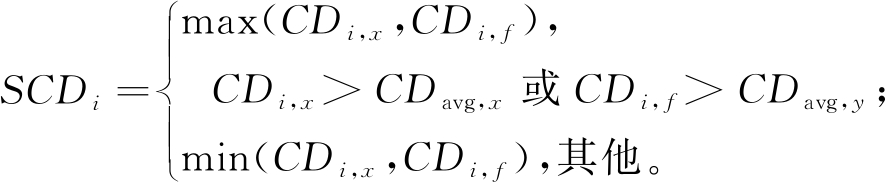
(1)
式中:CDi,x、CDi,f分别表示第i个个体在决策空间和目标空间的拥挤距离;CDavg,x、CDavg,y分别表示决策空间和目标空间的平均拥挤距离。
1.1.2 精英变异策略
在精英搜索阶段根据非支配排序和决策空间的拥挤距离选取种群的最优的一半作为精英变异池,采用差分进化算法中的DE/rand/2变异策略进行变异,这样可以有效提高解的质量,加快收敛速度。差分变异策略DE/rand/2定义见式(2):
Vi(t)=xr1(t)+F(xr2(t)-xr3(t))+
F(xr4(t)-xr5(t))。
(2)
式中:xr1、xr2、xr3、xr4、xr5是从变异池中随机选取的互不相同的5个个体;i=1,2,…,N,N为种群规模;Vi(t)表示第t代的第i个个体;F为DE的缩放因子,取值为[0,1]。
1.1.3 越界处理方法
经变异后的个体可能会落在决策空间以外,为此学者提出众多的修补方法,如文献[4]和文献[14]。本文提出一种新的越界处理方法,给首次越界的个体第2次变异的机会,变异方式如式(3)所示:
Vi,j(t)=xr1,j(t)-F(xr2,j(t)-xr3,j(t))-
F(xr4,j(t)-xr5,j(t))。
(3)
如果第2次变异后个体仍然越界,则按照式(4)进行修补:
(4)
式中:vi,j表示第i个个体第j维上的值;Uj、Lj表示决策空间的上下界。
1.1.4 精英搜索阶段实现步骤
Step 1 精英变异池更新:通过非支配排序和决策空间拥挤距离从种群P中选取最优的一半个体放入精英变异池。
Step 2 变异操作:通过式(2)对精英变异池中的个体进行变异。
Step 3 越界操作:执行按照式(3)、(4)。
Step 4 杂交操作:执行二项式交叉操作形成种群UP。
Step 5 选择操作:合并种群P和种群UP后,利用非支配解排序和特殊拥挤距离式(1)更新种群P。
1.2.1 分区搜索方法
Fan等[15]指出:搜索空间和目标空间共同决定了问题的复杂性。然而,在现实中很难根据目标空间降低问题的复杂性。因此,将搜索空间划分为若干子空间是降低问题复杂度的一种很有前途的方法。
在处理多模态多目标优化问题时,分区搜索的方法操作简单,且不会因种群环境过于复杂而出现恶化[10],可以在降低问题复杂度的同时有效地帮助算法在决策空间进行广泛搜索。本文采用的分区方法是从一个D(D≥2)维优化问题中随机选取Xa、Xb两个变量,并将Xa划分为Q个分段,将Xb划分为H个分段,从而把整个D维空间划分为Q×H个子空间。以3维空间为例,取Q=2、H=2可以将决策空间划分为4个子空间,如图2所示。
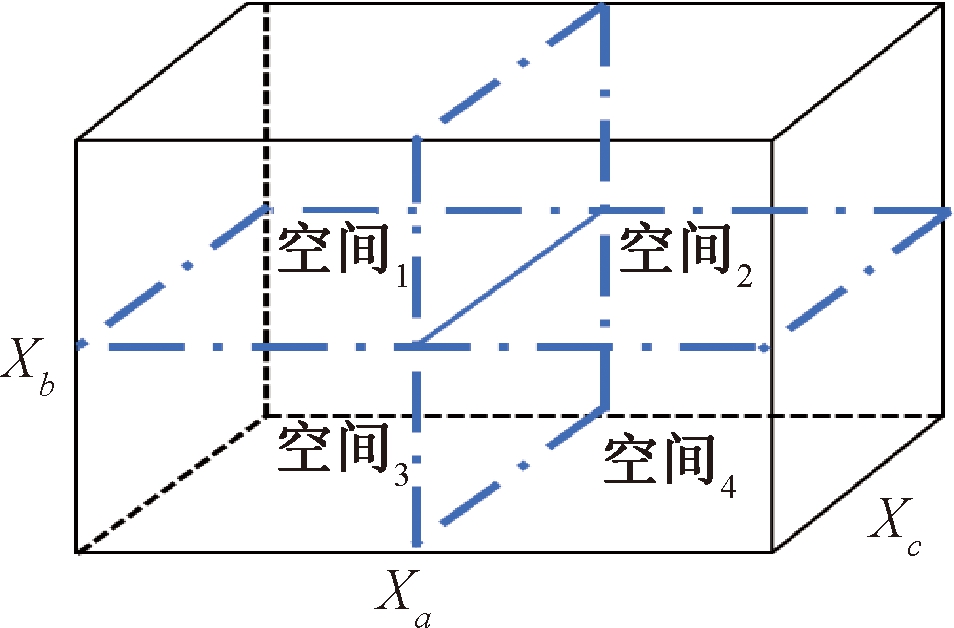
图2 3维4空间分区示意图
Figure 2 3-D and 4 spatial divisions diagram
1.2.2 分区搜索阶段变异策略
在算法的分区搜索阶段,为了在已有一定分布性且适应度值较好的种群内进行更广泛的搜索,将分区后子空间的全部个体作为变异池,通过式(2)来产生下一代个体。
1.2.3 分区搜索阶段实现步骤
Step 1 分区操作:将种群个体放入划分好的空间Sk中,k=1,2,…, Ns。其中Ns表示子空间个数。
Step 2 变异操作:依式(2)对子空间中个体进行变异。
Step 3 越界操作:执行按照式(3)、(4)。
Step 4 杂交操作:执行二项式交叉操作形成种群UP。
Step 5 选择操作:利用非支配解排序和特殊拥挤距离式(1)更新种群。
Step 1 初始化TS-MMODE参数以及种群,阶段值为ti,子空间个数为Ns。
Step 2 对种群进行精英搜索。
Step 3 判断当前迭代次数是否小于阶段值ti。若小于则跳转至Step 2继续执行;否则执行Step 4。
Step 4 对种群进行分区搜索。
Step 5 判断是否达到最大适应度评估次数,若没有达到则跳转至Step 4继续执行;否则执行Step 6。
Step 6 输出结果。
本文共采用18个多模态多目标测试函数[3]来验证算法的性能表现,分别是MMF1~MMF12、MMF13~MMF15(n=3)、Omni-test(n=3)、SYM-PART_simple和SYM-PART_rotated。
本文使用多模态多目标算法常用的评价指标:帕累托近似性 (PSP)[3],用来评估获取的PS与实际PS之间的相似程度。
在所有实验中,比较算法的参数设置均与原文献[3,4,6,7,16]参数相同,每个算法每个实验均独立运行30次,种群规模为800,最大评估次数为1.6×105次。
本文算法TS-MMODE涉及的参数有种群规模N、阶段值ti、子空间个数Ns、缩放因子F、交叉概率Cr。在本次实验中取F=0.5,Cr=0.9。针对阶段值ti和子空间个数Ns的设置会在第3节进行讨论。
由于本文提出的算法将进化过程分为精英搜索和分区搜索两个阶段,算法何时停止精英搜索阶段进入分区搜索阶段由阶段值ti决定。表1中的实验取阶段值ti分别为1、50、100和150,ti=1即表示算法在一开始就进行了分区。
表1展示了在18个测试函数中,不同的阶段值ti对TS-MMODE算法的PSP的影响。从表1中可以看出,有9个函数在ti取100时效果最好;在MMF5、MMF12和MMF14上ti取50时算法表现最好;ti取150时算法在MMF4、MMF7、MMF10、Omni-test(n=3)、SYM-PART_simple和SYM- PART_rotated上表现最为理想;而当ti=1时,与其他3种取值相比,在18个测试函数中没有任何一个可以取得最优结果。所以此实验证明分两阶段搜索在TS-MMODE算法中是很有必要的。
表1 TS-MMODE取不同阶段值时的PSP值
Table 1 PSP value when TS-MMODE takes different stage values
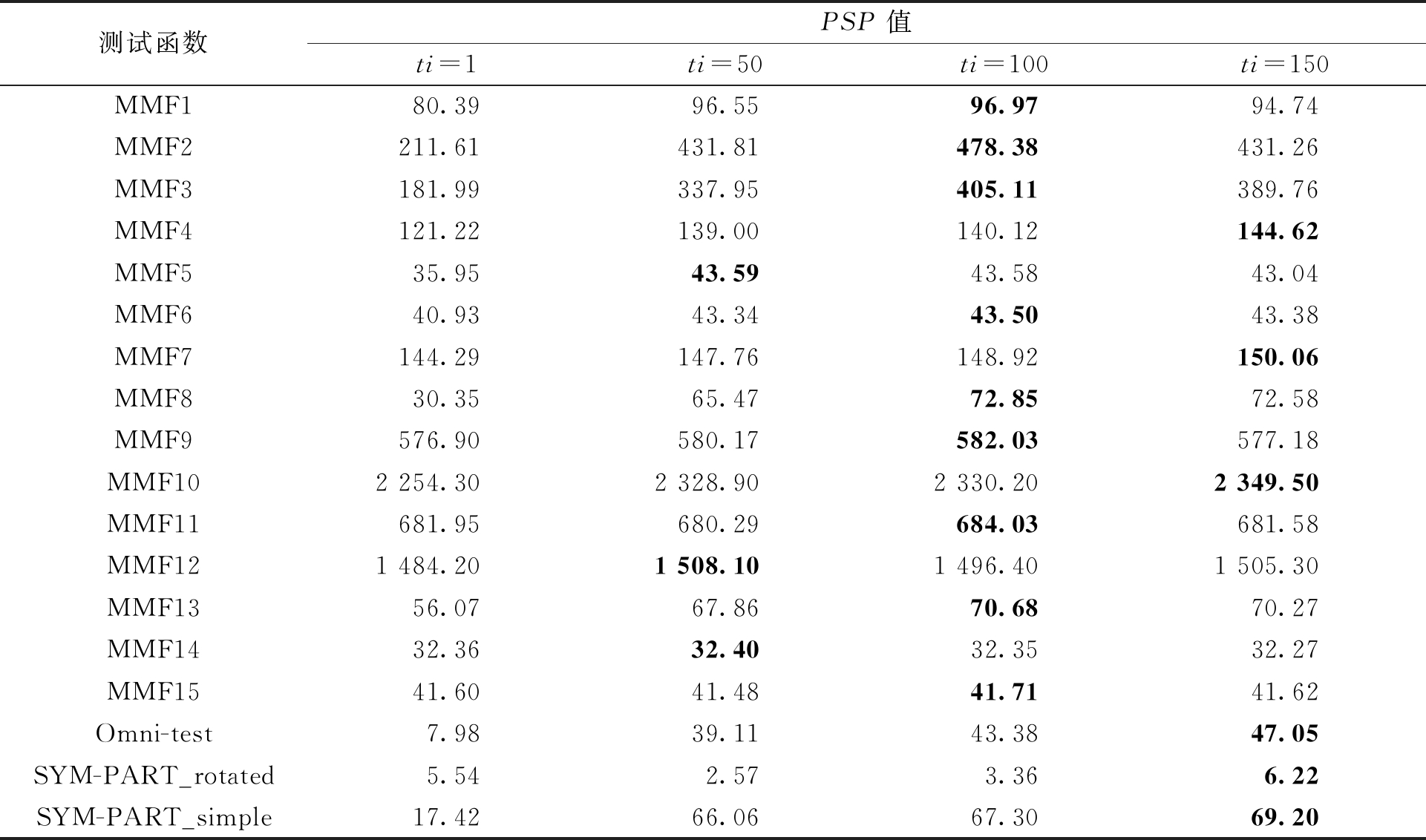
测试函数PSP值ti=1ti=50ti=100ti=150MMF180.39 96.55 96.9794.74 MMF2211.61 431.81 478.38 431.26 MMF3181.99 337.95 405.11 389.76 MMF4121.22 139.00 140.12 144.62 MMF535.95 43.59 43.58 43.04 MMF640.93 43.34 43.50 43.38 MMF7144.29 147.76 148.92 150.06 MMF830.35 65.47 72.85 72.58 MMF9576.90 580.17 582.03 577.18 MMF102 254.30 2 328.90 2 330.20 2 349.50MMF11681.95 680.29 684.03681.58 MMF121 484.20 1 508.101 496.40 1 505.30 MMF1356.07 67.86 70.6870.27 MMF1432.36 32.40 32.3532.27 MMF1541.60 41.48 41.7141.62 Omni-test7.98 39.11 43.38 47.05SYM-PART_rotated5.54 2.57 3.36 6.22SYM-PART_simple17.42 66.06 67.30 69.20
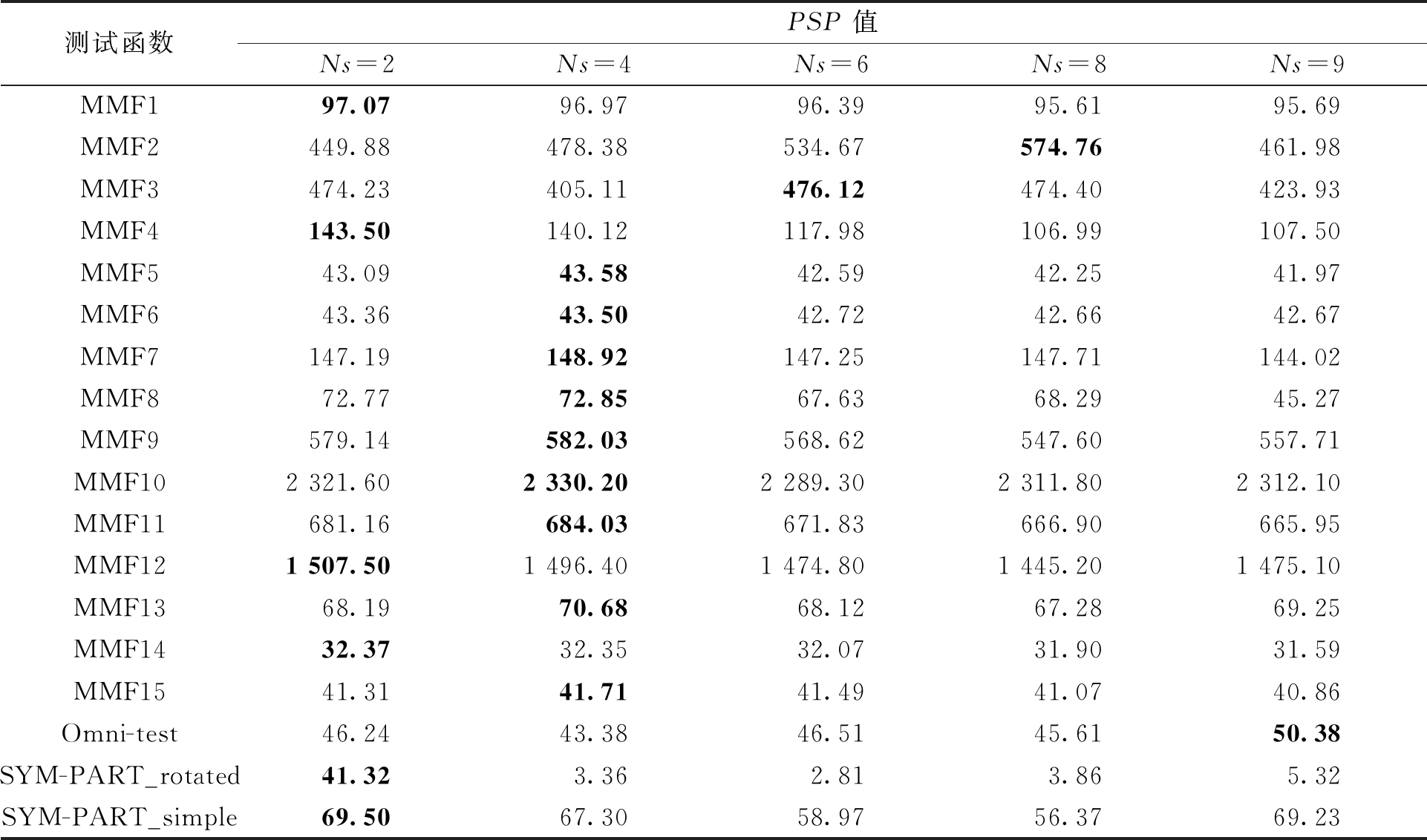
表2展示了当阶段值ti=100时,子空间个数Ns分别为2、4、6、8、9时对算法的影响。实验结果表明,在18个测试函数中有9个函数在Ns=4时效果最好;有6个函数在Ns=2时表现更为理想,且除SYM-PART_rotated外的其他5个函数与Ns=4时的结果相近。总体而言,对于TS-MMODE算法,当Ns=4时效果是最佳的。此外,阶段值ti和子空间个数Ns的不同取值对PF的影响很小,因此不再进行讨论。
表2 TS-MMODE子空间个数不同时的PSP值
Table 2 PSP value with different number of TS-MMODE subspaces
测试函数PSP值Ns=2Ns=4Ns=6Ns=8Ns=9MMF197.0796.9796.3995.6195.69 MMF2449.88478.38534.67574.76461.98 MMF3474.23405.11476.12474.40423.93 MMF4143.50140.12117.98106.99107.50 MMF543.0943.5842.5942.2541.97 MMF643.3643.5042.7242.6642.67 MMF7147.19148.92147.25147.71144.02 MMF872.7772.8567.6368.2945.27 MMF9579.14582.03568.62547.60557.71 MMF102 321.602 330.202 289.302 311.802 312.10 MMF11681.16684.03671.83666.90665.95 MMF121 507.501 496.401 474.801 445.201 475.10 MMF1368.1970.6868.1267.2869.25 MMF1432.3732.3532.0731.9031.59 MMF1541.3141.7141.4941.0740.86 Omni-test46.2443.3846.5145.6150.38 SYM-PART_rotated41.323.362.813.865.32 SYM-PART_simple69.5067.3058.9756.3769.23
如表3所示,为了进一步验证TS-MMODE算法的性能,本文引入常见的多模态多目标优化算法MO_Ring_PSO_SCD[3]、DN-NSGAII[7]、Omni-Optimizer[6]、MMODE[4]和经典多目标算法NSGAII[16],与本文算法的PSP值来进行比较。
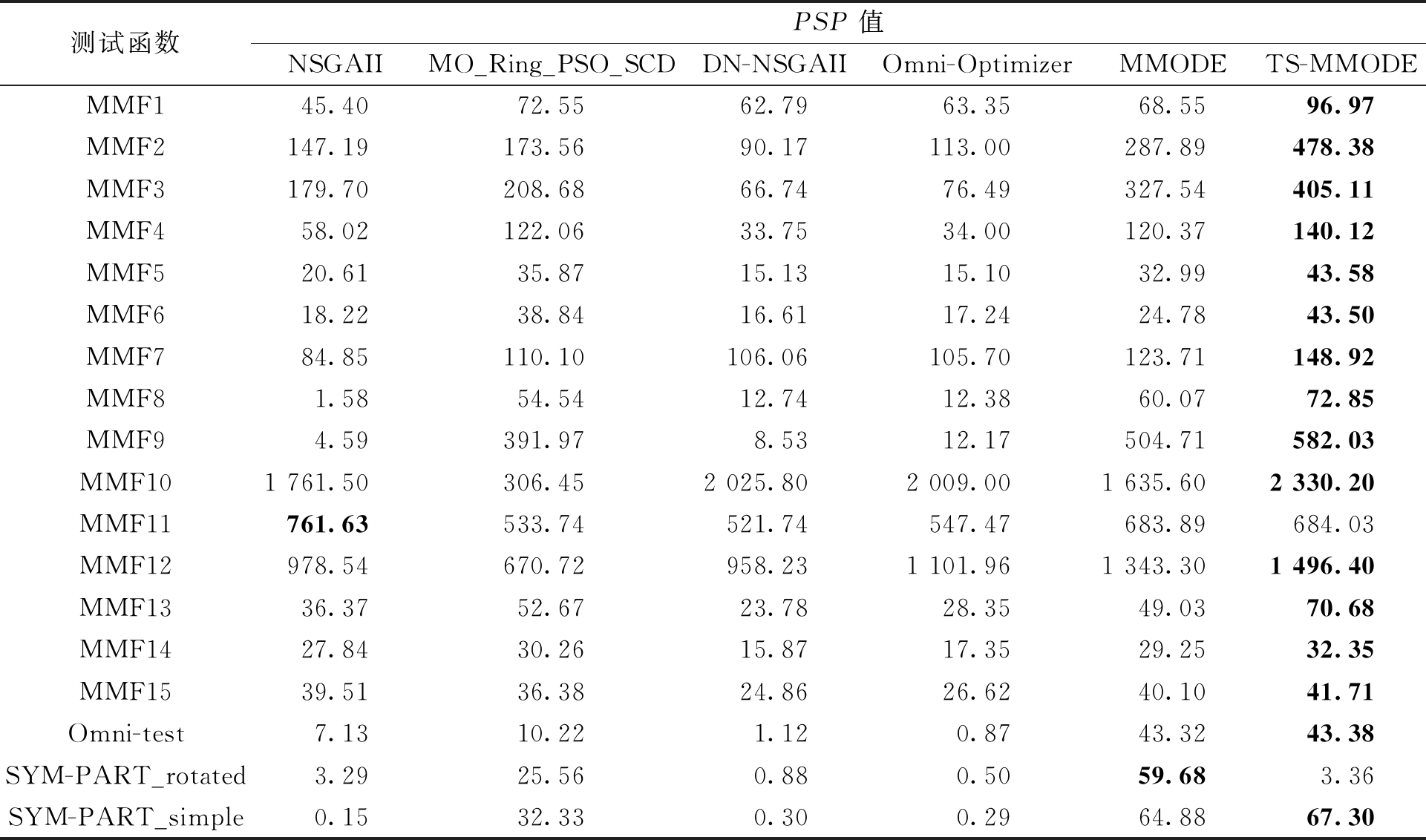
由表3可以看出,本文提出的TS-MMODE算法在18个测试函数中有16个函数的结果优于其他5个算法,虽然在MMF11中效果不如NSGAII,但是也高于其他4种多模态多目标优化算法。另外,与MMODE算法的比较中可以看出,在18个测试函数中仅SYM-PART_rotated这一函数的结果不如MMODE。
图3展示了TS-MMODE算法在PSP值提升较大的MMF2、MMF3、MMF7、MMF9、MMF10、MMF12这6个测试函数上获得的PF与真实PF。从图3中可以看出,TS-MMODE算法并没有因注重决策空间分布而损坏PF。
表3 6种算法在18个测试函数上的PSP值
Table 3 PSP values of 6 algorithms on 18 test functions
测试函数PSP值NSGAIIMO_Ring_PSO_SCDDN-NSGAIIOmni-OptimizerMMODETS-MMODEMMF145.40 72.55 62.79 63.35 68.55 96.97 MMF2147.19 173.56 90.17 113.00 287.89 478.38 MMF3179.70 208.68 66.74 76.49 327.54 405.11 MMF458.02 122.06 33.75 34.00 120.37 140.12MMF520.61 35.87 15.13 15.10 32.99 43.58 MMF618.22 38.84 16.61 17.24 24.78 43.50MMF784.85 110.10 106.06 105.70 123.71 148.92MMF81.58 54.54 12.74 12.38 60.07 72.85 MMF94.59 391.97 8.53 12.17 504.71 582.03 MMF101 761.50 306.45 2 025.80 2 009.00 1 635.60 2 330.20MMF11761.63 533.74 521.74 547.47 683.89 684.03 MMF12978.54 670.72 958.23 1 101.96 1 343.30 1 496.40MMF1336.37 52.67 23.78 28.35 49.03 70.68 MMF1427.84 30.26 15.87 17.35 29.25 32.35MMF1539.51 36.38 24.86 26.62 40.10 41.71 Omni-test7.13 10.22 1.12 0.87 43.32 43.38 SYM-PART_rotated3.29 25.56 0.88 0.50 59.683.36 SYM-PART_simple0.15 32.33 0.30 0.29 64.88 67.30
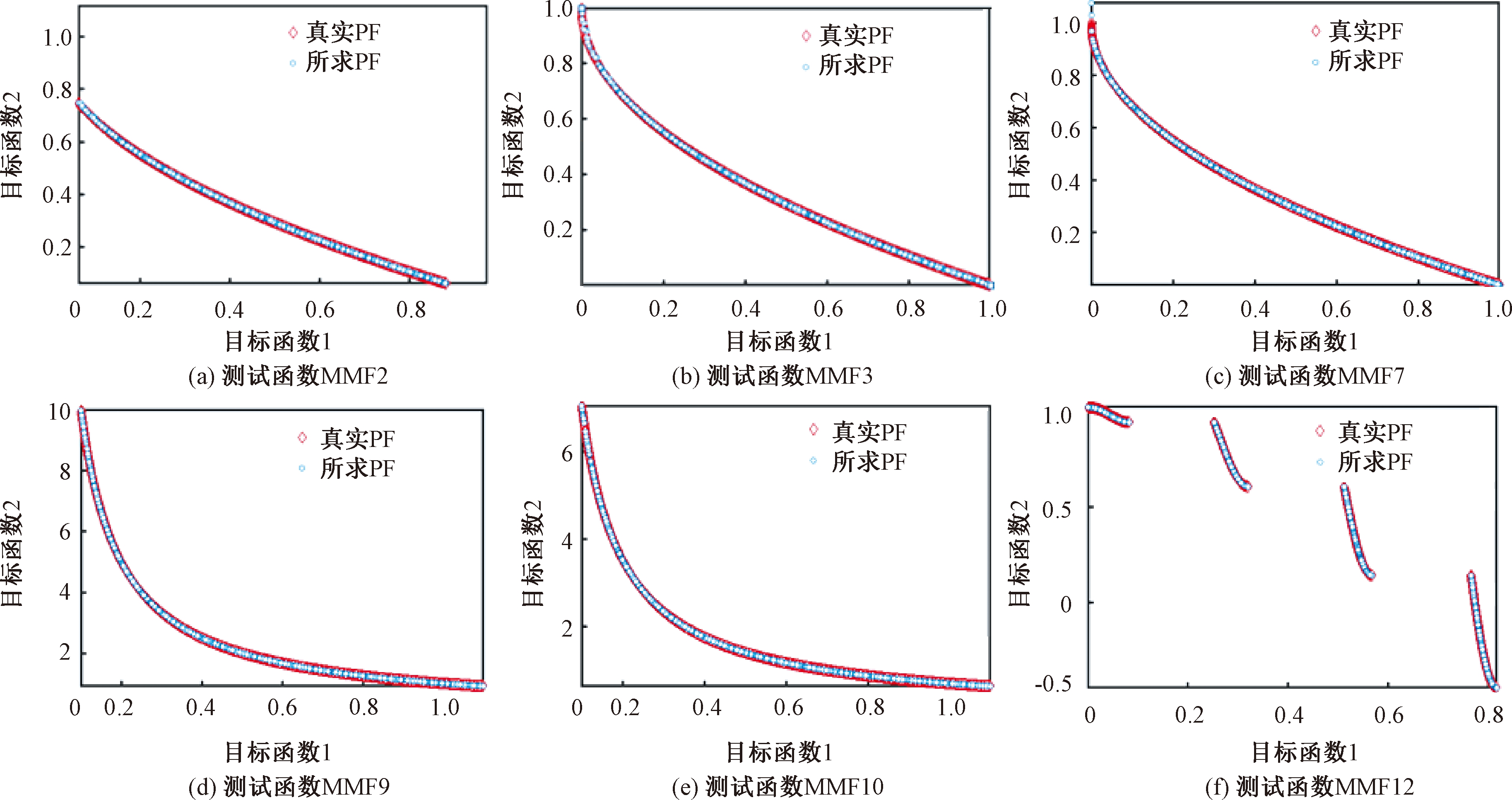
图3 TS-MMODE算法求得的PF与真实PF
Figure 3 Obtained PF by TS-MMODE algorithm and true PF
综上所述,本文提出的TS-MMODE算法在PF分布均匀的情况下大大提高了测试函数的PSP值,这主要是因为算法在精英搜索阶段有效地保证了解在目标空间的质量。在分区搜索阶段,对决策空间进行分区虽然很难提高PF的质量,但有效提高了解在决策空间的多样性和分布性,特别是对于一些PS几何结构相对复杂的测试函数,对决策空间进行分区可以更有效地定位解的位置并进行深度搜索。
针对多模态多目标优化问题,提出了一种两阶段搜索的多模态多目标差分进化算法(TS-MMODE),算法将进化过程分解为以发散搜索为主的精英搜索阶段和以深度搜索为主的分区搜索阶段。在精英搜索阶段,通过精英变异策略增加种群多样性;在分区搜索阶段,通过对决策空间的划分实现对子空间的深度搜索。和常见的5种经典算法进行了比较,实验结果表明,TS-MMODE算法在18个多模态多目标测试函数中有16个函数的PSP性能指标均优于其他5个算法,这表明本文提出的算法可以在维持目标空间解多样性的同时在决策空间搜索到分布更均匀的PS。
[1] 公茂果,焦李成,杨咚咚,等.进化多目标优化算法研究[J].软件学报,2009, 20(2): 271-289.
[2] 闫李,李超,柴旭朝,等.基于多学习多目标鸽群优化的动态环境经济调度[J].郑州大学学报(工学版), 2019, 40 (4): 8-14.
[3] YUE C T, QU B Y, LIANG J. A multi-objective particle swarm optimizer using ring topology for solving multimodal multi-objective problems[J]. IEEE tran-sactions on evolutionary computation,2017, 22(5): 805-817.
[4] LIANG J, XU W W, YUE C T, et al. Multimodal multi-objective optimization with differential evolution[J]. Swarm and evolutionary computation, 2019, 44:1028-1059.
[5] WANG Y, YANG Z L, GOU Y J, et al. A novel multi-objective competitive swarm optimization algorithm for multi-modal multi objective problems[C]//IEEE Congress on Evolutionary Computation (CEC). New York: IEEE, 2019:271-278.
[6] DEB K, TIWARI S. Omni-optimizer: a procedure for single and multi-objective optimization[C]// Evolutionary Multi-criterion Optimization, Third Inter-national Conference. Berlin: Springer, 2005: 47-61.
[7] LIANG J J, YUE C T, QU B Y. Multimodal multi-objective optimization: a preliminary study[C]//IEEE Congress on Evolutionary Computation (CEC). New York:IEEE,2016: 2454-2461.
[8] LIU Y, ISHIBUCHI H, NOJIMA Y, et al. A double-niched evolutionary algorithm and its behavior on polygon-based problems[C]// International Conference on Parallel Problem Solving from Nature. Berlin:Springer, 2018: 262-273.
[9] SHIR O M, PREUSS M, NAUJOKS B, et al. Enhancing decision space diversity in evolutionary multiobjective algorithms[C]// International Conference on Evolutionary Multi-Criterion Optimization. Berlin: Springer, 2009:95-109.
[10] FAN Q Q, YAN X F. Solving multimodal multi-objective problems through zoning search[J]. IEEE transactions on systems, man, and cybernetics: systems, 2019:1-12.
[11] QU B Y, LI Y, LIANG J, et al. A self-organized speciation based multi-objective particle swarm optimizer for multimodal multi-objective problems[J]. Applied soft computing, 2019, 86: 105886.
[12] ZHANG W Z, LI G Q, ZHANG W W, et al. A cluster based PSO with leader updating mechanism and ring-topology for multimodal multi-objective optimization[J]. Swarm and evolutionary computation, 2019,50: 100569.
[13] HU Y, WANG J, LIANG J, et al. A self-organizing multimodal multi-objective pigeon-inspired optimization algorithm[J]. Science China information sciences,2019,62(7):69-85.
[14] 汪慎文,丁立新,张文生,等.差分进化算法研究进展[J].武汉大学学报(理学版),2014, 60(4):283-292.
[15] FAN Q Q, LI N, ZHANG Y L, et al. Zoning search using a hyper-heuristic algorithm[J]. Science China information sciences,2019,62(9): 189-191.
[16] DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II[C]// International Conference on Parallel Problem Solving from Nature. Berlin: Springer, 2000:849-858.