0 引言
车联网是物联网在交通领域的典型应用,是一种基于无线通信进行信息交换的智能化网络形态,在保证道路安全等方面发挥了重要作用[1-2]。车联网中节点之间以及节点与路边设备都需要进行相互通信和数据交换,因此,频谱资源是车联网进行无线通信的基础和支撑性资源,对未来车联网的广泛应用具有重要的意义[3-4]。车联网的快速发展导致了频谱资源的供需矛盾日益显现和突出。美国、日本、中国、欧盟等国家和组织的无线电频谱管理部门均对车联网通信所需的频谱资源做了相应规划。目前主要是使用尚未分配的公用频谱资源,随着车联网频谱需求的爆发式增长,现有的方式将无法满足需求[5]。现在的频谱资源采用固定式分配,大部分频谱资源已经被占用,但已有研究表明,已分配的频谱利用率并不高,导致了频谱资源紧缺,但实际上部分频谱资源存在浪费的局面[6]。认知无线电技术提出了一种高效利用频谱资源的新思路,将频谱资源的使用者分为主用户(授权用户)和次用户(认知用户),实现了频谱的二次利用,在各个无线网络领域显示了巨大优势,如认知Ad hoc网,认知mesh网等[7-9]。在车联网中引入认知无线电技术,即形成了认知车联网,对解决车联网的无线频谱资源问题提供了全新的途径[10]。
目前,研究者对认知车联网展开了广泛而深入的研究,取得了很多有代表性的成果。频谱分配是认知车联网中的关键技术,即在认知车联网用户感知到空闲频谱后,如何将频谱资源分配给次用户使用,达到主用户和次用户的收益最大化,进而提高频谱使用效率。目前,传统认知无线电网络频谱分配有着较为丰富的研究成果,但这些算法均考虑的是静态的认知用户,并不适用于具有动态认知用户的车联网[10]。在认知车联网的研究方面,必须考虑认知车联网的动态连接性、高速移动性等特点。目前,在认知车联网的频谱分配方面,国内外尚处于起步阶段,相关研究成果还较为有限。Cheng等[11]研究了基于博弈论的多认知小区的频谱分配模型,未考虑多用户同时接入可能造成的干扰问题;Zhang等[12]模拟了车联网的运行场景,提出了最大化带宽总和的频谱分配算法;Jiang等[13]建立了车联网的频谱分配框架,以最大化频谱资源利用率为优化目标,未考虑授权频谱由于移动而造成的空闲。
传统的频谱分配可以分为图着色、博弈论、交易理论等解决方法[14]。基于图着色进行频谱分配在传统的认知无线网络分配中取得了非常好的效果[14]。基于此,本文对认知车联网的频谱分配问题采用图着色理论进行建模求解。由于此问题具有NP(non-deterministic polynomial)特性,显然,进化类算法是求解此问题的有效方法。免疫优化是一种有效的计算智能方法,其特有的克隆算子有效兼顾了局部搜索和全局搜索,并保证了较好的种群多样性[15-16],在工程应用领域得到了广泛应用。
基于此,本文考虑了认知车联网中授权用户的移动性、多认知用户之间的干扰等因素,采用图着色模型建立频谱分配的优化模型,以最大化认知用户的网络吞吐量为目标;基于车联网频谱分配问题的NP特性,进而提出一种基于免疫克隆优化的求解算法。实验结果表明,本文所提的频谱分配算法能得到较好的频谱分配效果,达到了主用户和认知用户的收益最大化。
1 认知车联网频谱分配问题建模
本文考虑一个基于路边基础设施的主用户网络,路边移动的车辆作为认知用户。路边基站提供无线通信频谱。认知车联网频谱分配问题简单描述为:车联网节点如何通过感知,机会接入授权频谱。对认知车联网用户,频谱分为占用(不可用)和可用两种。由于车联网中用户拓扑结构是动态变化的,作如下假设:①频谱池中有M个可用频谱,且具有相同的带宽和传输范围;②车联网应用中,随机分布着N个车联网节点,在相互不干扰的情况下,可以同时使用多个频谱M。
本文基于图着色模型,采用以下几个矩阵描述频谱分配问题。
(1)频谱可用矩阵L。L={ln,m|ln,m∈{0,1}}N×M表示频谱的有效性。其中,ln,m=1表示车联网用户n(1≤n≤N)可以使用频谱m(1≤m≤M);如果ln,m取值为0,则表示m不能被n使用。
(2)认知用户之间的干扰矩阵C。C={cn,k,m|cn,k,m∈{0,1}}N×N×M表示车联网用户n,k(1≤n,k≤N)如果同时使用空闲频谱m(1≤m≤M)时是否互相干扰。有干扰产生时,cn,k,m=1,否则,cn,k,m=0。当有干扰时,只能将频谱m(1≤m≤M)分配给一个认知用户使用。现实中,一般使用两个节点之间的传输半径和地理距离来判断[9]。
(3)无干扰分配矩阵AS。AS={an,m|an,m∈{0,1}}N×M。当频谱m分配给用户n时,an,m=1。必须注意的是,AS必须满足an,m×ak,m=0, 若cn,k,m=1,∀n,k<N,m<M(即满足矩阵C的要求)。
根据上面的分析,假设认知车联网用户n分配到了频谱m,则其获得的传输速率为
(1)
式中:w为频谱的带宽;ψ为认知车联网用户的发射功率;hn,m为用户n在频谱m上的信道增益;σ2为噪声方差;n∈1,2,…,N,m∈1,2,…,M。
假设认知用户在t时刻接入频谱m,可用时长至少为T,才能保证其在[t,t+T]数据传输正常完成。因此,在时长T内,认知车联网用户的吞吐量表示为[8]
(2)
式中:Pm(T)为可用频谱m的可用时长不小于T的概率。具体计算式为[14]
(3)
式中:TOFF,m~exp (λOFF,m)。
对频谱分配问题,本文的优化目标是对所有的认知车联网用户最大化其网络吞吐量:
(4)
通过分析,本文频谱分配建模为:在已知可用矩阵L、干扰矩阵C的情况下,寻求使所有认知车联网用户吞吐量最大的分配矩阵As。
可见,此问题为非线性0-1规划问题,具有NP难特性,具有较高的求解复杂度。计算智能算法由于对问题特征无严格的要求,适合对NP难问题的求解。作为一种计算智能算法,已有的研究表明,免疫克隆算法具有良好的优化性能。基于此,本文采用免疫克隆优化算法对该问题进行求解。
2 基于免疫优化的频谱分配方法
2.1 免疫优化算法
免疫优化算法是一种模拟人体免疫系统的优化算法,在工程应用领域显示出了巨大的潜力[15-16]。在免疫优化算法中,要求解的问题被映射为抗体,免疫优化算法通过种群初始化、克隆、变异、选择等策略实现抗体寻优,算法结束时,最优抗体即为算法的解。
2.2 算法的关键技术
(1)抗体编码。抗体编码是将实际问题映射为免疫抗体的过程。本文最终要得到频谱分配矩阵AS,所以最直观的方式是采用矩阵编码,即1个抗体是1个随机初始化的矩阵: AS={an,m∈{0,1}}N×M。
1个抗体编码的例子如下:
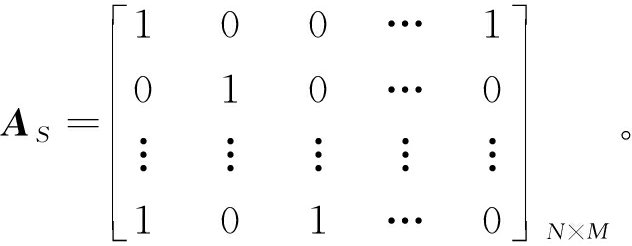
(5)
(2)修正抗体满足约束条件。由于随机生成的抗体和进化过程中产生的新抗体可能不满足矩阵C定义的无干扰约束条件:an,m×ak,m=0,若cn,k,m=1,∀n,k<N,m<M。因此,必须对抗体进行修正,满足约束条件。具体如下:对频谱m,若cn,k,m=1,则观察AS中第m列的第n行和第k行是否同时为1。若满足同时为1,则随机将其中某1个设置为0,即将AS修正为可行解。
(3)亲和度函数。由于要求最大的认知用户吞吐量,所以直接将式(4)作为亲和度函数。
2.3 算法具体实现
本文提出的认知车联网频谱分配过程如下。
步骤1 种群初始化。设进化代数t为0,采用随机的方式初始化1个大小为k的种群A,则: A(t)={A1(t),A2(t),…,Ak(t)},其中每个抗体Ai(t)(1≤i≤k)代表一个候选分配方案AS,并按照抗体修正方式保证其满足约束条件,设置最大进化代数为tmax。
步骤2 亲和度函数评价。按照式(4),计算种群中每个抗体Ai(t)(1≤i≤k)的亲和度f(Ai(t))并排序;选择亲和度较高的个体组成规模为s的记忆种群M(t),其中M(t)={A1(t),A2(t),…,AS(t)},s=0.2k。
步骤3 算法终止条件判断。如果达到最大进化次数gmax,算法终止。此时,将亲和度最高的抗体进行输出,即为最优的分配方案;否则,进化代数t=t+1,转步骤4。
步骤4 比例克隆。克隆M(t)中的优秀抗体得到种群B(t)。克隆操作Tc定义为
B(t)=Tc(M(t))=
[Tc(A1(t),Tc(A2(t),…,Tc(As(t)]。
(6)
为了尽可能保持优势抗体,克隆采取比例克隆,即根据抗体亲和度大小进行,对第i个抗体Ai(t)进行qi克隆,产生的抗体个数为
qi(t)=![]()
![]()
![]() 。
。
(7)
经过比例克隆的抗体总数为
(8)
式中:「·⎤表示向上取整;N(N>S)为克隆参数。
步骤5 克隆变异Tm。通过对种群B(t)实施变异操作Tm得到C(t),即C(t)=Tm(B(t))。本文的变异策略简单高效。由于是矩阵编码,所以,以概率pm直接对第m列进行变异,即将其中的1元素与0元素随机交换,实际上代表了将频谱m分配给另外一个认知用户n。同时,变异完成后要进行上面所述的约束处理,保证其为一个可行解。
变异后的种群为
C(k)={C1(t),C2(t),…,CQ(t)}。
(9)
步骤6 克隆选择TS。为了保持种群规模不变,如果Q>K,则计算C(t)中抗体的亲和度,选择k个亲和度高的抗体组成下一代种群A(t+1);如果Q<K,则随机生成(k-Q)个新抗体,选择前s个亲和度高的抗体更新记忆种群M(t+1),t=t+1,转步骤3。
2.4 算法特点和优势分析
(1)抗体采用矩阵编码,适合频谱分配问题,表示简单,交叉、变异等算子操作也容易实现。
(2)算法实现中保留了记忆种群,有利于算法快速收敛。
(3)比例克隆保证了优势抗体更容易进入到下一代,利于算法的寻优。
2.5 算法收敛性证明
设抗体种群空间为Ik={P:P=[P1,P2,…,Pk],Pg∈I,1≤g≤k},k为种群规模,抗体种群P(t)(第t代)在各种算子的作用下,种群演化过程表示为
(10)
定义1 算法收敛性。
设B*表示问题的全局最优解,ϑ(P)表示抗体种群P中包含的最优解个数。如果对于任意的初始状态P0,均有
![]() ϑ(P(t))≥1|P(0)=P0}=1。
ϑ(P(t))≥1|P(0)=P0}=1。
(11)
则称算法以概率1收敛到最优种群集。(P表示抗体种群,p表示概率,下面的证明中含义相同)。
定理1 本文算法是以概率1收敛的。
证明 记p0(t)=p{ϑ(P(t))=0}=p{P(t)∩B*≠∅},由贝叶斯条件概率公式有
p0(t+1)=p{ϑ(P(t+1))=0}=
{0|ϑ(P(t))=0}×p{ϑ(P(t))=0},
(12)
由ϑ(P)的定义可知,
p{ϑ(P(t+1))={0|ϑ(P(t))≠0}=0,
(13)
所以
p0(t+1)=p{ϑ(P(t+1))=
{0|ϑ(P(t))=0}×p0(t),
(14)
记
p{ϑ(P(t+1))≥1|ϑ(P(t))=0}≥ξ>0,
(15)
所以
p{ϑ(P(t+1))}≤1-ξ<1,
(16)
因此
0≤p0(t+1)≤(1-ξ)×p0(t)≤(1-ξ)2×
p0(t-1)…≤(1-ξ)t+1×p0(0),
(17)
因为
(18)
所以
![]()
(19)
故
(20)
因此
(21)
也就是
![]() ϑ(P(t))≥1|P(0)=P0}=1。
ϑ(P(t))≥1|P(0)=P0}=1。
(22)
于是定理1得证。
3 仿真实验与结果分析
在Windows环境下,利用NS-2搭建网络仿真平台。仿真实验中参数设置如下:仿真区域为1 000 m×1 000 m的矩形区域,随机分布主用户、认知用户和路边单元。其中,联网车辆移动情况按泊松点过程随机分布,矩阵L、C依照文献[12-13]生成,发射功率ψ为50 mW,频谱带宽ω为1 kHz,参数信道增益hm,i服从均值为1的瑞利分布,噪声功率σ2为10-5 W,时长T为1 s,N取值为1~20,M取值为1~30。免疫算法中,由于参数很难通过理论确定[16-17],只能通过大量的实验进行参数调整,最终参数设置如下:最大迭代次数tmax=200;种群规模k=30,s=0.2k=6,比例克隆参数nt=12。
为了验证算法的性能,与文献[12-13] 作了对比分析。算法验证了在不同的N、M的取值情况下算法的性能。
图1和图2是不同进化代数下,相关算法得到的车联网用户吞吐量总和。图1假设M=10,N=5;图2为M=20,N=10。从图1和图2中可以看出,随着迭代次数的增加,本文算法所得到的吞吐量保持增加,在算法运行到140代左右时,算法开始收敛,获得了较高的吞吐量。本文算法在优化目标网络吞吐量总和上优于相关算法(文献算法是确定性算法,与迭代次数无关),并且当频谱数量较大时,优势较为明显,说明本文算法提高了寻优能力。
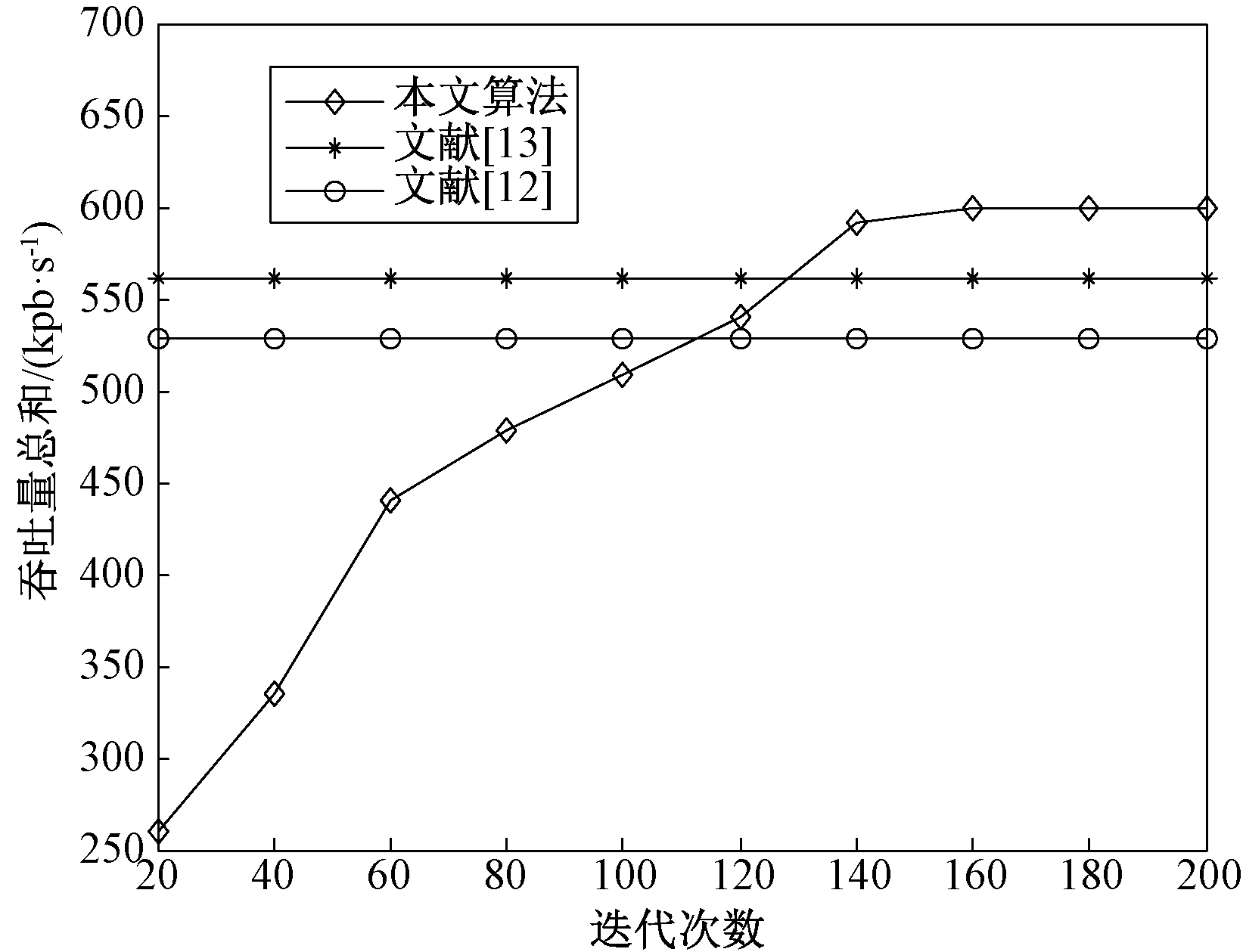
图1 算法性能比较(M=10,N=5)
Figure 1 Comparations of relative algorithm
(M=10,N=5)
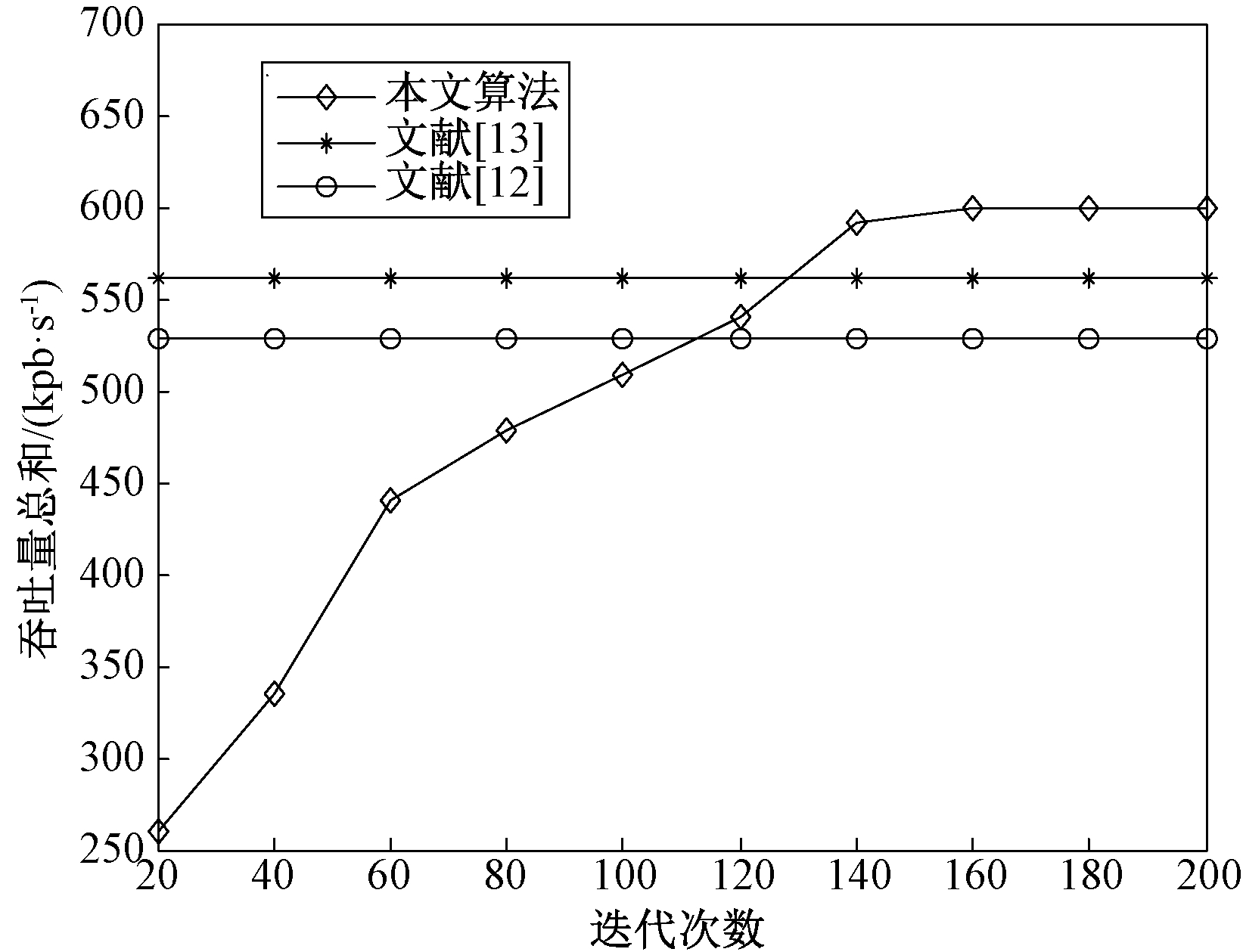
图2 算法性能比较(M=20,N=10)
Figure 2 Comparations of relative algorithm
(M=20,N=10)
同时,也通过实验验证了当可用频谱M固定(M=30),而认知用户数不同时,系统吞吐量的变化,实验结果如图3所示。可以看出,随着认知用户个数的增加,网络的总吞吐量在降低,相比于其他算法,本文算法下降较少,进一步验证了本文算法的各种策略是有效的。
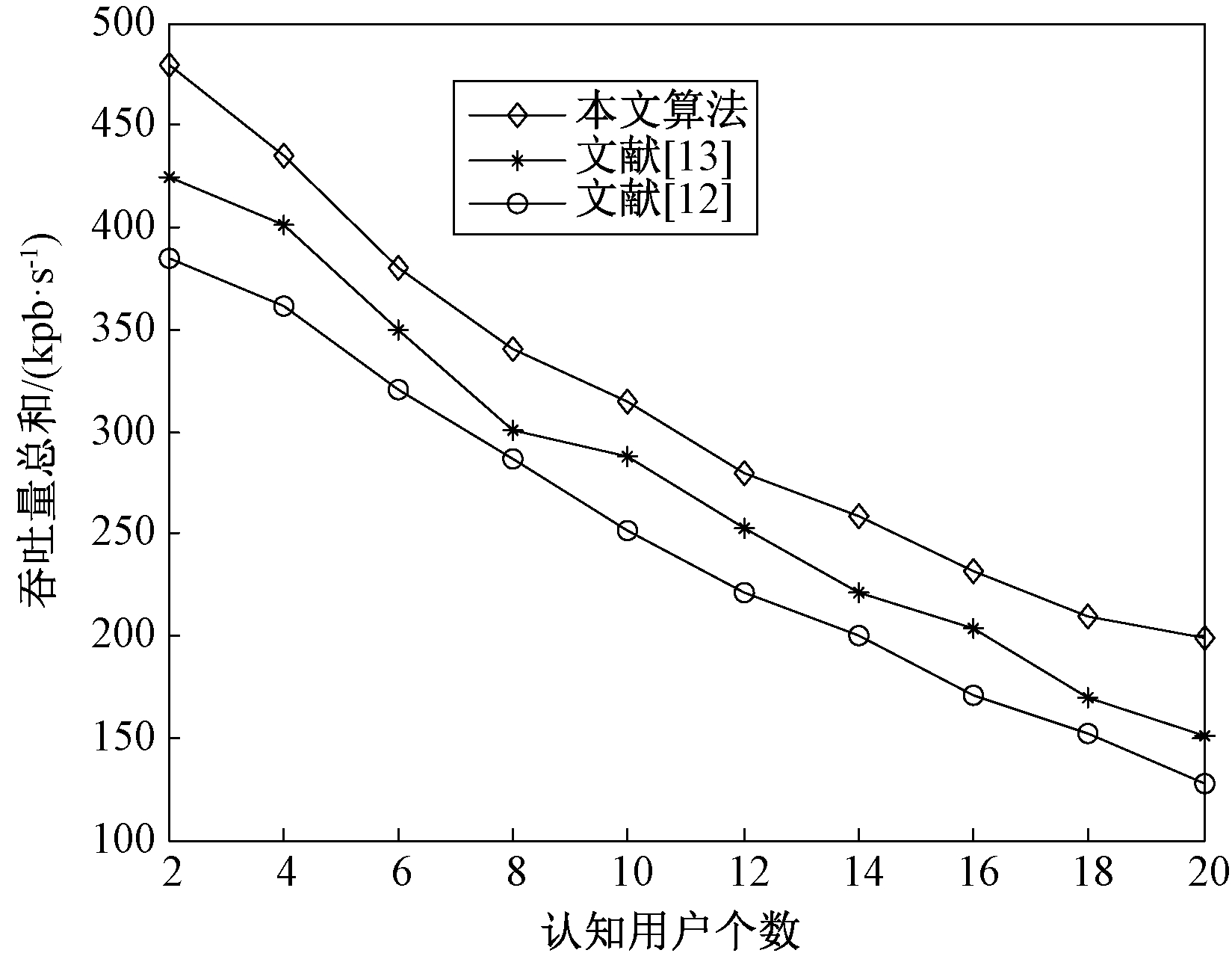
图3 认知用户个数与吞吐量总和的关系
Figure 3 Relationship between cognitive number
and throughput
此外,图4显示的是车联网用户数不变(N=10),而可用频谱数有效增加时,相关算法的性能表现。从图4可以看出,可用频谱数M越多,认知用户的吞吐量越大,这是因为有更多的频谱被分配给了认知用户。本文算法相比其他对比算法,吞吐量增加较多,验证了算法的优势。
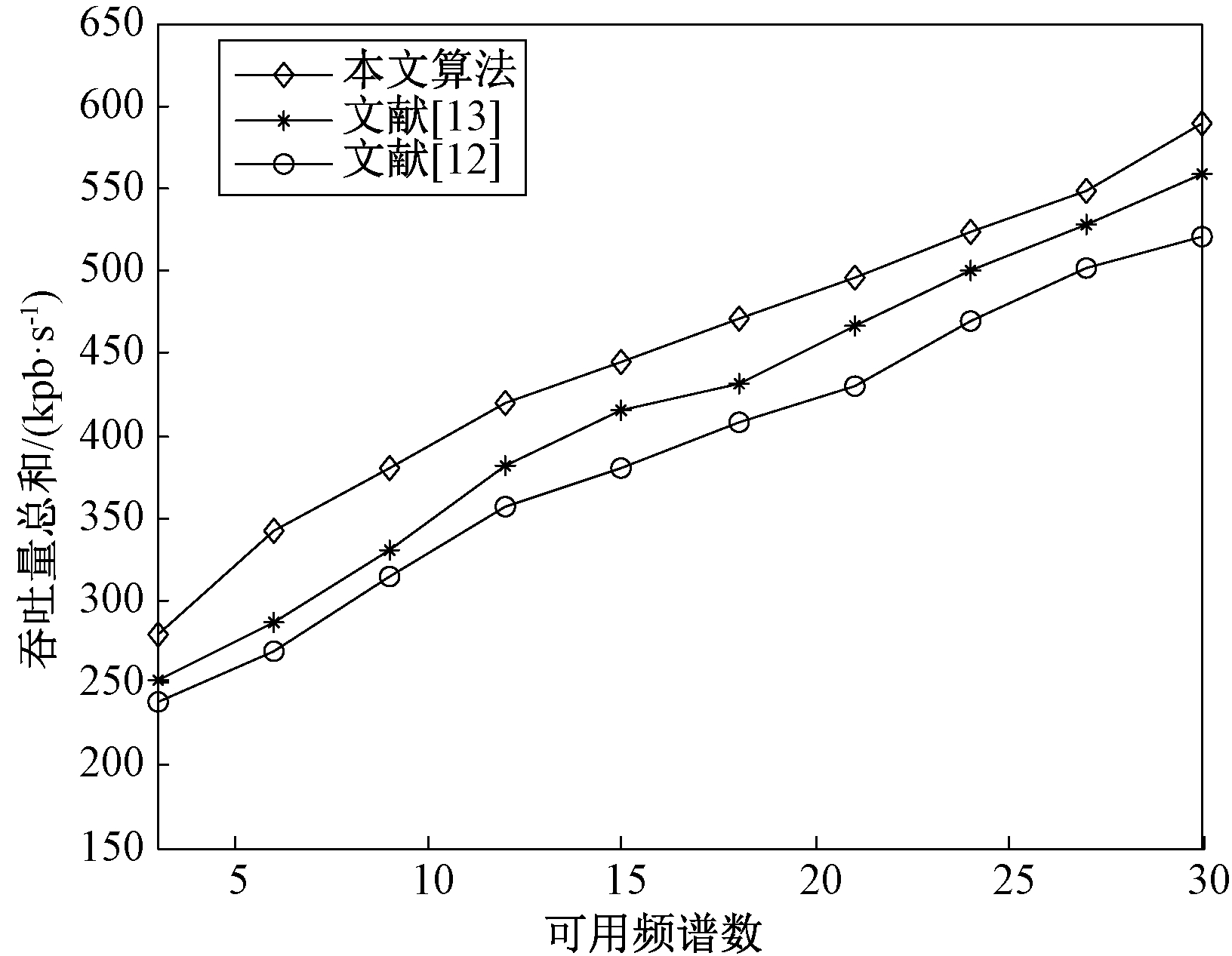
图4 认知用户吞吐量随可用频谱的变化
Figure 4 Throughput change with cognitive number
4 结论
针对认知车联网中的频谱分配问题,基于图论模型,将其建模为一个优化问题,并采用免疫算法进行求解。仿真结果表明,本文算法可以最大化认知用户的吞吐量,提高了频谱资源的利用效率。如何进一步优化认知车联网的场景设计,是下一步优化的工作。
[1] GOLI-BIDGOLI S, MOVAHHEDINIA N. A trust-based framework for increasing MAC layer reliability in cognitive radio VANETs[J]. Wireless personal communications, 2017,95(3):2873-2893.
[2] HE X X, ZHANG H, LUO T. Transmission capacity analysis for cellular based cognitive radio VANETs[J]. Wireless networks, 2017,23(7): 2215-2226.
[3] JOY E C, ZHANG S, LIU E, et al. Cognitive radio aided vehicular ad-hoc networks with efficient spectrum allocation and QoS guarantee[C]//22nd International Conference on Automation and Computing (ICAC). Piscataway: IEEE, 2016:156-161.
[4] FAWAZ K, GHANDOUR A, OLLEIK M, et al. Improving reliability of safety applications in vehicle ad hoc networks through the implementation of a cognitive network[C]//2010 17th International Conference on Telecommunications. Piscataway:IEEE, 2010:798-805.
[5] HE X X, SHI W S, LUO T. Survey of cognitive radio VANET[J]. KSII transactions on internet and information systems, 2014, 8(11):3837-3859.
[6] SINGH K D, RAWAT P, BONNIN J M. Cognitive radio for vehicular ad hoc networks (CR-VANETs): approaches and challenges[J]. Eurasip journal on wireless communications and networking, 2014, 2014:49.
[7] 柴争义, 王秉, 李亚伦. 拟态物理学优化的认知无线电网络频谱分配[J]. 物理学报, 2014, 63(22):437-442.
[8] CHEMBE C, NOOR R M, AHMEDY I, et al. Spectrum sensing in cognitive vehicular network: state-of-art, challenges and open issues[J]. Computer communications, 2017,97:15-30.
[9] HAN Y, EKICI E, KREMO H, et al. Resource allocation algorithms supporting coexistence of cognitive vehicular and IEEE 802.22 networks[J]. IEEE tran-sactions on wireless communications, 2017, 16(2):1066-1079.
[10] WANG T, SONG L Y, HAN Z. Coalitional graph games for popular content distribution in cognitive radio VANETs[J]. IEEE transactions on vehicular technology, 2013, 62(8):4010-4019.
[11] CHENG N, ZHANG N, LU N, et al. Opportunistic spectrum access for CR-VANETs: a game-theoretic approach[J].IEEE transactionson vehicular technology,2014,63(1):237-251.
[12] ZHANG L, LUO T, LIU W, et al. Cooperative spectrum allocation with QoS support in cognitive cooperative vehicular ad hoc networks[J]. China communication,2014,11(10):49-59.
[13] JIANG T, WANG Z Q, ZHANG L, et al. Efficient spectrum utilization on TV band for cognitive radio based high speed vehicle network[J]. IEEE transactions on wireless communications,2014,13(10):5319-5329.
[14] SOHAN T A, HAQUE H H, HASAN A, et al. A graph coloring based dynamic channel assignment algorithm for cognitive radio vehicular ad hoc networks[C]// 2016 International Conference on Networking Systems and Security (NSYSS). Piscataway: IEEE, 2016:110-117.
[15] 王艳丽,梁静,薛冰,等.基于进化计算的特征选择方法研究概述[J].郑州大学学报(工学版),2020,41(1):49-57.
[16] XIAO J K,LI W M,LIU B, et al. A novel multi-population coevolution strategy for single objective immune optimization algorithm[J]. Neural computing and applications, 2018,29(4):1115-1128.
[17] QI Y T, BAO L, MA X L, et al. Self-adaptive multi-objective evolutionary algorithm based on decomposition for large-scale problems: a case study on reservoir flood control operation[J]. Information sciences, 2016,367-368: 529-549.