0 引言
变压器是电力系统的关键设备,运行使用过程中,由于老化、电、热故障等原因会产生少量气体溶解于绝缘油中,各种气体成分含量及不同组分间的比例关系与变压器的健康状况密切相关[1-2],因此预测变压器油中溶解气体含量是诊断故障的前提条件。
目前常用的变压器油中气体含量预测方法主要有灰色理论、网络分析法、极端学习机、支持向量机与组合预测方法等。有许多学者对预测方法给予研究,在预测变压器油中气体含量方向均取得较好的效果。刘航等[3]采用考虑多因素的灰色关联分析法;代杰杰等[4]运用深度信念网络模型;刘亚南等[5]在短期负荷预测领域使用极端学习机的方法,预测效果良好,但其容易产生过拟合现象,并且极端学习的权值是随机给定的,使得该算法的稳定性不能得到保证;司马莉萍等[6]对支持向量机算法进行优化并取得较好的预测效果;肖燕彩等[7]采用灰色模型预测油中气体的未来趋势,灰色预测模型适用于随时间按指数规律单调增长趋势的预测,如果预测量是按指数规律变化,则预测精度较高,但变压器油中溶解气体含量并不一定按指数规律增长变化,因此预测结果存在偏差。
ARIMA模型已在气象、医学、交通、农林等研究领域得到广泛应用,并取得很好的效果,将该模型应用到变压器油中溶解气体含量预测中,并对此模型进行以下两点优化:
(1)结合自相关函数(ACF)和偏自相关函数(PACF)参数选择原则得到若干组模型,然后利用3种准则对模型进行优选;
(2)利用相关的残差检验方法对优选模型进行残差检验并对残差检验结果分析。
ARIMA模型可以根据系统输出的有限长度数据建立比较精确的、反应系统动态依存关系的数学模型,考虑了序列的依存性和随机波动的干扰性。优化后的ARIMA模型克服了已有预测方法的过拟合现象以及对预测输入量类型有限制等问题,并且使原有预测模型的精准度更高。
1 ARIMA模型的时间序列预测方法
ARIMA(p,d,q)模型实则为AR(p)模型和MA(q)模型的组合。ARIMA中的“I”意味着对不平稳时间序列进行差分处理,通过差分法可确定ARIMA(p,d,q)模型中的参数d。
AR(p)是自回归模型,该模型是变量在时刻t的响应xt与时刻t-1,t-2,…的响应xt-1,xt-2,…及t时刻进入系统的扰动的关系,而与前期的扰动无直接关系。
自回归模型必须满足平稳性要求。p阶自回归过程的公式如式(1)所示:
(1)
式中:xt是当前值;μ是常数项;p是阶数;γi是自相关系数;ξt是误差。
MA(q)模型是移动平均模型,该模型是指变量在时刻t的响应xt与时刻t-1,t-2…的响应xt-1,xt-2,…无直接关系,而与时刻t-1,t-2,…进入系统的扰动存在一定的关系,移动平均法能有效地消除预测中的随机波动,是自回归模型中误差项的累加。q阶自回归过程的公式如式(2)所示:
(2)
式中:q是阶数;ξt是误差;θi是消除随机波动的参数。
ARMA(p,q)是自回归移动平均模型,该模型为自回归与移动平均的结合[8-9],是指变量在时刻t的响应xt不仅与时刻t-1,t-2,t-3,…的响应xt-1,xt-2,…存在直接关系,而且与时刻t-1,t-2…进入系统的扰动存在一定的相关关系。公式如式(3)所示:
(3)
综上所述,建立ARIMA模型的条件:序列的取值依赖时间的变化但不一定是时间的严格函数;每时刻的取值具有一定的随机性;序列应满足平稳性或差分处理后满足平稳性的要求。
变压器油中气体含量值会根据变压器运行状况的变化发生变化,通过时间的变化体现,因此满足建立模型的条件。
2 预测方法介绍
2.1 预测方法概述
对一个不满足平稳性条件的序列,通过若干次差分确定差分阶数d值,将非平稳时间序列转化为平稳时间序列,此时ARIMA模型转换为ARMA模型,再对平稳时间序列通过自相关函数(ACF)和偏自相关函数(PACF)定阶,得到若干组p和q值。因此对应若干组模型,通过赤池信息准则(AIC)、贝叶斯信息准则(BIC)、汉南-奎因准则(HQC)对多组模型进行优选,利用4种残差图呈现残差检验结果,对优选模型的残差检验结果分析,残差满足要求后,利用最佳模型对时间序列预测。
2.2 预测步骤分解及示例
实验数据来自2013年6月至8月某500 KV变压器A相DGA监测数据,共采集86例数据,其中61例用于训练,25例用于测试。
样本数据反映气体含量值随时间变化的过程。以变压器过热故障为例,变压器在运行中由于过载、开关接触不良、引线夹件螺丝松动或接头焊接不良、涡流引起铜过热、铁芯漏磁、局部短路等原因导致变压器过热,而此类原因会使油中溶解气体含量值发生变化。ARIMA模型将气体含量值的累积性以及外界干扰的变化过程记录到训练过程中,在短时间内的变化均可预测到,由于篇幅原因,以H2含量的预测为例。
2.2.1 ADF单位根检验平稳性
样本序列经ADF检验显示不满足平稳性的要求,对样本数据差分处理,每进行一次差分处理后都要经ADF检验,直到满足平稳性为止。针对样本数据,一次差分处理就满足了平稳性的要求,因此ARIMA(p,d,q)模型中参数d为1。H2含量随时间变化曲线如图1所示。
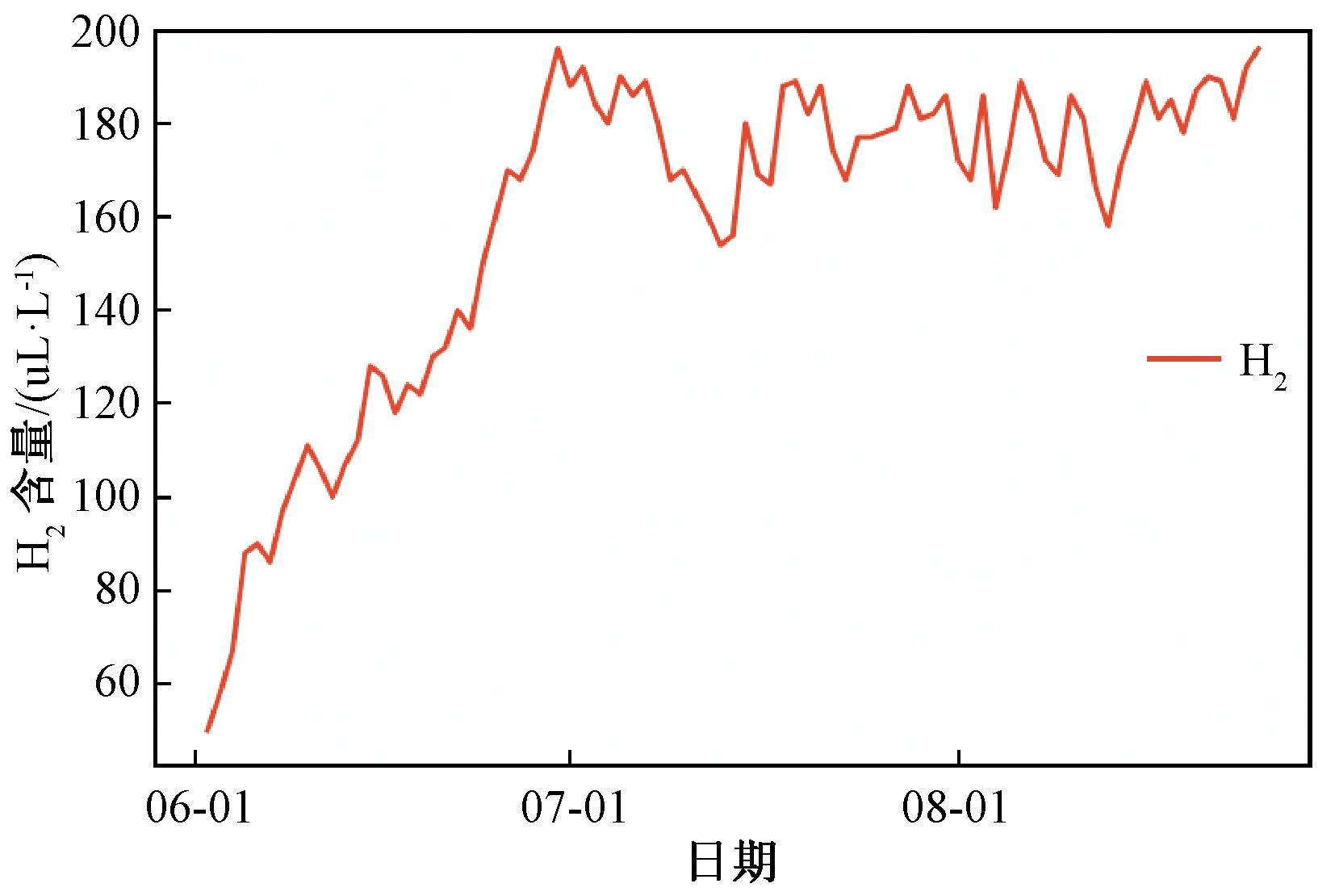
图1 H2含量随时间波动趋势图
Figure 1 The trend chart of H2 content fluctuation with time
ADF单位根检验过程:首先假设需要进行ADF检验的序列存在单位根,为非平稳序列,如果待检验的序列经程序计算得到的统计量Augmented Dickey-Fuller Test Statistic的值显著小于3个置信度Critical Value(1%,5%,10%)的临界值时;同时p-value接近于0,说明原假设不成立,判定正在接受检验的序列为平稳时间序列,否则继续进行差分运算[10-11]。
一阶差分图如图2所示,差分检验结果如表1所示,可判定经过差分处理的数据序列为平稳序列,满足定阶要求。
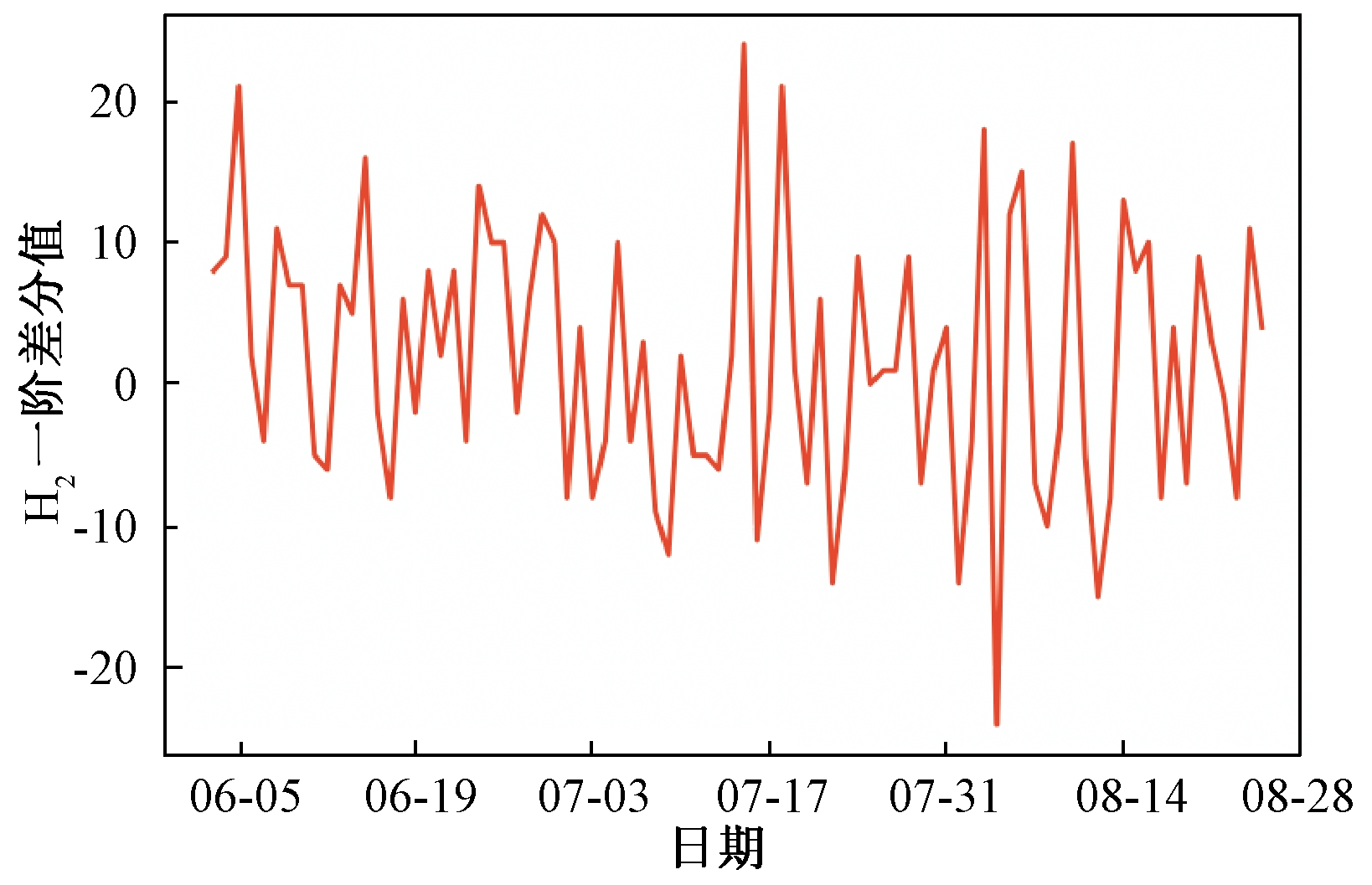
图2 H2一阶差分图
Figure 2 H2 first-order difference diagram
表1 ADF检验结果
Table 1 ADF test results
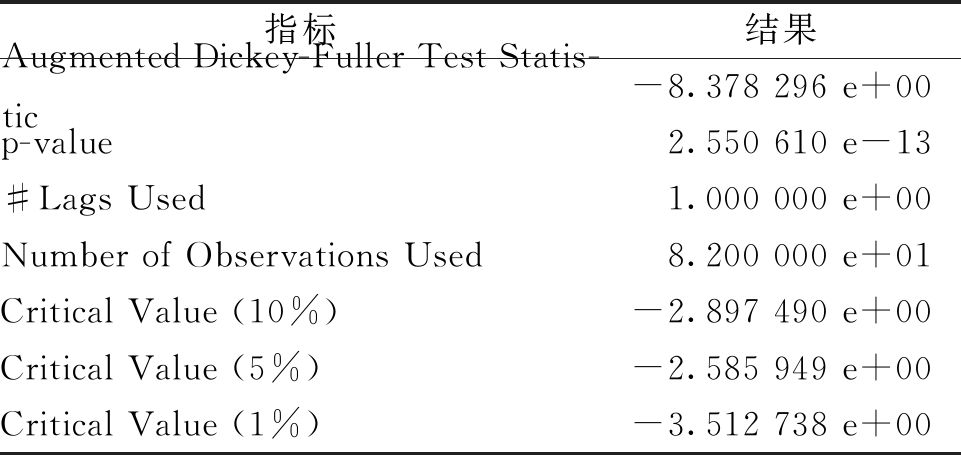
指标结果Augmented Dickey-Fuller Test Statis-tic-8.378 296 e+00p-value2.550 610 e-13#Lags Used1.000 000 e+00Number of Observations Used8.200 000 e+01Critical Value (10%)-2.897 490 e+00Critical Value (5%)-2.585 949 e+00Critical Value (1%)-3.512 738 e+00
2.2.2 ACF和PACF定阶
自相关函数ACF的k阶相关系数为
(4)
其中,ρk的取值范围为[-1,1]。
对平稳AR(p)模型,求滞后k阶自相关系数ρk时,ACF得到的不仅仅是xt与xt-k之间的相关关系,同时还受到中间k-1个变量xt-1、xt-2、…、xt-k+1的影响,且k-1个变量又都与xt-k具有相关关系,因此自相关系数ρk也受到k-1个变量的影响。偏自相关函数PACF有效删除了中间k-1个变量xt-1、xt-2、…、xt-k+1的影响,仅是xt-k对xt的相关关系。
AR(p)模型的参数值p,可由偏自相关函数的相关系数PACF(ρk)得到,同理MA(q)模型的参数q,可由自相关函数的相关系数ACF(ρk)确定,因此ARMA(p,q)模型的参数p和q要根据自相关函数ACF和偏自相关函数PACF[12]确定。图3和图4为样本数据经差分处理后的自相关函数图和偏自相关函数图。在对模型的阶数选择时依据原则如表2所示。
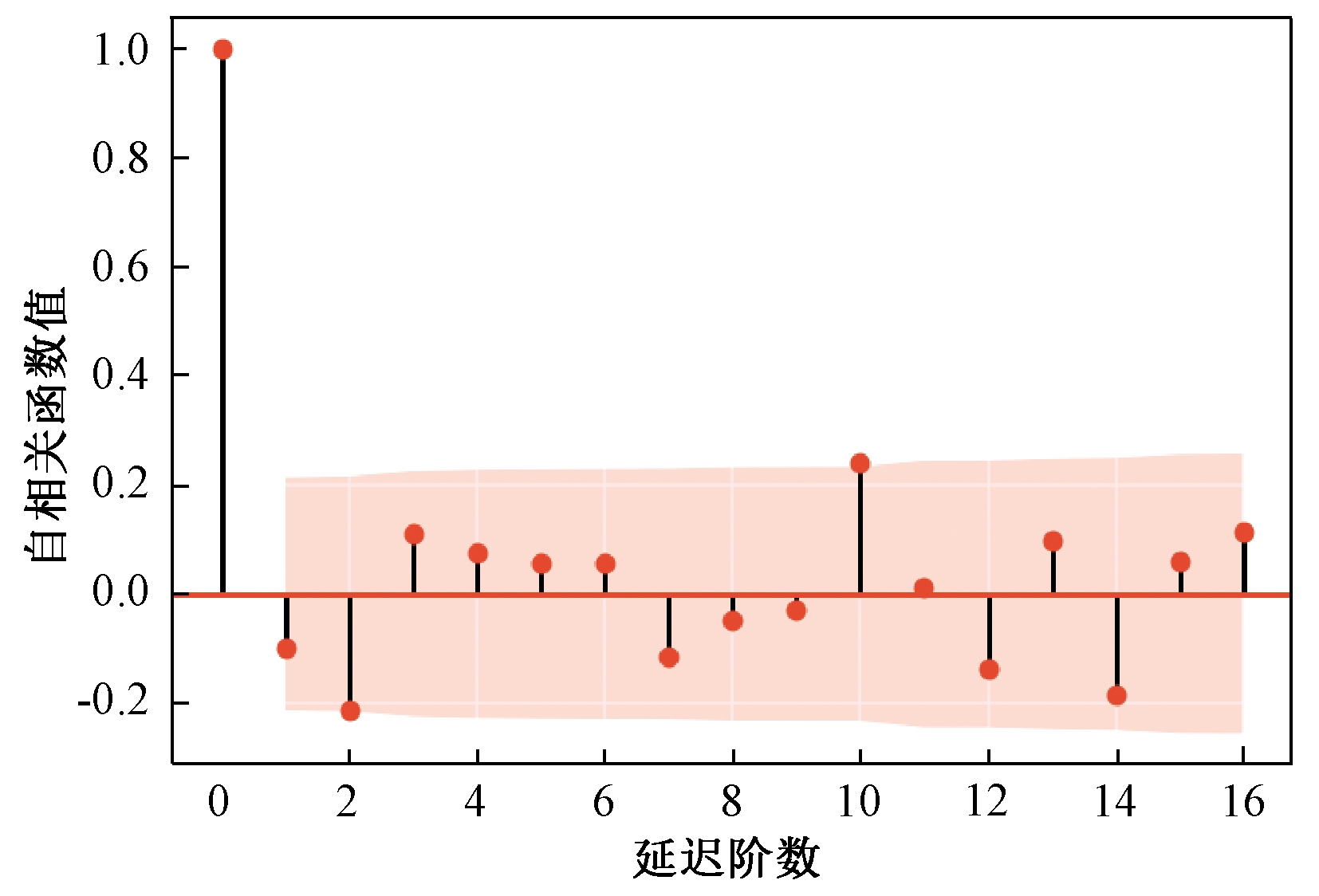
图3 自相关函数图
Figure 3 Autocorrelation function diagram
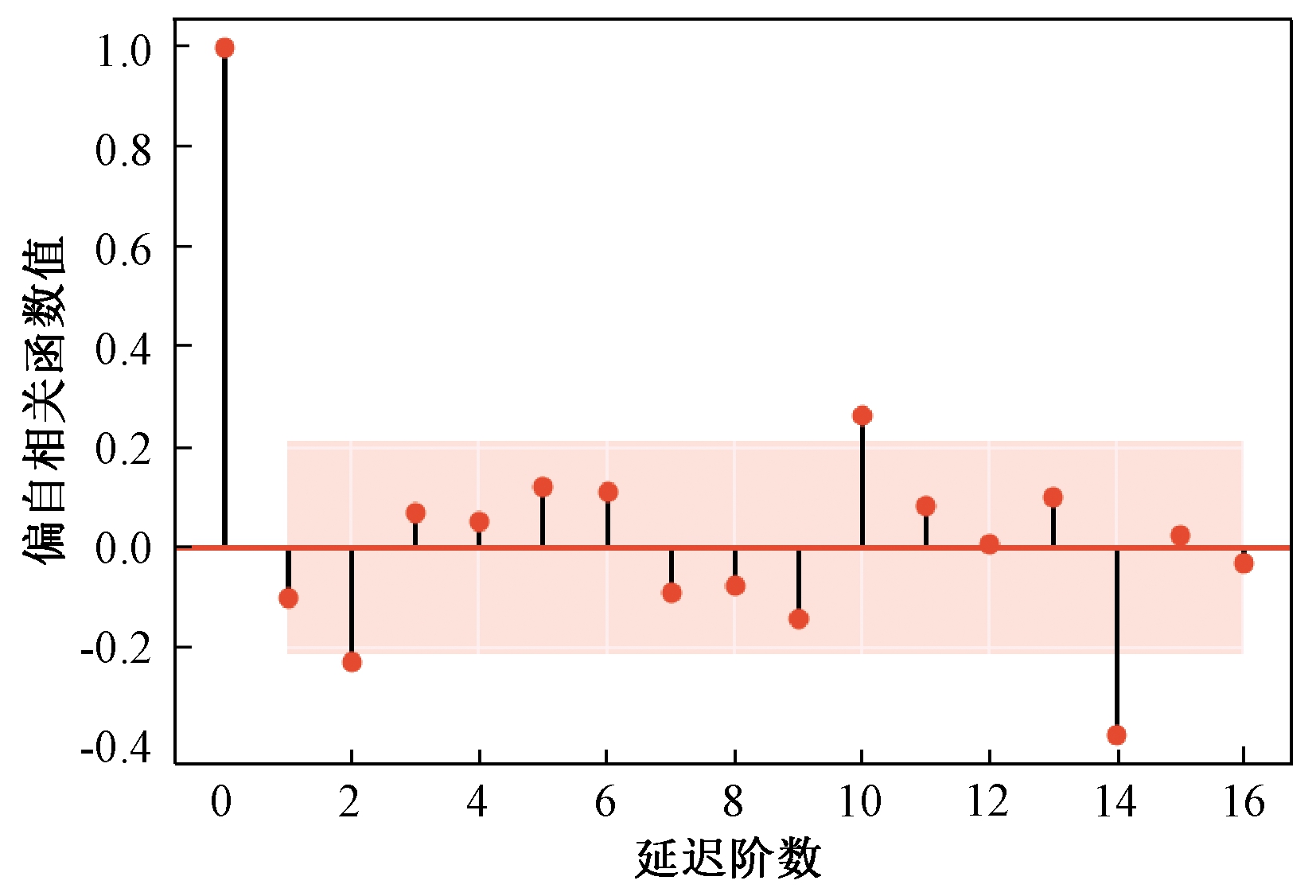
图4 偏自相关函数图
Figure 4 Partial autocorrelation function diagram
表2 阶数选择原则
Table 2 Order selection principle

模型ACFPACFAR(p)衰减趋于零p阶后截尾MA(q)q阶后截尾衰减趋于零ARMA(p,q)p阶后衰减趋于零p阶后衰减趋于零
2.2.3 模型优选
通过以上步骤得到9组ARMA(p,q)模型,为选出最优模型,利用AIC、BIC、HQC 3种准则判断[13],依据准则计算的结果如表3所示,用Y表示结果,则
YAIC=2m-ln(L);
(5)
YBIC=mln(n)-2ln(L);
(6)
YHQC=mln(ln(n))-2ln(L),
(7)
式中:m是模型参数的数量;n是样本数量;L是似然函数。
AIC、BIC、HQC准则对应的计算结果越小,则分别对应数据拟合的优良程度越高、模型的复杂度越低、模型的预测精度越高。
通过比较发现,3个准则中AIC和HQC的结果最小值对应的模型均为ARMA(2,2),而BIC准则对应的结果最小值为ARMA(0,0),由于ARIMA模型复杂程度本身不高,结合参数d为1,可确定ARMA(2,1,2)为最优模型。
表3 模型对应的3种准则计算结果
Table 3 Calculation results of three criteria corresponding to the model
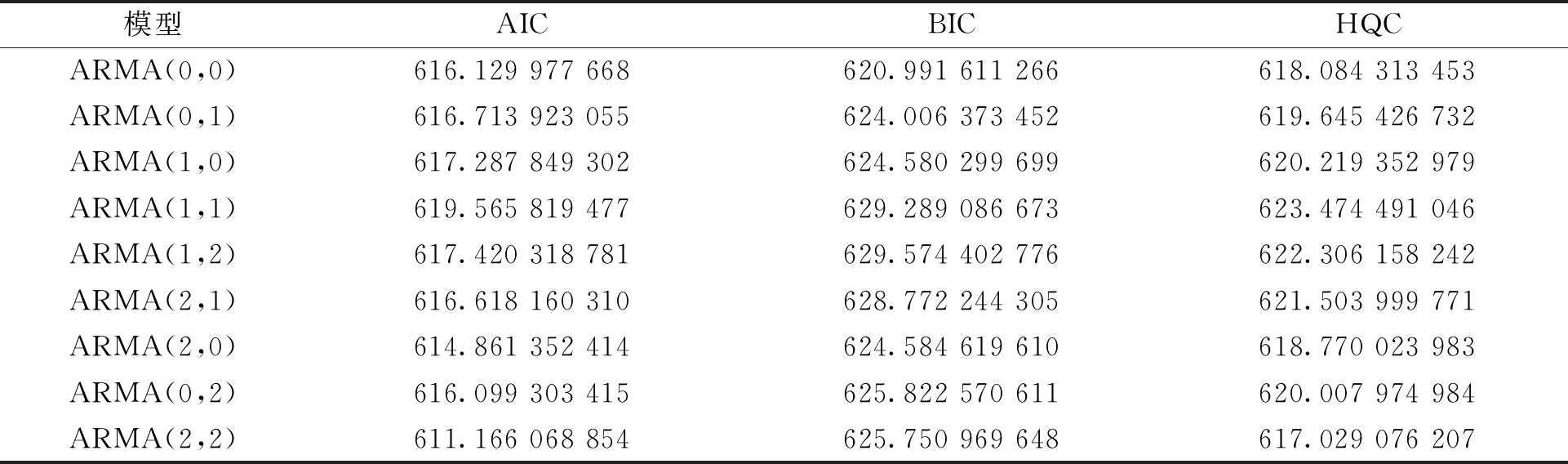
模型AICBICHQCARMA(0,0)616.129 977 668620.991 611 266618.084 313 453ARMA(0,1)616.713 923 055624.006 373 452619.645 426 732ARMA(1,0)617.287 849 302624.580 299 699620.219 352 979ARMA(1,1)619.565 819 477629.289 086 673623.474 491 046ARMA(1,2)617.420 318 781629.574 402 776622.306 158 242ARMA(2,1)616.618 160 310628.772 244 305621.503 999 771ARMA(2,0)614.861 352 414624.584 619 610618.770 023 983ARMA(0,2)616.099 303 415625.822 570 611620.007 974 984ARMA(2,2)611.166 068 854625.750 969 648617.029 076 207
2.2.4 残差检验
为确保模型的预测效果,对优选模型进行残差检验,残差是实际值与估计值的差,预测效果较好的模型的残差要体现出随机性和不可预测性。残差是正态分布说明残差是随机的,对随机误差有比较好的拟合[14]。
图5中大约有95%的标准化残差值在(-2,2)之间,服从正态分布;图6更直观地反映出残差服从正态分布;图7中大多数的点都落在符合规定的区间内,满足正态分布,残差满足要求;图8是一种散点图,图上的点近似地在一条直线附近,说明是正态分布,残差满足要求。
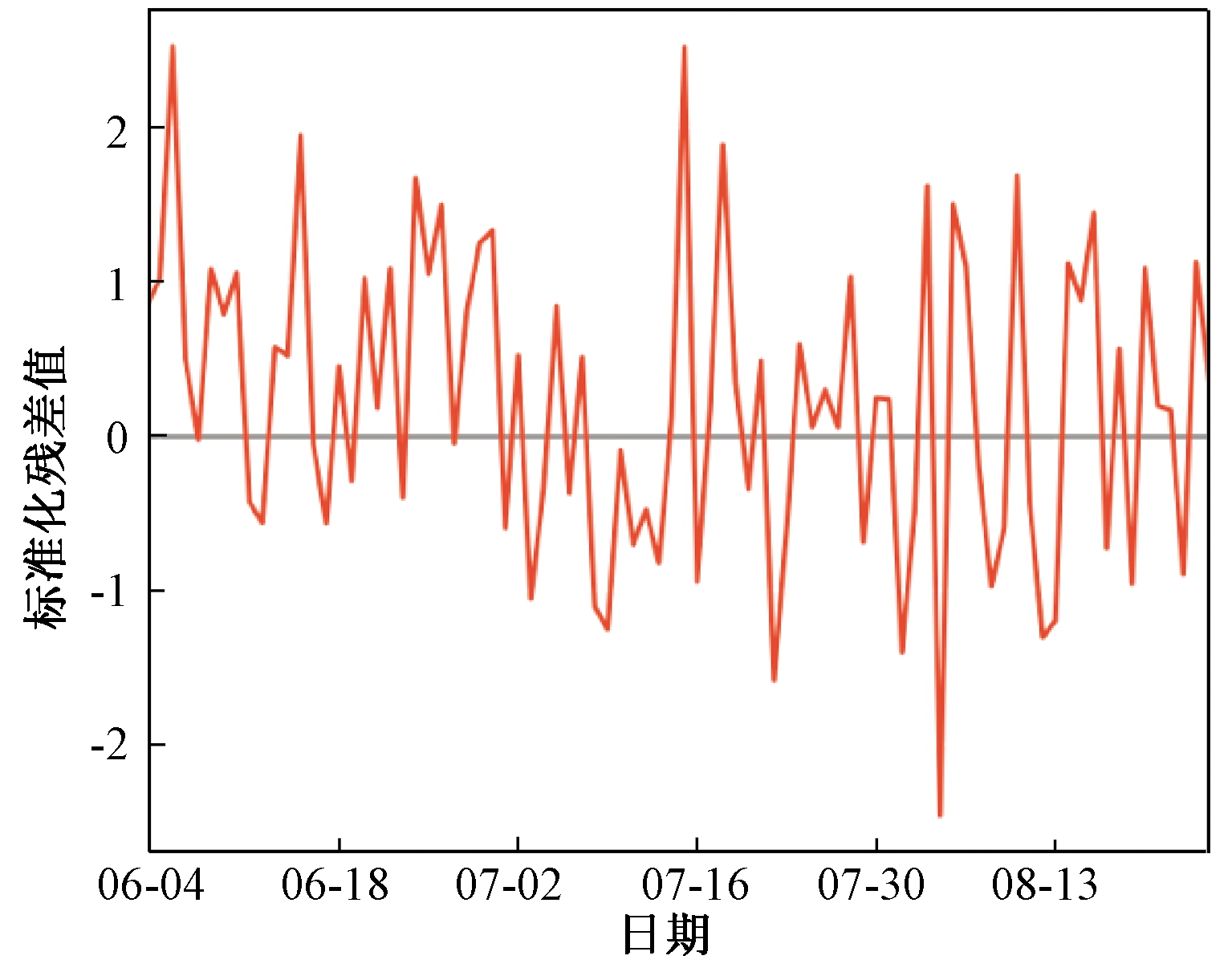
图5 标准化残差图
Figure 5 Standardized residual diagram
各图的横纵坐标没有量纲,因此以上针对各图的实际意义进行解释说明。
使用优选模型对测试数据进行预测,并与真实数据对比,结果如图9所示。从图9可以看出,预测数据与实际数据高度接近,能够反映变压器油中气体含量的变化趋势和数量关系。
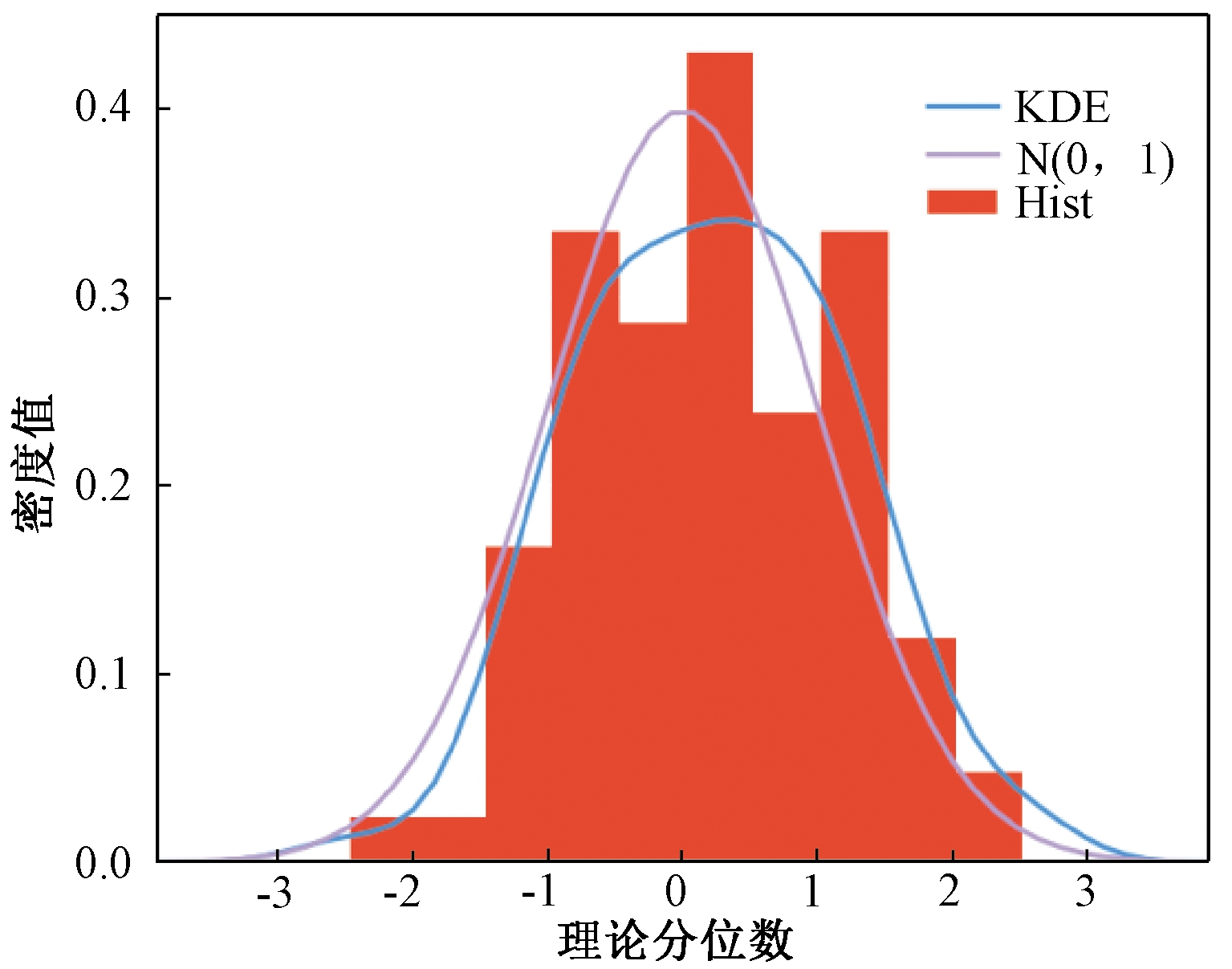
图6 残差的直方加密度估计图
Figure 6 Histogram density estimation of residuals
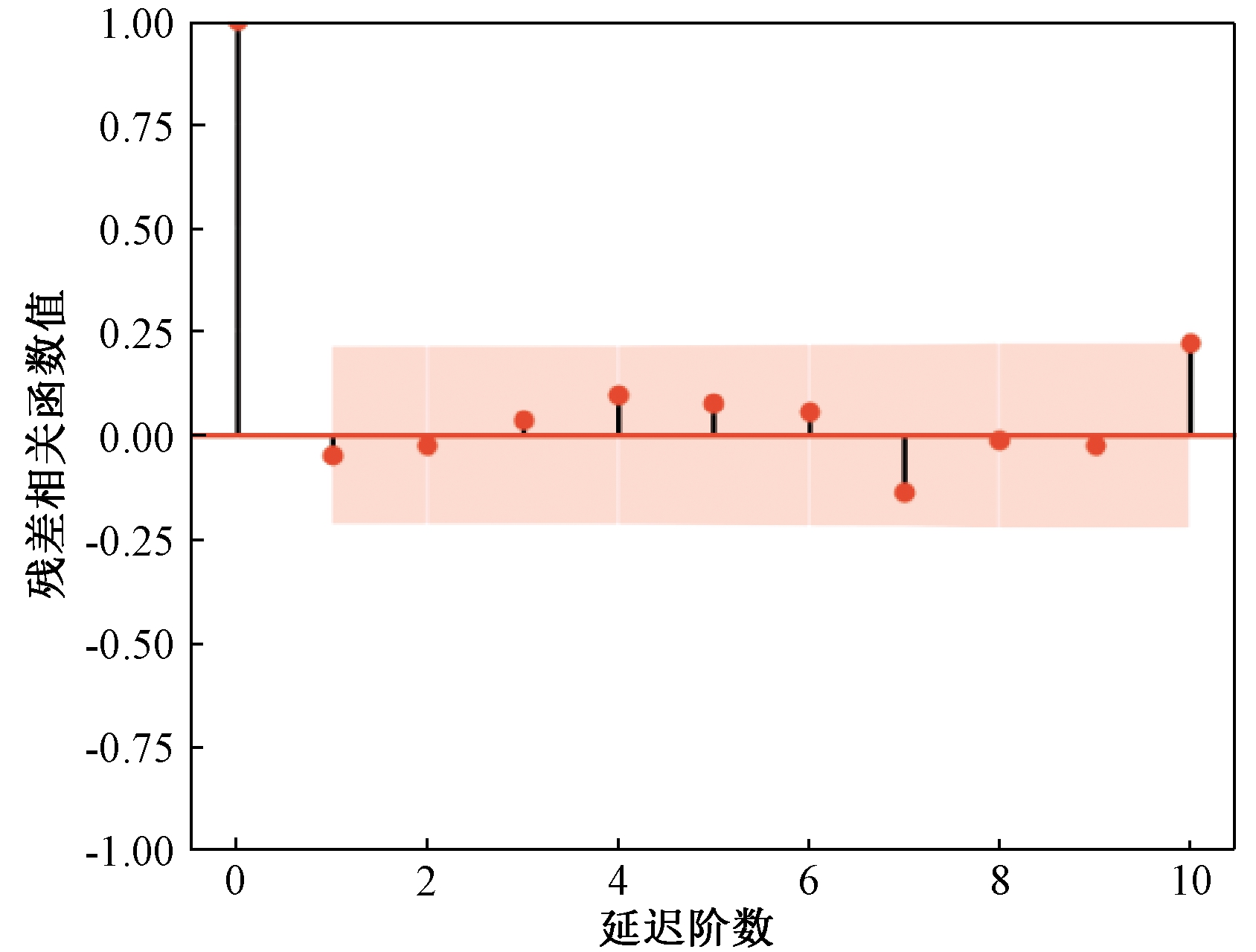
图7 残差的相关图
Figure 7 Correlation diagram of residuals
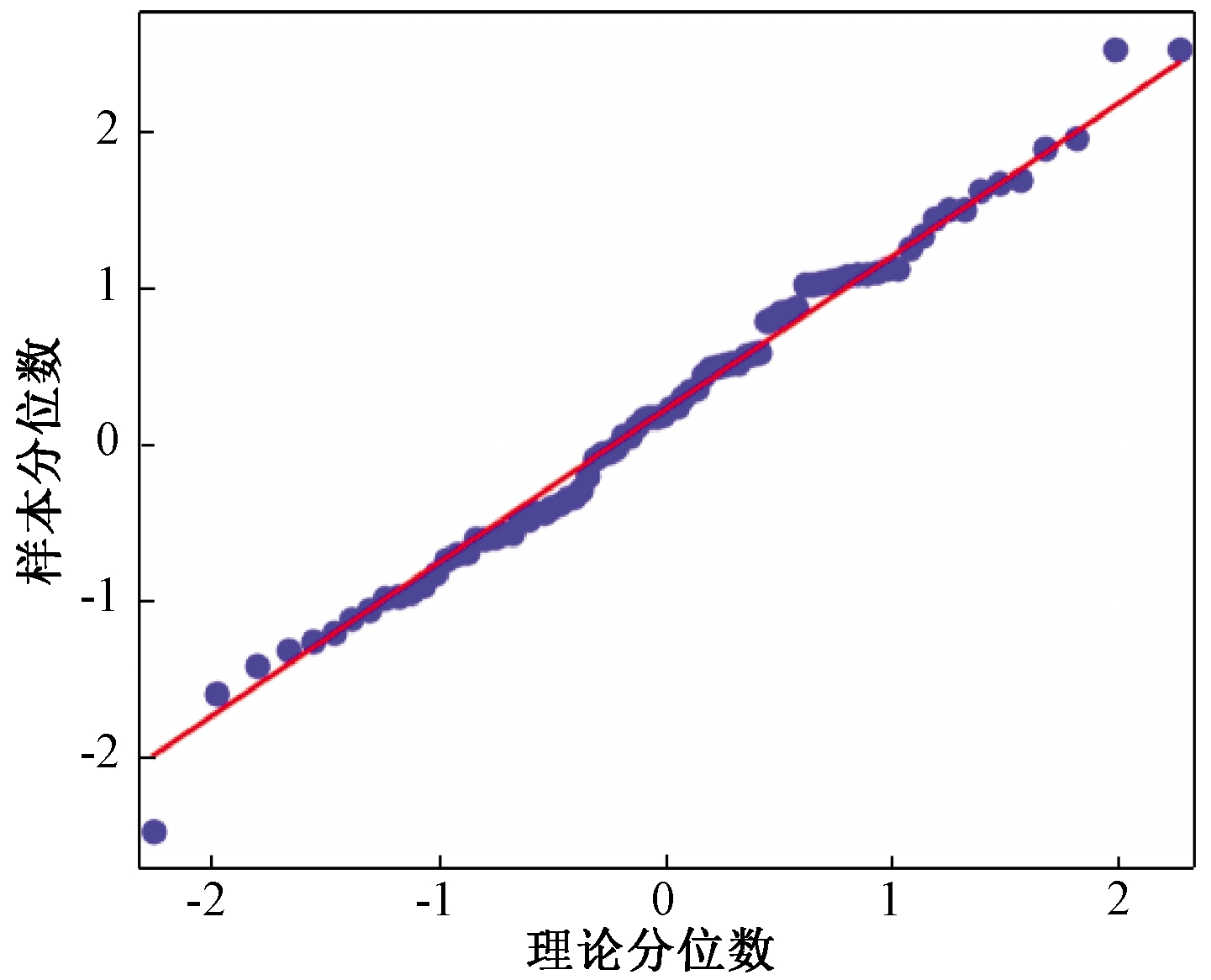
图8 残差的QQ图
Figure 8 QQ diagram of residuals
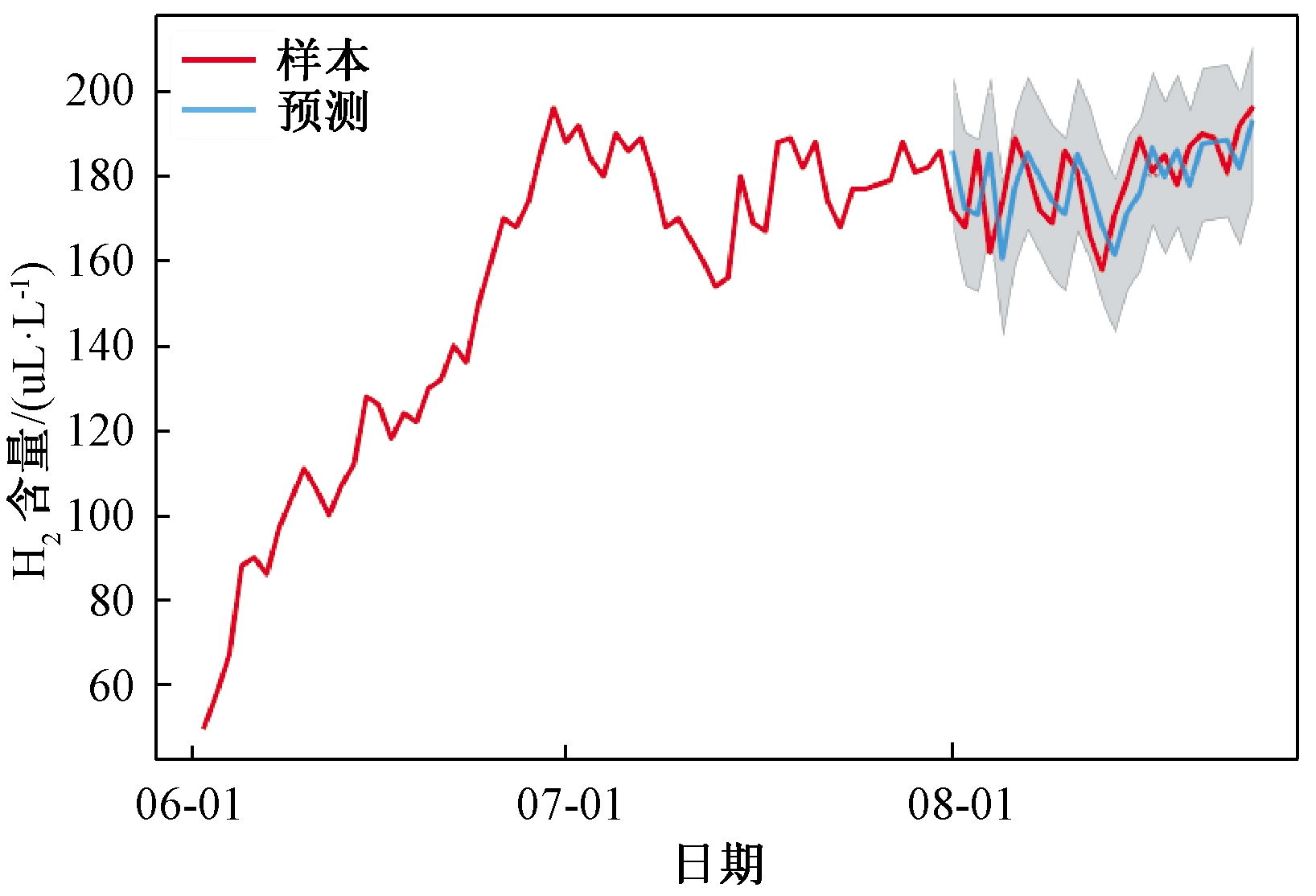
图9 预测趋势
Figure 9 Forecasting trends
3 预测方法对比与结果分析
为验证预测方法ARIMA模型的有效性,对同一组样本数据分别使用灰色预测模型GM、支持向量机预测模型SVM进行预测,预测结果如图10所示。
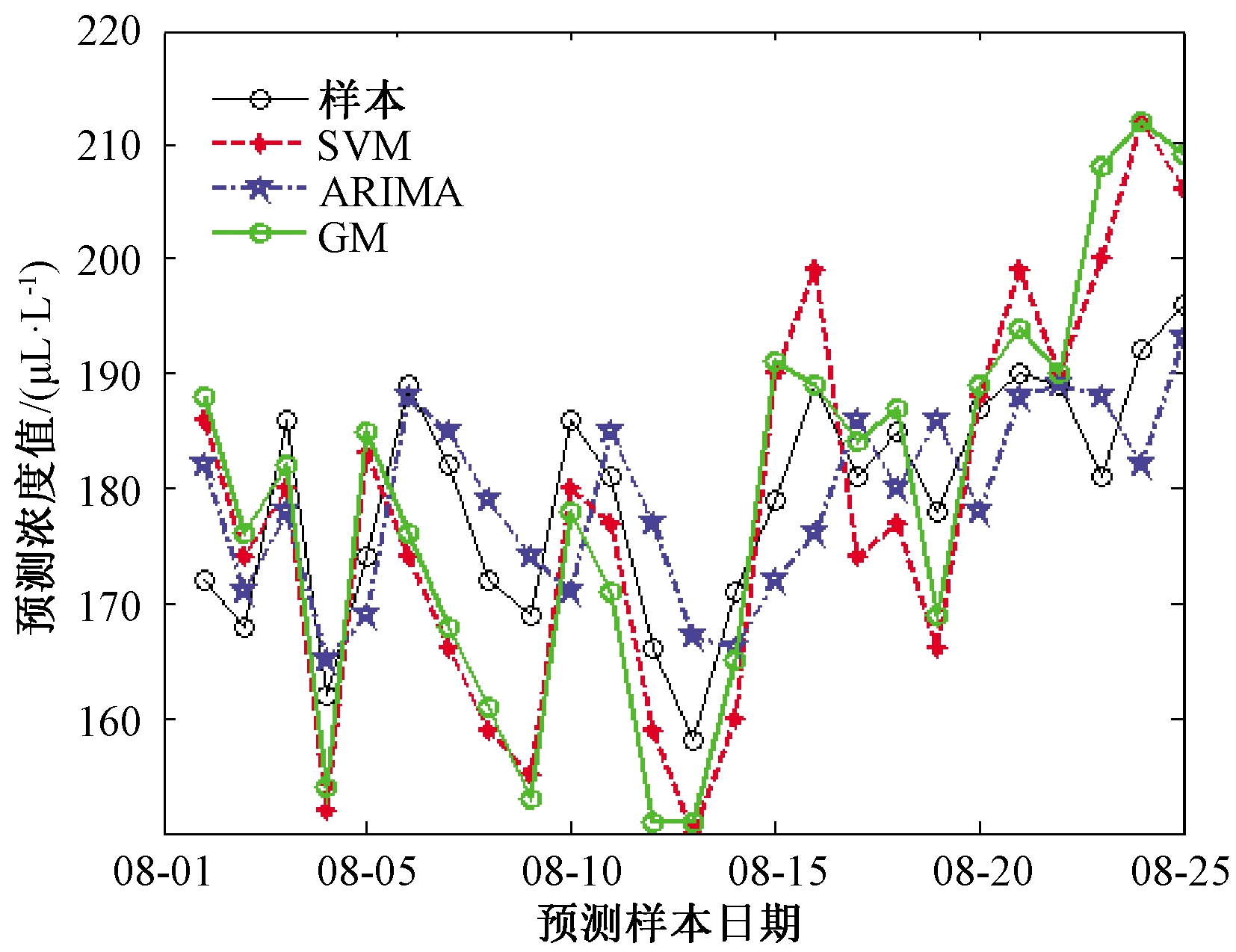
图10 模型预测值比较
Figure 10 Model prediction comparison
表4从3个维度讨论:①使用同一种长度的样本训练,预测相同的长度进行性能比较;②以预测结果的误差范围小于5%和10%的个数进行纵、横向比较;③使用3种长度的样本训练,预测不同的长度,对其性能优劣性比较。
表4 预测精度对比
Table 4 Prediction accuracy comparison
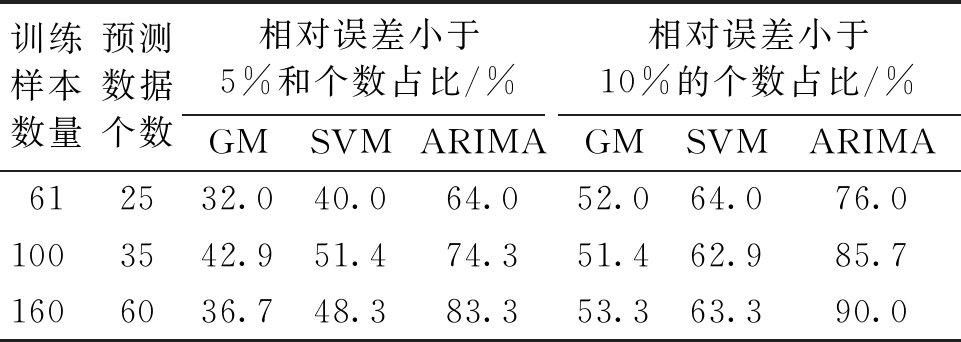
训练样本数量预测数据个数相对误差小于5%和个数占比/%相对误差小于10%的个数占比/%GMSVMARIMAGMSVMARIMA612532.040.064.052.064.076.01003542.951.474.351.462.985.71606036.748.383.353.363.390.0
从维度1来看,3种方法预测的准确度均以ARIMA模型的预测效果最好;从维度2来看,无论是误差小于5%还是小于10%的个数均以ARIMA模型最多;从维度3来看,当使用的训练样本数增加,预测长度也增加时,GM和SVM预测的准确度增加不够明显,例如当训练样本从61个增加到100个,预测长度从25个增加到35个时,预测准确度增加,但当训练样本增加到160个,预测长度增加到60个时,GM和SVM预测准确度几乎不变,ARIMA模型预测准确度会增加。
预测结果表明,ARIMA模型具有较好的性能,可用于变压器油中气体含量的预测。若每24 h采集一次数据,对表4中第一行数据而言,可以使用61 d的历史数据,预测未来25 d气体含量的变化趋势和数量关系,而第3行数据则显示,利用此前160 d的数据,可以预测此后60 d可能的结果。
4 结论
以变压器油中溶解的气体H2含量为对象建立模型,由于预测精度较高,其余气体含量均能较好地预测,总结ARIMA模型预测方法得到如下结论:
(1)用于对呈现对数、线性或随机性较强但趋势性较弱特性的数据序列预测,克服其他预测方法易存在的过拟合现象,预测误差较小,准确度高。
(2)具有训练样本长度越长、预测准确度越高的特性。
(3)只需导入数据,即可自动完成变压器油中溶解气体含量的预测,在此过程中不需要人为判断。
[1] 李振杰, 卞朝晖, 陈学民, 等. 变压器油色谱在线监测数据有效性评估[J]. 高压电器, 2018, 54(6): 158-163, 169.
[2] 杨志越,牛华宁.基于DGA的变压器状态监测与故障诊断技术研究[J].河北电力技术,2018,37(3):11-14.
[3] 刘航,王有元,梁玄鸿,等.基于多因素的变压器油中溶解气体体积分数预测方法[J].高电压技术,2018,44(4):1114-1121.
[4] 代杰杰,宋辉,杨祎,等.基于深度信念网络的变压器油中溶解气体浓度预测方法[J].电网技术,2017,41(8):2737-2742.
[5] 刘亚南, 范立新, 徐钢, 等. 基于非负矩阵分解与改进极端学习机的变压器油中溶解气体浓度预测模型[J]. 高压电器, 2016, 52(1): 162-169.
[6] 司马莉萍,舒乃秋,左婧,等.基于灰关联和模糊支持向量机的变压器油中溶解气体浓度的预测[J].电力系统保护与控制,2012,40(19):41-46.
[7] 肖燕彩,朱衡君,陈秀海.用灰色多变量模型预测变压器油中溶解的气体浓度[J].电力系统自动化,2006,30(13):64-67.
[8] PENG Y, YU B, WANG P, et al. Application of seasonal auto-regressive integrated moving average model in forecasting the incidence of hand-foot-mouth disease in Wuhan, China[J]. J Huazhong Univ Sci Technolog (Med Sci). 2017, 37(6):842-848.
[9] 杨高飞, 徐睿, 秦鸣, 等. 基于ARMA和卡尔曼滤波的短时交通预测[J]. 郑州大学学报(工学版), 2017, 38(2): 36-40.
[10] 严宙宁, 牟敬锋, 赵星, 等. 基于ARIMA模型的深圳市大气PM2.5浓度时间序列预测分析[J]. 现代预防医学, 2018, 45(2): 220-223, 242.
[11] MAHMUDAH U. Autoregressive integrated moving average model to predict graduate unemployment in Indonesia[J]. Practice and theory in systems of education, 2017, 12(1): 43-50.
[12] 岳继光,杨臻明,孙强,等.区间时间序列的混合预测模型[J].控制与决策,2013,28(12):1915-1920.
[13] 孙轶轩, 邵春福, 计寻, 等. 基于ARIMA与信息粒化SVR组合模型的交通事故时序预测[J]. 清华大学学报(自然科学版), 2014, 54(3): 348-353, 359.
[14] 滕志军,郭力文,吕金玲,等.基于时序信息分析的WSN贝叶斯信誉评价模型[J].郑州大学学报(工学版),2019,40(1):38-43.