0 引言
现实生活中很多优化问题都含有多个待优化目标,例如,工业生产问题中要求用较低的成本获得较高质量的商品[1],车辆调度问题中要求用较低的成本获得较高的服务质量[2]等,以上这些优化问题统称为多目标优化问题(multi-objective optimization problem, MOP)。MOP问题特点在于其多个优化目标之间往往相互冲突,即找不到一个解能同时使得所有目标取得最优。对于这类问题,传统的解决办法是取一组权重向量,把多目标优化问题转为单目标优化问题,而现代主流思想是利用进化算法为MOP问题求得一组折衷解,决策者根据偏好信息从中选择一个作为最终方案。
自多目标优化进化算法(multi-objective evolutionary alogrithm, MOEA)被提出后,研究者基于不同的视角和研究动机,提出大量经典MOEA算法。根据算法特征,大体可以分为如下几类:①基于Pareto占优机制的MOEA算法,利用Pareto支配关系对个体进行非支配排序,如NSGA-IISDR[3]、SPEAR[4]等。这类算法具有控制参数少,简单易实现等优点,但是在处理复杂前沿和高维目标问题时效果不理想。②基于目标分解的MOEA算法,核心思想是把MOP问题转化为多个简单子问题,如MOEA/D[5]、RVEA[6]、CDG-MOEA[7]等。这类算法运行效率高、收敛速度快,但是受权值向量分布的限制,在处理具有不规则Pareto前沿的MOP问题时性能不佳。③基于新型进化范例的MOEA算法,将性能优越的进化算法移植到多目标优化问题求解中,如基于粒子群优化的CMOPSO[8],基于差分进化算法的SMEA[9]等。这些算法拓宽了解决复杂MOP问题的途径,给从业人员提供更多的选择空间。④不同策略的MOEA集成算法,这类算法把优势互补的策略集成在一起,进一步提高算法的性能,如AOL-MOEA[10]、MSMOPSO[11]、BCEMOEAD[12]、MOEADDU[13]等。近年来,集成MOEA算法引起研究者广泛的关注,获得了很多集成框架和模型,取得了很好的效果。
受MOEA集成算法设计思想的启发,本文提出一种应用精英档案和反向学习的多目标差分进化算法 (EOL-MODE)。该算法创新之处在于:设置一个外部档案来保留进化过程中的非支配解,增强算法局部搜索能力,提高算法收敛速度;反向学习产生外部档案中的反向解,增强算法逃逸局部极值的能力,同时也增强解的多样性;网络约束分解对于Pareto前沿形状有较强的鲁棒性,特别适合处理前沿复杂的优化问题。EOL-MODE算法将3种策略有机集成,有效平衡算法的全局勘探能力和局部开采能力,以便解决复杂多目标优化问题。
1 基本概念
1.1 多目标基本概念
多目标优化问题可以定义为:
minimizeF(x)=(f1(x),…,fm(x))T,
subject to x∈Ω。
(1)
式中:Ω⊂Rn是决策空间;x=(x1,x2,…,xN)T是决策向量;F(x)是m维从决策空间映射到目标空间的目标函数。
定义1 (Pareto支配)假设x,y是多目标优化问题的可行解,称x支配y,当且仅当
∀i=1,2,…,m,fi(x)≤fi(y),
且∃j=1,2,…,m,fj(x)<fj(y)。
(2)
定义2 (Pareto 最优解集)如果解x*∈Ω不被任何别的解支配,x*就是 Pareto 最优解。由Pareto最优解构成的集合就是Pareto 最优解集。
定义3 (Pareto 前沿,PF)Pareto最优解集中的所有 Pareto 最优解在目标函数空间中对应的目标向量组成的集合。
多目标优化问题的最终目标就是在目标空间用一组解集去近似Pareto前沿,让解集尽量均匀分布在Pareto前沿面。
1.2 网格约束分解排序
网格约束分解的主要思想是把每个目标在理想点和边界点之间划分K个间隔,建立一个网格系统,求每个解在网格中的位置坐标。通过对位置坐标进行变换,选取每个目标子问题最小解。
定义4 (理想点)目标空间中所有解在每个目标上的最小值![]()
(3)
定义5 (边界点)目标空间中接近理想点的解集SP中的非支配解,在每个目标上的最大值![]()
(4)
(5)
定义6 (位置坐标)把每个目标划分成K个等距离的小区间,划分后每个小区间的宽度为dj:
(6)
解x沿第j个目标在网格中的位置gj(x):
(7)
式中:σ为一个极小的值,确保网格宽度d>0,同时每个解在网格位置坐标gj(x)>0。
定义7 (邻居解)解x在距离T之内的网格邻居:
![]() 。
。
(8)
定义8 (网格约束分解)基于网格约束方法划分并计算每个目标的子问题,对每个目标子问题排序,再按字典升序排序选择前N个较优解。第l个目标的第k个子问题的约束分解方法计算公式为:
minimize fl(x),subject to gj(x)=kj,
j=1,…,m,j≠l,kj∈{1,…,K},x∈Ω。
(9)
用网格约束分解排序来选择较优的个体,包括更新理想点和边界点,更新每个解的网格坐标,用约束分解排序来选择更优的个体进入下一次迭代过程。
算法1:网格排序选择。
输入:当前合并后种群P,种群规模N
输出:更新的种群P,理想点z*,边界点znad
1.按式(3)、 (4)更新z*和znad,更新网格系统
2.移除在边界点外的解P′
3.按式(7)更新种群P中每个解的位置坐标
4.if |P|<N then
5. 从P′中选择N-|P|个体,加入到种群P中
6.else
7. 按式(9)选择前N个解
8.end if
2 EOL-MODE算法
2.1 外部精英档案
在种群的进化过程中,通过差分进化(differential evolution,DE)[14]算法中的变异杂交策略不断地产生新解,但新解不一定会支配历史非支配解,因此设置一个外部档案来保存算法在进化中产生的非支配解[15]。这些非支配解是在迭代过程中获得的某种最优解,也被称为精英解,精英解携带一定的优良基因,加以利用可引导算法向最优解收敛。
初始时,外部档案为空,将初始种群中的非支配解保存到外部档案。在迭代过程中,利用网格约束排序算法对DE操作前后的种群进行选择,构造一个非支配解集合。并与上一代外部档案中的精英解进行合并,对外部档案中精英个体进行更新,维持种群的多样性。当外部档案中的解容量达到最大值时,要删除一些个体从而维持档案规模,并保持档案的多样性。
算法2:更新外部档案。
输入:合并后种群非支配解为Arc,档案最大规模为A
输出:更新档案中的非支配解
1.if |Arc| ≤A then
2. 利用非支配排序更新档案,除去被支配的个体
3.else
4. 执行算法1选出前A个最优个体
5.end if
2.2 反向学习策略
在求种群非支配解时,计算其反向解,将当前解和反向解同时参与竞争,提高搜索到最优解所在空间的概率,扩大解的搜索范围,使其跳出局部最优,引导种群找到最优解,从而提高算法向全局最优解收敛的速度。解xj在N维空间的反向解xj*计算如下:
xj*=k(aj+bj)-xj,xj∈[aj,bj]。
(10)
式中:k是0~1之间随机数,控制在搜索区间中。反向解的例子如图1所示。
图1 反向解的例子
Figure 1 An example of an opposition solution
以一定的反向学习代跳跃概率p对外部档案中的每一个精英解执行反向学习,生成精英反向解。让反向种群和当前种群共同参与进化竞争,保留优秀的个体进入下一代进行繁殖。
算法3:反向学习伪代码。
输入:种群非支配解Arc,反向学习代跳跃概率p
输出:反向学习种群GOA
1.GOA=∅
2.if rand(0,1)<p then
3. 按式(10)对Arc执行反向学习策略得到GOA
4.end if
2.3 EOL-MODE算法流程
受MOEA集成算法设计思想的启发,本文提出集成多种策略的EOL-MODE算法。以解的网格邻居NS作为交叉池,利用DE算法生成新的个体。对外部档案中精英个体进行反向学习,维持档案规模,直到满足终止条件。算法4描述了具体的算法步骤。
算法4:EOL-MODE算法。
输入:种群规模N,外部档案最大规模A,网格划分参数K,网格邻居距离参数T,杂交父代个体来自网格邻居解概率δ,评估次数FEsmax
输出:外部精英档案解Arc
1.随机生成规模为N的初始种群P,初始化档案Arc=∅,FEs=N
2.构造初始种群P的非支配解,存放到外部档案Arc中,按式(3)、(4)计算z*和znad,按式(7)计算每个解在网格系统的坐标
3.while (FEs<FEsmax)
4. Q=∅
5. for i=1 to|N|
6. if rand(0,1)<δ and |GN|<2 then
7. NS=GN(x,T)
8. else
9. NS=P
10. end if
11. 从交叉池NS中随机选择两个解,与xi用DE算法产生新个体,添加到集合Q中
12. end for
13. 对Arc执行算法3反向学习得到GOA
14. 合并种群P、子代种群Q、反向学习种群GOQ
15. 执行算法1选出前N个最优个体,构造其非支配解集Arc′
16. 合并Arc′与外部档案个体解Arc,按算法2更新并维持外部档案
17. 更新网格系统中当前解的位置坐标
18.end while
19.输出外部精英档案中非支配解Arc
3 实验仿真与结果分析
为了验证所提出的EOL-MODE算法的性能,选取UF系列问题进行测试,并与7个多目标优化算法进行对比,包括BCEMOEAD[12]、SMEA[9]、MOEADDU[13]、CMOPSO[8]、SPEAR[4]、RVEA[6]、NSGAII- SDR[3]。其中,UF1~UF7为2目标问题,UF8~UF10为3目标问题。
3.1 实验参数设置
由文献[7]可知,种群大小N和划分参数K存在一个隐含关系,N=θKm-1,其中θ=αm/β,α为子问题的最优平均解的个数,β为取决于PF形状的系数。
实验中2目标测试函数种群规模N=300,外部档案N=300,网格划分参数K=180,网格间距T=5;3目标测试函数种群规模N=600,外部档案N=600,网格划分参数K=30,网格间距T=1;反向学习代跳跃概率p=0.3;杂交个体来自网格邻居解概率δ=0.8;DE算子中缩放因子F=0.5,交叉概率CR=1。所有测试函数决策空间是30维,最大评估次数为300 000次,每个算法独立运行30次。
采用MATLAB R2019进行编程,选用的仿真平台为PlatEMO[16],64位Windows 8操作系统,电脑配置8G内存。
3.2 与其他算法的性能对比结果与分析
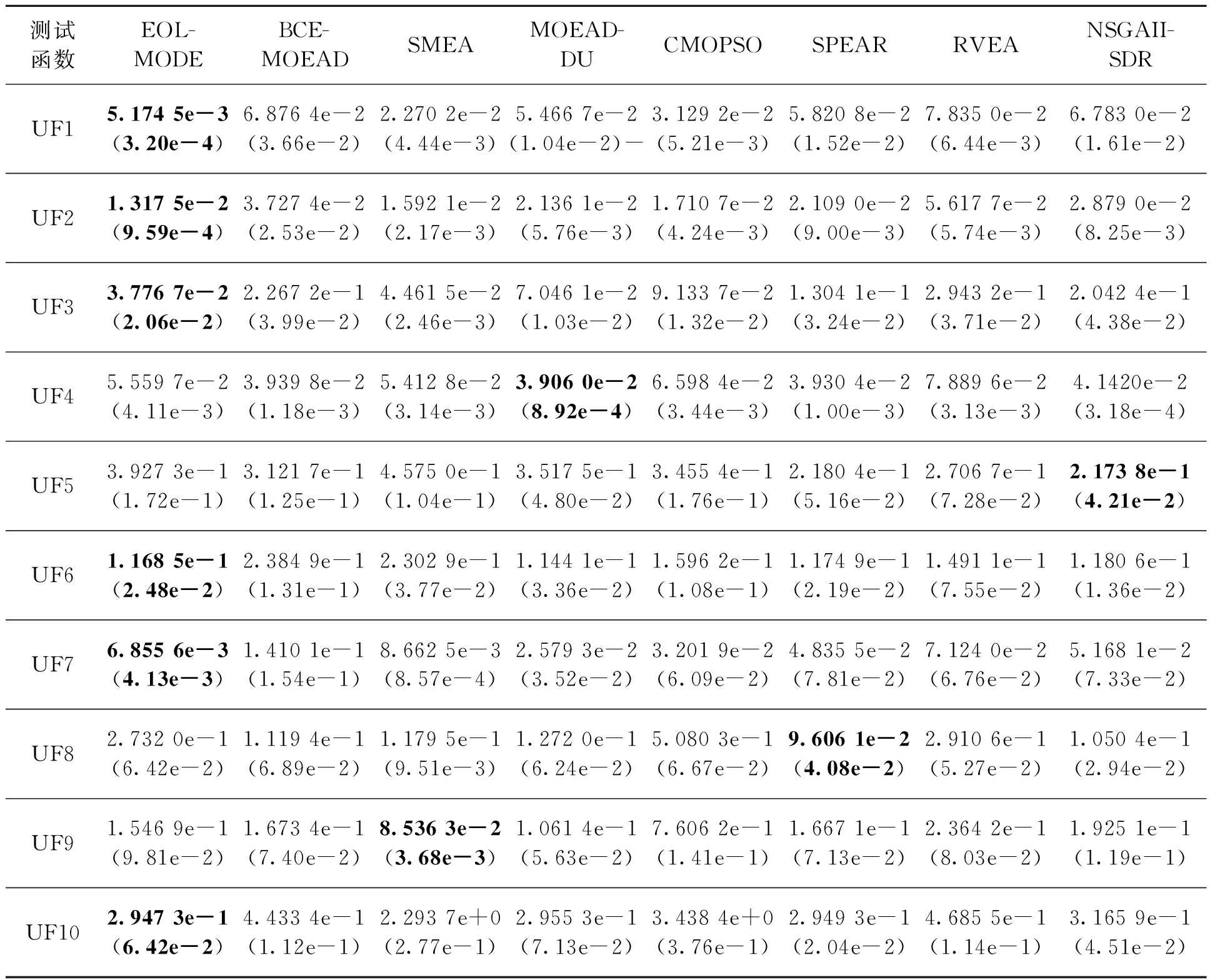
实验中选取反向迭代距离IGD作为评估指标。IGD是指真实PF中的点到所求Pareto解集中的解的最小距离的平均值,IGD值越小,越能更好地近似整个PF。文中对比8个多目标优化算法在10个测试函数的IGD性能如表1所示。其中,表1中每个函数第一行数据代表算法独立执行30次后取的均值,第二行括号内数据代表标准差值,下同,最优值用加粗字体显示。
从表1可以看出,EOL-MODE算法在大多数测试函数上的IGD性能指标都优于其他算法,处理UF1、UF3、UF7问题上相对于NSGAII-SDR等算法有数量级上的提升,虽然在UF4、UF5、UF8、UF9测试问题上EOL-MODE算法比其他算法要差一些,但性能差别不大。图2是8个算法在UF1测试函数上得到的Pareto前沿面。可以看出,本文提出的EOL-MODE算法在求解UF1问题时,算法具有较优的性能,求得的Pareto前沿面最接近真实前沿。
表1 8个多目标优化算法在10个测试问题上的IGD性能对比结果
Table 1 Comparison of IGD performance of eight multi-objective optimization algorithms on ten test problems
测试函数EOL-MODEBCE-MOEADSMEAMOEAD-DUCMOPSOSPEARRVEANSGAII-SDRUF15.174 5e-3 (3.20e-4)6.876 4e-2(3.66e-2)2.270 2e-2(4.44e-3)5.466 7e-2(1.04e-2)-3.129 2e-2(5.21e-3)5.820 8e-2 (1.52e-2)7.835 0e-2(6.44e-3)6.783 0e-2 (1.61e-2)UF21.317 5e-2 (9.59e-4)3.727 4e-2(2.53e-2)1.592 1e-2(2.17e-3)2.136 1e-2(5.76e-3)1.710 7e-2 (4.24e-3)2.109 0e-2 (9.00e-3)5.617 7e-2 (5.74e-3)2.879 0e-2 (8.25e-3)UF33.776 7e-2 (2.06e-2)2.267 2e-1(3.99e-2)4.461 5e-2(2.46e-3)7.046 1e-2(1.03e-2)9.133 7e-2 (1.32e-2)1.304 1e-1 (3.24e-2)2.943 2e-1 (3.71e-2)2.042 4e-1(4.38e-2)UF45.559 7e-2(4.11e-3)3.939 8e-2(1.18e-3)5.412 8e-2(3.14e-3)3.906 0e-2(8.92e-4)6.598 4e-2 (3.44e-3)3.930 4e-2 (1.00e-3)7.889 6e-2 (3.13e-3)4.1420e-2 (3.18e-4)UF53.927 3e-1(1.72e-1)3.121 7e-1(1.25e-1)4.575 0e-1(1.04e-1)3.517 5e-1(4.80e-2)3.455 4e-1 (1.76e-1)2.180 4e-1 (5.16e-2)2.706 7e-1(7.28e-2)2.173 8e-1 (4.21e-2)UF61.168 5e-1(2.48e-2)2.384 9e-1(1.31e-1)2.302 9e-1(3.77e-2)1.144 1e-1(3.36e-2)1.596 2e-1 (1.08e-1)1.174 9e-1 (2.19e-2)1.491 1e-1 (7.55e-2)1.180 6e-1 (1.36e-2)UF76.855 6e-3(4.13e-3)1.410 1e-1(1.54e-1)8.662 5e-3(8.57e-4)2.579 3e-2(3.52e-2)3.201 9e-2 (6.09e-2)4.835 5e-2 (7.81e-2)7.124 0e-2(6.76e-2)5.168 1e-2 (7.33e-2)UF82.732 0e-1 (6.42e-2)1.119 4e-1(6.89e-2)1.179 5e-1(9.51e-3)1.272 0e-1(6.24e-2)5.080 3e-1 (6.67e-2)9.606 1e-2 (4.08e-2)2.910 6e-1 (5.27e-2)1.050 4e-1 (2.94e-2)UF91.546 9e-1 (9.81e-2) 1.673 4e-1(7.40e-2)8.536 3e-2(3.68e-3)1.061 4e-1(5.63e-2)7.606 2e-1 (1.41e-1)1.667 1e-1 (7.13e-2)2.364 2e-1(8.03e-2)1.925 1e-1 (1.19e-1)UF102.947 3e-1 (6.42e-2)4.433 4e-1(1.12e-1)2.293 7e+0(2.77e-1)2.955 3e-1(7.13e-2)3.438 4e+0(3.76e-1)2.949 3e-1 (2.04e-2)4.685 5e-1(1.14e-1)3.165 9e-1 (4.51e-2)
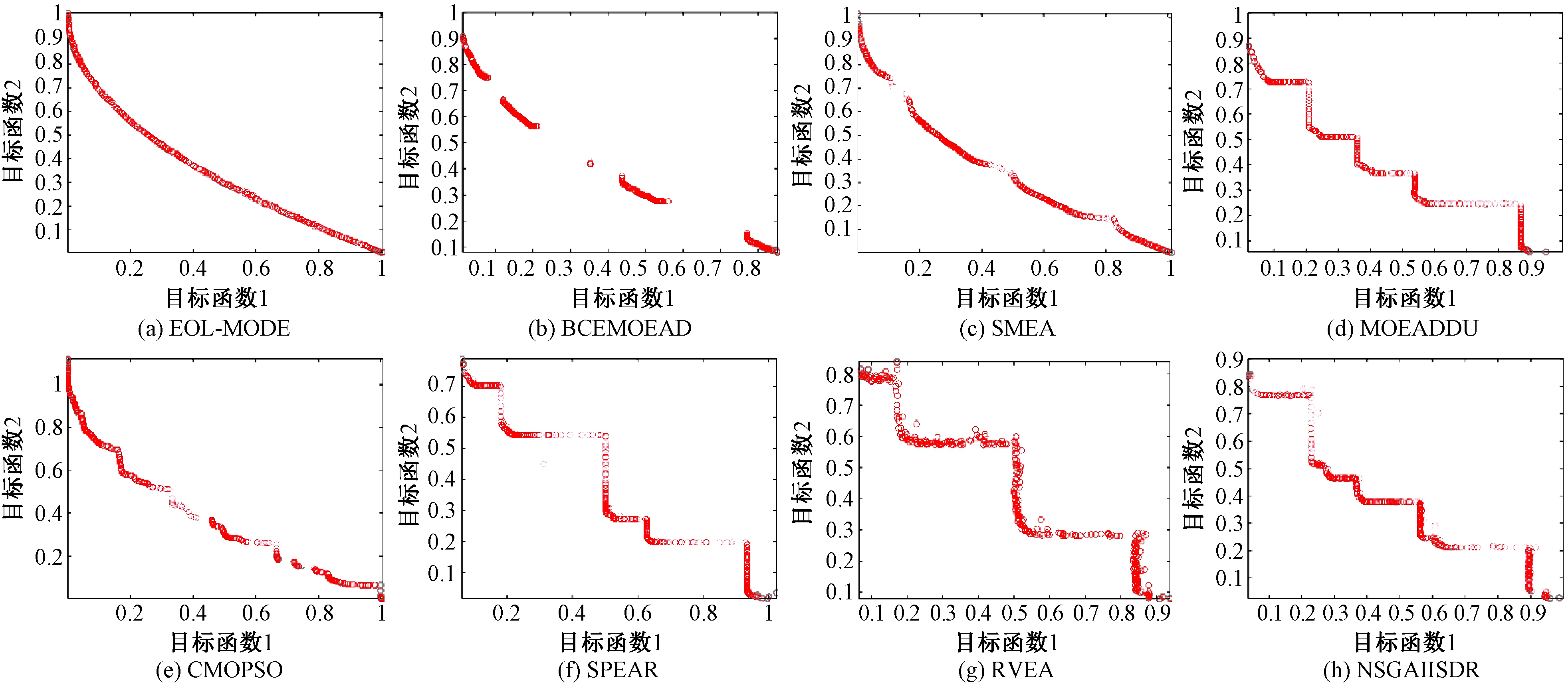
图2 8个算法在UF1测试问题上得到的PF
Figure 2 The final PF obtained by eight algorithms on UF1
图3是选取的8个算法在UF1测试函数上IGD结果对比,相比之下EOL-MODE算法取得的结果最好,收敛速度最快。
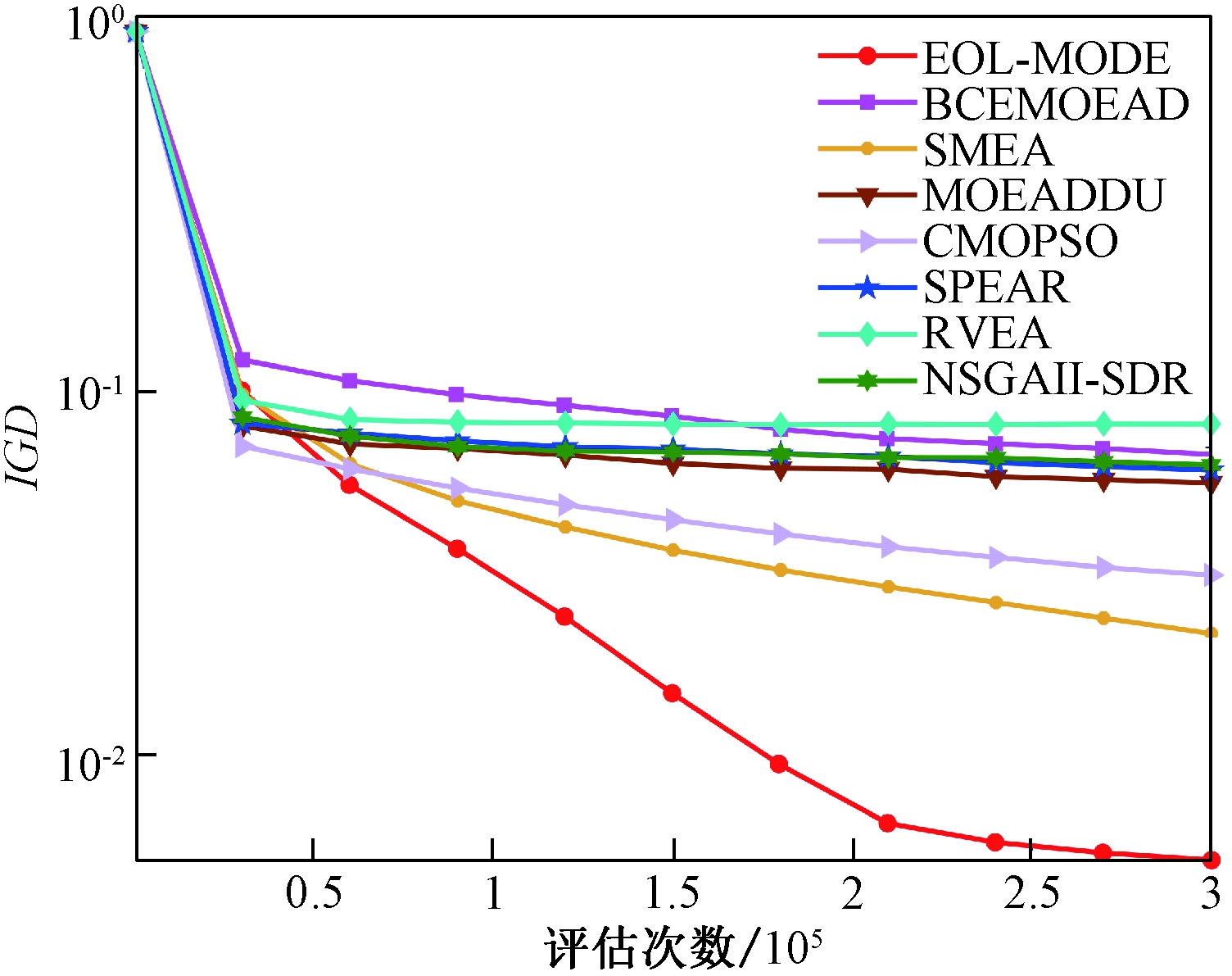
图3 IGD性能评估
Figure 3 The IGD performance of
function evaluation
3.3 集成策略有效性分析
为了检验外部精英档案和反向学习机制的有效性,对比只加入反向学习机制的算法(OL-MODE),和只加入外部精英档案的算法(EL-MODE),在UF1~UF10测试函数上进行实验,对比结果见表2。
从表2中可以看出,OL-MODE 只在UF3测试函数上获得较好的IGD指标值,这表明加入外部精英档案能让算法收敛的更快,提高算法求得解的质量。EL-MODE 在UF2、UF8测试函数上获得较好的IGD指标值,这表明加入反向学习策略,可以让种群在更广的范围内搜索到最优解。通过表中数据可以得出,加入精英档案机制更能引起算法性能的提升。结合这两种机制的EOL-MODE算法,在多样性和收敛性方面要更加有优势,证明了集成策略的有效性。
表2 3个算法的IGD性能对比结果
Table 2 The IGD performance of three algorithms

测试函数EOL-MODEOL-MODEEL-MODEUF15.174 5e-3 (3.20e-4)7.707 2e-3(5.81e-4)5.676 6e-3(3.28e-4)UF21.317 5e-2 (9.59e-4)1.465 3e-2(1.26e-3)1.2128e-2(1.39e-3)UF33.776 7e-2(2.06e-2)2.926 4e-2(1.58e-2)3.291 0e-2(2.51e-2)UF45.559 7e-2 (4.11e-3)5.561 9e-2(2.58e-3)5.571 0e-2(2.69e-3)UF53.927 3e-1(1.72e-1)4.004 9e-1(1.64e-1)4.265 7e-1(2.13e-1)UF61.168 5e-1(2.48e-2)1.742 5e-1(9.45e-2)1.722 8e-1(9.22e-2)UF76.855 6e-3(4.13e-3)1.371 7e-2(8.05e-3)1.032 1e-2(6.39e-3)UF82.732 0e-1(6.42e-2)2.228 1e-1(1.29e-1)1.811 5e-1 (1.23e-1)UF91.546 9e-1 (9.81e-2)2.307 6e-1(1.26e-1)1.919 1e-1(1.14e-1)UF102.947 3e-1(6.42e-2)2.495 1e+0(6.43e-1)1.483 2e+0(4.73e-1)
4 结论
为了更好地求解多目标优化问题,本文提出了EOL-MODE算法,利用外部精英档案来保存进化过程中的非支配解;引入反向学习机制来扩大解的搜索范围,增强解的多样性;求出每个解的网格邻居解,执行差分进化操作,实现局部搜索;利用网格约束分解排序选取较优解,提高算法收敛性,找到的解分布均匀,且多样性保持好。通过仿真实验,对精英档案和反向学习的有效性进行了评估。将该算法与多个多目标优化算法在UF测试函数上的性能进行了比较,结果表明,EOL-MODE算法具有很好的效果。下一步的工作是继续对算法进行优化,使算法在处理大规模问题时具有更好的稳定性。
[1] Van NIEKERK S G J,BREYTENBACH W J J,MARAIS J H.Developing an optimisation model for industrial furnace gaseous fuel distribution for energy cost savings[C]//2017 International Conference on the Industrial and Commercial Use of Energy (ICUE).New York:IEEE,2017:1-4.
[2] MONTOYA-TORRES J R,L PEZ FRANCO J,NIETO ISAZA S,et al.A literature review on the vehicle routing problem with multiple depots[J].Computers & industrial engineering,2015,79:115-129.
PEZ FRANCO J,NIETO ISAZA S,et al.A literature review on the vehicle routing problem with multiple depots[J].Computers & industrial engineering,2015,79:115-129.
[3] TIAN Y,CHENG R,ZHANG X Y,et al.A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization[J].IEEE transactions on evolutionary computation,2019,23(2):331-345.
[4] JIANG S Y,YANG S X.A strength Pareto evolutionary algorithm based on reference direction for multiobjective and many-objective optimization[J].IEEE transactions on evolutionary computation,2017,21(3):329-346.
[5] ZHANG Q F,LI H.MOEA/D:a multiobjective evolutionary algorithm based on decomposition[J].IEEE transactions on evolutionary computation,2007,11(6):712-731.
[6] CHENG R,JIN Y C,OLHOFER M,et al.A reference vector guided evolutionary algorithm for many-objective optimization[J].IEEE transactions on evolutionary computation,2016,20(5):773-791.
[7] CAI X Y,MEI Z W,FAN Z,et al.A constrained decomposition approach with grids for evolutionary multiobjective optimization[J].IEEE transactions on evolutionary computation,2018,22(4):564-577.
[8] ZHANG X Y,ZHENG X T,CHENG R,et al.A competitive mechanism based multi-objective particle swarm optimizer with fast convergence[J].Information sciences,2018,427:63-76.
[9] ZHANG H, ZHOU A M, SONG S M,et al. A self- organizing multiobjective evolutionary algorithm[J]. IEEE transactions on evolutionary computation, 2016, 20(5): 792- 806.
[10] 谢承旺,王志杰,夏学文.应用档案精英学习和反向学习的多目标进化算法[J]. 计算机学报, 2017, 40(3): 757-772.
[11] 谢承旺,邹秀芬,夏学文,等.一种多策略融合的多目标粒子群优化算法[J].电子学报, 2015,43(8): 1538-1544.
[12] LI M, YANG S, LIU X. Pareto or non-Pareto: bi-criterion evolution in multiobjective optimization[J].IEEE transactions on evolutionary computation, 2016, 20(5): 645-665.
[13] YUAN Y, XU H, WANG B,et al. Balancing convergence and diversity in decomposition-based many-objective optimizers[J]. IEEE transactions on evolutionary computation, 2016, 20(2): 180-198.
[14] STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of global optimization, 1997, 11(4): 341-359.
[15] CAO X J, LI G L, YE Q B,et al. Multi-objective optimization of permanent magnet synchronous motor based on elite retention hybrid simulated annealing algorithm[C]//2017 12th IEEE Conference on Industrial Electronics and Applications. New York: IEEE, 2017: 535-540.
[16] TIAN Y, CHENG R, ZHANG X Y,et al. PlatEMO: a MATLAB platform for evolutionary multi-objective optimization[J]. IEEE computational intelligence magazine, 2017, 12(4): 73-87.