0 引言
中国西部山区地形复杂，频繁的地震诱发了大量的滑坡，成为西部地区主要的地震灾害之一[1]。近年来，地震滑坡给我国西部地区造成了巨大损失[2-3]。2017年四川省新磨村滑坡与中国历史上几次大地震具有密切关系，强震降低了岩体的完整性，在强降雨作用下诱发了高位山体滑坡[4]。地震对滑坡的影响具有长期性，引起了国内外学者的重视。
目前，国内外众多学者采用数值计算的方法针对岩质边坡的动力响应开展了大量的研究。Che等[5]采用有限元方法对含不连续节理岩质边坡的地震动力响应进行了研究，探讨了节理分布对其动力响应的影响；Song等[6]采用有限元方法基于时频联合分析方法探究了含不连续结构面岩质边坡地震响应特征及其破坏变形机制；Liu等[7]采用有限元数值计算方法研究了含软弱夹层煤岩边坡的动力响应规律，探讨了软弱夹层对边坡动力响应规律的影响；赖杰等[8]采用数值计算方法研究了双排抗滑桩的坡面加速度响应规律及边坡的动力破坏特征；刘树林等[9]采用离散元软件UDEC对不同倾角顺层边坡的地震响应规律及破坏机制进行了研究，结果表明，软弱结构面及其倾角对边坡的动力响应特征影响较大；朱仁杰等[10]采用有限元方法对含贯通性结构面的岩质边坡地震响应规律进行了研究，分析了地震波场传播特性和动力演化规律。由此可知，采用数值模拟研究岩质边坡的动力响应特征已取得了较多的研究成果。
目前，模态分析主要用于结构及机械工程等动力特性方面的研究。采用模态分析方法可以较好地反映工程实体动力变形特征，但是，采用模态分析方法开展岩质边坡的动力响应方面的研究较少。本文以大型均质岩质边坡为例，采用有限元方法建立三维数值模型，通过对边坡进行模态分析，研究边坡固有频率与其动力变形特征的关系，分析均质边坡的动力放大效应，探讨坡表微地貌变化对边坡动力响应特征的影响，旨在为岩质边坡动力响应方面的研究提供一种新思路。
1 区域概况
研究区位于云南省西北地区的金沙江流域，区内地势总体上西北高东南低。区内河流和山脉的伸展方向与构造线方向整体上相一致。研究区处于欧亚板块与印度板块的缝合带，属青藏高原块区之川-滇块体，研究区所处的区域构造块体构造活动强烈，多条活动性断裂从研究区外围通过。以1996年丽江地震为例，强震诱发了研究区附近大量的滑坡。研究区边坡总体坡度为20°～30°，以均质边坡为研究对象，考虑坡表微地貌对边坡动力响应的影响，边坡地质概化模型如图1所示。边坡的岩性为玄武岩，通过现场勘查及室内岩石试验获取了边坡岩体的主要物理力学参数，如表1所示。
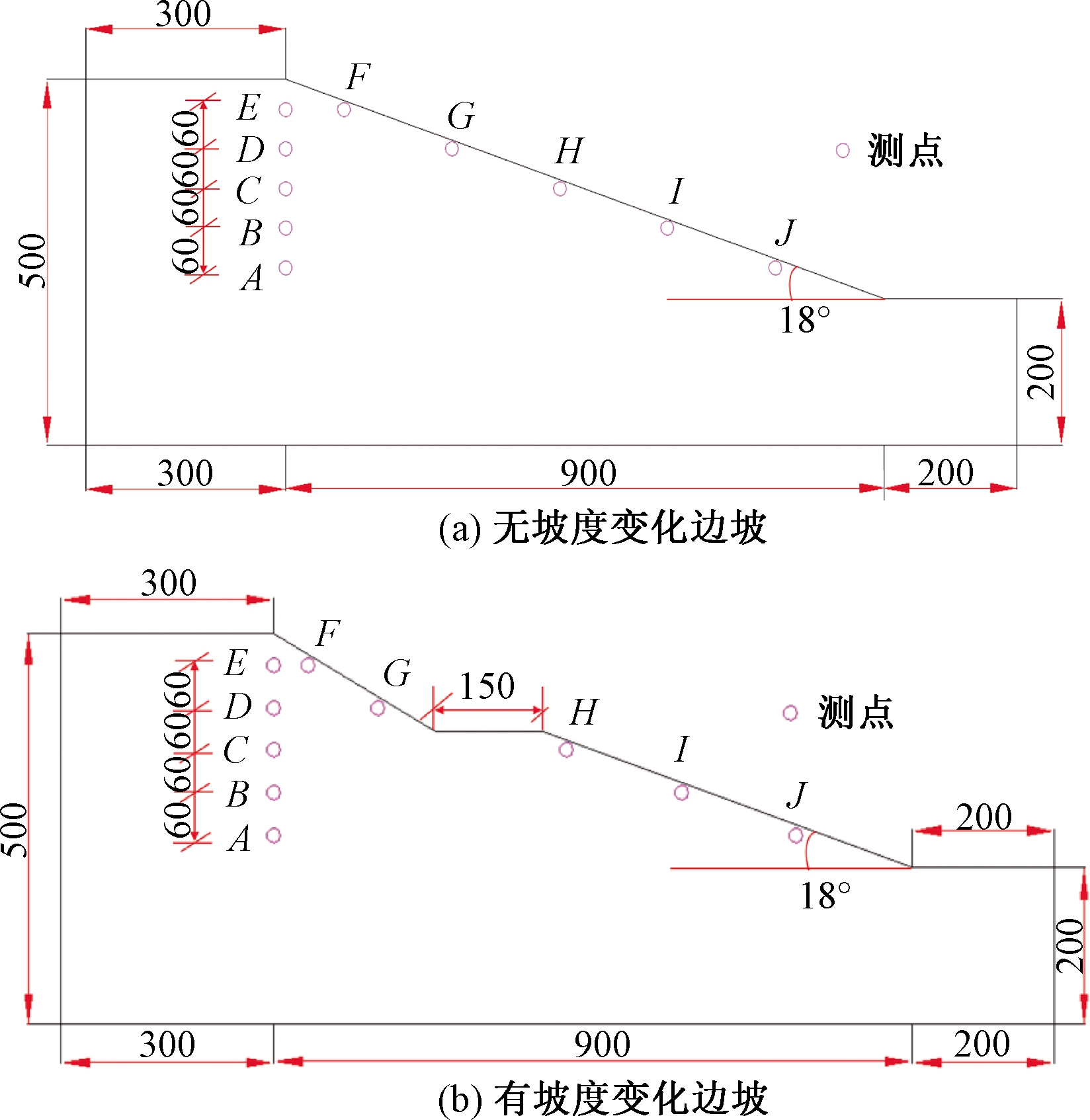
图1 大型均质边坡地质概化模型(m)
Figure 1 Geological generalization model of large homogeneous slope(m)
表1 边坡岩体物理力学参数
Table 1 Physico-mechanical parameters of the slope rock mass
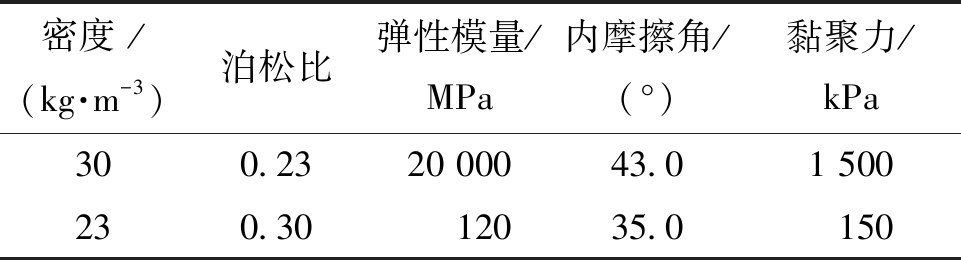
密度 /(kg·m-3)泊松比弹性模量/MPa内摩擦角/(°)黏聚力/kPa300.2320 00043.01 500230.3012035.0150
2 模态分析原理
模态指系统按照其固有频率进行自由振动时，系统内的各质点偏离原来平衡位置的位移满足某一比例关系。振型指系统按照某一固有频率振动时的振动形态，其中1阶振型为主振型。模态分析主要获取固有振型及固有频率，是结构动力分析的重要方法，也是动力频域分析的基本类型。有限元法是模态分析常用的方法，基于弹性力学原理，模态分析的动力控制方程如下[11]：
(1)
式中：M、C、K分别为质量矩阵、阻尼矩阵、刚度矩阵；F为随时间变化的外力荷载函数；
和
分别为模型的加速度矢量和速度矢量；U为模型的位移矢量，用于描述振型的模态分析。模态分析计算实际上是一种理论建模过程，主要采用有限元方法对振动工程实体进行离散，建立系统特征值问题的数学模型，采用各种近似方法对系统的特征值及特征矢量进行求解。由于阻尼难以精确地处理，因此通常忽略小阻尼系统的阻尼，此时计算得到的特征值及特征矢量为系统的固有频率及固有振型矢量[12]。在理想情况下，模态分析中不考虑外力和阻尼效应的影响。模态分析的动态控制方程可表示为[11]：
(2)
式(2)的特征方程为：
(K-ωi2M)U=0。
(3)
式中：ωi是第i个自然圆频率(i=1,2，…,n)。得到的固有频率fi为：
(4)
特征值所对应的特征向量是Ui，Ui表示固有频率fi下振动时的振型。1阶振型为主振型，模型的动力学特性主要由低阶振型控制，进行分析时仅考虑前几阶模态。
3 有限元模态分析
3.1 数值模型
根据边坡原尺寸建立有限元数值模型，包括模型1(坡表无坡度变化)和模型2(坡表有坡度变化)，如图2所示。模型尺寸为1 400 m×800 m×500 m，边坡坡度约为20°，岩体采用三角形网格进行建模，边坡的岩体物理力学参数如表1所示。有限元模态分析中边坡的变形属于小应变问题，在模态分析中采用弹性模型进行研究。采用ABAQUS隐式求解功能中的线性摄动分析步进行模态分析。
3.2 固有频率分析
采用有限元方法对2个模型进行模态分析，模型的前10阶固有频率如图3所示。由图3可知，2个模型的固有频率随着振型阶次增加而增加，模型1的前4阶固有频率分别为4.34、7.81、9.27、12.67 Hz，模型2的前4阶固有频率分别为4.21、7.53、8.25、11.25 Hz。2个模型的前2阶固有频率较为接近，而在第3阶之后模型1的固有频率明显大于模型2。这是由于模型2坡表处含有1个平台区域，在该区域坡度出现了较大的变化，改变了边坡的刚度，导致模型2的固有频率小于模型1。由此可知，相同条件下坡表坡度变化对边坡的固有频率具有影响，在一定程度上降低了边坡的固有频率。
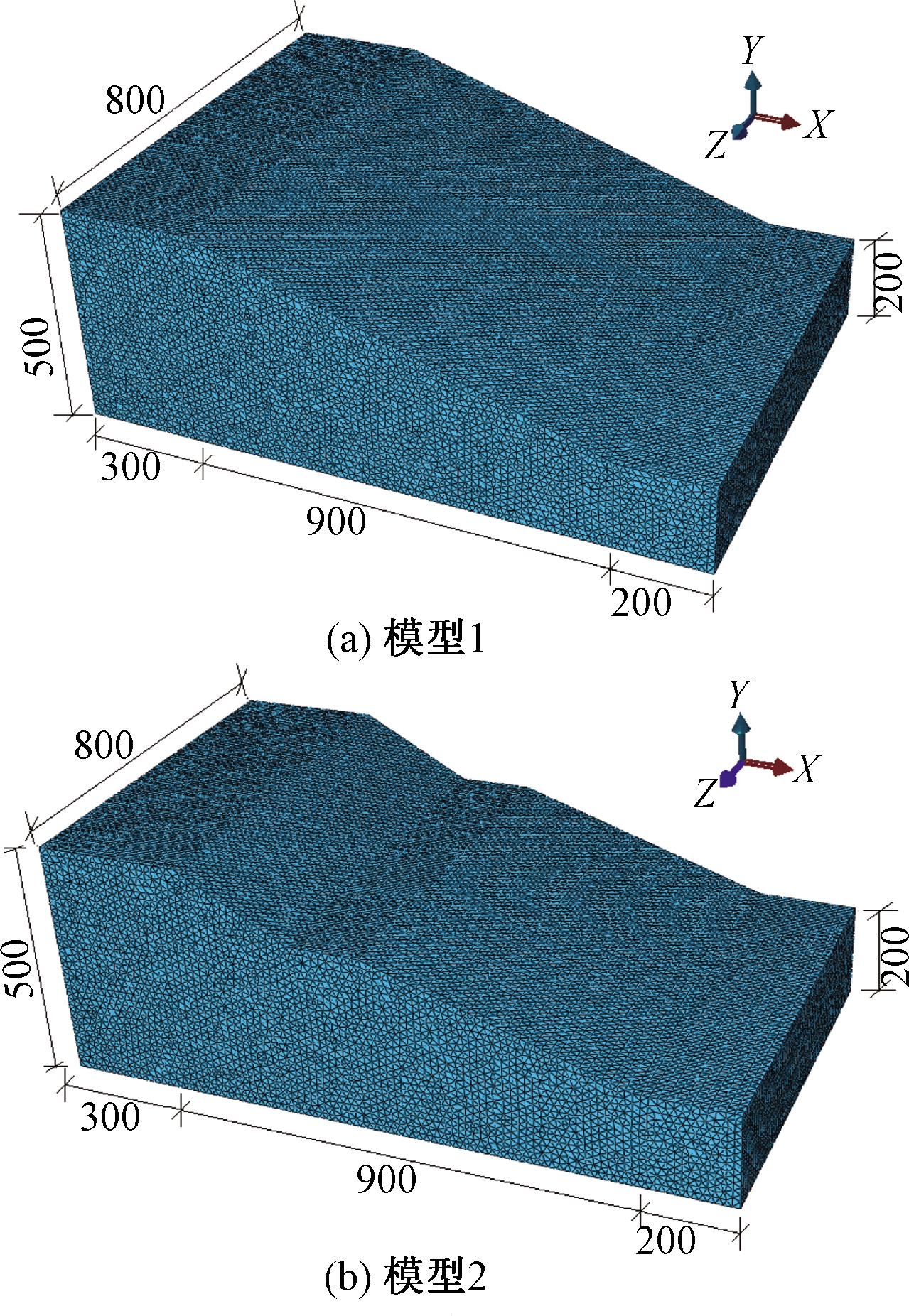
图2 三维有限元数值模型(m)
Figure 2 Three-dimensional finite element numerical model(m)
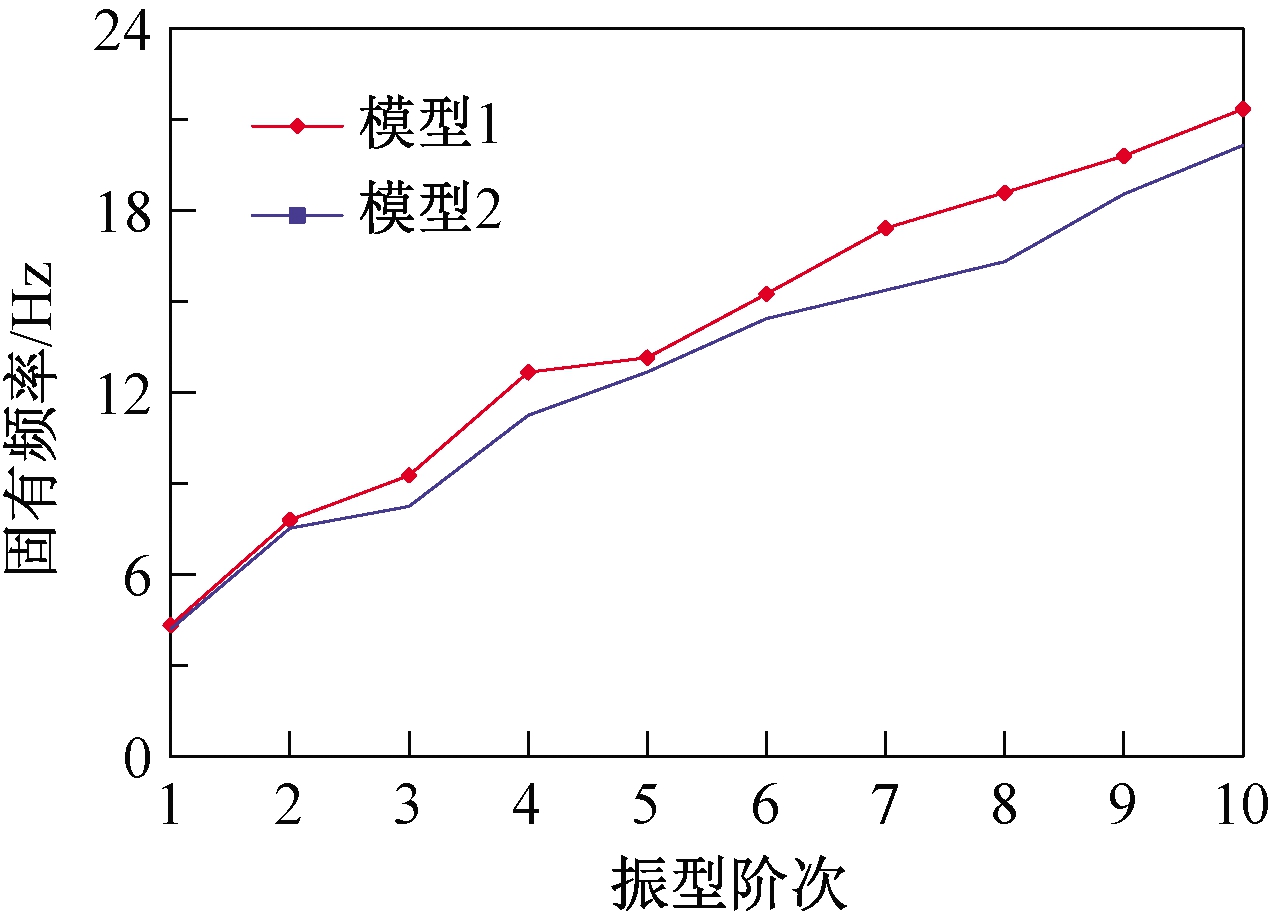
图3 模型固有频率
Figure 3 Natural frequencies of models
3.3 振型分析
低阶振型对模型的动力特性起着决定性的作用，因此，在模态分析中主要考虑前几阶振型[13]。边坡振型与其固有频率一一对应，振型分析可为边坡的动力破坏模式提供参考依据[11]。2个模型的振型如图4和图5所示，振型特征如表2所示。由图4和图5可知，2个模型的主要振型特征包括弯曲、拉伸、扭转变形及其组合。图4和表2表明：模型1的1阶模态振型特征主要表现为坡顶区域的弯曲变形特征，这说明地震作用下模型1的坡顶区域易发生变形破坏；2阶及3阶振型表现为坡顶区域的弯曲及拉伸变形；4阶及5阶振型特征表现为坡底及坡体中部的扭转变形；5阶以上的振型表现为弯曲、拉伸及扭转的组合变形特征。由图5和表2可知，模型2的1阶振型特征表现为坡顶区域的弯曲变形，这说明地震作用下坡顶及平台区域易发生变形破坏；2阶至5阶振型特征表现为平台区域的弯曲或扭转变形；5阶以上振型表现为坡底、坡顶及平台区域的弯曲、拉伸及扭转变形的组合变形。
图4 模型1振型分析
Figure 4 Vibration mode analysis of Mode 1
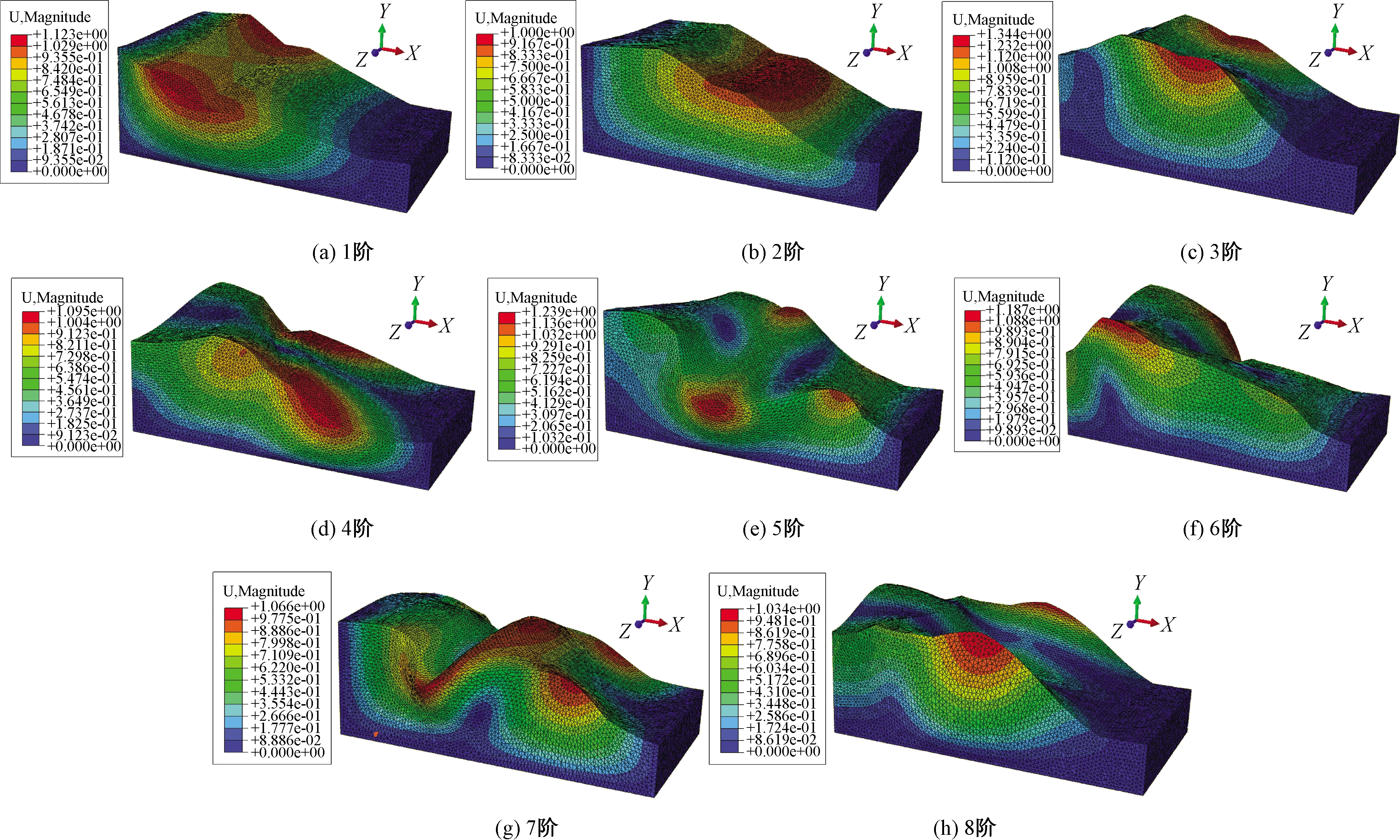
图5 模型2振型分析
Figure 5 Vibration mode analysis of Mode 2
表2 模型振型特征
Table 2 Vibration characteristics of models
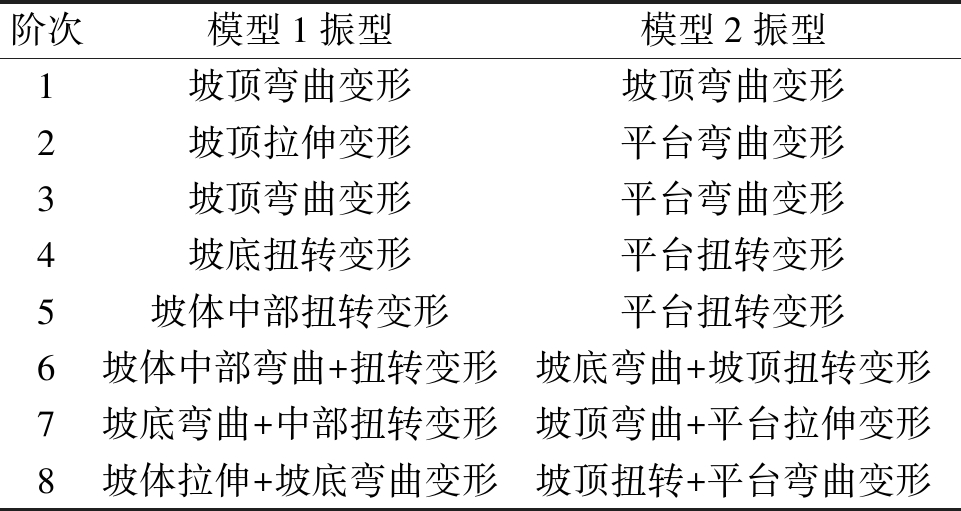
阶次模型1振型模型2振型1坡顶弯曲变形坡顶弯曲变形2坡顶拉伸变形平台弯曲变形3坡顶弯曲变形平台弯曲变形4坡底扭转变形平台扭转变形5坡体中部扭转变形平台扭转变形6坡体中部弯曲+扭转变形坡底弯曲+坡顶扭转变形7坡底弯曲+中部扭转变形坡顶弯曲+平台拉伸变形8坡体拉伸+坡底弯曲变形坡顶扭转+平台弯曲变形
由此可知，模型1的1阶及2阶振型主要表现为坡顶区域的整体性变形特征，3阶及以上振型表现为局部变形特征；模型2的1阶及2阶振型主要表现为坡顶及平台区域的整体性变形特征，3阶及以上振型表现为局部变形特征。也即低阶固有频率主要诱发边坡的整体变形，高阶(≥3阶)固有频率主要诱发边坡的局部变形。随着阶次增加，边坡的振型变得更为复杂。5阶以下振型主要表现为单一的变形特征，5阶以上的振型表现为多种变形的组合。本文模型边坡的模态分析结果与文献[13]采用振动台试验及有限元数值计算结果相吻合，岩质边坡的低阶固有频率及地震波的低频段主要与边坡的整体动力变形特征相关，而边坡高阶固有频率及地震波高频段与边坡的局部变形相关。
此外，与模型1相比，模型2的高阶振型特征主要表现为平台区域的变形，这是由于模型2平台区域的坡度变化较大，引起平台区域出现了应力集中现象，导致该区域的动力放大效应变大，坡表坡度变化对边坡的动力响应特征具有较大的影响。由图4和图5可知，2个模型边坡振型特征表现为相对位移Ud主要集中于坡表区域，这说明边坡的坡表区域的动力放大效应大于坡内，也即地震作用下坡表区域是最容易失稳的区域。
3.4 动力放大效应分析
1阶振型为边坡的主振型，1阶模态可以反映边坡的主要动力变形特征[11]。为进一步研究边坡的动力放大效应，1阶模态的边坡不同高程处测点相对位移Ud随相对高程的变化如图6所示，其中Ud为模型Z轴上的位移平均值。相对高程为边坡某点高程与坡高的比值，以坡脚处为高程0 m。由图6(a)可知，2个模型坡内的Ud随相对高程的增加而增加，这说明坡内的动力放大效应随高程增加而增加。图6(b)表明，模型1坡表的Ud随高程增加而呈增加趋势，但模型2坡表的Ud表现为明显的非线性增加趋势，在平台区域相对位移出现了突增现象，这说明坡表坡度变化对边坡的局部变形具有明显的放大效应。此外，模型2的Ud大于模型1，这说明坡度变化对边坡动力放大效应具有影响。结合图3、图4和图6可知，坡表的Ud远大于坡内，这表明坡表为动力放大区域。针对大型均质岩质边坡，詹志发等[14]采用振动台试验模拟研究了其动力响应特征，研究结果表明，大型均质边坡具有明显的高程动力放大效应，并且坡表的动力放大效应大于坡内，这与本文采用模态分析研究大型均质岩质边坡动力放大效应结果相吻合。
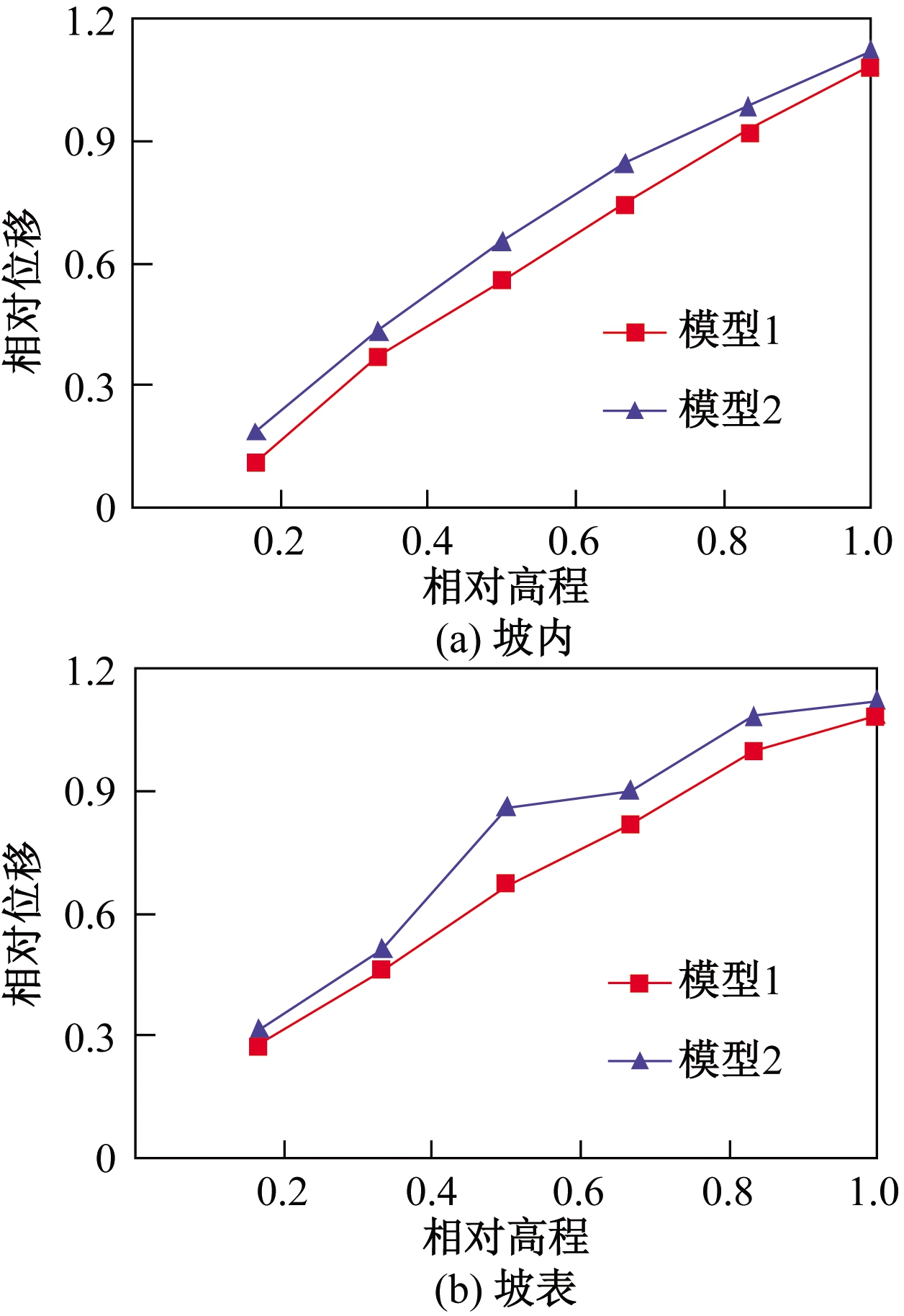
图6 1阶模态Ud随高程的变化
Figure 6 Change of Ud with elevation in the first-order mode
3.5 边坡动力变形机制
由上述分析可知，均质岩质边坡的低阶固有频率主要引起其整体性变形，高阶固有频率主要引起边坡的局部变形破坏。地震作用下均质边坡的地震破坏机制可以概括如下：地震波频率成分复杂，均质边坡的地震失稳破坏机制主要与地震波的卓越频率及边坡的固有频率密切相关；地震波低阶卓越频率与边坡低阶固有频率共振是导致滑坡触发的主要诱因；边坡的高阶固有频率主要使边坡出现局部变形，坡表局部变形累积到一定值时，将会在低阶固有频率作用下出现整体性的滑动破坏。模型1的地震破坏模式主要表现为坡顶区域的滑动破坏，模型2的地震破坏模式主要表现为坡顶区域及平台区域的滑动破坏。
4 结论
(1)均质岩质边坡的固有频率随阶次增加而增加，边坡具有高程及坡表动力放大效应。模型1的前4阶固有频率分别为4.34、7.81、9.27、12.67 Hz，模型2的前4阶固有频率分别为4.21、7.53、8.25、11.25 Hz；1阶模态相对位移随着高程增加而增加，坡表相对位移大于坡内。
(2)均质岩质边坡的固有频率与其动力变形特征密切相关。低阶固有频率主要诱发边坡的整体性变形，高阶固有频率主要诱发边坡的局部变形。边坡的振型特征随着阶次增加变得复杂，低阶振型主要表现为单一的变形特征，5阶以上的振型表现为多种变形的组合。
(3)坡度变化对边坡的固有模态及动力放大效应具有影响。坡度变化导致模型2的固有频率小于模型1，模型2的平台区域的放大效应明显变大。模型1的坡顶区域容易发生滑动变形破坏，模型2的坡顶及平台区域易出现滑动变形破坏。
[1] 宋丹青,王丰,梅明星,等. 水库蓄水对库岸边坡稳定性的影响[J]. 郑州大学学报(工学版), 2016,37(1):60-64.
[2] 徐锡蒙,郑粉莉,关颖慧,等. 2013年我国地震灾害时空特征与灾害损失分析[J]. 水土保持研究, 2015,22(4):321-325.
[3] DAI F C, XU C, YAO X, et al. Spatial distribution of landslides triggered by the 2008 Ms 8.0 Wenchuan earthquake,China[J]. Journal of Asian earth sciences, 2011, 40(4): 883-895.
[4] FAN X M, XU Q, SCARINGI G, et al. Failure mechanism and kinematics of the deadly June 24th 2017 Xinmo landslide, Maoxian, Sichuan, China[J]. Landslides, 2017, 14(6): 2129-2146.
[5] CHE A L,YANG H K,WANG B,et al.Wave propagations through jointed rock masses and their effects on the stability of slopes[J].Engineering geology,2016,201:45-56.
[6] SONG D Q,CHEN Z,CHAO H, et al. Numerical study on seismic response of a rock slope with discontinuities based on the time-frequency joint analysis method[J]. Soil dynamics and earthquake engineering, 2020, 133: 106112.
[7] LIU G W,SONG D Q,CHEN Z,et al.Dynamic response characteristics and failure mechanism of coal slopes with weak intercalated layers under blasting loads[J].Advances in civil engineering,2020(9):1-18.
[8] 赖杰,刘云,辛建平,等. 大理西站支护边坡振动台试验及数值模拟[J]. 浙江大学学报(工学版), 2020,54(5):870-878.
[9] 刘树林,杨忠平,刘新荣,等. 频发微小地震作用下顺层岩质边坡的振动台模型试验与数值分析[J]. 岩石力学与工程学报, 2018,37(10):2264-2276.
[10] 朱仁杰,车爱兰,严飞,等.含贯通性结构面岩质边坡动力演化规律[J].岩土力学,2019,40(5):1907-1915.
[11] 周逸飞,刘汉香,朱星,等. 含软弱夹层岩质边坡的模态分析及其对边坡地震动力响应影响的初步研究[J]. 地震工程与工程振动, 2020,40(1):223-232.
[12] REALE C, GAVIN K, PRENDERGAST L J, et al.Multi-modal reliability analysis of slope stability[J]. Transportation research procedia, 2016, 14: 2468-2476.
[13] SONG D Q, CHE A L, ZHU R, et al. Natural frequency characteristics of rock masses containing a complex geological structure and their effects on the dynamic stability of slopes[J]. Rock mechanics and rock engineering, 2019, 52(11): 4457-4473.
[14] 詹志发,祁生文,何乃武,等.强震作用下均质岩质边坡动力响应的振动台模型试验研究[J].工程地质学报,2019,27(5):946-954.