0 引言
饱和多孔介质热-流-固耦合问题不仅在传统的土力学、水文学等经典领域得到广泛应用，而且也广泛应用于核废料污染物处置、地热资源、热能贮存、人体关节软骨组织分析等工程领域。因此，研究饱和多孔介质的热力学性能的理论、数值方法及其应用有着重要的意义和广泛的背景。早在1955年，Biot[1]建立了有关饱和多孔介质的热弹性理论，已在众多工程领域成功地取得了许多研究成果[2-4]。在连续介质混和物公理体系和体积分数概念的基础上，De Boer[5]于2005年建立了更加精确完整的多孔介质热弹性理论，一些微观性质可以直接用来描述宏观性质，容易反映非线性效应。利用混合物理论，De Boer等[6]为一维流体饱和不可压缩多孔介质的动力学固结问题提供了解析解。Heider等[7]研究了波在饱和多孔半空间中的传播。在De Boer等[8]提出的多孔介质热力学本构关系的基础上，He等[9]给出了一种在热局部非平衡条件下的流体多孔介质的数学模型，Yang[10]建立了该模型的相应的Gurtin型变分原理，朱媛媛等[11]对空间轴对称流体饱和多孔热弹性柱体动力学特性进行了分析。但目前有关饱和多孔介质热-流-固耦合系统非线性理论和应用以及数值模拟的报道很少见。
为探索所提问题理论和数值方法分析及其可行性，笔者基于多孔介质混合理论(porous media theory， PMT)[5,8]，研究了在有限变形和热局部非平衡条件下，不可压流体饱和多孔热弹性半平面在表面温度载荷作用下的动力学特性。在建立该问题非线性数学模型的基础上，通过采用微分求积法(differential quadrature method, DQM)在空间域内建立离散问题的非线性数学模型，用二阶后向差分格式来处理时间导数，用Newton-Raphson法求解非线性代数方程组，从而可得到问题的数值结果，分析半平面的动力学特性。通过和De Boer等[6]的解析解的对比研究，表明本文方法是有效可靠的，具有计算量小、精度高等优点。
1 数学模型
考察图1所示平面直角坐标系xoz中饱和不可压多孔热弹性半平面的动力学问题。假设作用于半平面表面的载荷或者温度具有某种对称性，取oz轴为对称轴，由表面指向半平面内部的方向为正方向(图1)。
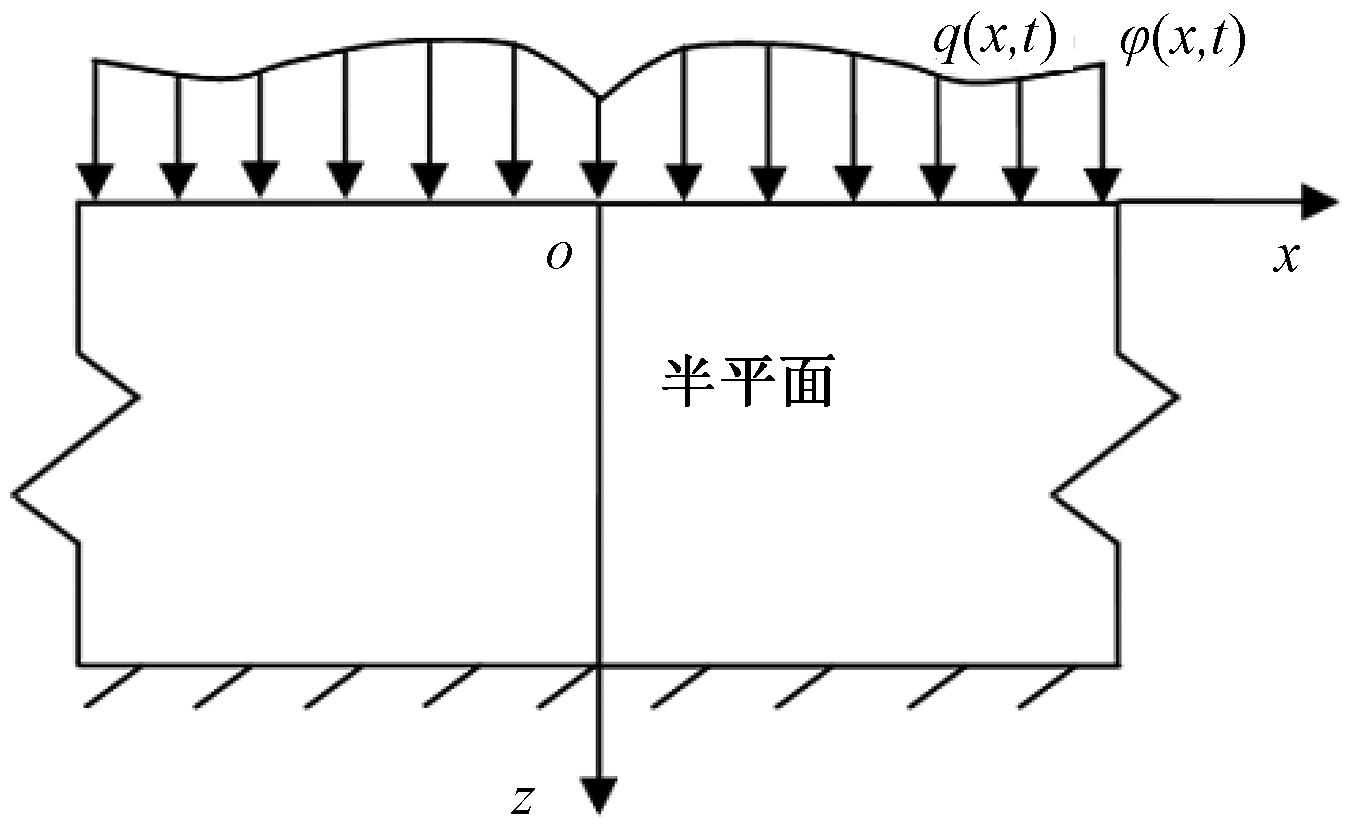
图1 半平面问题的数学模型
Figure 1 Mathematical model of half-plane problem
设平面处于热局部非平衡状态(固相介质和液相介质的变温不同)，并假设平面介质为各向同性线性热弹性多孔固相骨架和理想流体，根据PMT，在不可压和小流速的假设下，半平面的控制微分方程如下：
(1a)
(1b)
(1c)
(1d)
(1e)
Θ0βS(wx,x+wz,z)-eθθFS+
(1f)
Θ0βF(wx,x+wz,z)+eθθFS-ρFrF=0。
(1g)
其中，公式(1a)是质量守恒方程，公式(1b)～(1e)是动量和动量矩平衡方程，公式(1f)～(1g)是能量守恒方程。基本未知量为固相位移ux、uz，固相有效应力
相对流速wx、wz，有效孔隙压p，固相介质和液相介质的变温θS、θF。主要材料参数有体积分数na(a=S、F分别记为固相及液相)、宏观质量密度ρa(和微观质量密度ρaR关系为ρa=naρaR)、流固耦合系数Sv=(nF)2γFR/κF (其中γFR为液相有效比重，κF为达西渗透系数)，热交换因子βa，热传导系数kab、热能交换系数eθ,比热系数ca和热源强度ra、固相材料的Lame系数μS、λS，体积模量KS，热膨胀系数αS。并记系统的初始绝对温度为Θ0，θFS=θF-θS。
在有限变形的情况下，对于各向同性线性热弹性的固相材料，几何关系和本构关系为：
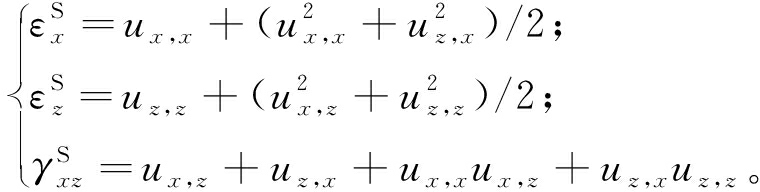
(2)
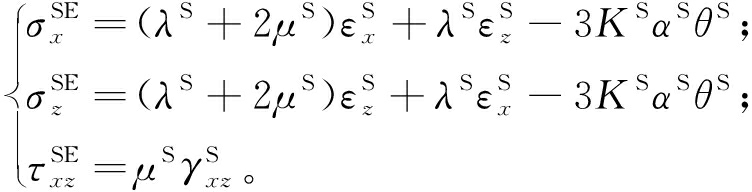
(3)
式中：
为固相的应变分量。
同时，固相材料的有效应力与总应力之间的关系为：
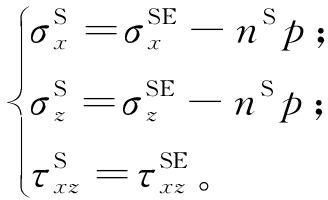
(4)
假设流体饱和多孔弹性半平面的上表面处于理想排水状态，同时承受变温φ(x,t)和垂直载荷q(x,t)的作用；底部为不排水刚性绝热底面；侧面不排水绝热且在x方向位移被约束 (图1)。设φ(x,t)和q(x,t)关于oz轴对称，可以在区域0≤x≤L0,0≤z≤H0内考虑问题，这时在热局部非平衡状态下，有如下边界条件和对称条件。
z=0时，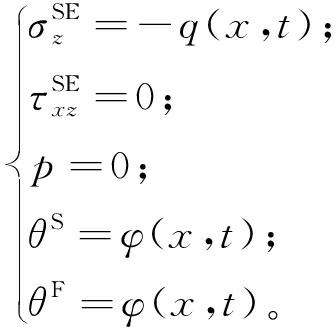
(5)
z=H0时，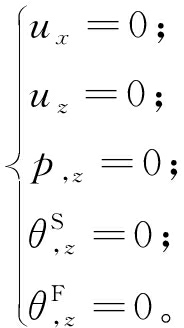
(6)
x=0时，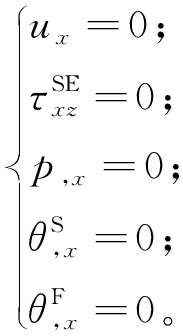
(7)
x=L0时，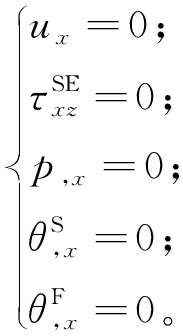
(8)
假设t≤0时半平面处于静止和热力平衡状态，在热局部非平衡状态下初始条件为：
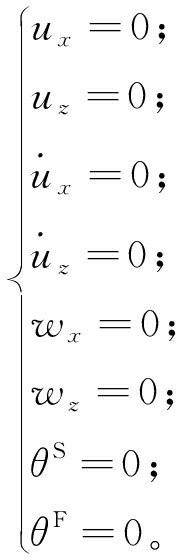
(9)
因此，式(1)～(8)构成了在热局部非平衡条件下流体饱和多孔热弹性半平面动力学问题的一个数学模型。当固相和液相介质的变温相同时，式(1)～(8)退化为热局部平衡条件下的数学模型。
不难看到，很难获得上述动力学问题的解析或半解析解。在本文中，对于热局部非平衡条件下的非线性数学模型在空间域中使用DQM离散，时间导数采用二阶后向差分格式处理，离散后的非线性代数方程组采用Newton-Raphson法迭代求解，可得到问题的数值模拟结果。
2 求解方法
1970年，Bellman等[12-13]提出了DQM。DQM具有公式简单、精度高、计算量少等优点，已有很多成功的应用[14-15]。DQM的基本思想是将函数的偏导数近似为离散点处相应函数值的加权和。由于DQM权函数的选取与特定问题无关，微分方程能DQ离散为相应的代数方程求解。
设半平面占有区域Ω={〈x,z〉|0≤x≤L0,0≤z≤H0}，分别在x、z轴方向布置Nx×Nz个节点，节点坐标为Chebyshev-Lobatto多项式的零点。根据DQM，未知函数ψ(x,z)对x的n阶偏导数可近似表示为：
(10)
式中： ψkη是在x=xk，z=zη节点处的函数值；
是n阶偏导数的权系数，本文由Lagrange插值多项式来决定。同时，可给出ψ(x,z)对z的m阶偏导数，权系数为
利用式(10)，在空间域内对数学模型(1)～(8)DQM离散化后，产生了关于时间t的微分代数方程组。使用二阶后向差分格式来处理关于微分代数方程组中的时间导数：
(11)
式中：Δt是时间步长；ψ(tn,x)是在时刻t=tn的函数值。
最后利用DQ离散的初始条件(9)，对离散化方程组进行Newton-Raphson迭代求解，从而可得到问题的数值结果。
3 分析与讨论
3.1 验证方法
忽略体积力的影响，De Boer等[6]分析了几何小变形和常温条件下不可压饱和多孔弹性介质的一维动力固结问题，并给出了在PMT下唯一的解析解。为了验证本文方法的正确性和有效性，本文在第1节给定的数学模型中设平面表面变温为φ(x,t)=0，从而可以认为在热局部非平衡条件下的解近似等于常温状态时的解，然后用一个高H0=10 m，宽L0=10 m的流体饱和多孔弹性体来模拟De Boer等[6]所考虑的类似问题，并与解析解进行比较。在验证中，分别考虑了阶梯载荷q(x,t)=q0h(t)和周期载荷q(x,t)=q0[1-cos(ωt)]的影响，其中，q0=3 kN/m2，ω=0.4 s-1，h(t)为Heaviside函数。本文计算中选取的材料是废料存储中使用的黏土材料[2]，材料参数见表1。
图2和图3分别给出了在阶梯载荷和周期载荷下，对称轴处不同深度的位移uz (沉降)，其中，实线和虚线分别对应了在7×7和9×9布点下利用本文方法得到的数值解，坐标点为文献[6]中的解析解。时间步长Δt=1 s。从图中看到，本文提供的数值结果与解析结果吻合良好，当布置结点数为7×7个时，便能得到令人满意的结果。说明用本文方法来计算流体饱和多孔弹性介质的动力学特性是有效的。
表1 材料参数
Table 1 Parameters of material
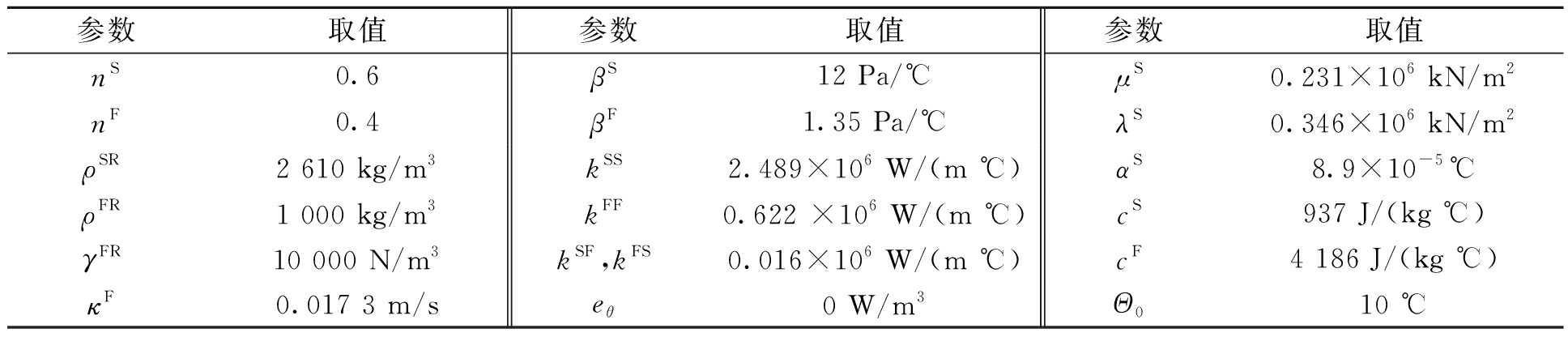
参数取值参数取值参数取值nS0.6βS12 Pa/℃μS0.231×106 kN/m2nF0.4βF1.35 Pa/℃λS0.346×106 kN/m2ρSR2 610 kg/m3kSS2.489×106 W/(m ℃)αS8.9×10-5 ℃ρFR1 000 kg/m3kFF0.622 ×106 W/(m ℃)cS937 J/(kg ℃)γFR10 000 N/m3kSF,kFS0.016×106 W/(m ℃)cF4 186 J/(kg ℃)κF0.017 3 m/seθ0 W/m3Θ010 ℃
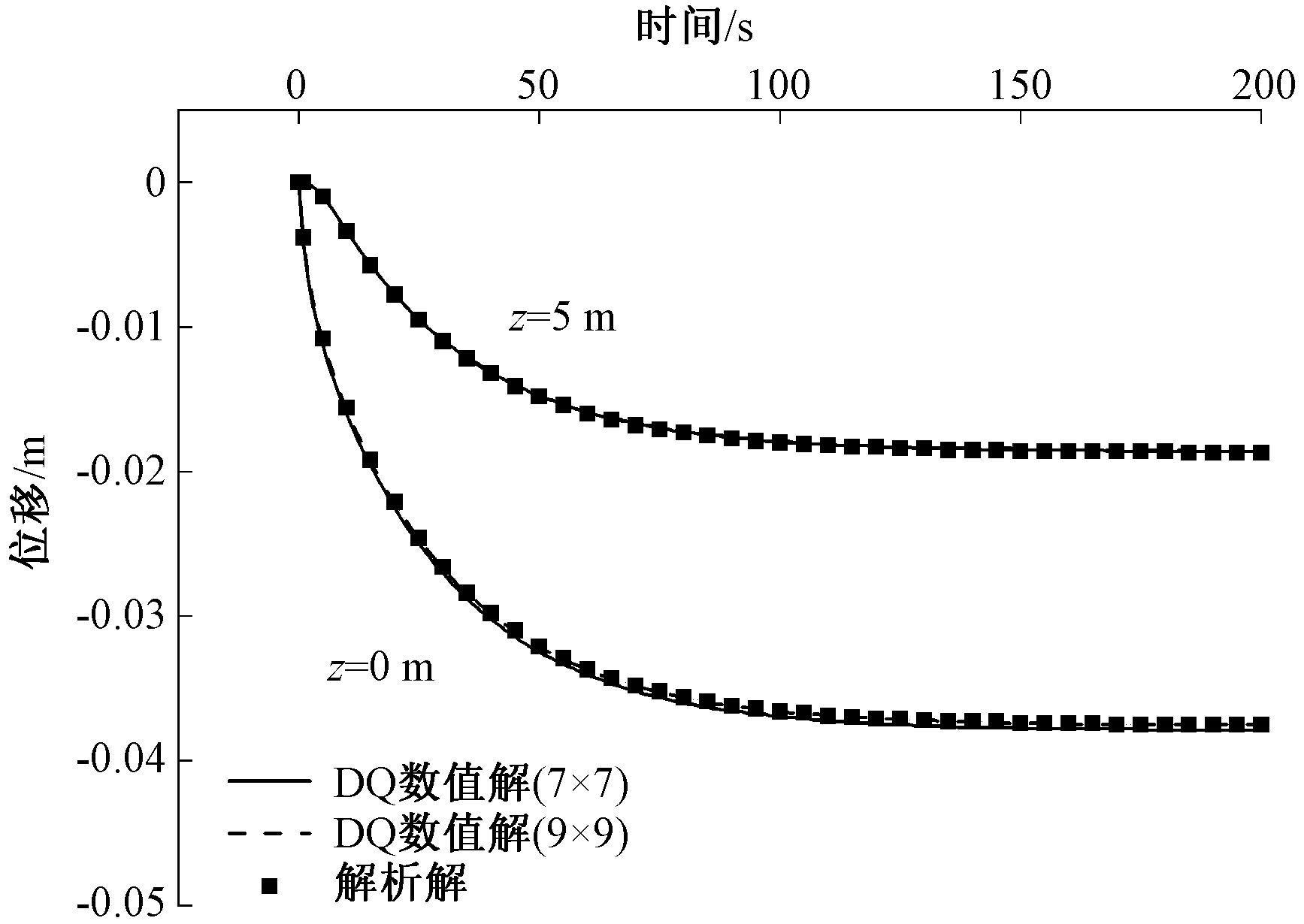
图2 位移时程曲线图(阶梯载荷)
Figure 2 Time-history curves of displacement
(step loading)
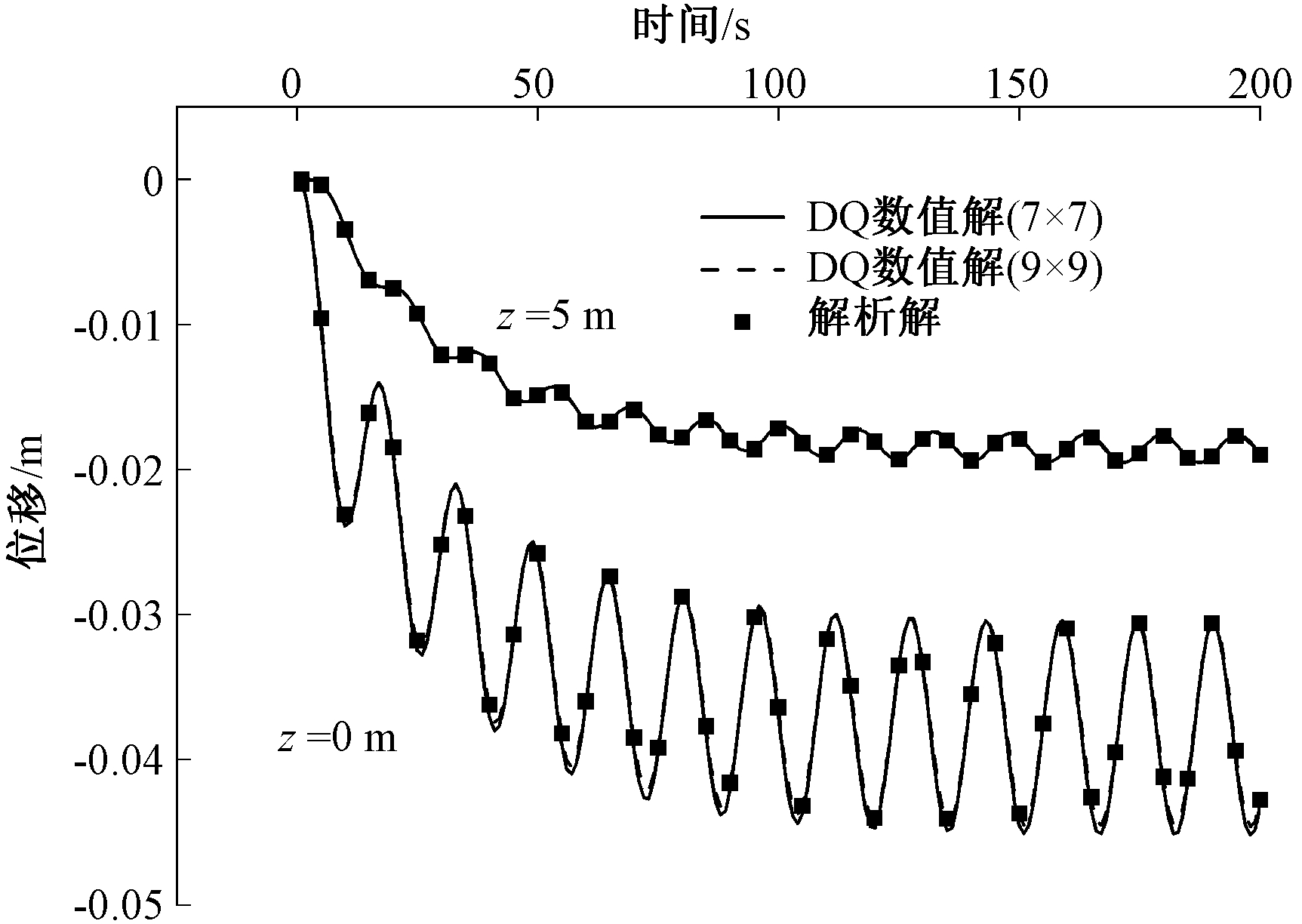
图3 位移时程曲线图(周期载荷)
Figure 3 Time-history curves of displacement
(cycle loading)
3.2 耦合系统的动力学特性分析
在热局部非平衡条件下，考察高(深)H0=10 m，宽L0=10 m的半平面域，边界条件由式(5)给定。考察表面阶梯温度载荷φ(x,t)=φ0h(t)的影响，其中φ0=10 ℃，h(t)是Heaviside函数。计算中布点数为7×7，时间步长Δt=1 s，表面垂直外载q(x,t)=3 kN/m2，材料参数见表1。
3.2.1 达西渗透系数κF的影响
图4显示了在热局部非平衡条件下，达西渗透系数κF对半平面对称轴(x=0)处未知量uz、wz、p及θS和θF的影响。图4(a)表明随着时间的逐渐增加，沉降uz最终达到相同的稳定状态。κF较大时，初始阶段固结速度比热传导快，导致热体积膨胀不明显，所以半平面的沉降uz大。图4(b)表明相对流速wz的变化趋势。当系统趋于稳定时，相对流速wz趋于零。但在初始阶段，平面内部的流速小于上表面附近，并且κF较大时流速的峰值较大。图4(c) 表明孔隙压p随着时间由初始孔压逐渐至零，半平面上表面附近孔隙压的面内部快，同时孔隙压的消散速度随κF增大而增大。消散速度较平图4(d) 表明固相和液相的温度从上表面传播到半平面深处，并且逐渐到达至给定的表面温度，最终达到等温状态。由于在热局部非平衡条件下，流固两相之间的温度是不同的，在给定的参数下，固相温度高于流相温度，并且在初始阶段温差明显。同时，κF对变温θS和θF的影响很小。
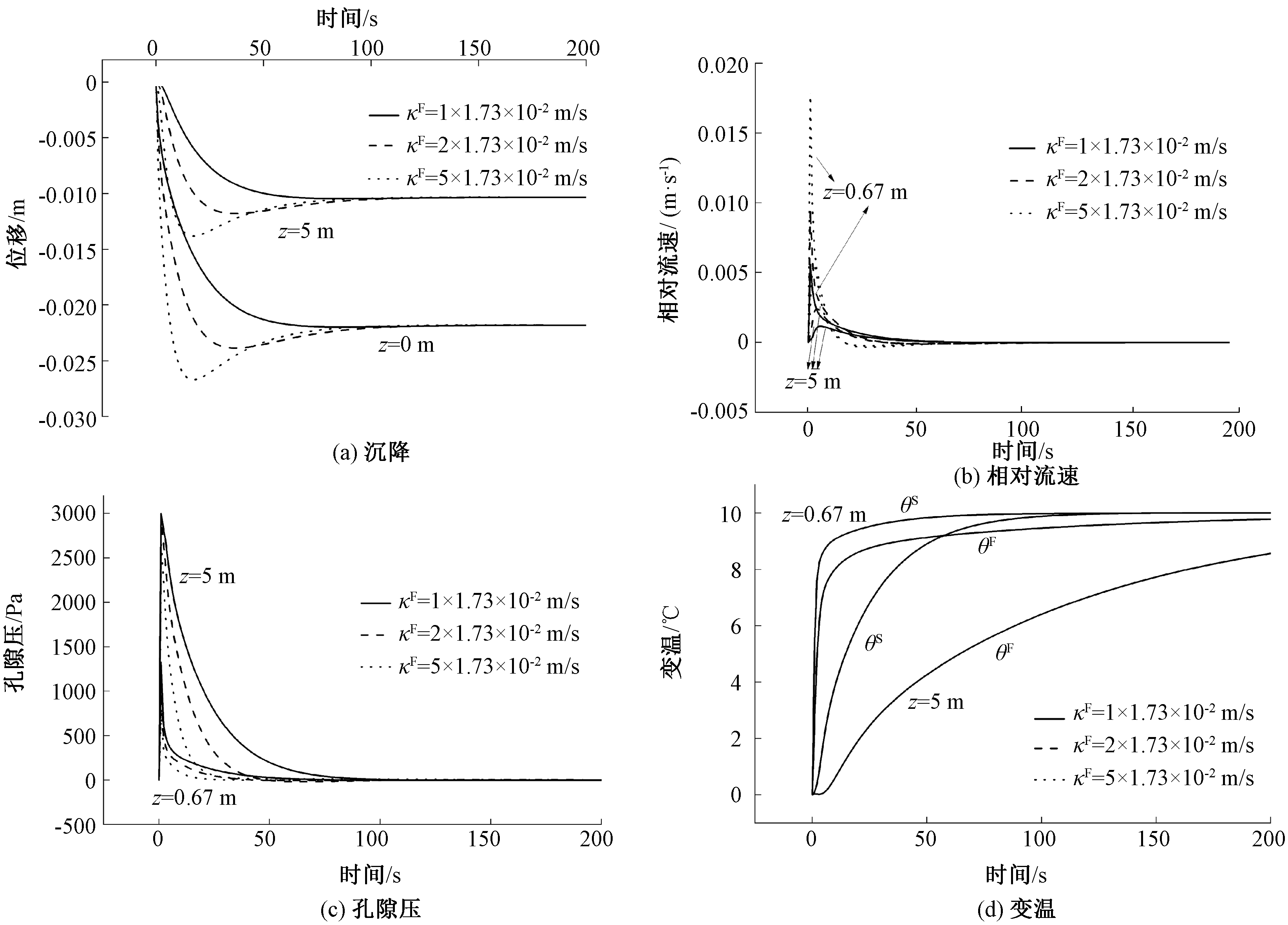
图4 达西渗透系数对半平面时-程曲线的影响
Figure 4 Effect of Darcy permeability coefficient on time-history curves of half-plane
3.2.2 热能交换系数eθ的影响
图5给出了在热局部非平衡条件下，不同物相之间热能交换系数eθ对半平面对称轴(x=0)处未知量uz及θS和θF的影响。同时，图5也给出了在热局部平衡条件下系统的时程曲线。在热局部非平衡条件下，随着eθ增大，固相温度降低并逐渐接近热局部平衡条件下系统的温度，而流相温度升高并逐渐接近热局部平衡条件下系统的温度，因此流固两相温差逐渐变小。另外，随着eθ增大，固相温度降低，在初始阶段系统热传导过程小于固结作用，沉降变大。
与此同时，笔者也考虑了热交换系数βS、βF和热传导系数kSS、kFF、kSF对半平面的影响。限于篇幅，仅列出结论如下：当热交换系数βS、βF较小时，流相和固相之间的耦合作用减弱，初始阶段半平面的沉降uz较大。当热传导系数kSS、kFF、kSF较大时，初始阶段时热传导比固结过程快，半平面的沉降uz较小，温度场达到等温状态所需的时间更短。
3.2.3 非线性的影响
图6给出了在热局部非平衡条件下，对称轴不同深度处沉降uz的几何非线性结果与相应的线性解的比较。可以看到，当载荷较小时(q(x,t)=3 kN/m2)，非线性解和线性解趋于一致。当载荷较大时(q(x,t)=30 kN/m2)，非线性解略大于线性解。
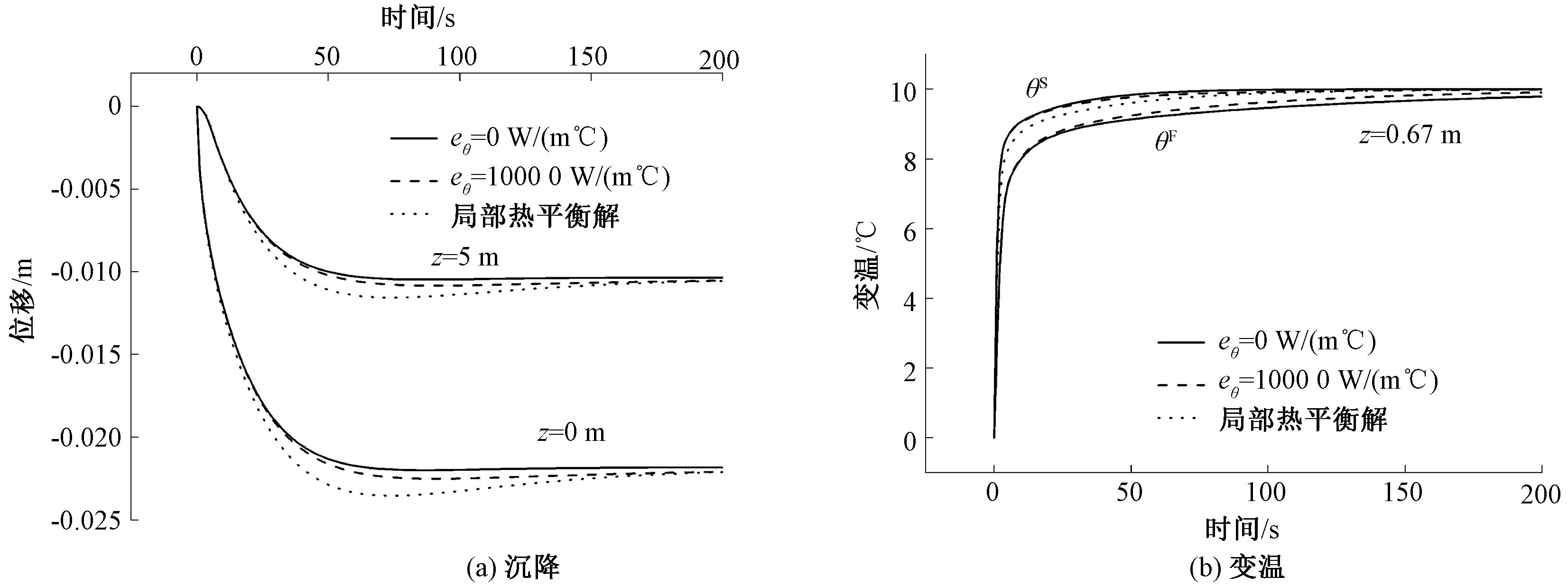
图5 热能交换系数对半平面时-程曲线的影响
Figure 5 Effect of energy exchange coefficient on time-history curves of half-plane
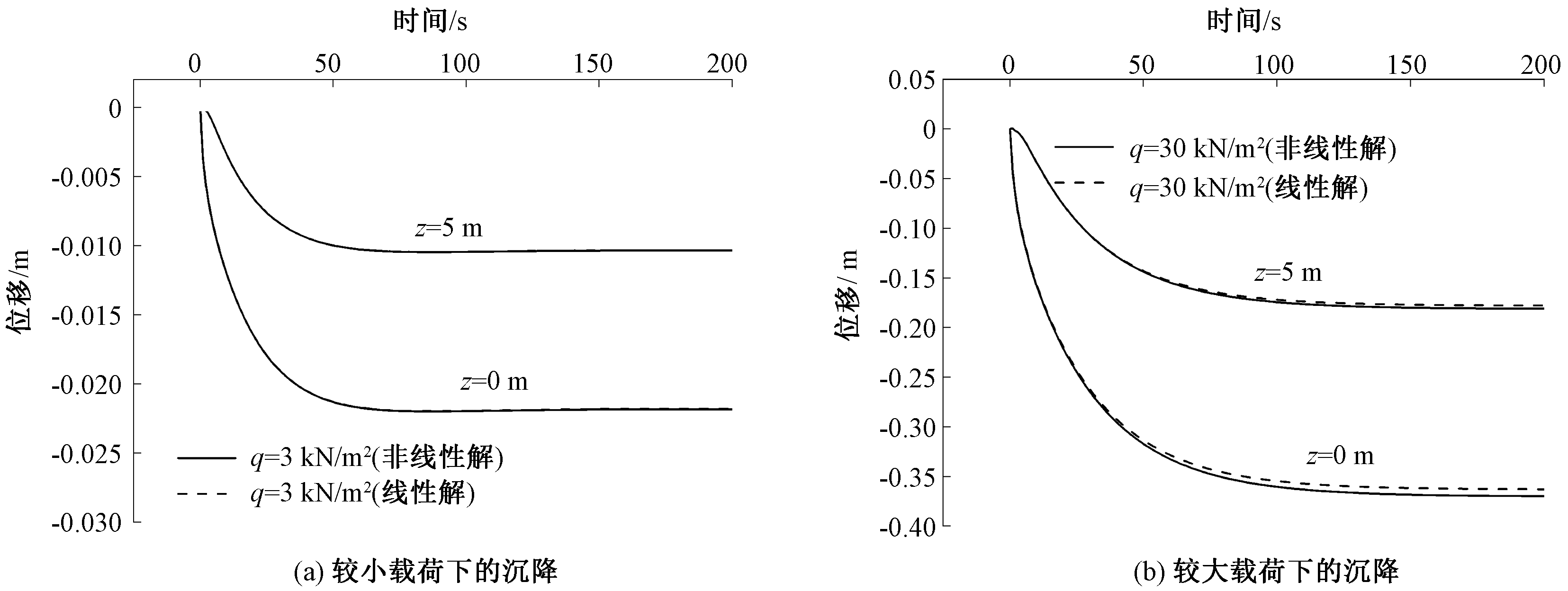
图6 非线性解与线性解的对比
Figure 6 Comparison between nonlinear solutions and linear solutions
4 结论
在几何非线性条件和热局部非平衡条件下，对流体饱和不可压多孔热弹性半平面在表面温度载荷作用下的动力学特性进行研究。首先基于PMT并考虑几何非线性和热局部非平衡的影响，给出了问题的数学模型；其次提出了一个系统的综合数值计算方法来模拟问题的数值结果，通过DQM和二阶后向差分格式分别在空间域和时间域离散数学模型，利用Newton-Raphson法求解非线性代数方程组，从而可得到问题的数值结果，分析半平面的动力学特性。
和现有解析解的对比研究验证了本文方法是正确可靠的，具有精度高、计算量小、数值稳定等优点。在此基础上，研究了在表面温度载荷作用下半平面的热力学特性，考察了系统的材料参数以及几何非线性对半平面动力学特性的影响，获得了一些有益的结论。
[1] BIOT M A.Theory of elasticity and consolidation for a porous anisotropic solid[J].Journal of applied physics, 1955,26(2):182-185.
[2] ZHOU Y,RAJAPAKSE R K N D,GRAHAM J.A coupled thermoporoelastic model with thermo-osmosis and thermal-filtration[J].International journal of solids and structures, 1998,35(34/35):4659-4683.
[3] 白冰.循环温度荷载作用下饱和多孔介质热-水-力耦合响应[J].工程力学,2007,24(5):87-92.
[4] 毕苏萍,时刚,高广运.饱和地基上铁路交通引起的地面振动分析[J].郑州大学学报(工学版),2010,31(3):73-76.
[5] De BOER R.Theoretical poroelasticity:a new approach[J].Chaos,solitons & fractals, 2005,25(4):861-878.
[6] De BOER R,EHLERS W,LIU Z F.One-dimensional transient wave propagation in fluid-saturated incompressible porous media[J].Archive of applied mecha-nics, 1993,63(1):59-72.
[7] HEIDER Y,MARKERT B,EHLERS W.Dynamic wave propagation in infinite saturated porous media half spaces[J].Computational mechanics, 2012,49(3):319-336.
[8] DE BOER R,KOWALSKI S J.Thermodynamics of fluid-saturated porous media with a phase change[J].Acta mechanica, 1995,109(1/2/3/4):167-189.
[9] HE L W,JIN Z H.A local thermal nonequilibrium poroelastic theory for fluid saturated porous media[J].Journal of thermal stresses, 2010,33(8):799-813.
[10] YANG X. Gurtin-type variational principles for dynamics of a non-local thermal equilibrium saturated porous medium [J]. Acta mechanica solida sinica, 2005, 18(1): 37-45.
[11] 朱媛媛,胡育佳,程昌钧,等.基于DQM的空间轴对称流体饱和多孔热弹性柱体动力学特性研究[J].振动与冲击,2017,36(23):83-91.
[12] BELLMAN R,CASTI J.Differential quadrature and long-term integration[J].Journal of mathematical analysis and applications, 1971,34(2):235-238.
[13] BELLMAN R,KASHEF B,CASTI J.Differential quadrature:a technique for the rapid solution of nonlinear partial differential equations[J].Journal of computational physics, 1972,10(1):40-52.
[14] 程昌钧,朱正佑.微分求积方法及其在力学应用中的若干新进展[J].上海大学学报(自然科学版),2009,15(6):551-559.
[15] 聂国隽,仲政.用微分求积法求解梁的弹塑性问题[J].工程力学,2005,22(1):59-62,27.