0 引言
类脑智能一直都是人工智能和机器人领域的研究重点。目前,已经出现的具有仿生机制的计算方法主要有蚁群算法[1]、神经网络算法[2]、遗传算法[3]、粒子群算法[4]等,这些方法都存在任务确定、离线学习、智能扩展性差、无法适应多变的环境等局限。针对这些缺点,受人脑神经系统、记忆机能及其信息加工机制的启发,研究人员提出了多种生物启发的认知计算模型,为实现更高层的认知和突破传统方法的局限提供了重要的研究思路。
Shanahan[5]将全局工作空间理论与内部模拟相结合,模拟人脑基底神经节、杏仁体、丘脑皮质等结构,构建了外部世界交互的外层回路和系统内部高层回路。Weng等[6]提出了自主心智发育的概念,构建了SAIL和Dav这2个人形机器人。Dirafzoon等[7]模拟螳螂的行为建立了可学习未知环境拓扑信息的模型,应用于机器人导航,验证了模型的高效性。Liu等[8]从情景记忆和生物启发的注意力系统的角度解决了机器人行为选择问题。Kawamura等[9]基于仿生发育机理提出一种大脑启发神经结构与空间认知和导航的计算模型,利用类海马电路存储目标位置,回忆出现的类似视觉模式,使机器人自主移动到目标位置。Islam等[10]提出一种基于拓扑的地图框架,实现了机器人在智慧城市中的自主导航,并且具有很高的决策效率和灵活的可操作性。针对动态环境中机器人的导航问题,Olcay等[11]设计了一种多机器人协作的导航框架,通过多个机器人的信息共享,为每个机器人找到一条合理的无碰撞路线,准确到达目标。Zeng等[12]提出一种贝叶斯吸引网络模型,模拟哺乳动物空间记忆回路的头朝向细胞和网格细胞的神经编码机制,通过积分单元和校准单元之间的竞争动力学来解决冲突,在室内和大型室外环境中均具有出色的性能。这些方法都在一定程度上解决了机器人导航问题,但都不具备通用性。为了找到一种通用的计算模型,Weng[13]通过对认知科学与神经生物学的研究,提出了一种类脑仿生计算模型,称为发育网络。
本文模型在发育网络的基础上进行改进。将发育网络内部的神经元个数以及连接由静态改为动态,模拟大脑皮层内部神经元的可塑性与再生功能。添加短时记忆区,模拟人脑长时记忆和短时记忆相互协调机理。机器人在执行任务时,利用状态转移机制不断地更新和积累知识。在非任务过程,机器人将自主学习到的环境和决策数据迁移到发育网络成为长时记忆。通过门限自组织机制确定网络中哪些神经元发生侧向激励,最后产生新的连接并记忆新的知识,实现与人类相似的自主学习与发育。网络的运行过程分为在线的自主探索学习过程和线下的非任务过程。在线探索过程主要进行新知识的短期记忆和学习,非任务过程主要进行更改或产生新的连接及短期记忆转为长期记忆。
1 算法原理
1.1 发育网络结构
发育网络[14-16]是一种模拟人脑发育规律的神经网络,最简单的发育网络结构示意图如图1所示。输入层模拟人类的感知系统,可以感知任何模态的信息,如视觉,听觉,味觉或触觉等;隐含层连接输入层和输出层,类似人类的大脑,指挥输出层输出相应的动作。输出层对应于人类的肌肉或腺体,直接与外界接触执行动作。
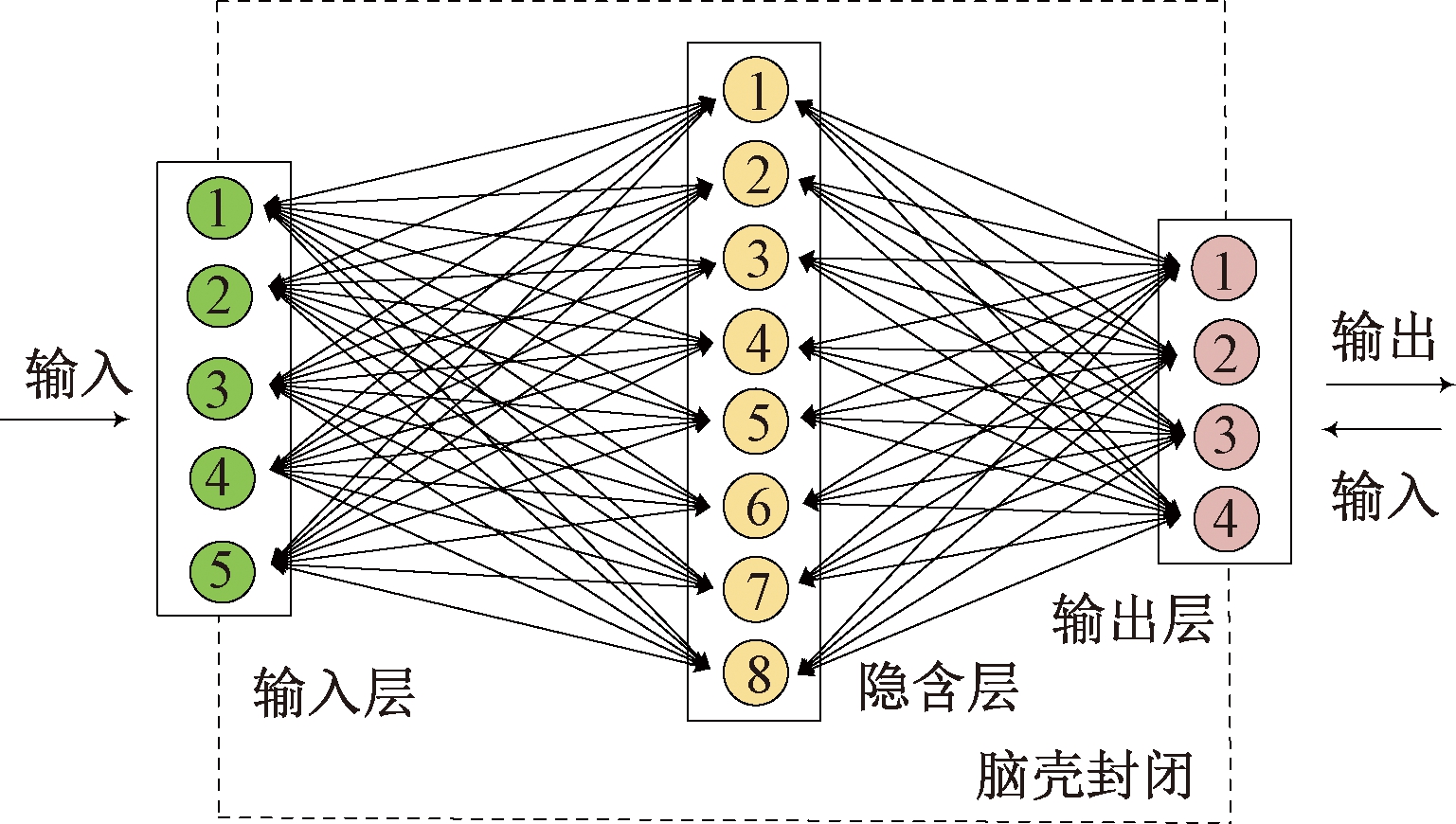
图1 最简单的发育网络结构示意图
Figure 1 Schematic diagram of the simplest developmental network structure
发育网络中,层与层之间均为静态或动态的双向连接。网络运行过程中,可根据需要对不同层之间的权值连接进行动态调节。但原始发育网络功能有限,对新环境的适应性较差。针对这些问题,对网络的结构和运行机理进行了改进。
图2为改进的发育网络结构图。输入层与隐含层、隐含层与输出层均为双向连接。若神经元之间连接权重为1,则表示2个神经元建立连接;若连接权重为0,则表示2个神经元之间没有连接。
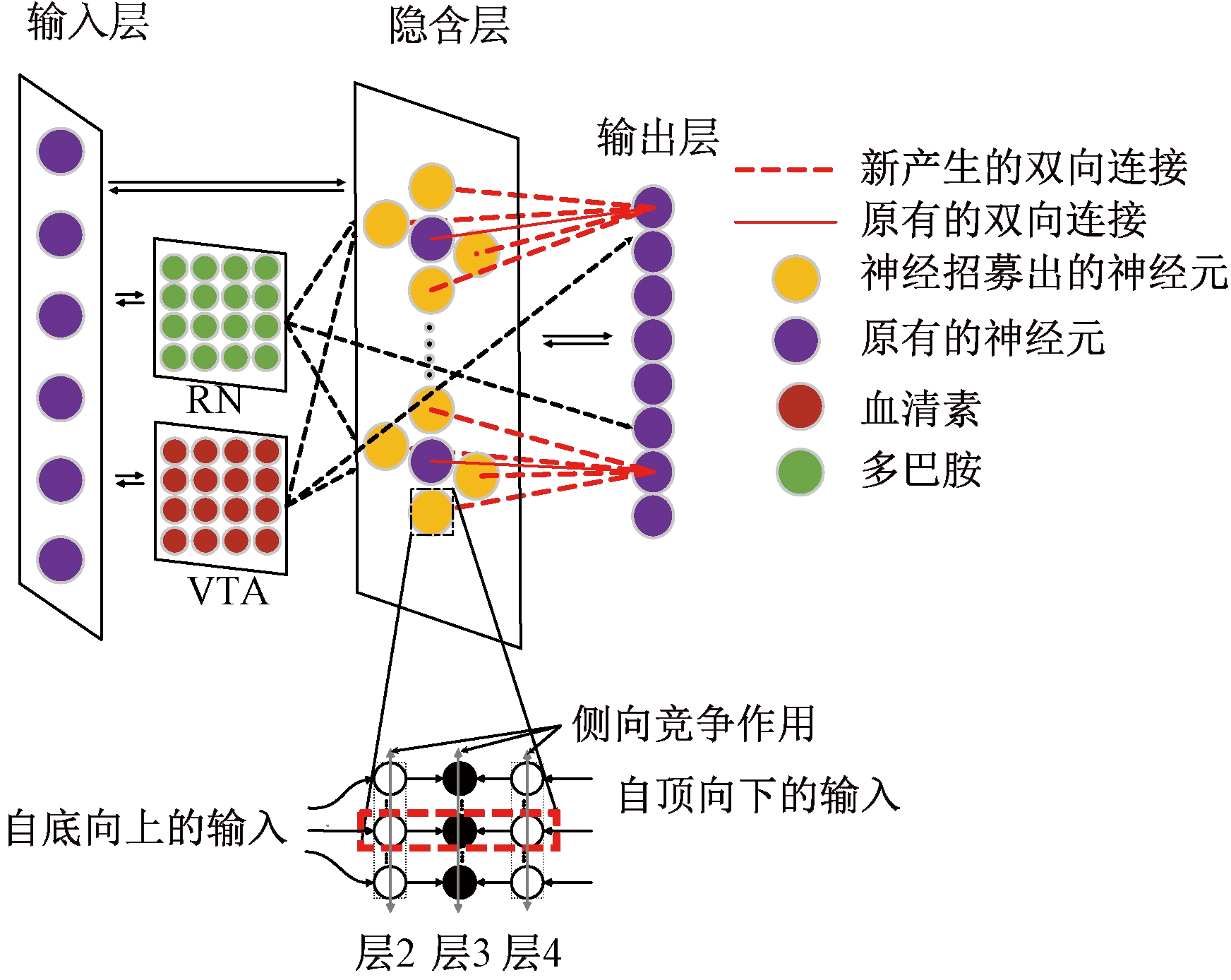
图2 改进的发育网络结构图
Figure 2 Improved developmental network structure diagram
从图2可以看出,神经元之间的连接有3种:输入层到隐含层、隐含层到输出层的连接称为自底向上的连接;由输出层到隐含层的连接称为自顶向下的连接;隐含层内的横向连接代表侧向竞争作用。红色矩形方框内的3个神经元是隐含层某一个神经元的放大图,层2和层4是功能层,依次处理自底向上的输入和自顶向下的输入。血清素来源于脑干中缝核(RN)释放的神经递质,与人所厌恶的动作有关,作用于几乎所有前脑区域,在网络中,具有惩罚作用。多巴胺来源于腹侧被盖区(VTA)或黑质致密部,与人所偏好或喜欢的动作有关,在网络中,具有奖励作用。这2种神经递质对网络的输出有微调作用。
1.2 网络计算
在时刻ta=0,设A={X,Y,Z}, N={V,G},V代表神经元的权重信息,G代表神经元的年龄信息。X、Y、Z分别表示输入层、隐含层、输出层的信息。
在时刻ta=1,2,…,n,对网络3个区域重复进行如下2个步骤。
步骤1 计算区域函数f:
(r′,N′)=f(b,t,N)。
(1)
式中:b和t分别为计算区域中响应向量为r时的自底向上和自顶向下的输入;r′、N′为更新后的变量。
步骤2 进行更新:N←N′,r←r′。
若X为智能体的传感器接口,那么x∈X,x一直处于被外界监督的状态;若Z为智能体的执行器接口,当且仅当在“教师”选择的情况下,Z才会处于被外界监督状态,如果不能被外界“教师”选择,Z会给出执行器的输出。只有当X、Y、Z至少都更新一次以后,整个发育网络才完成一次更新过程。
下面讨论区域函数f。A中的任一神经元有权值向量v=(vb,vt),对应区域的输入(b,t)。隐含层不仅有自底向上的输入b,还有自顶向下的输入t。隐含层中每一个神经元激活之前,要计算其能量值:
(2)
为模拟区域隐含层的侧向竞争机制,前k个获胜的神经元(前k个神经元的能量最大)被激活并进行更新。本文只考虑k=1,被激活的神经元可通过式(3)得到辨识:
(3)
式中:c为隐含层神经元的个数;vbi为隐含层第i个神经元自底向上的权重向量;vti为隐含层第i个神经元自顶向下的权重向量,计算得出第j个神经元的能量值最大,从而被激活。被激活神经元发放yj=1,其余神经元不发放。对于某个神经元,只有其前突触作用和后突触作用同时被激活,该神经元才能被激活,此时神经元的突触向量产生突触增益yjp,p为输入。其他没达到激活能量的神经元保持初始状态不变。激活后的神经元产生连接关系,随后其权值将被更新。当某个神经元j被激活后,它的权值更新依据Hebbian规则:
vj←ω1(nj)vj+ω2(nj)yjp。
(4)
式中:ω2(nj)为学习率,与神经元激活的次数有关;ω1(nj)为保持率。ω1(nj)+ω2(nj)=1,ω2(nj)的最简单形式是ω2(nj)=1/nj。输入p采样均值的递归计算方法:
(5)
式中:t′i为神经元的激活时间,神经元每激活一次,年龄增加1,有nj←nj+1。机器人在运动过程中受到血清素和多巴胺2种神经递质的调节,分别用奖励和惩罚来模拟2种神经递质的作用,β、α分别为惩罚值和奖励值, 机器人的决策方向与惩罚、奖励的方向的合成便是机器人最终的运动方向。
z=zi+αe1+βe2。
(6)
式中:z为最终决策方向;zi为智能体根据已学到的知识做出的决策;e2为奖励方向的单位向量;e1为惩罚方向的单位向量。
1.3 状态转移机制
在人类感知环境过程中,在第1个环境下训练感知任务,若将其放置在与第1个环境有相似特征的第2个环境下,通过认知学习机制,将导致学习效果迁移到第2个环境,这个过程称为状态转移。
研究表明,感知学习与决策相关的高级区域内的神经元活动变化相关联[17]。人脑在感知环境过程中,可以在线学习认知事物,并将自己记忆的环境和得出的决策变成短时记忆,在无外界输入信号也无对外输出时,仍可以进行回忆、推理、整理和保存短时记忆。如此反复,将短时记忆转换为长时记忆。模拟这种工作机理,使机器人在进行环境探索的过程中在线学习认知,此时发生状态转移,在执行任务的间隙或非工作状态下,即无感知信息输入和对外动作输出时,进行数据迁移,将感知到的环境位置信息与相应的决策建立关联。在后续的环境认知中,遇到类似的环境信息时,机器人可以做出比上次更好的决策,无须重新学习。
当发生状态转移时,在神经网络中会产生新的知识,该知识表现为环境和动作的组合信息。该组合是否正确、是否最佳,需要通过评价机制来决定,最终转换为长期记忆的知识均为最佳的组合。机器人在环境中运行时,不可避免会遇到未学习过的环境,因而做出的决策很差,此时会触发在线认知学习过程。将环境信息转化为输入信息p,神经元权重向量为v,计算环境信息与网络中记忆的环境信息的相似度:
(7)
当相似度低于设置的某一值时,说明是未学习过的环境,需要重新认识该环境并做出一个好的决策,此时由评价机制来决定决策的好坏。如在机器人导航任务中,评价机制:非工作状态下确定最佳运动方向时,在当前状态S1=(x1,x2,…,xn)下选择不撞上障碍物的行为决策为a,这导致机器人发生状态转移,机器人所处状态变为![]() 机器人达到最终目的的状态为
机器人达到最终目的的状态为![]() 通过式(8)计算转移后的状态S2和S的曼哈顿距离Ds来评价决策a,给状态S1下的决策空间A1=(a1,a2,…,an)中的每个决策一个差距评价,选出差距最小的作为状态S1下的最佳决策。
通过式(8)计算转移后的状态S2和S的曼哈顿距离Ds来评价决策a,给状态S1下的决策空间A1=(a1,a2,…,an)中的每个决策一个差距评价,选出差距最小的作为状态S1下的最佳决策。
(8)
其中,x1,x2,…,xn在不同的领域所代表的意义不同,状态中的元素个数及意义人为确定。例如在导航应用中,可使用x1和x2为智能体的横纵坐标。
状态转移机制可大幅减少训练需要的标记样本。在导航应用中,用F表示机器人决策方向,L表示环境信息(机器人、障碍物、目标的相对位置关系),不同的L和F代表不同的状态。图3中A代表的是源域,在源域的训练任务为源任务,B为目标域,C为目标任务。源域和目标域的特征空间不同但又存在相似特征,机器人在源域中进行训练,获得经验,将经验转移到另一种具有相似特征的目标域,源域和目标域具有相似的特征L,而具有不同的F,源域和目标任务具有相同的特征F,但具有不同的特征L。即从L1F2的学习效果转移到了L1F8和L2F2。
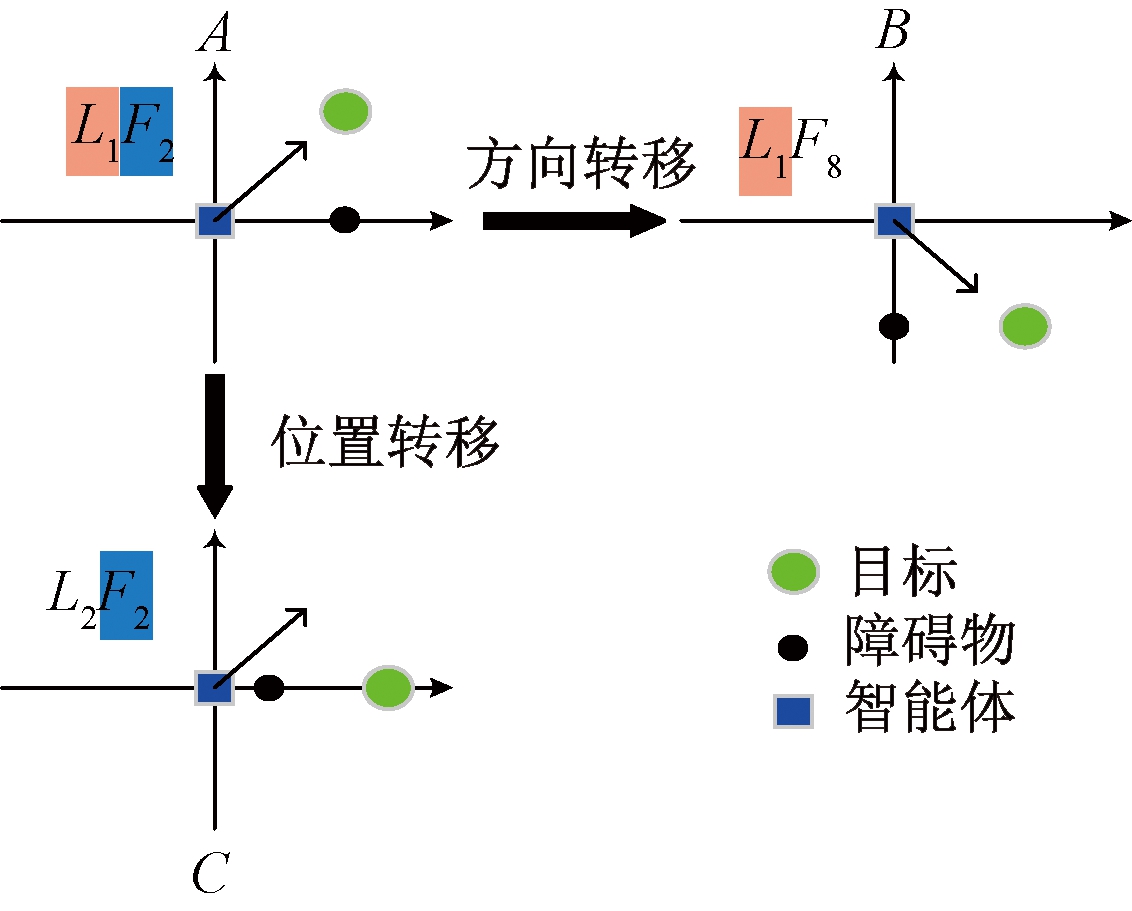
图3 状态转移示意图
Figure 3 Schematic diagram of state transition
智能体每一步都根据已经记忆的知识做出决策,因此,实际的位置情况和识别出来的位置情况是有差别的。假设实际输入向量x={x1,x2,x3,x4,x5,x6},输入网络后,根据top-k竞争法则,隐含层获胜神经元被激活,它的权重信息w={w1,w2,w3,w4,w5,w6},此时的识别误差为
(9)
设m为机器人在某环境下到达目标的过程中感知范围内有障碍物时步数的累加,则智能体完成整个复杂任务的平均识别误差为
(10)
式中:ψ表示环境最大直径与步长的比值;φ′表示平均识别误差,φ′越小,任务完成得越好,反之则越差。
1.4 非任务过程
非任务过程是指网络不关注任何刺激或任务时的神经交互,用来模拟当不关注或没有感知输入时候的大脑内部神经活动。这个过程是否改变网络连接取决于网络最近的经验。
当机器人处于空闲状态或执行任务结束后,进入数据处理非任务状态。在工作结束后,与该任务相关的大脑区域仍存在神经活动,该区域中被激活频率高的神经元在一段时间内仍保持着活跃状态,并且被重新激活的概率也高,这可能是由神经递质扩散引起的,例如活跃神经元释放的去甲肾上腺素[18]。这种机制减轻了人在执行任务时大脑的数据处理量。在智能体一次运动结束后进行非任务过程,如果没有其他神经元在同一概念区域内放电,则概念神经元(代表特定概念的输出层神经元)在非任务过程中触发的概率被建模为一个单调增长函数。
(11)
(12)
式中:nZi为输出层第i个神经元的激活次数;NZ为输出层神经元的激活次数总和。按照激活概率大小排序,激活前k个概率高于设定的阀值的输出层神经元,假设有4个神经元概率高于阀值,概率从大到小排序为pnr1、pnr3、pnr2、pnr5,则进入4次循环,依次进行反向输入数据、激活隐含层神经元、侧向激励、保存数据、建立新的连接。如第1次循环,输出层到隐含层的输入为[1,0,0,0,0,0,0,0],计算隐含层神经元响应,根据top-k竞争法则,激活前k个神经元(这些被激活的隐含层神经元均是属于第1类,即方向1的神经元,即只与输出层第1个神经元有连接且它们的能量值均为1),将这些神经元进行能量值缩放:
(13)
式中:ri为第i个神经元的能量值;k为激活的神经元总数。这些被激活的神经元发生侧向激励,激发出更多的神经元用于记忆新的知识,侧向激励的激活范围如图4所示。
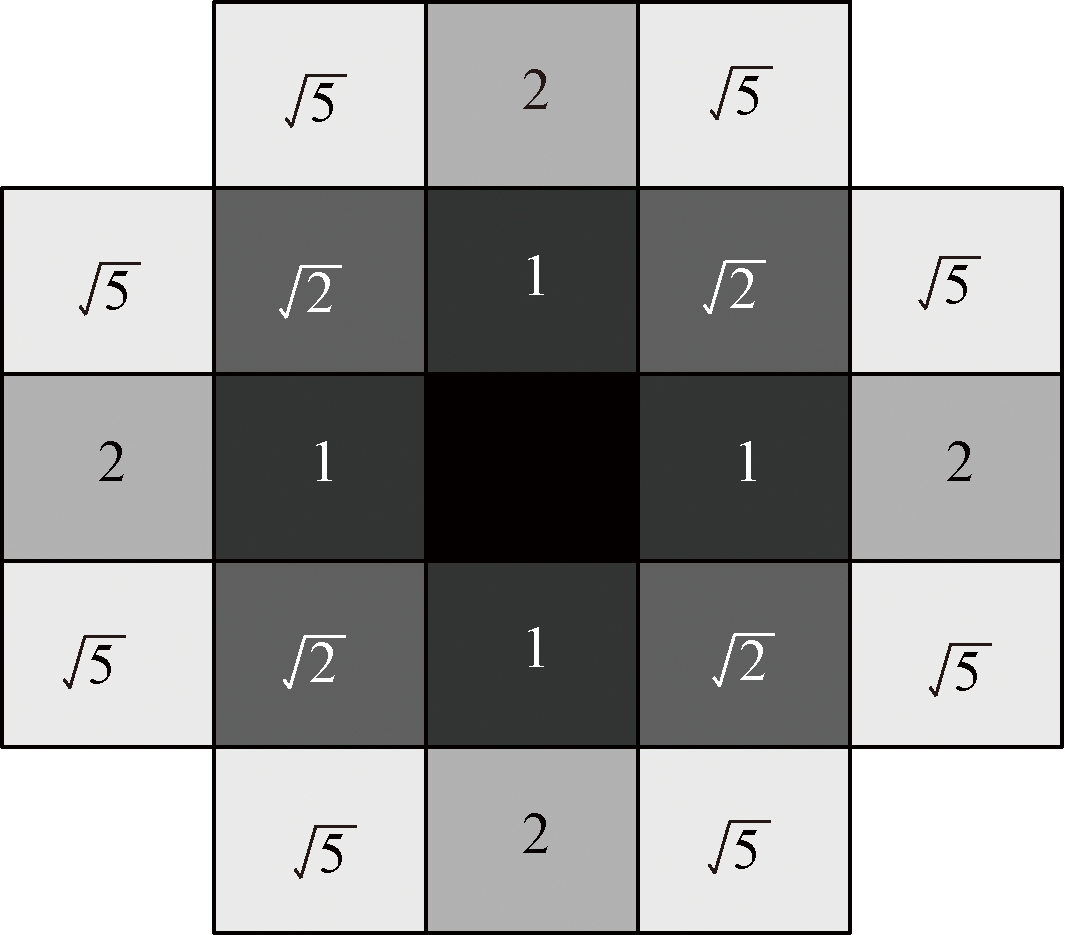
图4 侧向激励范围
Figure 4 Lateral excitation range
图4中每个方格代表1个神经元,里面的数字表示与激活神经元的距离,颜色越深代表激发出的神经元能量值越大,反之,则越小。侧向激励出的神经元能量值为
(14)
式中:r′ij表示第i个神经元激发出的第j个神经元;ri表示最初激活的第i个神经元。然后将隐含层所有神经元按照能量值大小排序,依次将上次测试运行过程中遇到的实际的未训练过的位置数据保存进激活的神经元中年龄为1的神经元,之后年龄加1(选择年龄为1的神经元可防止数据覆盖),然后将激发出的且保存了知识的隐含层神经元与输出层神经元建立连接,短时记忆变为长时记忆。
2 结果与分析
2.1 实验参数
根据输入向量的大小,设置了输入层6个神经元,隐含层10 000个神经元,输出层8个神经元。输出层的神经元分别代表8个行走方向。将输入层到隐含层、隐含层到输出层的权重向量初始化为0~1的随机数,从输出层到隐含层的权重向量初始化为0,隐含层和输出层每个神经元赋予年龄为1。输入的环境信息为
(15)
如图5所示,以智能体(小车)为坐标原点建立坐标系,θf表示由原点到目标的线段与x轴的夹角,θe表示由原点到障碍物的线段与x轴的夹角,df表示目标和智能体距离,de表示障碍物和智能体的距离。
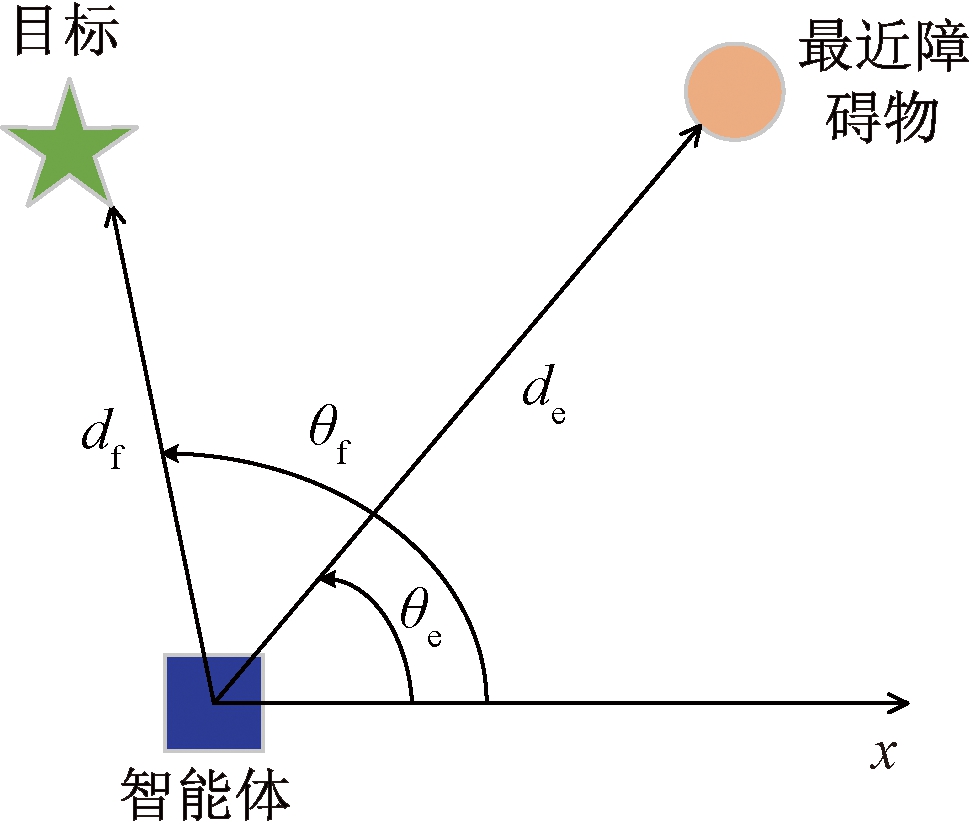
图5 相对位置示意图
Figure 5 Relative position diagram
2.2 结果与分析
启动小车之后,在MATLAB上训练控制小车的发育网络。 图6(a)为真实环境中小车的位置,图6(b)为与图6(a)对应的智能小车运行过程在RViz中的监控界面。图6(b)和实际的智能小车的运行路径一致,实时在电脑端显示智能小车的运动状态以及智能小车感知到的环境。

图6 机器人运行场景
Figure 6 Real scene of robot operation
在MATLAB上监控智能小车的实际位置,将智能小车的实际运行轨迹在MATLAB上进行绘制,智能小车5次运行路径图如图7所示。蓝色正方形代表智能小车,黑色形状代表实际环境中的障碍物,目标点为绿色五角星所在位置。
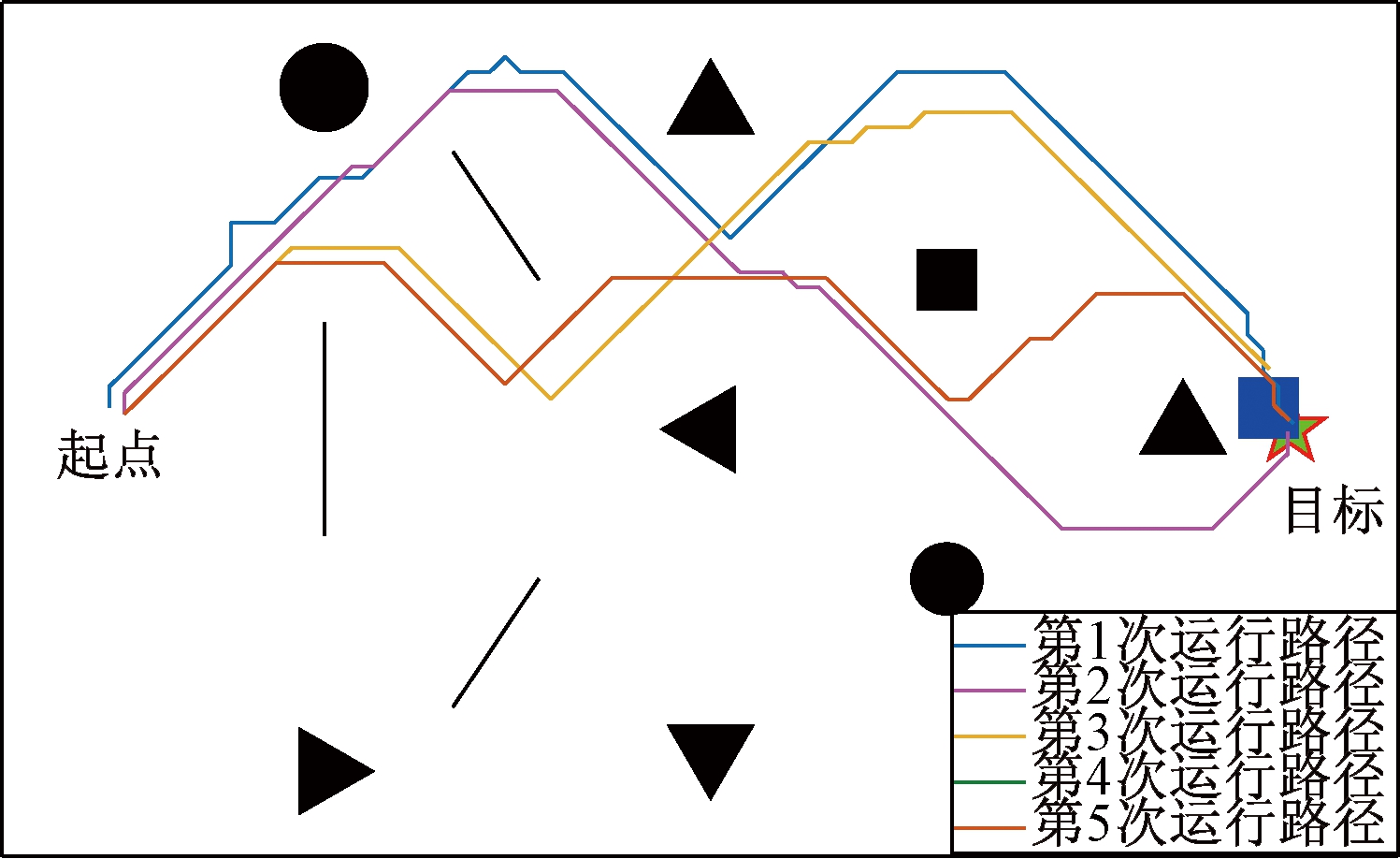
图7 智能小车运行轨迹
Figure 7 Smart car running track
由图7可以看出,由于机器人每次运行结束后都发生了状态转移,学习到了新的知识,所以每次运行的轨迹有所不同,智能体对路径所做出的调整趋于好的方向,到第4次和第5次时路径重合,网络做出的决策已不会再发生改变。
智能小车在环境中运行的各项数据如表1所示。由表1可以看出,随着运行次数的增加,智能小车所走的步数越来越少,知识量越来越多,平均识别误差也越来越小,最终趋于稳定。这也表明,智能小车在每次运行完,都进行了线下过程的转移学习,最终发生了位置环境的转移,学习到了更多新的环境信息,并可以做出一个好的决策。
表1 实验结果
Table 1 Test results
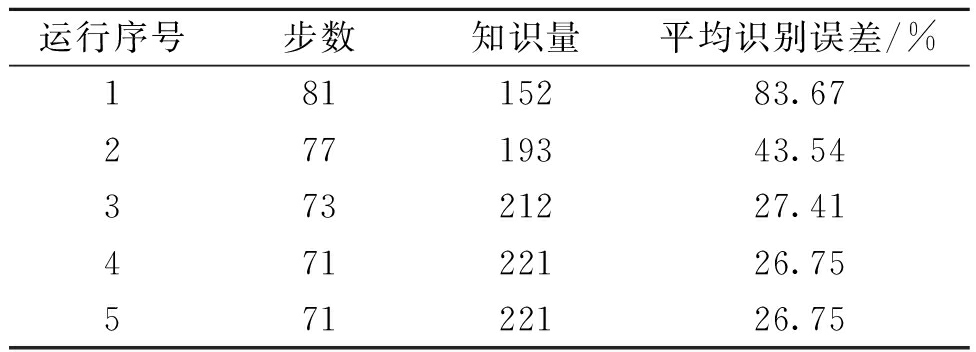
运行序号步数知识量平均识别误差/%18115283.6727719343.5437321227.4147122126.7557122126.75
2.3 对比实验
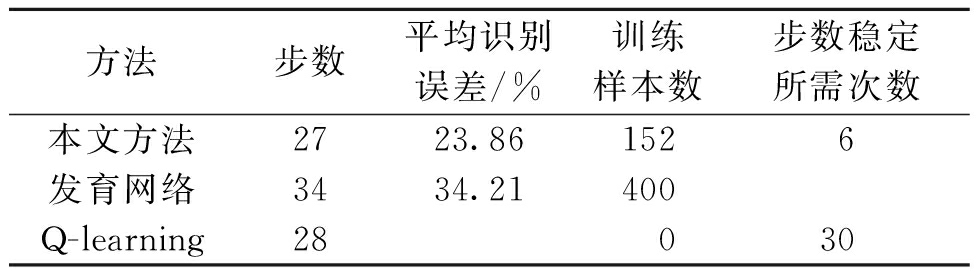
图8为所走的路径对比。在图8所示的仿真环境下用不同的方法来实现导航,路径对比见表2。表2中的步数表示学习或者训练完成之后的最终步数。平均识别误差表示在环境中的最终误差情况,由式(9)、(10)计算得出。由表2中数据可以得出,本文方法和Q-learning算法的路径相对较短,且与Q-learning方法得出的步数相差不大,虽然Q-learning不需要训练样本,但达到稳定状态的耗时较长,需要30次步数才稳定,而本文方法仅需要6次。由于Q-learning维护的是1张Q表,无法计算平均识别误差。发育网络算法的路径比较长,且不具有连续学习能力,所需训练样本多,每次运行都会选择一样的路径。因此,本文方法综合性能较好。
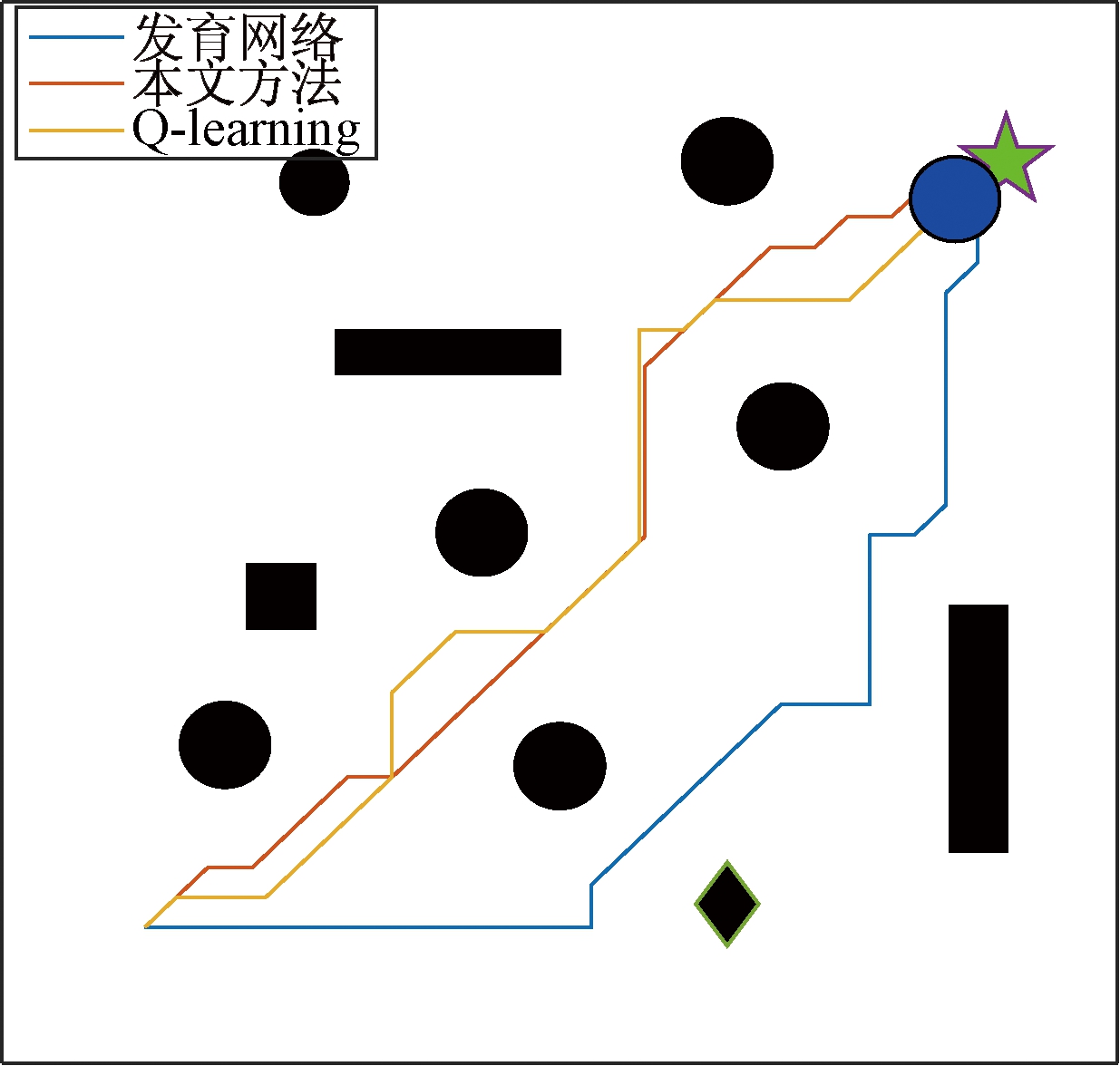
图8 路径对比
Figure 8 Path comparison
表2 不同方法结果对比
Table 2 Comparison of different methods
方法步数平均识别误差/%训练样本数步数稳定所需次数本文方法2723.861526发育网络3434.21400Q-learning28030
3 结论
本文提出一种仿生的机器人行为决策认知计算模型。该模型通过改进原始发育网络的结构,并增加非任务过程的运行机制,以及状态转移的方法,使改进的发育网络可以通过半监督的方法实现行为决策,克服了传统行为决策方法存在的未知环境适应性差以及针对不同环境需要重新编程等问题。未知环境下的自主机器人导航结果表明,本文方法在未知环境中经过3~5次的决策调整即可收敛到稳定状态,且决策效果不断改善。机器人可以通过不断积累知识应对各种复杂环境,在未知环境中具有很强的适应性。
目前的研究只考虑了距离智能体最近的障碍物的影响,只能保证局部的决策效果,所提模型难以保证整体的决策效果,考虑智能体感知范围的所有障碍物对智能体行为决策的影响是下一步研究的重点。
[1] 常玉林,汪小渟,张鹏.改进蚁群算法在交通分配模型中的应用[J].郑州大学学报(工学版),2017,38(2):41-44,49.
[2] 蔡婉贞,黄翰.基于BP-RBF神经网络的组合模型预测港口物流需求研究[J].郑州大学学报(工学版),2019,40(5):85-91.
[3] PATLE B K,PARHI D R K,JAGADEESH A,et al.Matrix-binary codes based genetic algorithm for path planning of mobile robot[J].Computers & electrical engineering,2018,67:708-728.
[4] 徐霜,万强,余琍.基于学习理论的改进粒子群优化算法[J].郑州大学学报(工学版),2019,40(2):29-34.
[5] SHANAHAN M.A cognitive architecture that combines internal simulation with a global workspace[J].Consciousness and cognition,2006,15(2):433-449.
[6] WENG J,MCCLELLAND J,PENTLAND A,et al.Artificial intelligence:autonomous mental development by robots and animals[J].Science,2001,291(5504):599-600.
[7] DIRAFZOON A,LOBATON E.Topological mapping of unknown environments using an unlocalized robotic swarm[C]//2013 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway:IEEE,2013:5545-5551.
[8] LIU D,CONG M,DU Y,et al.Robotic autonomous behavior selection using episodic memory and attention system[J].Industrial robot:an international journal,2017,44(3):353-362.
[9] KAWAMURA K,GORDON S.From intelligent control to cognitive control[C]//2006 World Automation Congress.Piscataway:IEEE,2006:1-8.
[10] ISLAM N,HASEEB K,ALMOGREN A,et al.A framework for topological based map building:a solution to autonomous robot navigation in smart cities[J].Future generation computer systems,2020,111:644-653.
[11] OLCAY E,SCHUHMANN F,LOHMANN B.Collective navigation of a multi-robot system in an unknown environment[J].Robotics and autonomous systems,2020,132:103604.
[12] ZENG T P,TANG F Z,JI D X,et al.Neuro bayes SLAM:neurobiologically inspired bayesian integration of multisensory information for robot navigation[J].Neural networks,2020,126:21-35.
[13] WENG J.Artificial intelligence:autonomous mental development by robots and animals[J].Science,2001,291(5504):599-600.
[14] SCASSELLATI B.Theory of mind for a humanoid robot[J].Autonomous robots,2002,12(1):13-24.
[15] WANG D S,WANG J H,LIU L.Developmental network:an internal emergent object feature learning[J].Neural processing letters,2018,48(2):1135-1159.
[16] WANG D S,XIN J B.Emergent spatio-temporal multimodal learning using a developmental network[J].Applied intelligence,2019,49(4):1306-1323.
[17] TAKEDA M.Brain mechanisms of visual long-term memory retrieval in primates[J].Neuroscience research,2019,142:7-15.
[18] SOLGI M,LIU T S,WENG J Y.A computational developmental model for specificity and transfer in perceptual learning[J].Journal of vision,2013,13(1):1-23.