0 引言
近年来,随着智能电网的快速发展,大量的非线性负载和冲击性负荷的增加,导致电流、电压发生畸变,电网的稳定性受到影响。精密的仪器设备对供电质量要求更高,实现电能质量扰动准确的检测,对改善和提高电能质量具有重要的意义。
目前国内外常用的电能质量扰动检测方法仍存在不少问题亟待解决,例如,短时傅里叶变换(short-time Fourier transform,STFT)在处理非平稳信号时,选择窗的固定性导致分辨率单一;采用S变换求取的S矩阵的冗余信息过多,干扰了特征的提取,影响了信号识别精度[1-2];而小波变换(wavelet transform, WT)中若不能保证基函数和分解尺度选取合适,则不能确保获得极佳的结果[3-4]。相较而言,希尔伯特-黄变换(Hilbert-Huang transform, HHT)更成熟,HHT具有很好的自适应性,很多极端情况均可适用,然而其不足之处在于会发生端部失真,产生模态混叠、虚假分量等相关弊端[5-6]。很多学者采用改进HHT的方法进行电能质量扰动的检测,其中胡雷等[6]采用移动平均法改进HHT算法,通过对HHT变换得到的幅频参数进行平滑处理,减小了其波动,实现电能质量扰动的检测,但容易发生模态混叠和端点效应的现象。最近几年变分模态分解(variational modal decomposition, VMD)被广泛地应用到信号处理中,其中黄传金等[7]提出了一种基于VMD的电能质量扰动检测新方法,VMD方法既可以处理不同时间支集的电能质量扰动信号,也可以分析频率相近的谐波和复合扰动,同时也避免了模态混叠的现象,得到的瞬时幅频分析结果更加精确,但VMD参数特征的选取主要依靠经验选取;罗亦泳等[8]对VMD参数选取进行了改进,提出采用最大相关系数法优化k值的选取方法,并将其运用到桥梁的固有频率和阻尼系数的识别,判断由于温度、多路径等环境因素导致桥梁发生的变化。
本文提出了一种基于能量收敛因子与粒子群优化(particle swarm optimization, PSO)的变分模态分解和希尔伯特变换(variational modal decomposition and Hilbert transform, VMD-HT)的电能质量扰动检测方法。其不仅避免了HHT容易发生模态混叠的缺陷,通过能量收敛因子和PSO自适应地选择最优的VMD参数k和α的值,电能质量扰动检测的精度、抗干扰性和容错能力都得到了有效的提高。
1 变分模态分解及改进
1.1 VMD算法原理
VMD算法的实质是将信号分解过程转变为求解变分问题的过程,将输入实值信号f分解为k个单分量调幅-调频的固有模态函数(intrinsic modal function, IMF)uk (t)。相应变分问题的目标函数把k个模态估计带宽之和最小且模态之和等于f作为约束条件,其数学模型表达式如下[9-10]:
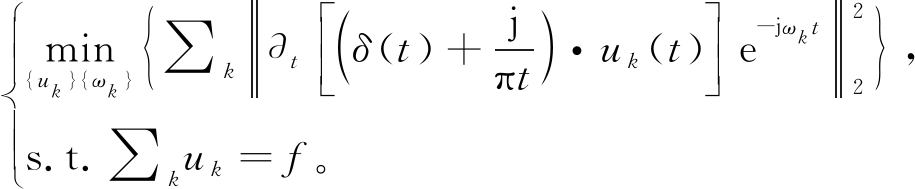
(1)
式中:δ(t)为狄拉克函数;ωk(t)、uk(t)分别为第k个IMF分量的中心频率、模态函数。
引入二次惩罚因子α和Lagrange乘数λ,构建Lagrange方程,如式(2)所示,求取式(1)最优解。
(2)
Lagrange方程采用交替方向乘子法(alternating direction method of multipliers,ADMM),不断迭代更新![]() 寻求该函数的最优
寻求该函数的最优![]() 的数学表达式为:
的数学表达式为:
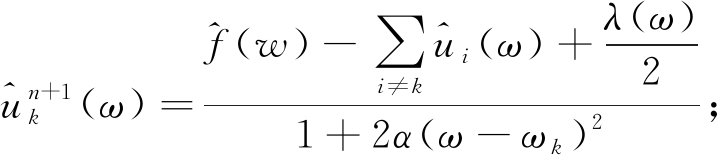
(3)
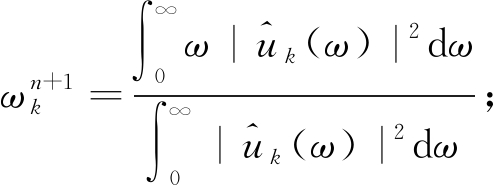
(4)
(5)
式中:^表示傅里叶变换;τ为保真系数;n为迭代次数。
VMD算法步骤如下:
步骤1 初始化![]() 和n(n=0);
和n(n=0);
步骤2 n←n+1,并由式(3)和式(4)更新![]() 和ωk;
和ωk;
步骤3 由式(5)更新![]() 的取值;
的取值;
步骤4 重复步骤2和步骤3,当式(6)满足时,停止迭代,输出结果,得到k个模态分量及其中心频率。
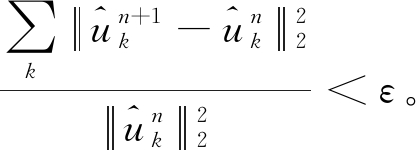
(6)
1.2 基于能量收敛因子确定k值
由于电能质量扰动检测点环境的不确定性,分解模态的个数k值很难确定最优值,这对VMD分解的自适应性和效果具有很大的影响。为了解决模态分量k值选取的问题,本文构造了能量收敛因子来确定VMD分解中的IMF分量k的个数,相邻k值分解后的余量与原始能量比值的差值满足阈值的条件,此时VMD分解相对完全,避免了频率相近造成的过分解和欠分解的现象。能量收敛因子计算过程即通过VMD算法将原始信号s分别分解为m个IMF分量与m+1个IMF分量,将信号分解为m个IMF的余量与s的能量的比值称为Em,将信号分解为m+1个IMF的余量与s的能量的比值称为Em+1,则Δmm+1=Em-Em+1,Δmm+1为能量收敛因子,其数学表达式如下:
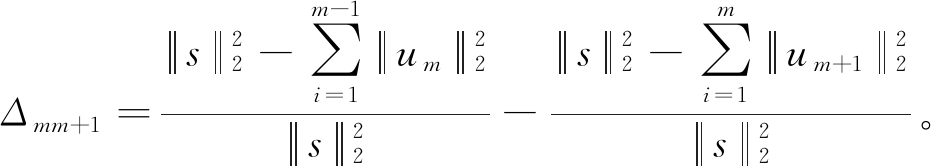
(7)
通过分析多组扰动信号的实验结果,本文阈值η取0.02。详细实现过程如下:
步骤1 初始化模态分量个数值m=1;
步骤2 运用VMD分解原理将原始信号分别分解为m和m+1个模态分量;
步骤3 分别计算模态分量个数为m和m+1的余量能量和原始信号s的能量;
步骤4 代入式(7),得能量收敛因子Δmm+1的值,并更新VMD算法分解的模态分量个数m=m+1;
步骤5 重复步骤2~4,直到达到能量收敛因子Δmm+1<η,迭代终止,即可自适应确定信号经过VMD算法分解的最优分解个数m=k。
1.3 基于PSO算法确定惩罚因子
惩罚因子α与分解的IMF分量的带宽成反比,α越小IMF带宽越大,相反α越大IMF带宽越小。PSO算法是一种群体随机搜寻、不断迭代寻优的过程,将个体粒子的极值与群体目前的最优解进行比较,通过不断地迭代和更新粒子的位置,获得全局的最优取值[12-13]。包络熵的大小用来评价信号的稀疏特性。通过对分解后每个模态分量进行处理,形成一个概率序列Pi,求出其熵值。信号x(i)的包络熵定义为:
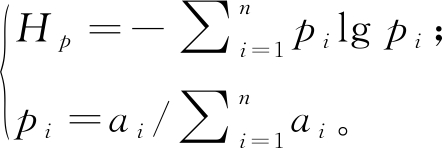
(8)
式中:a(i)为信号x(i)分解后的IMF分量经过Hilbert变换得到的包络信号。
经过VMD算法分解的模态分量中的噪音成分与包络熵的大小成正比,即噪音成分越多,包络熵越大;反之噪音成分越少,包络熵越小。不同粒子所处的不同位置代表惩罚因子α不同的取值,计算此时IMF分量的包络熵,即PSO的适应度函数,当包络熵具有最小值时,信号具有最佳的分解效果。因此将包络熵的最小值作为PSO算法在迭代寻优过程中的全局最优值。算法具体流程如图1所示。
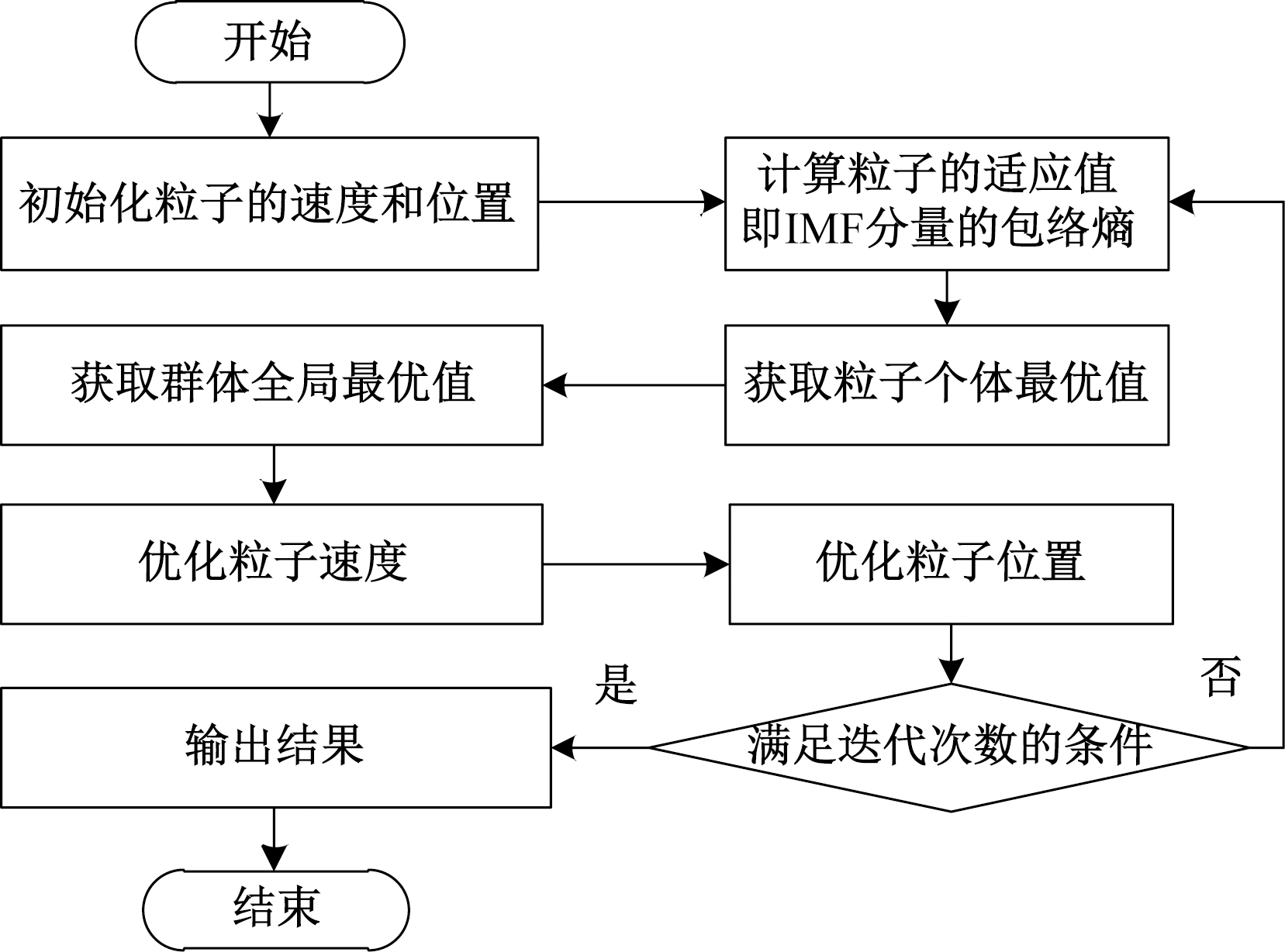
图1 PSO算法流程图
Figure 1 PSO algorithm flow chart
2 基于改进VMD-HT的电能质量扰动检测
首先对输入的电能质量扰动信号进行能量收敛因子的计算,确定k值;然后运用PSO优化算法确定惩罚因子α的取值,运用VMD算法将电能质量扰动信号x(t)分解成k个IMF分量之和;最后,通过Hilbert变换得到相应IMF分量的瞬时频率和瞬时幅值[14]。具体步骤如图2所示。
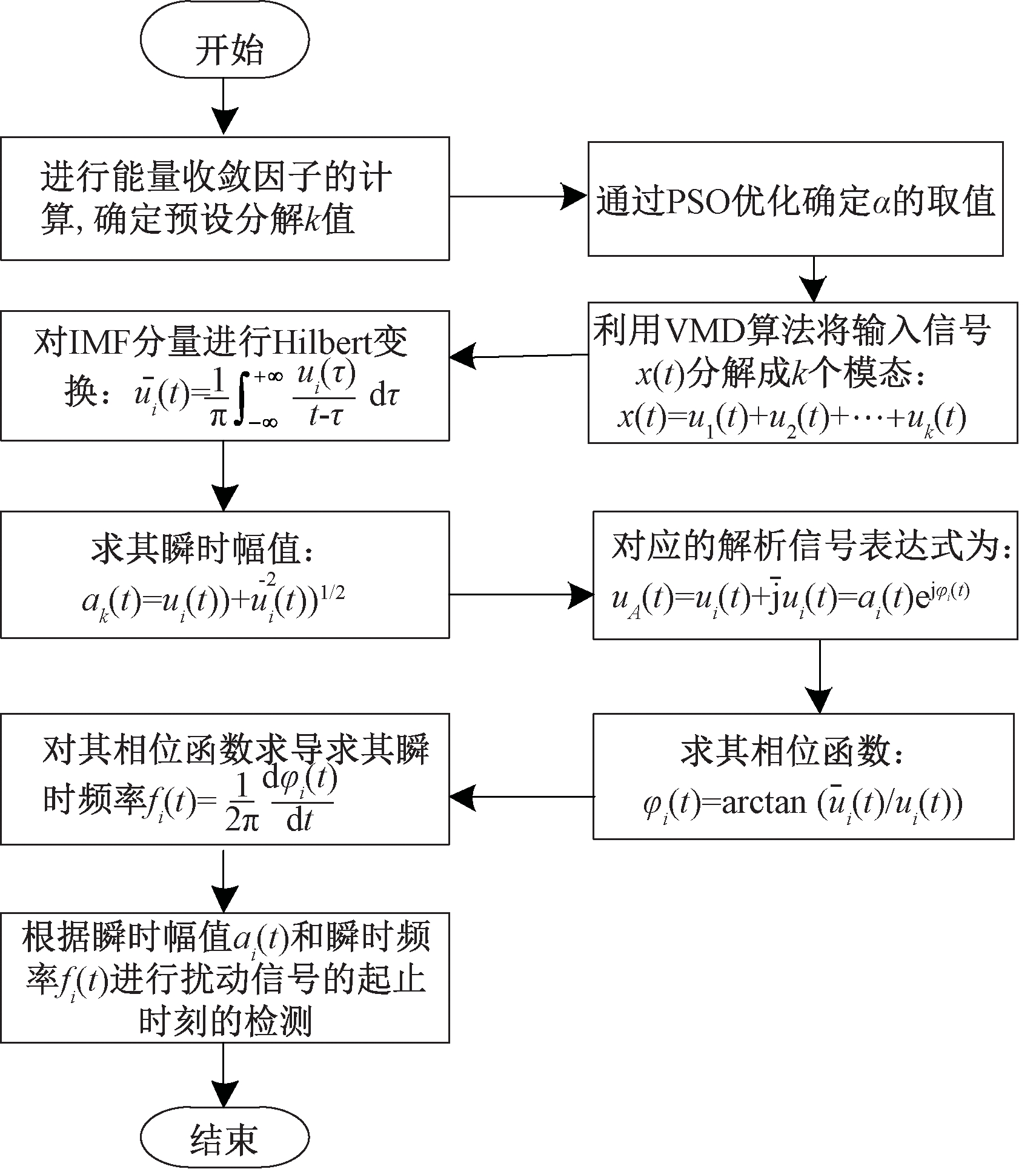
图2 改进VMD-HT算法流程图
Figure 2 Improved VMD-HT algorithm flow chart
3 仿真结果与分析
对电力系统中常见的单一电能质量扰动信号和复合扰动信号进行MATLAB仿真分析。电压暂降、中断等单一电能质量扰动信号构成简单,属于单一分量信号,本文直接进行Hilbert变换,分析其发生的起止时刻。暂态振荡、谐波等信号构成相对复杂,属于复杂分量信号,运用改进的VMD-HT对电能质量扰动进行检测,并将其与HHT检测结果进行对比分析。复合扰动信号其成分更加复杂,亦运用改进的VMD-HT对其进行扰动发生时刻的定位。
3.1 单一电能质量扰动
3.1.1 单一分量电能质量扰动
对某三相系统做仿真分析,其电压幅值为311 V、频率为50 Hz,采样频率f=1 000 Hz。设某一相的电压在0.15~0.25 s之间发生了电压暂降,其理想数学模型如式(9)所示,在0.2~0.3 s之间发生电压中断,其理想数学模型如式(10)所示。对单一分量电能质量扰动直接进行Hilbert变换,波形如图3、图4所示。其扰动发生的起止时刻(起始时刻t1、终止时刻t2)如表1所示。
(ε(t-0.15)-ε(t-0.25)))×cos ωt;
(9)
(ε(t-0.2)-ε(t-0.3)))×cos ωt。
(10)
表1 单一分量信号的检测误差分析
Table 1 Detection error analysis of single component signal

扰动类型理论值测量值t1/st2/sU/Vt1/st2/sU/V电压暂降0.1500.250190.00.1490.251195.8电压中断0.2000.3000.1990.300
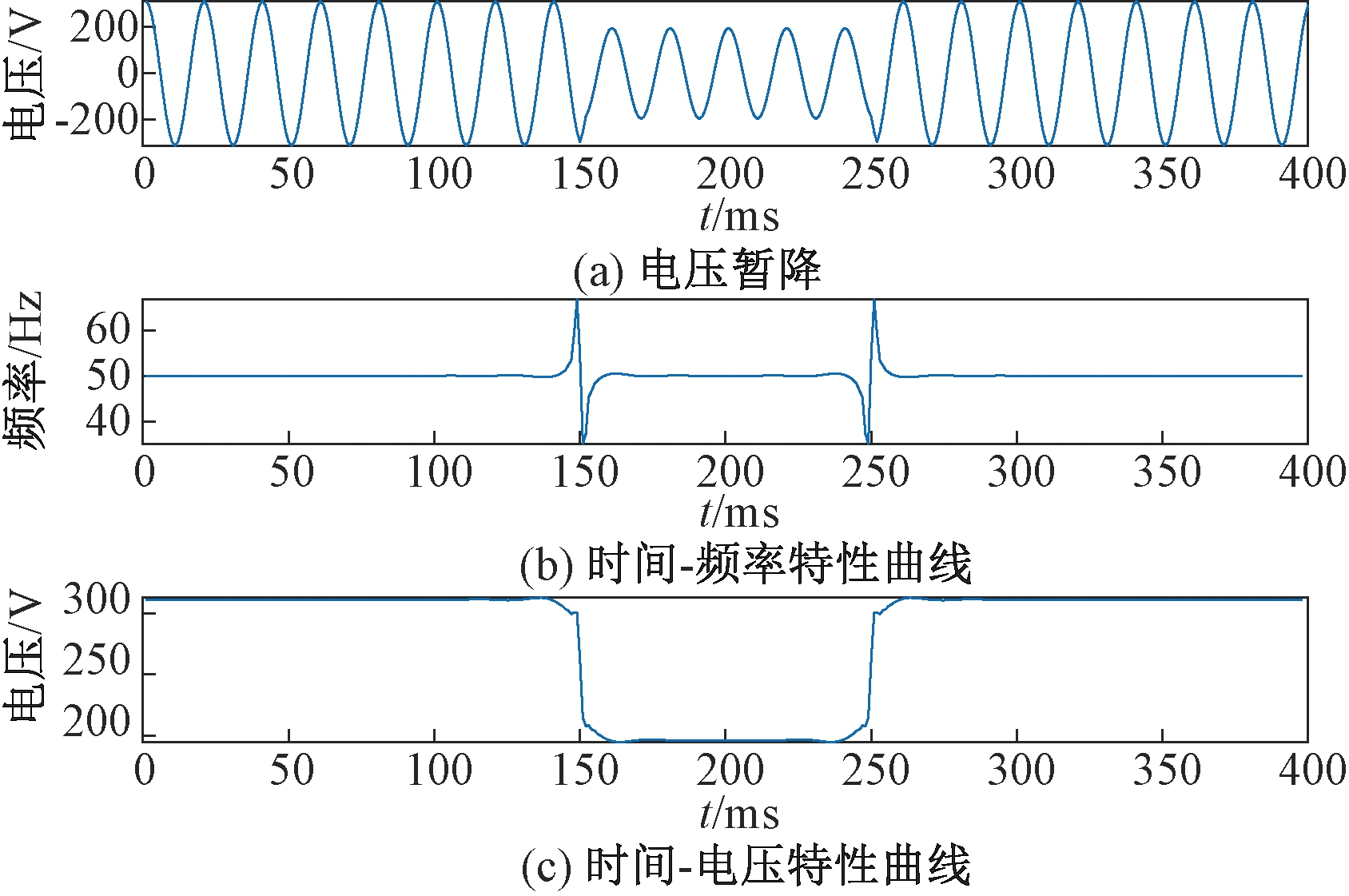
图3 电压暂降Hilbert变换
Figure 3 Voltage sag Hilbert transformation
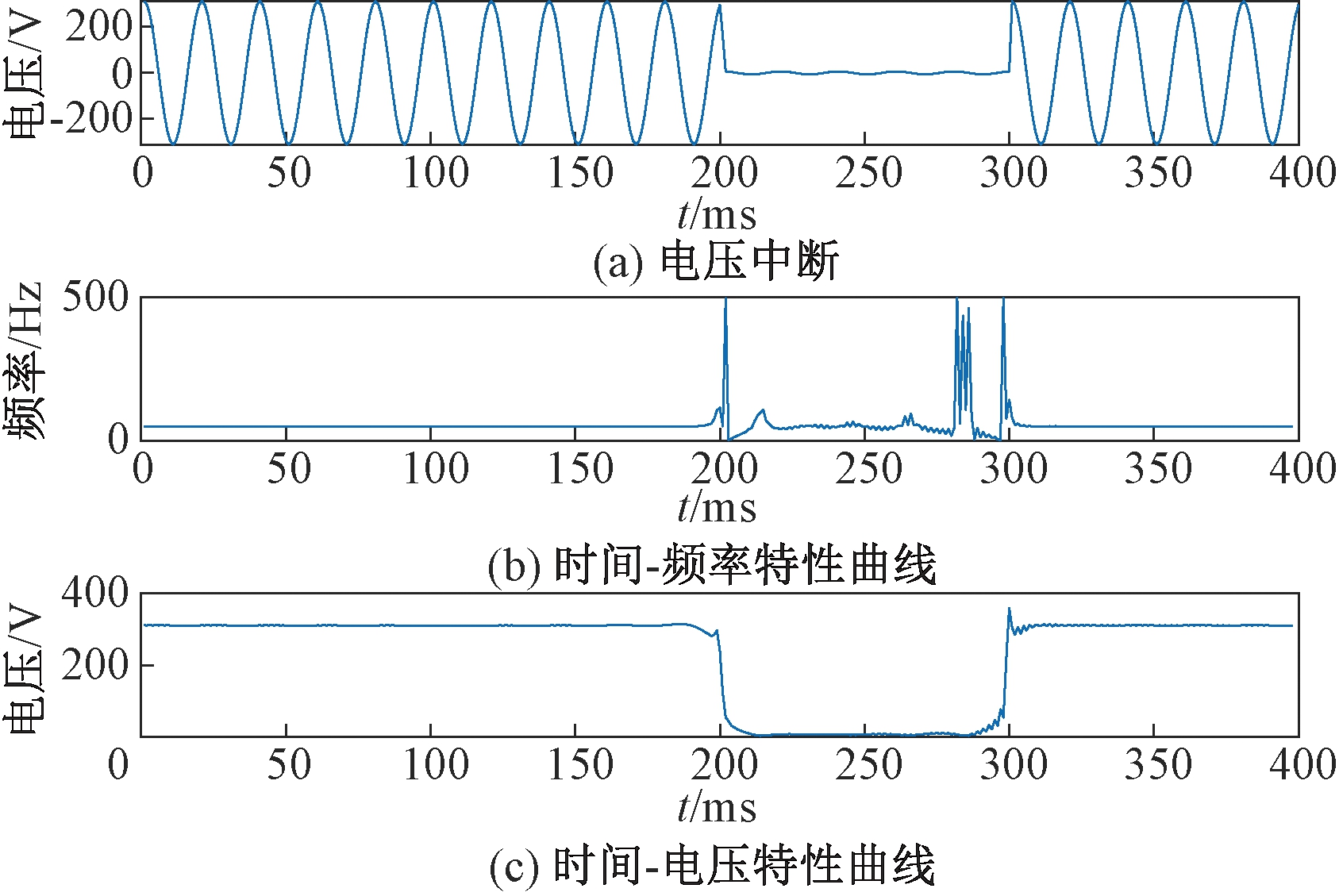
图4 电压中断Hilbert变换
Figure 4 Voltage interruption Hilbert transformation
3.1.2 复杂分量电能质量扰动
对于复杂分量的电能质量扰动,采用本文提出的能量收敛因子与PSO优化的VMD-HT进行检测,例如暂态振荡,其数学模型如下:
(ε(t-0.08)-ε(t-0.17))cos 3ωt)。
(11)
首先对暂态振荡扰动信号的分解模态个数k值进行确定,根据能量收敛因子的步骤计算出不同模态下Em的取值结果。当m=1、2、3,分别对应的Em取值为1、0.028 3、0.019 1。相邻模态的差值Δ12=0.971 7,Δ23=0.009 2<η,因此分解模态个数k值取2。
然后通过PSO算法对α取最优值,PSO参数种群个体数目N,学习因子C1、C2,最大迭代次数M,惯性权重最大值和最小值wmax、wmin,随机权重方差rande,其初始值设定如表2。
表2 PSO算法参数的初始值
Table 2 PSO algorithm parameter initialization
NC1C2Mrandewmaxwmin20022500.10.80.4
如图5所示,当迭代到第6代时,适应度函数趋于稳定并取到最小值,即包络熵最小,此时α=565 即原始信号经VMD算法分解效果最佳。
将暂态振荡扰动运用本文提出的改进VMD-HT电能质量检测方法进行仿真,其波形如图6、图7所示。
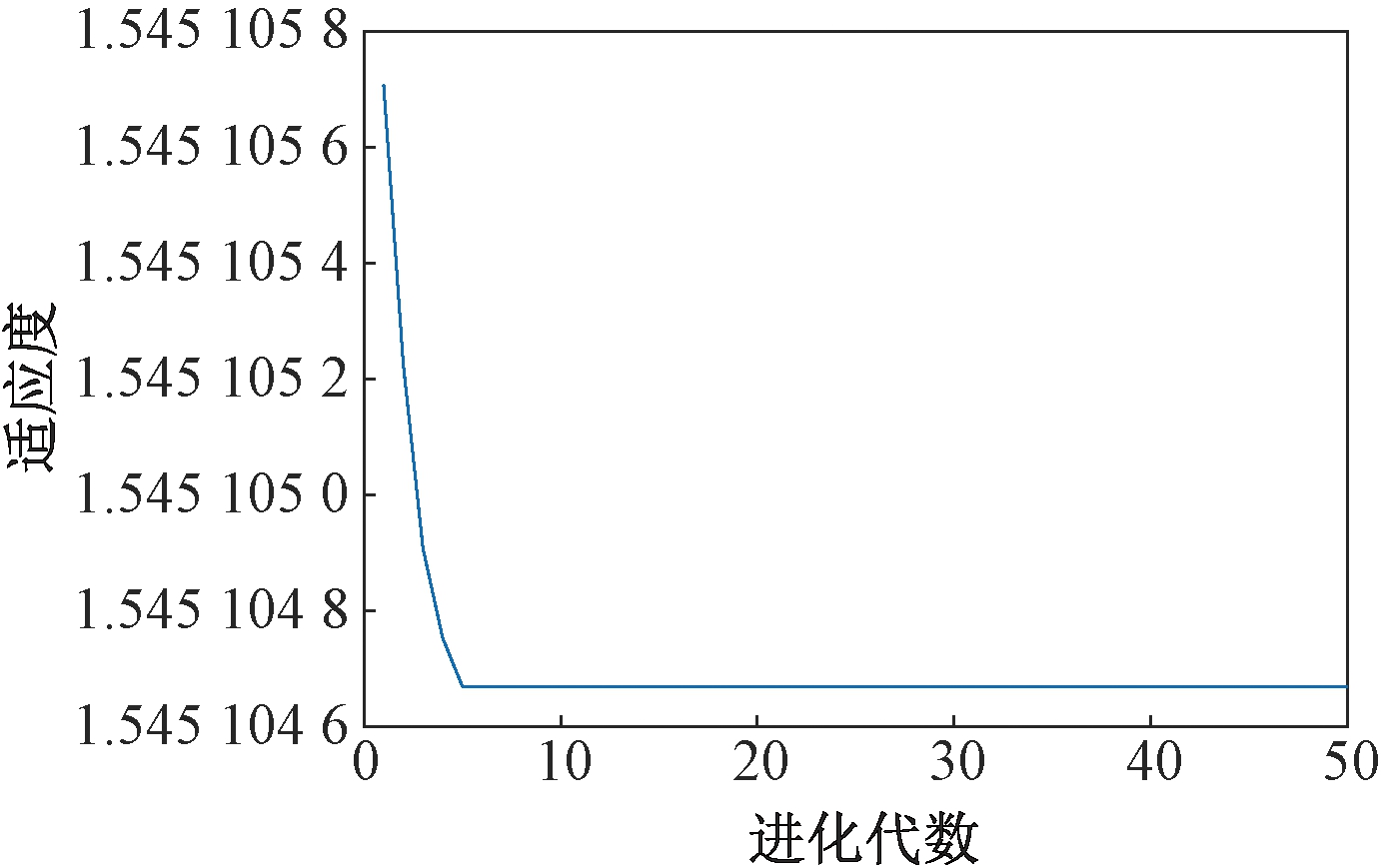
图5 暂态振荡适应度值随迭代变化图
Figure 5 Transient oscillation fitness value iterative change graph
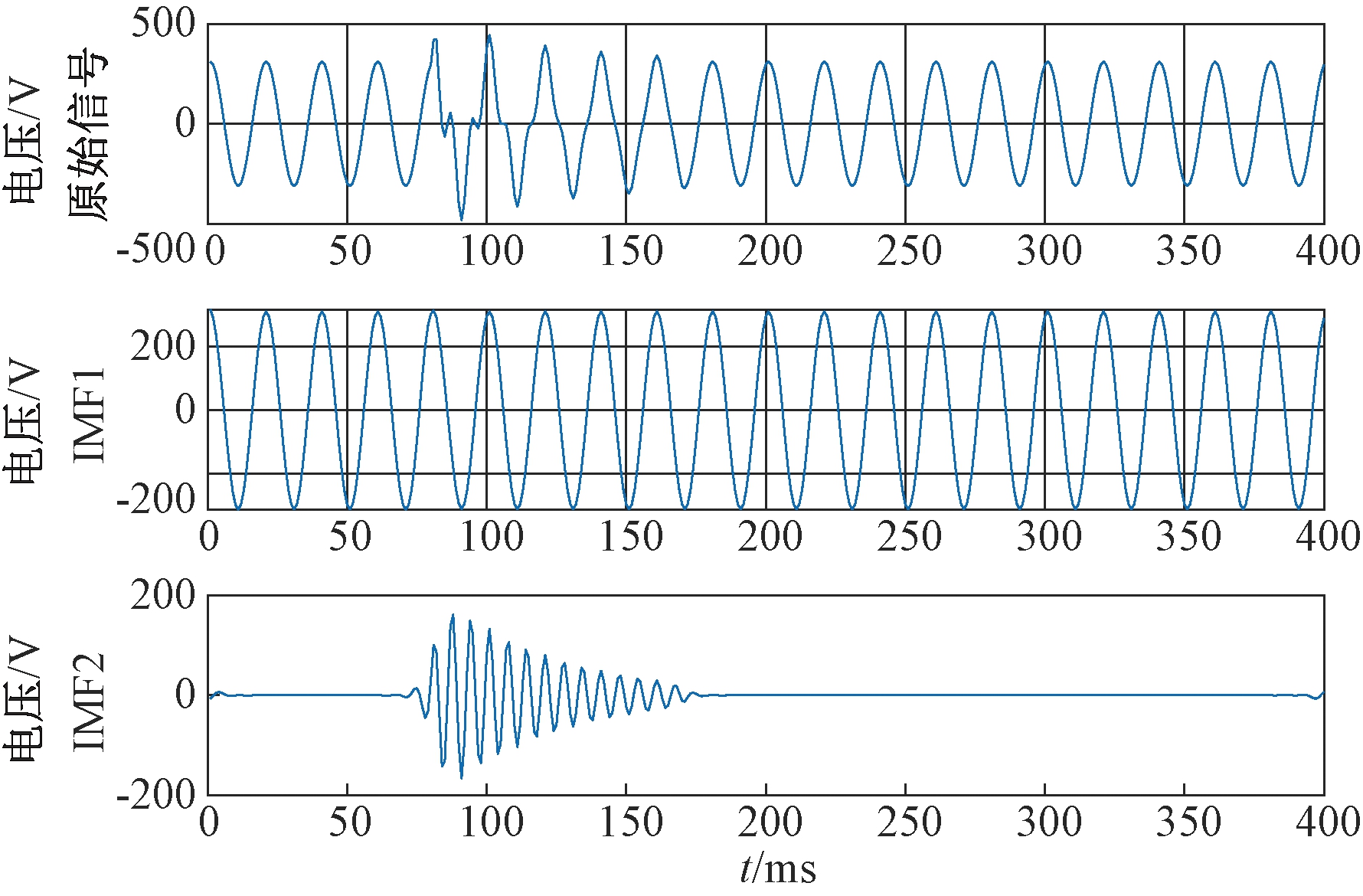
图6 暂态振荡VMD分解图
Figure 6 VMD exploded graph of transient oscillation
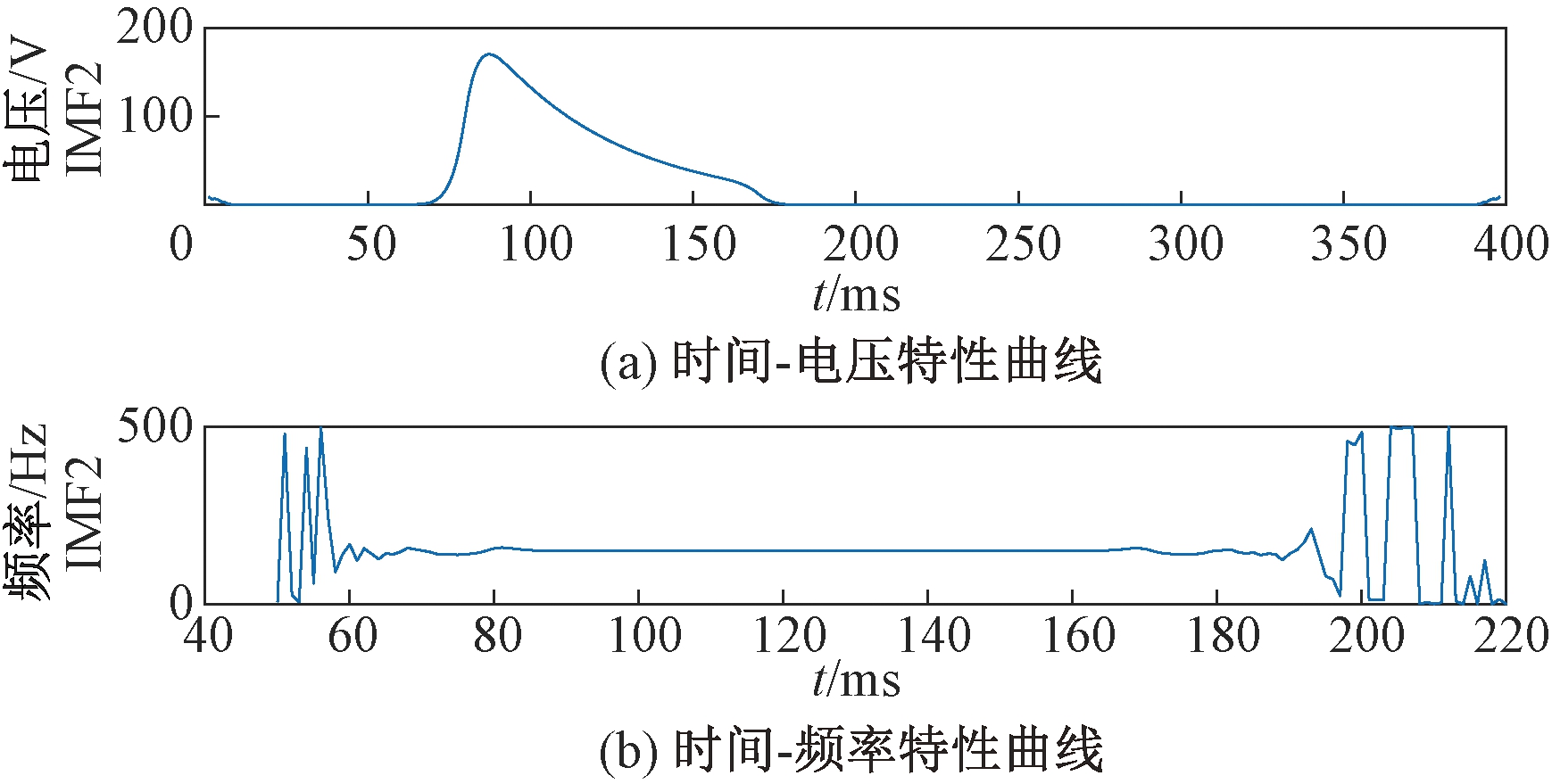
图7 暂态振荡VMD分解的模态分量Hilbert变换
Figure 7 Hilbert transform of modal component of transient oscillation VMD decomposition
然后再将理想的暂态振荡扰动信号进行HHT变换,对其起止时刻进行检测分析如图8、图9所示。通过分析两种不同算法的波形将其定位扰动发生的起止时刻进行对比,同时与加入20 dB白噪声的暂态振荡信号检测结果进行对比见表3。由表3可知,改进的VMD-HT算法在理想环境下检测扰动发生起始时刻的误差和终止时刻的误差均较HHT减少了0.001 s,在含有20 dB白噪声环境下检测扰动发生的起始时刻的误差和终止时刻的误差较HHT算法分别减少了0.007 s和0.006 s。实验表明,改进的VMD-HT具有很好的抗干扰性。通过对暂态振荡模型的起止时刻进行随机改变,并采用本文改进的VMD-HT进行检测,其测试值和理论值误差小于0.003 s的概率达99.84%,表明本文改进的VMD-HT方法具有较高的容错性。本文所提的改进VMD-HT算法较HHT具有更好的检测精度、抗干扰性和容错能力,同时其运行时间也略有增加,但相差不大。通过综合分析可知,改进的VMD-HT对暂态振荡的检测效果更好。
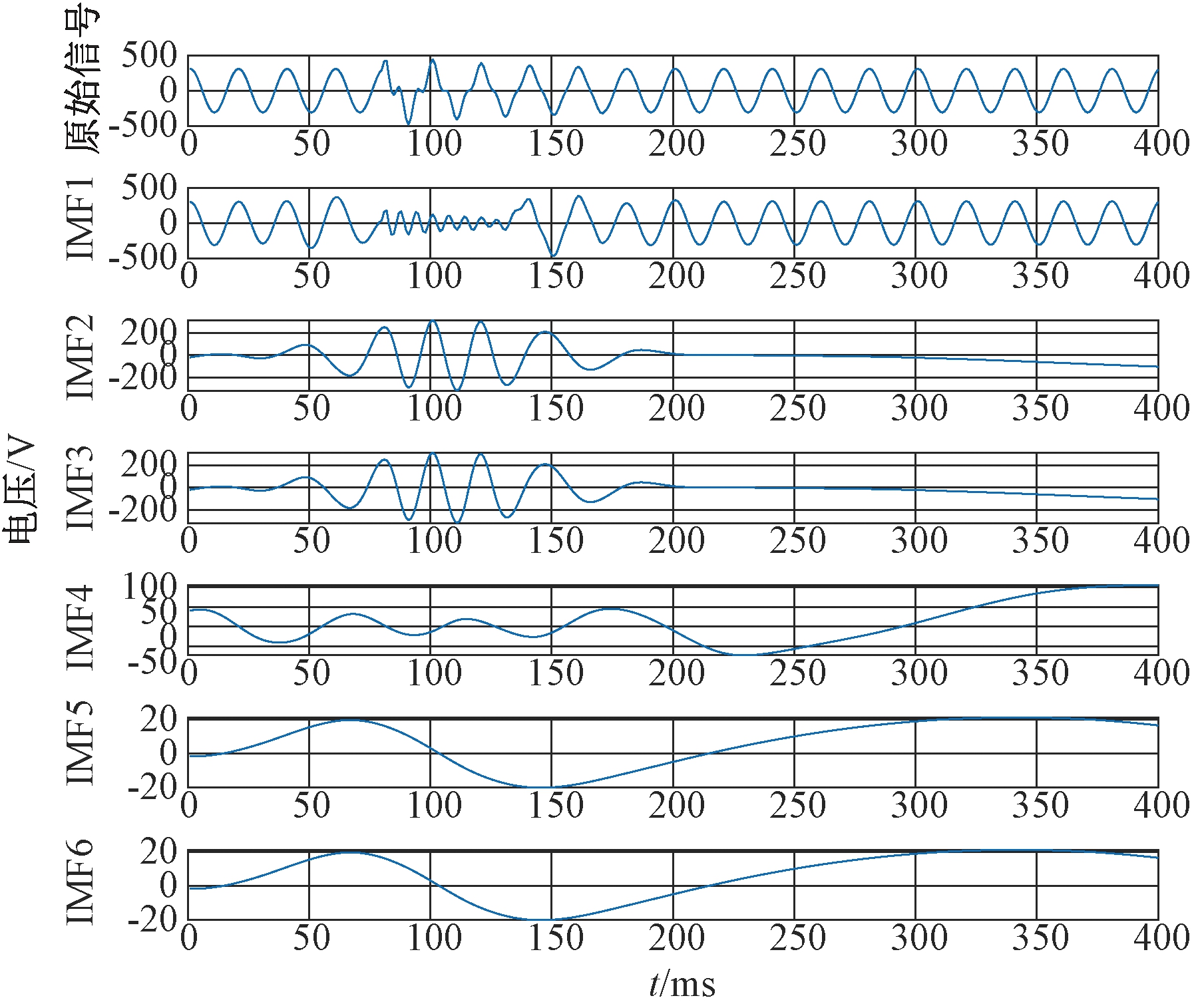
图8 暂态振荡EMD分解图
Figure 8 EMD exploded graph of transient oscillation
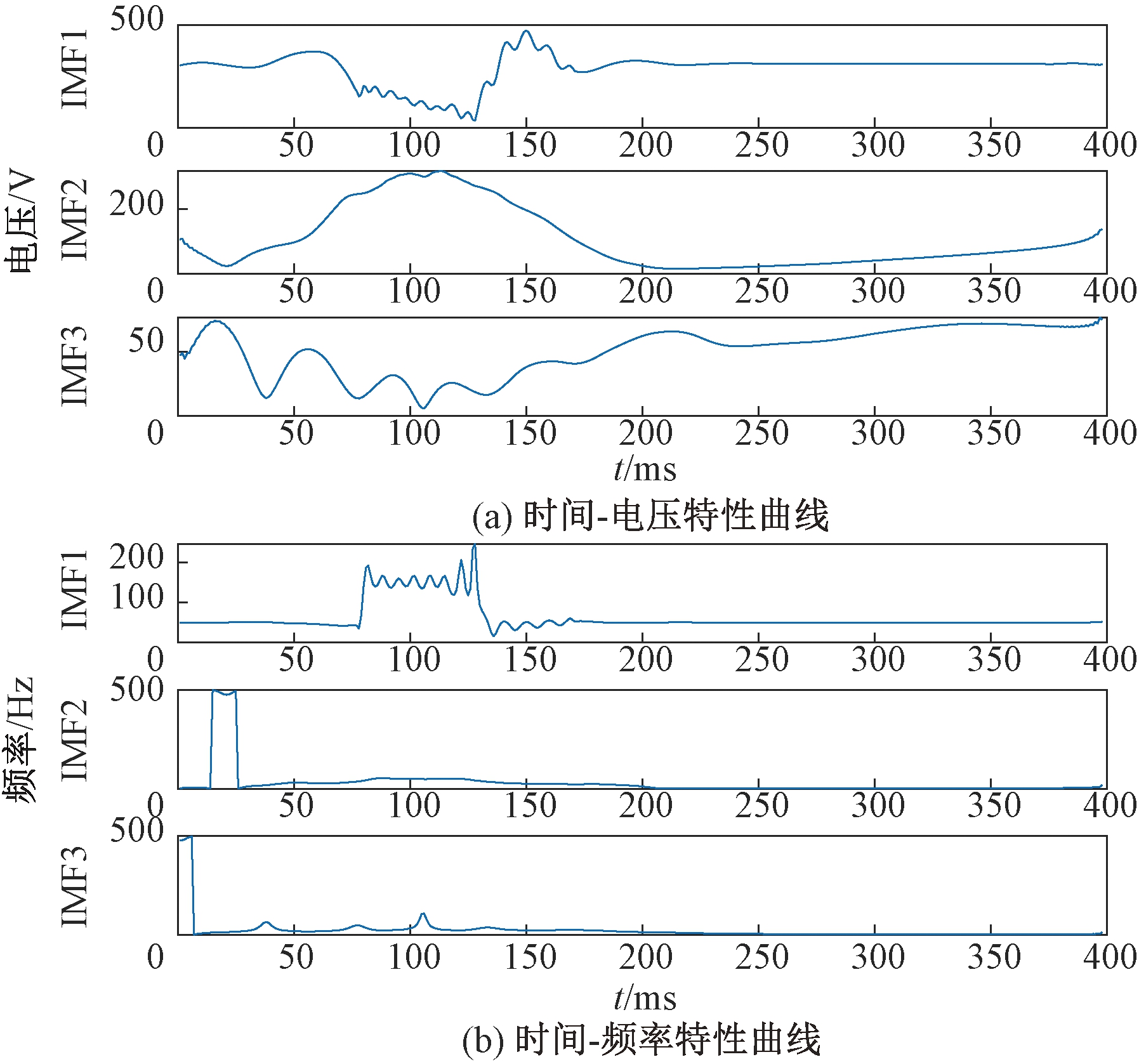
图9 暂态振荡HHT变换
Figure 9 Transient oscillation HHT transformation
表3 暂态振荡的扰动发生时间
Table 3 Time of disturbance of transient oscillation s
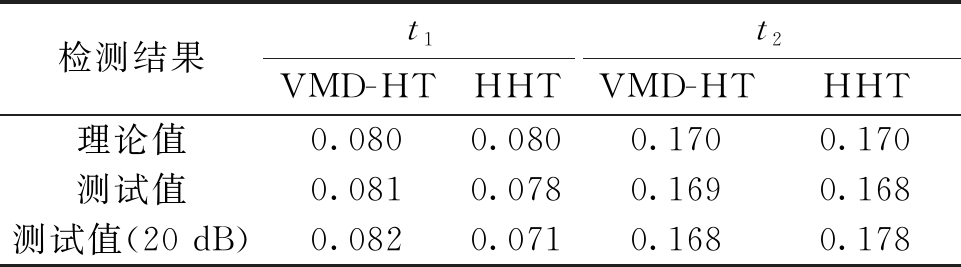
检测结果t1t2VMD-HTHHTVMD-HTHHT理论值0.0800.0800.1700.170测试值0.0810.0780.1690.168测试值(20 dB)0.0820.0710.1680.178
3.2 复合电能质量扰动
在电网中可能存在谐波+暂降的复合扰动信号。现设一突变谐波+暂降的信号,信号基波频率为50 Hz,在0.23~0.34 s时发生谐波突变,同时在0.12~0.17 s时发生暂降+谐波突变,其信号表达式为:
(ε(t-0.12)-ε(t-0.17))×cos 3ωt。
(12)
首先对谐波+暂降的扰动信号的分解模态个数k值进行确定,根据能量收敛因子的步骤计算出不同模态下Em的取值。当m=1、2、3、4时,其分别对应的Em取值为1、0.262 9、0.195 4、0.179 2,相邻模态的差值Δ12=0.737 1,Δ23=0.067 5,Δ34=0.016 2<η,因此分解模态个数k值取3。
图10所示为PSO优化算法的适应度值函数迭代变化图。当迭代到10代,α的取值129时,适应度函数值最小,即原始信号经VMD算法分解效果最佳。
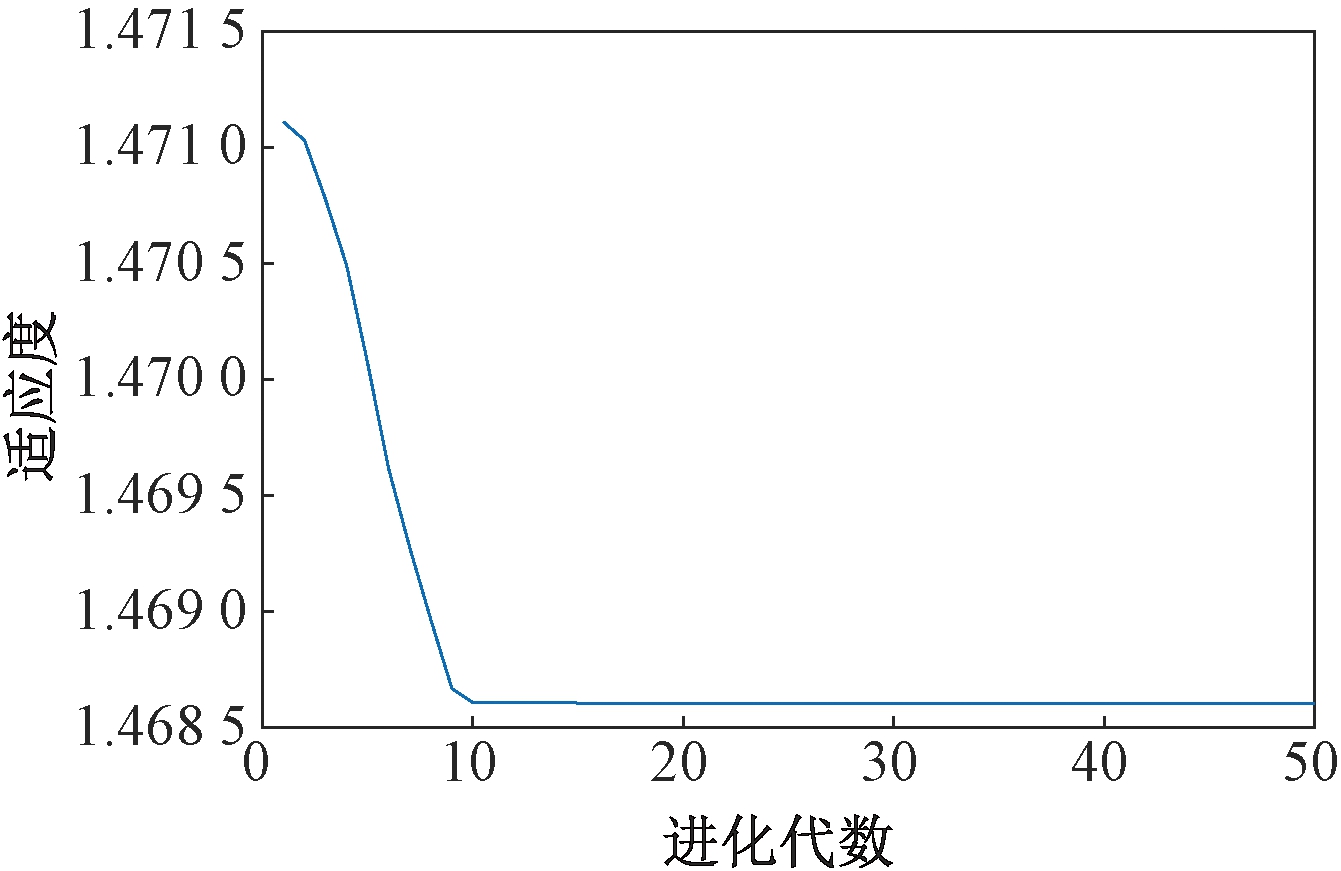
图10 谐波+暂降适应度值随迭代变化图
Figure 10 Harmonic and sag fitness value iteration change graph
将谐波+暂降的复合扰动信号运用本文改进的VMD-HT电能质量扰动检测分析方法进行仿真,得到波形如图11、图12所示。
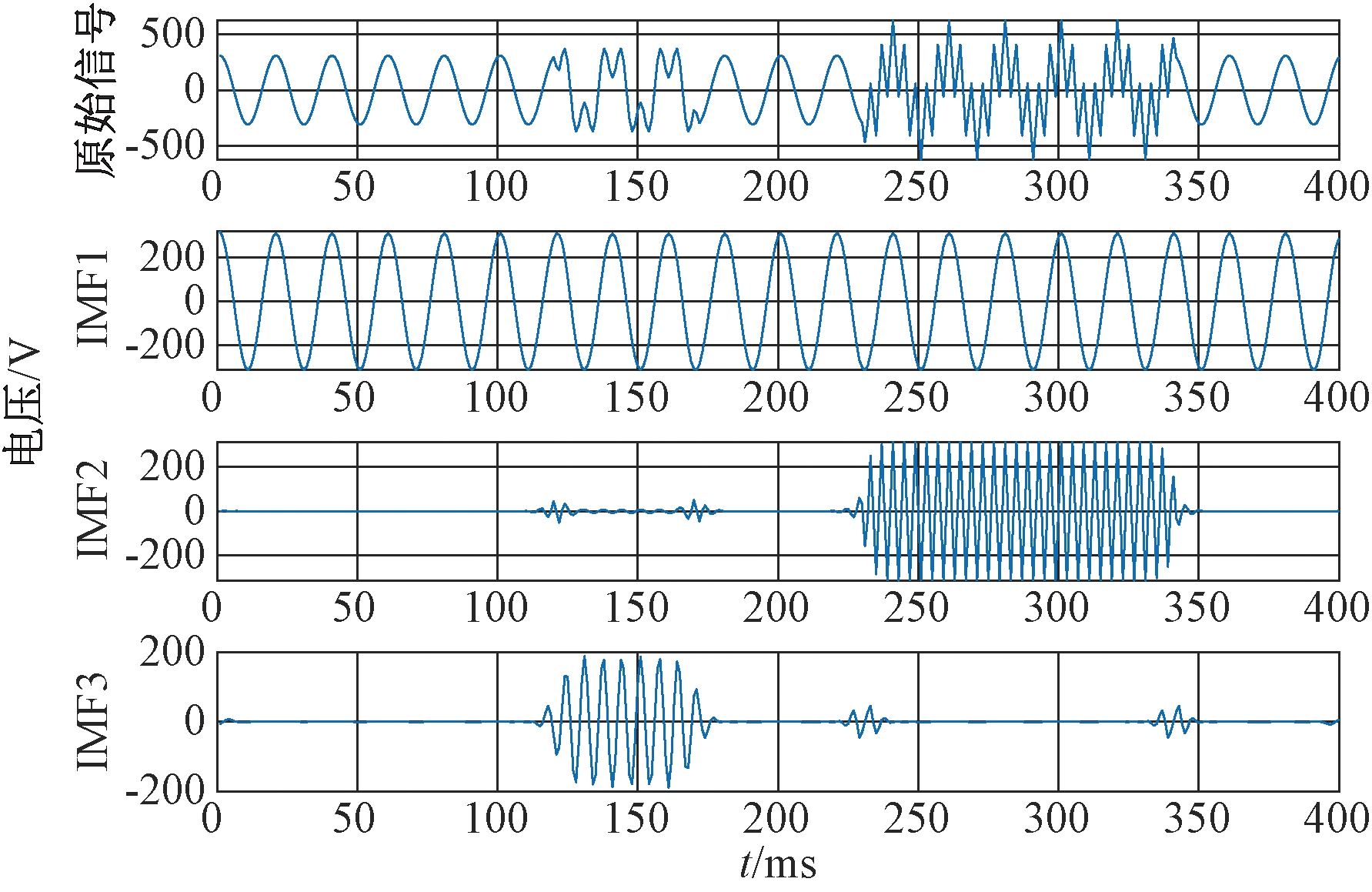
图11 谐波+暂降VMD分解图
Figure 11 VMD exploded graph of harmonics and sag
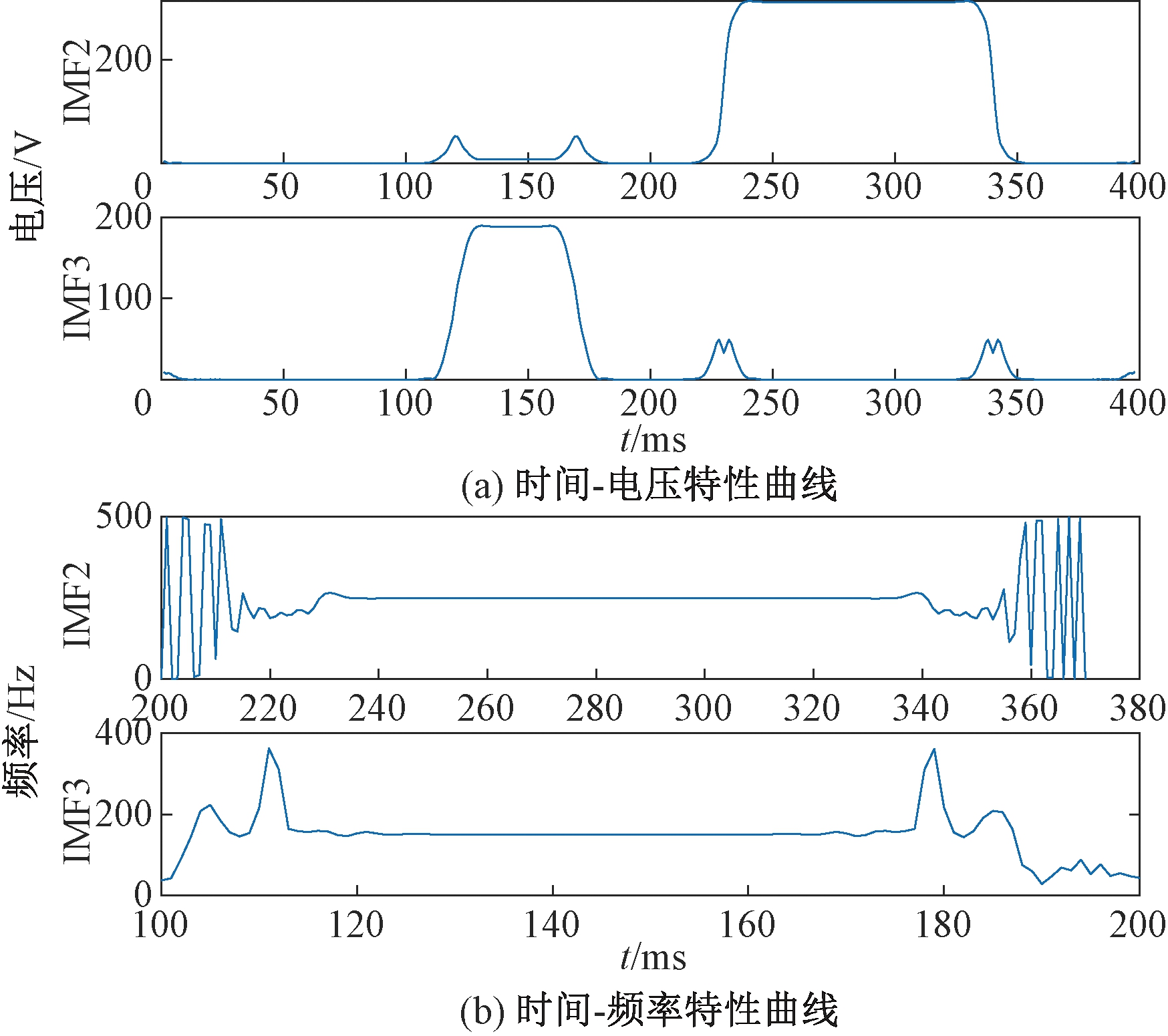
图12 谐波+暂降VMD分解的模态分量Hilbert变换
Figure 12 Hilbert transform of modal component of Harmonics and sag VMD decomposition
谐波+暂降的扰动信号HHT变换波形如图13、图14所示。将其定位扰动的起止时刻与改进的VMD-HT检测结果进行比较,同时与加入20 dB白噪声的谐波和暂降复合扰动检测结果进行对比,如表4所示。由表4可知,采用本文改进的VMD-HT算法在理想环境下较HHT而言,谐波检测起止时刻的误差分别减小了0.003 s和0.001 s,暂降起止时刻的检测误差均减小了0.002 s;在含有20 dB白噪声的环境下,谐波检测的误差分别减小了0.002 s和0.007 s,暂降检测误差分别减小了0.005 s和0.004 s。实验表明,本文提出的改进VMD-HT具有更好的抗干扰性。通过对谐波+暂降的复合扰动模型的起止时刻进行随机改变,并采用本文改进的VMD-HT进行检测,扰动起止时刻的测试值与理论值的误差在0.003 s以内的概率为99.55%,表明本文改进的VMD-HT方法具有较高的容错性。本文所提改进的VMD-HT算法较HHT检测的精度、抗干扰能力和容错性更高,同样其运行时间也略有增加,但相差不大。通过综合分析,本文所提的改进VMD-HT检测效果更好。
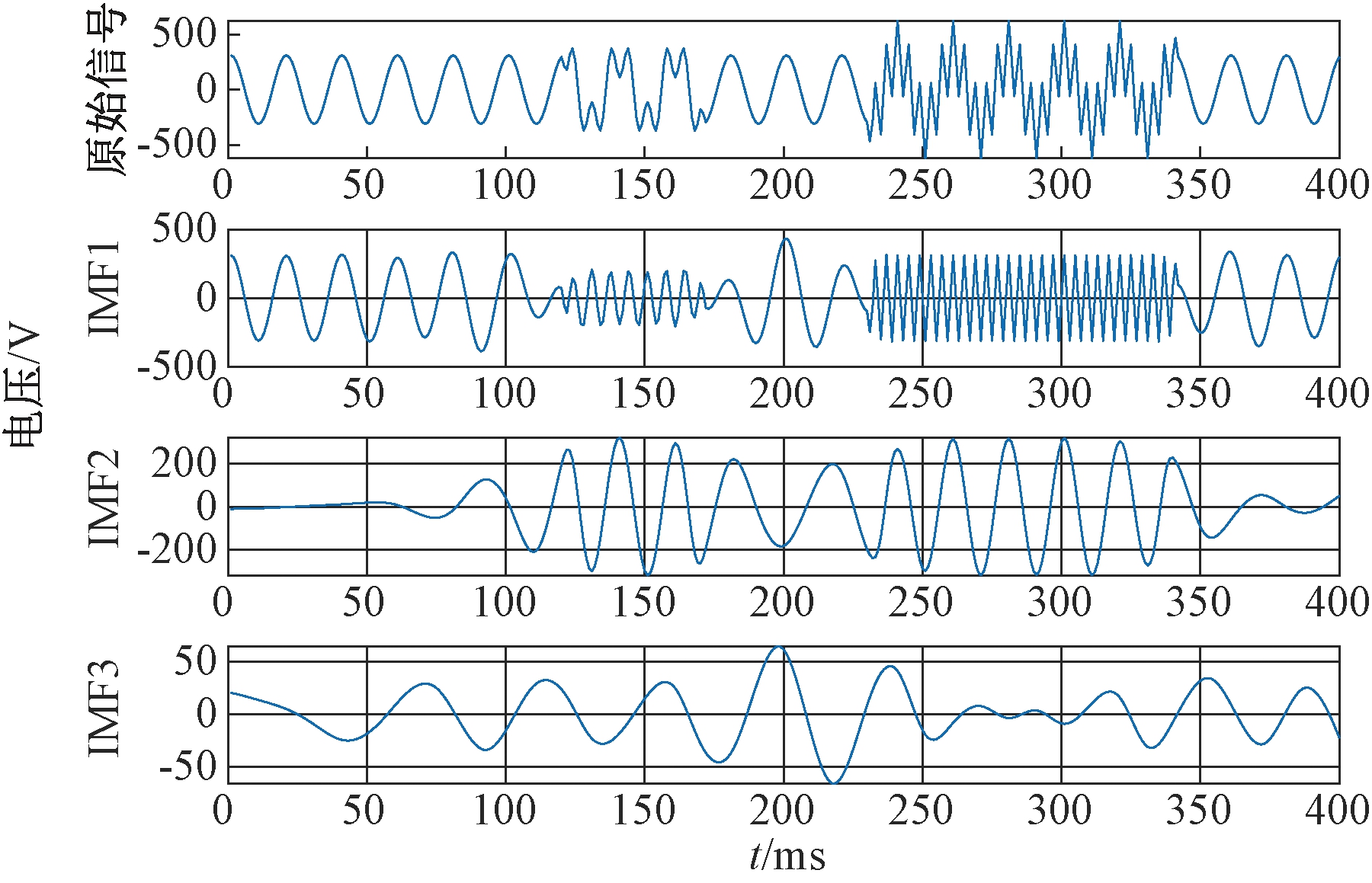
图13 谐波+暂降EMD分解图
Figure 13 EMD exploded graph of Harmonics and sag
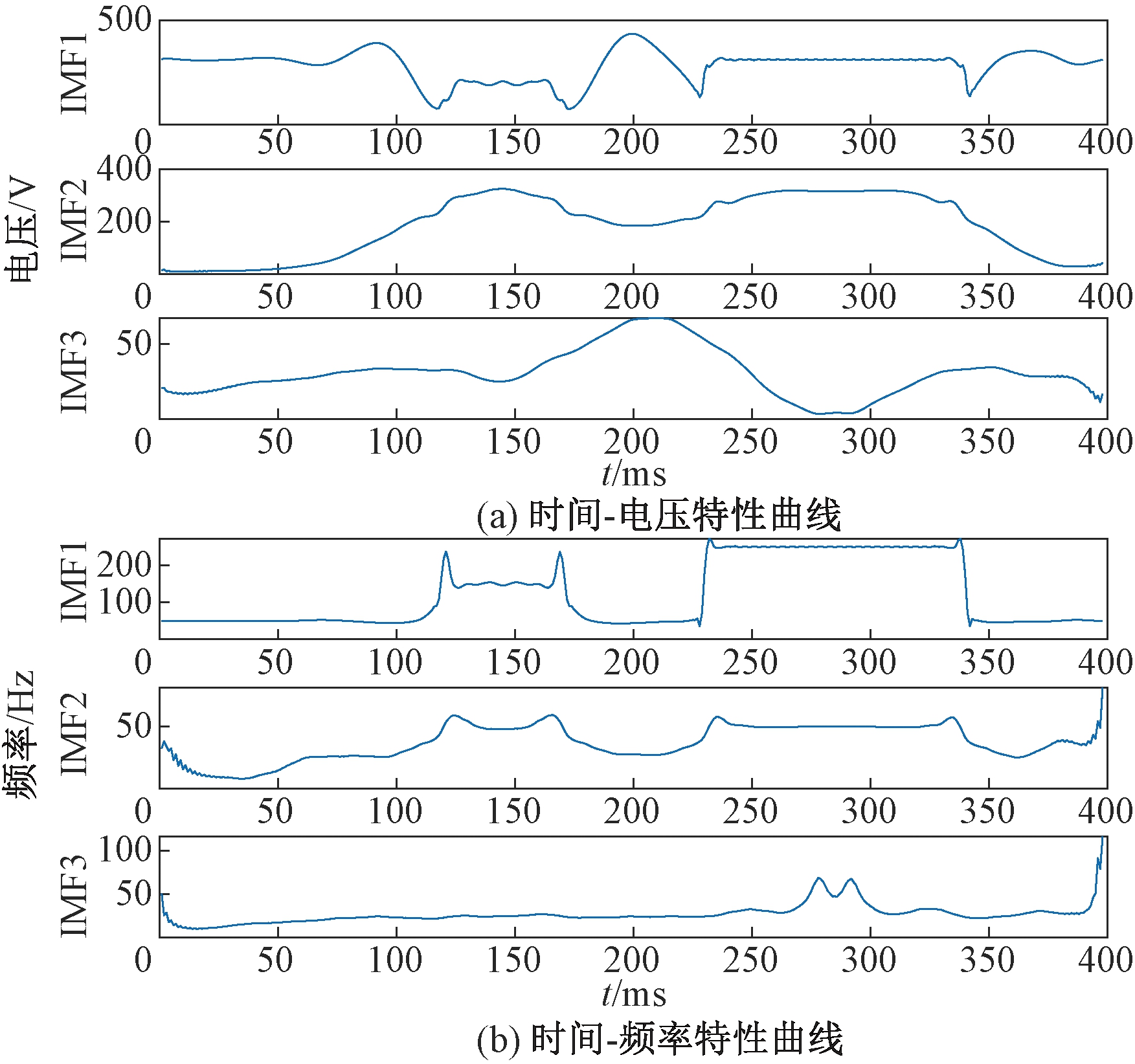
图14 谐波+暂降HHT变换
Figure 14 Harmonics and sag HHT transformation
表4 谐波+暂降的扰动发生时间对比
Table 4 Time of occurrence of Harmonics and sag disturbance s
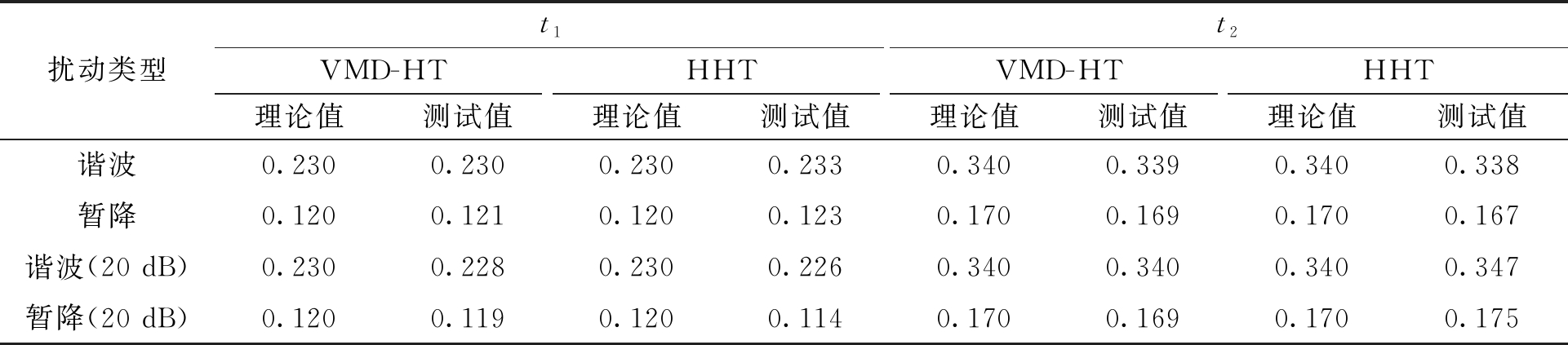
扰动类型t1t2VMD-HTHHTVMD-HTHHT理论值测试值理论值测试值理论值测试值理论值测试值谐波0.2300.2300.2300.2330.3400.3390.3400.338暂降0.1200.1210.1200.1230.1700.1690.1700.167谐波(20 dB)0.2300.2280.2300.2260.3400.3400.3400.347暂降(20 dB)0.1200.1190.1200.1140.1700.1690.1700.175
4 结论
提出一种优化的VMD-HT电能质量扰动检测方法,主要是通过引入能量收敛因子和粒子群优化算法寻优VMD参数k和惩罚因子α的取值,使得VMD分解达到最优效果,然后通过Hilbert变换进行扰动发生起止时刻的检测。相比于传统依靠经验选取VMD参数的方法和缺少数学基础的希尔伯特-黄变换对电能质量扰动的检测具有更好的检测效果。大量的对比实验表明,其暂态振荡检测误差在0.003 s内的概率达到了99.84%。谐波和暂降组成的复合扰动检测等实验也均验证了本文提出的能量收敛因子与PSO优化的VMD-HT电能质量扰动检测方法具有可行性。较HHT检测算法而言,本文方法提高了电能质量扰动检测的准确性、抗干扰能力和容错性。
[1] 任祖华,王柏林.基于多分辨率S变换的电压闪变检测[J]. 电力自动化设备, 2014, 34(1):27-31.
[2] 刘军,黄纯,江亚群,等.电能质量扰动分析中广义S变换算法的改进与实现[J]. 电力系统及其自动化学报, 2017, 29(3):35-41.
[3] 唐圣学,付滔,李志刚.基于自适应小波阈值去噪和HT-LMD的电能质量扰动检测方法[J]. 电测与仪表, 2017, 54(17):70-76.
[4] 王燕,李群湛,周福林.一种暂态电能质量扰动检测的新方法[J]. 中国电机工程学报, 2017, 37(24): 7121-7132,7426.
[5] 廖晓辉,赵肖健,梁恒娜.一种基于Hilbert-Huang变换的电力电缆故障测距方法[J]. 电力系统保护与控制,2017, 45(3):20-25.
[6] 胡雷,陈湘波,熊魁,等.基于改进HHT的电能质量扰动检测方法[J]. 电测与仪表, 2018, 55(21):105-111.
[7] 黄传金,周铜.基于变分模态分解的电能质量扰动检测新方法[J].电力自动化设备,2018,38(3):116-123.
[8] 罗亦泳,姚宜斌,黄城,等. 基于改进VMD的变形特征提取与分析[J].武汉大学学报(信息科学版),2020,45(4):612-619.
[9] 陈陈,李晓明,杨玲君,等.变分模态分解在电力系统谐波检测中的应用[J].电力系统保护与控制,2018,46(14):63-70.
[10] DRAGOMIRETSKIY K,ZOSSO D.Variational mode decomposition[J]. IEEE transactions on signal processing, 2014, 62(3): 531-544.
[11] 郑小霞,陈广宁,任浩翰,等.基于改进VMD和深度置信网络的风机易损部件故障预警[J].振动与冲击,2019,38(8):153-160,179.
[12] 蒋丽英,卢晓东,王景霖,等.基于PSO-VMD的齿轮特征参数提取方法研究[J].制造技术与机床,2017(11): 65-71.
[13] 龙志伟,肖松毅,王晖,等. 基于粒子群算法的水资源需求预测[J]. 郑州大学学报(工学版), 2019, 40(4): 32-35,47.
[14] 刘宏波.基于改进VMD-HT的电力系统低频振荡模态辨识[D].哈尔滨: 哈尔滨工业大学,2018.