0 引言
特征值分析法以状态空间模型为基础，是电力系统小干扰稳定性分析的常用方法之一[1]。随着现代电力系统规模不断扩大[2]，求解状态空间矩阵所需计算量急剧增大，国内外学者开始寻找快速形成状态矩阵的方法。
目前，国外通常采用拟合的方法求解状态矩阵，比如Saitoh等[3]用广域监测系统(WAMS)搜集各个离散时间点的值，并利用最小二乘法拟合出状态矩阵。国内有两种主流方法:一种是用解析的方法直接得出状态矩阵，该方法计算速度很快，但是预处理较困难；另一种则是利用插入式模拟技术(PMT)[4]，先将所有系统元件转化为两种基本传输模块，再利用传输模块两端的节点编号组成关联矩阵，最终得到状态空间方程。第2种方法较为灵活，适用于对元件内部模块间变量的监控和灵敏度计算，但是矩阵运算较多，渐渐陷入了矩阵“维数灾难”。因此，一些学者在该方法的基础上进行了改进，比如罗丹等[5]将状态矩阵形成过程中的相关算式进行QR优化和重组，通过矩阵降阶求逆的方法提高计算效率；胡崴[6]则是利用Hager算法缩减矩阵的外形，再引入并行计算提高计算效率，但是Hager缩减过程中没有与并行计算相结合，此过程本身也会耗费一定时间。除此之外，为了缩短特征值的计算时间，有些学者利用改进的Rayleigh商逆迭代法来获得机电模式的特征值:首先用相关因子将机电模式分组，再参照模型降阶的方法，计算出大规模电力系统机电模式特征值[7]。
在PMT的基础上充分利用相关矩阵的稀疏特性及Open MP技术的并行计算功能：首先将求解过程中的关键矩阵进行ILUTP预处理，合理舍弃掉一些非对角非零元素，使系数矩阵谱分布更集中，再采用Krylov子空间迭代法中的BICGSTAB算法，对得到的预处理模块进行快速迭代计算。ILUTP技术与BICGSTAB算法均能很好地与Open MP结合使用，进一步加快了迭代计算速度。稀疏矩阵存储采用行压缩矩阵存储的方法降低存储量，减小计算量，从而提高整体计算效率。
1 BICGSTAB算法及ILUTP技术
1.1 BICGSTAB算法
Krylov子空间迭代法[8]适用于求解大型线性方程组。给定线性方程组：
Ax=b。
(1)
式中：A∈Rn×n；x，b∈Rn。
设Km为m维子空间，一般投影方法是从m维仿射子空间x0+Km中寻找上式的近似解xm，x0为迭代初值，使相应的残差满足Petrov-Galerkin条件:
rm=b-Axm。
(2)
其中，要求rm与预设的约束空间Lm正交[9]。
记Km=Km(A,r0)为Krylov子空间，定义为：
Km(A,r0)=span{r0,Ar0,A2r0,…,Am-1r0}。
(3)
约束空间Lm的选择对迭代过程具有重要影响，本文中矩阵具有非对称性，故选用双正交化方法，取Lm=Km(AT,r0)，其中BICG法是双正交化方法中最典型的算法。
BICGSTAB算法[10]是在BICG的基础上发展起来的，其避免了BICG中对AT的计算，收敛速度比BICG更快。
对于n阶线性方程组Ax=b，假设初始的近似解为x0，第k次近似解为xk，相应的第k次残差为rk=b-Axk，r0是与
不正交的非零向量，
分别是与
有关的k阶Krylov子空间：
(4)
BICGSTAB算法在Krylov子空间Kk中选取序列，通过选择参数αk和βk，使得xk和rk满足rk∈x0+Kk且rk与
正交，同时，计算的残差向量rk和搜索方向pk为：
(5)
BICGSTAB算法能够在保证精度和稳定性的同时，达到快速收敛的效果。但是其收敛速度非常依赖于系数矩阵特征值的分布，所以在一些情况中，直接使用BICGSTAB算法会导致收敛速度很慢，甚至根本不能收敛[11]。可使用预条件技术将原线性方程组转化为更利于迭代收敛的线性方程组[11]，保证迭代过程不中断，提高收敛速度。
1.2 ILUTP预处理
相比于LU分解，不完全LU分解(ILU)可以减少内存占用，更适用于大型稀疏矩阵的计算[12]。该方法是在高斯消元的过程中强制舍弃掉一些非对角非零元素，从而得到有效的预处理子矩阵M,其中
和
分别为L和U的近似。
ILU预处理有很多种算法，不同算法的主要区别是在对
和填充的舍弃策略上。当填充满足某些条件，例如位置、大小或者是位置和大小的组合，即被舍弃[13]。
ILUT(p，τ)[14]是ILU预处理中一种具有双重阈值的算法(以下简称ILUTP)，其中τ表示舍弃阈值，若|aij|小于τ乘以第i行的2-范数，那么在(i,j)位置不引入填充，即舍弃aij；p表示最大填充个数，即分别在和的第i行保留p个绝对值最大的元素，并将其他元素舍弃。
ILUTP方法[15]的优势在于其可以降低分解因子中非零元素的个数，从而缩减不完全分解时间和预条件处理的迭代时间；同时，当矩阵性质较差时，可以通过调整参数τ与p的值来提高分解因子的质量，增强迭代有效性。但是在特定情况下，需要不断尝试才能预先选择出合适的参数τ和p，否则精度将无法得到保证。因此，最优值应当结合实际问题和矩阵特点来合理选定。
引入一个名为droptol(阈值)的参数以确定是否改变变量值，使得矩阵的系数谱变得更加集中，从而将矩阵转换为对角占优形矩阵，可提高计算效率。但是由于舍弃掉了一些非零元素，计算准确度无法保证，因此又引入一个名为tol(绝对误差限)的参数以保证计算精度。通过不断尝试，在速度和精度之间找出最佳平衡点。
2 状态空间方程的建立及特点分析
2.1 插入式建模技术
在插入式建模技术中，将电力系统描述为传输模块集合：非状态变量传输块(零阶)、状态变量传输块(一阶)和5类基本参数k、ka、kb、Ta、Tb，再根据各个系统元件和电力网络中传输模块两端的节点编号列出关联矩阵L:
(6)
式中：Xi和Mi分别为状态变量和非状态变量模块的输入;X和M则为状态变量和非状态变量模块的输出;R、Y对应系统输入、输出的列向量。
第n个零阶和一阶的传输块方程可表示为：
(7)
那么，所有零阶和一阶的传输块方程可表示为：
(8)
式(7)、式(8)中，kn为第n个零阶传输块的传输增益；K为由所有的kn组成的对角矩阵；Ka、Kb和Kt分别为所有一阶模块参数kan/Tbn、kbn/Tbn和Tan/Tbn共同组成的对角矩阵。
由式(6)～(8)消去Xi、Mi和M，得到电力系统状态空间方程如下:
(9)
其中，各系数矩阵的具体表达可详见文献[4]。
状态矩阵A的表达式为：
A=(I-Kt(L1-L3L9-1))-1×
(Ka(L1-L3L9-1L7)-Kb)。
(10)
式中：
为单位矩阵；L1～L6分块子矩阵均只由0和1组成；分块子矩阵L7～L9展示了零阶模块变量和一阶模块变量间的代数关系。
2.2 矩阵分析
基于插入式建模中节点电压和电流是非状态变量，节点导纳矩阵可以直接被插入到分块子矩阵L9中，得到下式：
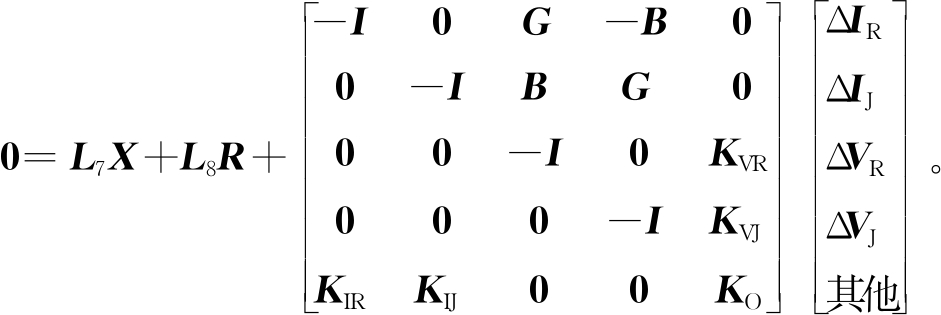
(11)
式中：G、B分别为导纳矩阵的实部和虚部；KVR、KVJ、KIR、KIJ和KO为非状态模块的参数矩阵；I为单位阵。
形成状态空间方程时，内存的需求主要取决于L9子矩阵，求解L9矩阵的逆矩阵是求解A矩阵的关键，也是计算过程中耗时最长的环节，因此加速求解L9逆矩阵可加快状态空间方程的形成。
L9系数矩阵为大型稀疏矩阵，其稀疏度随着数据增多而变高，所以可充分利用其稀疏特性优化求逆过程。对于大型非对称的稀疏矩阵，首先考虑用BICGSTAB 算法迭代。图1为L9矩阵的数据分布示意图，“×”表示非零元素，其余为零元素。观察图1可以看出L9矩阵条件数很大且为非对角占优矩阵，直接用BICGSTAB算法无法收敛，因此本文最终选用ILUTP结合BICGSTAB求解方程，迭代计算则采用Open MP技术的并行计算功能。
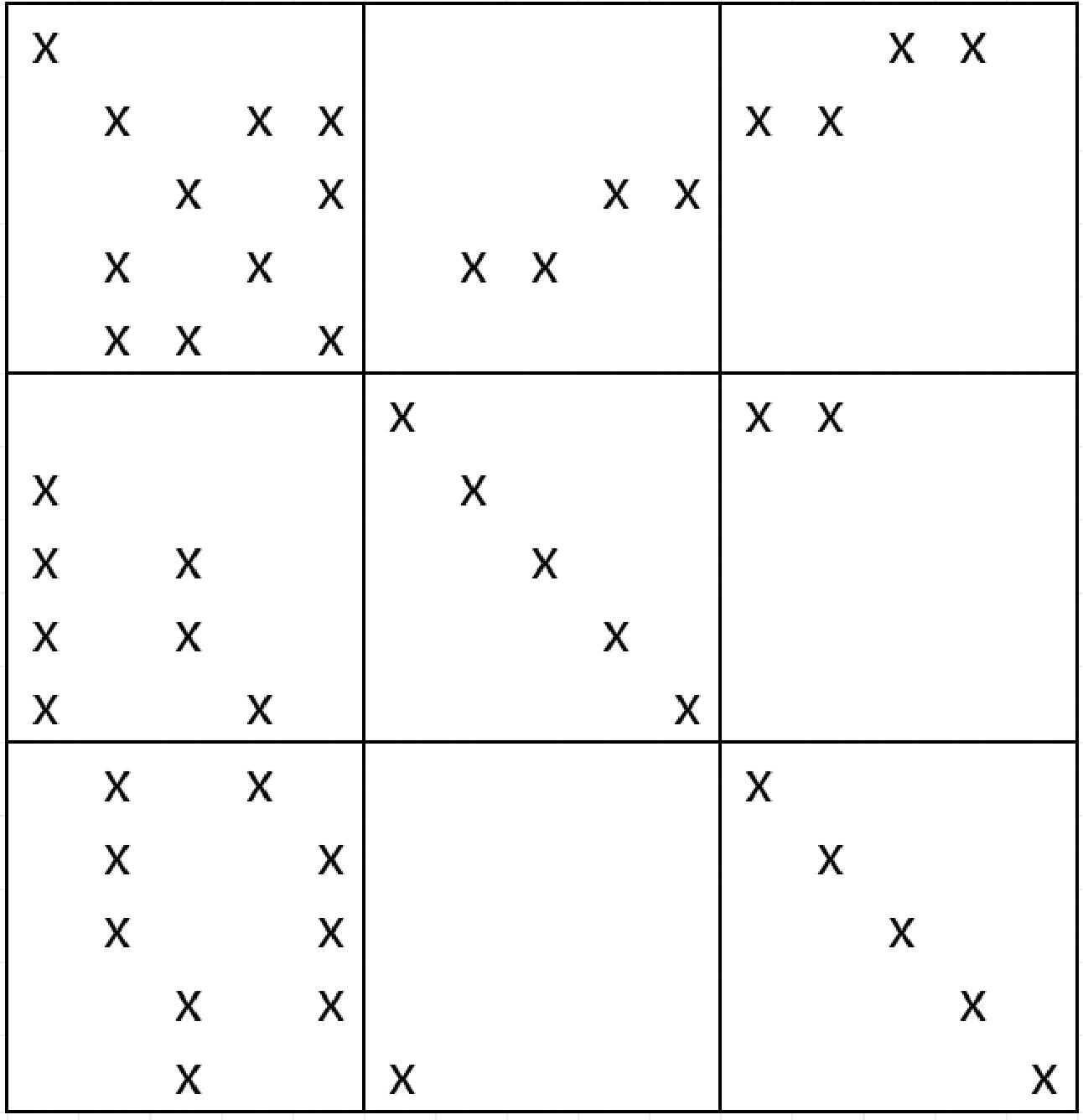
图1 L9矩阵
Figure 1 The L9 matrix
2.3 算法分析
L9矩阵为不对称的稀疏矩阵，原算法中直接求逆的时间复杂度为
优化算法的时间复杂度由ILUTP预处理算法与BICGSTAB算法的时间复杂度共同组成，为
其中n为正整数，表示迭代次数。此时，取T2<T1，则有n≥2，因此认为优化算法程序的时间复杂度始终小于原算法(除非计算时只迭代1次)。
并行处理是将原有单线程执行的程序变为多线程执行，增加线程并不会影响算法的时间复杂度，但是会提高执行效率。优化算法与原算法相比，与Open MP的并行功能结合度更高，因此执行效率更高，计算时间会有明显缩短。
3 加速求解状态矩阵的程序实现
本文求解状态矩阵A的步骤如下：
Step 1 输入稀疏矩阵A，矩阵采用行压缩存储；
Step 2 ILU分解，得到L、U矩阵;
Step 3 BICGSTAB，求解线性方程组Ax=b;
Step 4 求解方程组采用Open MP并行;
Step 5 输出结果，将L9的逆矩阵代入原程序，求A矩阵及特征值。
3.1 行压缩存储
鉴于稀疏矩阵A的特点，矩阵采用行压缩存储(CRS)[16]，该格式只显示保留每行第一个非零元素的位置，具体在图2所示例子中可以看到：假设有稀疏矩阵B，创建一个浮点型数组Val和两个整型数组Colind和Rowp。Val数组的大小为矩阵B中非零元素的个数，保存矩阵B的非零元素(按从上往下，从左往右的行遍历方式访问元素)；Colind数组和Val数组一样，大小为矩阵B的非零元素的个数，保存Val数组中元素的列索引；Rowp数组大小为矩阵B的行数，保存矩阵B的每行第一个非零元素在Val中的索引。该方法可以节省很多空间，只需要2nnz+n+1个存储单元，而不是n2个单元，其中nnz为稀疏矩阵中非零元素的个数。
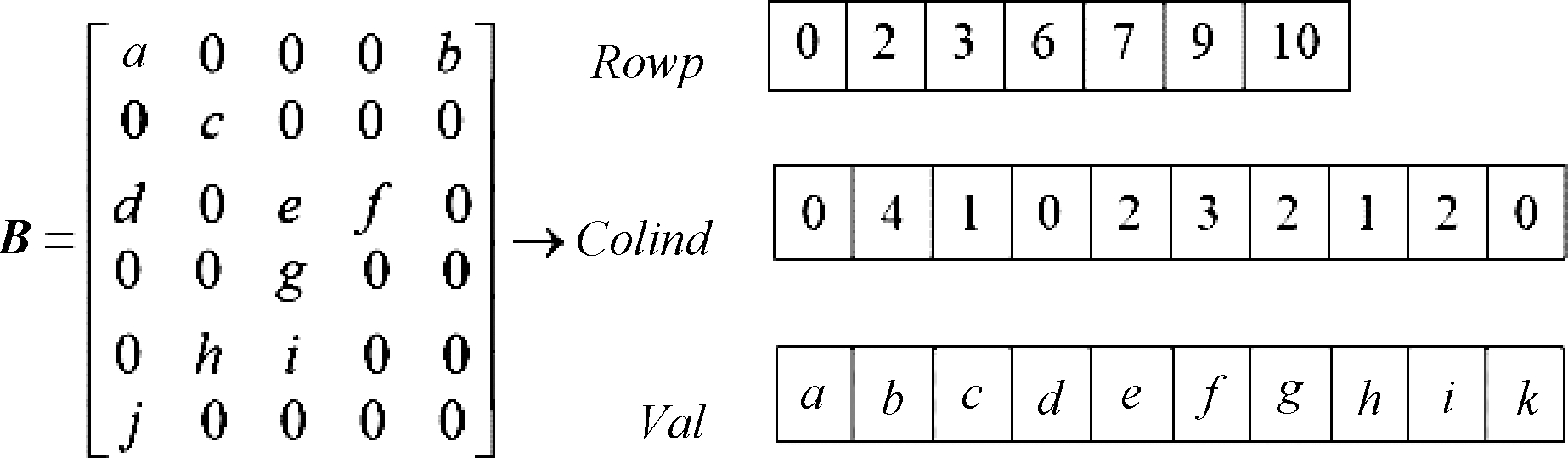
图2 稀疏矩阵B的行压缩示意图
Figure 2 Schematic of sparse matrix B using CRS
3.2 预处理参数设定
本文采用ILUTP预处理方法，将L9矩阵进行预处理，处理后得到的
矩阵增强BICGSTAB迭代的稳定性，加快收敛速度。ILUTP技术应用的关键在于对其中部分参数的设定，该研究中这些关键参数的具体设定如下:
integer::ILU_mode=1
real*8::droptol=0.001
integer::lfil=10
real*8::permtol=0.5
integer::mbloc=0
通过阈值来舍弃数值小的元素，从而影响生成的ILU矩阵大小。这个值设定得太小会导致无法收敛，太大则无法保证精度。本文经过多次修改对比，最终选用droptol_def=0.001，tol=0.000 01达到理想的平衡点。下降公差lfil用来控制L和U中每行限定的最大非对角元素个数，填充参数设定得较小是为了保证计算精度。列交换容差permtol合理的值通常介于0.5和0.01，本文矩阵维数很大，因此将列交换容差设为0.5。图3为预处理之后得到的L9矩阵的数据分布示意图，经过ILUTP预处理之后，矩阵转换为对角占优型矩阵，一方面更有利于BICGSTAB算法的求逆迭代，另一方面更易与Open MP的并行功能相结合。
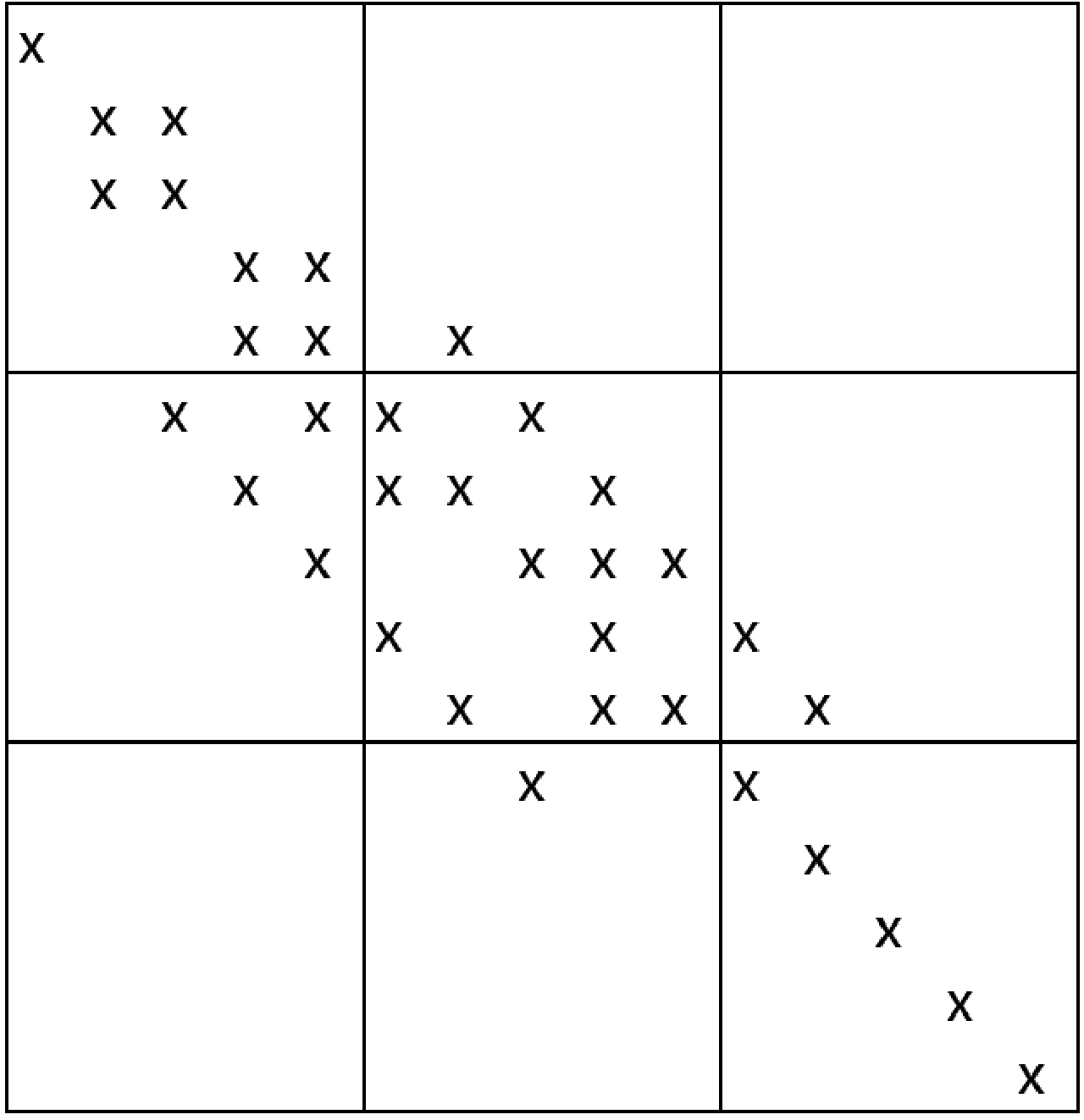
图3 转换后的L9矩阵
Figure 3 The transformed L9 matrix
3.3 BICGSTAB算法实现
程序中BICGSTAB算法流程如下：
Step 1 对于线性方程组Ax=b，给定初始值x0，最大迭代次数kmax，计算r0=b-Ax0，其中给定
使得内积
同时给定ρ0=α=ω0=1，ν0=p0=0，i=1；
Step 2 
pi=ri-1+β(pi-1-ωi-1vi-1)，vi=Api；
Step 4 xi=xi-1+αpi+ωis；
Step 5 若xi达到精度要求，则转Step 7；
Step 6 ri=s-ωit，i=i+1，若i<kmax，转Step 2；
Step 7 输出xi，算法结束。
3.4 Open MP并行实现
Open MP作为并行提速计算的一种工具，适合处理独立循环或者分开的子任务，程序编写简单，具有强扩展性，可支持Fortran等多种编程语言[8]。
在状态矩阵形成的程序中有很多DO循环语句，如对矩阵L1、L3、L7、L9赋值、对矩阵L9求逆过程中的迭代等，这些任务在程序执行过程中可以独立执行，因此结合Open MP进行并行处理。其中BICGSTAB算法中求解方程组时的并行语句如下：
!S|OMP Parallel
!S|OMP do Private(i,x0,x,bi)
do i=1,N
bi=0.d0; bi(i)=1.d0; x0=0.d0
call Precond(bi,x0)
x0=x0(Iperm(1:N))
call Bicgstab(bi，x0，x，max_it，tol)
a(1:N,i)=x(Iperm(1:N))
enddo
!S|OMP enddo
!S|OMP end Parallel
4 算例分析
某省电力网络的两个实际算例分别包含23台发电机和98台发电机，发电机均采用六阶发电机模型，励磁调节模块与原动机调速模块均为系统的实际参数。
程序采用Fortran语言编写，编写环境为Visual Studio 2010平台、Intel Fortran 12，在2.14 GHz 主频、32 GB 内存、8核计算机上运行实现。存储方式为行压缩存储形式。
通过对两种求解状态矩阵方法的所用时间进行比较来验证可行性。两种方法分别为原方法和现方法，均利用插入式建模技术及Open MP的并行功能。其中,原方法为文献[4]中基础的PMT方法，矩阵求逆采用直接LU分解法，矩阵存储采用三元组技术存储；现方法为预处理的不完全LU分解法，矩阵求逆采用BIGSTAB算法迭代求逆，矩阵存储采用行压缩存储技术。分别将原方法及现方法无并行所用时间、原方法及现方法加入并行所用时间进行比对，验证现方法的加速效果。
算例1为23台发电机，系统中包含90个节点，210条支路，状态矩阵的阶数为257阶。算例1中矩阵L1、L3、L9及状态矩阵A的阶数、非零元素个数和对应的稀疏程度如表1所示。本算例为了对比算法方面的改进，设为单线程执行，各方法运行时间的对比如表2所示。
表1 算例1中各矩阵的信息
Table 1 Information of each matrix in example 1
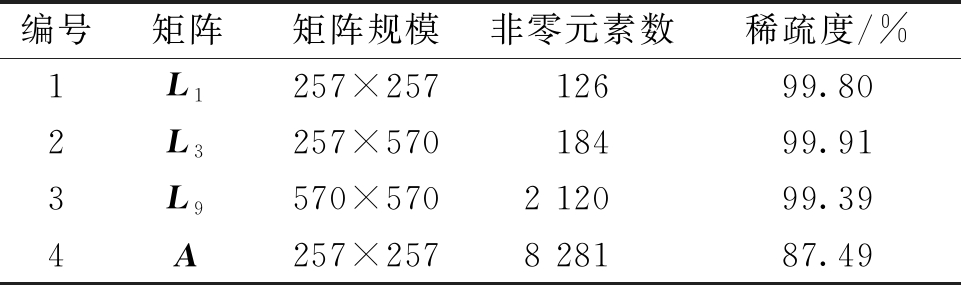
编号矩阵矩阵规模非零元素数稀疏度/%1L1257×25712699.802L3257×57018499.913L9570×5702 12099.394A257×2578 28187.49
表2 算例1中各方法的运行时间
Table 2 Run time of each method in example 1
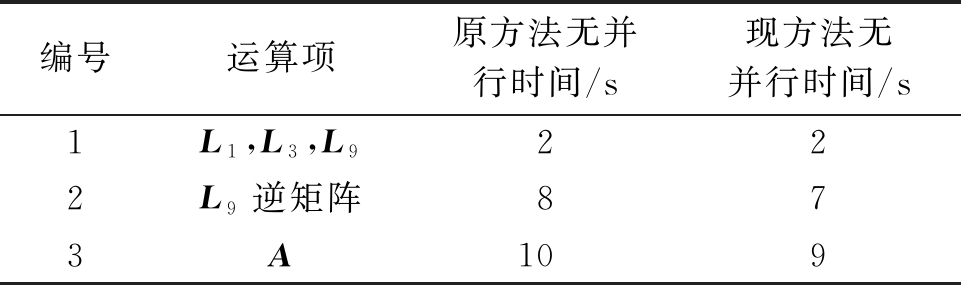
编号运算项原方法无并行时间/s现方法无并行时间/s1L1,L3,L9222L9逆矩阵873A109
由表2得出，在矩阵阶数较少时，BICGSTAB算法及预处理技术的运用对计算效率并没有非常明显的提高。
算例2为98台发电机，系统中包含2 394个节点，5 512条支路，状态矩阵的阶数为1 736阶。其中矩阵L1、L3、L9及状态矩阵A的矩阵规模、非零元素数和对应的稀疏程度如表3所示。算例2中加入了并行计算功能，为八线程执行，各方法运行时间的对比如表4所示。
表3 算例2中各矩阵的信息
Table 3 Information of each matrix in example 2
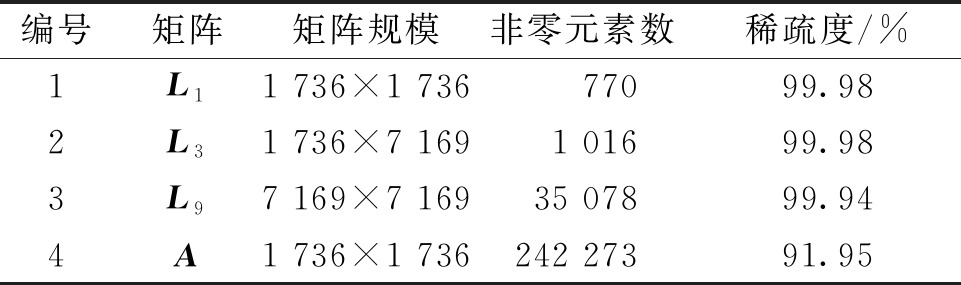
编号矩阵矩阵规模非零元素数稀疏度/%1L11 736×1 73677099.982L31 736×7 1691 01699.983L97 169×7 16935 07899.944A1 736×1 736242 27391.95
表4 算例2中各方法的运行时间
Table 4 Run time of each method in example 2
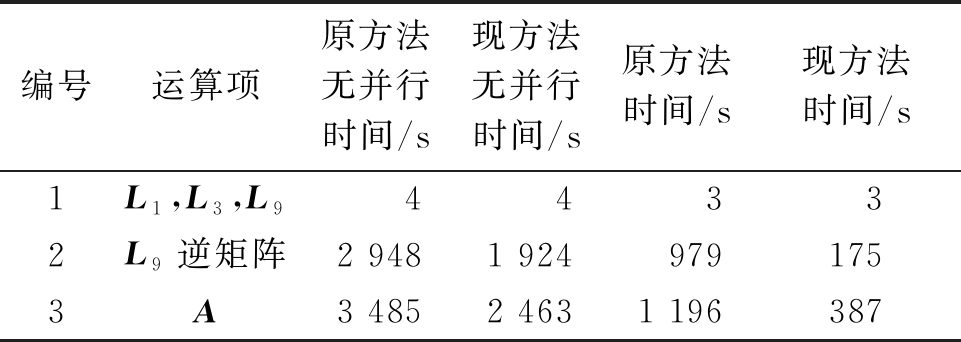
编号运算项原方法无并行时间/s现方法无并行时间/s原方法时间/s现方法时间/s1L1,L3,L9 4 4 3 32L9逆矩阵2 9481 9249791753A3 4852 4631 196387
综合各表中数据可得：当矩阵规模较小时，ILU预处理及BICGSTAB算法对运行时间有一定改善，但效果并不明显；当系统规模较大时，L9矩阵稀疏度增高，越来越接近于1，稀疏技术的利用率变高。
通过原方法无并行和现方法无并行的运算时间对比，说明ILUTP及BICGSTAB算法可以提高迭代速度；引入并行计算后，加速效果更加明显，并行加速比接近于3.
5 结论
在插入式模拟技术的基础上，对L9矩阵的求逆过程进行优化，利用矩阵的稀疏特性引入ILUTP预处理技术，并与BICGSTAB算法相结合，提高了迭代速度，使矩阵转化为更有利于并行计算的形式；然后通过行压缩存储技术和Open MP中的并行功能，加速了整个求逆过程；最后分别对两个不同规模的算例进行分析计算，验证了本文方法能够缩短状态矩阵形成的时间，有利于电力系统小干扰稳定性的计算与分析。
在之后的研究中，一方面可以尝试不同的算法转换矩阵形式，比如将L9矩阵变换成对角加边的形式，再进行并行化处理；另一方面也可尝试使用 Open MP+MPI 混合编程，利用不同的并行处理方式加快程序执行。
[1] 刘畅,刘卉,王克文.特征值分析法在地区电网稳定分析中的应用[J].电测与仪表,2012,49(9):43-46.
[2] 张振,刘艳红.基于特征值的单机无穷大电力系统随机稳定性分析[J].郑州大学学报(工学版),2018,39(4):58-63.
[3] SAITOH H,MIURA K,ISHIOKA O,et al. On-line modal analysis based on synchronized measurement technology[C]//Proceedings of International Conference on Power System Technology. New York: IEEE, 2002:817-822.
[4] 钟志勇,谢志棠,王克文.适用于电力系统动态稳定分析的元件建模新方法[J].中国电机工程学报,2000,20(3):30-33.
[5] 罗丹,王克文,王君亮.小干扰稳定分析中状态矩阵的快速形成[J].电测与仪表,2015,52(10):56-60,91.
[6] 胡崴. 构建电力系统状态矩阵的并行计算研究[D].郑州:郑州大学,2017.
[7] 王宁. 电力系统状态空间方程的优化降阶研究[D].郑州:郑州大学,2017.
[8] 李晓梅,吴建平.Krylov子空间方法及其并行计算[J].计算机科学,2005,32(1):19-20,40.
[9] 范晋军.基于MATLAB软件的大地电磁测深正演模拟研究[J].能源技术与管理,2019,44(2):155-156.
[10] 李晓梅,迟利华.并行求解大型稀疏线性方程组的研究概况[J].指挥技术学院学报,1999,10(3):1-8.
[11] 李月卉. 电磁场数值求解中迭代方法与预条件技术研究[D].成都:电子科技大学,2011.
[12] 张芡. 大规模稀疏线性系统的稀疏近似逆预处理技术[D].北京:清华大学,2013.
[13] MAYER J. Alternative weighted dropping strategies for ILUTP[J]. SIAM journal on scientific computing, 2006, 27(4):1424-1437.
[14] SAAD Y. Iterative methods for sparse linear systems[M]. Philadelphia: SIAM, 2003.
[15] 吴建平,刘兴平,王正华,等.二维三温能量方程组离散求解的两个新预处理技术[J].计算物理,2005(4):283-291.
[16] 周凌焱,刘成龙,张强,等.稀疏矩阵压缩技术在CPⅢ网平差中的应用研究[J].铁道科学与工程学报,2014,11(6):142-147.