0 引言
电力计量仪器的精度对于测量至关重要,需定期检测其精确度。而传统的数显式仪表不全都具备通信接口,无法直接获取标准测量仪表和被测仪表的数值,只能通过双相机分别采集其在快速升压和降压过程中的图像,自动识别仪表读数,最后对比标准表和被测表的结果,以判定被测表的精确度[1]。然而,在仪表数字变化时,部分仪表会出现严重重影,光照不均的影响也较为突出,使得仪表字符无法正常二值化。
针对光照不均的影响,常用的图像增强算法包括灰度变换方法和直方图均衡化[3-4]。Kim等[5]使用快速迭代直方图方法增强图像的对比度,同时使用移动模板对图像的各个部分进行部分重叠的字块直方图均衡化。近年来,Retinex理论[6]研究逐渐成为图像增强、去雾的热点,并衍生出多种改进算法,如单尺度Retinex(SSR)[7]、同态滤波的Retinex[8]、双边滤波的Retinex[9]。刘健等[10]提出了基于Retinex理论与LIP模型的低照度图像增强方法,在HSV颜色空间,结合引导滤波与高斯平滑估计图像V分量的照度分量,利用LIP模型替代传统对数运算。这些方法机制简单并且具有较低复杂度,然而都容易丢失图像细节和增加过多的噪声。
常用的二值化方法主要分为两大类:全局阈值算法和局部阈值算法。全局阈值算法主要包括大律法(Otsu)、最大熵法、迭代法等,主要适用于光照均匀、灰度直方图有明显双峰的图像。局部阈值算法主要包括Sauvola算法、Niblack算法、Bernsen算法等,主要适用于光照不均的图像。以上算法都只能分离仪表图像的背景,无法分离数字重影。
为克服图像光照不均而导致的二值化困难,笔者根据文献[11]的方法,分别对具有强光照、弱光照、无底光的图像进行增强。通过对RGB彩色图进行灰度化,以灰度图的灰度级分布统计量作为输入,利用误差反向传播神经网络(back propagation neural network,BPNN)建立仪表字符图像全局阈值预测模型,预测理想二值化全局阈值,以分离重影。
1 仪表字符识别流程
笔者结合提出的BP神经网络[12]阈值预测算法和改进LeNet-5的字符识别模型,提出了一种新的仪表字符识别方法,具体流程如图1所示,其中BP神经网络模型和改进LeNet-5模型的训练过程提前完成,未在流程图中画出,主要包括以下步骤:
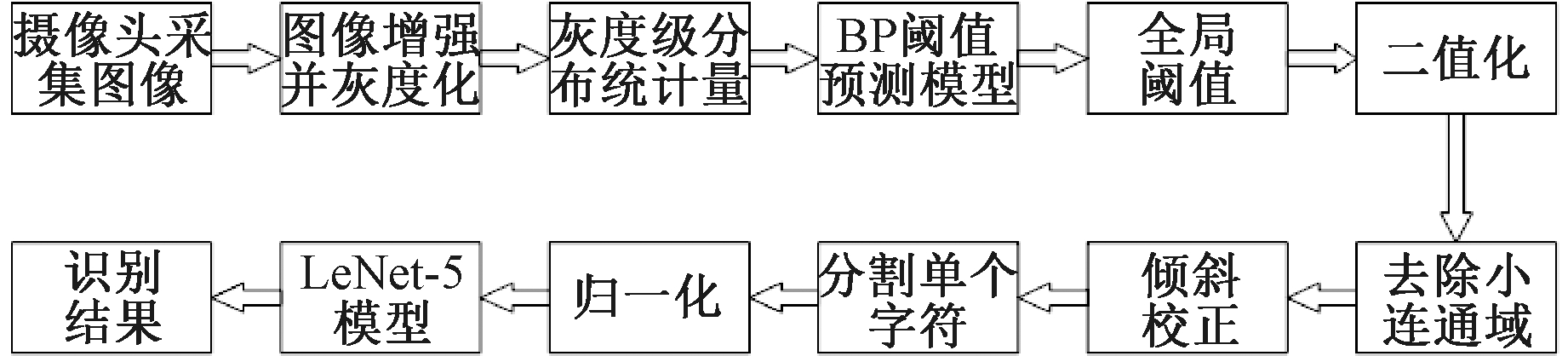
图1 仪表字符识别流程图
Figure 1 Flow chart of instrument character recognition
(1)摄像头采集图像,图像增强并灰度化。
(2)计算灰度图像的灰度级分布统计量,作为已经训练好的BP神经网络阈值预测模型的输入,预测理想的全局阈值,对图像进行二值化。
(3)去除二值图的小连通域,降低噪声对图像的影响。
(4)进行倾斜矫正,并将二值图分割成单个字符。
(5)对单个字符图像进行尺寸归一化,使其达到改进LeNet-5模型输入图像尺寸统一的要求。
(6)将尺寸归一化的图像输入到训练好的改进LeNet-5模型进行识别,得到仪表字符的识别结果。
其中,图像增强采用基于非线性函数变换的彩色图像校正方法,先将原始RGB图像转换到HSV颜色空间,对V分量采用多尺度加权高斯滤波的方式估计照射分量,然后根据估计光照分量的分布调整自适应增强函数的参数,得到两幅图像。利用图像融合从图像中提取重要信息来增强V分量。最后,将图像从HSV空间转换回RGB空间[11]。增强后的效果如图2所示。

图2 光照不均实验对比
Figure 2 Uneven illumination experiment comparison
从图2可以看出,增强后的图像相比原图亮度得以提高,整体对比度有明显提升,极大地提高了图像质量。增强后彩色图像的灰度化使用MATLAB的函数模型rgb2gray完成。
2 BP神经网络二值化阈值预测模型设计及优化
2.1 数据来源
为了验证本文算法的有效性,制作了一个含有复杂重影的仪表数字库。通过大恒MER-131-210U3C相机与50 mm镜头采集5 000张多种旋转角度、不同污渍同光照下电压快速变化时FLUKE289C万用表的图像,不同的污渍状态是通过在数字显示处加灰尘和水渍得到,采集过程中固定图像为1 141像素×317像素,并通过手动调整相机位置使得仪表数字全部出现在采集图像中,部分样本如图3所示。

图3 部分仪表数字样本
Figure 3 Digital sample of some instruments
2.2 样本预处理和标签制作
采集的样本需进行灰度化处理,再计算出样本的灰度级分布统计量。经分析发现,仪表字符中重影的灰度明显比真实数字低。图4(a)中显示的实际数字是31.936,而数字“1”、“9”和“3”有明显拖影,实际数字灰度偏暗,拖影数字偏亮,两者灰度存在明显区别,图4(a)对应的灰度直方图如图4(c)所示,根据灰度直方图手动调整二值化全局阈值,将灰度直方图分为前景和背景,前景则是最理想二值化结果,如图4(b)所示,二值化结果中无拖影,且数字完整,基本无噪声。
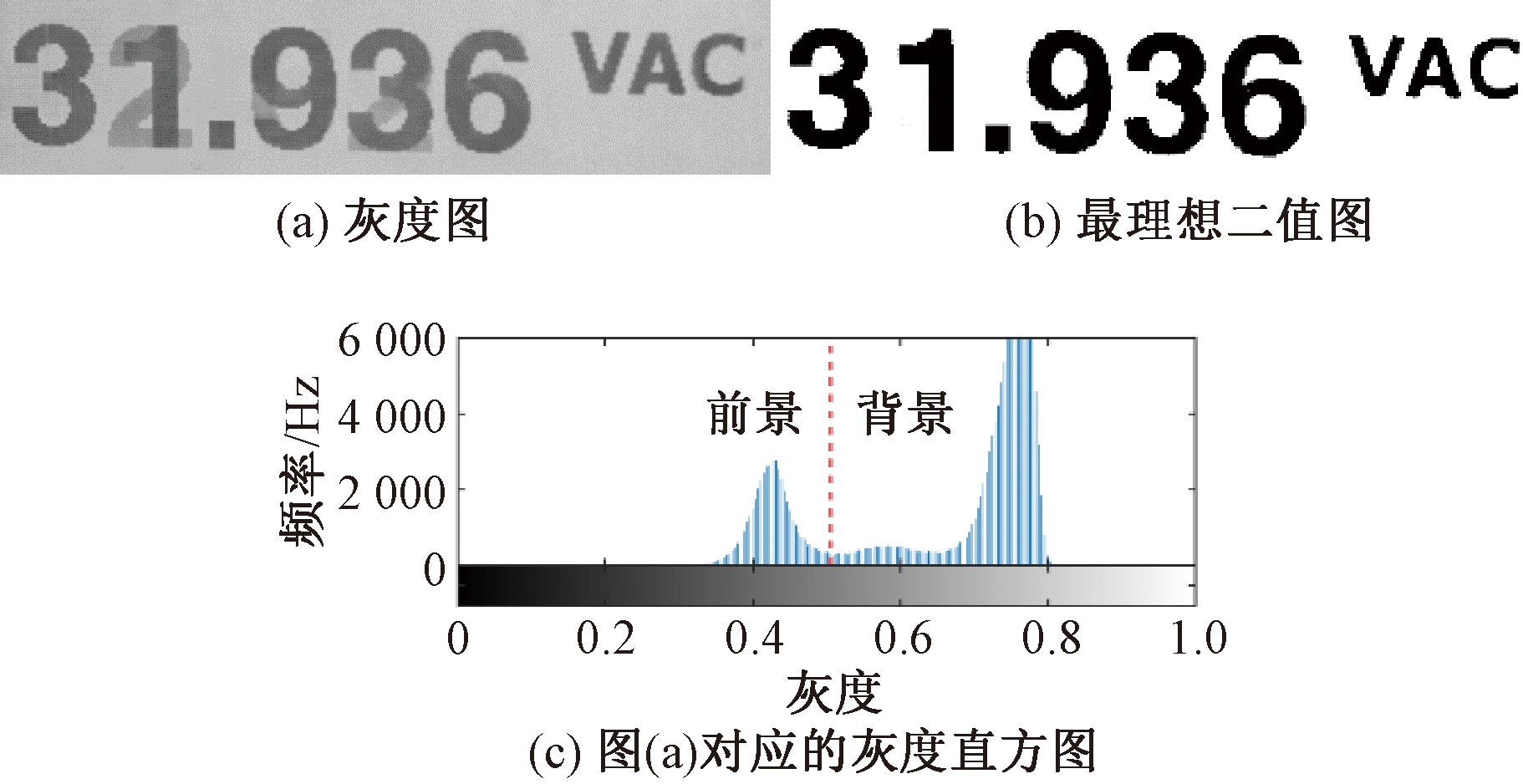
图4 重影字符的理想二值化过程
Figure 4 The ideal binarization process of ghost characters
灰度级分布统计量是灰度直方图数据的来源,直接反映了图像的灰度信息,包含了图片的拖影和真实数字以及背景的灰度信息,且与二值化全局阈值密切相关。笔者以灰度级分布统计量作为BP神经网络预测模型的输入,理想全局阈值作为网络的输出,对模型进行训练,并将预测值与实际值进行比较,最终实现BP神经网络[12]自动预测仪表数字图像的最佳二值化全局阈值。
在网络训练前,由于各灰度级统计量相差过大,导致网络的训练时间增加,甚至无法收敛。为保证网络的收敛速度和可靠性,必须对样本数据进行归一化处理。笔者采用最大值归一化处理:
(1)
式中:xn为样本的第n级灰度统计量;xmax为256维灰度级中最大灰度统计量;![]() 为xn归一化之后的输出值。归一化后BP阈值预测网络的输入量归一化到[0,1]。
为xn归一化之后的输出值。归一化后BP阈值预测网络的输入量归一化到[0,1]。
通过BP神经网络训练输出全局阈值的训练标签根据经验选取。从拍摄的图像库中选取4 000张样本,选取每个样本合理的全局阈值的最小值和最大值,并取平均值作为参考标准,手动调整直到图像清晰,此时对应的阈值即是理想二值化阈值,训练样本的数量为留下的4 000张样本的60%,测试样本为剩余的40%。
对训练样本进行预处理并制作阈值标签后,设计BP阈值预测网络的参数,使其能够通过样本的灰度级分布统计量预测出理想的二值化全局阈值。需要设计的参数包括隐含层的层数和节点数、节点转移函数和训练函数。
2.3 隐含层的层数和节点设计
在实际应用中,隐含层一般为1~2层,节点数大多根据以下经验公式[13]选择:
(2)
式中:l为隐含层节点数;n为输入节点数;m为输出节点数;a为1~10的整数。
BP阈值预测网络输入为256维的灰度级分布统计量,输出为单输出,则n和m分别设置为255和1,即隐含层节点数的范围为17~26。笔者选取不同的节点数和网络层数对网络进行训练,比较不同情况下的均方根误差ERM和相关系数R2[14]来评价训练网络的好坏。均方根误差衡量实际值和预测值之间的偏差,其值越小,模型越好。相关系数衡量预测值与实际结果的精确度,其值越接近于1,越精确。均方根误差和相关系数计算公式如下:
(3)
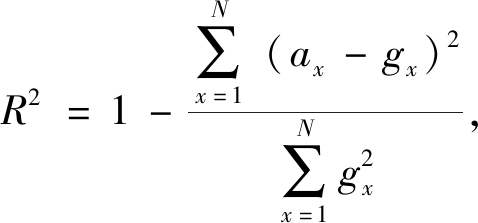
(4)
式中:N表示测试样本总数;ax为第x个样本的理想阈值;gx为第x个样本的预测阈值。
图5给出了不同隐含层数和节点数下的均方根误差值和相关系数,其中第2层隐含层的节点数为0时,代表只有1个隐含层。由实验结果可以看出,当有两个隐含层且节点数都为25时,均方根误差最小,相关系数最接近于1,此时隐含层的层数和节点数最优。因此,选取最优的隐含层结构为两隐含层,各层的节点数均为25。
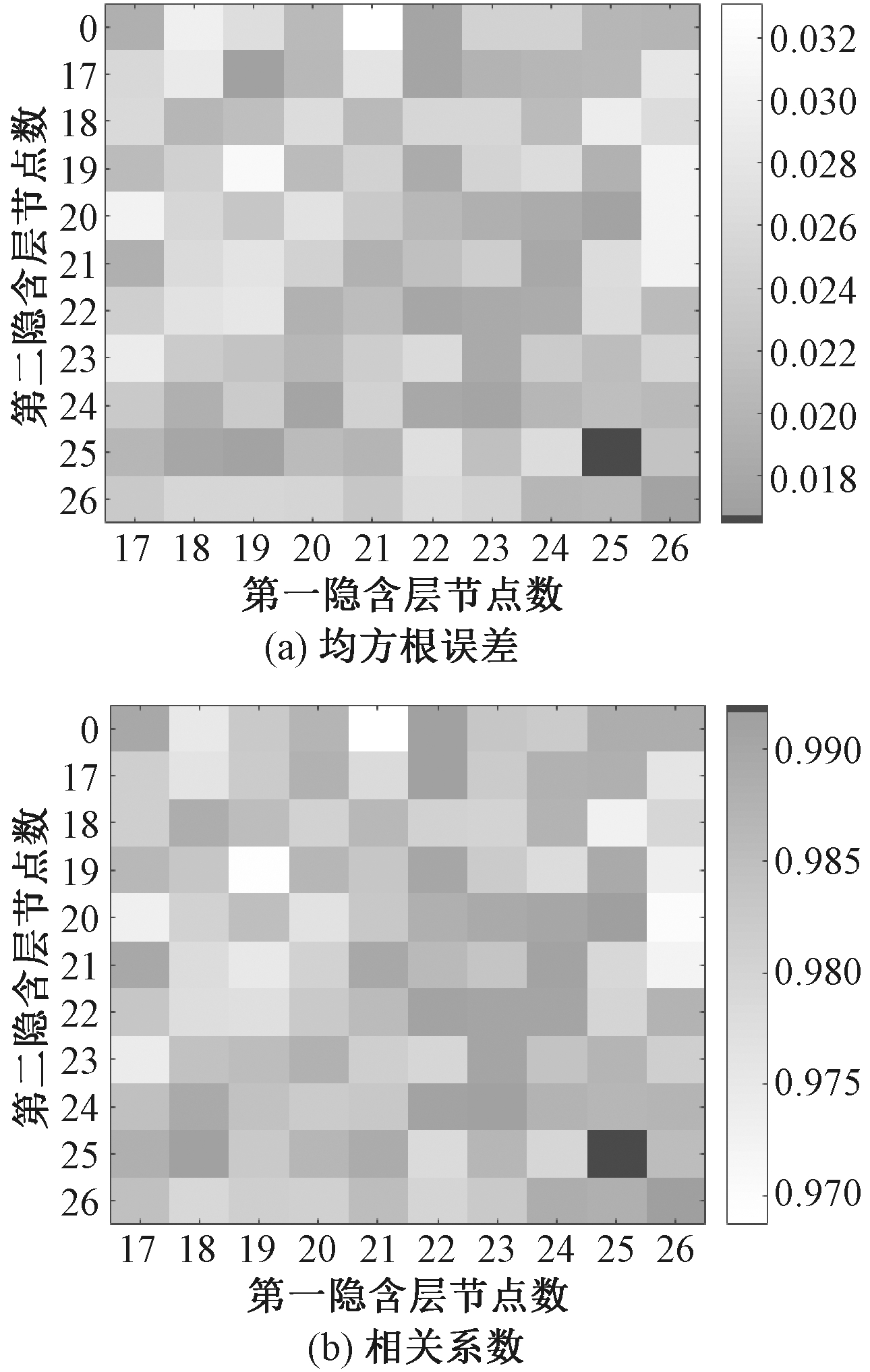
图5 不同隐含层数和节点数下的均方根误差和相关系数
Figure 5 Root-mean-square error and correlation coefficient under different hidden layers and nodes
2.4 节点传递函数的选择
节点传递函数对于预测的精度有着重要的影响[15],笔者在Logsig、Purelin和Tansig 3种节点传递函数中进行选择。不同节点传递函数的训练结果如表1所示,由表1可以看出,当隐含层和输出层函数都为Tansig时,相关系数最接近于1,均方根误差也最小。因此,笔者选择Tansig作为隐含层和输出层的节点传递函数。
表1 不同节点传递函数的训练结果
Table 1 Training results of transfer functions of different nodes
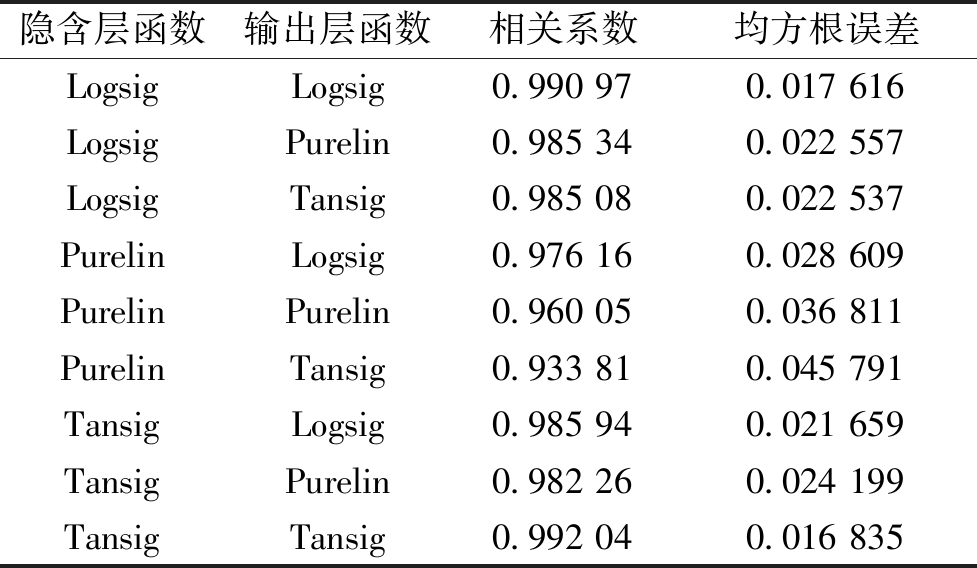
隐含层函数输出层函数相关系数均方根误差LogsigLogsig0.990970.017616LogsigPurelin0.985340.022557LogsigTansig0.985080.022537PurelinLogsig0.976160.028609PurelinPurelin0.960050.036811PurelinTansig0.933810.045791TansigLogsig0.985940.021659TansigPurelin0.982260.024199TansigTansig0.992040.016835
2.5 训练函数的选择
BP训练函数根据网络的输入和目标期望输出,修正BP网络的权值和阈值,最终达到设定的网络性能指标,其直接影响BP模型的预测精度[16]。笔者分别对Traingdx、Traingdm、Traingd、Trainrp、Trainlm、Traincgb和Trainscg等7种训练函数进行了测试,对比实验结果见表2。由表2可以看出,Traingdm训练函数对应模型的相关系数最接近于1,均方根误差也最小,优于其他6种训练函数。因此,笔者选择Traingdm作为BP训练函数。
表2 不同训练函数的训练结果
Table 2 Training results of different training functions
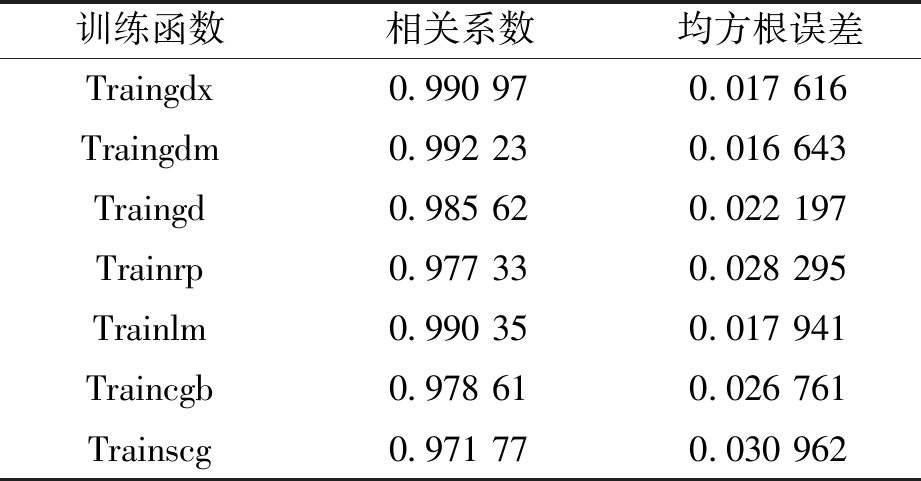
训练函数相关系数均方根误差Traingdx0.990970.017616Traingdm0.992230.016643Traingd0.985620.022197Trainrp0.977330.028295Trainlm0.990350.017941Traincgb0.978610.026761Trainscg0.971770.030962
3 阈值分割实验及字符识别
实验环境如下:Windows 10系统,Intel Core i5处理器,8 GB内存,编程软件为MATLAB2017a。
3.1 阈值分割实验
笔者选取大律法、最大熵法、迭代法、Sauvola算法、Niblack算法和Bernsen算法等6种经典的全局阈值和局部阈值算法作对比。实验所用的样本均是增强后的实验样本,结果如图6所示,各二值化方法的时间比较如表3所示。不同二值化算法的单张样本处理时间由相同条件下处理1 600张测试样本的总时间取平均求得。
表3 不同二值化算法的时间比较
Table 3 Time comparison of different binarization algorithms
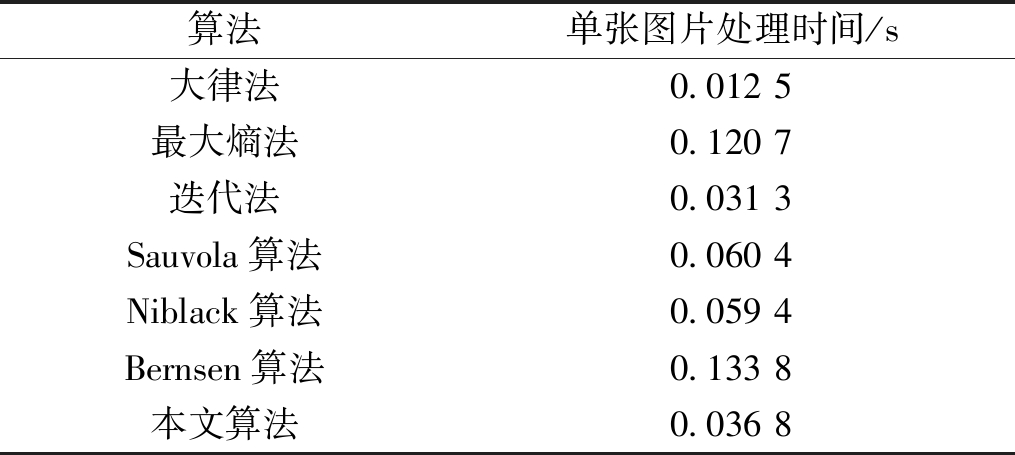
算法单张图片处理时间/s大律法0.0125最大熵法0.1207迭代法0.0313Sauvola算法0.0604Niblack算法0.0594Bernsen算法0.1338本文算法0.0368

图6 不同算法的二值化结果
Figure 6 Binary results of different algorithms
由实验结果可以看出,笔者提出的BP预测阈值的二值化方法效果最好,基本能分离重影;而其他6种方法二值化效果较差,无法分离重影。而且增强后二值化能分割出完整的字符。说明了本文算法的有效性。单个样本的处理时间仅0.036 8 s,仅比大律法和迭代法慢,说明本文算法的实时性较好,满足仪表字符的快速识别要求。而本文算法的网络结构简单,由于输入层和最终输出层结点数量是确定的,可以视为常量,中间的隐含层节点数均设定为25,反向传播的时间复杂度和前馈计算相同,所以对一个样本的前馈计算时间复杂度应该是O(N)。
3.2 倾斜矫正和字符分割
倾斜矫正算法[17]采用先创建最小外接矩形并计算出倾斜角度,后仿射变换,具体过程如图7所示。

图7 校正算法流程图
Figure 7 Flow chart of calibration algorithm
字符分割算法采用投影法,包括垂直投影和水平投影两步,可以很好地对经过倾斜矫正的二值化仪表字符进行分割。分割过程如图8所示,由图8可以看出,数字、小数点和“VAC”字符水平投影的区间不同。
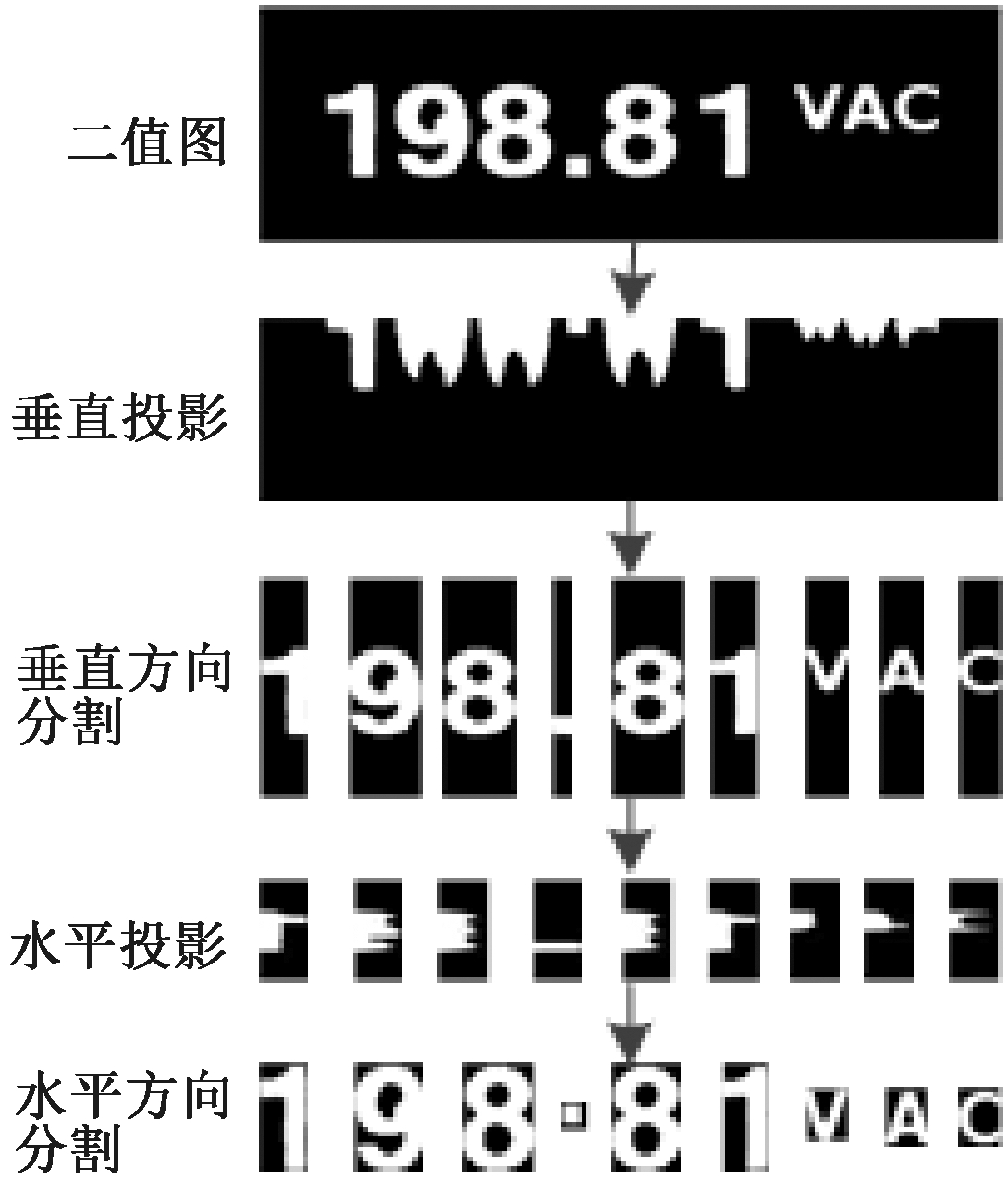
图8 投影法分割流程图
Figure 8 Flow chart of projection method
笔者主要考虑电压变化下仪表数字识别,而“VAC”字符不会随电压改变而改变,小数点可以直接通过水平投影区间判断,只需要识别重影数字,因此,在分割时只保留数字。
3.3 重影字符识别实验
LeNet-5是适用于手写字符识别的经典卷积神经网络,主要包括1个输入层、1个输出层、2个卷积层、2个池化层和3个全连接层。笔者对LeNet-5进行了改进,并应用于仪表字符识别,主要改进如下:
(1)LeNet-5使用的sigmoid激活函数会出现梯度消失问题且泛化能力差,而ReLU可以很好地解决此问题,并且收敛速度更快,故采用ReLU替换sigmoid函数。
(2)使用RMSprop优化算法可以解决学习率选择困难和避免陷入局部最小值的问题,且收敛速度更快,因此采用RMSprop优化算法更新权重和偏置。
对于采集的重影字符库,传统大律法二值化后单个字符图像如图9所示,图像包含大量重影,难以辨别显示的数字。然而,本文算法分割得到单个字符如图10所示,图像基本不包含重影,可以达到识别要求。

图9 大律法二值化单个字符部分样本图
Figure 9 A part of sample image of the binarization of a single character in the Great Law

图10 本文算法分割后单字符部分样本图
Figure 10 Part of Sample image of single-character after segmentation algorithm in this paper
将训练样本和测试样本分割后的单个字符进行数字归类,制作数字标签,使用训练样本和测试样本分别对改进LeNet-5模型进行训练和测试。
改进LeNet-5和原始的LeNet-5参数设置如下:输入图像为32像素×32像素,训练周期为3 000,batch size为64,学习率为0.000 1。SVM使用的LIBSVM工具包,采用线性核函数。HOG特征提取使用的是MATLAB自带函数,其cell size设置为3×3。各参数由多次实验取平均值得到。
实验结果如表4所示,由表4可以看出,改进LeNet-5和其他方法都能达到很高的识别率,表明本文二值化算法性能好,二值化后样本区分度高,但是改进LeNet-5不需要手动提取特征,在单个样本识别速度上比其他方法更快,虽然改进LeNet-5训练时间更长,但是训练过程可以预先完成,不影响实时识别。因此,改进LeNet-5更适合仪表数字的实时识别。
表4 字符识别结果
Table 4 Character recognition results
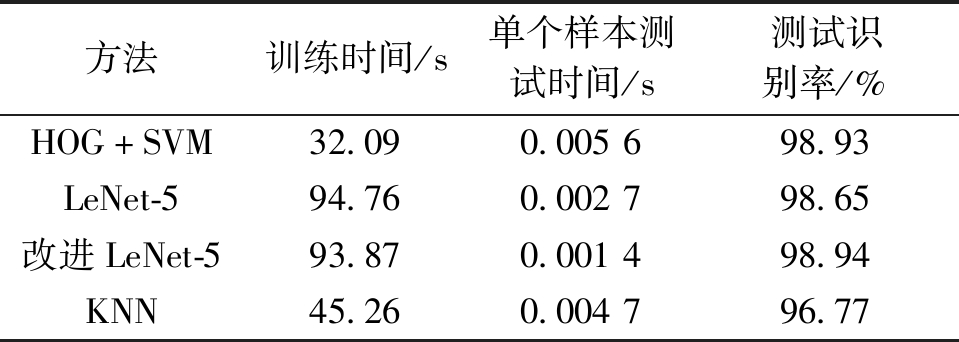
方法训练时间/s单个样本测试时间/s测试识别率/%HOG+SVM32.090.005698.93LeNet-594.760.002798.65改进LeNet-593.870.001498.94KNN45.260.004796.77
根据本文提出的仪表重影字符识别方法,并通过MATLAB设计GUI交互界面,可以准确识别出仪表重影字符上显示的数字,如图11所示。
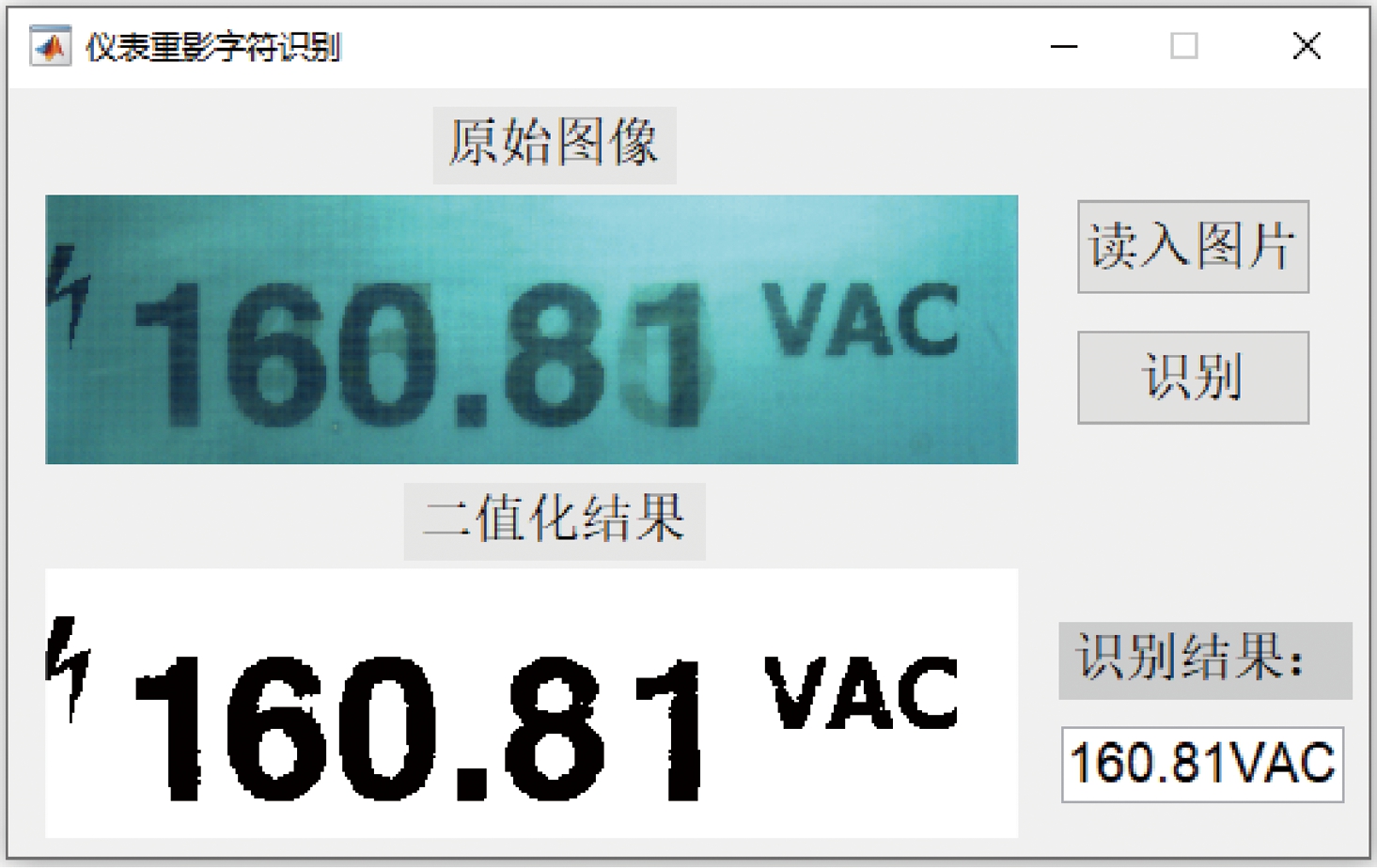
图11 仪表重影识别交互界面
Figure 11 Instrument ghost recognition interactive interface
4 结论
笔者提出了一种基于BP神经网络的二值化方法,根据重影数字图像的灰度级分布统计量预测理想二值化全局阈值,在不同光照情况下该二值化方法能够有效地消除仪表数字刷新时形成的重影。并采用改进LeNet-5对分割后的二值化单个字符进行识别。实验结果表明,提出的二值化方法优于现有的大律法、最大熵法、迭代法、Sauvola算法、Niblack算法和Bernsen算法,改进LeNet-5网络优于传统HOG+SVM算法和原始的LeNet-5网络,具有很高的实用价值。
[1] 孙国栋,梅术正,汤汉兵,等.基于密度特征与KNN算法的最优特征维数选择[J].现代电子技术,2018,41(16):80-83.
[2] 李智成,李文婷,梅术正,等.基于机器视觉的高压计量数显表自动校对系统[J].电测与仪表,2017,54(20):105-109,121.
[3] 李娜.利用灰度变换法增强数字图像[J].北京工业职业技术学院学报,2009,8(3):36-39.
[4] KANDHWAY P,BHANDARI A K,SINGH A.A novel reformed histogram equalization based medical image contrast enhancement using krill herd optimization[J].Biomedical signal processing and control,2020,56:101677.
[5] KIM J Y,KIM L S,HWANG S H.An advanced contrast enhancement using partially overlapped sub-block histogram equalization[J].IEEE transactions on circuits and systems for video technology,2001,11(4):475-484.
[6] 梁琳,何卫平,雷蕾,等.光照不均图像增强方法综述[J].计算机应用研究,2010,27(5):1625-1628.
[7] JIN H,TU L,DENG X.Night image enhancement algorithm based on retinex theory[J].International journal of advancements in computing technology,2011,3(10):291-298.
[8] 董静薇,徐博,马晓峰,等.基于同态滤波及多尺度Retinex的低照度图像增强算法[J].科学技术与工程,2018,18(22):238-242.
[9] 任崇巍.基于双边滤波和Retinex算法的货车图像预处理方法[J].现代城市轨道交通,2019(6):39-43.
[10] 刘健,郭潇,徐鑫龙,等.基于Retinex理论的低照度图像增强技术[J].火力与指挥控制,2019,44(9):139-143.
[11] WANG W C,CHEN Z X,YUAN X H,et al.Adaptive image enhancement method for correcting low-illumination images[J].Information sciences,2019,496:25-41.
[12] 查刘根,谢春萍.应用四层BP神经网络的棉纱成纱质量预测[J].纺织学报,2019,40(1):52-56,61.
[13] 夏克文,李昌彪,沈钧毅.前向神经网络隐含层节点数的一种优化算法[J].计算机科学,2005,32(10):143-145.
[14] 冉成科,夏向阳,杨明圣,等.基于日类型及融合理论的BP网络光伏功率预测[J].中南大学学报(自然科学版),2018,49(9):2232-2239.
[15] 范伟,林瑜阳,李钟慎.基于BP神经网络的压电陶瓷蠕变预测[J].计量学报,2017,38(4):429-434.
[16] 李标,王磊,朱金营,等.BP网络训练函数选取及其岩土工程应用分析[J].西部探矿工程,2008,20(10):58-60.
[17] 李少辉,周军,刘波,等.基于机器视觉和神经网络的低质量文本识别研究[J].机电工程,2018,35(9):1006-1010.