0 引言
无刷直流电机(brushless dc motor)因其依靠电子换相，同时又具备直流电机带载能力强、动静态特性好等优点，被广泛应用于各种控制系统中[1]。由于传统无刷直流电机的换相所依靠的位置传感器不易准确安装、易受环境干扰等缺点限制了电机在很多场合的使用，因此文献[2]提出用无位置控制技术来判断转子位置成为当今研究热点。目前国内外学者针对无位置控制技术的研究提出过很多方法，按照检测原理的不同可分为反电动势法、磁链法、续流二极管法、电感法和状态观测器法等。文献[3-4]通过捕获反电动势过零点来指导电机换相，但在静止或低速状态下反电动势为零或很小,无法找到准确换相点，故低速状态下并不适用。文献[5]利用磁链法检测转子位置，适用于整个速度范围，但低速状态下由于电流积分导致累积误差较大且计算结果易受电机参数变化的影响。文献[6]通过检测悬空相二极管有无电流流过来指导电机换相，但该方法电机转矩脉动较大，同时二极管的换相干扰不好滤除。文献[7-8]通过多次检测绕组电感来获取换相点，但不适用于负载变化的情况。文献[9-10]利用状态观测器法将电机的转速、电压、电流等变量作为状态观测量，根据数学模型建立状态观测器来估算转子位置，在电机控制系统中取得了很好的效果。
滑模观测器结构简单、抗干扰性能强，相较于其他观测器更适用于电机控制，但传统滑模观测器由于符号函数的高频切换使观测到的波形存在剧烈的抖振现象，对此文献[11]提出用饱和函数作为系统切换函数，但对抖振的削弱并不明显，仍需对系统滤波补偿。笔者将sigmoid函数应用于滑模观测器，并根据Lya-punov定理推导出可随转速变化的滑模增益，使系统抖振得到很好的削弱，实现了较宽范围内的反电动势估计。根据线反电动势的特性，得到电机的换相信号和速度估计值应用于电机闭环控制系统中。仿真和实验结果验证了该观测器的有效性。
1 BLDCM数学模型
图1为无刷直流电机主电路原理图，假设电机处于理想状态下。
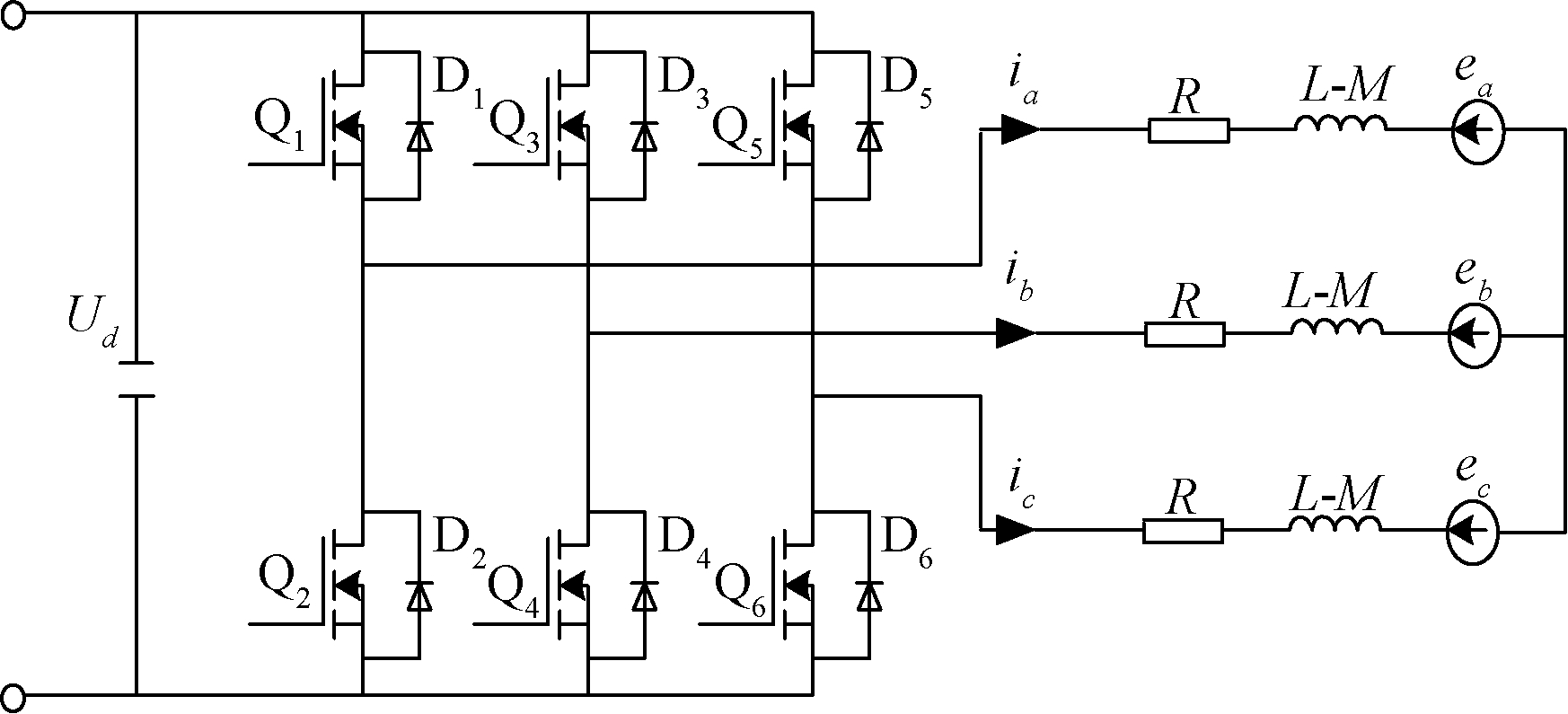
图1 无刷直流电机主电路原理图
Figure 1 Main circuit schematic diagram of brushless dc motor
由于相电压无法准确得到，笔者通过线反电动势指导电机换相，可得到线电压模型：
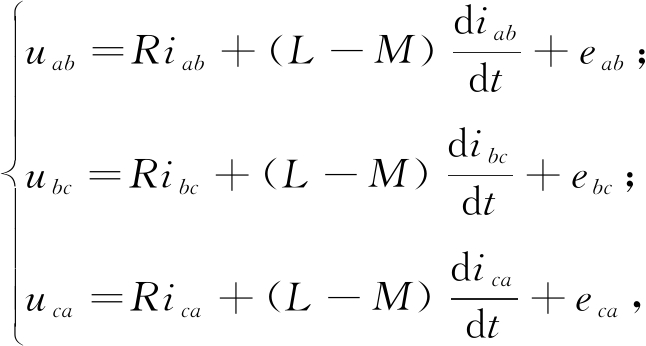
(1)
式中：uab、ubc、uca为绕组线电压，V；iab、ibc、ica为相电流差，A； eab、ebc、eca为线反电势，V； L和M为绕组自感和互感，H；R为相电阻，Ω。
2 BLDCM无位置控制系统设计
2.1 改进滑模观测器的设计
线反电动势eab、ebc、eca之和为0，所以只需观测eab、ebc，且可以认为在每个采样期间其导数为0。结合方程式(1)，可得传统的滑模观测器[9]：
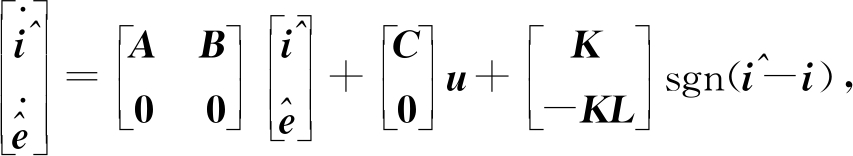
(2)
式中：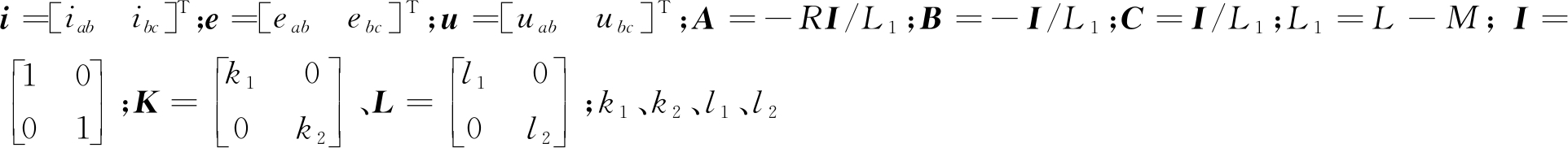
为滑模增益；
为相电流差和反电动势的观测值;sgn为符号函数。
当观测器观测的两相电流之差与实际相电流差不同时，为了使滑模观测器运行在滑模面上，此时的
项相当于反馈控制系统中的负反馈，使两相电流之差尽快逼近实际值[12]。由于符号函数在0处的突变，使其观测的反电动势存在剧烈的抖振现象，笔者利用sigmoid函数的连续光滑特性来削弱抖振，sigmoid函数如下式所示：
(3)
式中：f(t)为sigmoid函数，函数曲线示意图如图2所示;参数a决定了曲线的斜率，用于不同速度环节。增大a可以加快滑模趋近速度，但加剧了系统抖振，为了削弱系统抖振，取a=1。
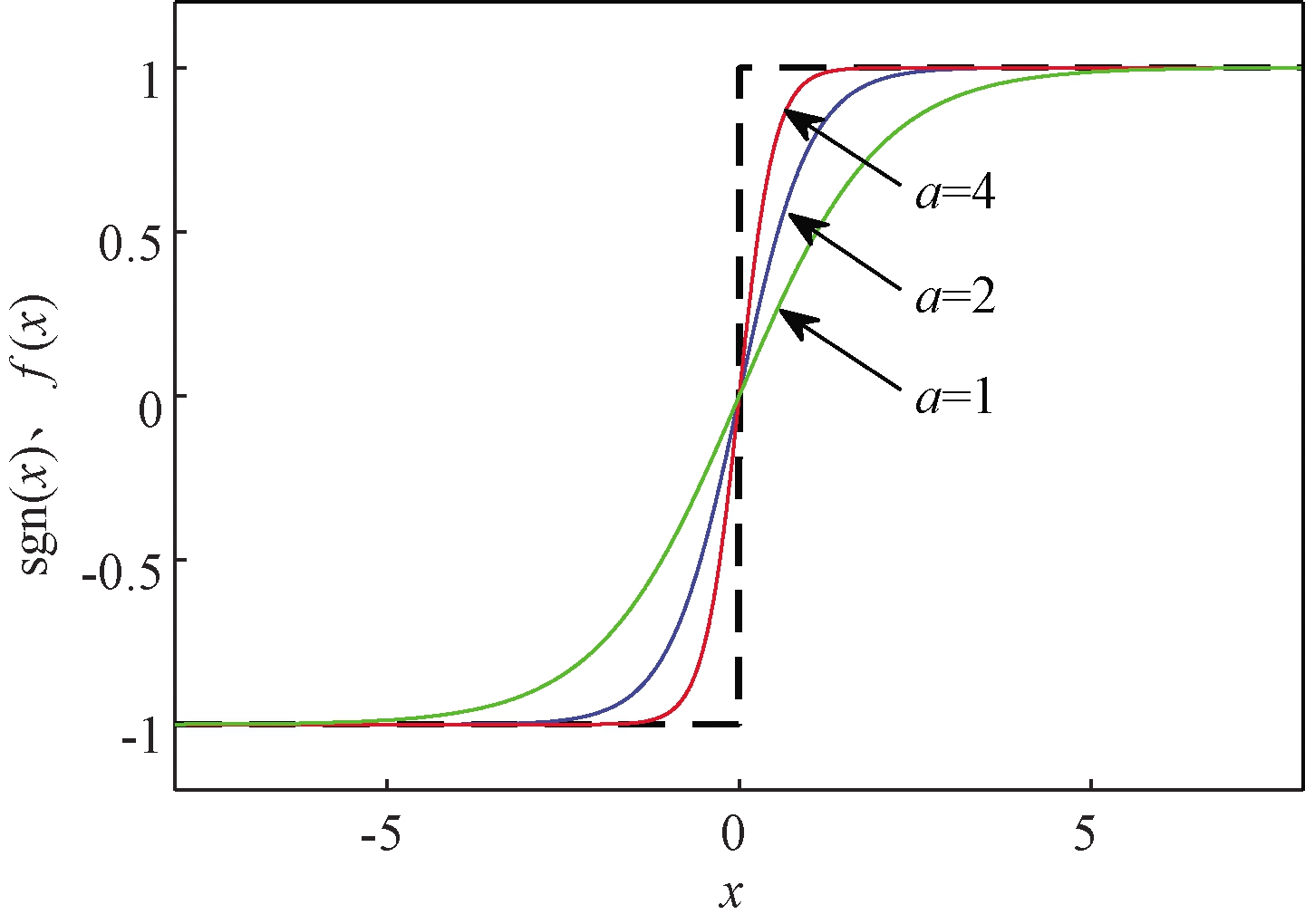
图2 符号函数、sigmoid函数
Figure 2 Symbol function,sigmoid function
应用sigmoid函数得到的改进滑模观测器为：
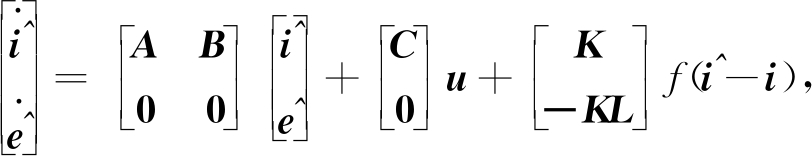
(4)
将式(4)减去电机状态方程，可得[12]：
(5)
式中：
分别为相电流差和反电动势的观测误差。
2.2 改进滑模观测器的增益选取
根据滑动模态存在性要求，观测器在有限时间内进入滑动模态的条件为
定义Lyapunov方程为：
(6)
对Vi求导，并将式(5)和
代入，可得
的充分条件为：
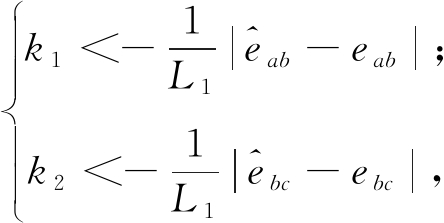
(7)
系统进入滑动模态后，有
代入式(5)，得
(8)
根据Lyapunov稳定性判定定理，取：
(9)
对上式求导，并将式(8)和
代入，可得Ee收敛到0的充分条件为：
(10)
滑模增益的选取至关重要，理想的滑模增益使系统尽快趋近于滑模面，同时抖振较小。传统滑模观测器是通过式(7)选取一个固定值，若选取不当则无法准确观测到反电动势，给位置和速度估计带来误差。为了尽快趋近滑模面，通常选用较大的滑模增益，但在低速时高频切换会加剧系统抖振，使反电动势的观测误差增大。因此最佳的滑模增益应该能随转速变化，笔者提出一种新的滑模增益，能给出较宽速度范围的最佳取值。取
(11)
由式(7)得：
(12)
式中：
为固定增益；
为反馈转速；ke为反电动势系数。
根据上述分析，笔者所提滑模观测器控制框图如图3所示。
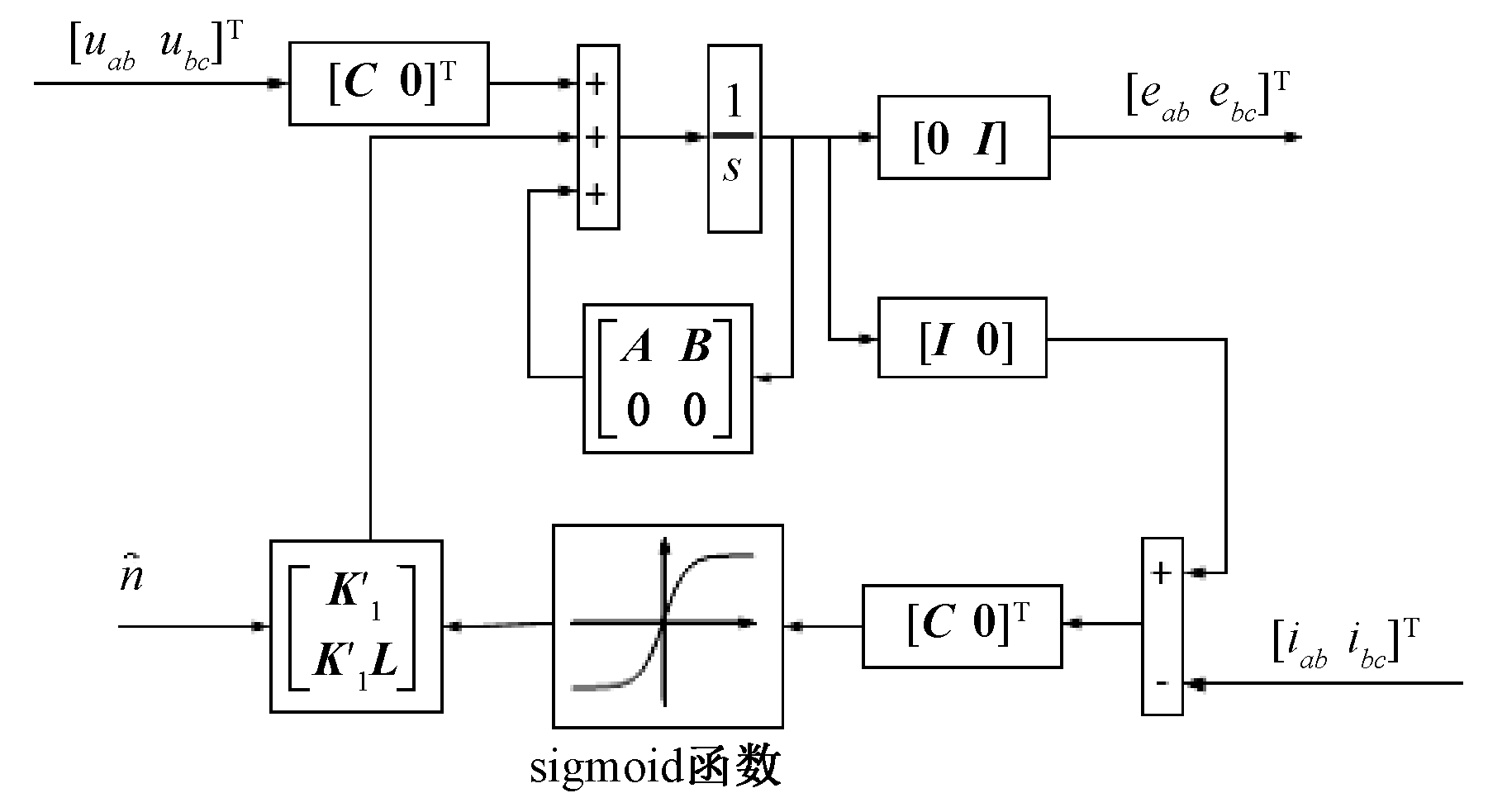
图3 改进滑模观测器框图
Figure 3 Block diagram of improved sliding-mode observer
2.3 基于线反电动势的换相策略与速度估计
对于三相六状态控制的无刷直流电机，在一个电周期内，其霍尔信号、相反电动势和线反电动势的关系如图4所示。
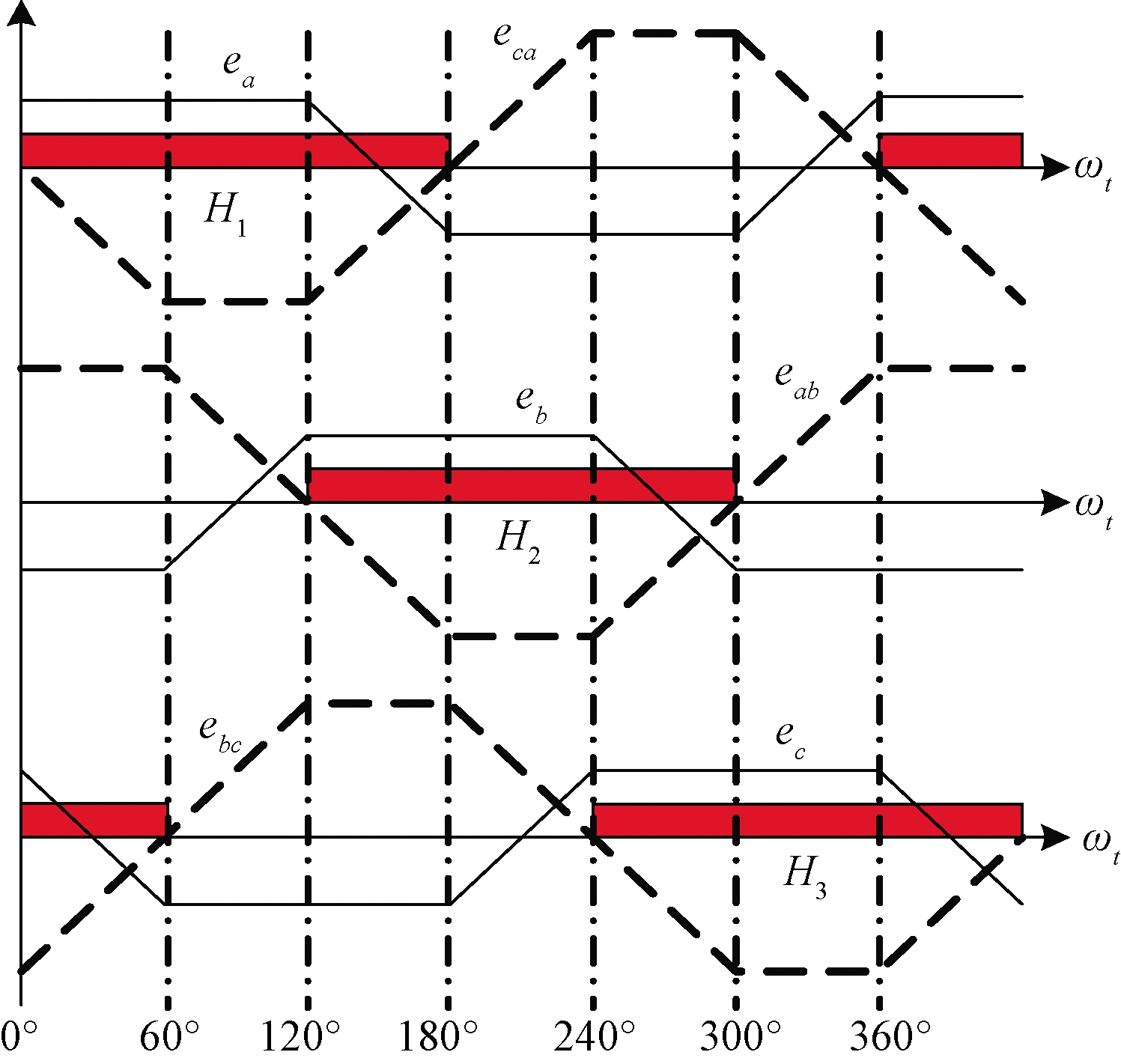
图4 无刷直流电机反电动势与换相信号的关系
Figure 4 The relationship between brushless dc motor back-EMF and commutation signal
由图4知，线反电动势eab、ebc、eca相互之间的正负关系共有六种状态，每种状态值对应一种霍尔信号值，所以改进滑模观测器观测到线反电动势后，即可根据线反电动势的符号判断出此时的导通相。
由线反电动势最大值与电机转速的关系可得：
Em=2ken,
(13)
式中：Em为线反电动势的幅值；n为电机转速。
线反电动势呈梯形波周期变化，每导通相均有一线反电动势处于最大值，如表1所示。电机转动过程中，通过线反电动势符号可得此时的线反电动势最大值，再根据式(13)可求出当前转速。
表1 线反电动势符号、霍尔信号和线反电动势最大值的关系
Table 1 Relation between line back-EMF symbol, Hall signal, and line back-EMF maximum
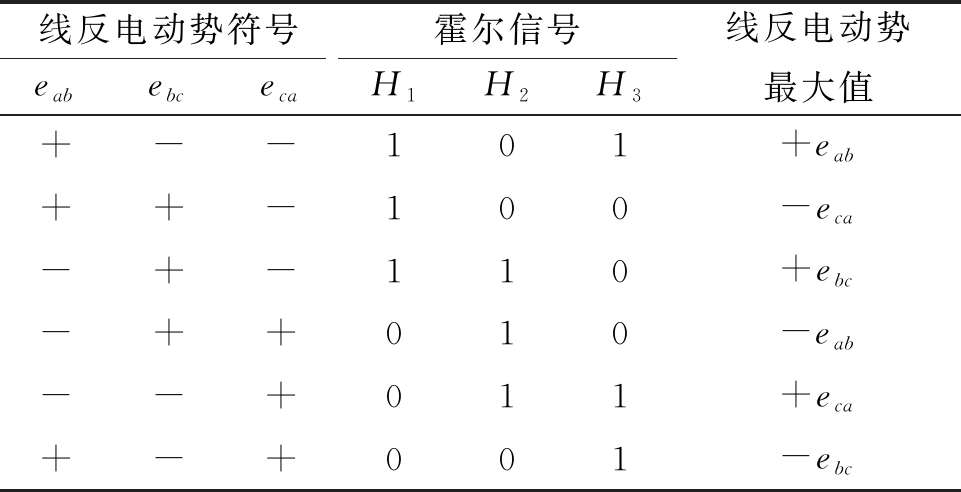
线反电动势符号霍尔信号eabebcecaH1H2H3线反电动势最大值+--101+eab++-100-eca-+-110+ebc-++010-eab--+011+eca+-+001-ebc
3 仿真分析
根据上述所提改进滑模观测器，笔者搭建了如图5所示的simulink仿真模型，电机仿真参数的设置与实验电机参数保持一致，如表2所示。 控制模型采用双闭环控制和三段式启动，并采用pwm-on的调制方式。滑模增益选取为给定增益
与反馈转速相乘构成随转速可变的滑模增益。
图6、7给出了负载T=TN条件下，电机转速分别为400 r/min、3 000 r/min时传统滑模观测器和改进滑模观测器的线反电动势观测值。通过对比发现，传统滑模观测器在低速时抖振非常剧烈，高速时的抖振虽较低速有所减弱，但仍无法找到准确换相点。笔者所提观测器的滑模增益随转速变化，在低、高速均可得到更加平滑准确的线反电动势观测值。得到线反电动势观测值之后，将线反电动势真实值与线反电动势观测值做差，得到线反电动势观测误差值，图8、9分别为转速在400 r/min、3 000 r/min时两种滑模观测器的线反电动势观测误差曲线。结合图8、9可知，转速为400 r/min、3 000 r/min时，传统滑模观测器线反电动势观测误差最大值分别为±0.23 V、±1.15 V，改进滑模观测器线反电动势观测误差最大值分别为±0.07 V、±0.52 V，与传统滑模观测器观测误差最大值相比，改进滑模观测器在转速为400 r/min、3 000 r/min时，线反电动势观测误差最大值分别降低了70%、54.8%，有效地提高了线反电动势观测精度。图10为转速在400 r/min时两种观测器线反电动势得到的换相信号估计值与实际值对比。由于滤波的影响，使得传统滑模观测器换相信号估计值滞后于实际换相信号一定角度，易造成电机换相失败；而改进滑模观测器获得的换相信号接近重合于真实换相信号，满足电机换相要求。
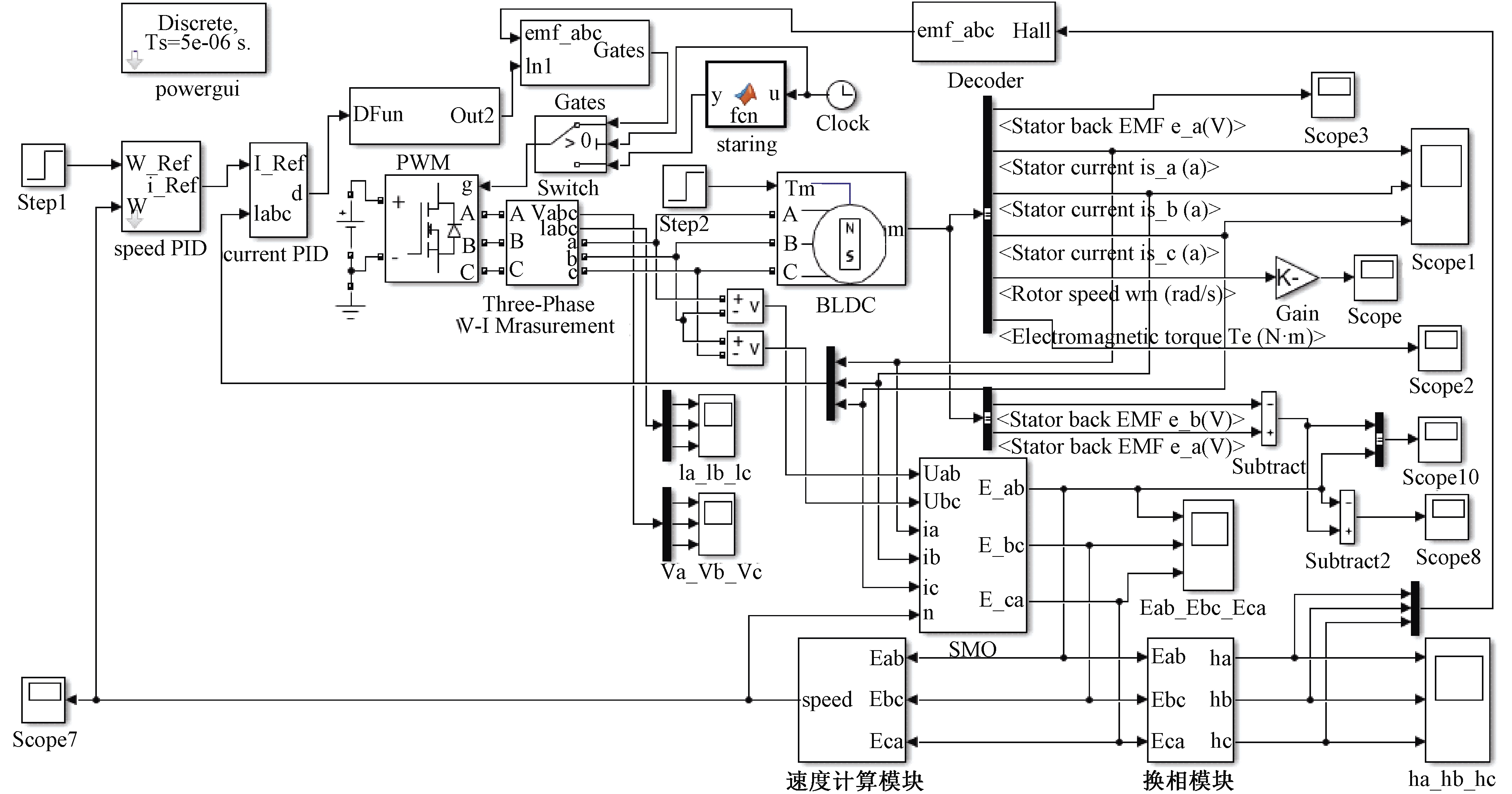
图5 无刷直流电机simulink仿真模型
Figure 5 The simulink simulation model of brushless dc motor
表2 仿真实验选用电机参数
Table 2 Motor parameters selected in this paper
参数参数值额定电压/V24额定功率/W26额定转速/(r·min-1)3 000极对数4线电阻/Ω1.8线电感/mH0.54
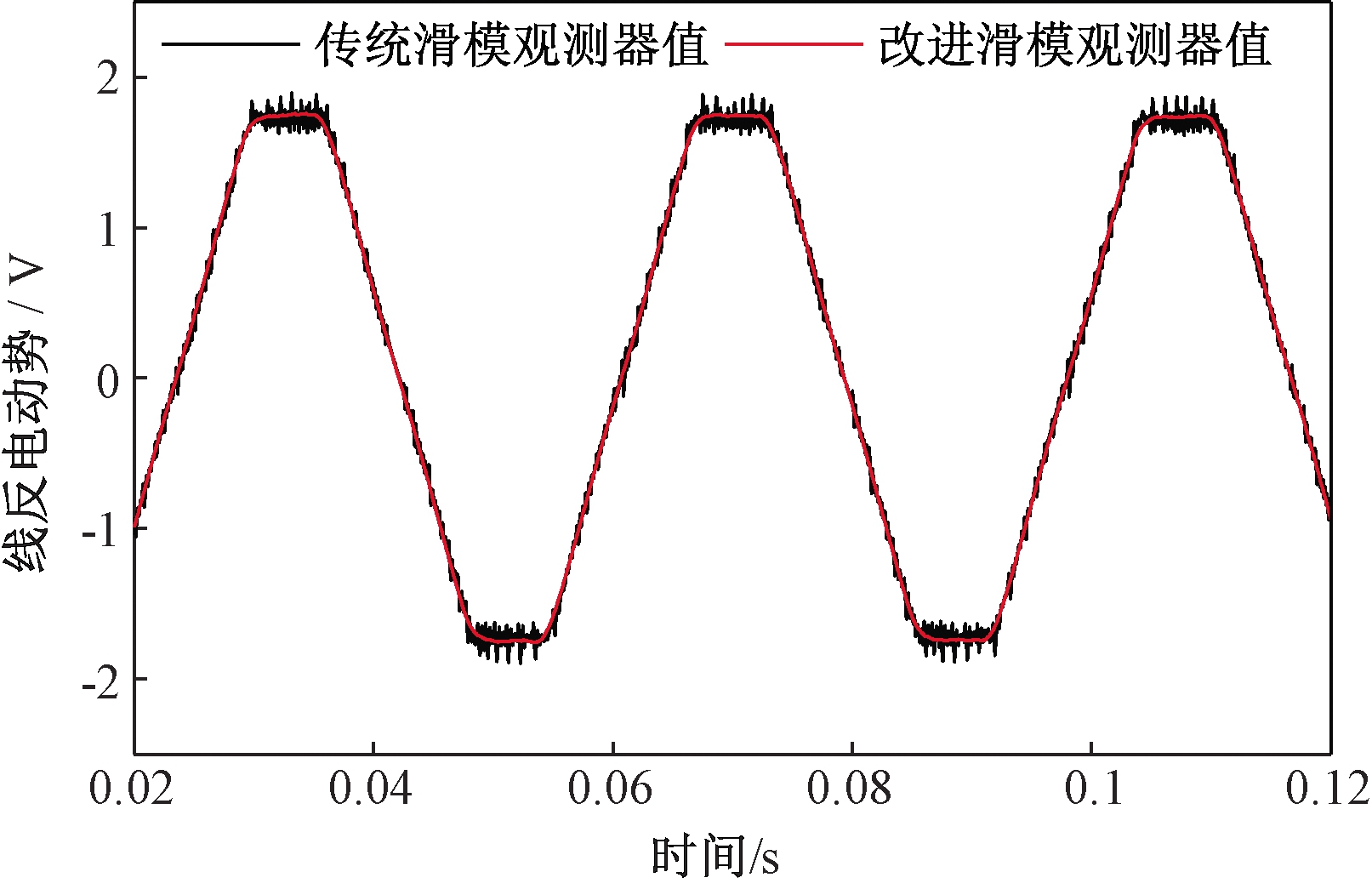
图6 转速为400 r/min时线反电动势观测值
Figure 6 The measured value of line back-EMF at 400 r/min
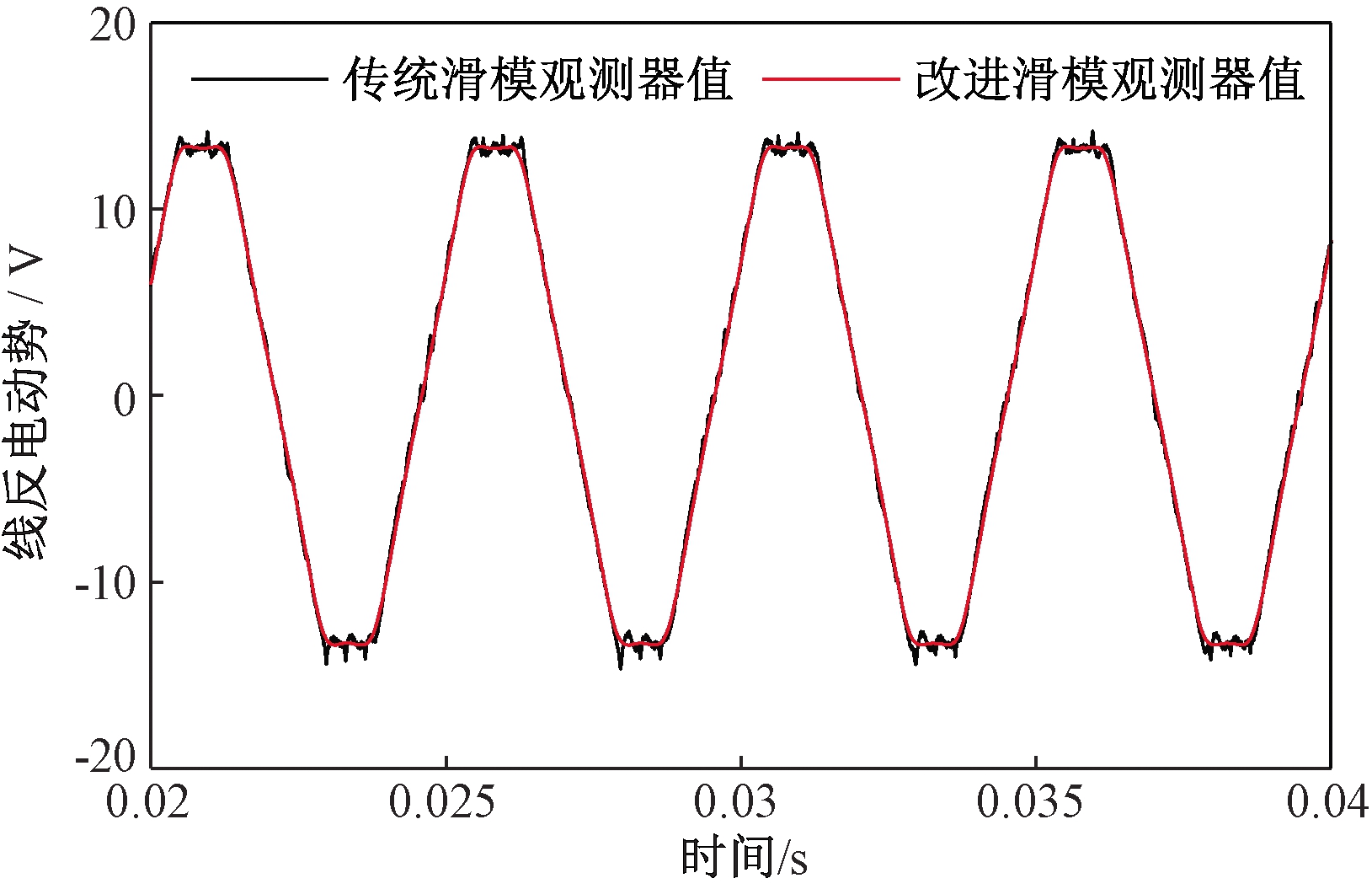
图7 转速为3 000 r/min时线反电动势观测值
Figure 7 The measured value of line back-EMF at 3 000 r/min
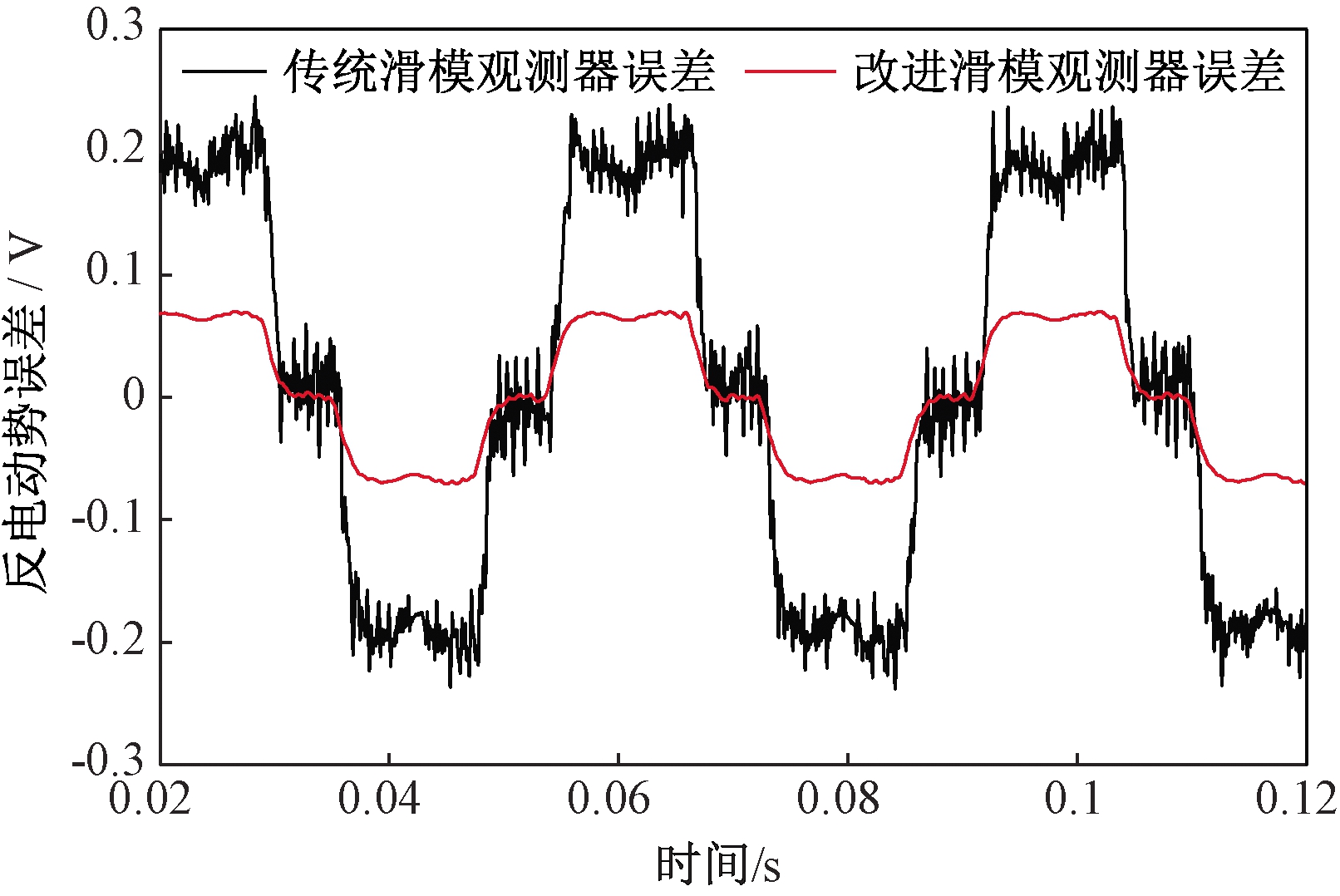
图8 转速为400 r/min时两种观测器线反电动势观测误差曲线
Figure 8 The line back-EMF error observation curves of two kinds of observer at 400 r/min
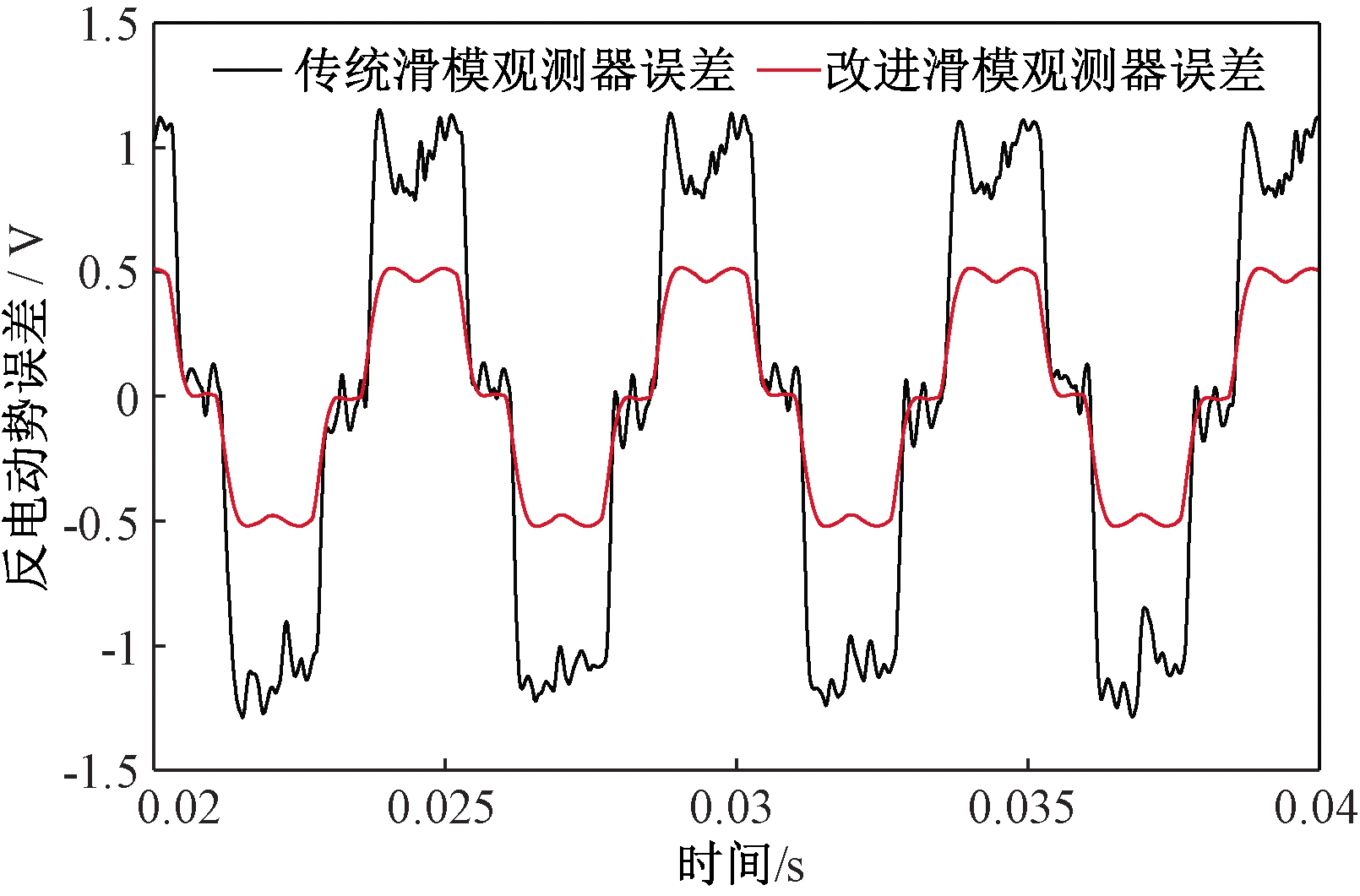
图9 转速为3 000 r/min时两种观测器线反电动势观测误差曲线
Figure 9 The line back-EMF error observation curves of two kinds of observer at 3 000 r/min
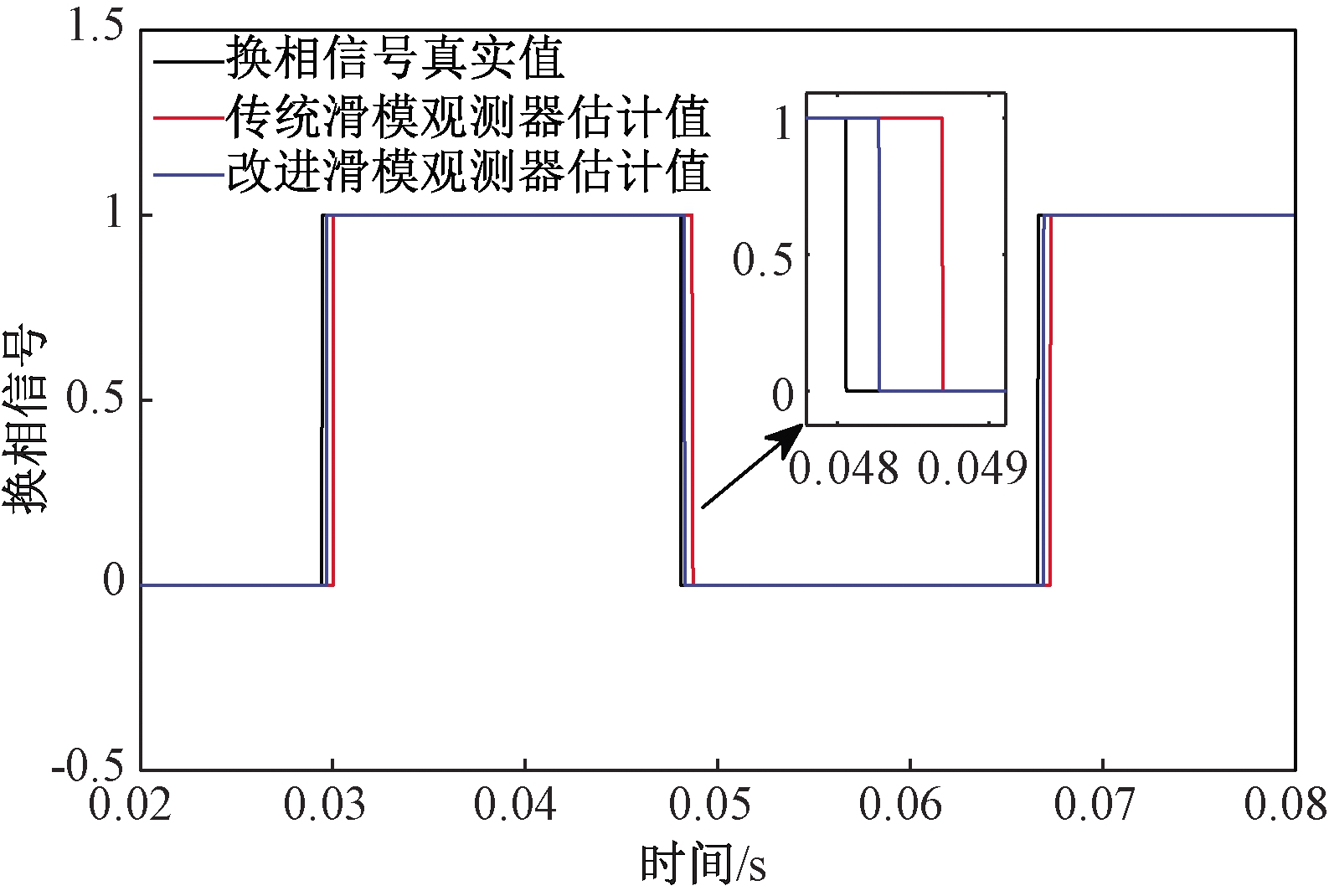
图10 转速为400 r/min时换相信号估计值与实际值
Figure 10 Commutation signal estimate value and actual value at 400 r/min
图11是在负载转矩T=TN条件下，改进滑模观测器在电机给定转速突变前后的观测结果。由图可见，改进滑模观测器在转速为400 r/min和3 000 r/min时均可得到平滑准确的反电动势观测值，给定转速突变后，改进滑模观测器的估算转速能够快速无静差地跟踪实际转速，提高了控制系统的鲁棒性。
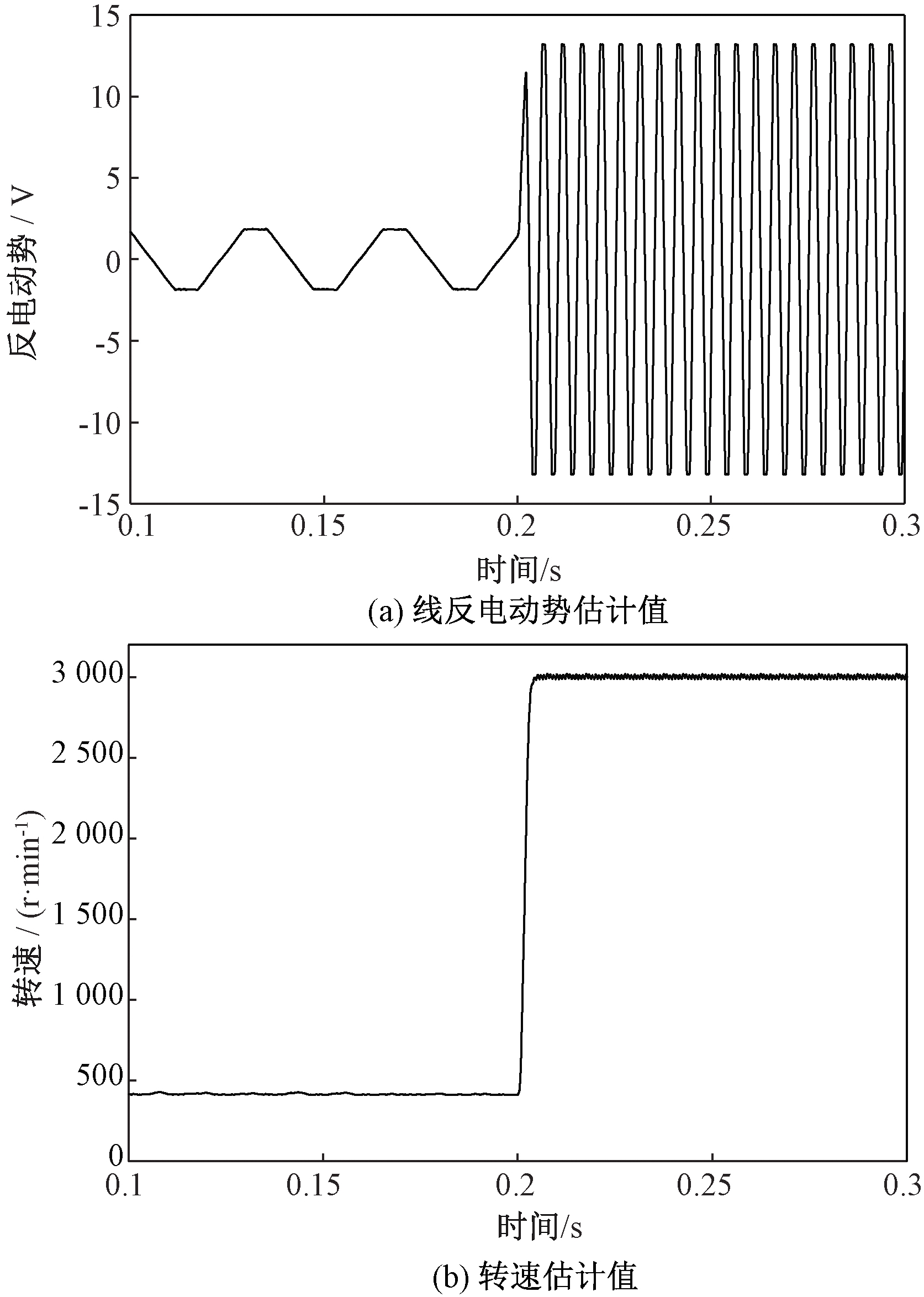
图11 转速突变时改进滑模观测器的观测波形
Figure 11 The observation waveform of improved sliding-mode observer when the speed changes suddenly
4 实验验证
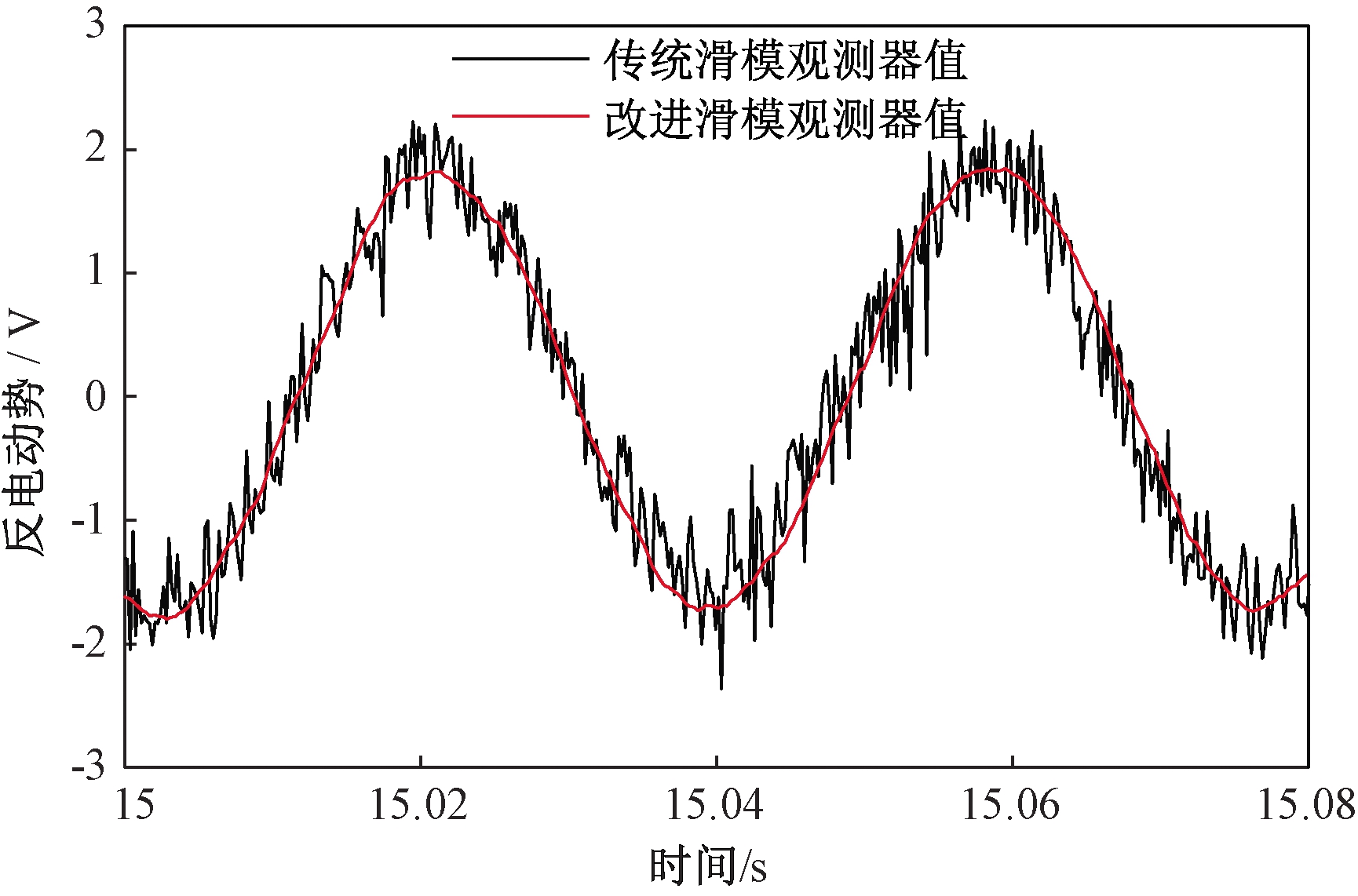
图12 转速为400 r/min时线反电动势观测值
Figure 12 The measured value of line back-EMF at 400 r/min
现以一台4对极的无刷直流电机来估算其线反电动势，电机供电选用输出为24 V的直流电压源，控制电路板用DC-DC电源供电，控制芯片为DSP-TMS320F28335。电流电压采集模块采集模拟量送入DSP的AD接口用于控制器估算反电动势，控制器根据估算出的线反电动势判断出换相信号控制电机换相。为了验证估算换相信号的准确性，实验中给电机内部的霍尔传感器供电，采集霍尔信号与换相信号估计值进行对比。在转速为400 r/min、3 000 r/min条件下，采用两种观测器的线反电动势观测值如图12、13所示。通过对比发现，传统滑模观测器由于符号函数的高频切换带来剧烈的抖振现象，且低速状态下抖振尤为剧烈，与仿真一致；而改进滑模观测器依靠sigmoid函数的连续光滑特性和可变滑模增益，在不同转速状态下均可将系统抖振削弱至可接受范围内，得到的线反电动势更加平滑，更加接近真实值。图14为电机转速在3 000 r/min条件下，通过两种观测器的线反电动势得到的换相信号。传统滑模观测器由于抖振的影响，在换相点处出现了干扰脉冲，容易导致电机换相错误；改进滑模观测器由于抖振被有效地削弱，换相信号消除了干扰脉冲，且几乎与换相信号真实值重合，无相位延迟现象，因此显著提高了无刷直流电机无位置控制系统的性能。
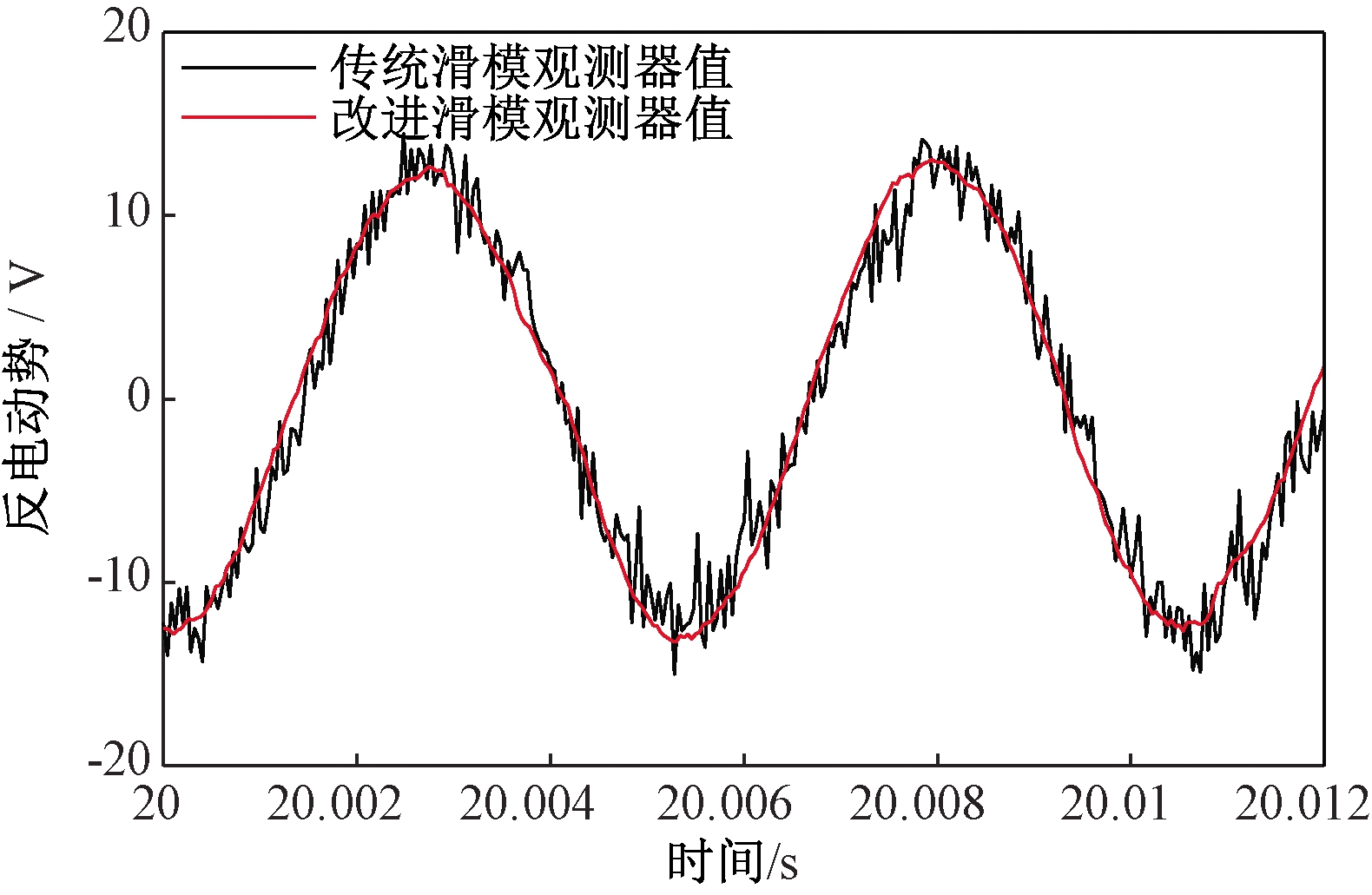
图13 转速为3 000 r/min时线反电动势观测值
Figure 13 The measured value of line back-EMF at 3 000 r/min
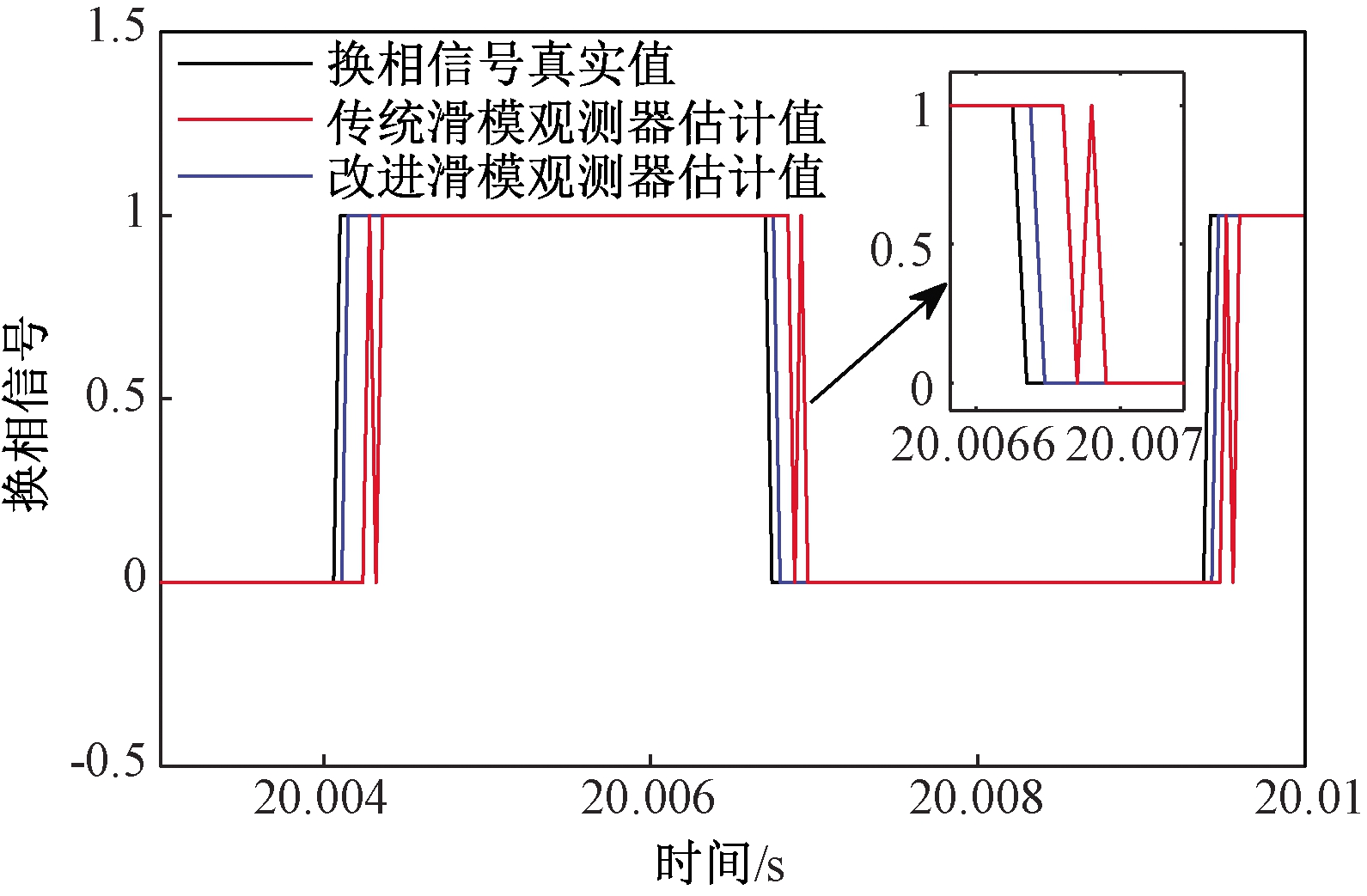
图14 转速为3 000 r/min时两种滑模观测器换相信号估计值与真实值对比
Figure 14 Commutation signal estimate value and actual value of improved sliding mode observer at 3 000 r/min
5 结论
为了克服剧烈抖振现象对传统滑模观测器的影响，提出将sigmoid函数应用在观测器中，并基于Lyapunov稳定性判据，推导出可随转速变化的滑模增益。基于线反电动势的特性，根据其符号变化和幅值得到电机换相信号和速度估计值并用于电机闭环控制。 simulink仿真和实验结果表明：改进的滑模观测器削弱了系统抖振，在较宽转速范围下均可获得更加平滑的线反电动势观测值，减小了线反电动势观测误差，得到更加准确的换相信号和速度估计值；所提方法能够快速响应电机转速变化，能够无静差地跟踪给定转速，提高了无刷直流电机无位置控制系统的性能。
[1] 夏长亮.无刷直流电机控制系统[M].北京:科学出版社,2009:1-20.
[2] LONG B, CAO B G, JIANG H, et al. Position tracking controlling system of position sensorless BLDCM by using SMC[C]//Proceedings of the 2nd IEEE/ASME international conference on mechatronic and embedded systems and application. Beijing, China:IEEE, 2006:1-5.
[3] LAI Y S, LIN Y K. Novel back-EMF detection technique of brushless DC motor drives for wide range control without using current and position sensors[J]. IEEE transaction on power electronics,2008,23(2):934-940.
[4] 郑路,倪忠进,倪益华，等.基于反电动势法无刷直流电机换相新方法[J].微电机,2019,52(3):69-74.
[5] 白国长,张宇昕.钻井力矩电机新型无位置传感器控制方法[J].郑州大学学报(工学版),2017,38(3):68-72.
[6] 官二勇,宋平岗,余晓毓.基于续流二极管检测法的无刷直流电动机[J].防爆电机,2005,40(1):24-28.
[7] LAI Y S, SHYU F S, TSENG S S. New intial position detection technique for three-phase brushless DC motor without position and current sensors[J]. IEEE transastions on industry applications, 2003, 39(2):485-491.
[8] 黄科元,陈忠强,黄守道.一种基于电感饱和效应的电流差值检测永磁同步电机转子初始位置的方法[J].电工技术学报, 2018, 33(7): 1508-1515.
[9] 史婷娜,肖竹欣,肖有文,等.基于改进型滑模观测器的无刷直流电机无位置传感器控制[J]．中国电机工程学报, 2015, 35(8): 2043-2051.
[10] 张震,沈学珂,程欣.永磁同步电机全速范围内无位置传感器控制[J].郑州大学学报(工学版),2019,40(2): 35-40.
[11] 杨奔,刘景林,卫丽超.基于优化的滑模观测器永磁同步电机无位置传感器控制研究[J].微电机, 2015, 48(11):52-57．
[12] 郭鸿浩,周波,左广杰，等.无刷直流电机反电势自适应滑模观测[J].中国电机工程学报, 2011, 31(21): 142-149.