0 引言
随着经济水平的提高，分布式电源(distributed generation，DG)接入配电网技术应运而生[1]。但分布式电源并网引起的电压变化等一系列问题，使配电网系统中电压无功控制的难度加大[2]。然而，需求响应(demand response，DR)对配电网可调节资源的利用可充分发挥电力系统各个部分多元协调调度的作用[3]。
DR对改善负荷分布，优化资源配置等具有明显的优势。根据响应特性和运行方式，DR可分为可中断负荷(interruptible load，IL)和可转移负荷[4](transferable load，TL)。此外，随着泛在电力物联网技术的发展，DR对DG资源优化配置的影响过程已经被提进日程。国内外学者对DR参与下的新能源配电网中电压无功优化的早期研究，集中于对DR的单一规划进行分析探究，文献[5]通过DG和DR的协同作用的规划探究，研究了DR对DG投资进程的影响。文献[6]对DR的建模分析，研究需求侧DR项目的水平对DG渗透率和电网稳定运行的影响。文献[7]建立含DG参与下的配电网中储能系统和DR之间协同优化规划模型，与现有方法制定的运行方式相比,论证了所提方案的合理性。以上文献虽考虑了需求侧的影响，但是建模比较简单，仅有一个优化变量参与系统优化，鉴于需求侧模型的复杂性，需对其进行精细化建模，为应对DR的多样性，应多角度建立不同模型以符合实际情况。
另外，目前对模型的求解一般采用粒子群算法、遗传优化算法、模拟退火算法等[8-11]智能优化方法或传统非线性规划、二次规划等传统算法。智能算法易陷入局部最优解，传统算法求解速度慢，以二阶锥规划为代表的凸优化在电压无功优化得到了广泛的应用。文献[12-14]建立电压无功协同优化模型，将所建立的配电网网络模型转化成锥优化模型，从而使模型大大简化，易于求解。
针对上述研究背景，建立了IL和TL模型，以网络运行成本最小为目标函数，以电容器组(capacitors banks，CB)和电抗器组(reactor banks，RB)、微型燃气轮机(micro-turbine generator，MTG)、静止无功补偿器(static var compensator，SVC)、储能装置(energy storage system，ESS)和可中断可转移负荷等为控制变量，对电网电压无功协同优化。通过变量替换，将原始混合整数非线性模型线性化，建立混合整数二阶锥规划模型，最后通过IEEE33节点配电系统测试的结果检验所提模型的正确性。
1 主动配网优化模型
1.1 目标函数
综合考虑配电网和各可控资源等调度主体的利益，现建立优化目标函数如下：
C=
(1)
式中：t表示时段；T表示周期；Δt表示调度周期时间间隔；ij表示支路；N表示数量；c代表相对应的
分别为主网购电量、PVG弃电量、WTG弃电量、可中断负荷的负荷中断量、可转移负荷的负荷转移量、储能装置的充电量、储能装置的放电量、MTG的燃气量;rij表示支路电阻；
表示支路电流。
1.2 运行约束
1.2.1 支路潮流约束
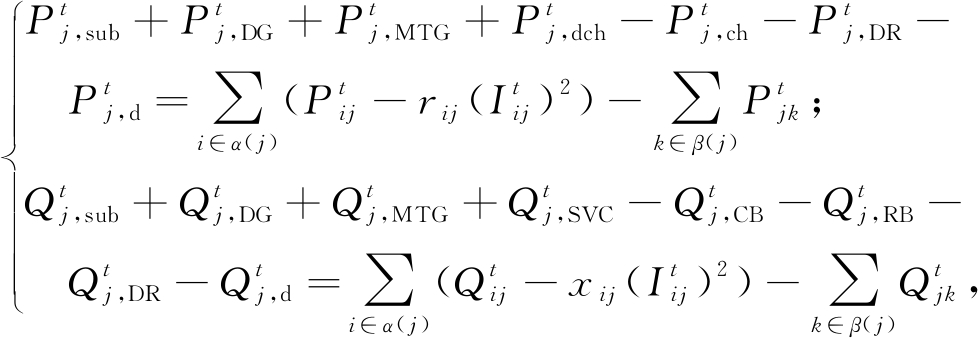
(2)
(3)
(4)
式中：xij为支路ij的电抗；α(j)、β(j)分别为以j为末(首)端节点的支路首(末)端节点集合；
为电压幅值；
和
分别为节点和支路上的有功功率、无功功率；
为DG注入有功功率、加入需求响应后的有功功率、电力负荷有功功率；
分别为变电关口、DG、MTG、SVC、CB、RB、DR和电力负荷的无功功率。
1.2.2 安全约束
(5)
式中：
分别为节点电压幅值上限下限和电流幅值限值。
1.2.3 变压器关口功率约束
(6)
式中：
为变压器有功功率上下限值；
为变压器无功功率上下限值。
1.2.4 CB与RB的运行约束
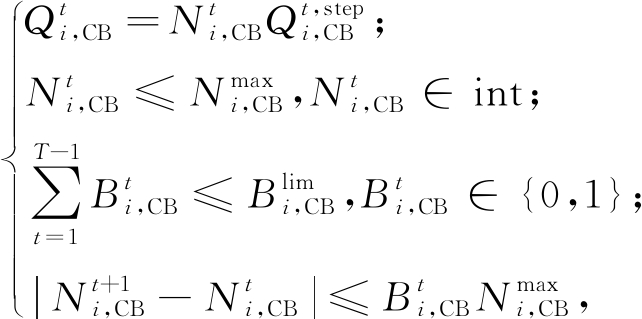
(7)
式中：
为CB的每组电容器的无功功率；
为CB的投运组数；
为CB 最大投运组数；
为CB最大投切次数；
为0-1变量，表示CB的投切组数的变化情况，取1时改变，取0时不变，其中RB模型类似，同时对RB的各参数进行限制约束。
1.2.5 储能装置运行约束
(8)
(9)
(10)
(11)
式中：
分别为ESS充放电功率上限；ηi,ch、ηi,dch为充放电效率系数；
为状态变量，为1时充电，为0时放电；
为t时刻第i节点的电量；
为考虑ESS寿命等因素后电量上下限值。
1.2.6 燃气轮机运行约束
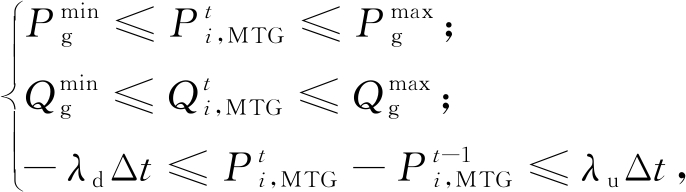
(12)
式中：
为燃气轮机的有功功率的最小值最大值；
为无功功率的最小值最大值；λd为微型燃气轮机的爬坡速率；λu微型燃气轮机的滑坡速率。
1.2.7 分布式电源出力约束
(13)
式中：
为DG在t时刻的最大有功出力；φ为功率因数。
1.2.8 静止无功补偿器运行约束
(14)
式中：
和
分别为SVC的无功功率的上下限值。
1.3 需求响应模型
现考虑需求侧可中断可转移负荷来实现对系统的灵活性调节。
1.3.1 可中断负荷
可中断负荷约束主要包含中断量、中断次数、中断持续时间、中断时间间隔的约束。
(15)
(16)
(17)
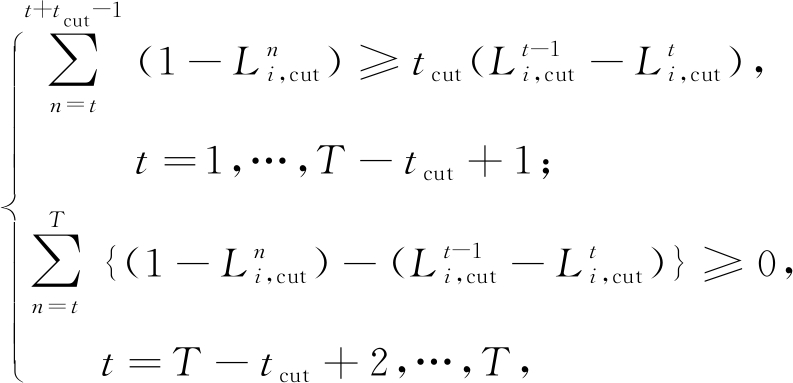
(18)
式中：Pcut.max为可中断负荷最大中断量；Ncut 为可中断负荷最大中断次数；Tcut 为可中断负荷最大中断持续时间；tcut 为可中断负荷最大中断时间间隔；
为可中断负荷i的状态变量，当为0时表示不中断，为1时表示中断。
1.3.2 可转移负荷约束
(19)
(20)
(21)
式中：Ptr.in.max、Ptr.out.max为可转移负荷可转入转出的最大功率；
为可转移负荷i的状态变量，当为0时表示无功率转入，为1时表示有功率转入。 需求响应参与调度后的总负荷为
(22)
(23)
2 优化模型的锥化
二阶锥规划将难于求解的优化模型转化成易于求解的二阶锥模型，使复杂变量用特殊形式的锥集表示，简化了原来的模型，具有收敛快，求解方便的特点。其中二阶锥规划的标准形式为
(24)
式中：f(x)为目标函数；Ax=b为线性约束函数；x∈RN、A∈RM×N、b∈RM；K为锥约束函数。一般形式：
(25)
根据二阶锥的特点，对非线性目标函数和约束条件通过引入变量替换的线性转换后，将配电网一般模型转换为二阶锥规划模型，即将混合整数非线性规划(MINLP)问题转化为混合整数二阶锥规划(MISOCP)问题，令
(26)
将上式替换目标函数和约束条件中对应的电流和电压项，可得功率平衡约束：
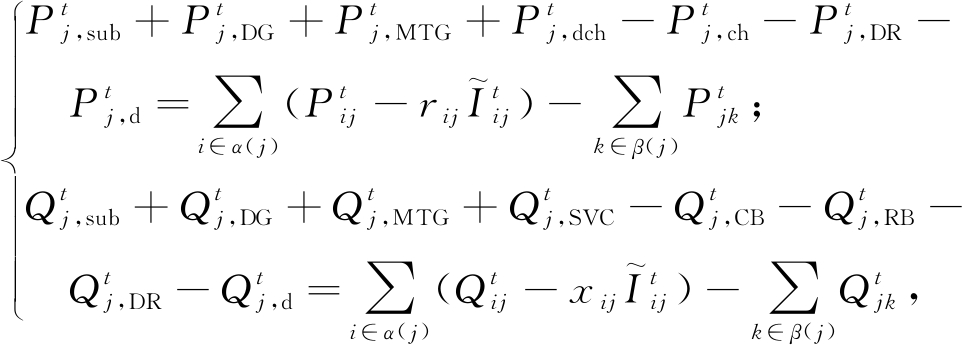
(27)
(28)
(29)
进一步等价变形转化为如下二阶锥形式
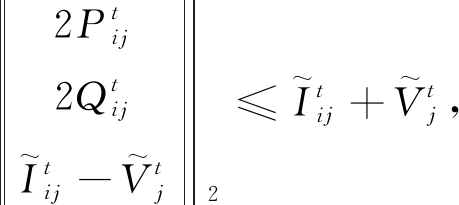
(30)
安全约束变为
(31)
3 算例分析
3.1 基础数据
为验证本文模型的合理性，在Yalmip上建模， 在Matlab R2016b环境下基于CPLEX12.7 算法包进行程序计算，采用修改的 IEEE 33 节点算例进行求解分析。接入光伏机组单位容量为400 kW,其接入节点为10、13、24、27；接入风电机组单位容量为1 000 kW，其接入节点为7、31。系统的日风光负荷曲线见图1，其中数据为以峰值为基值的标幺化结果。节点5、13接入CB(CB5,CB13)，节点6、27接入RB(RB6,RB27);二者最大投切次数均为5次，安装组数均为6组，每组补偿功率为0.05 Mvar；节点5、25接入SVC(SVC5，SVC25)，其可调范围±1 Mvar；节点17、29接入ESS(ESS17，ESS29)，参数见表1，节点4接入MTG，参数见表2。
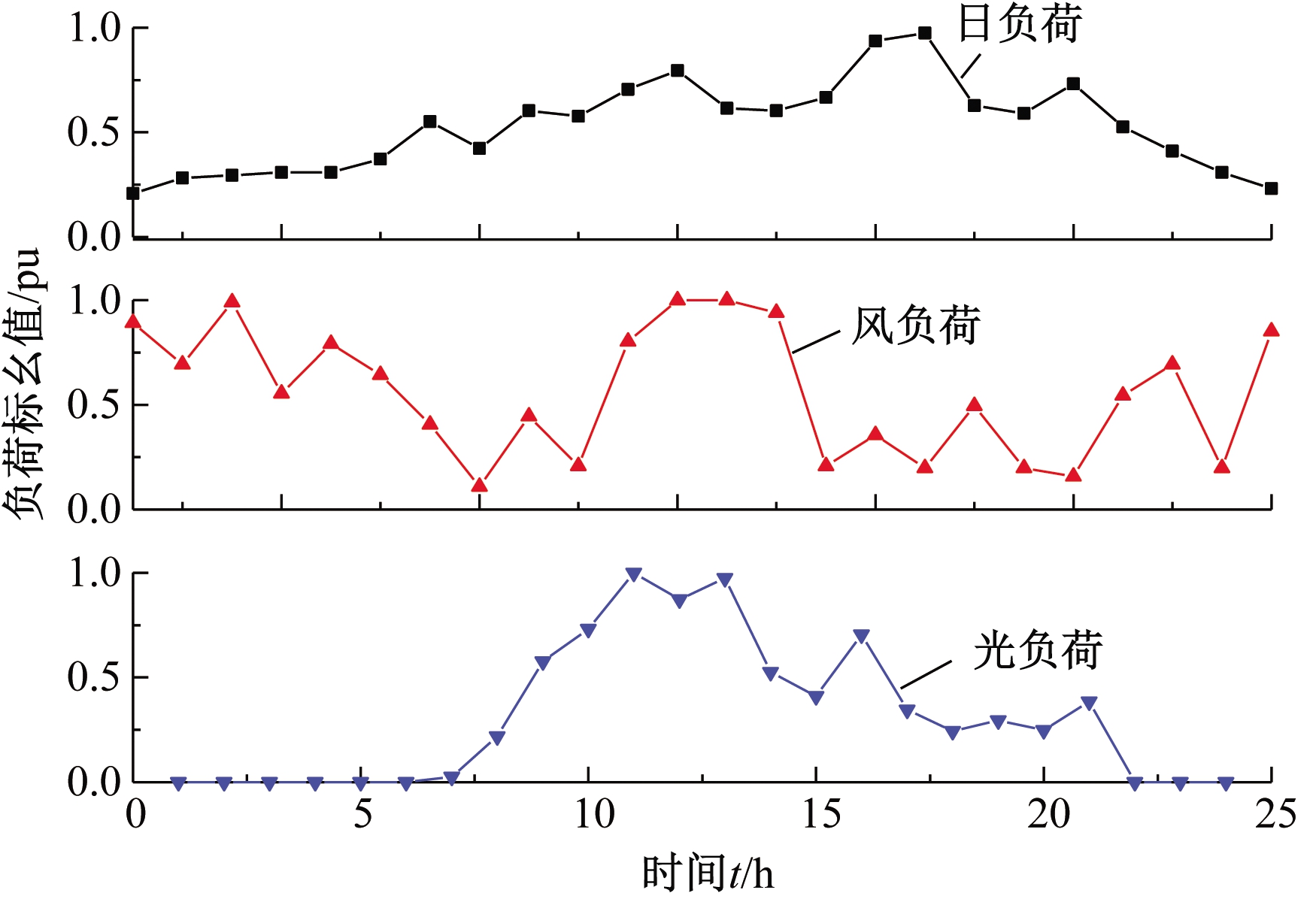
图1 日风光负荷曲线
Figure 1 Daily wind load normalization curve
表1 储能装置参数
Table 1 Energy storage device parameters
参数充放电效率最大充放电功率/kW容量/kW充电成本/元放电成本/元数值0.938 12401 2000.60.4
表2 燃气轮机参数
Table 2 Gas turbine parameters
参数有功最小值/kvar有功最大值/kvar爬坡/滑坡速率发电成本/元数值04002000.69
由于可控负荷具有多样性的特点，现假设有2种可中断负荷和3种可转移负荷：中断负荷接入节点类型一为8、32，类型二为24、30；可转移负荷接入节点7、14、25，其具体参数如表3、4所示。现选取弃风弃光成本为1元/(kW·h)，网损成本为0.4元/(kW·h)，主网购电分时电价00：00～9：00为0.25元/(kW·h)、15：00～18：00为0.45元/(kW·h)，其他为0.65元/(kW·h)。
表3 可中断负荷参数
Table 3 Interruptible load parameters
类型最大中断持续时间/h最小调度时间间隔/h最大中断次数调度成本/元最大中断容量/kW类型13140.5120类型24250.4150
3.2 优化结果及分析
3.2.1 电压无功优化结果分析
现取所建模型与一般主动配电网优化模型对比分析，图2给出了优化前后23：00全网的电压分布，可见通过协调电网中的DR与无功补偿设备优化后，电压偏差明显减小，平稳性明显提升，且所有节点电压均符合安全运行要求。由图2可以看出，末端节点电压偏移情况较为严重，现取节点18的电压变化曲线来进一步验证模型的优化性，如图3所示。直观可见，节点18电压幅值曲线整体向上移动，接近额定电压幅值，电压偏差显著减小。故优化后的模型对电压波动具有改善作用，提高了系统的稳定性。
表4 可转移负荷参数
Table 4 Transferable load parameters
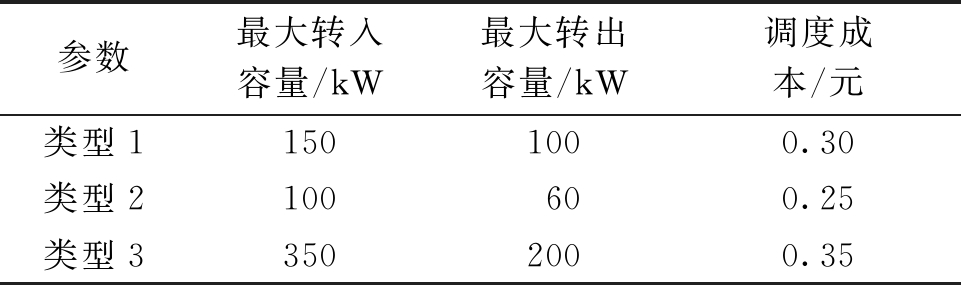
参数最大转入容量/kW最大转出容量/kW调度成本/元类型11501000.30类型2100600.25类型33502000.35
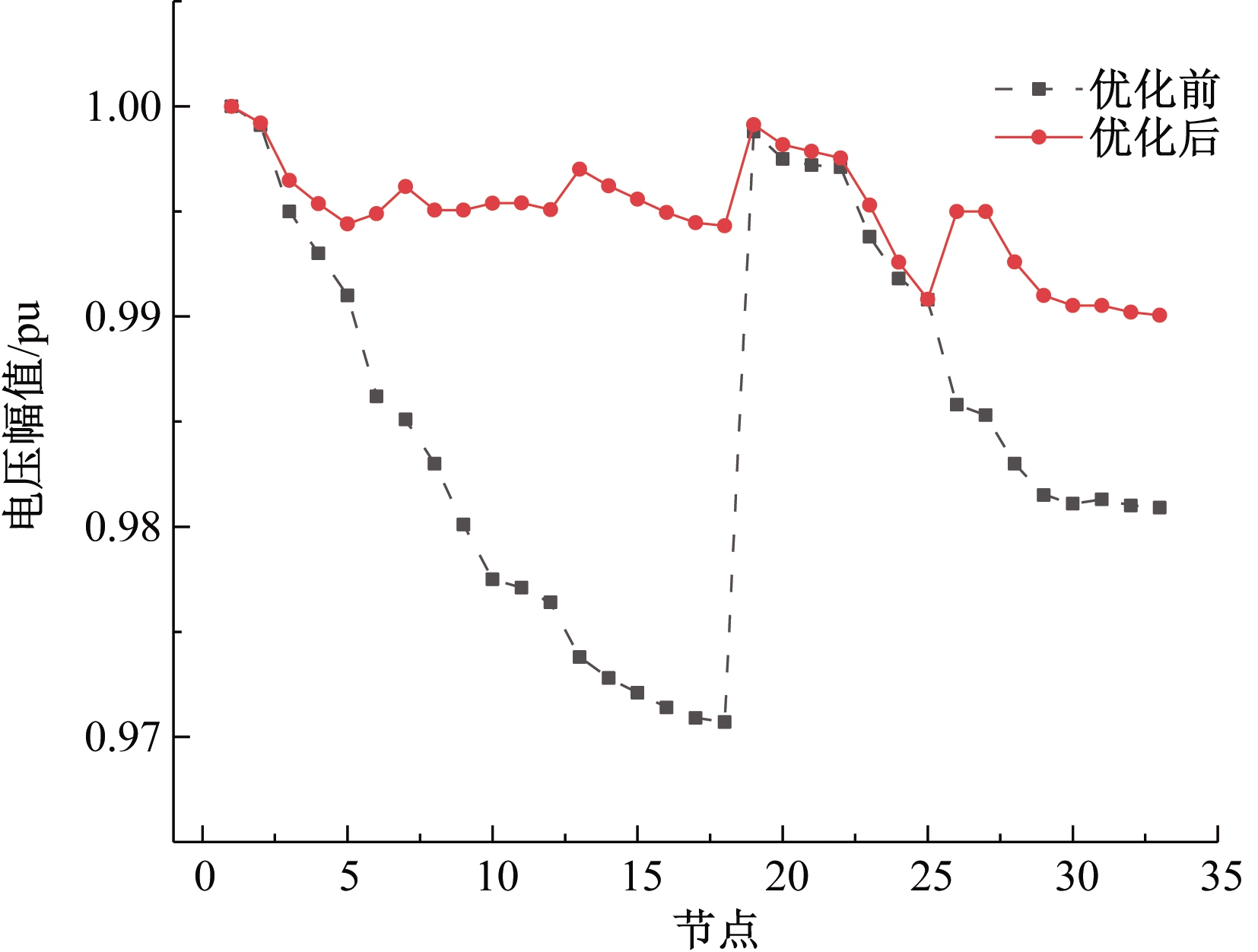
图2 23：00优化前后系统电压分布
Figure 2 Voltage distribution after optimization at 23:00
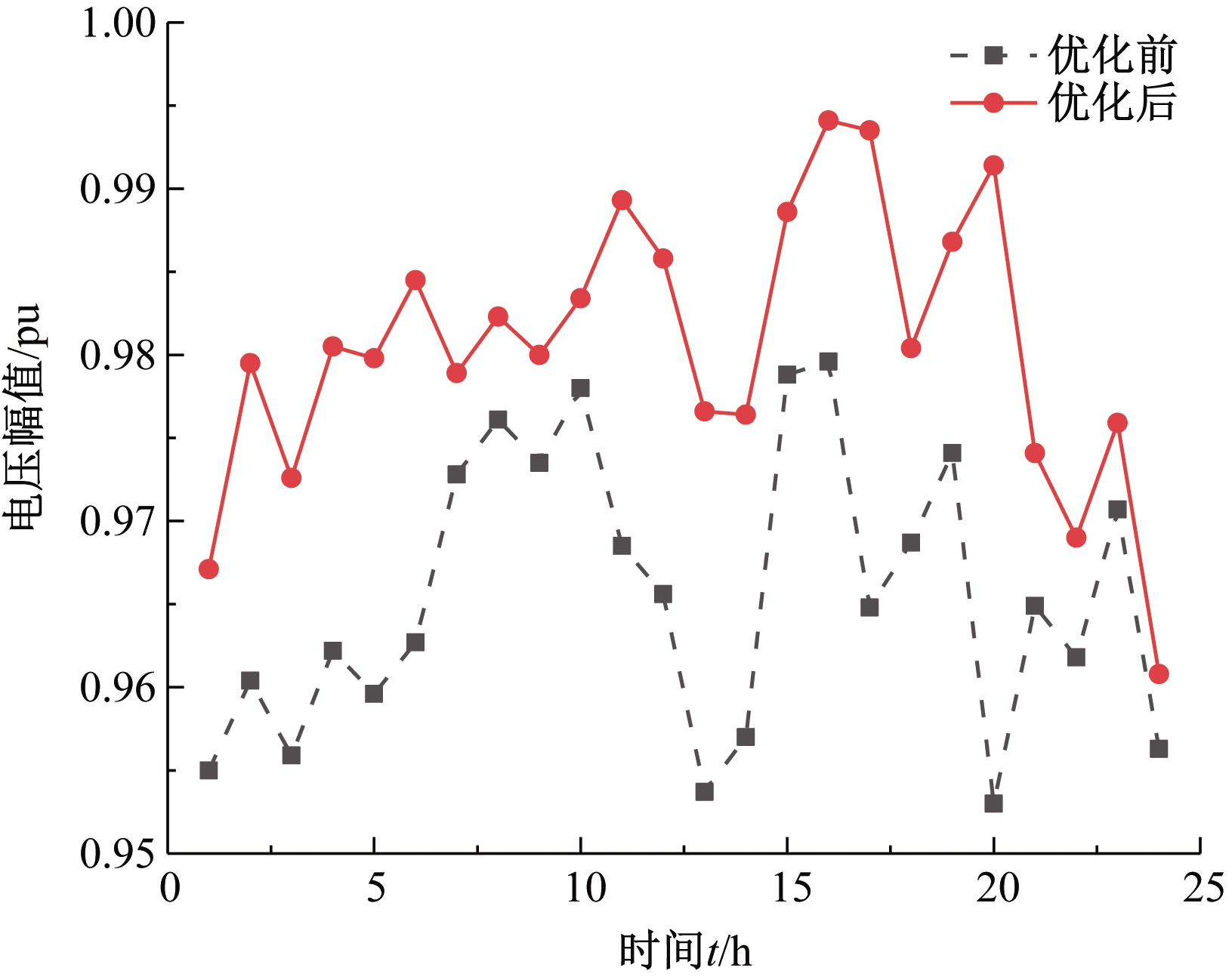
图3 优化前后节点18日电压波动曲线
Figure 3 Node18 voltage curve before and after optimization
表5给出节点18优化前后电压偏差对比，其最大日电压偏差和平均电压值都显著降低，电压平稳性提高，由此论证模型对电压优化的合理性和正确性。
3.2.2 补偿装置运行策略分析
如图4所示随着ESS的充放电，总电量表现出相应的变化幅度，结合日风光负荷曲线来看，DG出力增加时ESS储存电量增加，当负荷值达到顶峰时，ESS储存的电量开始逐步减少，实现了ESS稳定电网电压、降低线路损耗的作用，使充放电处于动态平衡状态。如图4由于SVC5距离根节点相对较近，其日运行策略在滞相与进相之间来回变换；又由于接入DG的容量不大，且为保证电压质量，SVC25大多时候滞相运行，整体上SVC的运行策略主要为容性补偿。现取CB13 和 RB27， 可以看出，在 DG 接入的配电网中，当CB13投运次数增加时，相对应的RB27的投运组数降低，反之亦然，二者达到一种动态平衡状态。所以 CB 和 RB 之间的相互协调有效地保证了电网电压的质量，提高了系统的稳定性。
表5 节点18优化前后电压偏差对比
Table 5 Comparison of voltage deviation before and after optimization of node 18
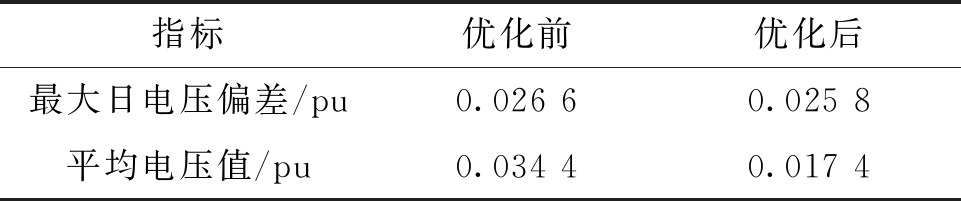
指标优化前优化后最大日电压偏差/pu0.026 60.025 8平均电压值/pu0.034 40.017 4
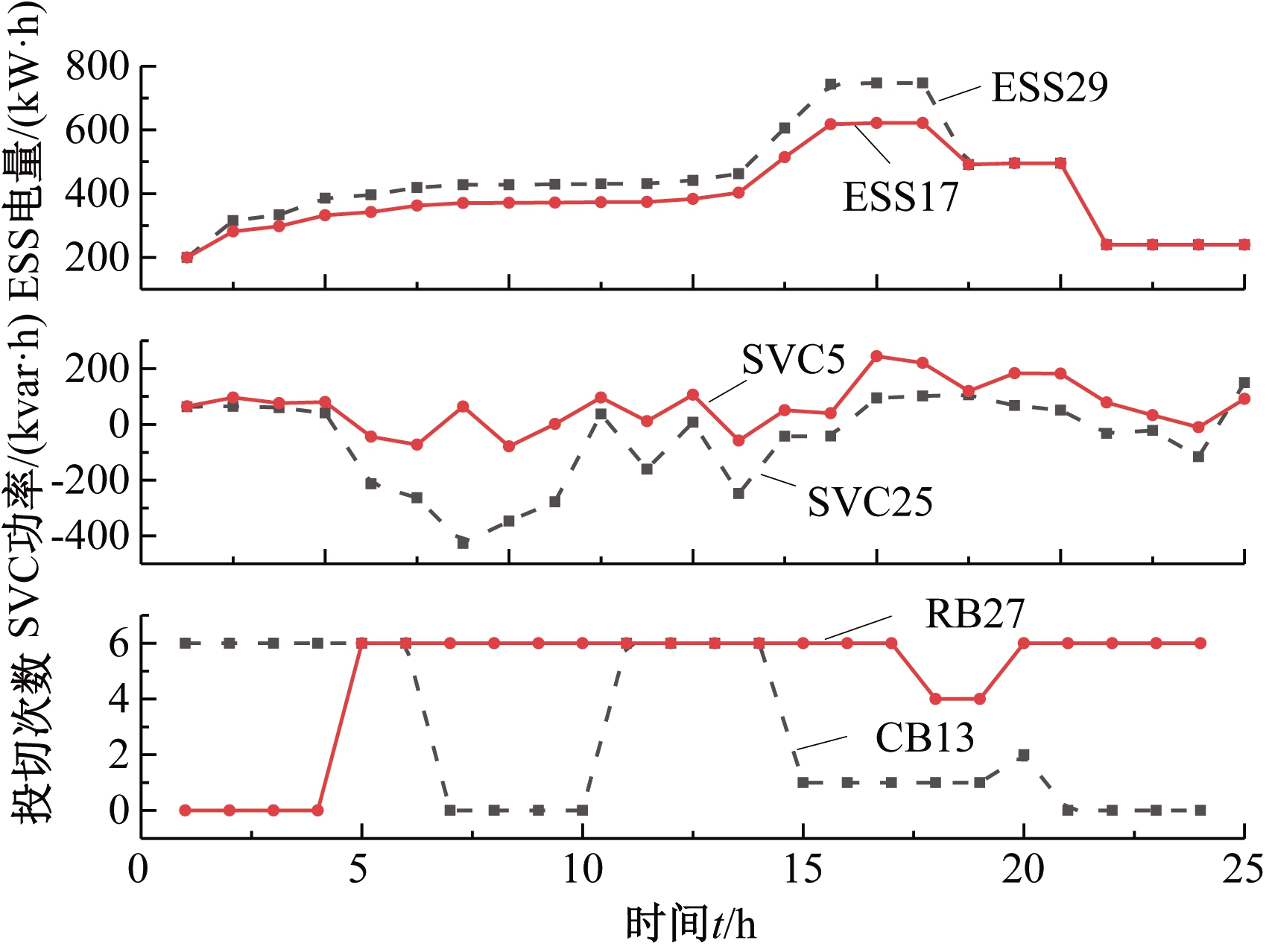
图4 补偿装置运行策略
Figure 4 Compensation device operation strategy
3.2.3 需求响应对网络优化的作用分析
为有效分析DR对系统电压无功优化作用，现提出两种方案：方案1：考虑DR；方案2：不考虑DR。图5给出23∶00时两种方案的系统电压分布，对比图3得，采用方案2与优化前的电压比较，由于储能等一些有功无功补偿装置的作用，电压偏差发生一定变化，但变化幅度不大。方案1中节点24和节点25由于可控负荷的影响，相比于其他节点出现一定程度的电压波动，整体来看，节点电压平稳，网络电压得到改善，稳定性进一步加强。可见，通过对DR的控制，一定程度可有效改善全网潮流分布，提高电压质量。
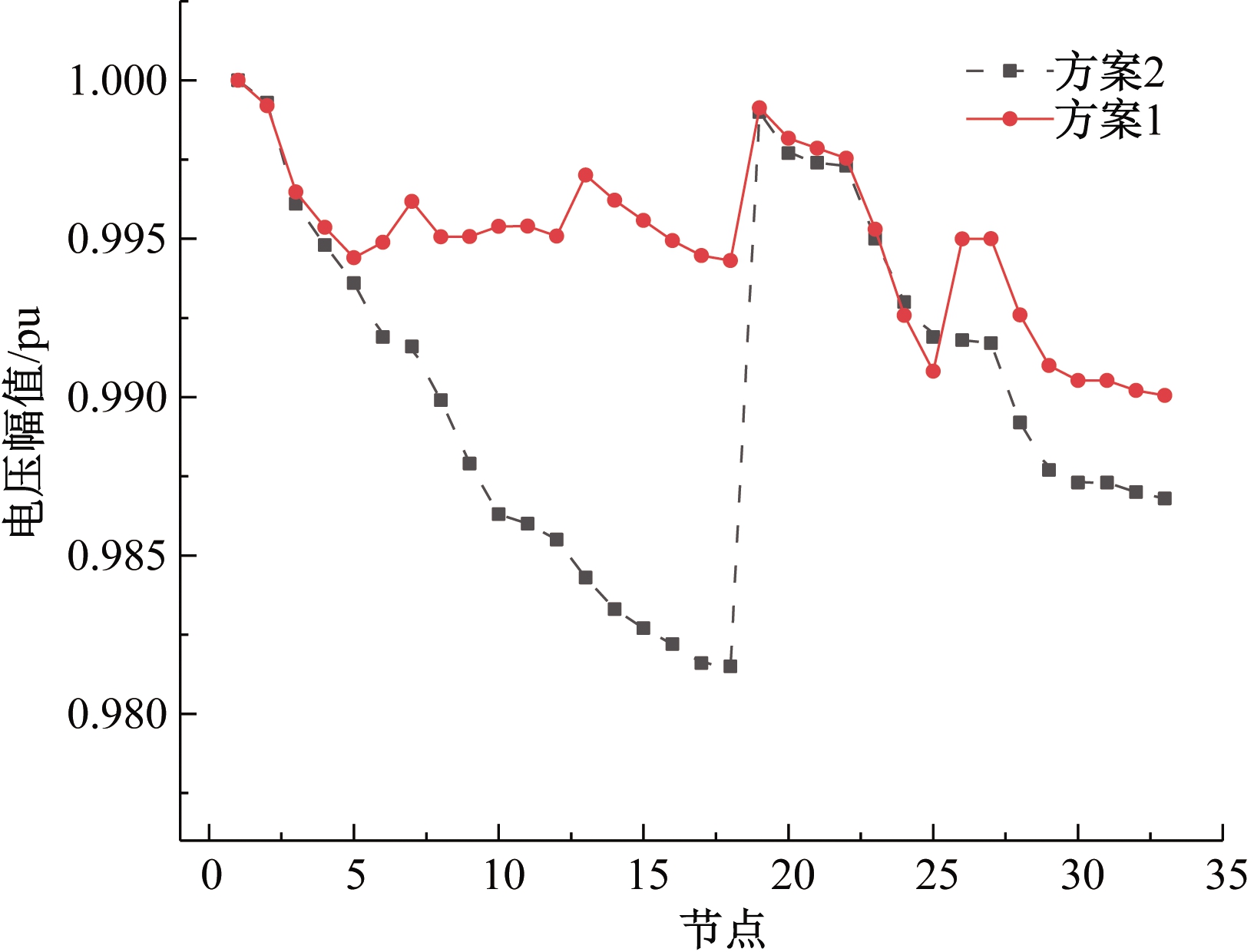
图5 23:00两种方案的电压分布
Figure 5 Voltage distribution of two schemes at 23:00
方案1中购电、网损、总运行成本为12 743、7 930、23 232元，相应成本在方案2中分别为13 152、8 463、23 913元。对比发现，方案1总运行成本小于方案2总运行成本，方案1中增加DR调度，在不同时刻增加或切除部分可调度负荷，购电成本、网损成本都有所降低。从结果来看，方案1中可中断负荷和可转移负荷成本为86元和340元，相比于允许可中断和可转移最大容量，成本不大，即需求响应在电网运行中参与度不大，部分可参与DR的负荷没被利用，因此可根据电网和DG发电成本制定合理的价格补偿策略，增加更多可控负荷参与电网调度中，以适应未来配电网的发展。总之，计及DR时，可有效降低网络损耗和改善电网电压。
3.2.4 算法验证
为验证MISOCP的可行性，现将其与MINLP进行对比分析，对MINLP运用粒子群智能算法求解。如表6，可见，直接求解MINLP耗时长，而转化为MISOCP后，求解速度大大提高。
表 6 不同算法下的求解信息对比
Table 6 Comparison for solution information under different algorithms
模型类型求解算法时间/sMISOCPCPLEX4.59MINLP粒子群算法29.48
4 结论
(1)在主动配电网中，由ESS、SVC、CB、RB等无功补偿装置及DR的协调作用，在保证电压质量的前提下可有效消纳分布式能源，提高了能源的利用率。
(2)计及需求响应后，配电网运行成本降低，网损下降，电压得到改善。因此，有效地将需求响应纳入配电网的优化调度中，可提高电网的安全性、经济性。
[1] 范明天, 张祖平, 徐丙垠, 等. 2017年第24届国际供电会议综述[J]. 供用电, 2017, 34(11): 28-36.
[2] 沈鑫, 曹敏. 分布式电源并网对于配电网的影响研究[J]. 电工技术学报, 2015, 30(S1): 346-351.
[3] 梁俊文, 林舜江, 刘明波, 等. 主动配电网分布式鲁棒优化调度方法[J]. 电网技术, 2019, 43(4): 1336-1344.
[4] 刘小聪. 基于需求响应的大规模风电消纳调度策略研究[D]. 南京：东南大学, 2015: 1-111.
[5] 谭心怡, 吕林, 高红均, 等. 考虑DG功率非线性特性和综合负荷建模的DG和DR协同规划[J]. 电网技术, 2018, 42(9): 2958-2966.
[6] 于娜, 李伟蒙, 黄大为, 等. 计及可转移负荷的含风电场日前调度模型[J]. 电力系统保护与控制, 2018, 46(17): 61-67.
[7] 李秀磊, 耿光飞, 季玉琦, 等. 主动配电网中储能和需求侧响应的联合优化规划[J]. 电网技术, 2016, 40(12): 3803-3810.
[8] 薛金花, 王德顺, 郁正纲, 等. 基于风电可调节不确定代价的风光柴储联合优化调度[J].郑州大学学报(工学版), 2019, 40(5): 73-79.
[9] 陈兰芝, 王克文. 基于粒子群算法的24小时综合无功协调优化[J]. 电测与仪表, 2016, 53(12): 107-110.
[10] 马晖军. 分布式光伏接入配电网的电压稳定性研究[D].北京：华北电力大学, 2017.
[11] 杨胡萍, 李威仁, 左士伟, 等. 基于改进遗传算法的电力系统无功优化[J]. 郑州大学学报(工学版), 2015, 36(6): 66-69.
[12] 章健, 熊壮壮, 王明东, 等. 基于二阶锥规划的主动配电网动态无功优化[J]. 郑州大学学报(工学版), 2019, 40(1): 32-37.
[13] 刘一兵, 吴文传, 张伯明, 等. 基于混合整数二阶锥规划的主动配电网有功-无功协调多时段优化运行[J]. 中国电机工程学报, 2014, 34(16): 2575-2583.
[14] 郭清元, 吴杰康, 莫超, 等. 基于混合整数二阶锥 规划的新能源配电网电压无功协同优化模型[J]. 中国电机工程学报, 2018, 38(5): 1385-1396.