0 引言
滚动轴承故障占旋转机械故障的大约30%,主要采用频谱分析来进行故障识别,提取故障特征的质量决定了评估方法的有效性[1-2]。包络分析是滚动轴承检测中的一项重要技术,能够从强背景噪声中有效提取故障频率。
滚动轴承故障结构件的缺陷在载荷作用下会引起高频共振(10 kHz以上),包络分析可以从其他结构件的振动中提取故障信息。文献[3]提出了粒子群算法选取带通滤波器,提升了包络分析性能,诊断了滚动轴承的内圈、外圈以及滚动体故障;Klausen等[4]提出了多窄带的滚动轴承的包络分析方法,和多种确定窄带的方法进行比较,有效地自动检测出滚动轴承故障;文献[5]提出使用经验小波变换分解信号,改进了阈值函数对噪声占比大的模态进行降噪,使用峭度和包络谱进行故障识别;文献[6]提出了使用Hilbert包络和零阶谐振器的算法,和Hilbert-Huang变换进行了比较,有效地诊断了轴承的早期故障。
谱峭度(spectrum kurtosis,SK)是由Dwyer提出的,Antoni将其应用到了故障诊断中,谱峭度可以自适应地选择带通滤波器,有利于提取滚动轴承的故障信息。陈东毅等[7]研究了改进经验模态分解在轴承的应用,并结合谱峭度,有效提取了步态信号的特征频率;田晶等[8]研究了Birge-Massart阈值降噪和集合经验模态分解(ensemble empirical mode decomposition,EEMD)谱峭度,提高了故障的信噪比,提取了滚动轴承的内圈、外圈故障特征;Lei等[9]提出了小波包变换估计谱峭度自适应设计滤波器,克服了传统谱峭度提取瞬态特征的缺陷,准确诊断了轴承的微弱故障。频带熵同样可以自适应选择带通滤波器,文献[10]研究了EEMD结合改进频带熵(frequency band entropy,FBE),从强背景噪声中提取了故障频率;李华等[11]提出了使用奇异值分解(singular value decomposition,SVD)降噪和FBE设计带通滤波,有效地提取了轴承故障频率。
综上所述,本文提出了一种全矢频带熵(full vector frequency band entropy,FV-FBE)的算法,采用频带熵理论计算时频分布的频带熵,依据熵最小原则设计双通道信号的带通滤波器,对滤波后的信号采用全矢Hilbert包络解调,得到全矢包络谱,通过实验证明了FV-FBE可以有效诊断滚动轴承故障。
1 全矢谱理论
在全矢故障诊断与故障预测系统中,两个传感器相互垂直安装获取振动信号,数据采集系统将振动数据进行信号调理、滤波、模数转换,对设备进行运行状态评估和预测故障。转子运行时,传感器获得的信号是椭圆轴心轨迹在相应方向上的投影,因此单传感器不能全面反映设备的振动,需要进行信息融合。
设{xn}与{yn}为全矢故障诊断与预测系统采集到的时域信号,进一步构成复序列,即{zn}={xn}+j{yn}。对{zn}进行傅里叶变换得到{Zn}={ZRn}+j{ZIn}。全矢谱理论定义椭圆轨迹长半轴为主振矢Ran,椭圆轨迹短半轴为副振矢Rbn,主振矢和x轴夹角为αn,椭圆轨迹相位角为φn,并推理得到:
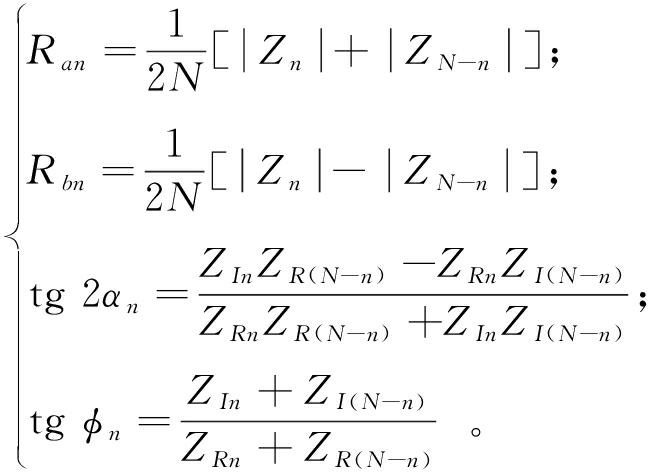
(1)
2 频带熵
峭度是一种全局指标不适合在强背景噪声下提取故障特征,谱峭度作为局部指标具有一定的抗噪能力。依据谱峭度的最大值,可以设计带通滤波器的带宽和中心频率,而频带熵是根据最小值设计带通滤波器的带宽和中心频率。频带熵的定义从传统的幅值熵出发,幅值熵可以用来表征信号频率的复杂度情况,信号能量主要在几个频率时,幅值熵就会很小,相反幅值熵就会较大。设时域信号x(t)的幅值谱为X(i),i=1,2,…,N,则可以得到:
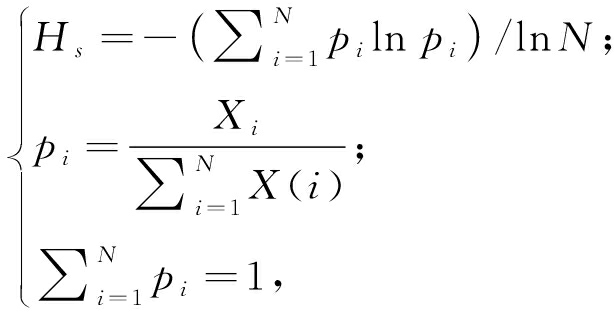
(2)
式中:Hs是信号x(t)的幅值熵。从式(2)可以看出幅值熵可以表示频域复杂程度,而频带熵表示时频域复杂程度。
短时傅里叶变换(short-time Fourier transform, STFT)可以对每个频率进行细致的分析,采用STFT对信号x(t)进行分析得到下式:
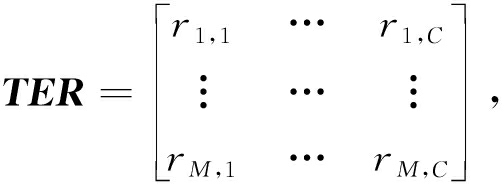
(3)
式中:M是频率点数;C=N/L;L是窗函数移动的步长。则单个频率分量的频带熵表示如下:
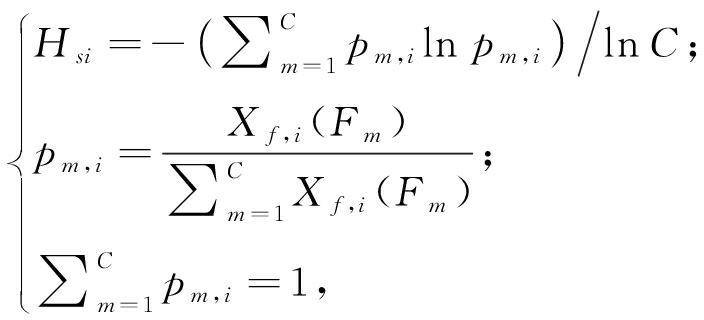
(4)
式中:Fm是频率Xf,i沿时间轴的谱分布。最后计算得到的各个频率的频带熵如下:
Hsf=(Hs1,Hs2,…,HsM)。
(5)
通过改变STFT不同的窗口大小,当频带熵取最小值时,则是所需要设计的带通滤波器的中心频率,带宽可以使用Δf=1.5fs/Nw来计算,其中fs为采样频率,Nw为窗口大小。
3 全矢Hilbert包络解调
滚动轴承各部件局部故障会产生典型的加速度信号,对其信号进行包络解调能够提取调制信号获得更多的诊断信息。当滚动体撞击外圈或内圈的局部故障时,会产生冲击响应,激发轴承和传感器整体结构的高频共振。同样滚动体的故障撞击内圈或外圈时也会产生类似情况,但其故障特征最为微弱。
这一系列滚动轴承故障产生的冲击响应振幅被两个因素调制。其一冲击的强度取决于滚动部件所受的载荷,而载荷通常是由故障通过载荷区的速度控制的;其二传感器是固定的,故障移动时传递路径的传递函数会随之变化,因此外圈故障磨损较大时会产生转频调制,内圈故障必然产生转频调制。
常用的包络解调方法有希尔伯特算子解调、广义检波滤波解调、能量算子解调以及复解析小波解调等。全矢Hilbert包络解调,解决了单通道Hilbert包络解调结果的片面性,得到的包络谱幅值更加准确可靠。信号x(t),y(t)进行Hilbert变换可得解析信号,如下式:
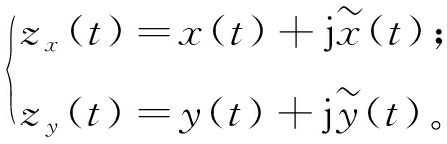
(6)
继续由式(6)得到x(t),y(t)双通道信号的包络,如下式:
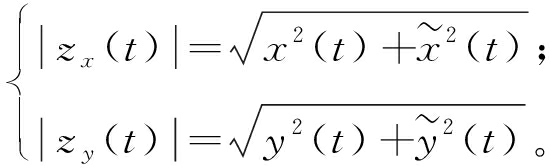
(7)
式(7)得到了双通道的包络信号,并结合全矢谱理论,即可得到全矢包络谱。
4 FV-FBE算法流程
滚动轴承故障缺陷产生的能量非常小,通常只占总能量的千分之一不到,难以通过频率分析识别故障,而包络分析的关键在于选择一个好的带通滤波器,然而对于固定参数的带通滤波器不能随着轴承工况的变化而改变,因此自适应寻找实际的共振带尤为重要。频带熵可以有效地自适应设计带通滤波器参数,全矢频带熵算法更进一步改善了单通道信号分析不完整、不精确的局限性,更有利于检测故障,算法步骤如下:
(1)使用全矢故障诊断与预测系统采集旋转机械振动信息x(t),y(t);
(2)依据频带熵最小设计带通滤波器参数带宽Δf和中心频率;
(3)依据设计的带通滤波器对双通道信号进行滤波处理;
(4)对滤波后的双通道信号作全矢Hilbert包络解调,得到全矢包络谱。诊断流程图如图1所示。
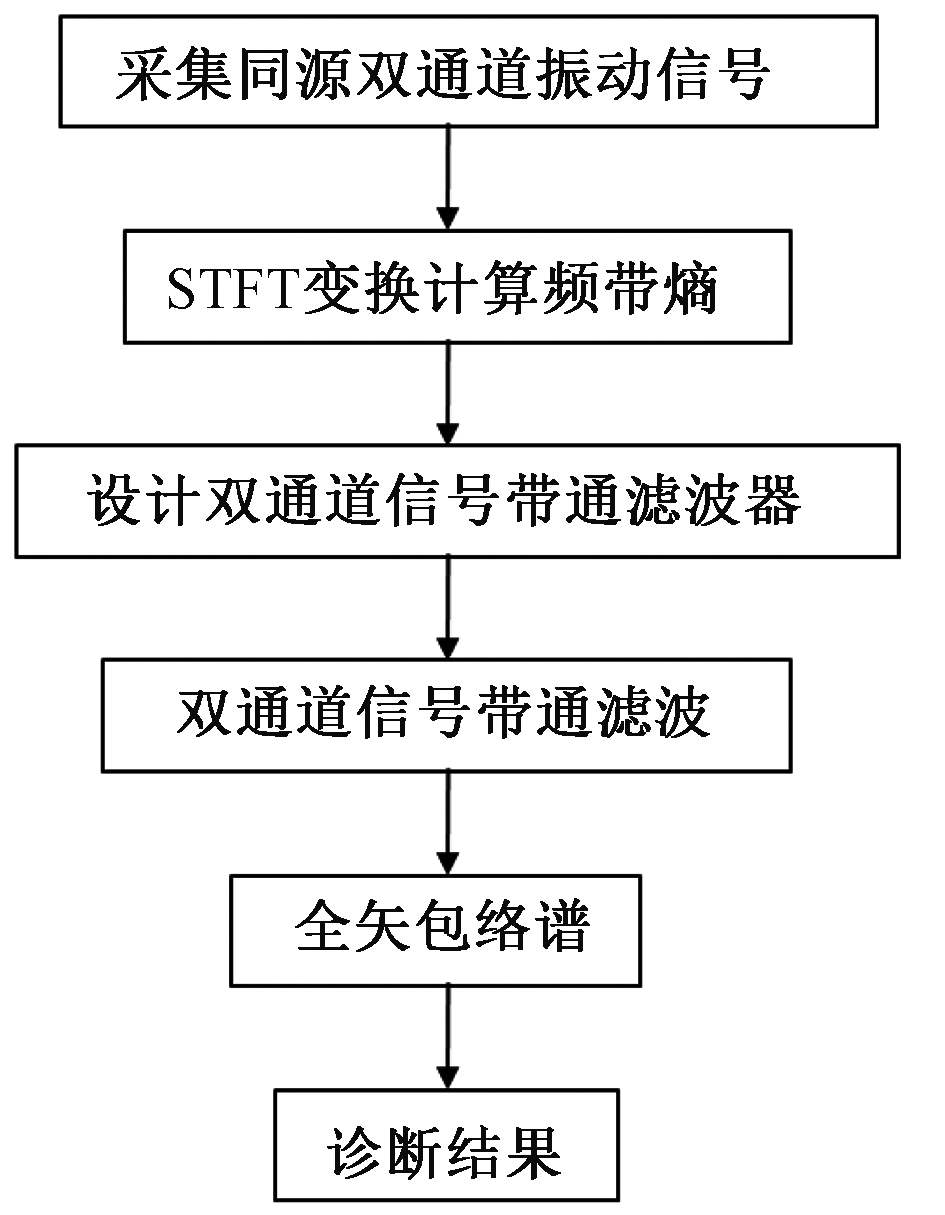
图1 FV-FBE诊断算法
Figure 1 FV-FBE diagnosis algorithm
5 实验验证
为了验证FV-FBE算法的正确性,使用美国辛辛那提大学智能维护中心提供的轴承数据。实验设备如图2所示。图2中电机为交流电机,转速为2 000 r/min,转轴上安装4个轴承,轴承型号为ZA-2115双列滚子轴承,滚动体个数16个,节圆直径为71.5 mm,滚子直径为8.4 mm,接触角为15.17°,使用摩擦带驱动主轴转动。转轴径向施加的载荷为6 000 lbs,使用两个互相垂直的PCB 353B33加速度传感器,此时满足FV-FBE算法的前提条件,采用频率fs=20 kHz,每次采集20 480点,共有2 155组数据。实验结果后期轴承3出现了内圈故障,故障频率为294 Hz。
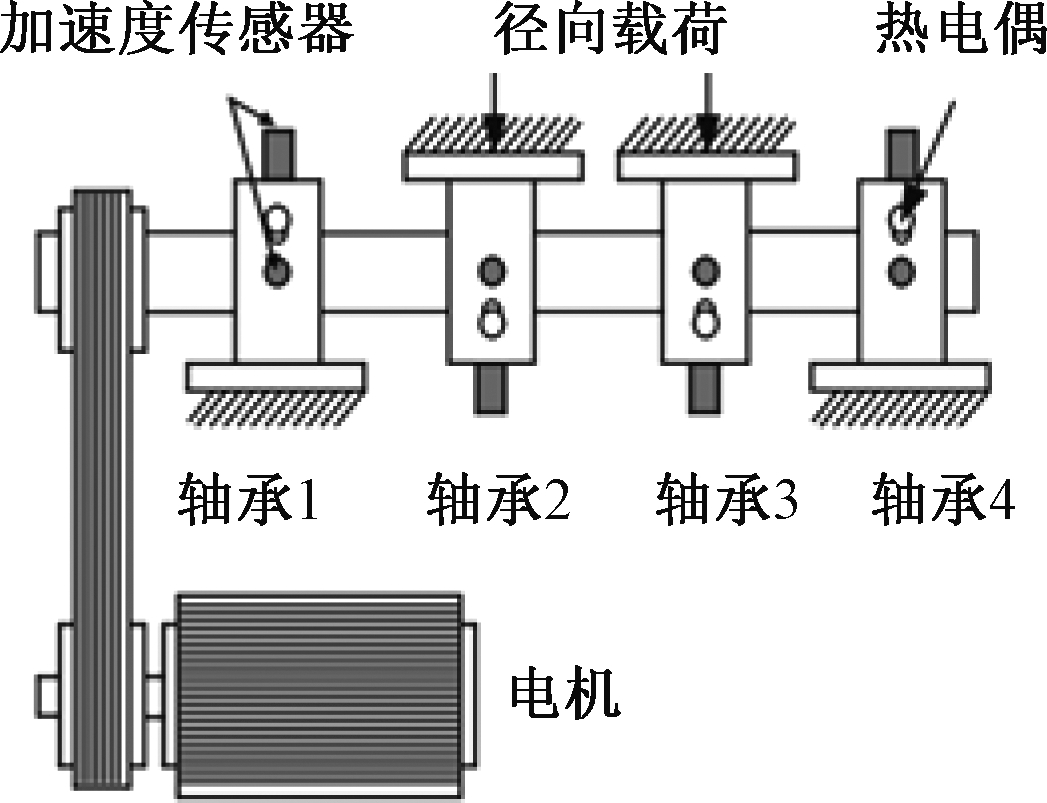
图2 实验装置图
Figure 2 Diagram of experimental device
轴承3信号的双通道时域波形图及其包络谱如图3所示,记其同源双通道依次为X和Y,从时域波形图以及包络谱中难以发现故障的特征信息,说明了滚动轴承故障信号的复杂性,只采用包络分析难以提取故障特征频率,因此需要进行更进一步的算法改善。
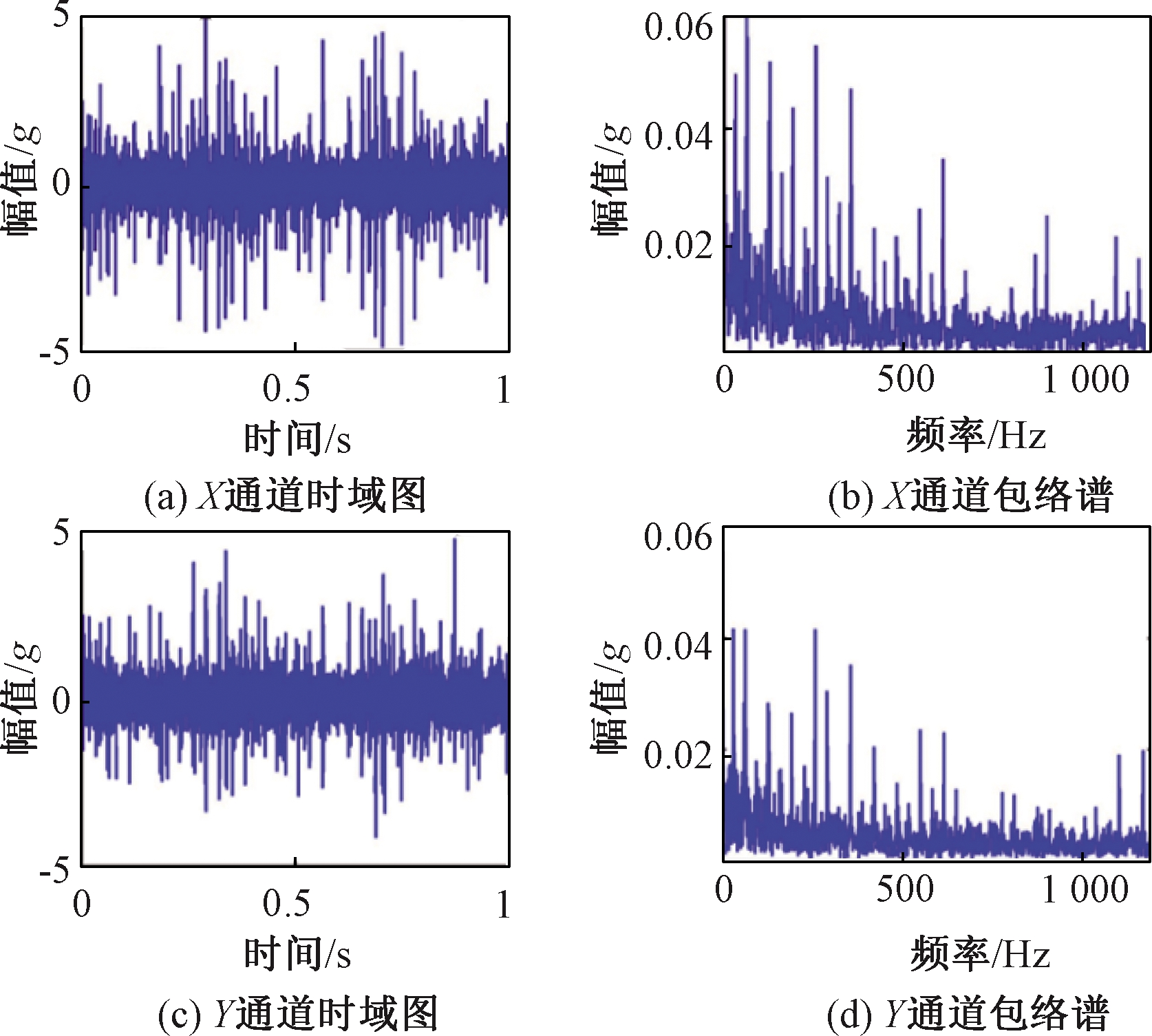
图3 信号时域图及包络谱
Figure 3 Time-domain diagram and envelope spectrum of signal
为了从强背景噪声中全面准确提取出轴承的微弱故障信息,采用频带熵理论对X通道进行分析。取STFT窗口长度Nw=32、64、128、256、512计算频带熵,得出Nw=128时频带熵取值最小,对应的频带熵大小为0.877 6,其所在频率为2 657 Hz,由此设计X通道滤波器带宽Δf=1.5fs/Nw=234.37 Hz,中心频率为2 657 Hz。
同样继续采用频带熵理论对Y通道进行分析,依次取STFT窗口长度Nw为32、64、128、256、512计算频带熵,得到Nw=256时频带熵取值最小,对应的频带熵大小为0.884 8,其所在频率为4 532 Hz,由此设计的Y通道滤波器带宽Δf=1.5fs/Nw=117.18 Hz,中心频率4 532 Hz。频带熵计算结果如图4所示。
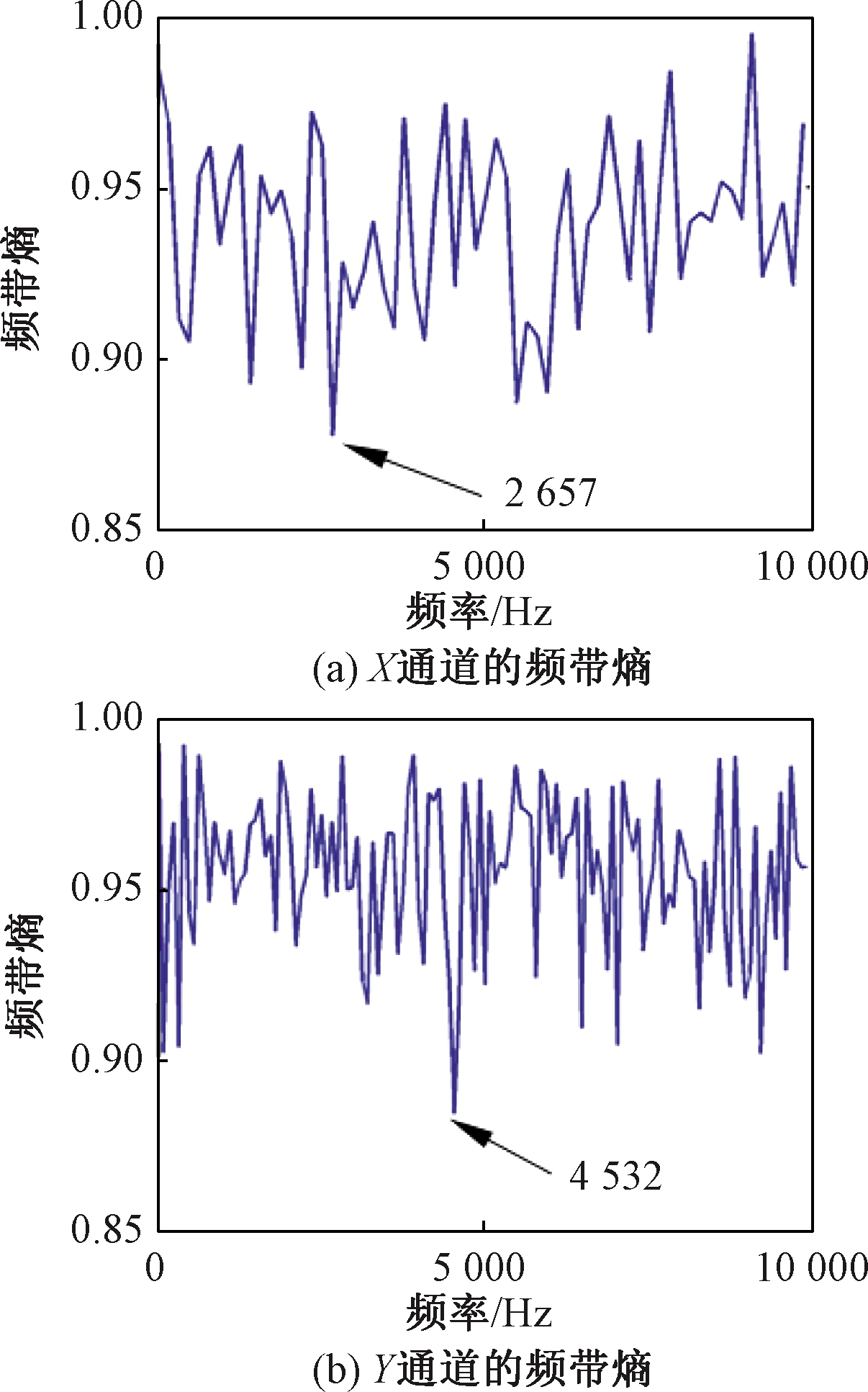
图4 双通道的频带熵图
Figure 4 Frequency band entropy of two channels
根据频带熵最小原则设计带通滤波器,分别对双通道信号进行滤波,并得到x(t),y(t)的包络谱如图5所示。X通道含有内圈故障频率294 Hz,以及转频33 Hz的2×成分;Y通道内圈故障信息较为微弱,说明故障信息提取不全面,单通道分析存在片面性。
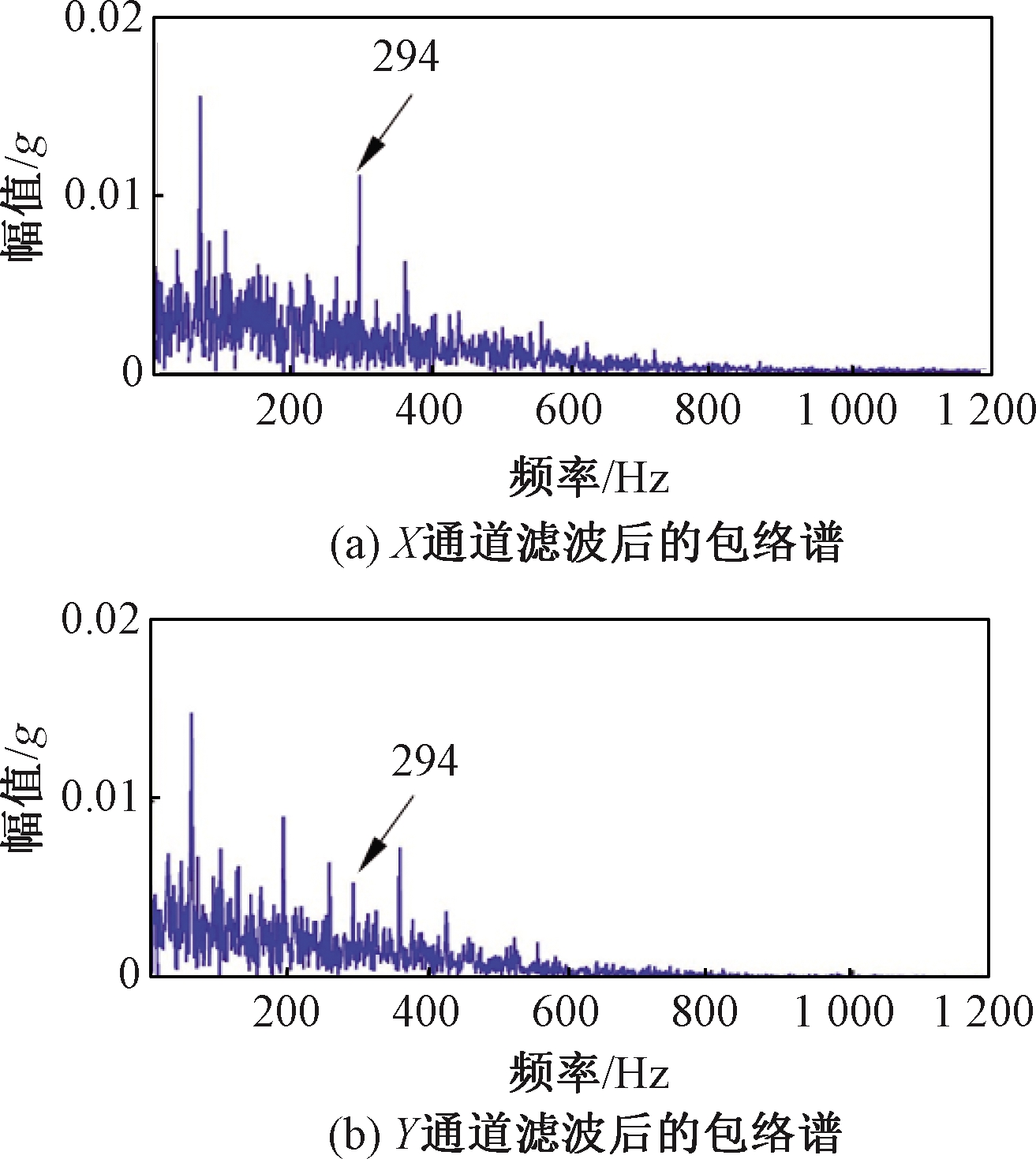
图5 双通道的包络谱
Figure 5 Envelope spectrum of two channels
为了解决单通道分析结果的片面性,进行全矢Hilbert包络解调,得到全矢包络谱,如图6所示。从图6中可以看到内圈故障频率294 Hz,及其转频33 Hz的2×、6×成分,相比于原始包络谱全面准确地提取出了故障频率。
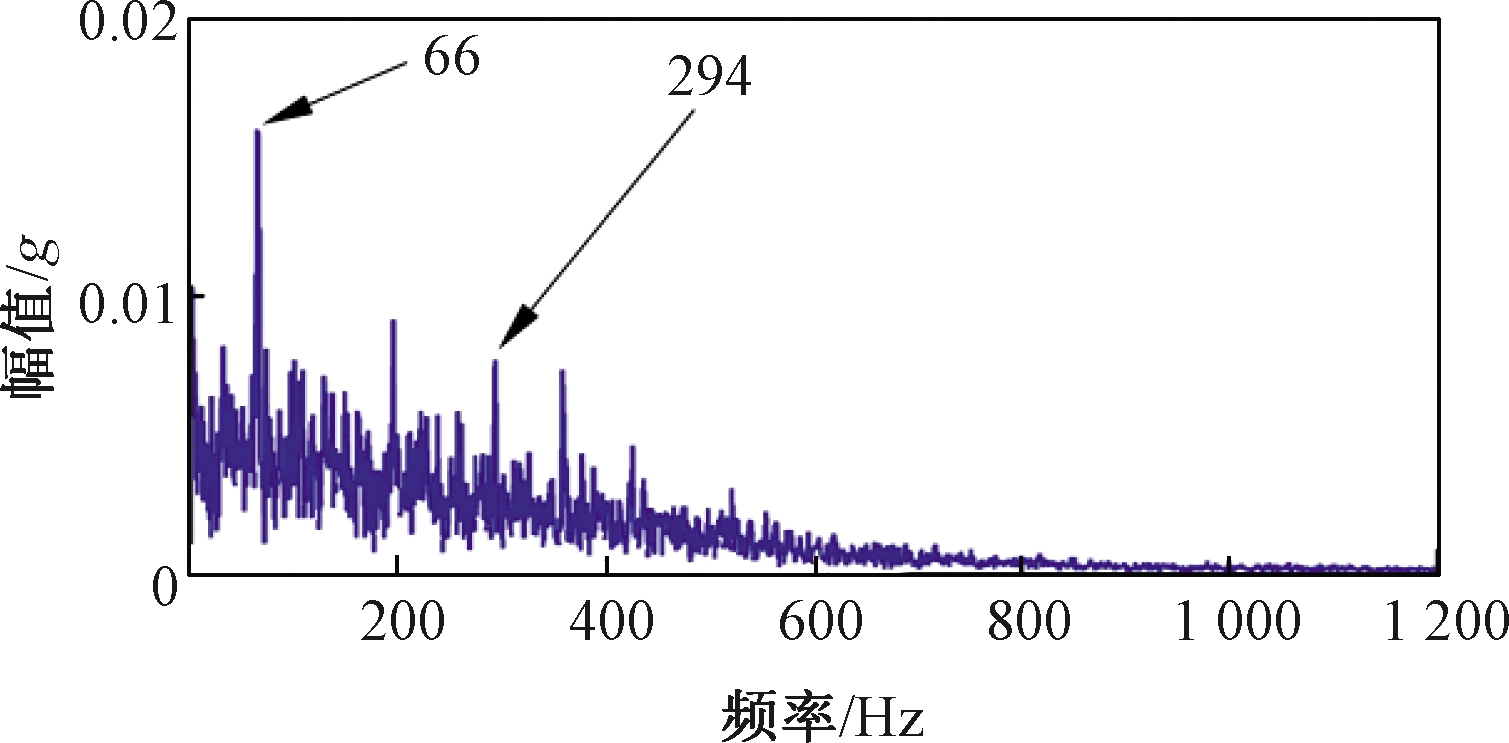
图6 全矢频带熵包络谱
Figure 6 Full vector frequency band entropy envelope spectrum
为了验证全矢频带熵提取故障信息的有效性,和谱峭度进行对比。图7为快速谱峭度自适应滤波得到的全矢包络谱,图中包含内圈故障频率294 Hz及其调制频率261 Hz、327 Hz,并且还包含转频33 Hz的2×、4×、5×、6×、7×成分,故障频率的幅值小于转频的2×幅值,噪声干扰成分较多。
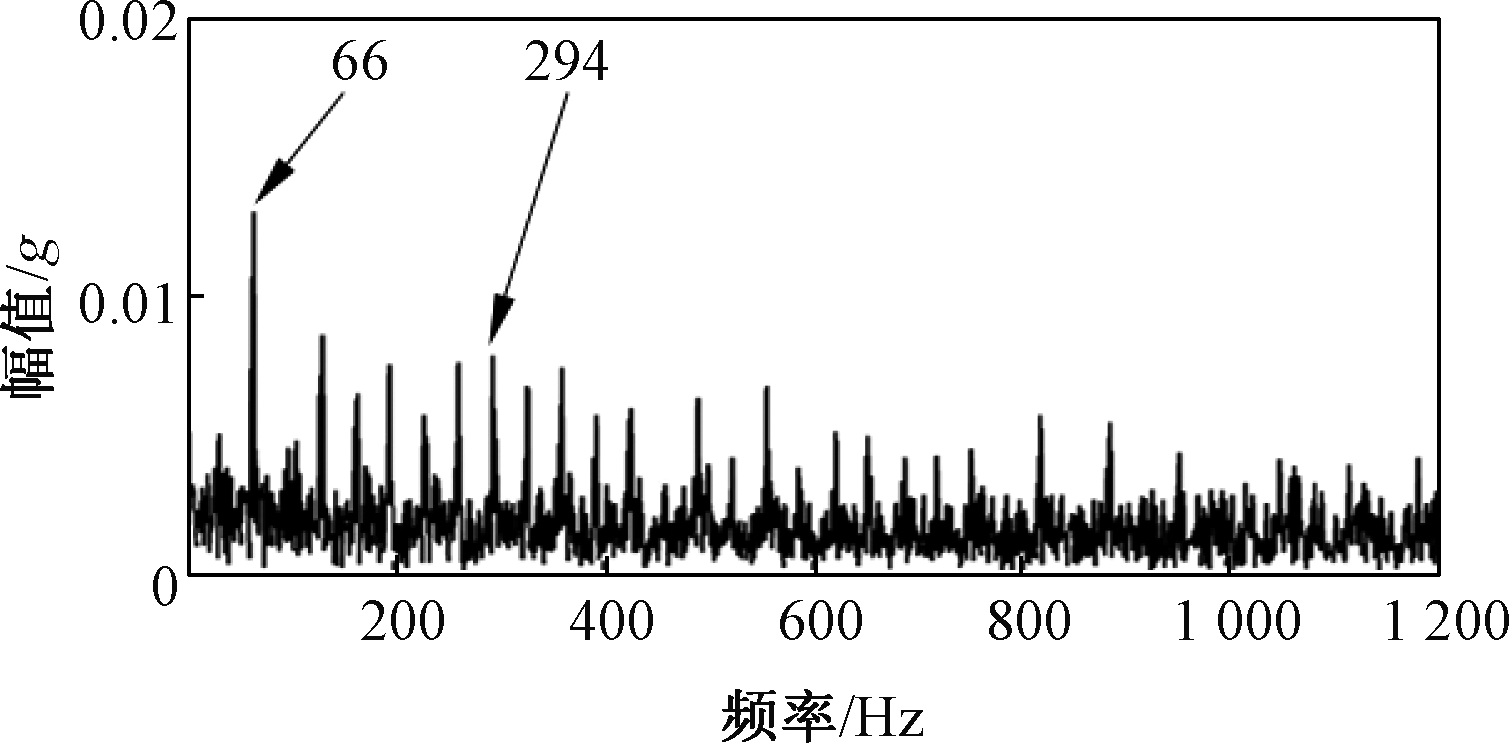
图7 谱峭度得到的全矢包络谱
Figure 7 Full vector envelope spectrum obtained by spectrum kurtosis
通过对比图6和图7,看出频带熵自适应滤波得到的全矢包络谱中能量集中在滚动轴承的内圈故障频率,噪声频率成分相对较小;谱峭度自适应滤波得到的全矢包络谱能量不仅分布在滚动轴承的内圈故障频率,还分布在转频的倍频成分,干扰性较大。由此可以看出全矢频带熵算法得到的全矢包络谱能够减小低频离散噪声的干扰,具有良好的抗干扰性,能够很好地提取出故障的频率信息,原因在于频带熵的算法具有一定的抗冲击干扰能力,提取的是幅值相对稳定存在的冲击成分,受幅值调制的影响相对较小。
6 结论
(1)全矢频带熵算法自适应滤波得到的全矢包络谱可以有效地提取滚动轴承的故障信息,克服了单通道信号提取故障信息不全的问题,避免了因此导致的诊断失误,并减少了滤波器设计环节人工选取参数的误差,提升了滚动轴承的故障诊断准确率,能够有效地从强背景噪声中自适应提取出故障的特征频率。
(2)和谱峭度得到的全矢包络谱相比,频带熵提取的是幅值相对稳定存在的冲击成分,即可在保留故障信息的前提下减小其他结构成分以及低频离散噪声的干扰,为后续的滚动轴承故障诊断研究提供了参考依据。
[1] 郝伟,林辉翼,郝旺身,等. 基于全矢稀疏编码的滚动轴承故障识别方法[J]. 郑州大学学报(工学版),2019,40(3):31-35.
[2] 李凌均,金兵,马艳丽,等. 基于MEMD与MMSE的滚动轴承退化特征提取方法[J]. 郑州大学学报(工学版),2018,39(4):86-91.
[3] TYAGI S, PANIGRAHI S K. An improved envelope detection method using particle swarm optimisation for rolling element bearing fault diagnosis[J]. Journal of computational design and engineering,2017,4(4):305-317.
[4] KLAUSEN A, ROBBERSMYR K G, KARIMI H R. Autonomous bearing fault diagnosis method based on envelope spectrum[J]. IFAC-PapersOnLine,2017,50(1):13378-13383.
[5] CHEGINI S N, BAGHERI A, NAJAFI F. Application of a new EWT-based denoising technique in bearing fault diagnosis[J]. Measurement, 2019,144:275-297.
[6] KUMAR K, SHUKLA S, SINGH S K. A combined approach for weak fault signature extraction of rolling element bearing using Hilbert envelop and zero frequency resonator[J]. Journal of sound and vibration, 2018,419:436-451.
[7] 陈东毅,陈建国,李玉榕. 改进经验模态分解与谱峭度法的步态信号特征分析[J]. 福州大学学报(自然科学版),2019,47(5):630-634.
[8] 田晶,王英杰,刘丽丽,等. 基于Birge-Massart阈值降噪与EEMD及谱峭度的滚动轴承故障特征提取[J].航空动力学报,2019,34(6):1399-1408.
[9] LEI Y G,LIN J,HE Z J,et al. Application of an improved kurtogram method for fault diagnosis of rolling element bearings[J]. Mechanical systems and signal processing,2011,25(5):1738-1749.
[10] LI H, LIU T, WU X,et al. Application of EEMD and improved frequency band entropy in bearing fault feature extraction[J]. ISA transactions,2019,88:170-185.
[11] 李华,刘韬,伍星,等. 基于SVD和熵优化频带熵的滚动轴承故障诊断研究[J].振动工程学报,2018,31(2):358-364.