0 引言
2016年年底，中国已建成各类水库大坝98 460 座，其中90%以上为土石坝[1]。常见的土石坝病险事故除洪水漫顶以外，主要还包括坝坡失稳、渗流异常和坝体开裂等[2]。开裂破坏是土石坝常见的隐患和导致土石坝变形破坏的主要原因之一。土石坝开裂会使大坝挡水功能不能得到充分发挥，甚至导致坝体溃决，严重影响大坝系统的服役寿命[3]。据统计，国内由裂缝问题引起的土石坝病险事故，在大型水库大坝中约占39%，小型水库土坝裂缝问题更多；而国外建造的高土石坝中，约有25%存在裂缝，有的已经导致溃坝事故[4]。工程经验表明，土石坝坝体开裂的原因除了施工期的加载变形以外，主要是在运行期发生的变形。当前，中国早期建造的土石坝多数已经达到正常使用年限[5]，对土石坝开裂破坏风险进行分析可以为病险事故判定提供依据。
根据《水库大坝安全评价导则》中对于变形分析的要求，部分学者从多角度对土石坝裂缝进行了定性或定量的研究。李雷等[6]根据土体拉应变试验，考虑拉应变的不确定性，采用一次二阶矩法计算坝体抗裂可靠度；刘远等[7]利用沉降观测资料，计算土石坝由裂缝引起的变形失事概率；彭翀等[8]采用有限元分析方法估算高土石坝是否会发生表面张拉裂缝等。
此类研究或采用有限元方法定性判断土石坝运行期间是否会产生裂缝，或考虑变量的随机性采用传统可靠度分析方法计算破坏概率。而在实际工程中，由于计算参数中存在着模糊性，变量的精确均值难以确定；且开裂破坏准则也存在模糊性，土体由稳定状态到开裂状态存在着过渡区域。考虑到土石坝裂缝产生时变量和失效准则的不确定性，本研究开展土石坝开裂破坏风险模糊分析。
1 土石坝开裂破坏风险模糊分析
变形与稳定分析是土石坝结构安全评价的重点，但坝体变形和破坏理论尚需完善[9]。就土石坝开裂破坏而言，大坝运行的安全可靠性依赖于坝体材料抵抗坝体变形产生的应力和应变的能力[10]，而土体的应力应变和极限应力应变均为随机变量，具有不确定性。
1.1 土石坝开裂破坏的不确定性分析
坝体裂缝是一种结构变形破坏，其中较为典型的是横向张拉裂缝破坏。这种裂缝常发生在坝体表面与两岸交界附近，会贯穿坝的防渗体，并在渗流作用下继续发展，因而危害极大[11]。坝体裂缝的产生受多重因素影响，如蓄水作用、流变变形、湿化变形，以及坝体的形状尺寸、土层分布、施工质量等，且这些因素都具有不确定性。对这些随机变量逐一考察会使模型构建复杂化，因此仅对土石坝易产生横向裂缝处土体的核心参数，即土体的水平拉应变和极限拉应变进行不确定性分析。
(1)极限拉应变Xtf。Xtf表征土体的抗拉强度，反映了土体抵抗开裂的能力，主要取决于土颗粒大小、干密度、含水率、孔隙率和容重等，服从正态、对数正态或极值Ⅰ型分布。极限拉应变与形成裂缝的类型有关，但与作用水头ΔH无关。Xtf值既可以根据经验公式计算，也可以通过原状土拉应变试验结果确定。
(2)水平拉应变Xx。Xx表征一定水位条件下土体的抗拉强度，是校核土体变形稳定的重要参数。水平拉应变和库水位、土体的干密度、含水率、内摩擦角和重度等多个变量有关，其值可根据有关公式计算得出。
坝体某点在各种作用下的应变效应即土体水平拉应变Xx，可采用倾度法来计算[7]。取坝头上3点a、b、c，其实测沉降量分别为s1、s2、s3，则该点的水平拉应变Xx如式(1)所示：
(1)
式中：C为河谷影响系数；Hmax为最大坝高；Δl为两测点间距离。
影响坝体各点沉降的因素很多，如坝体剖面尺寸、筑坝材料、施工质量、坝基地质条件及水库水位的变化等，且都具有不确定性。根据中心极限定理[12]，影响沉降量的随机变量序列无论它们原来服从何种分布，当数量足够多时，随机变量序列的综合值以正态分布为极限分布。因此认为s1、s2、s3均服从正态分布，所以Xx服从正态分布[6]。
1.2 土石坝开裂破坏风险评估模型
压实黏性土体在应力大于土体抗拉强度时先出现多条细微裂隙，随着这些裂隙逐渐扩大，裂纹加深，最终断裂[13]。一般认为，当裂缝产生处土体的水平拉应变Xx大于极限拉应变Xtf时，就会发生开裂。由此，开裂破坏发生的条件如式(2)所示：
Xx>Xtf，
(2)
式中：Xx为水平拉应变；Xtf为极限拉应变。
在实际工程中，土性参数在时间和空间存在可变性，因此某一区域基岩材料参数取值存在不确定性。在工程试验中，试验误差及试验与实际情况的差异也会引起材料参数的模糊性。由于土性参数的理论取值和实际值之间存在偏差，往往出现实际拉应变尚未达到理论极限拉应变时土体已经开裂，而实际拉应变超出理论极限拉应变时土体仍然完好的情况。另一方面，目前土石坝裂缝产生的评判缺乏统一标准[14]，开裂破坏也没有绝对明确的界限，即土体开裂准则中存在模糊性。为了描述土体开裂的过渡过程，引入模糊数∈[15]，同时综合考虑土体应变参数中存在的模糊性，则土石坝开裂破坏的风险评估模型如式(3)所示：
μZ(Z)μXtf(Xtf)μXx(Xx)f(Xx)dXx，
(3)
式中：μZ(Z)为系统的极限状态方程Z对开裂破坏这一模糊事件的隶属函数；μXtf(Xtf)、μXx(Xx)分别为理论极限拉应变、水平拉应变的隶属函数；f(Xx)为坝体材料水平拉应变的概率密度函数。
2 开裂破坏模糊风险率的求解
2.1 求解方法
风险率计算常用的方法主要有蒙特卡罗(Monte Carlo)法、一次二阶矩法、JC法、实用分析法和优化法等[16]。蒙特卡罗法又称随机模拟试验法，采用此方法计算复杂系统失事概率，能避免繁琐的积分运算，计算结果具有较好的计算精度和适用性[17]。土石坝开裂破坏风险率求解的具体方法：首先，通过沉降数据分析，对沉降量进行模拟，得到变量的抽样样本；然后，在样本中随机抽取数据代入极限状态方程，判断是否会开展裂缝并统计开裂的次数；最后，计算出发生开裂破坏次数与总抽样次数的比值，得到的频率值视为破坏风险值[18]。
2.2 求解步骤
利用式(3)求解土石坝开裂破坏模糊风险率时，要首先计算具有隶属函数和模糊变量的积分式，而确定隶属函数是相当困难的。通过引入模糊集理论中水平截集[19]的概念，利用α-水平截集，原有的模糊量可以转化为区间数的形式，从而在计算中消除了变量的模糊性。模糊变量的处理[20]如式(4)～(6)所示：
(Xx)α=[Xx+0.1Xx(α-1),Xx+
0.1Xx(1-α)];
(4)
(Xtf)α= [Xtf+0.1Xtf(α-1),Xtf+
0.1Xtf(1-α)];
(5)
∈=[δ(α-1)，δ(1-α)]。
(6)
由此可得模糊风险率，如式(7)和式(8)所示：
(7)
(8)
式中：
分别为模糊风险率区间上、下限；δ为极限状态下允许的最大裕度。
式(7)、(8)可以采用传统的可靠度方法计算，结果得到模糊风险率区间如式(9)所示：
(9)
由式(1)可知，f(Xx)的不确定性与沉降量有关，而坝体的沉降量和库水位密切相关，故对式(7)、(8)进行离散化处理，如式(10)、(11)所示：
(10)
(11)
式中：
为给定水位区间
时，土体实际水平拉应变大于理论极限拉应变的概率值；
为土体水平拉应变在某一水位hi下的条件概率密度函数；n为划分的库水位区间数；
为库水位区间频率。
求解时，先进行水库调洪计算，得出
然后，通过蒙特卡罗模拟，计算的值；最后，根据式(11)可得土石坝开裂破坏模糊风险率。
3 实例分析
毛尖山水库大坝为黏土心墙土石坝，坝顶长210 m，最大坝高为72.2 m。水库总库容为0.48亿m3，正常蓄水位为365.0 m。工程于1959年1月进行坝体大面积填筑，由于施工控制不当，施工期发现心墙与下游砂壳界面上有连续裂缝。发生的剪切裂缝深9.5 m，最大缝宽10 mm，因此在1963—1964年施工期间对大坝裂缝多次进行灌浆处理，效果良好，最终工程于1964年下半年顺利竣工。大坝变形监测系统包括37个竖向位移监测测点，各测点水平相距20 m。分析1963年6月开始观测至2002年11月7日的变形监测资料，在两岸岸坡与坝体接触部位，以及堆石料和心墙上下游接触部位附近计算得到的变形倾度值大于1%。但由于这种错切变形一般发生在坝体内部，土体承受较大的压应力，因此一般不会形成张拉裂缝威胁坝体的整体稳定和心墙的安全。
该坝右坝肩边坡陡峭，是该工程的重点薄弱部位。由于心墙在施工期间已进行灌浆加固，因此在后期运行过程中仅选择坝顶右岸沉降点372-1、372-2、372-3的观测值进行土石坝开裂破坏的风险分析。参照已有资料选取计算参数：河谷影响系数C=0.3，最大坝高Hmax=72.2 m，测点间距Δl=20 m；土体极限拉应变服从正态分布，其均值为1.98‰，标准差为0.64‰[21]。沉降实测结果统计成果如表1所示。
表1 沉降实测结果统计表
Table 1 Statistical table of measured settlement results
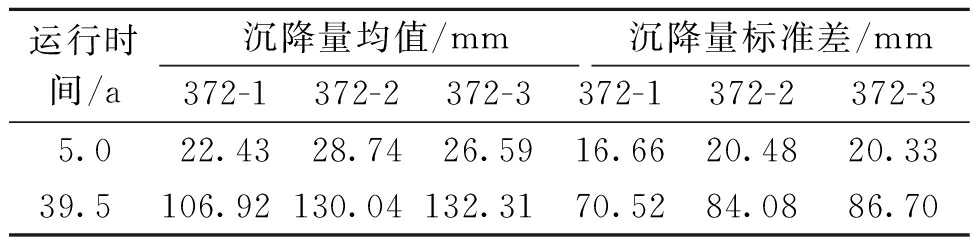
运行时间/a沉降量均值/mm沉降量标准差/mm372-1372-2372-3372-1372-2372-35.022.4328.7426.5916.6620.4820.3339.5106.92130.04132.3170.5284.0886.70
采用笔者提出的风险模型分别计算大坝运行5 a和39.5 a后的开裂破坏模糊风险率。通过分析长系列变形监测资料，发现观测数据和库水位关系相关性较差，因此采用极限状态方程g(*)=Xx-Xtf=0直接进行风险分析。利用蒙特卡罗方法对沉降资料进行模拟，根据式(1)得到土体水平拉应变参数：运行5 a时模拟应变参数均值为-0.23‰，标准差为1.32‰；运行39.5 a时模拟应变参数均值为-0.55‰，标准差为5.45‰。在对变量进行模糊化处理的基础上，基于
计算模糊风险率。利用MATLAB进行10万次模拟之后，计算结果相对稳定，概率精度满足工程实际要求。大坝运行5 a后的分析结果如表2和图1所示。
表2 运行5 a后开裂破坏模糊风险率区间
Table 2 Fuzzy risk interval of cracking failure after five years of operation
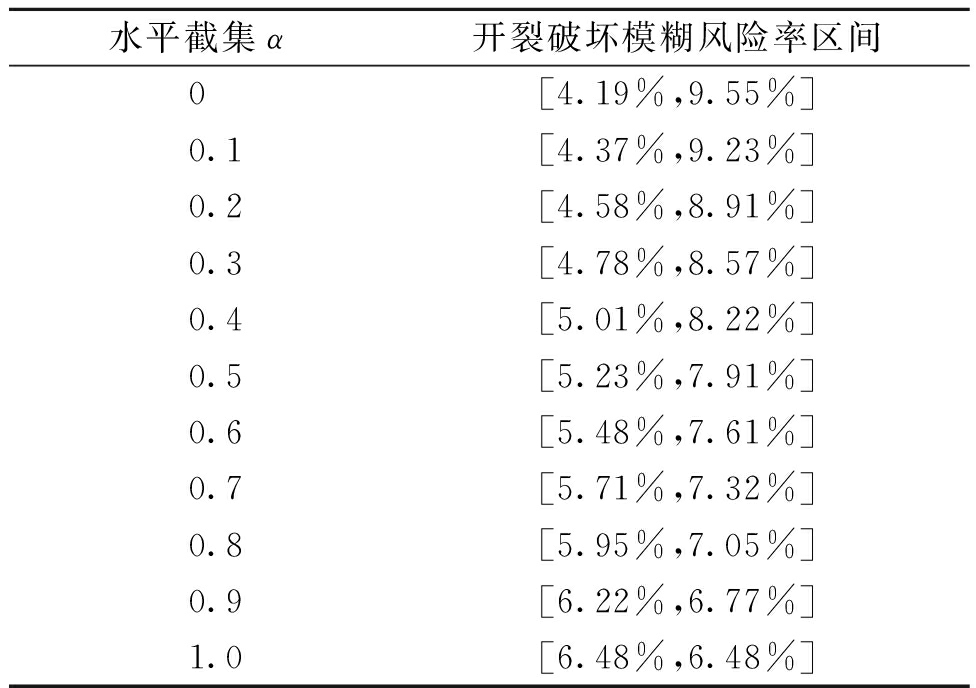
水平截集α开裂破坏模糊风险率区间0[4.19%,9.55%]0.1[4.37%,9.23%]0.2[4.58%,8.91%]0.3[4.78%,8.57%]0.4[5.01%,8.22%]0.5[5.23%,7.91%]0.6[5.48%,7.61%]0.7[5.71%,7.32%]0.8[5.95%,7.05%]0.9[6.22%,6.77%]1.0[6.48%,6.48%]
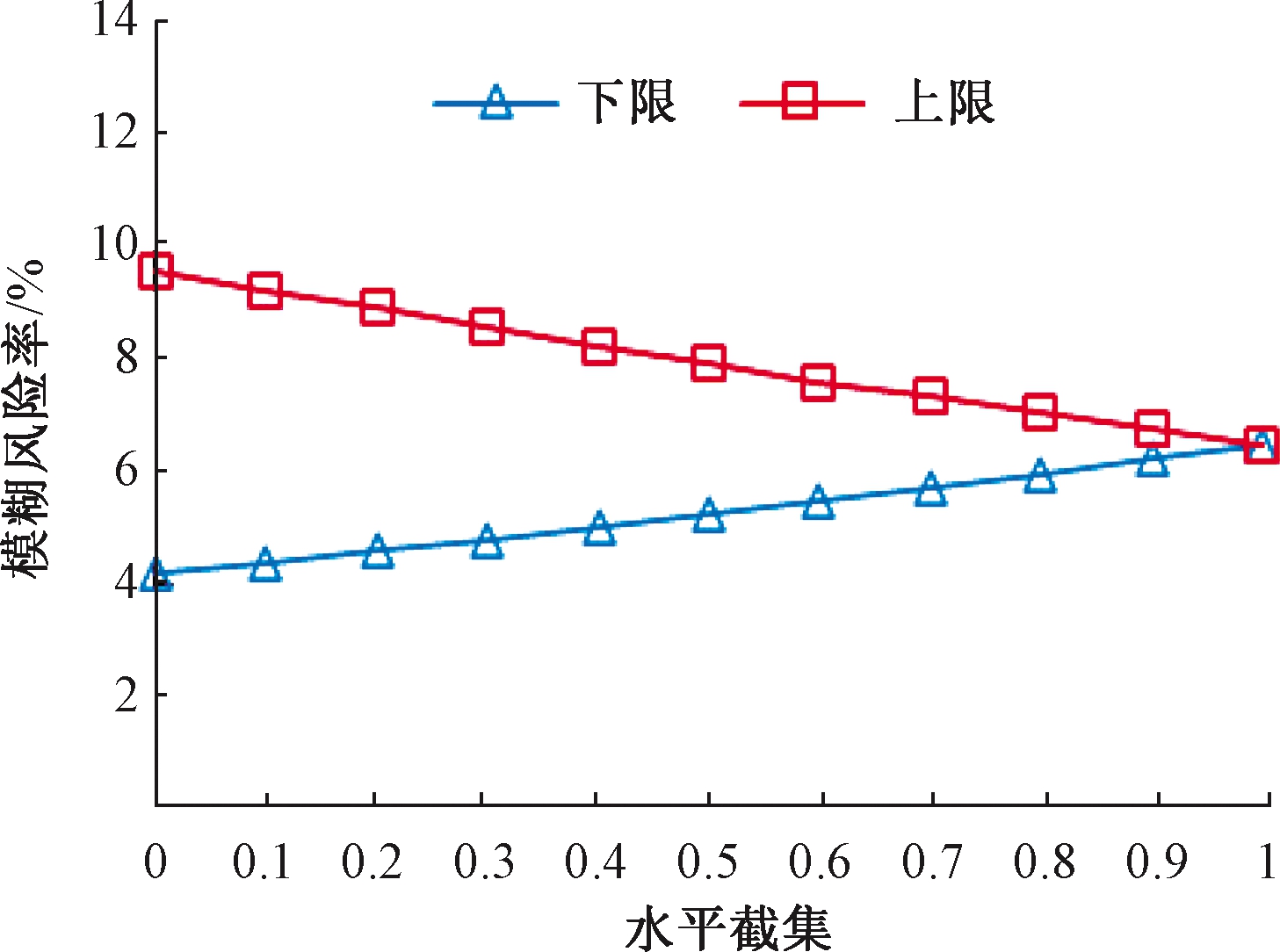
图1 不同截集水平下的模糊风险率
Figure 1 Fuzzy risk rate under different cut set levels
采用不同方法计算土石坝运行5 a和39.5 a后开裂破坏风险率如表3所示。
表3 开裂破坏风险率计算结果统计表
Table 3 Statistical table of calculation results of cracking failure risk rate
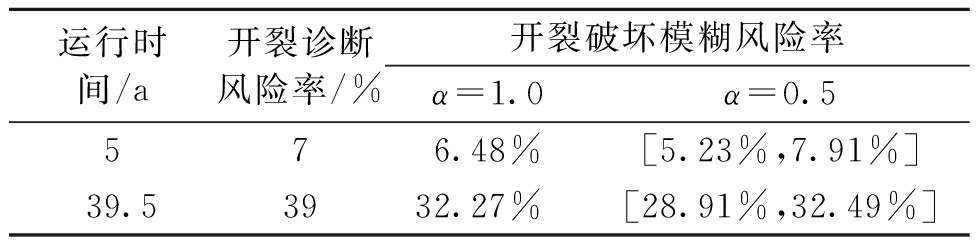
运行时间/a开裂诊断风险率/%开裂破坏模糊风险率α=1.0α=0.5576.48%[5.23%,7.91%]39.53932.27%[28.91%,32.49%]
对上述图表进行分析可知：
(1)考虑了变量的模糊性后，得到土石坝开裂破坏的模糊风险率区间如表2所示。根据表2和图1，水平截集α=0时，开裂破坏模糊风险率的变动范围最大，此时的风险区间对开裂破坏判定来说参考意义不大；α=1.0时，没有考虑设计参数的模糊性，开裂风险率为6.48%，这个计算结果与文献[21]中对毛尖山水库大坝运行5 a后进行开裂分析诊断得到的破坏概率7%近似，证实了采用蒙特卡罗模拟计算的可行性。
(2)表2中不同截集水平下的风险区间表示不同程度的开裂风险。平等地考虑各变量的模糊性，在表2中选取α=0.5时的模糊风险率作为开裂破坏风险，在大坝运行5 a时
表明其发生开裂破坏的风险率为5.23%～7.91%，平均风险率为6.57%。从工程风险角度分析，坝顶右岸产生横向裂缝的概率在这个风险率区间内变动相对较小，风险上下限可以为进一步的风险评价提供参考；且这个风险区间的平均风险率与大坝开裂分析诊断得到的风险概率近似，因此认为风险分析结果一致。
(3)考察大坝运行到2002年底开裂破坏风险，在表3中取α=0.5时得到风险率区间为[28.91%，32.49%]。这个风险率区间比大坝开裂分析诊断得到的开裂破坏概率39%要合理，因为在1973年坝顶右坝肩部位发现裂缝后又进行了灌浆处理，坝顶应力状态发生改变，而采用传统可靠度方法计算未考虑这一工程措施的影响。由于灌浆效果良好，土体抗拉能力增强，根据式(7)可知，风险区间下限更有参考价值。文献[21]得出的大坝开裂分析诊断结论认为，要特别注意坝顶右岸横向裂缝的产生，而从模糊风险区间下限判断，实际上裂缝开展的可能性大为降低。
4 结论
笔者综合考虑影响土石坝开裂破坏风险因素的随机性和模糊性，引入模糊集理论，建立了土石坝开裂破坏风险评估模型。求解模型时隶属函数难以确定，采用水平截集处理变量模糊性，将模糊量转化为区间数后即可应用蒙特卡罗方法计算模糊风险率。将建立的风险模型应用于毛尖山水库大坝的开裂破坏分析中，并将计算结果与采用传统可靠度方法得出的大坝变形健康诊断结果对比分析，验证了该模型的可靠性和合理性。计算结果表明：大坝运行5 a后，改进方法与传统方法得出的评价结论一致；大坝经过灌浆处理以后，根据改进方法得出风险评价结果比传统方法更符合工程实际。
[1] 中华人民共和国水利部. 2016年全国水利发展统计公报[M]. 北京: 中国水利水电出版社, 2017.
[2] MA J, YANG J, LI S Y, et al. Application of fuzzy analytic hierarchy process in the risk assessment of dangerous small-sized reservoirs[J]. International journal of machine learning and cybernetics, 2018, 9(1): 113-123.
[3] SU H Z, HU J, WEN Z P. Service life predicting of dam systems with correlated failure modes[J]. Journal of performance of constructed facilities, 2013, 27(3): 252-269.
[4] 韩朝军,朱晟. 土质防渗土石坝坝顶裂缝开裂机理与成因分析[J]. 中国农村水利水电, 2013(8): 116-120.
[5] 李宗坤, 葛巍, 王娟, 等. 中国大坝安全管理与风险管理的战略思考[J]. 水科学进展, 2015, 26(4): 589-595.
[6] 李雷, 盛金保. 土石坝安全度综合评价方法初探[J]. 大坝观测与土工测试, 1999,23(4): 22-24,28.
[7] 刘远, 王振宇, 刘国华, 等. 土石坝失事量化风险评估方法研究[J]. 水力发电, 2005, 31(3): 44-47.
[8] 彭翀,张宗亮,张丙印,等. 高土石坝裂缝分析的变形倾度有限元法及其应用[J]. 岩土力学, 2013, 34(5): 1453-1458.
[9] 宁保辉, 来亦姝, 王春磊, 等. 前坪水库大坝应力变形及抗水力劈裂研究[J]. 人民黄河, 2019, 41(5): 122-125.
[10] 邓刚,徐泽平,吕生玺,等. 狭窄河谷中的高面板堆石坝长期应力变形计算分析[J]. 水利学报, 2008, 39(6):639-646.
[11] 张琰, 王建国, 张丙印, 等. 土坝裂缝开展的无单元法数值模拟[J]. 岩土工程学报, 2009, 31(5): 727-731.
[12] 纪宏伟. 关于中心极限定理的解读[J]. 江西电力职业技术学院学报, 2019, 32(3): 82-84, 87.
[13] 胡磊, 张云, 史卜涛, 等. 重塑黏土抗拉特性试验研究[J]. 水文地质工程地质, 2017, 44(4): 98-104, 110.
[14] 于沭, 邓刚, 温彦锋, 等. 土石坝裂缝数值模拟方法研究[J]. 水利水电技术, 2014, 45(1): 152-157.
[15] 李宗坤, 韩瑞芳, 刘文立. 土石坝渗透破坏模糊风险分析[J]. 大坝与安全, 2007(1): 17-20.
[16] 罗国武, 区军雄. 土石坝坝坡失稳模糊风险分析[J].水利与建筑工程学报, 2012, 10(1):173-176.
[17] 李宗坤, 葛巍, 王娟, 等. 土石坝建设期漫坝风险分析[J]. 水力发电学报, 2015, 34(3): 145-149.
[18] 马海云, 党建武. 基于蒙特卡罗的软件测试技术的研究与实现[J]. 郑州大学学报(工学版), 2007, 28(4): 55-58.
[19] 郭平功,童丽萍. 基于α截集法的生土窑居模糊随机可靠度分析[J]. 郑州大学学报(工学版), 2012, 33(6): 112-116.
[20] SU H Z, WEN Z P. Interval risk analysis for gravity dam instability[J]. Engineering failure analysis, 2013, 33: 83-96.
[21] 侯玉成. 土石坝健康诊断理论与方法研究[D]. 南京: 河海大学, 2005.