0 引言
塔式太阳能发电是一种具有广阔发展前景的新能源技术。在塔式系统中，定日镜场成本约占总投资成本的40%～50%，其布局方式直接影响到整个镜场的集热效率，优化定日镜场布局十分必要。
目前对定日镜场布局的研究多为单目标，优化问题常见的目标函数有年均加权光学效率、平均能源成本等，然而单目标无法为决策者提供多而优的选择方案。Richter等[1]将发电量、密度分布、均匀性3个目标函数聚合转化为单目标问题求解，然而这种方法要求决策者有足够的先验知识。张宏丽等[2]基于多目标遗传算法将单位能量成本与投资成本作为多目标函数，得到了两者之间的关系。总体来说，国内外缺乏对定日镜场布局的多目标优化研究。
多目标进化算法(multi-objective evolutionary algorithm, MOEA)基于种群进化的并行性，每次迭代能求得一组 Pareto最优解集。典型MOEA有非支配排序遗传算法(NSGA-II)[3]、多目标粒子群算法(MOPSO)、改进的强度帕累托进化算法(SPEAII)[4]以及由张青富等[5]提出的基于分解的多目标进化算法(MOEA/D)。 MOEA/D收敛速度快，解集分布性好，被广泛应用到工程实际中[6]。近年来许多学者提出了对MOEA/D的改进算法，主要有：1)改进权重生成策略；2)改进子问题分解方法；3)采用效率更高的计算资源分配方法；4)采用不同的进化繁殖策略。
笔者在MOEA/D基础上对种群初始化、变异交叉因子以及归一化目标函数进行改进，并建立椭圆形定日镜场优化模型，提出了基于改进的MOEA/D多目标定日镜场布局优化算法。实验表明，改进的MOEA/D在定日镜场布局问题上表现明显优于NSGA-II算法和基本MOEA/D算法。
1 建立定日镜场模型
1.1 定日镜场初始布局
首先采用径向交错法[7]生成初始镜场。图1中定日镜的特征长度为
镜场分为3个区域，相邻两排定日镜径向间距ΔRmin约等于边长为DM的等边三角形的高：
ΔRmin=DMcos 30°-h≈DMcos 30°=
(1)
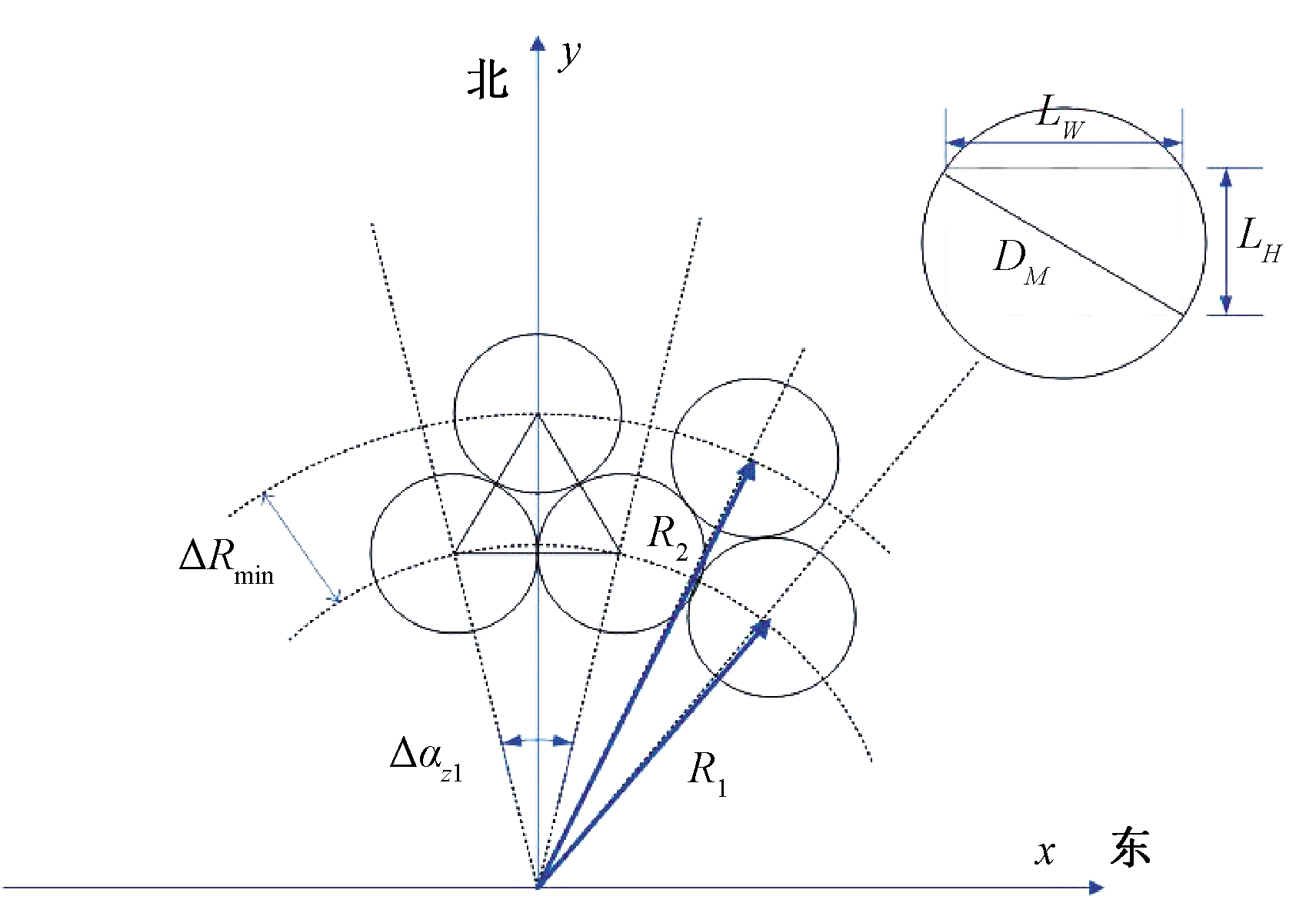
图1 径向交错布局
Figure 1 Diagram of radial staggered configuration
第一排定日镜的半径R1与塔高Ht的比值通常为0.75。R1确定后，由式(2)可得第一排相邻定日镜的角间距Δαz1，根据式(3)可得区域一每排定日镜的数量Nhel1。
Δαz1=2arcsin[DM/(2R1)]≈DM/R1；
(2)
Nhel1=2π/Δαz1=2πR1/DM。
(3)
同一排相邻定日镜的方位间距随每排半径的增加而增加，当两定日镜间可再放一台新的定日镜时，一个区域布置完成，开始排布下一个新的区域，因此，第二、第三个区域第一排相邻定日镜的方位角间距分别为：
Δαz2=Δαz1/2≈DM/R2⟹
R2≈2(DM/Δαz1)=2R1；
(4)
Δαz3=Δαz1/4≈DM/R3⟹
R3≈4(DM/Δαz1)=4R1。
(5)
每个区域的定日镜排数分别为：
N rows1=(R2-R1)/ΔRmin≈round(R1/ΔRmin)；
(6)
Nrows2=(R3-R2)/ΔRmin=2·R1/ΔRmin；
(7)
Nrows3=(R4-R3)/ΔRmin=4·R1/ΔRmin。
(8)
本实验主要算例参数:塔高120 m，第一排半径为87.5 m，第一区域共6排，每排放置35台定日镜；第二区域共12排，每排70面定日镜；第三区域共25排，每排140面定日镜。一共4 550台定日镜，最大半径676 m，占地面积为1.435 6×106 m2。为了证明所提方法在小型镜场中同样有效，补充算例二：塔高80 m，第一排半径60 m, 第一区域4排，每排24面定日镜；第二区域8排，每排48面定日镜；第三区域16排，每排96面定日镜。一共2 016面定日镜，最大半径为444 m,占地面积为6.193 21×105 m2。
1.2 定日镜场光学效率模型
任意时刻每一面定日镜的光学效率为：
ηopt=ηcosηatmηrefηintηs&b，
(9)
式中：ηcos为余弦效率，即入射光线与镜面法线夹角的余弦值;ηatm为大气衰减效率，由大气散射与吸收引起，采用Biggs等[8]提出的公式计算；ηref 为镜面反射率，由定日镜本身材料结构决定；ηint为拦截效率，是接收器接收到的太阳辐射与定日镜反射太阳辐射的比值，与定日镜跟踪误差、太阳形状误差、像散误差等有关，计算方法参见文献[9]；ηs&b为阴影遮挡效率，采用Sassi[10]提出的几何投影法来计算。
定日镜场年均综合光学效率计算公式如下：
(10)
式中：ts、tr分别为日落和日出时间。
定日镜场占地面积计算公式如下：
Sarea=π×amax×bmax，
(11)
式中：amax、bmax分别代表定日镜场最外圈椭圆的长轴和短轴的长度。
1.3 多目标椭圆定日镜场优化模型
在北半球，接收塔北面的定日镜余弦效率更高而阴影遮挡损失严重；太阳高度角比较小的时候，靠近东西轴方向的定日镜阴影遮挡损失更严重。为了提高布局的灵活性，笔者提出椭圆形定日镜场布局, 每一圈定日镜在x、y轴方向的增量为：
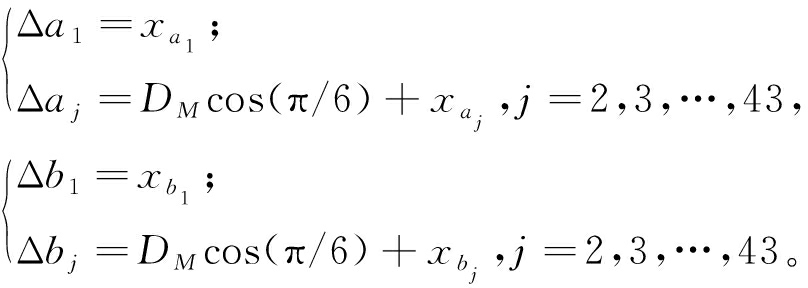
(12)
式中:xaj,xbj∈[0,3DM]。
圆形是椭圆形布局的一种特例，椭圆布局能够让每一面定日镜更有可能排布在其光学效率最优的位置。多目标定日镜场布局优化模型为：
min F=(f1,f2)，
(13)
式中：
f1=Sarea=πamaxbmax；
(14)
(15)
2 基于分解的多目标进化算法
2.1 MOEA/D
基于分解的多目标进化算法MOEA/D 根据一组预先生成的均匀权重向量将多目标问题分解为一系列单目标子问题，每个子问题的最优解对应于Pareto前沿面上的一个解。这些单目标子问题充分利用邻域子问题当前解提供的信息，用基于种群的进化算法共同迭代进化。
初始权重向量满足λi≥0且
常采用均匀分布的权重向量。
分解方法是MOEA/D的核心部分，有权重聚合法、切比雪夫加权法、基于惩罚的边界交叉法[5]。其中，切比雪夫加权法既能处理Pareto面为凸形又能解决其为凹形的问题。采用该方法，每个待优化的子问题可以表示为如下形式：
(16)
式中：
是参考点，对最小化问题有
2.2 改进的MOEA/D
2.2.1 初始种群生成策略的改进
佳点集法[11]：初始种群的质量对遗传算法的全局收敛性和算法的搜索效率有直接影响。用基于佳点集理论的取点法代替随机法可以使个体在解空间中更加可靠地均匀分布，提高算法稳定性。
在t维空间取佳点的方法如下:
Pn(k)={({r1·k},…,{ri·k},…,{rt·k}),
k=1,2,…,m}，
(17)
式中：
为满足p≥2 t+3的最小素数;或者取ri={ei}，1≤i≤t;{ri·k}表示取其小数部分。定义如下映射将单位立方体空间中的点映射到具体可行解空间T：f:H→T。
(18)
式中:1≤i≤t,1≤k≤m, t是空间的维数，m是取点数。
用以上两种方法在一个单位二维空间取400个点。如图2所示,随机法生成的点分布比较杂乱，密度不均匀，并且会出现多点重合的现象，而用佳点集法没有以上问题。
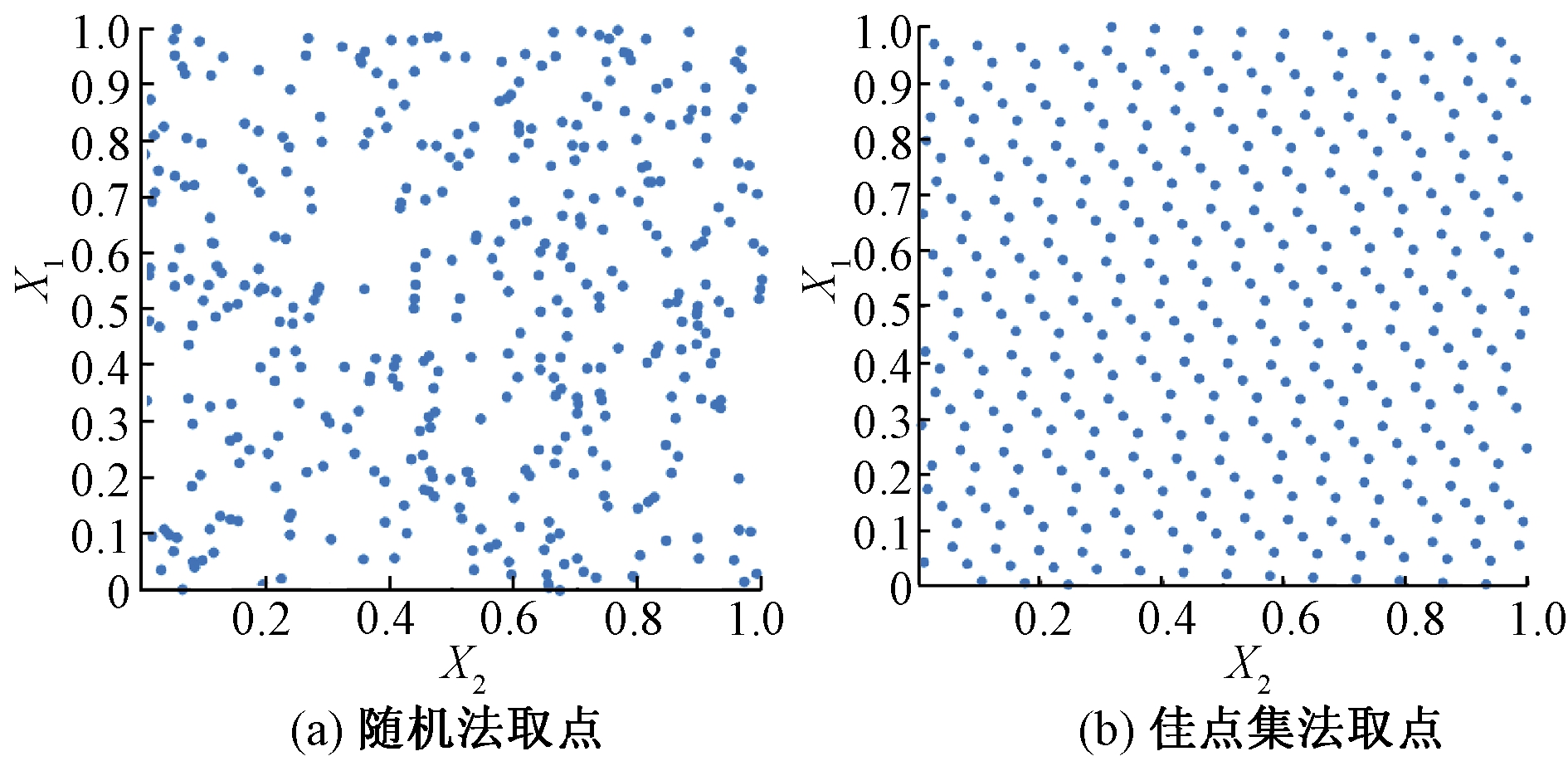
图2 初始种群生成策略比较
Figure 2 Comparison between two initial population generation strategies
反向学习[12]：在生成初始种群时考虑反向个体，选择二者中适应度值更佳的个体组成初始种群，能有效提高算法的精确度和收敛速度。个体反向解定义为：对P=(x1,x2,…,xn)，xi∈[ai,bi]， 反向点
其中
2.2.2 目标函数值稳定归一化
实际问题的目标函数一般有不同的量纲， 其目标值也在不同的数量级上。本例中，若采用未归一化的MOEA/D算法，将总是向最小化占地面积方向进化，仅能得到边界几个Pareto解。为了解决这一问题，现有研究常采用动态更新参考点的方法，即用每一次迭代得到的目标函数最大值和最小值对目标函数归一化。然而这一方法使原目标函数动态变化，算法进化不稳定。
针对定日镜场布局这一具体问题，通过第一部分的分析可知：镜场在最密布局时，占地面积最小(算例一：1.435 6×106 m2，算例二：6.193 21×105 m2)，综合光学效率最低(算例一：0.454 8，算例二：0.464 7)。采用简单单目标优化算法得到最高光学效率,具体过程不再赘述，得到最大效率值(算例一：0.547 7，算例二：0.589 7)，此时占地面积算例一：4.599 4×106 m2，算例二：2.435 6×106 m2。 Pareto前沿各目标函数最小值、最大值为(下式为算例一，算例二类似)：
(19)
目标函数稳定归一化表示为：
(20)
2.2.3 动态交叉因子
在MOEA/D的进化更新阶段，采用模拟二进制交叉(SBX)和多项式变异。由父代个体
生成子代个体
(21)
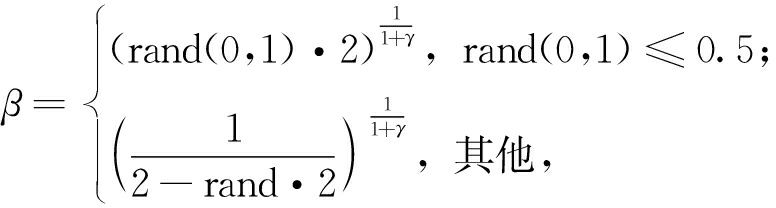
(22)
式中:γ为遗传交叉分布指数，当γ值较大时，生成的子代离父代较近，反之离父代较远。在进化初始阶段，应采用较小的交叉分布指数，提高种群多样性；在进化后期，应缩小搜索范围，加快收敛速度。基于此思想，笔者采用动态的交叉分布指数，γ由当前代数决定。计算公式如下：
γ=γo+ξ·normrnd(μ,σ)，
(23)
式中：初始值γo为2；高斯随机函数的均值μ=1；方差σ=1；ξ是用来控制随机扰动幅度的步长，用S型对数函数确定,
(24)
式中：T为最大迭代次数;t为当前代数;k用来控制变化速率，此处取k=20。
2.3 基于MOEA/D-HFL多目标镜场布局算法
步骤1 初始化。
(1)设置EP=∅。初始化迭代次数Gen=0。采用上文2.2.2部分介绍的方法设置参考点。
(2)初始化权重向量。计算权重向量之间的欧几里得距离，距离权重向量i最近的T个权重的索引集记为：B(i)=[i1,…,iT]，则λi1,…,λiT对应为 λi的T个相邻权重向量。
(3)生成初始种群。在决策空间利用佳点集生成一个初始种群Pop1，采用反向学习策略生成它的反向种群Pop2，选取适应度好的个体组成算法的初始种群。
步骤2 遗传进化。从B(i)中随机选取r1,r2，且r1≠r2≠i。根据式(21)、(22)进行模拟二进制交叉，其中交叉分布指数由式(23)、(24)确定。接着进行多项式变异。对变异生成的个体进行范围修正。
步骤3 更新邻域子问题的解，更新外部存档集。
步骤4 判断迭代停止条件。
步骤5 输出结果，输出目标值和对应Pareto最优解集,并采用模糊隶属度函数得到最优折中解。
3 实验
为验证提出算法的有效性，对两种不同规模的定日镜场进行多目标优化布局。同时，将所述算法得到的结果与基本MOEA/D以及NSGA-II算法得到的结果进行比较。本实验基于多目标进化PlatEMO平台[13]。
3.1 定日镜场及算法参数设置
定日镜场具体参数见表1。算法种群大小均为N=100;最大迭代次数为Gmax=300;MOEA/D邻域大小T=20; 遗传算法各控制参数已在上文指出。其中，基本MOEA/D和NSGA-II的固定遗传交叉分布指数为20，参见文献[3，5]。每个算法独立运行10次。
表1 定日镜场参数
Table 1 Parameters of the heliostat field
参数镜场地理经度镜场地理纬度镜场海拔高度/km定日镜长/m定日镜宽/m镜场区域数量数值97°22'E37°22'N3.512.39.753参数定日镜反射率定日镜坡面误差/rad定日镜跟踪误差/rad太阳形状误差/rad接收器半径/m接收器高度/m数值0.90.94×10-30.63×10-32.51×10-349
3.2 算法评价指标HV
Hypervolume(HV)超体积指标由解集中的个体与参考点在目标空间中所围成的超立方体的体积计算得到。用HV可以综合评价解集的收敛性与分布性，HV值越大,说明算法的综合性能越好。
(25)
式中：λ代表勒贝格测度;υi代表参考点和非支配个体构成的超体积;S代表非支配集。
3.3 模糊隶属度函数
获得Pareto解集后，引入模糊隶属度函数表示各个目标的满意度，模糊隶属度函数定义如下：
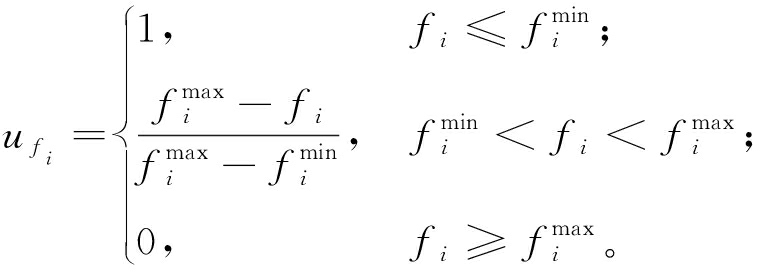
(26)
对于每个解，用下式求其标准化满意度值：
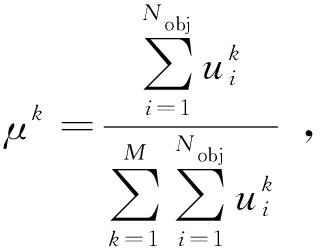
(27)
式中：M为Pareto解集中解的个数；Nobj为目标函数个数。标准化满意度最大的解就是最优折中解。
3.4 实验结果与分析
算例一：图3～5分别是3种算法得到的最接近平均HV时的Pareto前沿图。红色星号代表最优折中解。从横纵坐标所在的范围看，NSGA-II和基本MOEA/D的Pareto前沿局限于较窄的区域，说明这两种算法容易陷入局部最优，而MOEA/D-HFL得到的Pareto前沿分布更广，解集两端的开发性更好，能提供更多且更高质量的方案。 MOEA/D算法得到的Pareto前沿均比NSGA-II得到的前沿分布更加均匀。
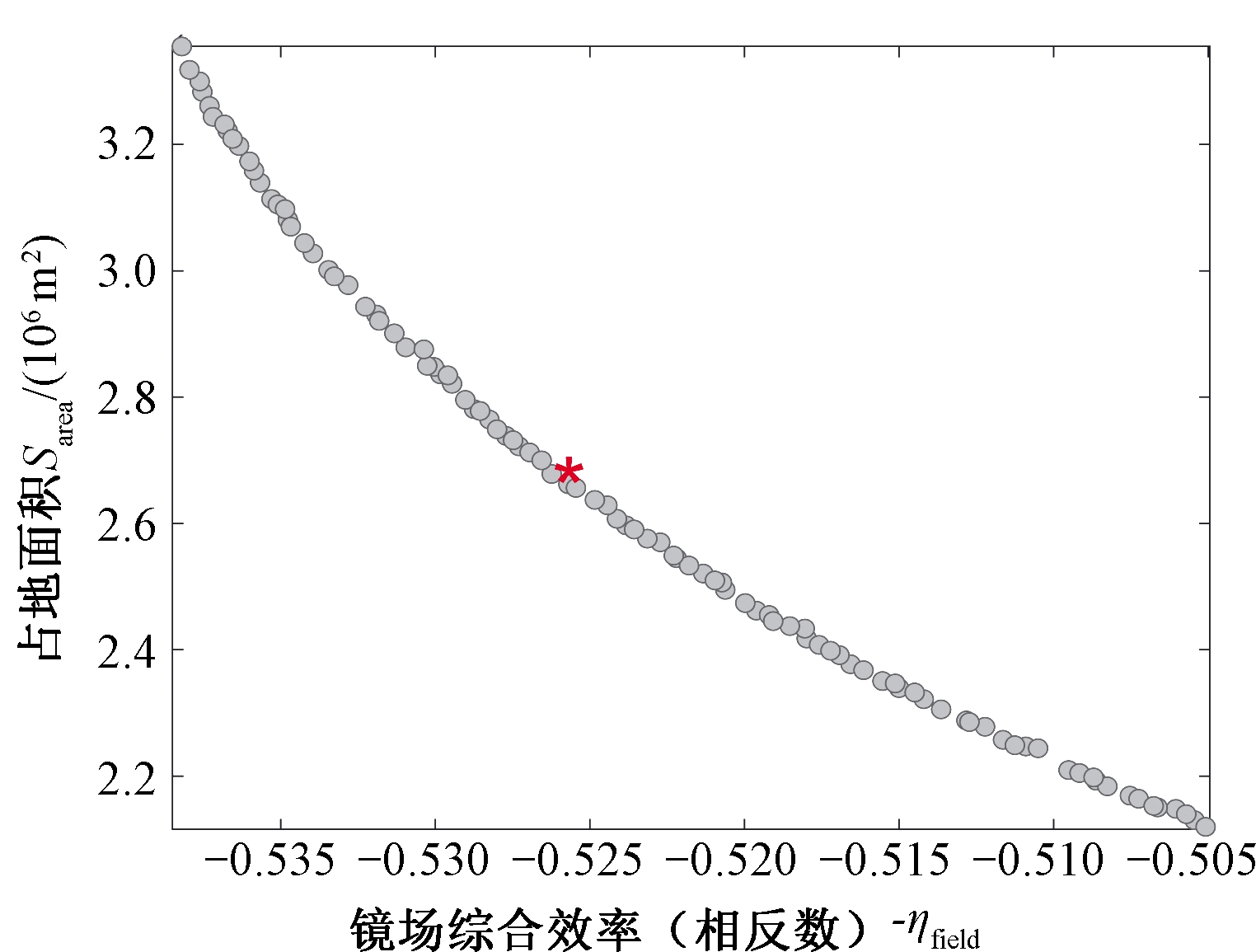
图3 算法NSGA-II所得Pareto前沿
Figure 3 Pareto front obtained from NSGA-II algorithm
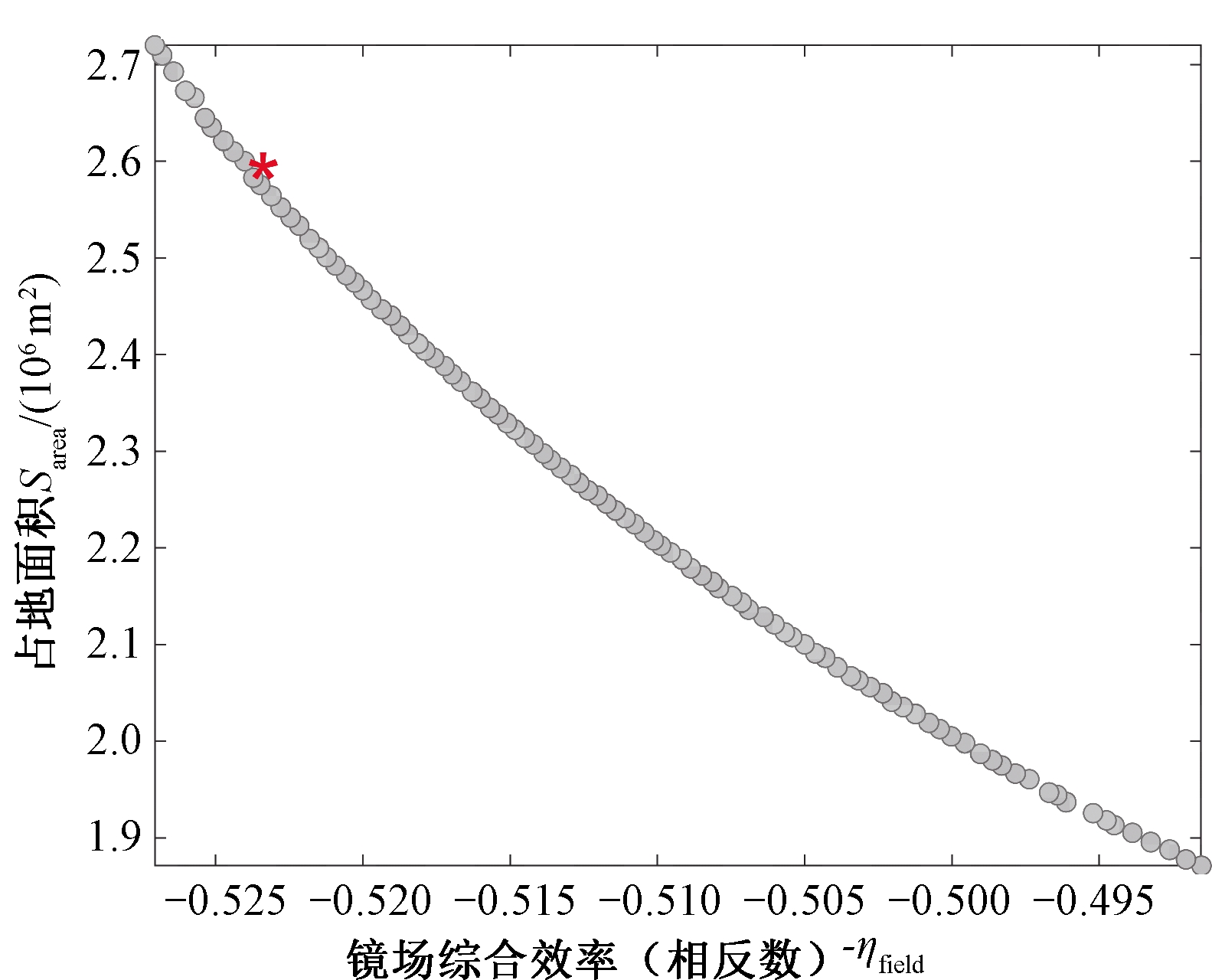
图4 基本MOEA/D算法所得Pareto前沿
Figure 4 Pareto front obtained from basic MOEA/D algorithm
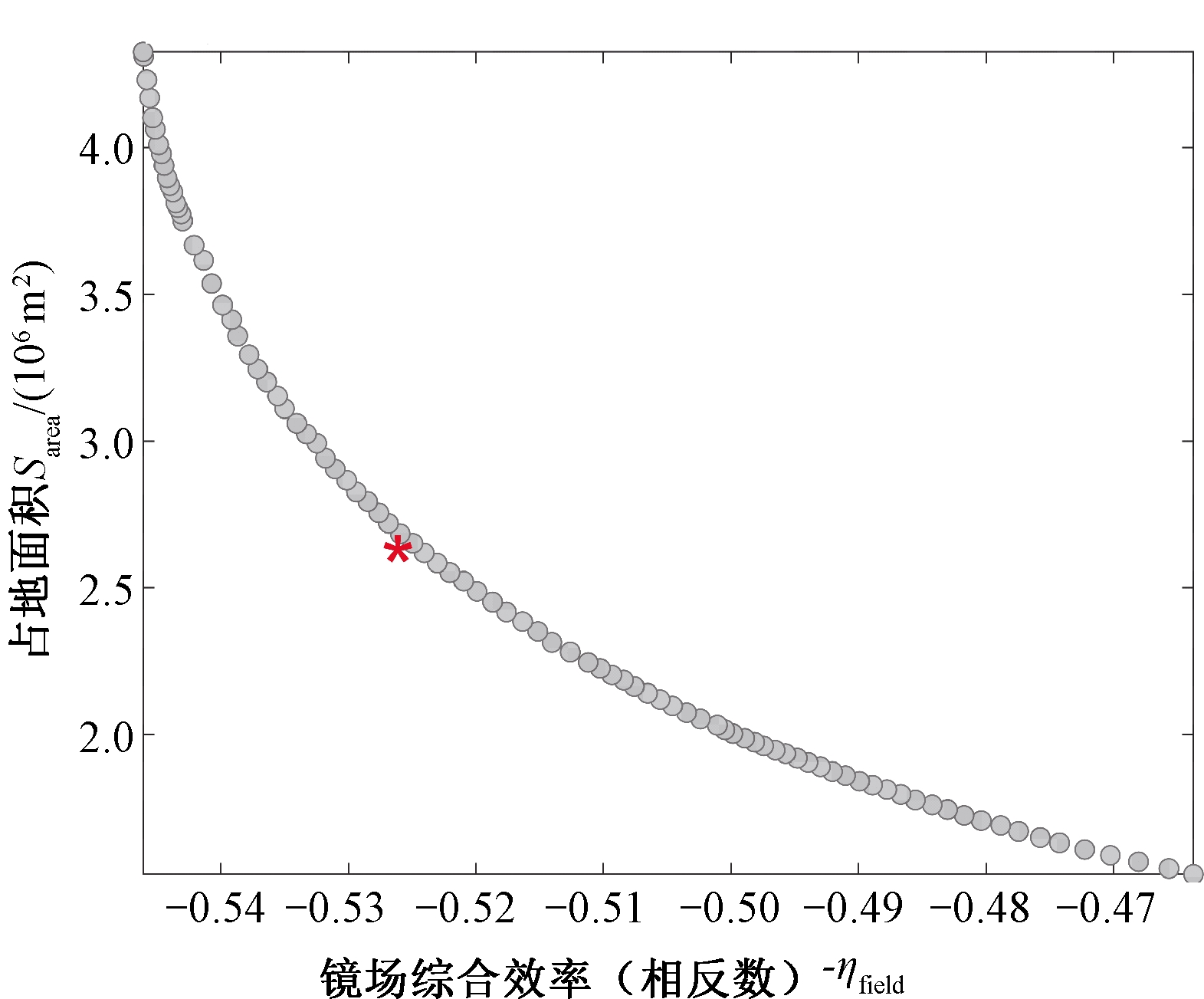
图5 算法MOEA/D-HFL所得Pareto前沿
Figure 5 Pareto front obtained from MOEA/D-HFL algorithm
表2列出了3种算法得到的极端解和最优折中解对应的目标函数值。对比可知，在极端解方面，MOEA/D-HFL得到的最大光学效率和最小占地面积均优于另两种算法,其最大光学效率为0.546 1，最小占地面积为1.523×106 m2。在最优折中解方面，MOEA/D-HFL得到的最优折中解光学效率最高，为0.527 4，而占地面积略大于基本MOEA/D。NSGA-II得到的折中解占地面积最大， MOEA/D所得光学效率最低。综合比较，MOEA/D-HFL得到的极端解和最优折中解质量最好。图6是由MOEA/D-HFL最优折中解得到的定日镜场布局图。
表2 试验结果(算例一)
Table 2 Experimental results (case 1)
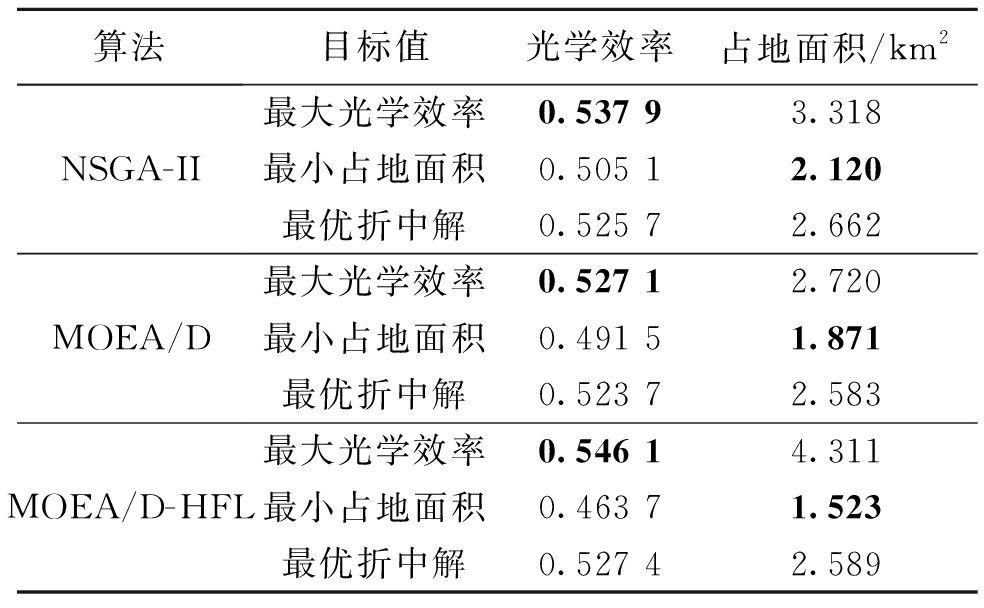
算法目标值光学效率占地面积/km2NSGA-IIMOEA/DMOEA/D-HFL最大光学效率0.537 93.318最小占地面积0.505 12.120最优折中解0.525 72.662最大光学效率0.527 12.720最小占地面积0.491 51.871最优折中解0.523 72.583最大光学效率0.546 14.311最小占地面积0.463 71.523最优折中解0.527 42.589
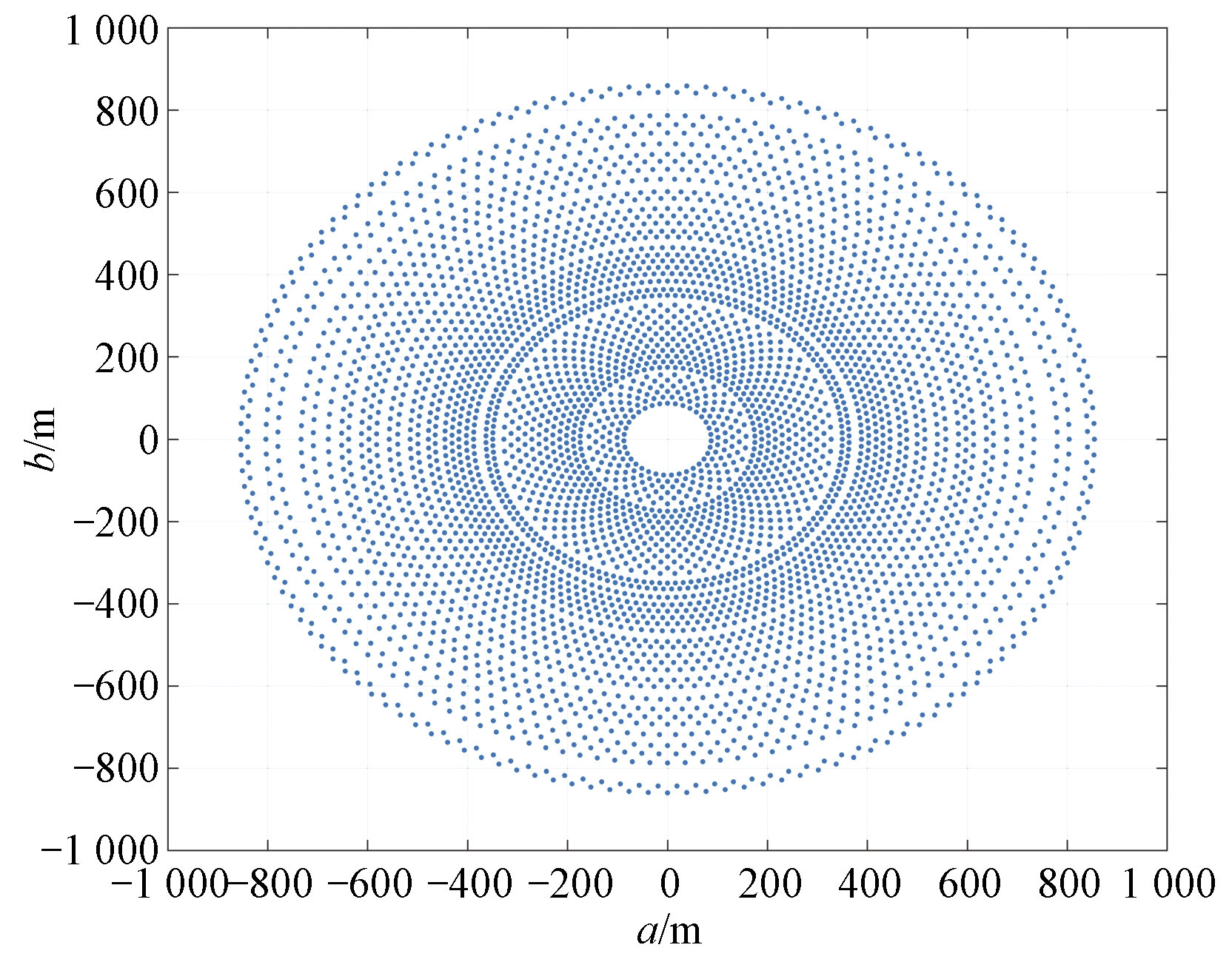
图6 多目标定日镜场布局最优折中解优化结果
Figure 6 Optimal compromise solution
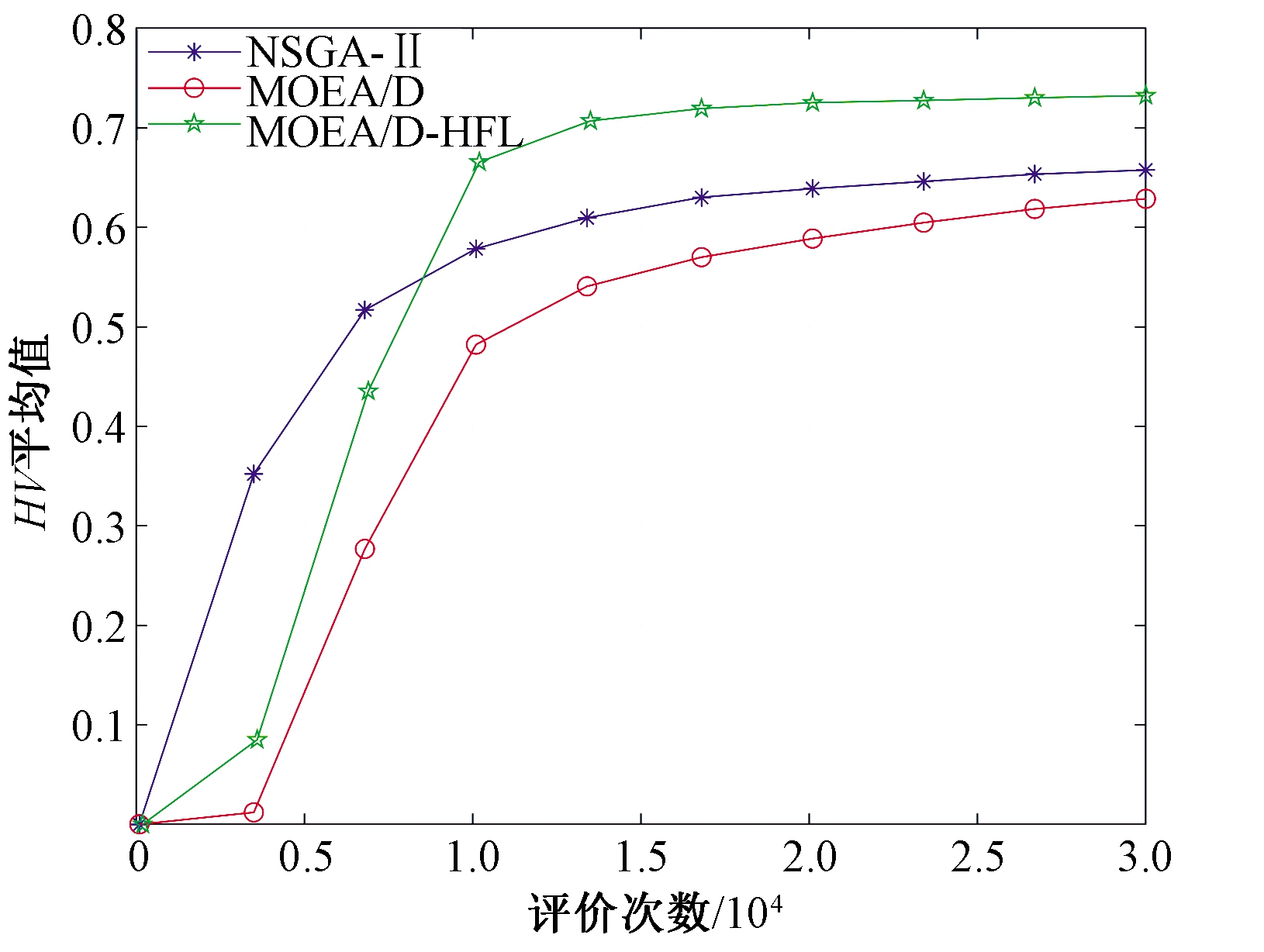
图7 3种算法HV进化曲线对比
Figure 7 Comparison among the curves of HV of the three algorithms during the evolution
图7为算法在进化过程中HV值变化曲线。NSGA-II在算法搜索前期收敛速度较快，但是后期陷入局部最优，最后得到的HV明显低于MOEA/D-HFL；MOEA/D在收敛速度和解集质量方面均不理想；而MOEA/D-HFL最终能够获得最高的HV。
表3列出了3种算法独立运行10次得到的HV平均值和标准差。对比可知，MOEA/D-HFL的 HV平均值最大，标准差最小，说明其Pareto前沿的收敛性和分布性最好，且算法稳定性最佳。基于佳点集和反向学习的初始种群生成策略使得MOEA/D-HFL具有较高的搜索精确度和稳定性，目标函数值稳定归一化使其具有更高的鲁棒性，交叉分布参数的动态变化使得进化搜索过程更加高效。 NSGA-II和基本MOEA/D不能获得理想的Pareto前沿，容易陷入局部最优，且参考点动态变化使MOEA/D聚合优化函数动态变化，算法不稳定。
表3 3种算法在多目标定日镜场布局优化问题上的HV平均值和标准差(算例一)
Table 3 Average and standard deviation of the HV by the three algorithms on multi-objective heliostat field layout optimization (case 1)
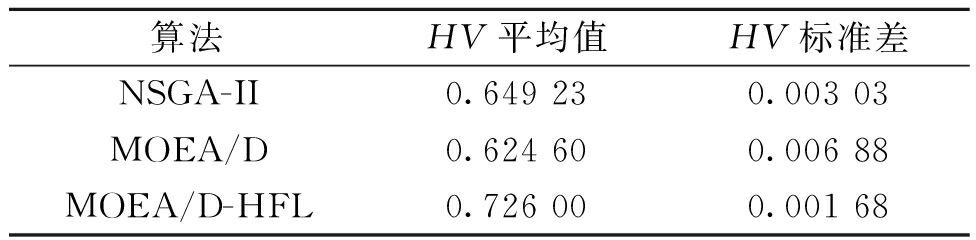
算法HV平均值HV标准差NSGA-II0.649 230.003 03MOEA/D0.624 60 0.006 88MOEA/D-HFL0.726 00 0.001 68
算例二：表4为算例二中3种算法得到的极端解和最优折中解对应的目标函数值。对比可知，在极端解方面，MOEA/D-HFL得到的最大光学效率和最小占地面积值均优于另外两种算法,其最大光学效率值为0.587 4，最小占地面积为6.363×105 m2。在最优折中解方面，MOEA/D-HFL得到的光学效率最高，为0.562 6。 表5列出了3种算法的HV平均值和标准差，对比可知，MOEA/D-HFL的HV平均值最大，标准差最小，因此可以证明该算法具有更好的收敛性、分布性以及稳定性。
表4 试验结果(算例二)
Table 4 Experimental results (case 2)
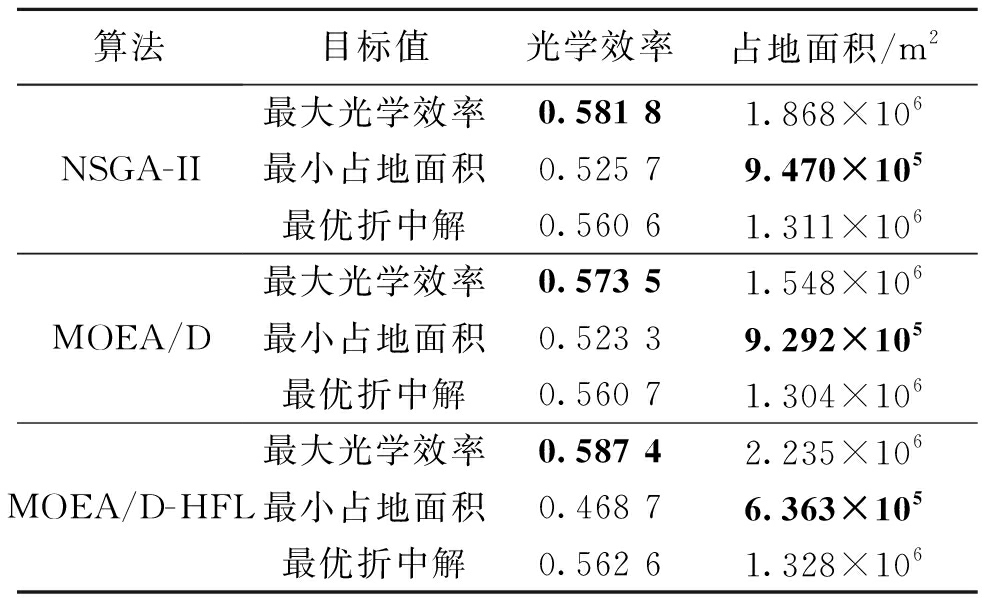
算法目标值光学效率占地面积/m2NSGA-IIMOEA/DMOEA/D-HFL最大光学效率 0.581 81.868×106最小占地面积0.525 79.470×105最优折中解0.560 61.311×106最大光学效率0.573 51.548×106最小占地面积0.523 39.292×105最优折中解0.560 71.304×106最大光学效率0.587 42.235×106最小占地面积0.468 76.363×105最优折中解0.562 61.328×106
表5 3种算法在多目标定日镜场布局优化问题上的HV平均值和标准差(算例二)
Table 5 Average and standard deviation of the HV by the three algorithms on multi-objective heliostat field layout optimization (case 2)
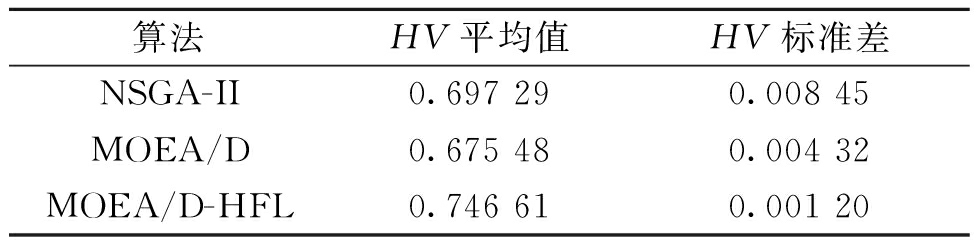
算法HV平均值HV标准差NSGA-II0.697 290.008 45MOEA/D0.675 48 0.004 32MOEA/D-HFL0.746 61 0.001 20
综合对比考虑，与NSGA-II和基本MOEA/D相比， 笔者提出的MOEA/D-HFL能够获得分布性和均匀性更好的Pareto前沿，且极端解和最优折中解质量更好，能给决策者提供很好的方案。
4 结论
以定日镜场年均综合光学效率和镜场占地面积为双重优化目标，建立了定日镜场椭圆布局多目标优化模型。在求解算法上提出了MOEA/D-HFL算法，该算法采用基于佳点集和反向学习的初始种群生成策略提高初始种群的质量和稳定性；采用稳定的目标函数值归一化方法，并且引入交叉分布指数动态变化机制，使得算法更加高效。对比实验结果表明，MOEA/D-HFL求得的Pareto前沿面具有更好的分布性和均匀性，更加接近真实Pareto前沿，能获得更高质量的极端解和折中解，为定日镜场布局问题提供了良好的解决方案。
[1] RICHTER P, FRANK M, 
BRAHM E. Multi-objective optimization of solar tower heliostat fields[C]//RUSSO G, CAPASSO V, NICOSIA G,et al. Progress in industrial mathematics at ECMI 2014. Cham Switzerland: Springer, 2016: 771-778.
[2] 张宏丽, JUCHLI I, FAVRAT D, 等. 塔式系统定日镜场的热经济性优化设计[J]. 太阳能学报, 2009, 30(1): 55-60.
[3] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197.
[4] KIM M, HIROYASU T, MIKI M, et al. SPEA2+: improving the performance of the strength pareto evolutionary algorithm 2[C]//YAO X,EDMUND K B,JOSÉ A,et al. Parallel problem solving from nature - PPSN VIII.Berlin： Springer, 2004:742-751.
[5] ZHANG Q, LI H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]. IEEE transactions on evolutionary computation, 2007, 11(6): 712-731.
[6] 朱晓东, 王颖, 杨之乐, 等. 启发式多目标优化算法在能源和电力系统中的典型应用综述[J]. 郑州大学学报(工学版), 2019, 40(5): 1-12.
[7] LIPPS F W, VANTHULL L L. A cellwise method for the optimization of large central receiver systems[J].Solar energy, 1978, 20(6): 505-516.
[8] BIGGS F, VITTITOE C N. The helios model for the optical behavior of reflecting solar concentrators[R]. Albuquerque, NM， USA: Sandia labs, 1979.
[9] COLLADO F J, GUALLAR J. Fast and reliable flux map on cylindrical receivers[J]. Solar energy, 2018, 169: 556-564.
[10] SASSI G. Some notes on shadow and blockage effects[J]. Solar energy, 1983, 31(3): 331-333.
[11] 邱傲, 项铁铭. 基于佳点集原理的多维竞争文化入侵杂草算法[J]. 杭州电子科技大学学报(自然科学版), 2016, 36(3): 89-93.
[12] TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence[C]//International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC′06). Vienna, Austria: IEEE, 2005:695-701.
[13] TIAN Y, CHENG R, ZHANG X Y, et al. PlatEMO: a MATLAB platform for evolutionary multi-objective optimization[educational forum][J]. IEEE computational intelligence magazine, 2017, 12(4): 73-87.