0 引言
剪叉式升降工作平台是一种用于高处作业的专用大型机械设备，其主要举升构件称为叉臂，由矩管和钢板焊接而成。由于升降平台具有作业面高、受动载荷作用、焊接接头形式复杂、载荷循环次数高等工作特点，对设备的耐久性和安全性提出极高要求，国标要求设备的可靠工作载荷循环次数达10万次以上[1]。升降平台一旦发生疲劳失效，会严重威胁高空作业人员的人身安全。为保证升降平台的使用寿命及安全运行，在设计阶段有必要对升降平台进行疲劳寿命仿真预测。
近年来，针对工程焊接结构的疲劳寿命分析，国内外诸多学者进行了研究。Ye等[2]利用钢桥面板开肋焊接接头，基于主S-N曲线对钢桥进行疲劳寿命评估。Pang等[3]计算获得了四点弯曲切削焊接钢管疲劳寿命，并与BS标准下的结果进行了对比。潘权等[4]提取剪叉臂在服役中的应力集中区域，通过名义应力法对剪叉臂疲劳寿命进行预测。徐杰[5]依据焊缝S-N曲线和天线梁疲劳寿命模型,获得了随机振动激励下天线梁的疲劳寿命分布。李向伟[6]以装甲钢T型焊接接头为研究对象进行仿真计算与疲劳试验,以获得重载货车的疲劳寿命。刘治华等[7]采用有限元分析理论并结合ncode疲劳分析软件，对飞碟游乐设备驱动轴进行了疲劳仿真研究。
升降平台在进行举升作业时，剪叉臂的位置、角度时刻都在变化，载荷环境非常复杂，焊缝多且易发生疲劳失效。在对这种含大范围刚体运动的焊接构件进行疲劳寿命分析时，上述文献研究均进行了某种程度的简化处理，包括：1)不建立焊缝的有限元模型，焊接强度取实际焊缝位置的应力作为焊缝应力；2)选取某些特定位置固定运动构件，或对焊接接头构件进行疲劳分析。显然，现有方法未能准确模拟运动焊接构件的实际承载状态。对此笔者提出一种新的疲劳分析方法，该方法在待分析构件的连体随动坐标系中建立该构件包括焊缝的有限元模型，将整机多体动力学仿真分析获得的铰链时变载荷映射到构件连体坐标系中作为疲劳载荷谱。通过上述构件连体坐标系的引入及载荷处理，可有效避免由于构件的大范围刚体运动给有限元建模及分析带来的困难。依据BS标准提供的S-N试验数据进行疲劳仿真获得其疲劳寿命分布，为包含大范围刚体运动的焊接构件疲劳寿命预测提供一种有效的数值分析方法。
1 焊缝疲劳寿命预测基本原理
相对于金属材料，焊接接头的疲劳有其特殊性。由于焊接接头有应力集中、残余应力、焊接缺陷的存在，焊缝疲劳裂纹更易产生，大大缩短了焊接构件服役的时间。由于焊接接头微观结构的不均匀性，其疲劳寿命表现出统计特性[8]，其研究理论是基于大量疲劳试验数据建立的[9-10]。
英国BS7608标准在基于名义应力的疲劳设计中最有代表性，它给出了不同等级、不同存活率下焊缝的S-N曲线数据。该数据可适用于屈服强度200～960 MPa的焊接材料，且考虑了焊接接头应力集中以及焊接残余应力的影响[10]。BS标准认为小应力循环对疲劳也有贡献，其S-N曲线是一条双斜率曲线，没有水平拐点。考虑到工程问题的复杂性，低于疲劳极限的小应力循环损伤的S-N曲线更加保守安全。按照焊接接头上焊缝的几何位置以及载荷与焊缝的相互关系，可确定其对应的焊缝级别。对于任意级别的焊接接头，其应力范围S与达到疲劳极限时的循环次数N之间的关系为：
SmN=C，
(1)
式中：m为材料特性；C为常数，对于不同级别的焊缝两者的取值不同，其数值由试验确定。
式(1)两边取对数可得：
lg N=lg C-mlg S。
(2)
标准S-N曲线存活率为50%，即仅有一半试验品能达到预期疲劳寿命。出于安全性的考虑，通常向下取两个标准差[11]，上式变为：
lg N=lg C-mlg S-2σ，
(3)
式中：σ为疲劳寿命的标准差，对应置信度P=97.5%。
BS标准基于miner线性损伤累积理论计算时变载荷引起的损伤。应力循环引起的疲劳损伤定义如下：
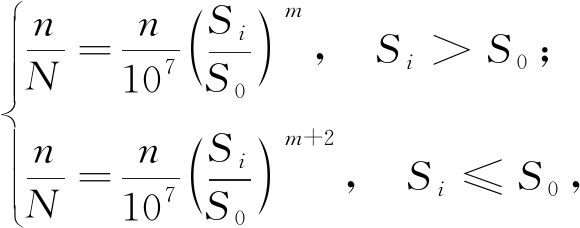
(4)
式中：N为应力水平下Si的应力循环数；S0为N=107时的应力幅值；l是应力水平级数。
如果
则认为发生破坏。
2 升降平台构件虚拟疲劳试验
叉臂是升降平台的主要承力部件，各叉臂的运动状态与受力状态极为相似。为验证方法的可行性，可取一典型叉臂计算其疲劳寿命，其他叉臂可通过相同的方法进行计算。从工程应用反馈来看，油缸下叉臂处疲劳寿命较低，且焊缝形式较复杂，取该叉臂进行疲劳寿命计算更具代表性，具体流程见图1。
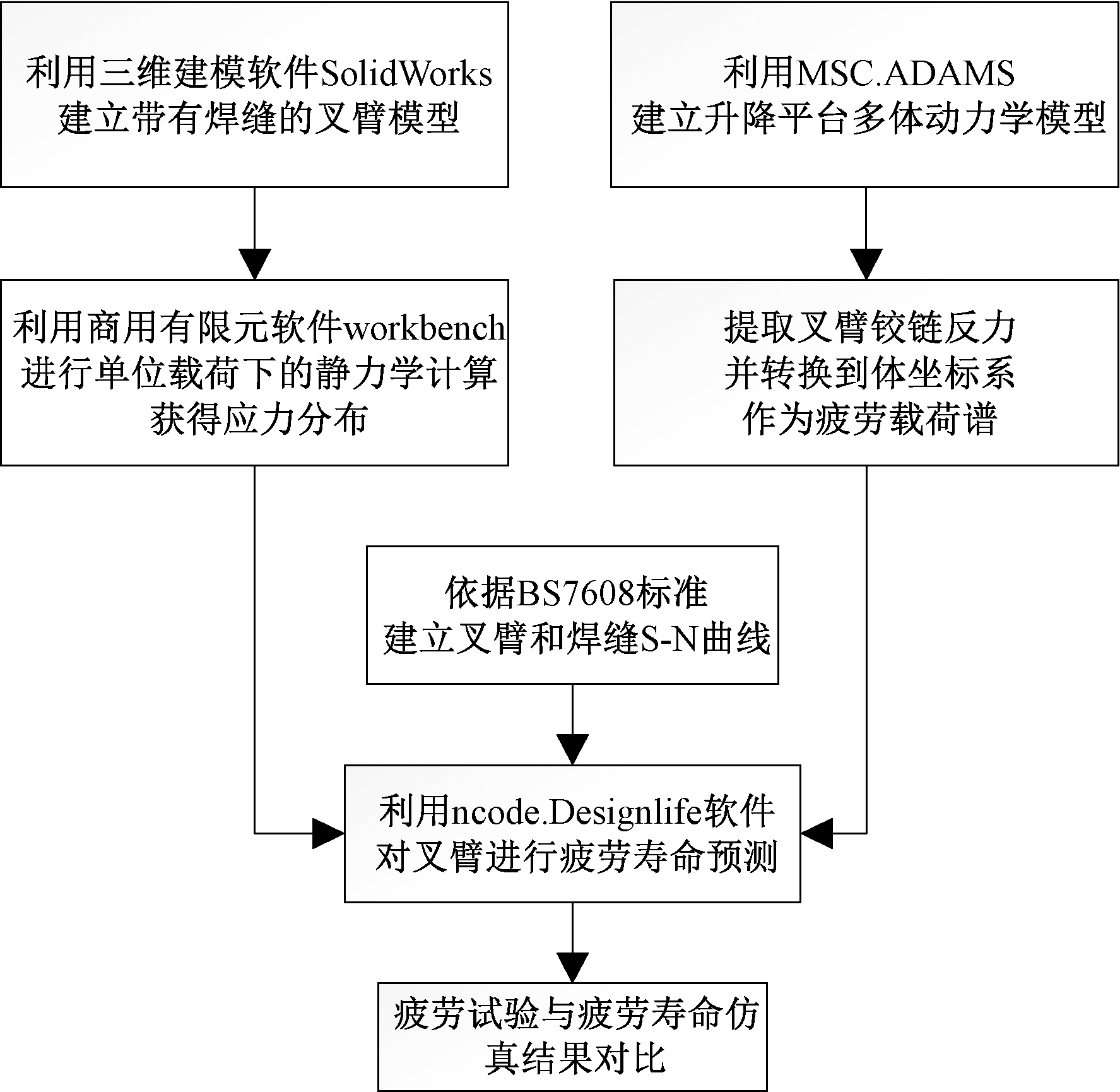
图1 疲劳寿命计算流程图
Figure 1 Flow chart of fatigue life calculation
2.1 有限元模型的建立
叉臂受力状态如图2(a)所示。ncode软件对每一通道载荷数据独立编谱，需要多个单一载荷下的应力分布。由于运动构件只有支反力，没有固定边界条件，有限元刚度矩阵奇异，有限元结果不能求解。依据图2(b)所示原理对叉臂的边界条件进行转化，其核心是利用静定边界条件的支反力代替构件的铰链载荷，既不影响构件的变形和应力结果，又消除了分析构件的刚体运动。
图2 叉臂受力状态及边界条件转化
Figure 2 Scissors rods′ stress state and boundary conditions conversion
基于SolidWorks平台建立带有焊缝的叉臂三维几何模型，主要焊缝位置如图3所示。焊缝宽度为
(t为板厚)，焊缝角度为45°。将三维几何模型导入Workbench中，采用实体单元对叉臂及焊缝分别进行单元划分[12]。其中母材单元尺寸为0.5 t，对焊缝单元尺寸分别用0.5 t、0.2 t、0.1 t、0.05 t进行单元划分，分别加载求解，进行网格收敛性分析。提取4号焊缝焊趾处的应力，见图4。从图中可以看出，单元尺寸小于等于0.1 t时，焊趾处的应力分布几乎不再发生变化，故取焊趾处单元尺寸为0.1 t。在Workbench中定义5个载荷步，在每个载荷步中分别施加静定边界条件和不同位置方向的单位载荷，如图5所示进行求解，获得5个单一载荷下的应力分布。
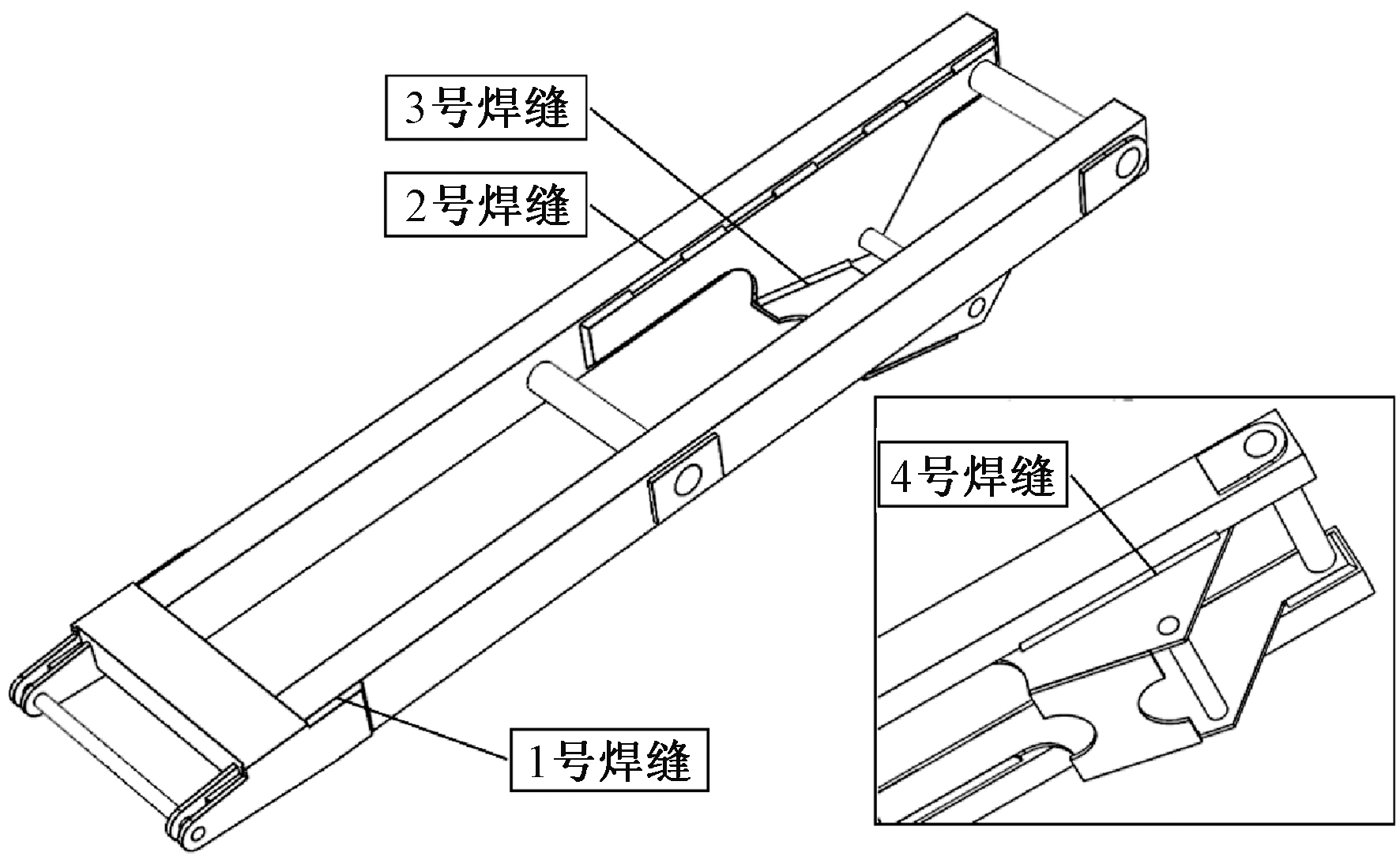
图3 叉臂焊缝编号
Figure 3 Scissors rod weld numbering
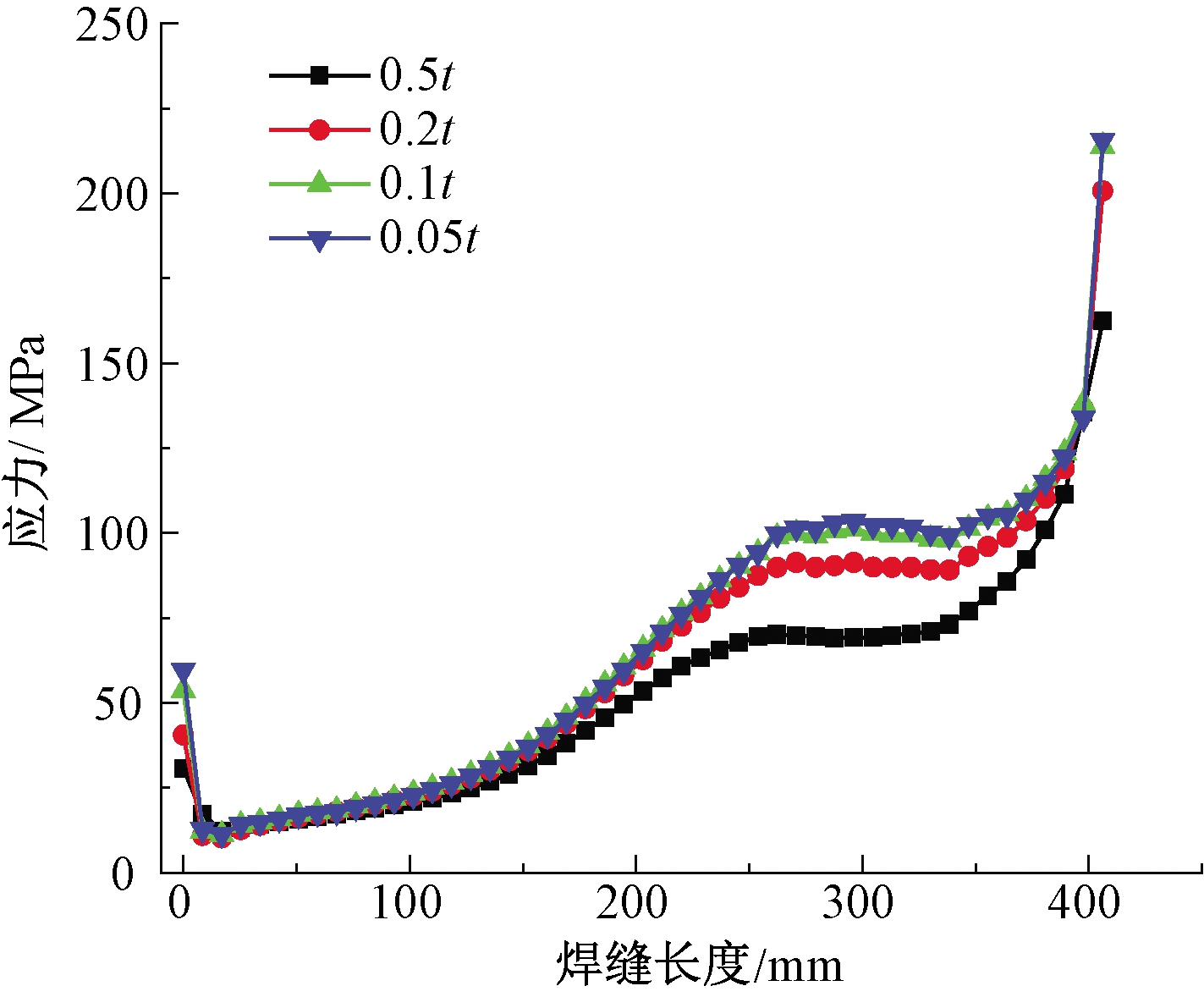
图4 叉臂焊趾处应力图
Figure 4 Stress diagram at welding toe of scissors rod
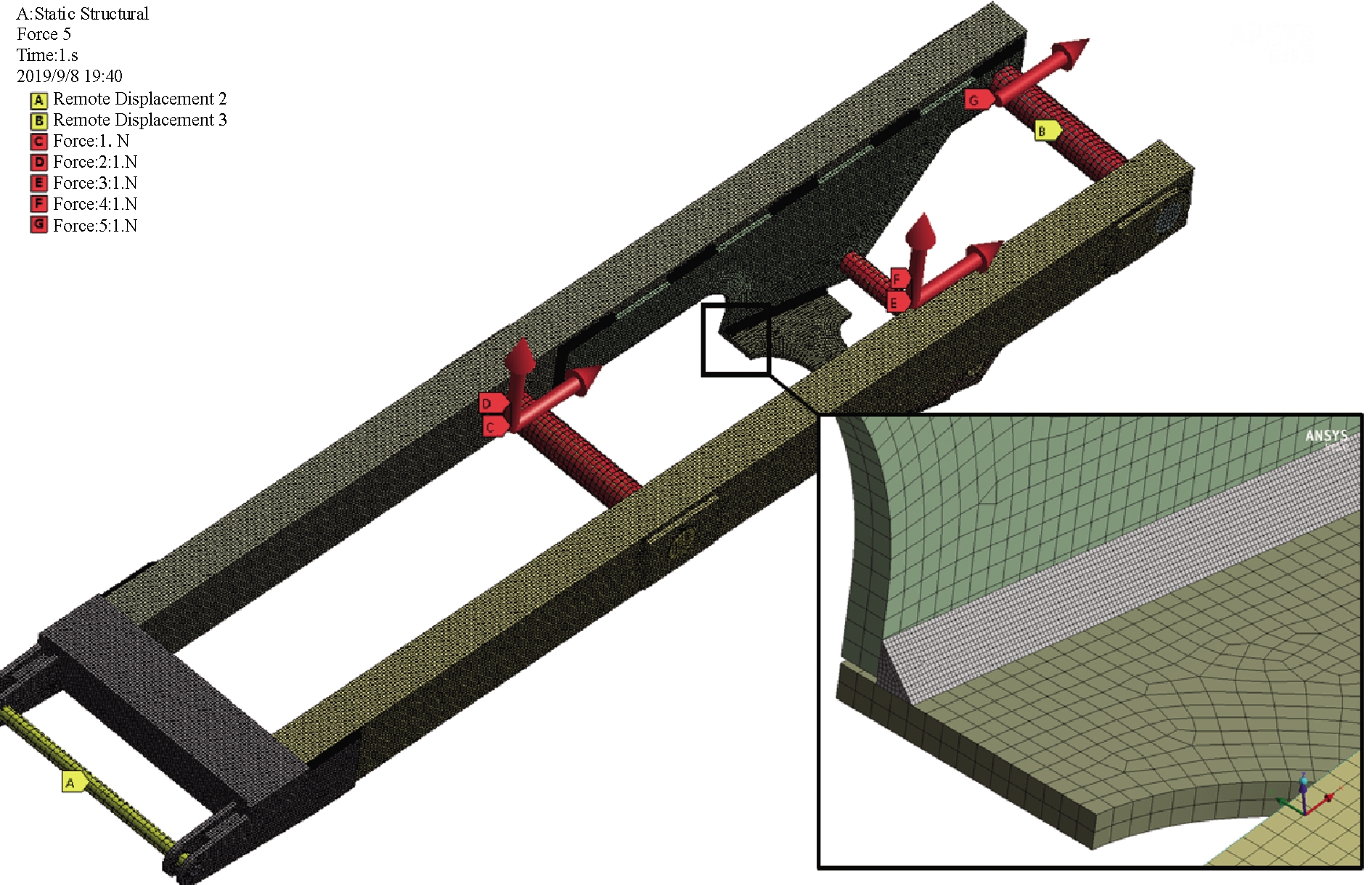
图5 叉臂有限元模型
Figure 5 Finite element model of scissors rod
2.2 时变载荷谱的获得
基于多体动力学软件MSC.ADAMS建立了剪叉式升降平台整机多刚体动力学系统模型，以获得叉臂疲劳载荷谱。模型中包括底盘、叉臂、油缸、平台等14个相对运动部件。升降平台的实际工作状态存在过约束现象。如按实际施加约束，ADMAS会随机去除冗余约束使运动状态得以求解，但铰链反力仿真结果存在不确定性。在分析升降平台的运动状态以及各约束作用后，对铰链进行了精简和替换，使其部件自由度和约束自由度相统一，模型约束施加情况如表1所示。整机共约束83个自由度，连同在油缸处施加的1个位移驱动约束，约束自由度总数为84，使系统总体自由度为0，分析类型为运动学分析。
表1 升降平台约束副汇总
Table 1 Summary of lifting platform constraints
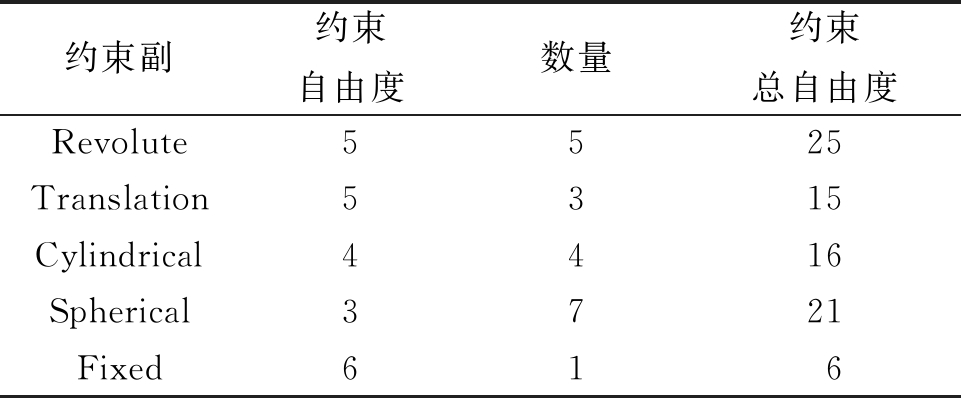
约束副约束自由度数量约束总自由度Revolute5525Translation5315Cylindrical4416Spherical3721Fixed616
GB 25849—2010标准规定升降平台从收藏位置开始举升，举升到最高工作位置回缩，再回到收藏位置为一个疲劳循环周期[1]。为油缸施加正弦位移驱动，周期为60 s。测量升降平台上平台的速度、加速度如图6、图7所示。从图中可以看出，最大举升速度0.34 m/s，最大加速度0.052 m/s2，均符合国标对疲劳校核的要求。
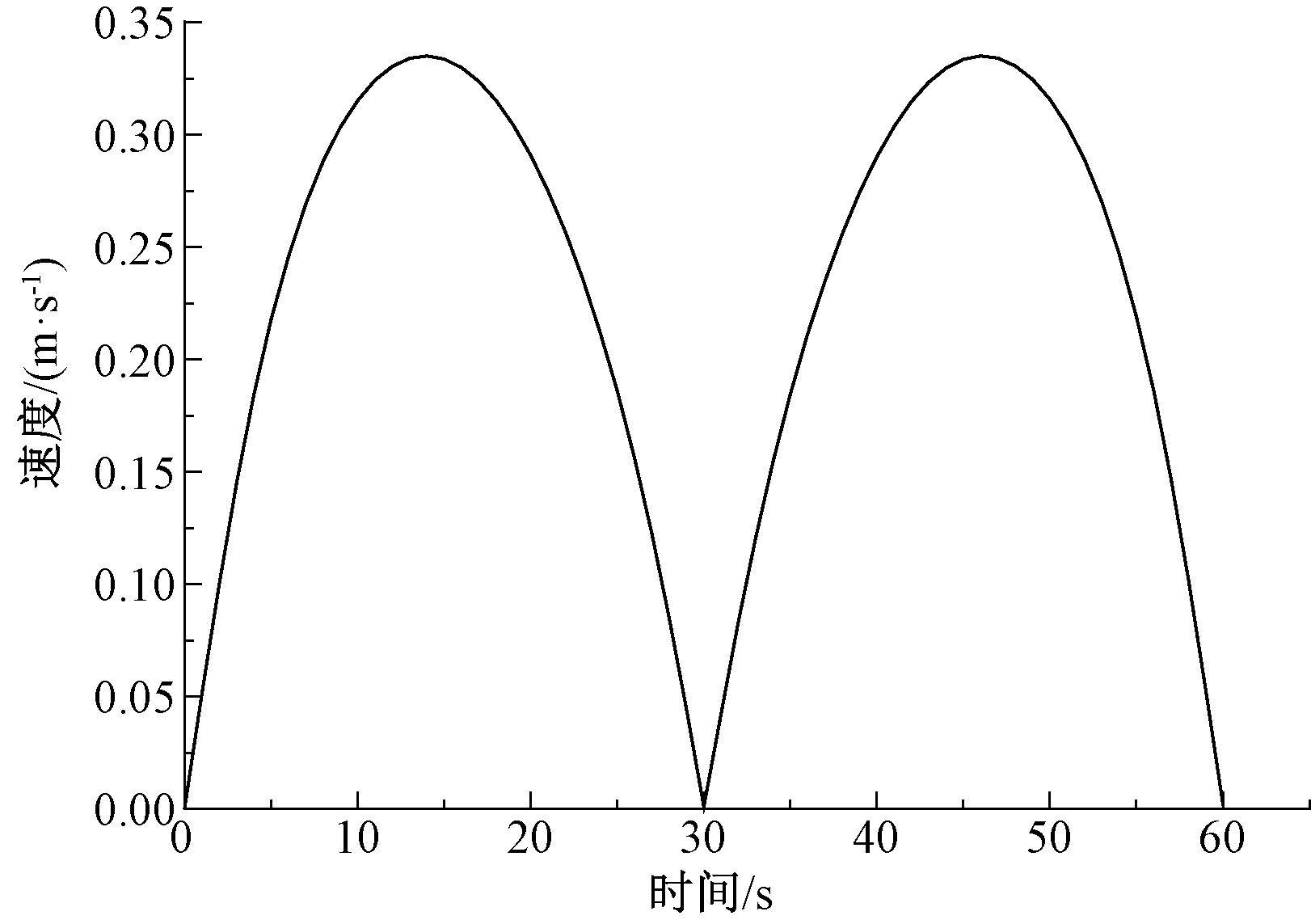
图6 升降平台举升速度
Figure 6 Lifting speed of lifting platform
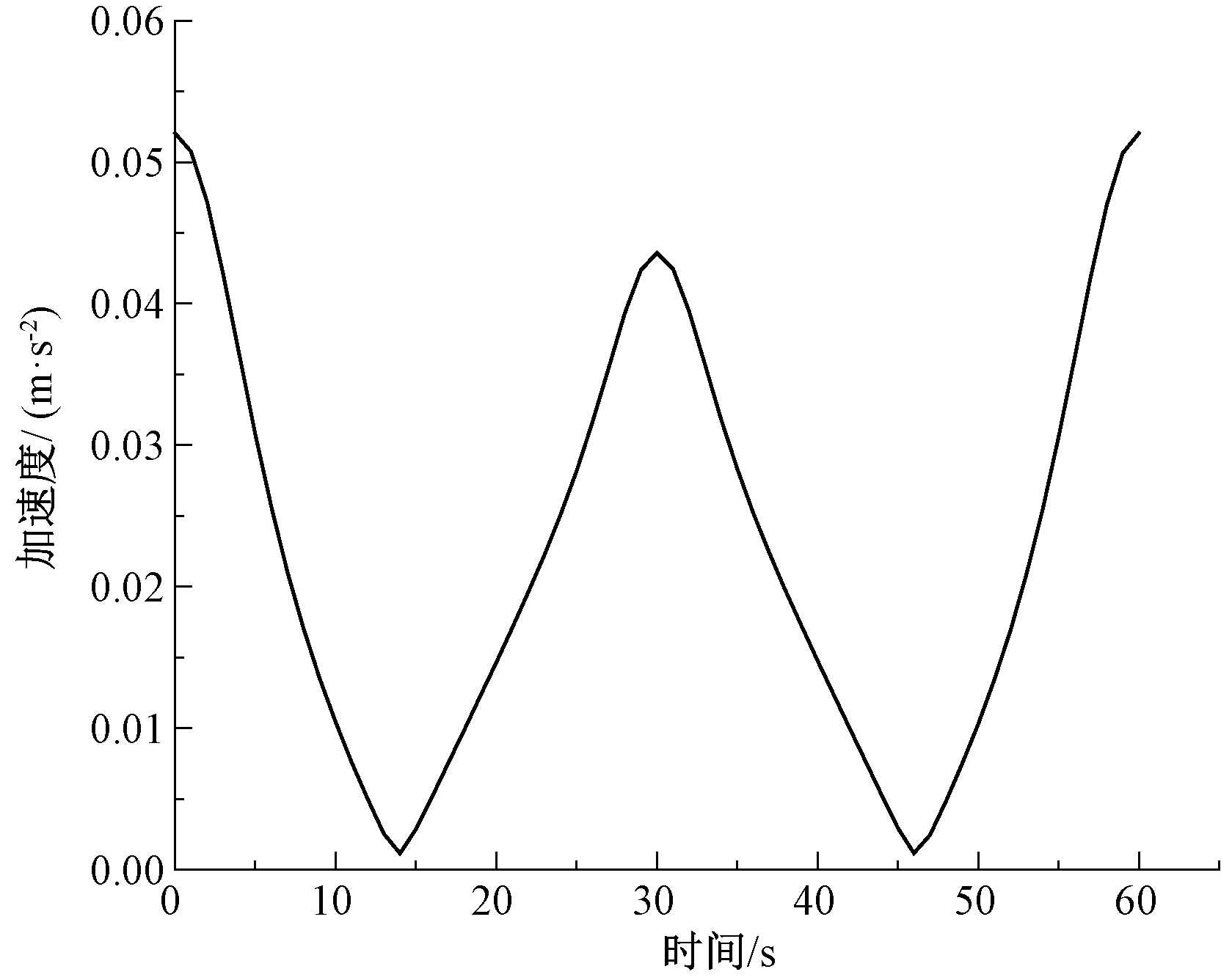
图7 升降平台举升加速度
Figure 7 Lifting acceleration of lifting platform
提取叉臂各约束副时变铰链反力。应该注意的是MSC.ADAMS的约束反力是基于GCS(全局坐标系)获得，相对GCS各部件存在大范围刚体位移，不能直接作为部件的疲劳载荷谱。依据图8所示原理，测量叉臂LCS(部件连体坐标系)与GCS的角度α，将部件的约束反力从GCS映射到LCS中，3.1节中叉架的有限元模型正是基于其自身的部件连体坐标系建立，可视为该叉架的空间位置固定，以消除部件的刚体运动对有限元建模的不利影响。映射到该叉架臂连体坐标系LCS后的单一方向时变铰链载荷谱如图9所示，其中纵坐标数值表示该方向铰链载荷的大小。5个通道的载荷谱分别与5个单位力作用下的有限元应力结果相乘并线性叠加即可得到5通道载荷谱共同作用下的时变应力场。
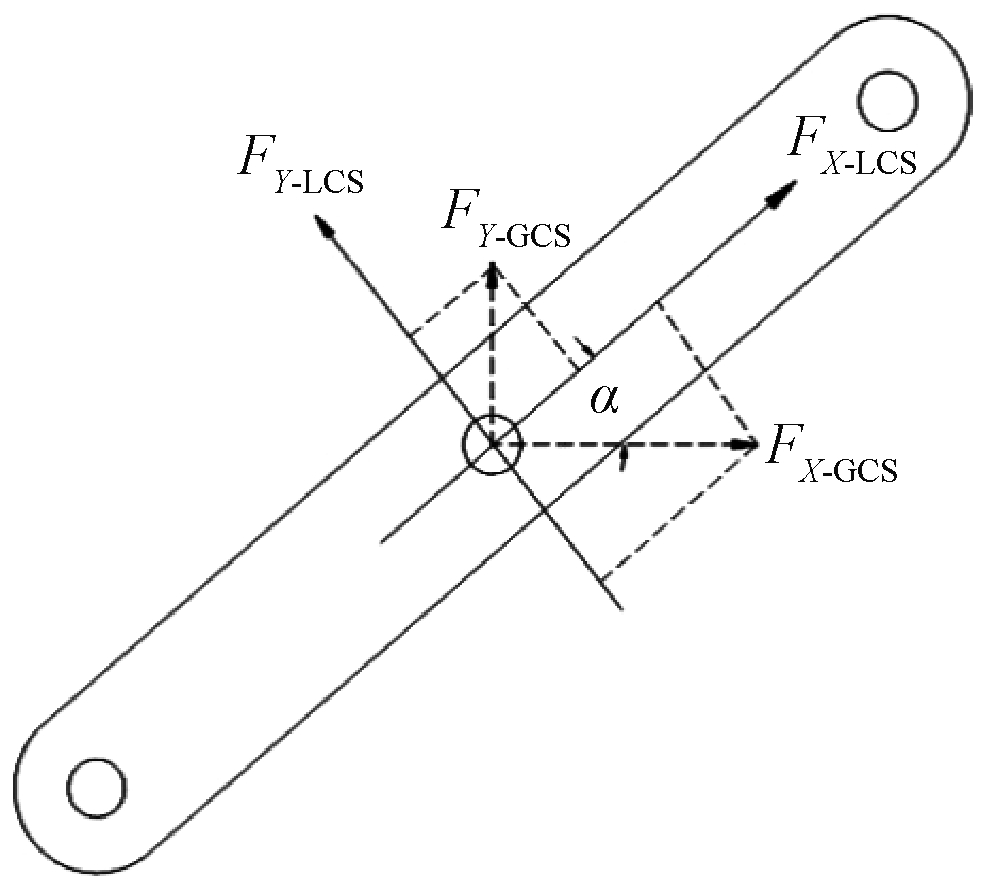
图8 坐标系映射原理
Figure 8 Principle of coordinate system mapping
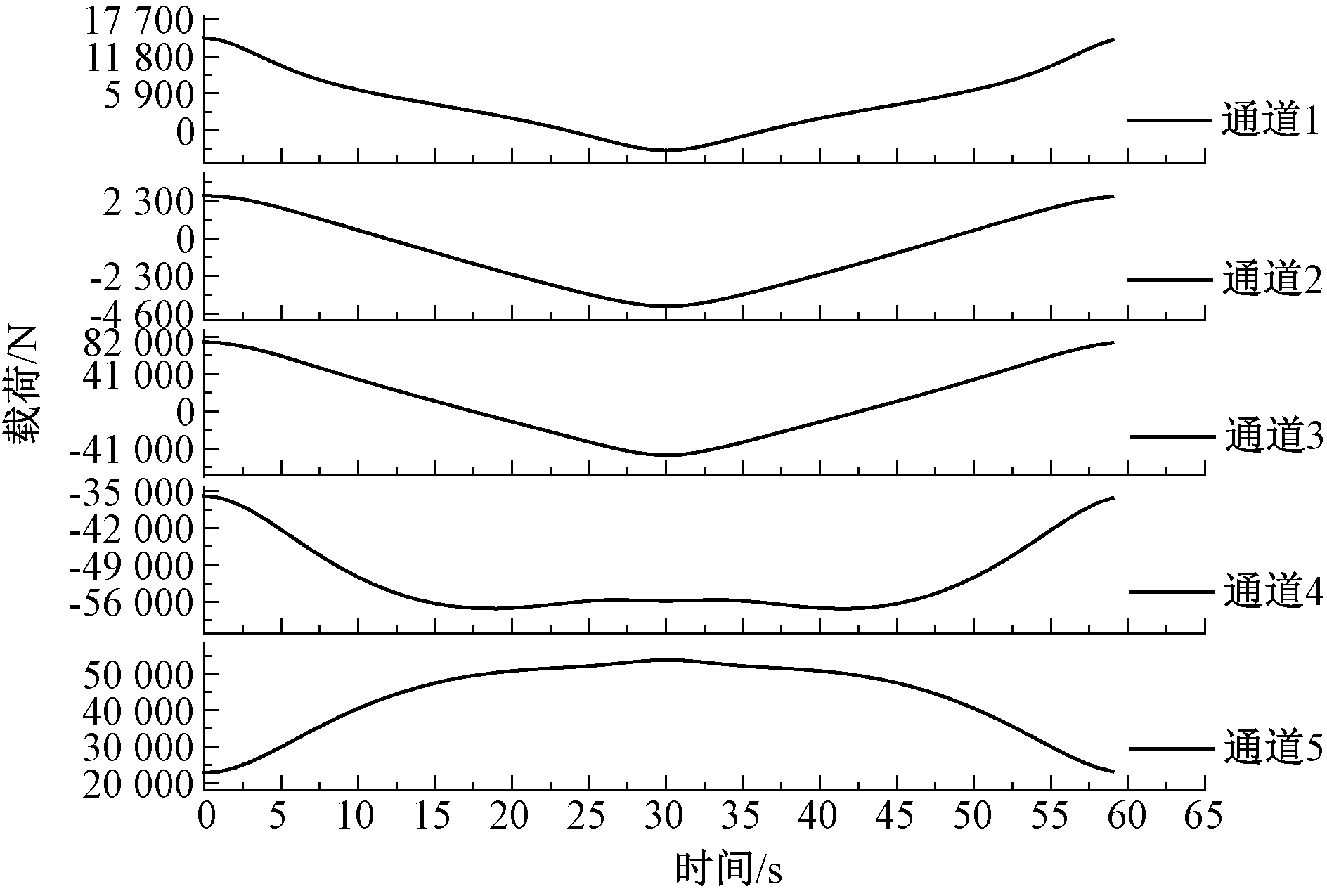
图9 叉臂铰链载荷谱
Figure 9 Load spectrum of scissors rod hinge
2.3 虚拟疲劳试验
将叉臂应力分布结果和疲劳载荷谱导入ncode.Designlife软件中进行虚拟疲劳试验。叉臂材料为Q345，其S-N曲线按照经验公式施加；根据焊接接头类型和受力方向，焊缝S-N曲线应用式(2)，取BS标准中的G级曲线数据，并向下取两个标准差，焊缝S-N曲线参数如表2所示[10]。
表2 BS标准G级S-N曲线数据
Table 2 Class G S-N curve data of BS standard
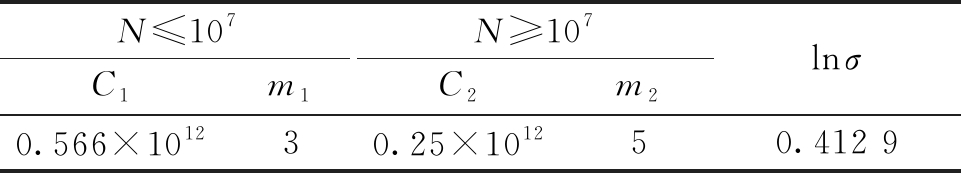
N≤107N≥107C1m1C2m2lnσ0.566×101230.25×101250.412 9
由于BS标准的S-N曲线已经考虑了焊缝本身的应力集中及残余应力，因此在疲劳仿真中不再重复计算。Q345材料和焊缝的S-N曲线分别如图10、图11所示。
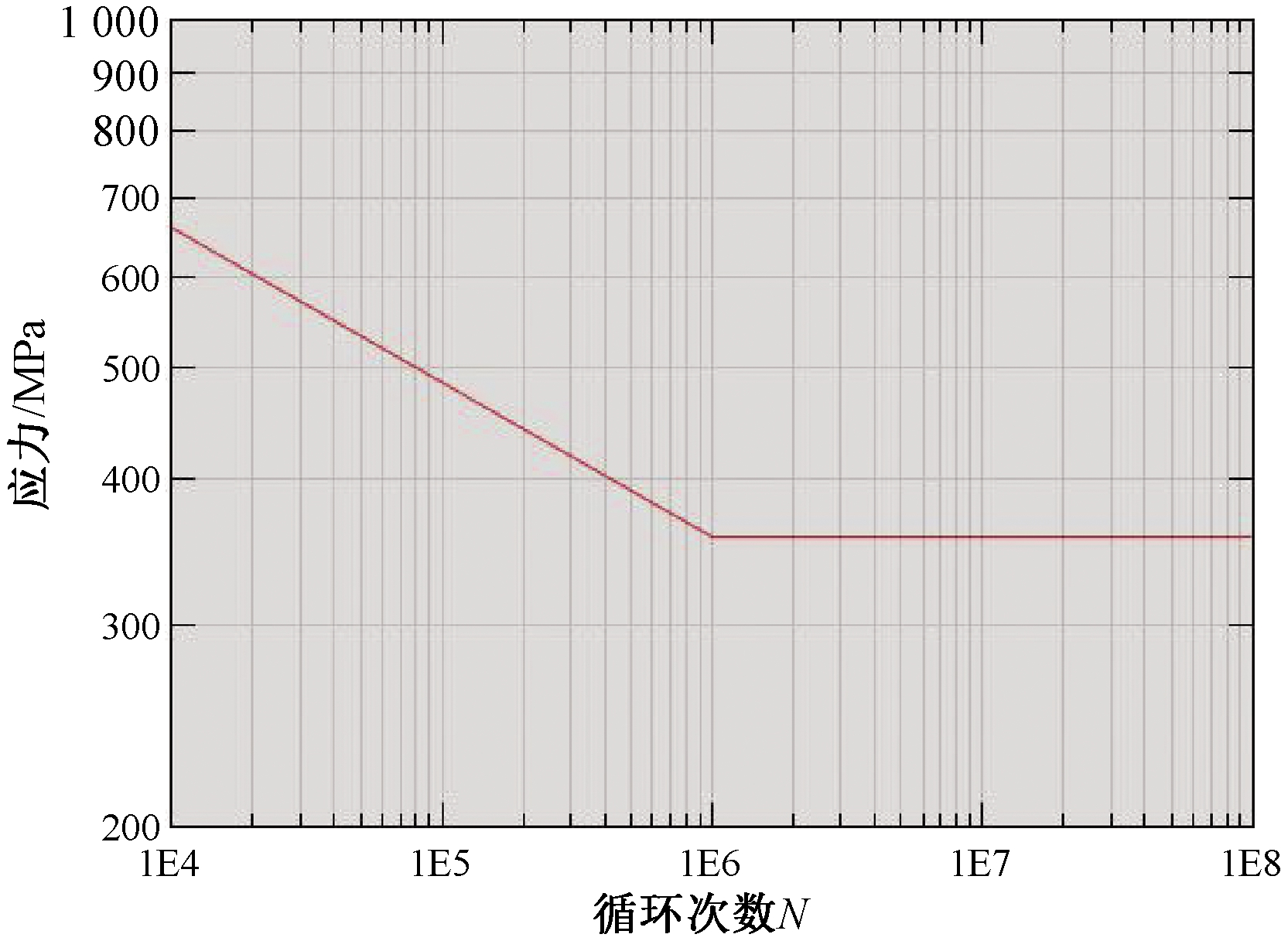
图10 Q345材料S-N曲线
Figure 10 S-N curve of Q345
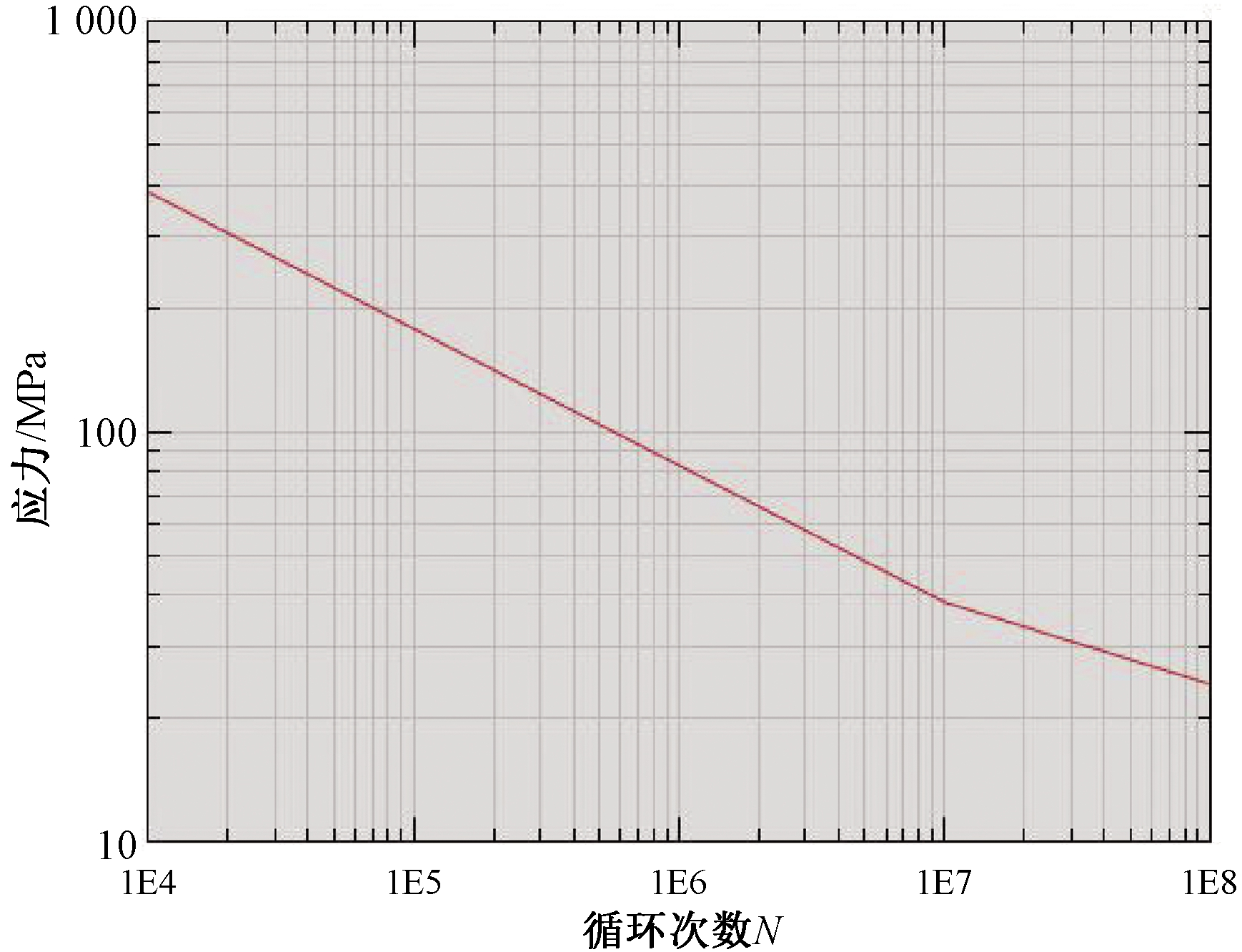
图11 BS7608标准G级焊缝S-N曲线
Figure 11 Class G weld S-N curve of BS7608 standard
图12为叉臂的疲劳寿命分布云图。从图中可以看出，母材疲劳寿命均大于8.72×1013，可认为具有无限疲劳寿命；焊缝处的疲劳寿命相对较低，疲劳寿命最低点位于4号焊缝起始位置，其节点编号为4783，疲劳循环次数为28 050。
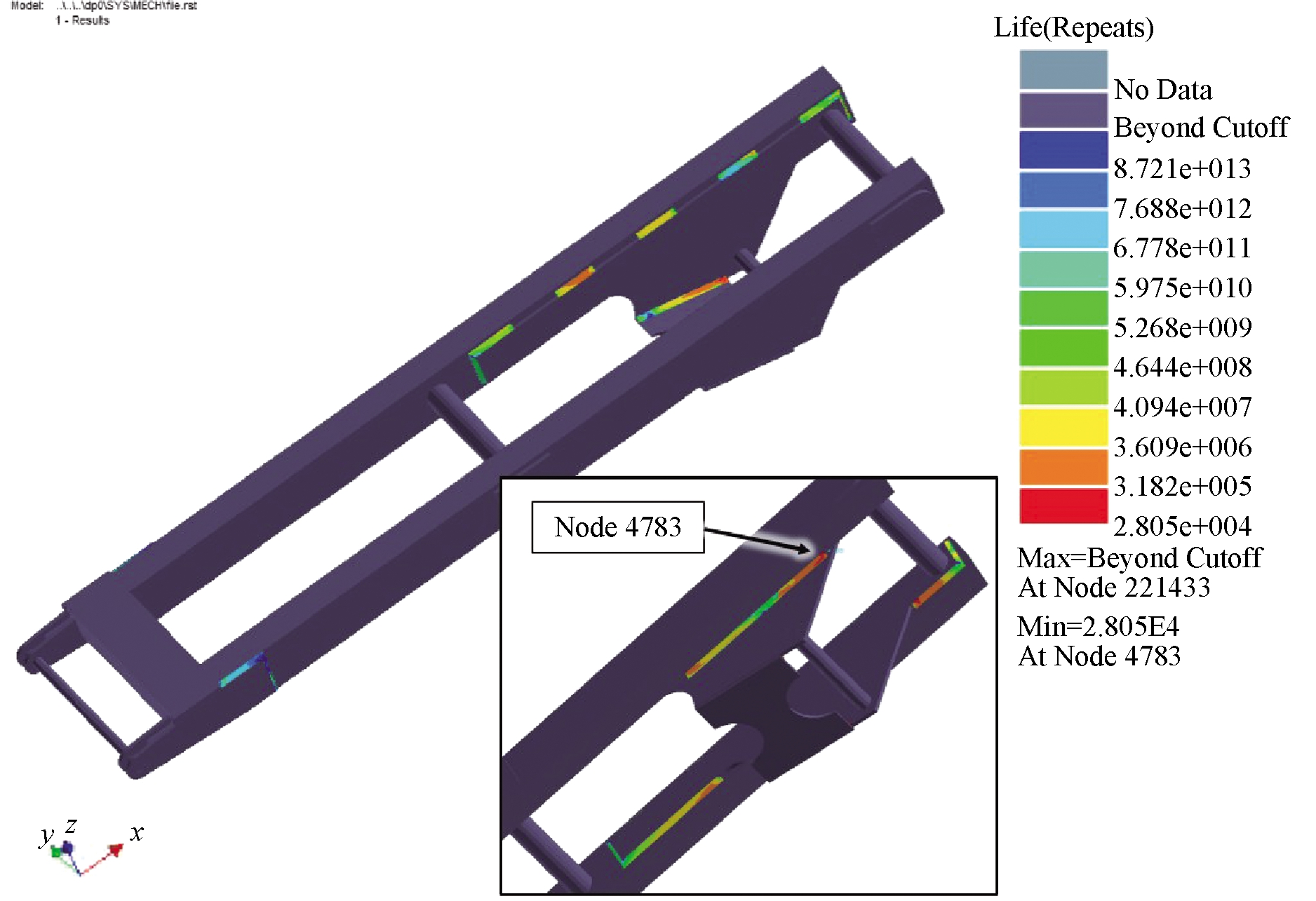
图12 叉臂疲劳寿命分布云图
Figure 12 Fatigue life distribution cloud of scissors rod
3 升降平台疲劳试验
为验证疲劳仿真方法及结果的正确性，建立了该型号升降平台的试验样机，将其调整至正常工作状态后，在试验现场进行疲劳试验。由于疲劳试验持续时间较长，为使试验能够长期稳定进行，使用外接液压泵站作为动力源。对样机平台施加额定载荷，载荷位置依照标准施加。升降平台从起升到升至最大高度，再下降至原来的位置为一个载荷循环。每个载荷循环时长为1 min，每次载荷循环结束后间隔20 s进行下次循环，记录载荷循环次数。载荷循环每进行5 000次，停机检查样机是否有零部件损坏及疲劳开裂现象，允许对样机进行简单维修以保证试验正常进行，如发现疲劳开裂即停止疲劳试验。试验现场如图13所示。
图13 升降平台疲劳试验现场
Figure 13 Fatigue test site of lifting platform
该疲劳试验进行到45 000次停机检查时，在油缸下叉臂矩管与油缸贴板焊缝处发现疲劳开裂，说明该叉臂至少能承受40 000次的额定载荷循环而不发生疲劳破坏。裂纹位置如图14所示。
图14 疲劳试验开裂位置
Figure 14 Fatigue test crack location
对比疲劳试验与疲劳仿真结果，疲劳试验裂纹产生位置与仿真焊缝疲劳寿命较低的4号焊缝位置相吻合，但循环次数有30%的差异。二者结果存在一定差异的原因可从两方面分析：原因一是构件的试验疲劳寿命值可视为一个服从概率分布的随机量；原因二是该仿真疲劳寿命值考虑了疲劳寿命分布方差，是在存活率97.5%条件下得到的构件疲劳寿命，即保证在该试验条件下，97.5%的构件疲劳试验循环次数会大于28 050次。高存活率的疲劳仿真寿命可确保疲劳仿真结果在工程应用中的安全性。故利用该疲劳仿真方法可有效获得构件疲劳寿命分布趋势及最小疲劳寿命发生部位，且所得仿真疲劳寿命值具有一定预测意义。
4 结论
通过疲劳仿真及疲劳试验可以看出，提出的疲劳仿真流程可较为准确地预测剪叉式升降平台焊接结构疲劳开裂起始位置以及疲劳寿命。该方法可有效对含刚体运动构件焊缝疲劳寿命进行预测，为运动构件焊接结构的疲劳寿命计算及抗疲劳设计提供了一种新的建模及分析方法。
[1] 中国国家标准化管委会. 移动式升降工作平台-设计计算、安全要求和测试方法:GB 25849—2010[S].北京：中国标注出版社，2011.
[2] YE X W, SU Y H, JIN T, et al. Master S-N Curve-based fatigue life assessment of steel bridges using finite element model and field monitoring data[J]. International journal of structural stability and dynamics, 2019，19(1):1940013.
[3] PANG J H L, HOH H J, TSANG K S, et al. Fatigue crack propagation analysis for multiple weld toe cracks in cut-out fatigue test specimens from a girth welded pipe[J]. International journal of fatigue, 2017,94:158-165.
[4] 潘权, 张哲, 贺尚红, 等. 剪叉式高空作业平台剪叉臂疲劳寿命分析及预测[J]. 食品与机械, 2017,33(5):119-124.
[5] 徐杰. 动车组转向架悬挂件随机振动疲劳寿命预测[D]. 成都：西南交通大学, 2015：42-49.
[6] 李向伟. 基于ESS法的重载货车焊缝疲劳仿真[J]. 大连交通大学学报, 2013,34(5):85-88.
[7] 刘治华, 刘博见, 许伟超, 等. 飞碟游乐设备驱动轴疲劳失效分析[J]. 郑州大学学报(工学版), 2017,38(5):91-96.
[8] 胡毓仁, 李典庆, 陈伯真. 船舶与海洋工程结构疲劳可靠性分析[M]. 哈尔滨：哈尔滨工业大学出版社，2010：87-89.
[9] 日本标准协会. 铁路车辆-转向架-转向架构件通则：JIS E 4207：2004[S].东京: JARI/JSA, 2004.
[10] British Standard Institute. Guide to fatigue design and assessment of steel structures：BS7608:2014+A1:2015[S]. London: BSI Standards Limited, 2015.
[11] 兆文忠, 李向伟, 董平沙. 焊接结构抗疲劳设计理论与方法[M]. 北京：机械工业出版社，2017.
[12] 李冬林, 王强. 基于有限元的角焊缝建模的探讨[J]. 湖北工业大学学报, 2009,24(2):76-77.