0 引言
柔顺机构是一类依靠柔性构件的弹性变形进行运动、力和能量传递的新型机构形式[1]，具有减少构件数量和装配时间、无摩擦磨损和传动间隙、精度及可靠性高、可实现微型化等优点，在轻型、微型化工程领域有着广泛的应用前景[2]。
柔顺机构的工作原理决定了在运行中柔顺杆件必然经历大变形过程，这给精确建模带来了极大困难。为了简化大变形柔顺杆的建模所提出的伪刚体模型方法[3]，采用具有等效力-杆端位移关系的刚体构件模拟柔性杆件的变形，成功地架起了刚性和柔性机构设计理论之间的桥梁。由于该模型含有一个转动副，因此被称为1R伪刚体模型[4-5]。虽然在一定范围内1R伪刚体模型也能给出一定精度的杆端运动轨迹，但其对大变形柔顺杆的近似精度不高。为了提高模型精度，通过增加模型中转动副个数或考虑轴向变形影响，改进的2R、3R以及PR伪刚体模型相继被提出[6-8]。
随着应用范围的拓广，工程中对柔顺机构的性能及运动精度都提出了更高要求。系统动力学特性不仅影响运动精度，还直接关系到既定功能的实现。为此，一些学者将伪刚体模型方法推广到柔顺机构动力学研究[9-11]。但伪刚体模型缺乏对柔顺杆大变形进行精确描述的能力，从而限制了其在柔顺机构精确动力学仿真分析中的应用。
柔顺杆件属于大变形柔性梁，基于刚性截面假设的建模方法需处理梁截面的大转动问题。为了避开大转动引起的数值困难，Shabana[12]提出的绝对节点坐标方法(absolute nodal coordinate formulation, ANCF)选取整体坐标系下节点的绝对位置矢量和梯度矢量作为单元参数，构造了一种描述单元任意刚体运动的单元变形场。ANCF梁单元节点力可依据连续介质力学理论计算，并具有常质量矩阵、系统方程不含惯性力和科氏力项等优点。因此该方法一经提出便引起普遍关注，已发展出包含梁、板壳及一般实体等ANCF单元族，并被应用于车辆、航天、仿生等实际工程[13-15]。最近李鹏飞等[16-17]采用ANCF方法研究了平面固定-导向柔顺机构和柔顺双稳态机构的变形与驱动力变化规律，并进行了数值仿真和实验研究。疲劳破坏是机械系统设计过程中所要考虑的重要问题[18]。由于工作过程中柔顺杆件处于循环往复的大变形状态，因此精确应力应变分析对于柔顺机构设计及疲劳寿命分析极为重要，而上述研究未曾涉及这一问题。
应用ANCF梁单元研究了大变形柔顺杆的动力学建模问题，并精确计算了柔顺杆件的动态应变分布；考虑柔顺杆端部铰接处对局部变形的影响，提出了一种含端部变形约束的平面ANCF梁单元；采用最新提出的应变分解法(strain split method, SSM)[19]考察了ANCF梁单元闭锁问题对柔顺机构动力学特性的影响。
1 绝对节点坐标梁单元
1.1 单元形函数
平面ANCF梁单元内任意一点的位置矢量可以表示为r(x)=S(x)e，其中x=[x, y]T为单元物质坐标，单元形函数矩阵S和单元参数列阵e分别为[20]
(1)
平面ANCF梁单元的变形梯度表示为
其中rx=Sxe，ry=Sye。根据连续介质力学理论(general continuum mechanics, GCM)，Green-Lagrangian应变为
(2)
利用Green-Lagrangian应变矩阵ε的对称性，定义Green-Lagrangian应变列阵εv=(ε11 ε22 2ε12)T。与Green-Lagrangian应变ε功共轭的第二类Piola-Kirchhoff应力σ也可以定义列阵形式
对于线弹性材料，本构方程为σv=Eεv，其中弹性矩阵E为
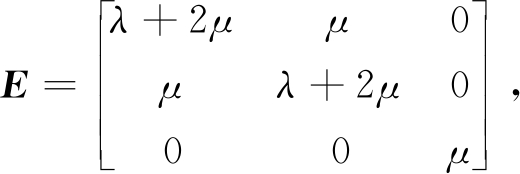
(3)
式中：拉梅常数λ=(Ev)/((1+v)(1-2v));μ=E/(2(1+v))，其中E为弹性模量，v为泊松比。
1.2 平面ANCF梁单元的控制方程
平面ANCF梁单元内力虚功率可以表示为：
其中单元节点力列阵Qs为
(4)
式中:V代表梁单元的体积域。
平面ANCF梁单元的惯性力虚功率可以表示为
其中ρ为材料密度，梁单元质量矩阵为
(5)
由上式可知，ANCF梁单元的质量矩阵M为常数阵。
不失一般性，假设单元上p点作用有集中力Fp，包含重力在内的体力密度为fe，则单元外力虚功率为：
其中单元外力列阵Qe为
(6)
式中:Sp为p点物质坐标xp对应的形函数矩阵Sp=S(xp)。
利用虚功率原理，平面ANCF梁单元的虚功率方程为
(7)
式中：单元广义节点力列阵为F=Qs-Qe。根据单元参数速率虚变分
的独立性可以得平面ANCF梁单元的控制方程为
(8)
2 含端部变形约束的ANCF梁单元
2.1 铰接节点处的运动学关系
ANCF梁单元节点力的推导过程基于大变形理论，对单元变形量没有任何限制，适用于大变形柔顺杆的建模。由于放松了刚性截面假设，一般情况下节点处的梯度矢量
不能满足单位正交关系。在柔顺机构中，柔顺杆与其他杆件或基座最常见的连接方式为固接与铰接，通常连接处有刚度加强处理措施，局部变形也将会受到约束作用。为了模拟这种约束，采用ANCF梁单元建模时假设端部为刚性截面，该节点处的梯度矢量保持为单位正交矢量。
不失一般性，设定节点1为变形受约束节点，如图1所示。根据假设：节点1处的梯度矢量
和
为单位正交矢量，因此存在转角α1可将梯度矢量表示为
(9)
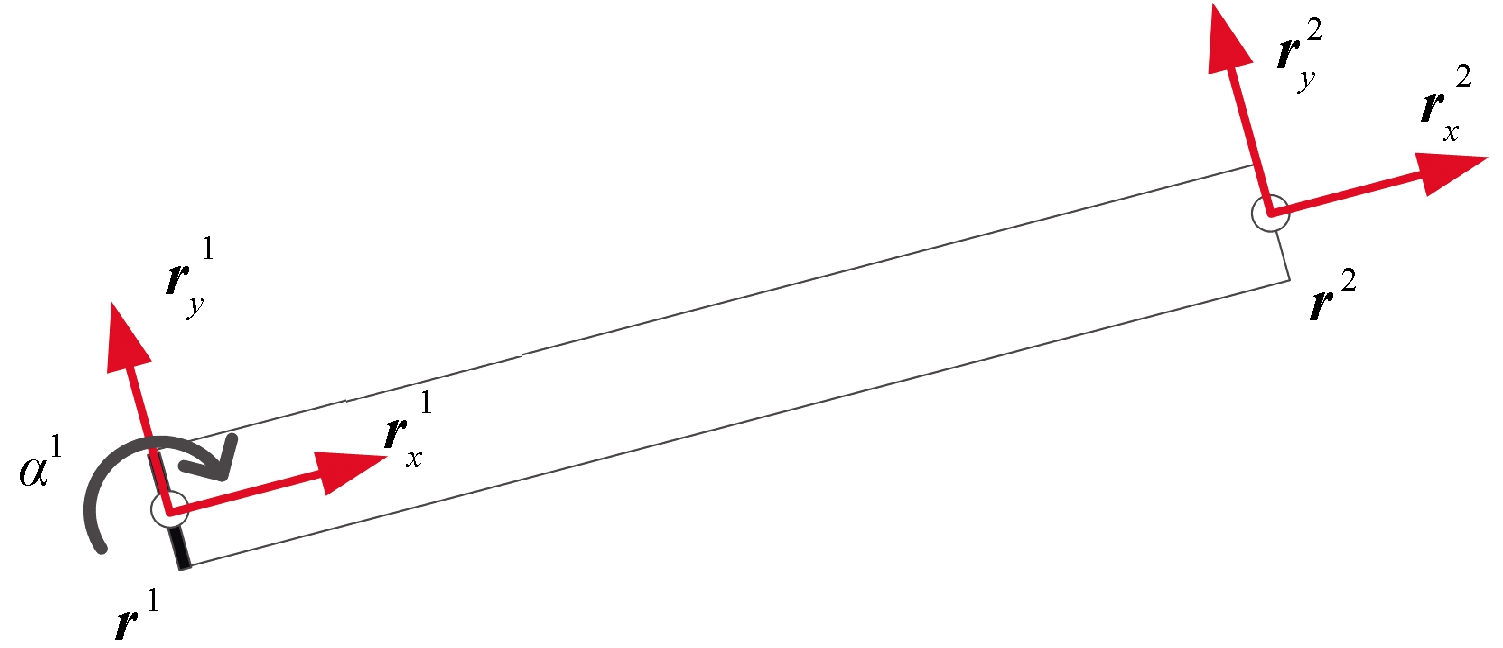
图1 含端部变形约束的ANCF梁单元
Figure 1 ANCF beam element with one nodal constrain
对上式求时间t的导数可以得到速度方程
(10)
因此在节点1处就定义了两组节点参数e1和p1，其中
为传统平面ANCF梁单元节点参数，
为将不独立梯度矢量参数和替换为独立转角参数α1所组集形成的新的节点参数。根据式(10)，这两组节点参数的时间变化率
和
存在如下变换关系:
(11)
式中：节点速度变换矩阵B1为
(12)
2.2 含端部变形约束ANCF梁单元的有限元列式
对于含端部变形约束ANCF梁单元，约束端节点1选取包含转角的独立节点参数
非约束端节点2仍选取节点参数
则新的单元参数列阵为
根据节点速度变换关系式(11)，有如下单元参数速率变换关系：
(13)
含端部变形约束ANCF梁单元控制方程只需将原ANCF梁单元虚功率方程式(7)中的单元速度参数
和加速度参数
替换为新的单元独立参数
和
便可以得到
(14)
式中：含端部变形约束ANCF梁单元的质量阵
和广义力列阵
分别为
(15)
3 ANCF梁单元的闭锁问题
同传统有限元法一样，ANCF单元也存在诸如剪切闭锁、泊松闭锁、体积闭锁等现象。ANCF梁单元闭锁现象源于单元位移插值函数沿轴向与截面内方向的阶次不同，使梁的弯曲变形耦合有过多剪切，表现为弯曲刚度过大、弯曲挠度变小。将最新提出的ANCF闭锁缓解技术SSM方法[19]应用于柔顺机构仿真分析，以考察ANCF梁单元闭锁问题对柔顺机构动力学特性的影响。
根据SSM方法，单元内任意点的位置矢量r可以分解为r=rc+yry，其中rc为梁截面形心处的位置矢量，梯度矢量可以表示为
相应的变形梯度也可以分解为两部分，即
将其代入Green-Lagrangian应变表达式就可以得到
(16)
式中：εc=(1/2)(JcTJc-I)为与梁形心线变形相关的应变量；εk=(1/2)(JcTJk+JkTJc+JkTJk)为与截面变形、弯曲及曲率相关的高阶量。
将分解得到的这两个应变εc和εk分别表示为列阵形式即：
相应的第二类Piola-Kirchhoff应力列阵可以表示为
(17)
式中：材料弹性矩阵Ec和Ek分别为
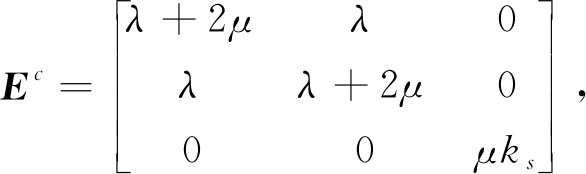
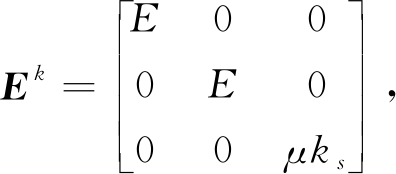
(18)
式中：剪切修正系数ks=10(1+v)/(12+11v)。
将修正后的Green-Lagrangian应变表达式和本构方程代入平面ANCF梁单元内力虚功率，可以得到采用SSM方法计算的ANCF梁单元节点力为
(19)
4 数值算例
不考虑ANCF梁单元闭锁，直接基于连续介质力学方法(GCM)计算单元节点力对应的仿真结果记作ANCF/GCM；采用缓解ANCF单元闭锁的SSM方法计算单元节点力对应的仿真结果记为ANCF/SSM。作为参照，在ADAMS中采用大变形梁类部件模块FE_Part搭建相应仿真模型，仿真结果记作ADAMS。
4.1 柔性单摆
柔性摆长度为L=1 m，截面面积为A=0.1×0.1 m2，材料弹性模量为E=2.1×106 Pa，材料密度为ρ=7 800 kg/m3，泊松比为v=0.27，在沿-Y方向重力作用下由图2所示水平位置自由下落，重力加速度为g=9.81 m/s2。
图2 柔性单摆
Figure 2 Flexible pendulum
本算例选取较小的材料弹性模量，自由下落过程中单摆产生较大变形。采用ANCF梁单元离散，左端旋转铰所在节点处采用含端部变形约束ANCF梁单元建模。最终形成的单摆系统刚柔耦合动力学方程采用MATLAB刚性方程求解器ode15s仿真求解，设定仿真时间为1 s。仿真求解时，柔性单摆均被等分为5个单元，图3～4给出了单摆末端节点位置坐标的时间变化曲线。
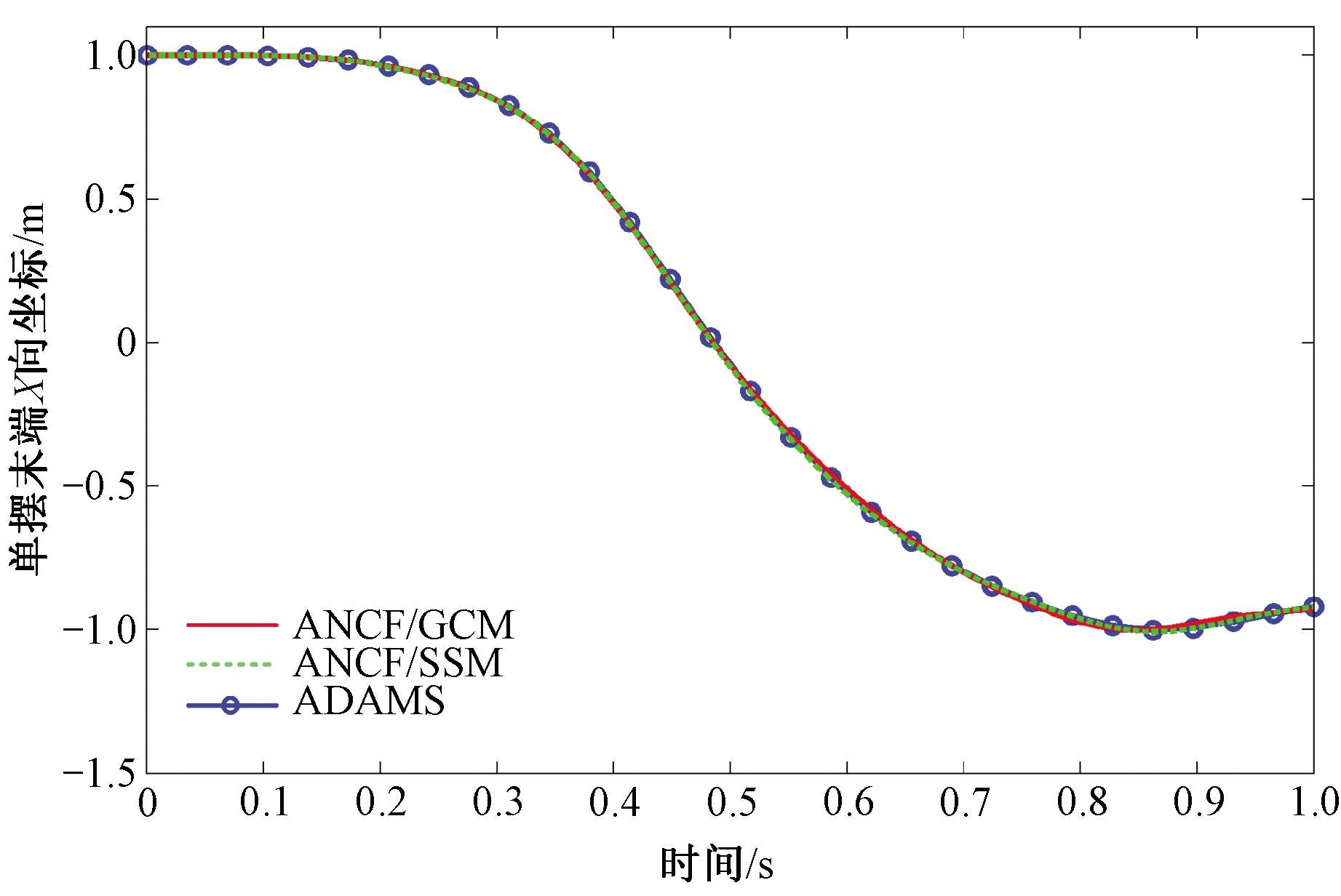
图3 柔性单摆末端节点X方向位置坐标
Figure 3 Position coordinate component in X direction of end point in flexible pendulum
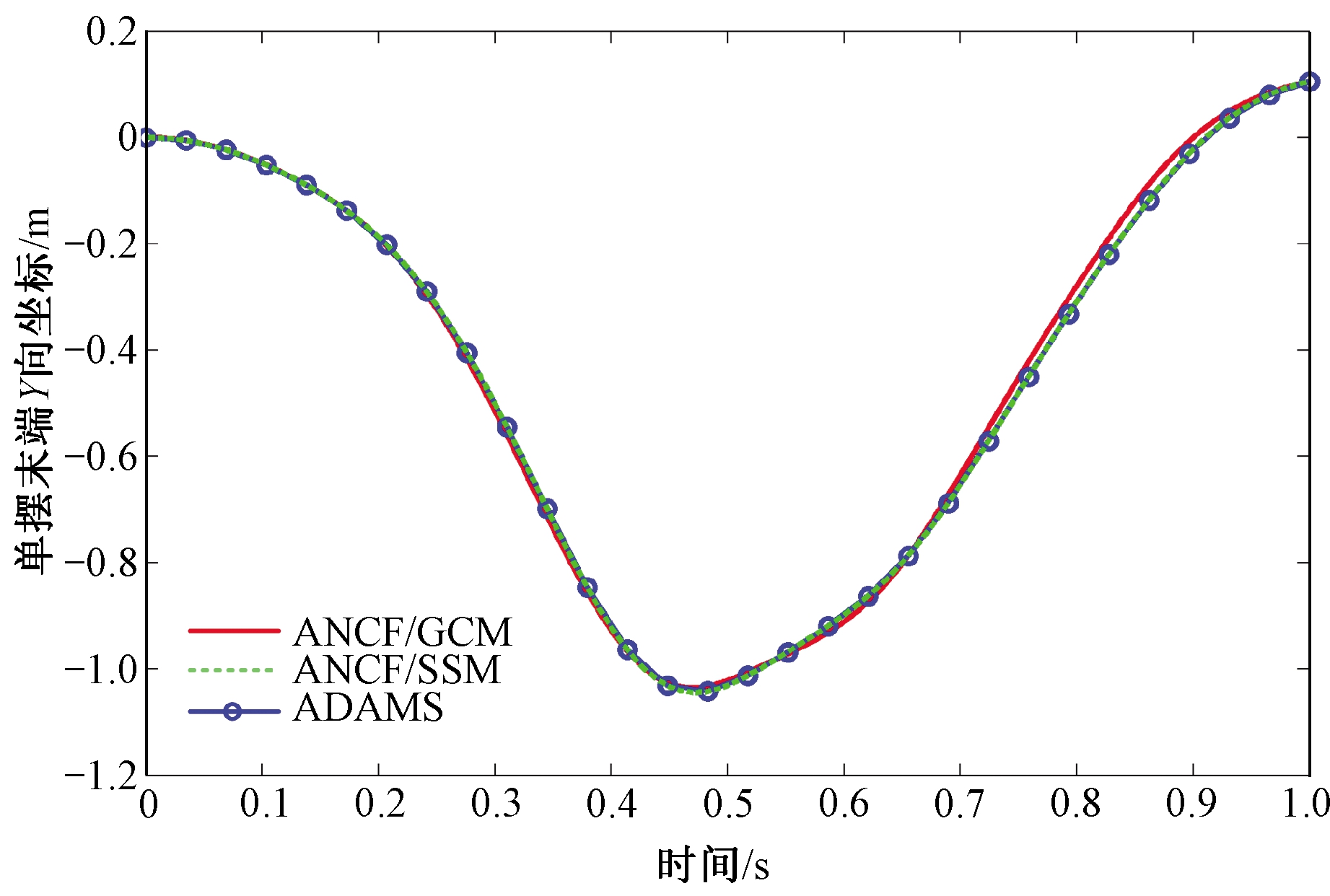
图4 柔性单摆末端节点Y方向位置坐标
Figure 4 Position coordinate component in Y direction of end point in flexible pendulum
由图3～4首先可以看出，采用ANCF梁单元得到的单摆算例仿真结果能够与商业软件ADAMS结果很好地吻合。这初步表明了笔者所提出的含端部变形约束ANCF梁单元的可行性与正确性。因为采用SSM方法修正单元节点力有效缓解了ANCF梁单元闭锁，因此得到了比直接基于GCM方法更好的数值结果。
ANCF梁单元基于连续介质力学基本理论，可以更方便更精确地计算单元内应力应变分布情况。图5给出了不同时刻柔性单摆的变形及正应变云图。
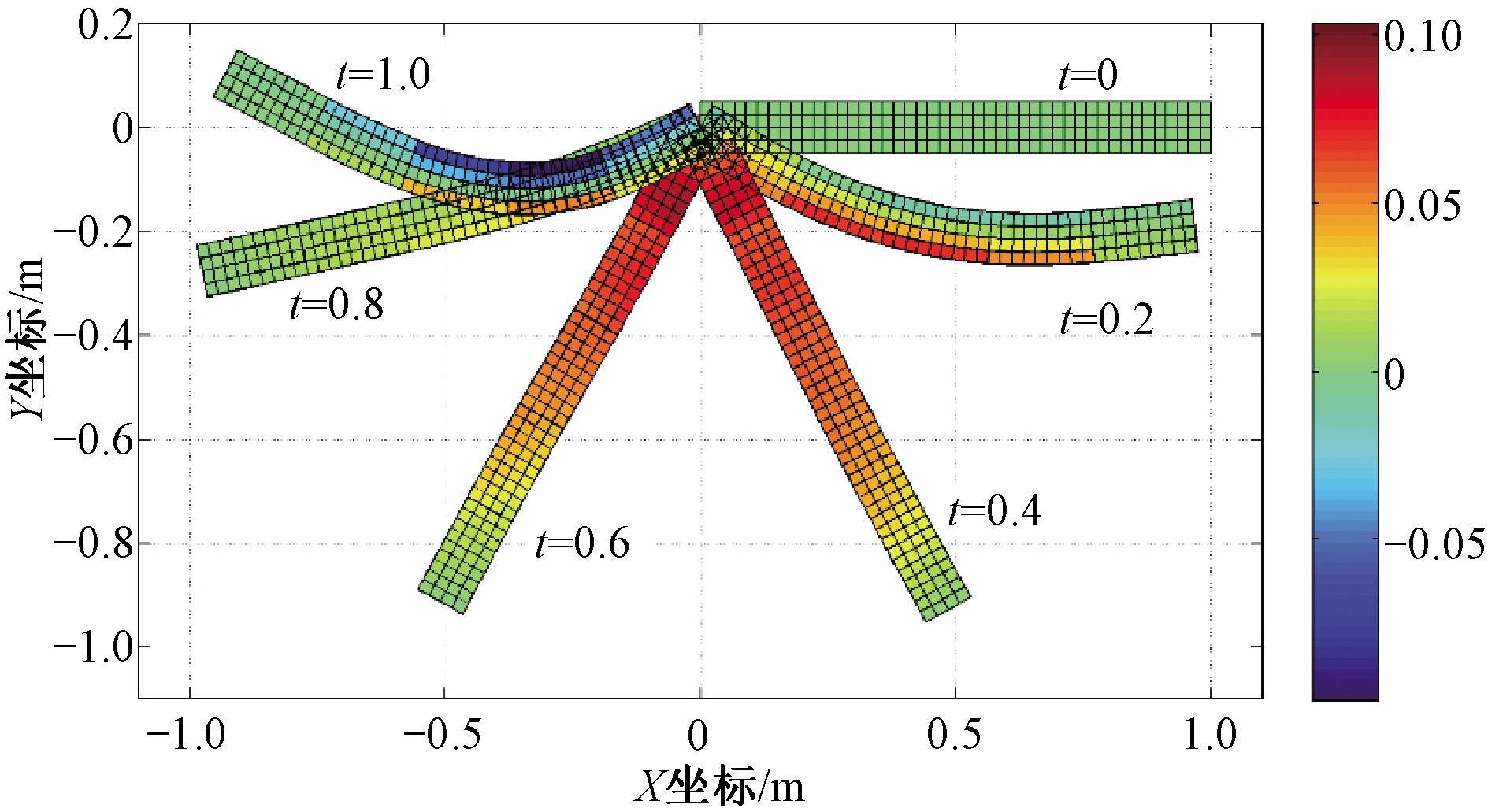
图5 柔性单摆的正应变云图
Figure 5 Distribution of normal strain of the flexible pendulum
4.2 柔顺四连杆机构
柔顺四连杆机构中刚性杆AB、刚性杆BC和柔顺杆CD的长度分别为
刚性杆AB和刚性杆BC的密度为ρAB=ρBC=7 800 kg/m3，截面面积为AAB=ABC=0.1×0.1 m2；柔顺杆CD的材料密度为ρCD=2 000 kg/m3，截面面积为ACD=0.04×0.04 m2，材料弹性模量为E=300×106 Pa，泊松比为v=0.27。柔顺四连杆机构受到作用在旋转铰A处的驱动扭矩M=50sin(πt) N·m及沿-X方向重力g=9.81 m/s2作用，其初始状态如图6所示。
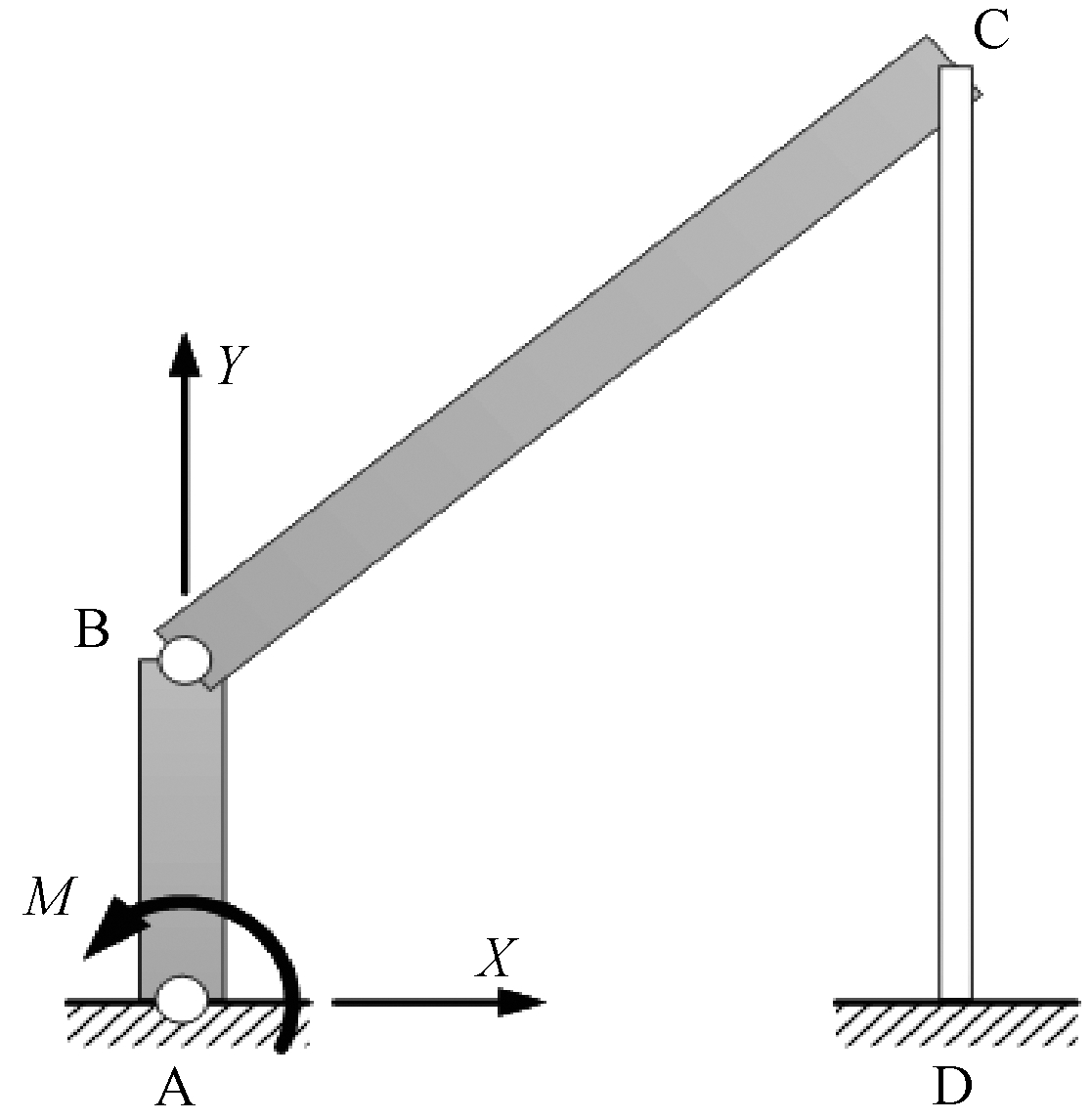
图6 柔顺四连杆机构
Figure 6 Compliant four-bar linkage
在这个算例中，刚性杆AB和BC采用刚体建模；柔顺杆CD均匀划分为5个梁单元，分别采用基于GCM和SSM的ANCF梁单元进行建模。对于包含柔顺杆端部节点C和节点D的单元仍采用含端部变形约束ANCF梁单元建模。图7～8给出了采用上述3种方法得到的仿真时间为1 s的柔顺杆顶端C点位置坐标的时间变化曲线。
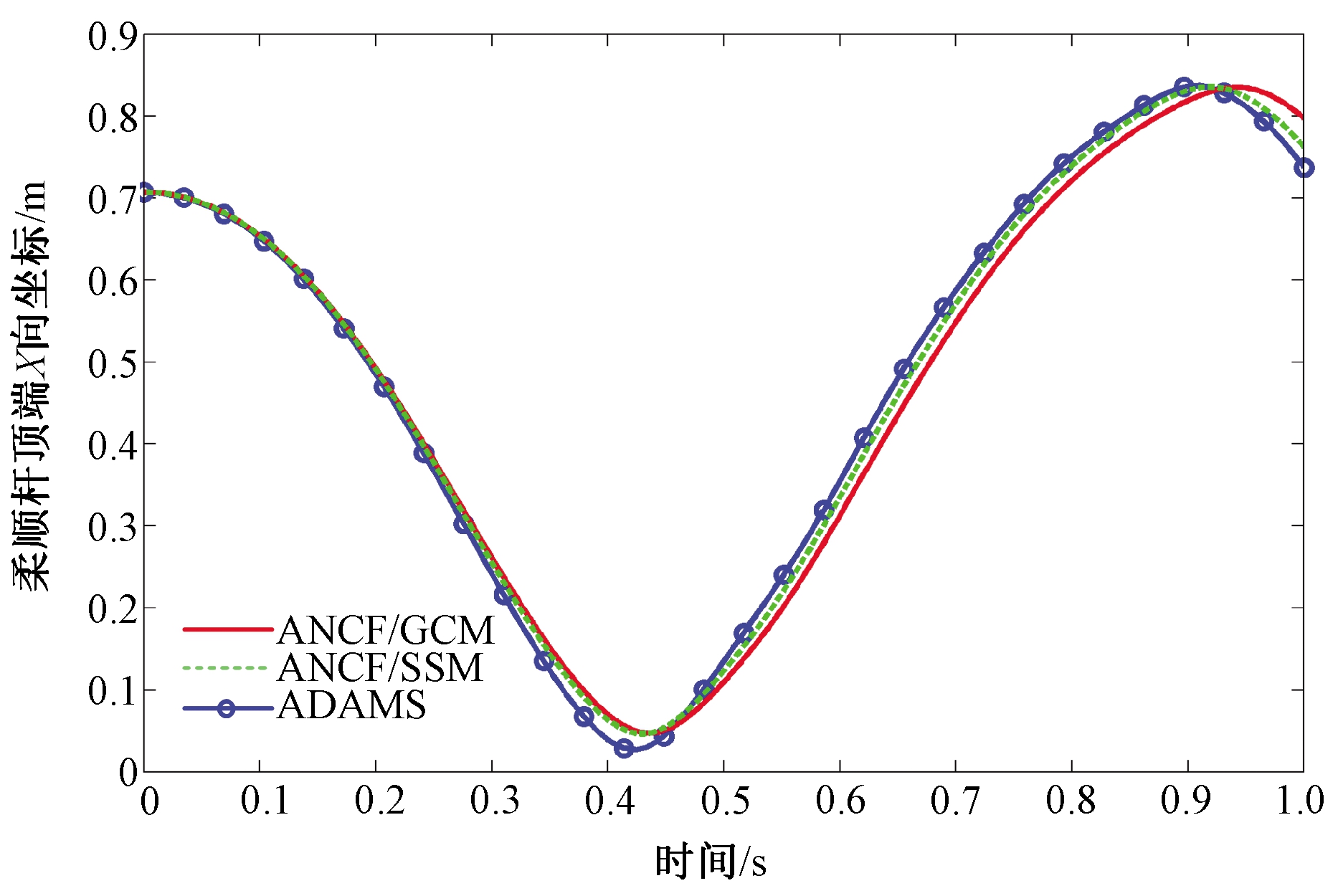
图7 柔顺杆顶端C点X方向位置坐标
Figure 7 Position coordinate component in X direction of point C in the compliant rod
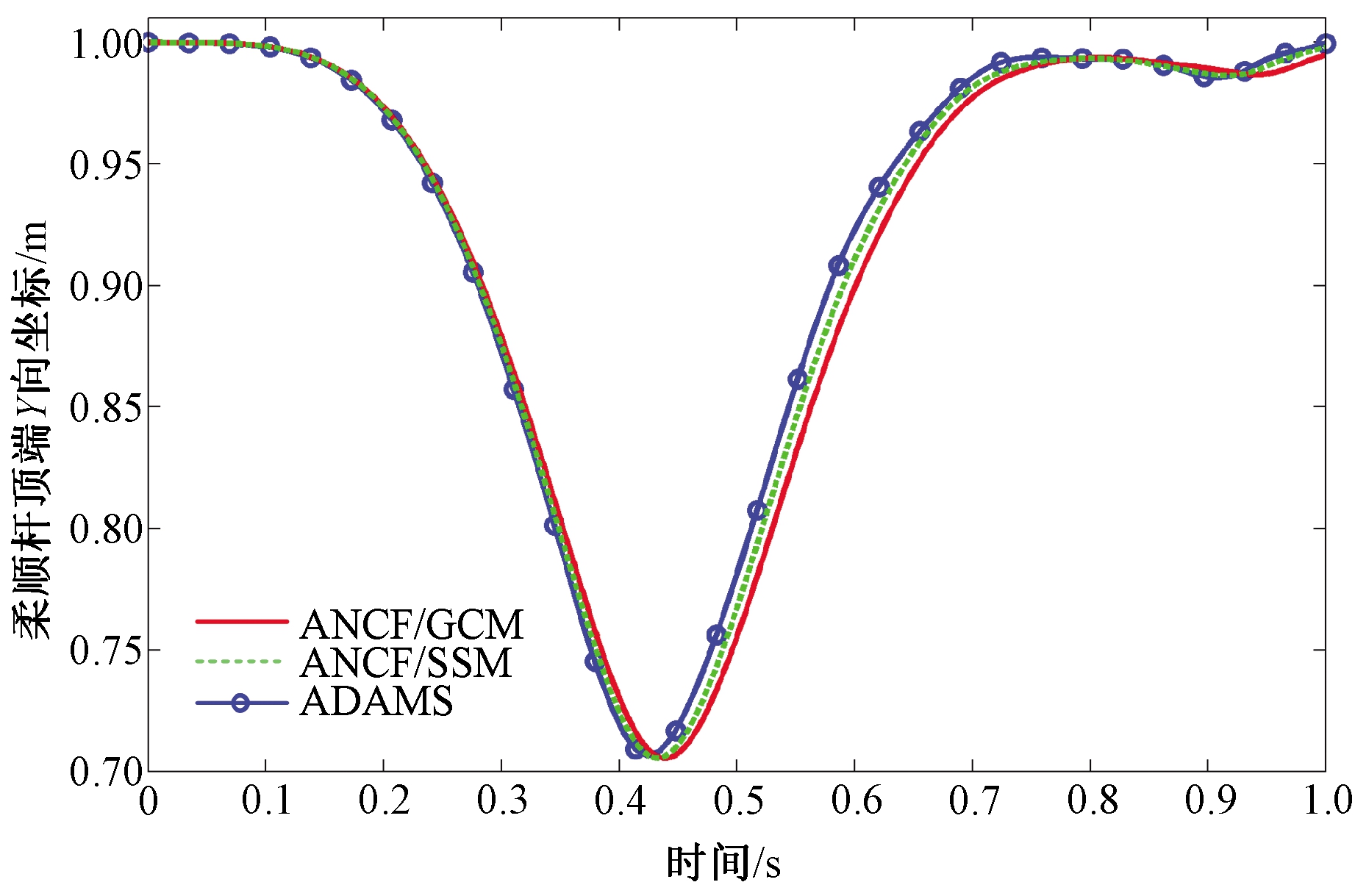
图8 柔顺杆顶端C点Y方向位置坐标
Figure 8 Position coordinate component in Y direction of point C in the compliant rod
从图7～8可以看出，采用ANCF梁单元所得数值结果与商业软件ADAMS相吻合。这也表明了ANCF梁单元适用于柔顺机构建模和动力学分析。从图中还可以看出，ANCF梁单元闭锁问题使得当单元发生较大变形时，单元表现为过于刚硬。因此，采用SSM闭锁缓解方法的数值结果(ANCF/SSM)好于不考虑闭锁问题所对应的数值结果(ANCF/GCM)。
柔顺四连杆机构在运行中必然会伴随柔顺杆件的往复变形。因此在设计和分析柔顺机构时，对工作过程中柔顺杆所受应力应变进行分析具有重要意义。图9给出了柔顺四连杆机构在不同时刻的运动变形情况及柔顺杆的正应变云图。
图9 柔顺四连杆机构正应变分布
Figure 9 Distribution of normal strain of the compliant four-bar linkage
由应变分布云图可知，在柔顺机构运行过程中柔顺杆的最大正应变出现在柔顺杆两端。因此在进行柔顺四连杆设计和疲劳寿命分析时都需要将柔顺杆两端看作危险截面给予重点核算。
5 结论
基于绝对节点坐标方法系统地研究了柔顺机构动力学建模问题，得到的结论如下：
(1) 采用平面ANCF梁单元建立了大变形柔顺四连杆机构的动力学模型；
(2) 在充分考虑柔顺杆铰链连接处变形特征基础上，提出了含端部变形约束的平面ANCF梁单元；
(3) 基于连续介质力学理论，精确计算了包含动力学效应的柔顺杆应变分布，为柔顺机构疲劳分析奠定了基础。
[1] HOWELL L L． Compliant mechanisms[M]． New York: John Wiley and Sons, 2001．
[2] 高峰． 机构学研究现状与发展趋势的思考[J]． 机械工程学报, 2005, 41(8): 3-17．
[3] HOWELL L L, MIDHA A, NORTON T W. Evaluation of equivalent spring stiffness for use in a pseudo-rigid-body model of large-deflection compliant mechanisms[J]. Journal of mechanical design, 1996, 118(1): 126-131.
[4] 于靖军, 毕树生, 宗光华, 等. 基于伪刚体模型法的全柔性机构位置分析[J]. 机械工程学报, 2002, 38(2): 75-78.
[5] 李海燕, 张宪民, 彭惠青. 大变形柔顺机构的驱动特性研究[J]. 机械科学与技术, 2004, 23(9): 1040-1043.
[6] SU H J． A pseudorigid-body 3R model for determining large deflection of cantilever beams subject to tip loads[J]． Journal of mechanisms and robotics, 2009, 1(2): 021008．
[7] 冯忠磊, 余跃庆, 王雯静． 柔顺机构中大变形柔性梁的2自由度伪刚体模型[J]． 机械设计与研究, 2010, 26(3): 41-43．
[8] 余跃庆, 周鹏． 柔顺机构PR伪刚体模型[J]． 北京工业大学学报, 2013, 39(5): 641-647．
[9] 李茜, 余跃庆, 常星. 基于2R伪刚体模型的柔顺机构动力学建模及特性分析[J]. 机械工程学报, 2012, 48(13): 40-48.
[10] 余跃庆, 徐齐平. 柔顺机构PR伪刚体动力学建模与特性分析[J]. 农业机械学报, 2013, 44(3): 225-229.
[11] 余跃庆, 张娜. 含拐点的柔顺机构动力学建模及分析[J]. 北京工业大学学报, 2018, 44(4): 489-496.
[12] SHABANA A A． An absolute nodal coordinate formulation for the large rotation and deformation analysis of flexible bodies． Technical report MBS96-1-UIC[R]. Department of mechanical engineering, University of Illinois at Chicago， 1996．
[13] PATEL M, ORZECHOWSKI G, TIAN Q, et al. A new multibody system approach for tire modeling using ANCF finite elements[J]. Proceedings of the institution of mechanical engineers, part K: journal of multi-body dynamics, 2016, 230(1): 69-84.
[14] K
ODOWSKI A, RANTALAINEN T, MIKKOLA A, et al. Flexible multibody approach in forward dynamic simulation of locomotive strains in human skeleton with flexible lower body bones[J]. Multibody system dynamics, 2011, 25(4): 395-409.
[15] 刘昊, 魏承, 田健, 等. 空间充气展开绳网捕获系统动力学建模与分析[J]. 机械工程学报, 2018, 54(22): 145-152.
[16] 李鹏飞, 曹博宇, 汪振宇, 等. 含非线性大变形构件的柔顺机构建模与分析[J]. 振动与冲击, 2019, 38(11): 110-115.
[17] 李鹏飞, 曹博宇, 汪振宇, 等. 一种外LET柔顺半铰的动力学建模与分析[J]. 中国机械工程, 2019, 30(14): 1727-1733.
[18] 刘治华, 刘博见, 许伟超, 等. 飞碟游乐设备驱动轴疲劳失效分析[J]. 郑州大学学报(工学版), 2017, 38(5): 91-96.
[19] PATEL M, SHABANA A A． Locking alleviation in the large displacement analysis of beam elements: the strain split method[J]． Acta mechanica, 2018, 229(7): 2923-2946．
[20] OMAR M A, SHABANA A A． A two-dimensional shear deformable beam for large rotation and deformation problems[J]． Journal of sound and vibration, 2001, 243(3): 565-576．