0 引言
2019年的“两会”期间，国家电网公司提出了关于建设“泛在电力物联网”的报告。“泛在电力物联网”以能源互联网和物联网为主体，旨在实现电网朝着智慧能源的方向发展[1]。在能源互联网中，DG是必不可少的。然而随着分布式电源DG在电源结构中的比例日渐提高，DG发电的随机性和间歇性对电网的运行和调度带来了不稳定性和困难，甚至某些地方因此出现了大规模的“弃风”、“弃光”现象[2]。储能系统ESS的可充、放电特点，可在一定程度上缓解因DG并网带来的功率波动问题，同时能起到 “削峰填谷”的作用[3]。
由于技术、材料等限制，储能系统ESS的投资成本与其容量大小有关，且十分高昂，所以如何尽可能地用较小的容量使其在电力系统中发挥较大的作用成为了研究的热点。关于电力系统中储能容量优化的研究已经取得了不少的成果[4-5]。文献[6]针对大量DG及电动汽车接入电网产生的问题，结合储能容量、日负荷曲线等因素，提出了一种改进区间控制的储能出力模型，并进一步利用点估计概率潮流算法分析DG、电动车及ESS接入对配网的影响，然后通过仿真实验证实此方法具有改善配网电压和降低系统功率的作用。文献[7]利用抽水储能的方式来平滑DG的功率波动，以实现“水光”互补，并通过实际数据证明其可行性。文献[8]抛弃传统的蓄电池储能系统，利用光热电站储热发电来调峰，降低火电调峰的成本。但上述文献仅利用ESS进行“削峰填谷”，或只平滑DG的功率输出。若将ESS应用于含有DG的配网中，在对DG功率波动进行平滑的同时，也可起到“削峰填谷”的作用，降低“调峰”压力。
基于经验模态分解EMD的方法，对所得样本进行筛选和分解，在有效降低含DG配网功率波动率的前提下，根据分解结果构成新的功率曲线作为目标功率，再考虑ESS充放电效率及SOC(荷电状态)约束，给出了满足经ESS补偿后的目标功率所需的ESS最小容量方案。
1 样本选取原则及EMD处理
1.1 样本选取原则
平滑含DG配网功率波动，需要大量的DG输出功率和DG所在配网的负荷功率数据并进行筛选。由于电网一般以天为单位运行，故数据片段长度可选为1 d(由于光伏发电具有间歇性，可选择一天内光伏出力的时间段为单位)。在选择光伏数据时，要考虑到温度和光照强度对出力的影响，温度过高或阴雨天气会造成光伏出力不足的情况，在选择时要剔除这些数据，否则可能使计算得到的ESS容量过小或过大，从而无法起到平滑功率的作用或造成投资过大。风电则需考虑到季风的影响。算例选取了2018年全年的光伏发电功率输出以及所在配网的用电负荷数据，按春、夏、秋、冬四季中光伏发电权重，分别随机抽取30 d(春，夏，秋)和15 d(冬)的光伏发电及所在配网的负荷数据，去掉雨雪天等对光伏发电不利的极端天气后，其余每天同一时刻数据相加求平均值作为样本。现实中，需要根据样本所在环境，增减取样天数，以应对DG发电的随机性、季节性对ESS容量选取的影响。
1.2 样本EMD的处理
设含DG配网功率随时间变化的信号为P(t)，进行EMD处理的步骤如下：
(1)识别出信号P(t)所有极值点，并分别拟合出P(t)的上、下包络线Eup(t)、Elow(t),计算其均值为m1(t)。
(2)将P(t)减去m1(t)得到n1(t),将n1(t)视为新的P(t)，重复步骤(1)，经过k次筛选，直到n1k(t)是基本IMF(本征模函数)分量。
(3)令c1(t)为n1k(t)，则c1(t)为从P(t)中得到的第一个基本模式分量，残部分量r1(t)为：
r1(t)=P(t)-c1(t)。
(1)
(4)若残部分量rn(t)的极值点数仍多于2个，需重复步骤(1)、(2)、(3)，则
rn(t)=rn-1(t)-cn(t)。
(2)
P(t)最终可表示为：
(3)
EMD方法可以认为是对原始信号信息的分解、分配过程，如果从这个角度来理解EMD，它就是一种自适应滤波方法。
2 ESS功率及容量的确定
2.1 ESS功率的确定
为确定ESS的补偿效果，需要引入功率波动率作为评价指标。设一定时间段内功率波动率为Fb,其可由下式表示:
(4)
式中：sP为时间段内功率的标准差，反映了负荷的分散程度；
为均值，反映了负荷的集中程度。式(4)可综合反映负荷的变化情况。
为保证ESS的连续运行，应确定合理的ESS功率输出，并保证ESS有足够大的充放电功率。ESS功率可以通过以下步骤获得。
(1)确定含DG配网的功率PZS，并对其进行EMD处理。假设PZS由DG的输出功率及用电负荷构成，分别由PDG和PTL表示。其间的关系可表示为：
PTL-PDG=PZS;
(5)
PTL,n-PDG,n=PZS,n,
(6)
式中：PTL,n、PDG,n、PZS,n分别为第n个采样点对应PTL、PDG、PZS的输出功率，n∈{1，2，…，Ns}，Ns为采样点个数。
(2)经过EMD处理得到目标功率PDR后，确定 ESS 所需最大充放电功率为其额定功率。ESS对外输出功率可由PES表示，则
PES=PDR-PZS。
(7)
由式(5)～(7)得到的ESS充放电功率PES绝对值的最大值即为ESS额定功率，即
PES,N=max|PES,n|。
(8)
当PES,n为正值代表ESS放电，为负值则代表充电；由于在没有DG并网时负荷从电网吸收的功率全部由电网提供，所以PTL也是原日负荷功率。
(3)确定ESS的实际输出功率。由于化学电池的特性，其在充放电过程中会有些许损耗，因此ESS在运行过程中也会产生损耗。若用η表示ESS的综合效率，则根据ESS的功率额定值，可确定ESS实际充放电功率，用PESO表示[9]为
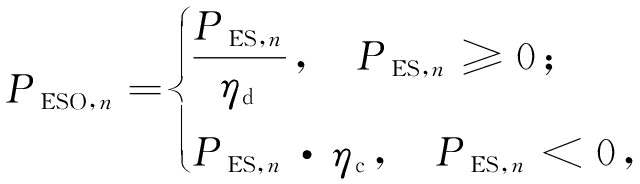
(9)
式中：ηd与ηc分别为ESS的放电和充电效率；n为样本采样个数。设充电效率与放电效率相等，则
(10)
此外，为保证ESS运行的可持续性，需尽量选择满足ESS运行一个周期内充放电量累积为0或近似等于0的样本片段，即
(11)
根据公式E=PT，因时间相同，可知能量的平衡表现在功率的平衡上，可将储能补偿的功率值进行纵坐标上的平移。平移量ΔP可通过迭代求得，平移后曲线波动率不变[5]。
2.2 ESS容量的确定
(1)由ESS实际输出功率对样本片段内充放电量进行累加，可得到ESS在时间点上相对于初始状态的能量波动[5]， 即
(12)
式中：PESO,n为ESS实际输出功率数据；Ts为采样周期，s。Ts/3 600的意义在于将单位“s”换算为“h”。
(2)在获取整个样本片段内的能量波动后，计算其最大与最小值之差，考虑ESS荷电状态的限制，可得到ESS的额定容量：
(13)
式中：Cup、Clow分别为ESS运行中SOC上、下限约束；maxEES,m、minEES,m分别为在整个样本周期内ESS相对于初始状态的最大和最小能量值；在理想情况下，Cup=1，Clow=0，考虑到实际运行时为避免充电过量和放电过量而影响ESS的寿命，一般取Cup=1，Clow=0.3[10]。
2.3 SOC初始值确定及容量校验
SOC表示ESS剩余能量水平， 且0≤SOC≤1。当SOC为1时，表明ESS完全充满；当SOC为0时则表明ESS放电完全。ESS的SOC过低会造成ESS中电极活性物质损伤。其中，铅酸蓄电池会造成“不可逆硫酸盐化”，造成大量结晶盐附着在电极上；较为昂贵的锂电池则会造成正负电极的永久损伤。这些都会影响ESS使用寿命，造成充电困难，增加运营、维护成本，因此需要对SOC的范围进行约束，并控制其在此范围内运行。由式(13)得到ESS容量后，需对SOC的运行范围进行校验，判断计算得出的容量是否满足约束，计算式如下[11]：
(14)
式中：C0、Cm分别为SOC的初始值和第m个采样时间段结束后SOC值。
若由式(13)所得ESS容量满足需求，则SOC必运行在以下约束范围内[12]：
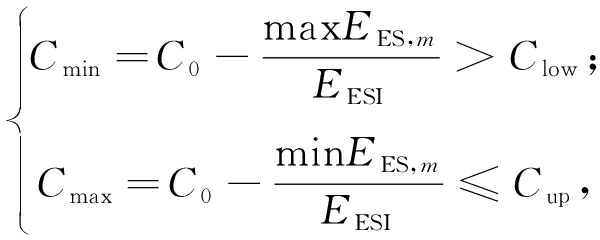
(15)
式中：Cmax和Cmin分别为ESS运行时的最大和最小SOC值，由式(15)得出ESS容量需满足的条件为：
(16)
由式(13)、(15)、(16)可得ESS初始SOC状态为：
(17)
由文献[9]可知，在满足SOC约束范围的ESS额定容量确立之后，相对应的唯一满足运行约束范围的SOC初值也就确定了，这需要对ESS采用一定控制策略，并通过一段时间的运行达到稳态，即可得到满足[11-12]。
3 算例分析
样本中DG数据为河南某地光伏电站采样数据，采样点间隔为5 min，电站最大输出功率为1.8 MW，电压为10 kV；配网联络线功率为DG同网数据，电压为10 kV,其功率在30 min内最大波动率为53.46%。ESS综合效率η取88%，则ηd、ηc均为93.1%；ESS运行过程中SOC的上限取1，下限取0.3[10]。
所需样本数据主要通过历史记录获得，并利用前述样本选取方法对所得数据进行计算筛选。由于光伏发电具有间歇性，白天发电而夜间不发电，且夜间日负荷功率波动较小，可关闭ESS提高其使用寿命，因此数据片段长度为早上6:30至下午18:30，此时段同时为光伏出力时段。结果如图1所示。
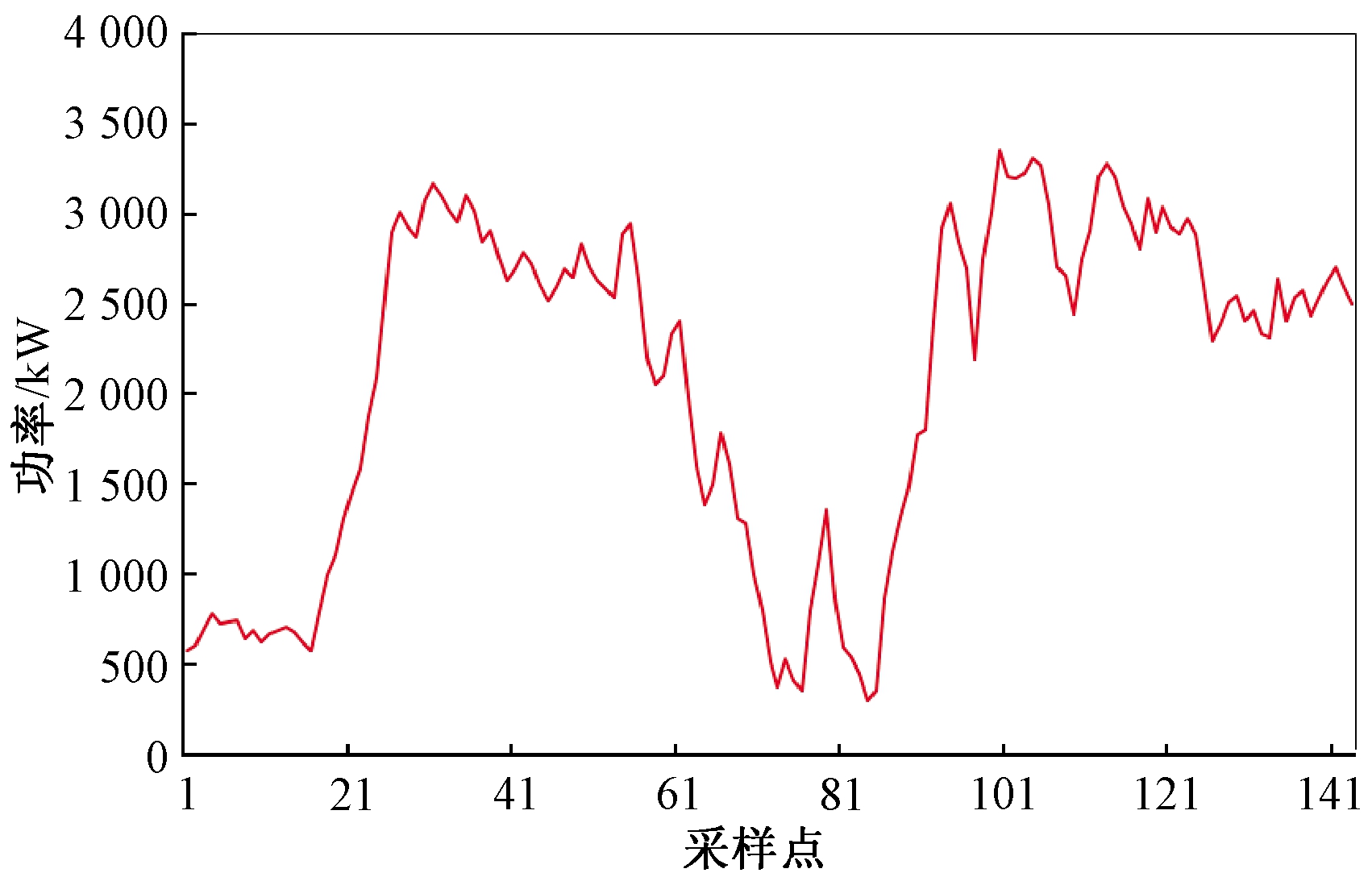
图1 含DG功率样本
Figure 1 Power samples containing DG
将图1功率数据样本进行EMD处理，分解结果如图2所示，得到4个IMF分量和一个余量R，根据分解结果重构出3条功率曲线，如图3所示。3条重构功率曲线30 min内最大波动率以及所需的ESS容量的计算结果如表1所示。
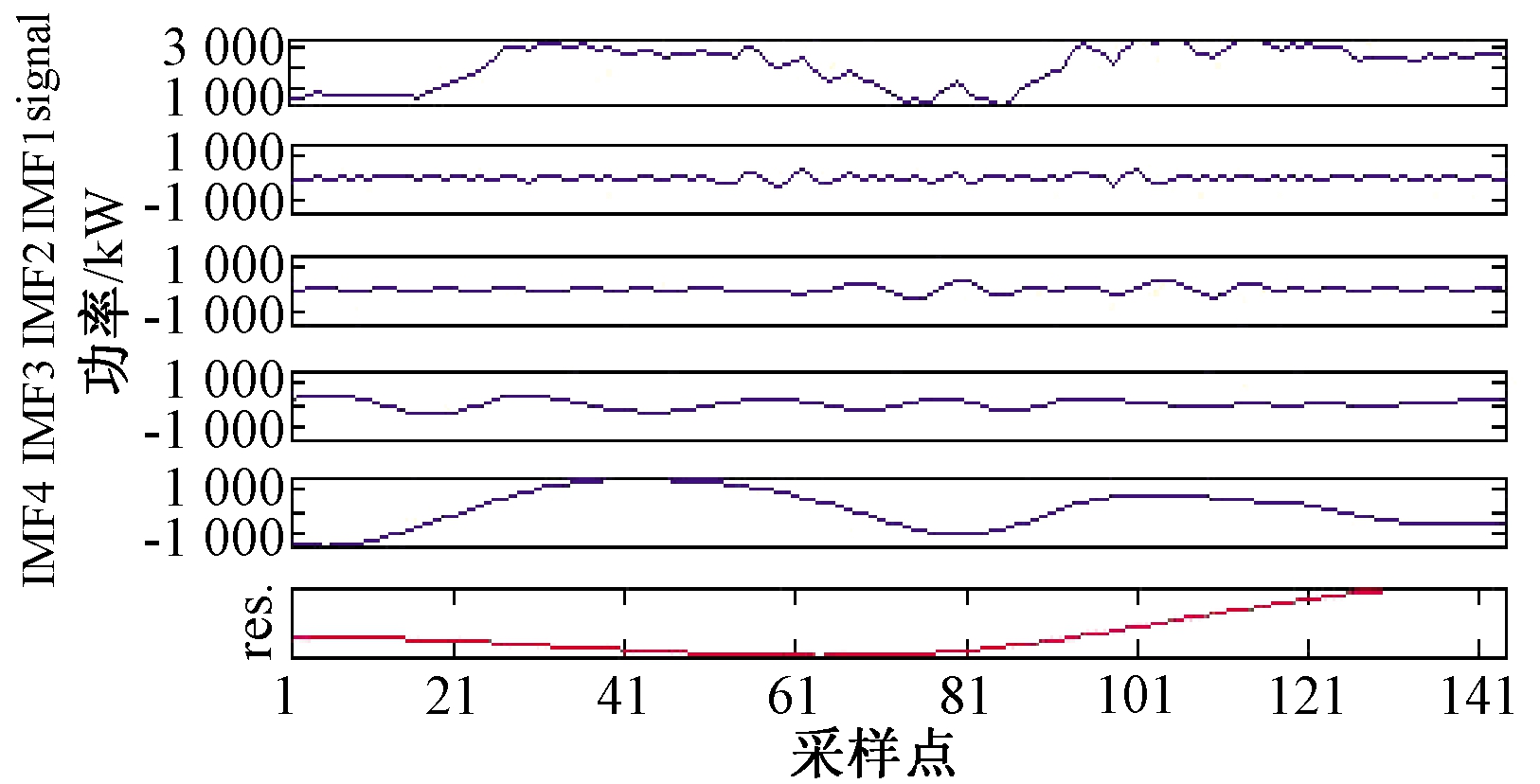
图2 EMD结果
Figure 2 Empirical mode decomposition results
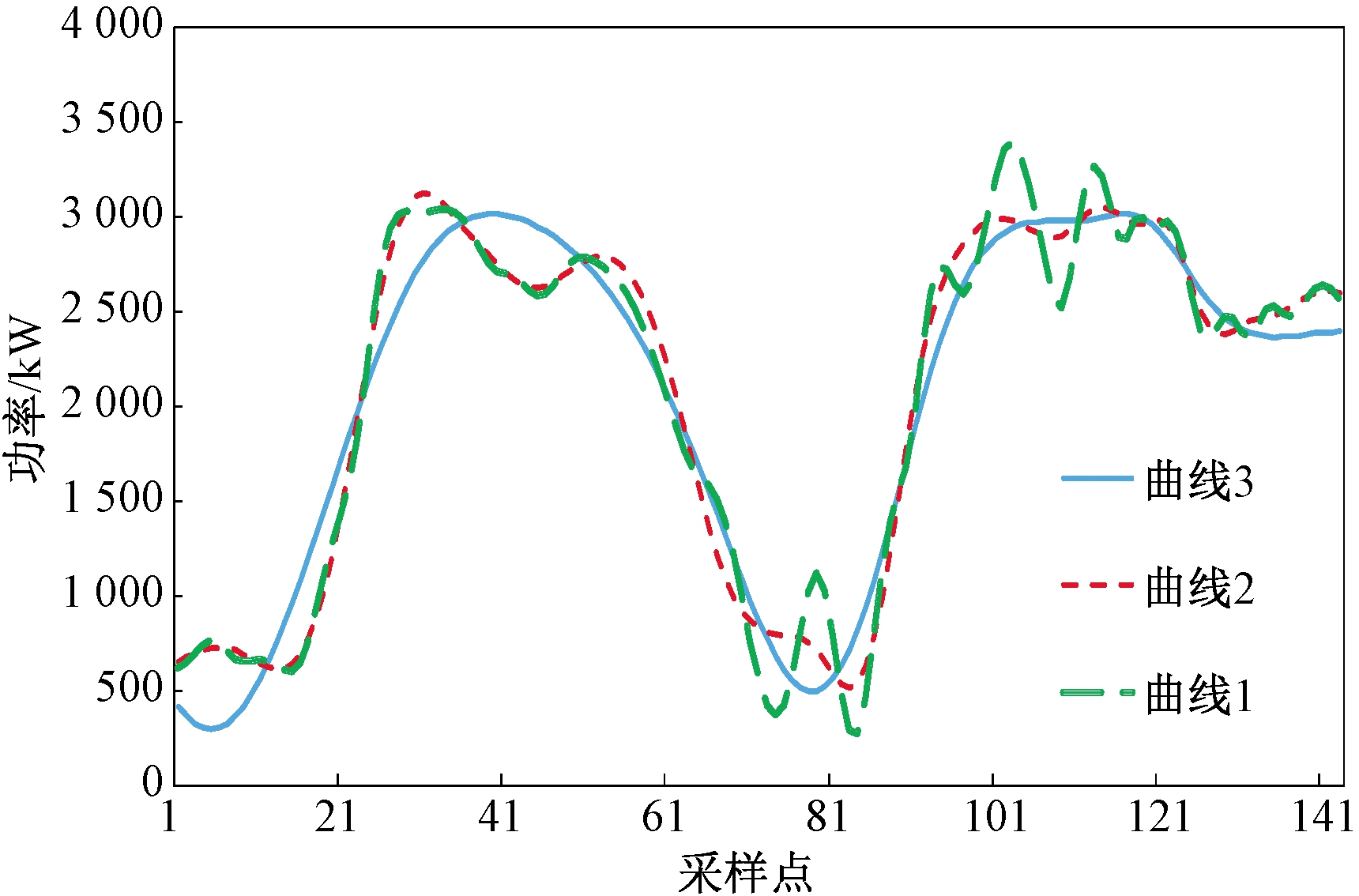
图3 重构功率曲线
Figure 3 Reconstruction power curves
表1 计算结果
Table 1 Computed results
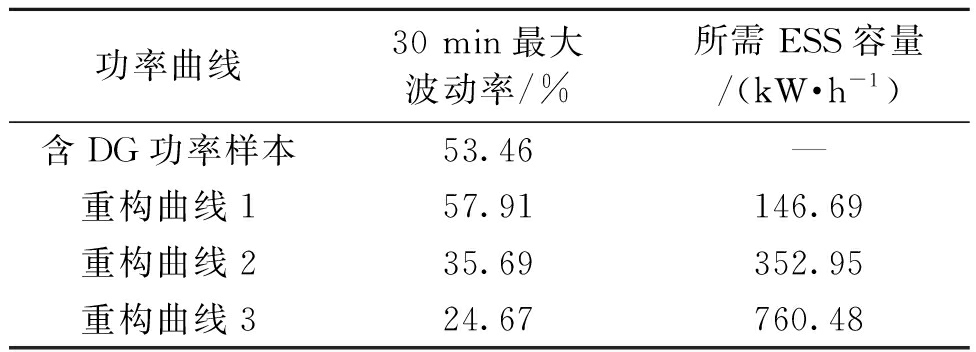
功率曲线30 min最大波动率/%所需ESS容量/(kW·h-1)含DG功率样本53.46—重构曲线157.91146.69 重构曲线235.69352.95 重构曲线324.67760.48
由图3和表1可知：3条重构曲线在30 min内的最大波动率分别为57.91%，35.69%和24.67%。曲线2和曲线3在30 min内最大波动率相对原样本均有所减小。相对于曲线2来说，曲线3对应需要的ESS容量较大，这表明平滑功率所需的ESS投资也较大[13]，但平滑效果也最好。
以曲线3为目标功率曲线，则为确保ESS在考虑充放电效率的情况下在所选时间片段内充放电电量相等，可将PESO整体向上平移，迭代得ΔP=43.79 kW。根据式(9)～(11)对得到的理论ESS输出功率进行充放电效率与电量平衡修正后得到ESS实际输出功率，如图4所示。根据式(7)、(12)、(13)、(17)可确定储能额定功率为831.245 kW，容量如表1所示，SOC初始值为64.32%。对ESS的SOC进行校验，校验结果如图5所示，可见运行过程中SOC的最大值和最小值分别为100%和30%，正好等于SOC的上下限，如图5虚线所示；且系统从开始运行至结束时充放电累计为0，如图5实线所示，故该系统可连续正常运行。
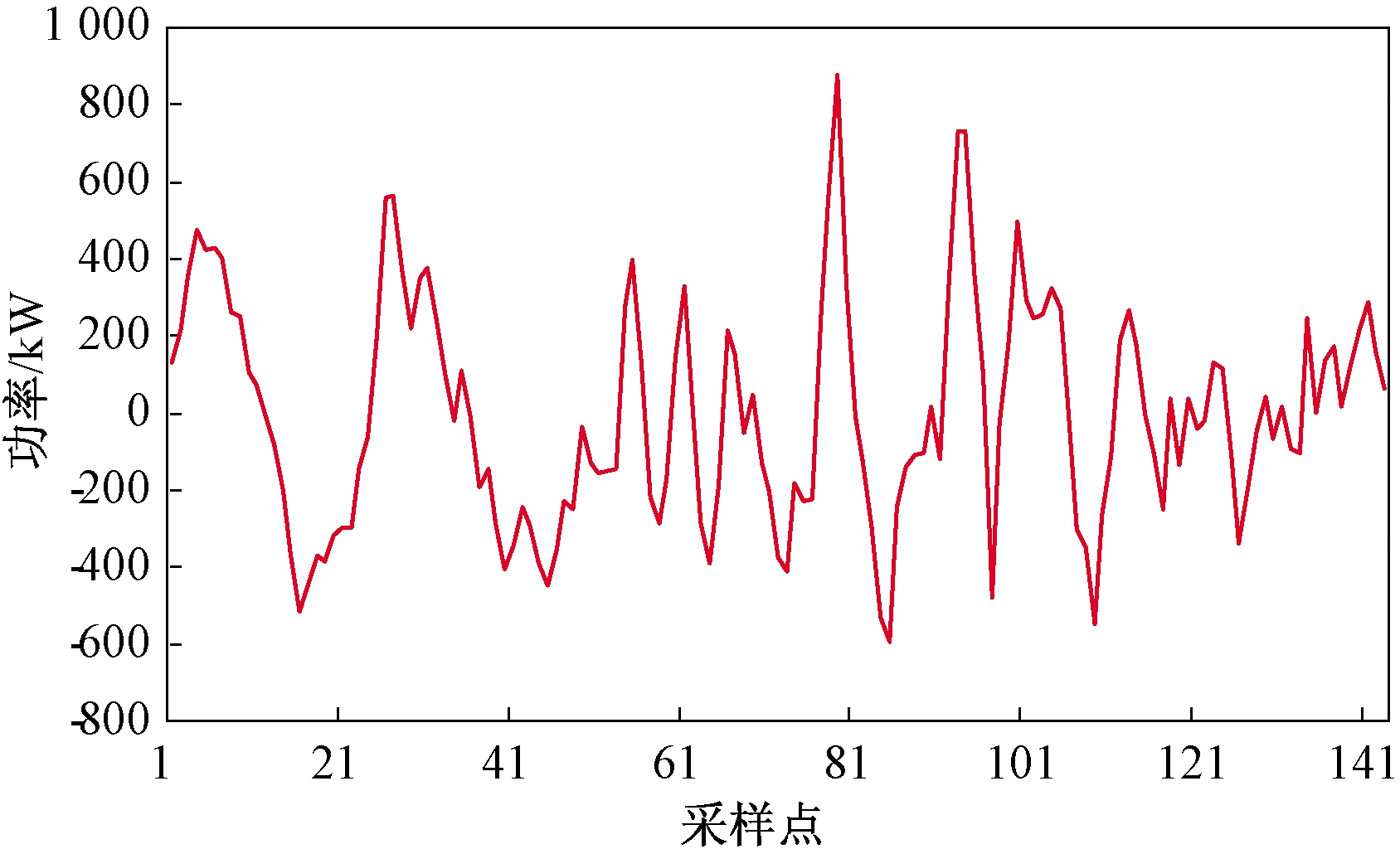
图4 ESS实际充放电功率
Figure 4 ESS actual charge and discharge power
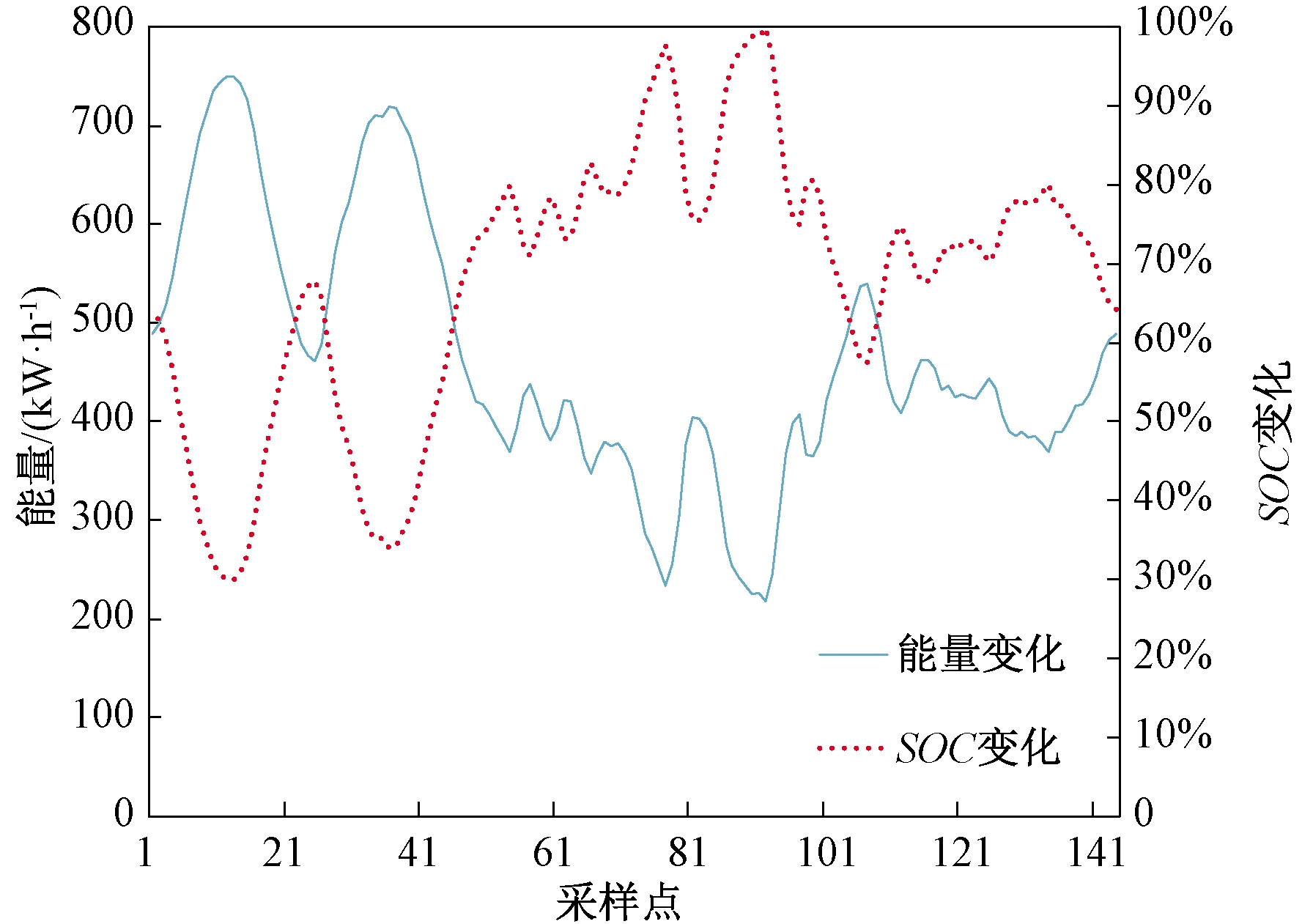
图5 校验结果
Figure 5 Calibration results
4 结论
为改善DG对配电网功率波动的影响，研究了一种基于EMD的平滑含DG配网功率波动的储能容量优化方法，以某地区的实际含DG配网功率样本为算例，考虑ESS充放电效率以及ESS的荷电状态约束，可得到以下结论：
(1)该方法可有效平滑含DG配网功率波动，能以较小的储能容量使功率最大波动率从53.46%降低至24.67%，且系统可正常稳定地运行。同时，该方法也具有一定的“削峰填谷”作用，可降低电力系统“调峰”的压力，提高电网经济性。
(2)就目前的技术而言，储能系统的成本较高，由本文计算方法得出的储能容量所需投资较大，在实际设计过程中应充分考虑储能成本与各方面的利益关系。
[1] 陈麒宇.泛在电力物联网实施策略研究[J].发电技术,2019,40(2):99-106.
[2] 范高锋,张楠,梁志锋,等.我国“三北”地区弃风弃光原因分析[J].华北电力技术,2016(12):55-59.
[3] 宁阳天. 基于削峰填谷的储能系统调度模型研究[D].北京：华北电力大学,2015.
[4] 孟顺,谢桦.基于经验模态分解的平滑可再生能源功率波动的储能容量优化[J].电源学报，2014,12 (5):7-11,18.
[5] 王成山,于波,肖峻,等.平滑可再生能源发电系统输出波动的储能系统容量优化方法[J].中国电机工程学报,2012,32(16):1-8.
[6] 李雪,宋彦龙.蓄电池储能运行控制对有源配电网影响研究[J].郑州大学学报(工学报)，2019,40(5)：32-38,51.
[7] JURASZ J, CIAPA
A B. Solar-hydro hybrid power station as a way to smooth power output and increase water retention[J]. Solar energy,2018,173:675-690.
[8] 崔杨,杨志文,严干贵，等.降低火电机组调峰成本的光热电站储热容量配置方法[J].中国电机工程学报,2018,38(6):1605-1611,1896.
[9] 王成山,于波,肖峻,等.平滑微电网联络线功率波动的储能系统容量优化方法[J].电力系统自动化,2013,37(3):12-17.
[10] LILIENTHAL P, LAMBERT T,GILMAN P, et al. HOMER.V.2.68beta[EB/OL].(2009-07-24)[2020-01-01].http://www.homerenergy.com/.
[11] YOSHIMOTO K, NANAHARA T, KOSHIMIZU G. Analysis of data obtained in demonstration test about battery energy storage system to mitigate output fluctuation of wind farm[C]//2009 CIGRE/IEEE PES Joint Symposium Integration of Wide-Scale Renewable Resources Into the Power Delivery System. Calgary, AB,Canada：CIGRE/IEEE,2009:1-5.
[12] YOSHIMOTO K, NANAHARA T, KOSHIMIZU G. New control method for regulating state-of-charge of a battery in hybrid wind power/battery energy storage system[C]//Power Systems Conference and Exposition. Atlanta, GA, USA:IEEE,2006:1244-1251.
[13] 段俊东,栗维冰,薛静杰.基于经济调度的光伏并网系统储能容量研究[J].河南理工大学学报(自然科学版),2015,34(6):860-866.