0 引言
现实中多目标优化问题[1]的Pareto前沿面往往是不连续的[2]、退化的[3]、倒置的[4]等非规则的形式，这类问题也被称为具有非规则Pareto前沿面的多目标优化问题[5]。多目标进化算法[1](multi-objective evolutionary algorithms，MOEAs)已被证明是解决多目标优化问题的有效途径，但现有算法大都假设问题的Pareto面是连续均匀地分布在目标空间的，在具有非规则Pareto前沿面的问题上表现不佳。这是由于，首先，基于指标的MOEAs[6]中，针对规则Pareto前沿面设计的指标不一定适用非规则Pareto前沿面，非规则Pareto前沿面问题中无效区域的个体可能使指标更好；其次，基于支配关系的MOEAs[5]针对规则Pareto前沿面设计的多样性保持机制无法保持非规则Pareto前沿面的多样性；第三，分解类的MOEAs[7]中预先设置的均匀分布的权值向量不能很好匹配非规则Pareto前沿面的分布，导致有效区域计算资源不足；最后，基于协同进化的MOEAs[8]中，基于决策变量分解的协同进化算法难以解决具有复杂依赖关系的问题，而使用目标函数分解的协同进化算法保持群体多样性比较困难。
近年来，研究者们针对非规则Pareto前沿面多目标优化问题设计了新的进化算法。本文将这些进化算法根据其实现方法分为调整参考向量类、固定参考向量加辅助方法类、参考点类、聚类和分区类，并进行分类综述。
1 基础概念及典型问题
1.1 相关概念
目前较通用的多目标优化问题的数学描述如式(1)所示[1]：
Min F(x)=(f1(x),f2(x),…,fm(x))T，
(1)
x=(x1,x2,…,xn)T∈D。
式中：x为含n个决策变量的决策向量；D⊆
n称为决策空间；F(x)∈m是m个目标函数fi(x)组成的目标向量，i=1,2,…,m，目标向量构成目标空间。
定义1：支配解和非支配解。设xA、xB∈D是式(1)的两个可行解，称xA支配xB，记作xA
xB，当且仅当：
(2)
对于这两个可行解，称xA为非支配解，xB为被支配解。可行解集中的非支配解被称为Pareto最优解，其在目标空间的映射构成Pareto前沿面。
定义2：退化的Pareto前沿面。一般来说，一个m目标的多目标优化问题有一个m-1维的Pareto前沿面，当其Pareto前沿面的维数小于m-1时，称该前沿面为一个退化的Pareto前沿面[3]。有冗余的目标、有约束等原因会造成退化的Pareto前沿面。
定义3：均匀分布的参考点和参考向量。在基于分解的进化算法中经常要用到均匀分布的参考点，一般是指Das等[9]提出的单纯型格法，参考点的个数
由目标维数m和每个边的分段数H决定。参考点之间的欧氏距离相等。
定义4：理想点、最底点和最坏点。种群中每个目标的最小值构成的点称为最小值点，整个可行目标空间中的最小值点叫作理想点；种群中的非支配个体的每个目标的最大值构成的点称为最底点；整个可行目标空间中的最大值构成的点称最坏点[10]。
1.2 典型非规则Pareto前沿面测试问题
在DTLZ[11]系列可扩展的测试问题中，三目标及以上的DTLZ5，DTLZ6问题具有退化的Pareto前沿面，两目标及以上的DTLZ7问题具有不连续的Pareto前沿面。IDTLZ1、IDTLZ2[12]有倒置的Pareto前沿面。图1为三目标Pareto前沿面，其中三目标DTLZ1为规则的Pareto前沿面。
在WFG[13]系列可扩展的测试问题中，两目标及以上的WFG2问题具有分段的Pareto前沿面，三目标及以上的WFG3问题具有退化的前沿面。在MaF[14]系列可扩展的测试问题中，三目标及以上的MaF6、MaF8、MaF9、MaF13有退化的Pareto前沿面，MaF7、MaF11有不连续的Pareto前沿面，MaF1和MaF4有倒置的Pareto前沿面。在UF[15]系列测试问题中两目标的UF5、UF6和三目标的UF9都有不连续的Pareto前沿面。有些文献认为具有凹的、凸的或者有凹有凸的连续均匀Pareto前沿面问题也属于非规则Pareto前沿面问题，但本文所指的非规则Pareto前沿面问题并不包括连续均匀分布的这类问题。
另外，现实生活中也存在较多具有非规则Pareto前沿面的问题：例如，选矿问题具有不连续的Pareto前沿面[16]；汽车设计中的碰撞可靠性问题是一个三目标的具有不连续的Pareto前沿面的问题；汽车侧面碰撞问题的Pareto前沿面只分布在目标空间的部分区域[4]；多速齿轮箱设计问题和暴雨排水系统问题具有退化的Pareto前沿面[17]；碳纤维形成过程中的六级牵伸参数优化问题具有不连续的Pareto前沿面[5]。
2 非规则前沿面多目标进化算法
目前，进化算法处理具有非规则Pareto前沿面的多目标优化问题的思路主要可分为4种： ①根据种群分布调整参考向量分布；②固定参考向量结合辅助方法；③参考点；④聚类和分区，另外还有少数的其他方法。不同类型的、用于解决具有非规则Pareto前沿面的多目标优化问题的MOEAs算法如表1所示。
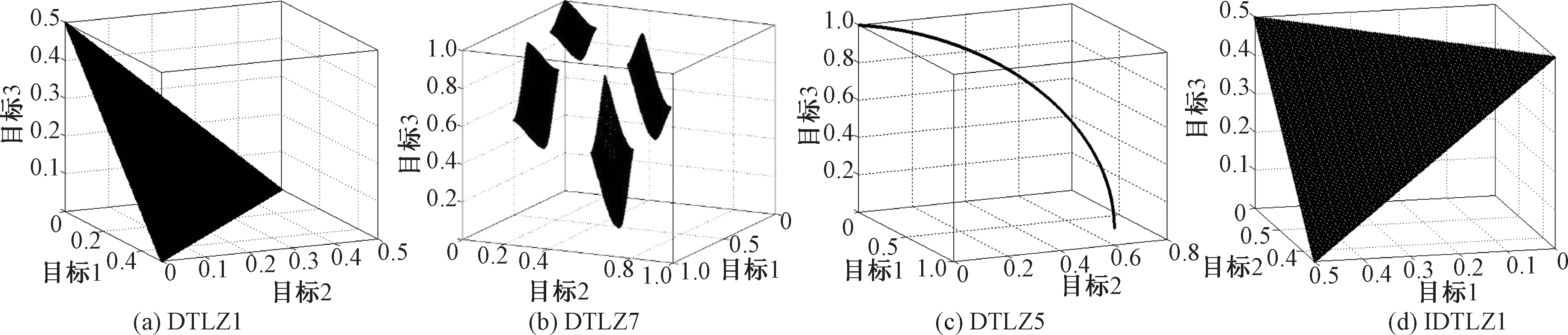
图1 三目标Pareto前沿面
Figure 1 The Pareto fronts of three-objective optimization problems
表1 用于解决具有非规则Pareto前沿面的多目标优化问题的MOEAs分类
Table 1 MOEAs for solving multi-objective optimization problems with irregular Pareto fronts
方法类型实现途径代表性算法调整参考向量固定参考向量+辅助方法参考点聚类和分区生成新参考向量,替换原有参考向量A-IM-MOEA[18],RVEA*[19], A-NSGA-III[4],A2-NSGA-III[12],MOEA/D-AWA[7],MOEA/D-ABD[2],MOEA-HD[20],MaOEA/D-2ADV[21],MOEA/D-TPN[22],SRV-TSL[23],PICEA-w[24],DMOEA/D[25]个体自身转化为参考向量,替换原有参考向量iRVEA[26],MOEA/D-AM2M[27],DDR[28]机器学习预测Pareto面分布,据此调整参考向量DEA-GNG[29],CLIA[30]非支配排序或外部库MOEA/D-AED[31],BCE-MOEA/D[32]一个参考向量选择多个个体MOEA/D-SAS[33],ASEA[34]在种群中产生参考点集F-DEA[35],RPEA[36],AR-MOEA[37], CA-MOEA[5]基于全局参考点MaOEA-CS[38],MOEA/D-MR[39],PAEA[40],PaRP/EA[41]聚类MaOEA/C[42],EMyO/C[43]分区MOEA-PPF[44],RdEA[45],CDG-MOEA[46]
2.1 根据种群分布调整参考向量的方法
预先设置的固定参考向量体系无法很好地匹配不规则前沿面的形状，造成计算资源的浪费。常用的解决方法就是调整参考向量的分布，使之更加适配不规则前沿面的分布。
在这类算法中，一些算法根据参考向量关联的个体数量来评价目标空间的个体拥挤度情况，并据此调整原有参考向量。比如，A-NSGA-III[4]和A2-NSGA-III[12]的每一代在拥挤的区域增加参考向量，删除没有个体关联的参考向量。这两个算法的区别在于增加参考向量的方法:A-NSGA-III是以原始的参考点为中心做单纯型格增加新的参考点以构成参考向量；而A2-NSGA-III是以原始的参考点为一个角点做单纯型格增加新的参考点以构成参考向量。然而该算法增加参考向量的效率低，且删除程序的启动条件在某些问题中可能很难满足，越来越多的参考向量会浪费很多不必要的计算资源。
MOEA/D-AWA[7]在一定代数后，根据外部库评估的拥挤度对参考向量进行调整，删除拥挤区域的参考向量，增加稀疏区域的参考向量。这个算法的问题在于，拥挤度评价在目标高维情况下计算量大，且算法对某些参数敏感。A-IM-MOEA[18]早期用一个随机向量代替一个关联个体数最多的向量，后期用一个随机向量代替一个关联个体数最少的向量。RVEA*[19]中，如果一个参考向量没有任何个体与之关联，该参考向量就会被一个随机产生的参考向量替代。然而随机产生的参考向量无法保证种群的均匀分布。iRVEA[26]在RVEA的框架下设置了两组方向向量，一组是固定的，一组不固定，不固定的参考向量中每代用与其他个体夹角最大的个体去构造新的方向向量，代替一个无效的方向向量。另外RVEA的APD选择可能会漏掉很多好解，所以又采用了第二准则去选择。MaOEA/D-2ADV[21]一开始用目标轴向量引导种群收敛；当检测到种群不再收敛时，以有个体关联的向量为有效向量，按有效向量之间的夹角从大到小排序，两两之间产生中点向量为新的参考向量，直到达到种群规模。这个方法在具有凹型前沿面的问题上表现一般，且只使用目标轴向量作为方向向量搜索区域太窄，很难引导收敛。MOEA/D-TPN[22]把整个进化进程分为两个阶段，把种群分为中间种群和边缘种群，根据第一阶段检测到的两个种群的拥挤度对比情况决定是否进入第二阶段——更新参考向量；同时，改进的差分进化[47]算子用于产生不重复的新个体。一些算法随机产生新的参考向量，再与原有参考向量共同进行对比调整。如PICEA-w[24]的每一代都随机产生新的参考向量，然后根据两个准则筛选参考向量：①该参考向量使候选解的适应度更高；②如果有两个适应度一样的参考向量，则选择与候选解向量角度大的，以此来保证收敛性和多样性。然而，每一代都产生新参考向量集并重新计算适应度需要大量的计算资源，比较低效。一些算法先估计Pareto前沿面的分布情况，再生成匹配的参考向量。DMOEA/D[25]每隔一定代数，用当前种群估计PF面，再在估计的PF面上以个体在每个子目标的投影等距插值取点，再将这些点分组计算平均值以生成参考向量。MOEA/D-ABD[2]是针对不连续非规则面的一种算法。该算法每隔一定代数通过计算权重向量与其关联的个体之间的偏差来检测Pareto前沿的不连续部分，并根据每个连续部分的长度调整权重向量的数量。该算法只适用于两目标问题，而且算法中的一些参数的阈值比较难确定。MOEA-HD[20]将子问题分为不同的层次，并根据高层次搜索结果自适应调整低层次子问题的搜索方向，缺点是只能处理2个或3个目标的优化问题。一些算法用个体本身产生参考向量。MOEA/D-AM2M[27]是一种根据当前个体自适应产生参考向量的方法，该算法在处理退化的Pareto前沿面问题上表现较好。DDR[28]用个体和原点构造向量，以已选个体为聚类中心进行聚类，选择当前个体为聚类中心的类中适应度最好的个体。它每次只产生一个参考向量，并相应选择一个个体。SRV-TSL[23]通过特定的中心向量来缩放参考向量，用以处理凹或凸面的问题，TSL用多样性较好的候选解及其两两的中点设置为新的参考向量用以处理退化的或不连续面的问题。这两个方法可以协同工作，并嵌入基于参考向量的高维多目标进化优化算法。然而SRV的缩放方法不适合反向的Pareto前沿面。
近年来，机器学习被用于更准确地调整参考向量。CLIA[30]将每一代的参考向量标记为有效的和无效的，再用增量支持向量机进行学习，用学习的结果判断哪些是有效的参考向量，并删掉无效的参考向量，用A-NSGA-III的方法增加参考向量,接着用基于向量的PDM指标筛选适应度更好的个体。这里的PDM指标类似于MOEA/D的PBI和RVEA的APD指标，由收敛性项(个体每个目标的平均值)和多样性项(个体到关联的参考向量的距离)构成。这个算法中嵌套学习模型的做法本身比较占用资源，并且没有考虑到种群分布的变化性，早期个体的分布往往不能准确反映Pareto前沿面的真实情况。DEA-GNG[29]用增长型神经气网络(GNG)学习权重向量的拓扑结构，再用学习到的信息调整参考向量分布。PF的拓扑结构是由一个改进的GNG模型学习的，筛选已知的解作为信号输入。参考向量通过结合GNG网络中的节点和一组均匀分布的参考向量来进行调整。每个参考向量的标量函数都是根据相应节点和从其发出的边之间的角度来调整的。这两种适应机制增强了进化算法的搜索能力。
总体来说，根据种群分布调整参考向量分布的方法是有效的，不论是根据当前种群分布情况还是综合考虑若干代种群分布变化去调整参考向量分布，都能一定程度上弥补固定参考向量的不足。但是，由于远离Pareto前沿面时，种群中存在大量被支配个体，这些个体的分布并不能反映真实Pareto前沿面的分布情况，对于参考向量的调整有误导作用。如何辨别真正有效的收敛方向是这类算法的一个关键。
2.2 固定参考向量合并其他辅助方法
虽然根据种群调整参考向量的方法达到了一定效果，但也有一些算法仍然是基于固定的参考向量体系，另外增加了其他适应非规则Pareto前沿面的辅助加强收敛性或多样性的方法。
比如，BCE-MOEA/D[32]设置了两个种群，一个基于非支配排序法，另一个沿用MOEA/D，这两个种群同时产生新个体，同时进化，用非支配排序方法筛选两个种群的最终个体。MOEA/D-SAS[33]的每个参考向量找距离自己夹角最近的若干个个体按适应度排序，再在最后一个选择层，依次选择与其他个体的夹角最大的个体。ASEA[34]首先把每个个体关联给与自己夹角最小的向量，有效向量关联的当代的未被选择的个体中，先用收敛性排序，再以其与子问题及相邻子问题中已选个体的最小夹角排序，夹角大的优先选择，这个过程循环直到达到种群规模。MOEA/D-AED[31]在算法中建立了一个外部库，用于储存分解的方法筛选出的适应度高(切比雪夫函数值小)的非支配个体，用一个基于自适应ε非支配排序的方法来控制外部库的规模，这样来弥补固定参考向量的方法在处理非规则Pareto前沿面问题时每一代得到的个体数太少的缺陷。
这类方法大都用一些辅助的手段来弥补固定参考向量方法在处理非规则Pareto前沿面时选出的个体数目不足的缺陷。然而当有个体关联的参考向量数量非常少时，辅助的收敛或多样性保持手段会对算法性能起决定性作用，而基于分解的算子则失去了应有的功能。
2.3 参考点的方法
参考点的思想也被用于处理非规则Pareto前沿面问题，这其中有一个参考点对应选择种群中一个个体的方法，也有用最小值点或最底点作为全局参考点的方法。
一个参考点对应选择种群中一个个体的方法有：RPEA[36]每隔一定代数，用当前非支配个体中拥挤距离较大(不拥挤)的个体通过在每个目标轴上的平移产生参考点，再选择种群中距离这些参考点加权欧氏距离最小的个体。AR-MOEA[37]算法提出一个改进的IGD指标——IGD-NS，在初始的均匀分布的参考点的基础上，根据种群的分布，找距离参考点最近的个体和非支配个体建立外部库，选有个体关联的参考点和与这些参考点向量夹角最大的外部库个体作为新的参考点，删除无效的参考点。然后，进行非支配排序，在最后一个待选择的非支配面，根据新的参考点集，删除使整个种群的IGD-NS指标更小的个体，直到达到所需种群规模。F-DEA[35]首先用传统的Das and Dennis方法产生均匀分布的参考点，然后选择有个体关联的参考点中拥挤距离较大的参考点作为聚类中心，对合并的父子种群进行聚类，选择每个类中模糊适应度值最好的个体。CA-MOEA[5]先对当前种群进行非支配排序，再在临界非支配面用基于分层聚类方法将个体聚为所需数目的类，然后计算每个类的聚类中心作为参考点，依次选择距离参考点最近的、拥挤区域的、稀疏区域的个体。
用最小值点、最底点或最大值点作为全局参考点的算法有：MOEA/D-MR[39]将种群分为两个子种群，其中一个种群以当前的最小值点作为参考点，另一个种群以当前非支配种群的最大值点作为参考点。用这样双参考点的方法避免前沿面的凹和凸带来的参考向量分布不均匀的问题。PAEA[40]中，一个父代会产生两个子代，在这3个个体中分别选择以最小值点为参考点和以最大值点为参考点的情况下适应度最高的两个个体。再在剩下的种群中依次选择夹角最小的两个个体，留下其中距离原点更近的那一个。然而，算法默认子代的收敛性比父代好，而这种情况并不总是成立。PaRP/EA[41]先用非支配排序，如果第一非支配面个体数超过种群数目，则用归一化后距离向量最近的几个非支配个体到超平面的平均距离和原点到超平面的平均距离做对比。如果更近，则判断为凸面，用最底点作为参考点，距离参考点近的个体适应度高；如果更远，则判断为凹面，用最小值点作为参考点。距离参考点更远的，适应度更高，如果距离一样，则判断为线性，个体每个目标值的和越小适应度越高。另外，算法用个体向量之间的夹角度量多样性，与其他个体夹角越大，适应度越高。这个算法只检测了Pareto前沿面的凹凸性，对其他非规则形状没有特别处理。MaOEA-CS[38]先用轴向量寻找与之夹角最小的边界个体，并用边界个体的每个目标的最大值构造最底点，将目标值小于最底点的和大于最底点的分为两个子集。如果目标值小于最底点的个体数大于所需种群规模，则依次选择与其他个体最小夹角最大的个体；若目标值小于最底点的个体数不足，则从目标值大于最底点的个体中依次选与最小值点距离最近的个体。
基于参考点的方法中，参考点的设置对于算法的性能有决定性的影响。因此，如何设置更有效的参考点，从而引导种群高效地收敛并保持多样性，是这类算法的关键。
2.4 聚类和分区的方法
由于非规则Pareto前沿面的分布不可预知，将当前种群通过聚类或者分区的方法分为若干个子问题，找寻子问题的最优解从而构成最终的解集也是一个比较好的途径。
EMyO/C[43]把聚类思想应用于高维多目标优化问题，将欧氏距离最近的个体聚为一个类，每个类中再选择距离预先设定的全局参考点最近的个体。然而，基于种群计算出的理想点不能保证正确的收敛方向，而且简单地根据欧氏距离聚类也不能对个体进行有效的划分。MaOEA/C[42]用K-means聚类结合分层聚类，选择方向轴为K-means聚类的聚类中心，将整个种群均分为m(m为目标数目)份。在m个子区域中，分别先用非支配排序，把前几个面个体挑出来，再用基于角度的分层聚类，把整个目标空间分为所需种群规模数量的子问题，每个子问题依次选离轴最近的个体和收敛性最好的个体。RdEA[45]根据种群分布预测Pareto前沿面的几何形状，并提出一种区域划分的方法将目标空间分区，在每个分区中选择离参考点更近或离区域中心点更近的个体。然而判断个体位于哪个区域比较困难，且算法中存在难以确定的参数。CDG-MOEA[46]对当前种群建立网络，每个个体按网格中的位置编序，优先选择序号小的个体。MOEA-PPF[44]首先根据个体之间的拥挤距离判断优化问题的Pareto前沿面上的间断点，并在考虑间断点的基础上将目标空间划分为若干子空间，在每一子空间中采用MOEA/D得到一个外部保存集，再综合所有外部保存集组成问题的最终Pareto解集。该算法比较适合有分段的Pareto前沿面的问题。
聚类和自适应分区的方法在处理非规则Pareto前沿面问题上有较好的表现。聚类的优势在于它是基于种群的分区，每一个子区域都有个体，不浪费计算资源，劣势在于当分类不均匀时会导致种群的分布不均匀，而且聚类的方法计算复杂度较高。再者，聚类也无法辨别真正有Pareto前沿面的区域。而网格分区方法虽然分区更加均匀，却容易造成计算资源的浪费，且算法性能对网格尺寸敏感。
3 结论和展望
近几年来，随着多目标进化优化算法的发展，以往基于规则的Pareto前沿面设计的进化算法无法很好解决具有非规则Pareto前沿面的多目标优化问题，于是具有非规则Pareto前沿面的多目标优化问题逐渐受到关注，并涌现出许多针对性的算法。
本文首先简要介绍了MOEAs的研究概况，将现有MOEAs分为指标类、支配关系类、分解类和协同进化类4个大类，分别简要介绍这4类算法以及在处理具有非规则Pareto前沿面多目标优化问题上的缺陷；接着，给出了非规则Pareto前沿面多目标进化优化领域的一些概念，并整理了典型的非规则Pareto前沿面多目标优化测试问题。在文章的主要部分，从调整参考向量、固定参考向量结合其他辅助策略、参考点、聚类和分区4个大方向对相应类型的算法进行简述，分析了每个类型算法的特点和设计关键。
尽管运用MOEAs处理具有非规则Pareto前沿面问题已经取得了一定成效，但现有算法一般只在部分非规则Pareto前沿面问题上表现较好，适应所有种类的非规则Pareto前沿面问题的算法还有待开发，更加智能的、可以辨别和处理多类型非规则Pareto前沿面的MOEAs是未来的研究重点。这里给出一些可能的发展方向：首先，目前大都用单一的方法来处理非规则Pareto前沿面多目标优化问题，用多种方法混合可能可以取长补短，提高算法性能；第二，机器学习的方法也可以与进化算法进行融合，比如迁移学习，多任务的方法等；第三，决策变量或目标数量的高维[48]给问题带来更大的难度，这方面的研究还有很大空间；第四，动态的具有非规则Pareto前沿面的多目标优化问题的研究还是空白，有待开发；第五，数据驱动的、具有非规则Pareto前沿面的多目标优化研究以及算法在实际具有非规则Pareto前沿面的多目标优化问题上的应用研究也有待加强。
[1] 雷德明, 严新平. 多目标智能优化方法及其应用[M]. 北京: 科学出版社, 2009.
[2] ZHANG C J, TAN K C, LEE L H, et al. Adjust weight vectors in MOEA/D for bi-objective optimi-zation problems with discontinuous Pareto fronts[J]. Soft computing-a fusion of foundations, methodologies and applications, 2018, 22(12):3997-4012.
[3] ISHIBUCHI H, MASUDA H, NOJIMA Y. Pareto fronts of many-objective degenerate test problems[J]. IEEE transactions on evolutionary computation, 2016, 20(5):807-813.
[4] JAIN H, DEB K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: handling constraints and extending to an adaptive approach[J]. IEEE transactions on evolutionary computation, 2014, 18(4):602-622.
[5] HUA Y, JIN Y, HAO K. A clustering-based adaptive evolutionary algorithm for multiobjective optimization with irregular Pareto fronts[J]. IEEE transactions on cybernetics, 2019, 49(7): 2758-2770.
[6] BADER J, ZITZLER E. HypE: an algorithm for fast hypervolume-based many-objective optimization[J]. Evolutionary computation, 2011, 19(1):45-76.
[7] QI Y T, MA X L, LIU F, et al. MOEA/D with adaptive weight adjustment[J]. Evolutionary computation, 2014, 22(2):231-264.
[8] ANTONIO L M, COELLO C A C. Coevolutionary multiobjective evolutionary algorithms: survey of the state-of-the-art[J]. IEEE transactions on evolutionary computation, 2018, 22 (6):851-865.
[9] DAS I, DENNIS J E. Normal-boundary intersection: a new method for generating the Pareto surface in nonlinear multicriteria optimization problems[J]. SIAM journal on optimization, 1998, 8(3):631-657.
[10] WANG H D, HE S, YAO X. Nadir point estimation for many-objective optimization problems based on emphasized critical regions[J]. Soft computing, 2017, 21(9):2283-2295.
[11] DEB K, THIELE L, LAUMANNS M, et al. Scalable test problems for evolutionary multiobjective optimization[J]. Evolutionary multiobjective optimization, 2005:105-145.
[12] JAIN H, DEB K. An improved adaptive approach for elitist nondominated sorting genetic algorithm for many-objective optimization[J] Evolutionary multi-criterion optimization, 2013, 7811:307-321.
[13] HUBAND S, BARONE L, WHILE L, et al. A scalable multi-objective test problem toolkit[J]. Lecture notes in computer science, 2005, 3410:280-295.
[14] CHENG R, LI M Q, TIAN Y, et al. A benchmark test suite for evolutionary many-objective optimization[J]. Complex & intelligent systems, 2017, 3(1):67-81.
[15] ZHANG Q F, ZHOU A, ZHAO S Z, et al. Multiobjective optimization test instances for the CEC 2009 special session and competition[J]. Mechanical engineering,2008,8:16283.
[16] YU G, CHAI T Y, LUO X C. Multiobjective production planning optimization using hybrid evolutionary algorithms for mineral processing[J]. IEEE transactions on evolutionary computation, 2011, 15(4):487-514.
[17] SAXENA D K, DURO J A, TIWARI A, et al. Objective reduction in many-objective optimization: linear and nonlinear algorithms[J]. IEEE transactions on evolutionary computation, 2013, 17(1):77-99.
[18] CHENG R, JIN Y C, NARUKAWA K. Adaptive reference vector generation for inverse model based evolutionary multiobjective optimization with degenerate and disconnected Pareto fronts[J]. Evolutionary multi-criterion optimization, 2015, 9018:127-140.
[19] CHENG R, JIN Y C, OLHOFER M, et al. A reference vector guided evolutionary algorithm for many-objective optimization[J]. IEEE transactions on evolutionary computation, 2016, 20(5)：773-791.
[20] XU H, ZENG W H, ZHANG D, et al. MOEA/HD: a multiobjective evolutionary algorithm based on hierarchical decomposition[J]. IEEE transactions on cybernetics, 2019, 49(2): 517-526.
[21] CAI X Y, MEI Z, FAN Z. A decomposition-based many-objective evolutionary algorithm with two types of adjustments for direction vectors[J]. IEEE transactions on cybernetics, 2018, 48(8)：2335-2348.
[22] JIANG S Y, YANG S X. An improved multiobjective optimization evolutionary algorithm based on decomposition for complex Pareto fronts[J]. IEEE transactions on cybernetics, 2016, 46(2):421-437.
[23] LIANG Z P, HOU W J, HUANG X, et al. Two new reference vector adaptation strategies for many-objective evolutionary algorithms[J]. Information sciences, 2019, 483:332-349.
[24] WANG R, PURSHOUSE R C, FLEMING P J. Preference-inspired co-evolutionary algorithms using weight vectors[J]. European journal of operational research, 2015, 243(2):423-441.
[25] GU F, LIU H L, TAN K C. A multiobjective evolutionary algorithm using dynamic weight design method[J]. International journal of innovative computing, information and control, 2012, 8(5B): 3677-3688.
[26] LIU Q Q, JIN Y C, HEIDERICH M, et al. Adaptation of reference vectors for evolutionary for evolutionary many-objective optimization of problems with irregular Pareto fronts[C]// 2019 IEEE Congress on Evolutionary Computation (CEC). New York: IEEE, 2019:1726-1733.
[27] LIU H L, CHEN L, ZHANG Q F, et al. Adaptively allocating search effort in challenging many-objective optimization problems[J]. IEEE transactions on evolutionary computation, 2018, 22(3)：433-448.
[28] HE X Y, ZHOU Y R, CHEN Z F, et al. Evolutionary many-objective optimization based on dynamical decomposition[J]. IEEE transactions on evolutionary computation, 2019, 23(3): 361-375.
[29] LIU Y P, ISHIUCHI H, MASUYAMA N, et al. Adapting reference vectors and scalarizing functions by growing neural gas to handle irregular Pareto fronts[J]. IEEE transactions on evolutionary computation, 2020, 24(3):439-453.
[30] GE H, ZHAO M D, SUN L, et al. A many-objective evolutionary algorithm with two interacting processes: cascade clustering and reference point incremental learning[J]. IEEE transactions on evolutionary computation, 2019, 23(4)：572-586.
[31] LI H, DENG J D, ZHANG Q F, et al. Adaptive epsilon dominance in decomposition-based multiobjective evolutionary algorithm[J]. Swarm and evolutionary computation, 2019, 45：52-67.
[32] LI M Q, YANG S X, LIU X H. Pareto or non-Pareto: bi-criterion evolution in multi-objective optimization[J]. IEEE transactions on evolutionary computation, 2016, 20(5):645-665.
[33] CAI X Y, YANG Z X, FAN Z, et al. Decomposition-based-sorting and angle-based-selection for evolutionary multiobjective and many-objective optimization[J]. IEEE transactions on cybernetics, 2017, 47(9):2824-2837.
[34] LIU C,ZHAO Q,YAN B, et al. Adaptive sorting-based evolutionary algorithm for many-objective optimization[J]. IEEE transactions on evolutionary computation, 2019, 23(2):247-257.
[35] DAS S S, ISLAM M M, ARAFAT N A. Evolutionary algorithm using adaptive fuzzy dominance and reference point for many-objective optimization[J]. Swarm and evolutionary computation, 2019, 44: 1092-1107.
[36] LIU Y P, GONG D W, SUN X Y, et al. Many-objective evolutionary optimization based on reference points[J]. Applied soft computing, 2017, 50：344-355.
[37] TIAN Y, CHENG R, ZHANG X Y, et al. An indicator-based multiobjective evolutionary algorithm with reference point adaptation for better versatility[J]. IEEE transactions on evolutionary computation, 2018, 22(4):609-622.
[38] CAI X Y, SUN H R, ZHU C Y, et al. Locating the boundaries of Pareto fronts: a many-objective evolutionary algorithm based on corner solution search[EB/OL]. (2018-06-08)[2020-09-15]. https://arxiv.org/abs/1806.02967.
[39] WANG Z K, ZHANG Q F, LI H, et al. On the use of two reference points in decomposition based multiobjective evolutionary algorithms[J]. Swarm and evolutionary computation, 2017, 34: 89-102.
[40] ZHOU Y R, XIANG Y, CHEN Z F, et al. A scalar projection and angle-based evolutionary algorithm for many-objective optimization problems[J]. IEEE transactions on cybernetics, 2019, 49(6): 2073-2084.
[41] XIANG Y, ZHOU Y R, YANG X W, et al. A many-objective evolutionary algorithm with Pareto-adaptive reference points[J]. IEEE transactions on evolutionary computation, 2020, 24(1):99-113.
[42] LIN Q Z, LIU S B, WONG K C, et al. A clustering-based evolutionary algorithm for many-objective optimization problems[J]. IEEE transactions on evolutionary computation, 2019, 23(3): 391-405.
[43] DENYSIUK R, COSTA L, ESP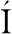
RITO SANTO I. Clustering-based selection for evolutionary many-objective optimization[C]// International Conference on Parallel Problem Solving from Nature.Berlin: Springer, 2014:538-547.
[44] 封文清,巩敦卫. 基于在线感知Pareto前沿划分目标空间的多目标进化优化[J].自动化学报, 2020,46(8):1628-1643.
[45] PAN L Q, HE C, TIAN Y, et al. A region division based diversity maintaining approach for many-objective optimization[J]. Integrated computer-aided engineering, 2017, 24(3): 279-296.
[46] CAI X Y, MEI Z W, FAN Z, et al. A constrained decomposition approach with grids for evolutionary multiobjective optimization[J]. IEEE transactions on evolutionary computation, 2018, 22(4): 564-577.
[47] 汪慎文,杨锋,徐亮,等. 离散差分进化算法求解共享单车调度问题[J].郑州大学学报(工学版),2019,40(4):48-53.
[48] 梁静,刘睿,瞿博阳,等.进化算法在大规模优化问题中的应用综述[J].郑州大学学报(工学版),2018,39(3):15-21.