0 引言
由于同步调相机的大容量、暂态性能优越等特点,已应用于特高压直流站的快速电压支撑[1-4]。采用主变高压侧电压控制的电力系统电压调节器(power system voltage regulator,PSVR),可有效改善系统侧的动态电压特性。陈新琪等[5]分析PSVR的工作原理,依据现场试验结果研究发电机PSVR在提高机组对系统动态无功支撑中的作用;周晓渊等[6]在单机无穷大系统上,从特征值和时域仿真两方面进行分析;陈新琪等[7]利用PSCAD,仿真分析PSVR在六机实际系统中的影响;Nocuchi等[8-9]提出了不同形式的发电机高压侧电压控制器的结构和控制策略;石祥建等[10]分析了大型同步调相机的PSVR控制策略。
对于PSVR参数整定,陈新琪等[11]面向常规发电机,提出类似于电力系统稳定器(power system stabilizer,PSS)的参数整定方法,对PSVR增益系数的取值考虑电压稳定性,对时间常数的设置考虑对系统功角振荡阻尼的增强,并与PSS的阻尼特性协调。
由于调相机仅输出无功功率,不同于发电机,励磁相关控制环节对机组功角特性的影响要小的多。需通过分析调相机的动态无功电压特性、动态功角特性,进行PSVR的参数整定或调整。对PSVR相关的电压动态性能分析,现有文献大多采用时域仿真方法[2-11],尚未见到直接利用大系统电压稳定的特征值分析。
笔者以河南电网新增大容量同步调相机为例,分析调相机的动态特性,提出针对调相机PSVR的参数调整方法。调整PSVR移相环节时间常数,降低PSVR对功角的影响。计算不同系统运行方式、不同调相机无功出力下的电压振荡模式,确定PSVR增益系数调整范围,并进行功角振荡模式的核算。为调相机PSVR参数整定提供参考。
1 大容量调相机与PSVR
鉴于800 kV特高压直流天中线、青豫线及其他规划线路陆续接入河南电网,于2019年在河南邵陵站投运两台隐极式同步调相机以提高对系统动态无功电压的支撑能力。
调相机采用单元接线方式,通过升压变压器接入500 kV母线。额定容量300 Mvar,额定电压20 kV。励磁调节器为电力系统分析综合程序(PSASP)中的12型。
励磁电压控制如图1所示,采用从主变高压侧取控制信号的PSVR(PSASP中8型PSS)。PSVR的控制框图如图2所示,主要参数包括:增益系数Kqv、变送器时间常数Tqv、3个移相环节的时间常数、限幅环节参数。
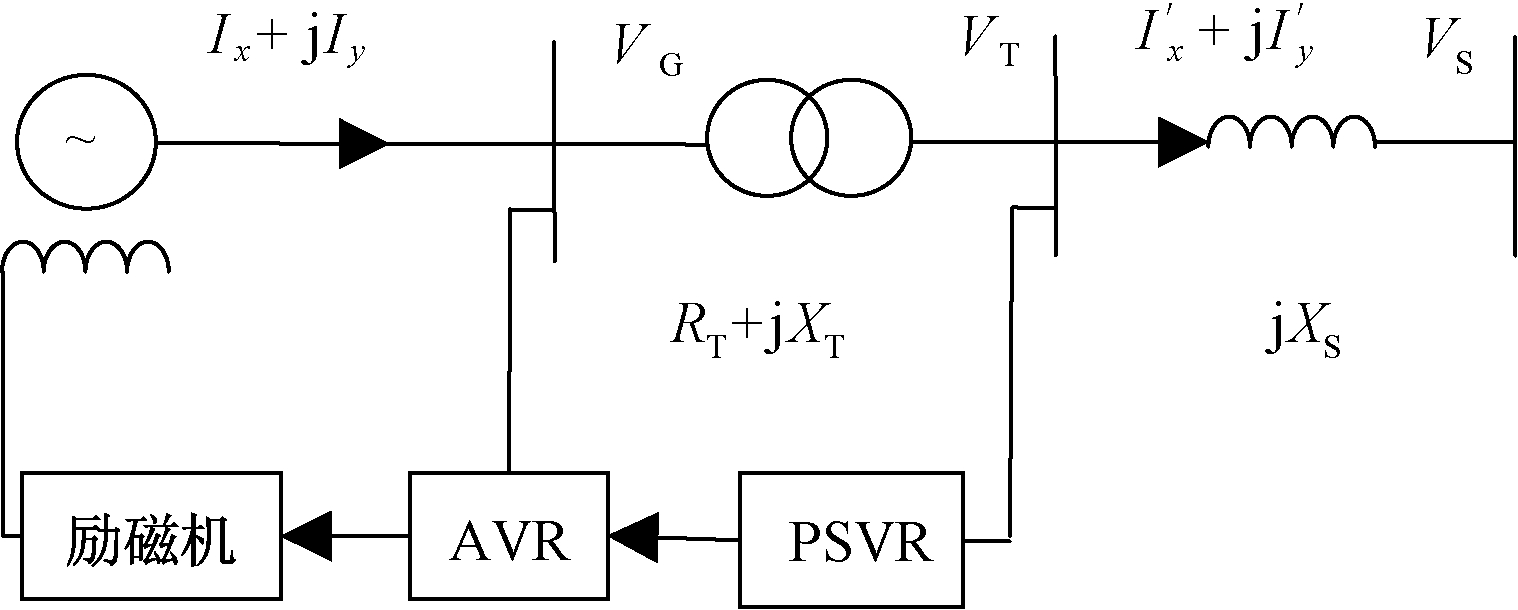
图1 调相机励磁控制
Figure 1 Excitation control of the synchronous condenser
图2 PSVR控制框图
Figure 2 Control block diagram of PSVR
由于调相机的运行方式不同于发电机,需要根据调相机的运行状况,分析PSVR对系统电压稳定和功角稳定的影响,合理调整PSVR参数。
2 调相机动态特性分析
先从单机无穷大系统模型[12]计算调相机及控制系统的幅频相频特性,分析无功出力、PSVR参数对调相机动态特性的影响。
对图1所示的单机无穷大系统,发电机采用六阶模型,相关微分方程和代数方程可表达为式(1)~(13)。
(1)
(2)
(3)
(4)
p2δ=[Pm-Pe]Ω0/M;
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
式中:p为微分算子;其他变量含义符合常规习惯,并参见图1。
将式(1)~(13)线性化,加上励磁系统、PSVR的相关方程,构成单机无穷大系统的微分、代数方程组。
经算式处理,可分别得到计算调相机的功角特性、电压特性的解析表达式:
ΔM=FMδ(p,VGx,VGy,Ix,Iy)Δδ;
(14)
(15)
式中:ΔM、Δδ分别为转矩和功角;ΔVT、ΔVS分别为图1中变压器高压母线、系统母线电压偏差量。FMδ、FTS均为微分算子的函数,并受调相机运行状态影响;由于计算中取p=jω,尽管式(15)右侧的ΔVS为实数,但左侧为复数。篇幅所限,略去具体表达式。
2.1 调相机无功出力对P-δ特性的影响
功率基准100 MV·A,不计PSVR,分别取调相机无功出力0、0.5、1、1.5、2、2.5、3 p.u.,相应的有功出力为P=-0.06Q,按式(14)计算功角扰动对电磁转矩的影响,幅频特性如图3所示,7条曲线几乎重叠。
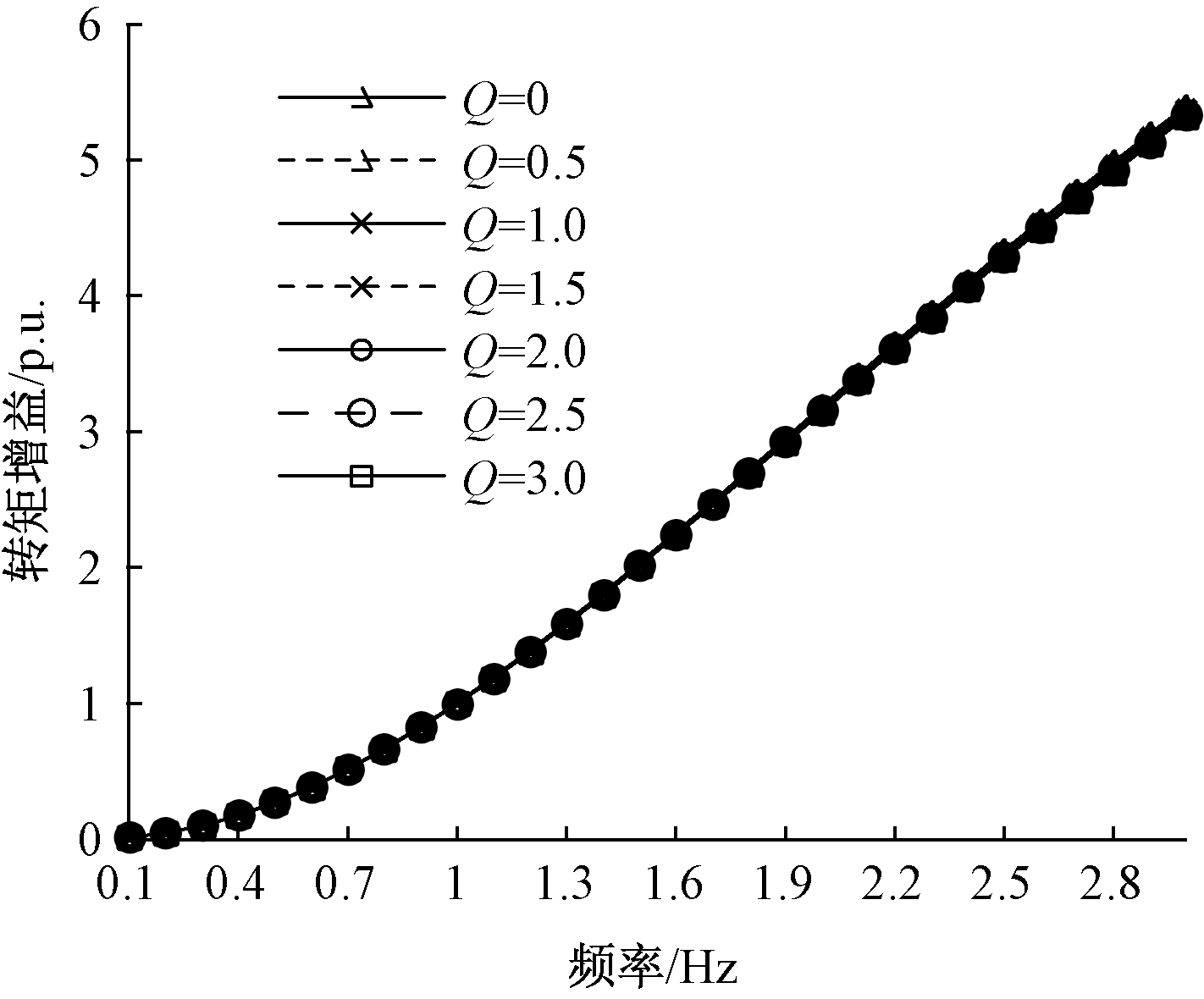
图3 不同调相机无功出力下的转矩幅频特性
Figure 3 Torque amplitude frequency characteristics under different reactive power outputs of condensers
由图3可知,单机无穷大系统下,调相机无功出力变化对转矩的影响可略去。但后文的全系统特征值计算表明,调相机无功出力变化会影响系统的潮流分布,对相关特征值的影响虽小,但不可忽略。
2.2 计及PSVR的调相机VT-VS特性
PSVR的主要功能是改善电压VT的动态性能,因此计算VS变化对VT的影响。
PSVR参数取实际值:![]() 其余参数为0。
其余参数为0。
调相机无功出力为1.0 p.u.。VT-VS相频特性曲线示于图4,最大相移51.8°。
幅频特性体现VS变化对VT的影响,属于正常的电压无功关系,未给出。图4的相频特性体现系统电压VS变化对![]() 的幅角的影响,电压幅角的变化将影响到调相机有功功率的波动,当然影响到功角稳定特性。
的幅角的影响,电压幅角的变化将影响到调相机有功功率的波动,当然影响到功角稳定特性。
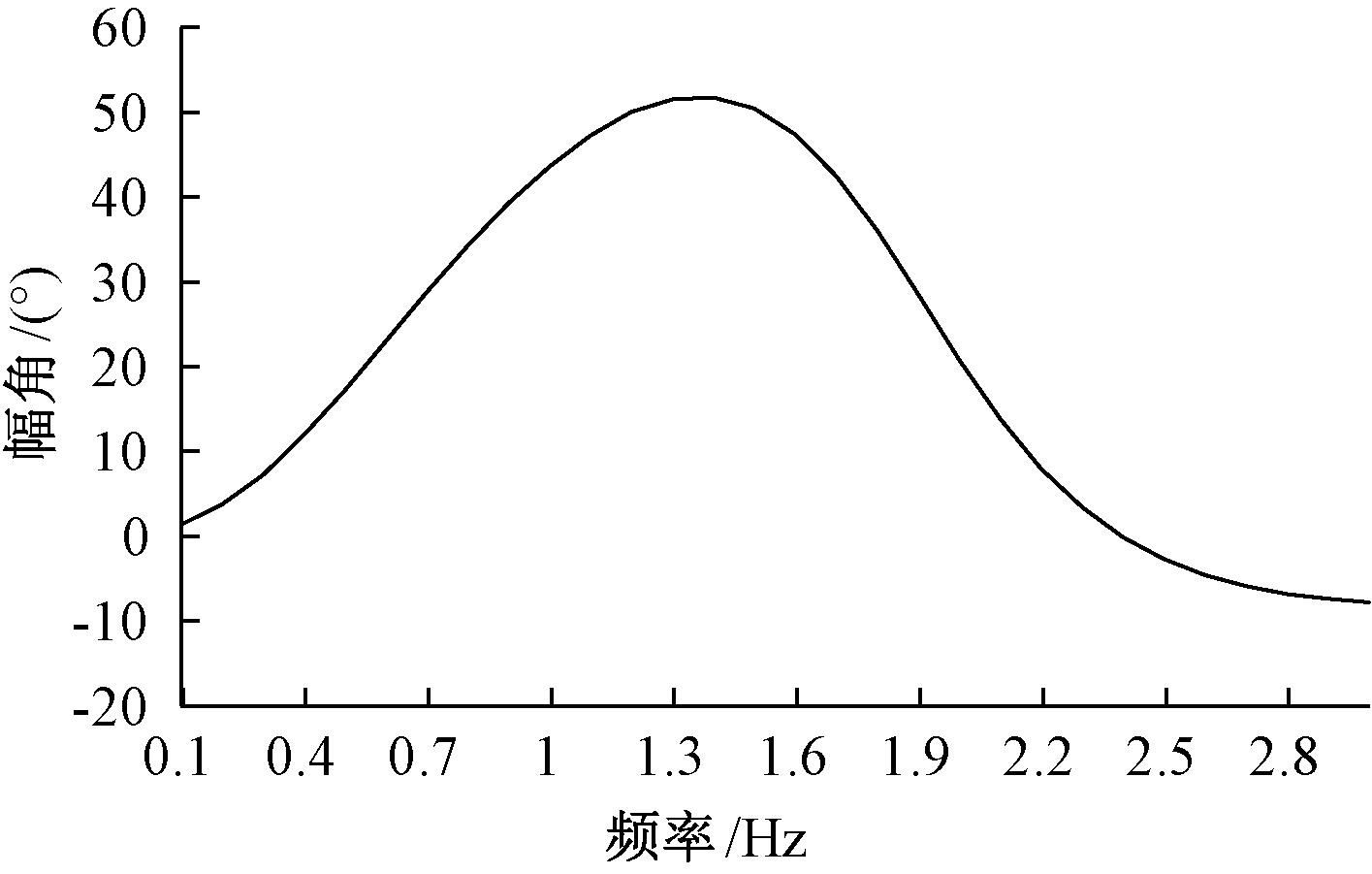
图4 含PSVR的调相机VT-VS相频特性
Figure 4 VT-VS phase frequency characteristic of the condenser employing PSVR
相频特性值越小,对有功功率、功角稳定特性的影响也越小。为描述方便,计算相频特性曲线的均方根:
(16)
本文中,N=30。图4中相频特性的均方根为36.182 6。
本文中调相机PSVR时间常数的调整目标就是最小化相频特性曲线的均方根:
min θRMS。
(17)
3 PSVR参数调整与特征值计算
对调相机而言,由于有功出力为0,其动态电压无功特性、功角特性不同于常规发电机。2.1节的分析说明,调相机无功出力变化对转子转矩的影响几乎可略去;2.2节的分析说明,由于控制环节的作用,电压幅值的变化会一定程度影响到电压幅角和调相机的功角特性。
在调相机上采用PSVR的目的是改善电压VT的动态性能。PSVR参数调整应针对调相机电压稳定特性,但同时兼顾功角稳定性。
因此,笔者对PSVR参数的调整,考虑4个方面内容。
(1)PSVR时间常数调整:通过调相机的相频特性,按式(16)、(17)调整PSVR移相环节的时间常数,减小对调相机功角特性的影响。
(2)PSVR增益系数调整:通过全网小干扰稳定特征值计算,保证调相机相关电压振荡模式的稳定性和阻尼比,确定PSVR增益系数的取值上限。
(3)功角振荡模式校核:同样是通过全网小干扰稳定特征值计算,保证调相机相关功角振荡模式的稳定性和阻尼比,校核或进一步调整PSVR增益系数的取值上限。
(4)考虑多种运行方式:分别在河南电网峰、平、谷3种典型运行方式以及调相机不同无功出力下,计算系统稳定性,调整PSVR增益系数上限值。
有关河南电网的小干扰稳定特征值计算,利用PSASP中导出的数据、本课题组多年来编写的计算程序[13-14]进行。计算环境为Intel Visual Fortran Composer XE 2011,8线程并行计算。
对于机电振荡模式,计算状态变量中各发电机功角、转速的参与因子,利用参与因子计算各模式的机电相关比,确定调相机参与的机电振荡模式以及各模式中的各发电机参与度,不再赘述。
对于电压振荡模式,计算状态变量中各发电机电势的参与因子,利用参与因子计算各模式的电压相关比,确定调相机参与的电压振荡模式以及各模式中的各发电机参与度。
4 PSVR参数调整算例
4.1 PSVR时间常数调整
在初始PSVR参数下,图4中相频特性的均方根为36.182 6。调整PSVR其余两个移相环节的时间常数值,改变相频特性曲线。当![]() 时,调相机VT-VS相频特性曲线如图5所示,最大相移18.6°,相频特性的均方根由原来的36.182 6下降为12.761 7,降低了无功电压对功角特性的影响。
时,调相机VT-VS相频特性曲线如图5所示,最大相移18.6°,相频特性的均方根由原来的36.182 6下降为12.761 7,降低了无功电压对功角特性的影响。
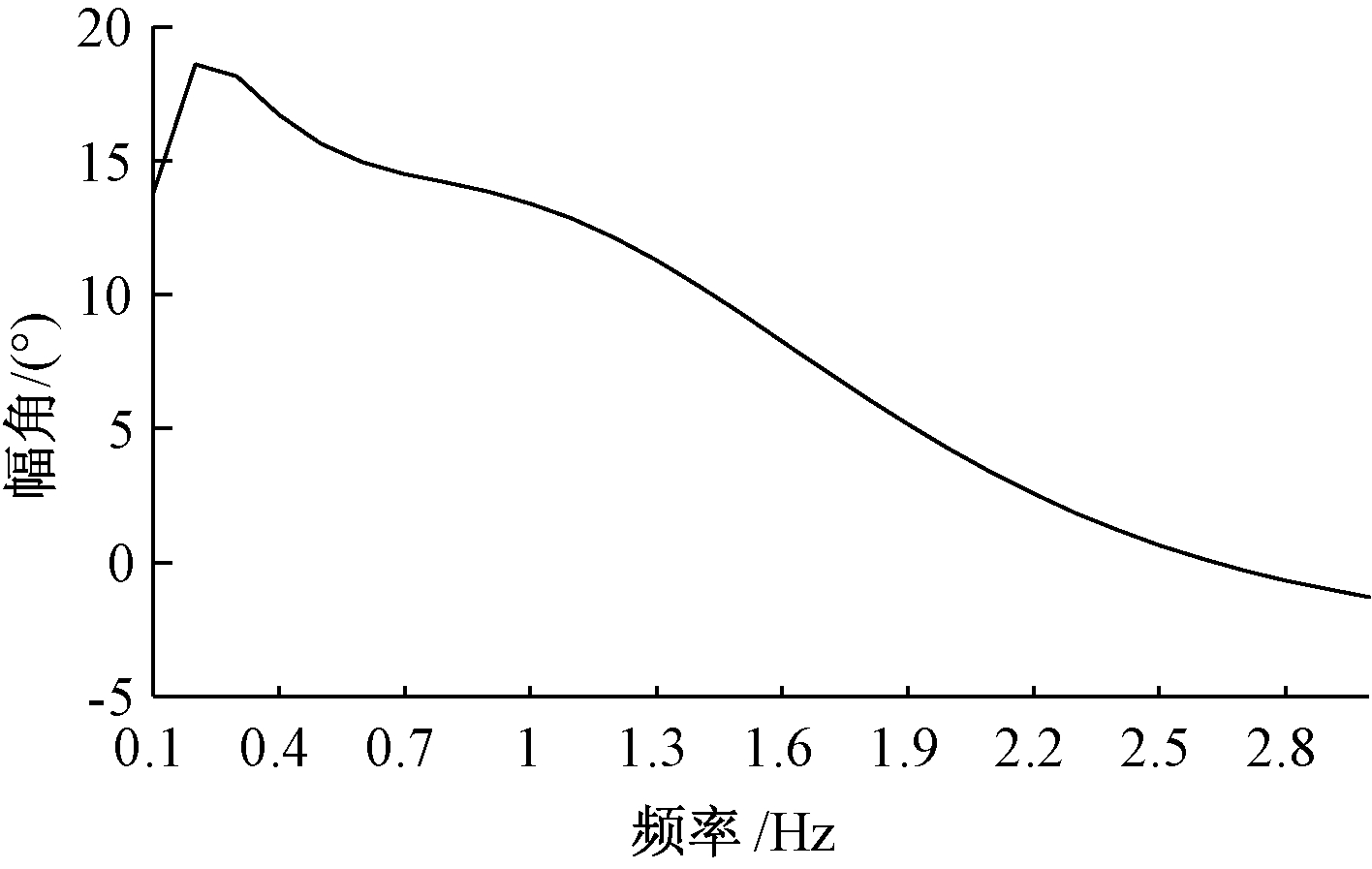
图5 调整PSVR时间常数后的调相机VT-VS相频特性
Figure 5 VT-VS phase frequency characteristic of the condenser with PSVR time constants adjusted
4.2 调相机相关的电压振荡模式
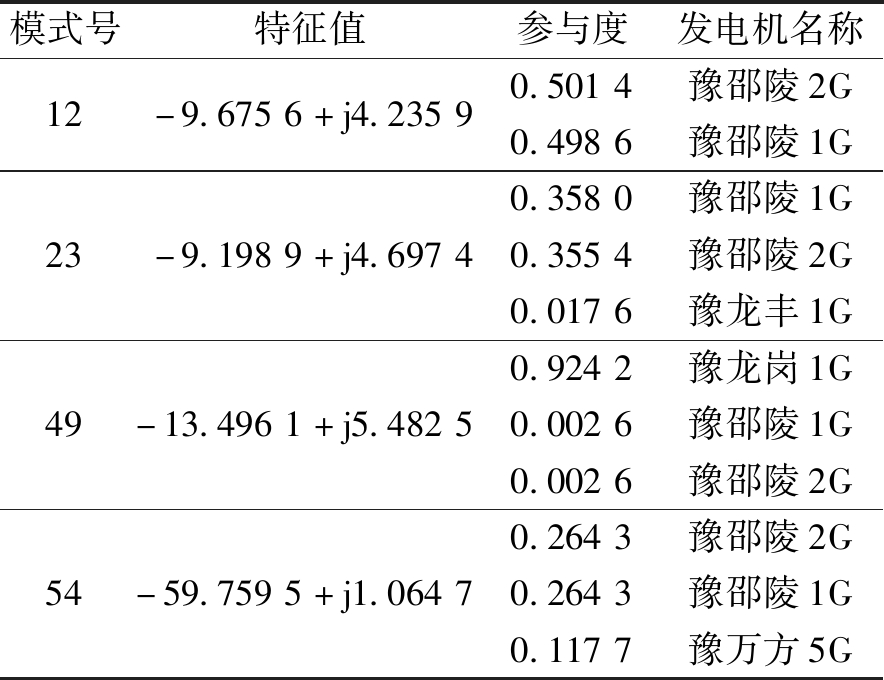
平运行方式下,不计PSVR,河南电网94台发电机,1 736个特征值。与调相机相关的电压振荡模式有4个,列于表1,振荡频率分别为0.67、0.87、0.75、0.17 Hz,后3个模式中未列出参与度更小的机组。
表1 与调相机相关的电压振荡模式
Table 1 Voltage oscillation modes relevant to condensers
模式号特征值参与度发电机名称12-9.6756+j4.235923-9.1989+j4.697449-13.4961+j5.482554-59.7595+j1.06470.5014豫邵陵2G0.4986豫邵陵1G0.3580豫邵陵1G0.3554豫邵陵2G0.0176豫龙丰1G0.9242豫龙岗1G0.0026豫邵陵1G0.0026豫邵陵2G0.2643豫邵陵2G0.2643豫邵陵1G0.1177豫万方5G
共3种类型:①模式12,为调相机之间的无功电压振荡模式;②模式23、54,调相机为主,其他机组参与的振荡模式;③模式49,其他机组为主,调相机参与的振荡模式。
4.3 PSVR增益系数调整
(1)平运行方式下的Kqv上限。在河南电网平运行方式下,PSVR的时间常数采用4.1节确定的值,增益系数Kqv从-0.6开始逐渐增大,计算系统的特征值,利用参与因子确定与调相机相关的电压振荡模式。最终结果列于表2。
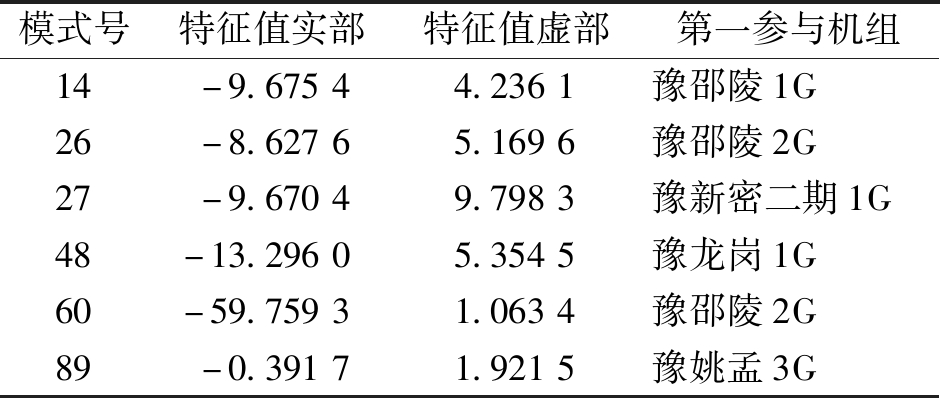
表2 平运行方式下Kqv=24时调相机相关电压模式
Table 2 Voltage oscillation modes relevant to condensers under the flat-operation mode with Kqv=24
模式号特征值实部特征值虚部第一参与机组14-9.67544.2361豫邵陵1G26-8.62765.1696豫邵陵2G27-9.67049.7983豫新密二期1G48-13.29605.3545豫龙岗1G60-59.75931.0634豫邵陵2G89-0.39171.9215豫姚孟3G
当Kqv为0时,调相机仅参与4个振荡模式,见表1。随着增益系数变化,调相机参与的振荡模式数变多。当Kqv从0逐渐增大到24时,相关电压振荡模式稳定。增益系数达到25时,出现一个正实部特征值,不稳定。因此,平运行方式下,Kqv应不大于24。
(2)峰运行方式下的Kqv上限。在峰运行方式下,电网有129台发电机,2 381个特征值。当Kqv从0逐渐增大到67时,相关电压振荡模式稳定,列于表3;Kqv达到68时,不稳定。
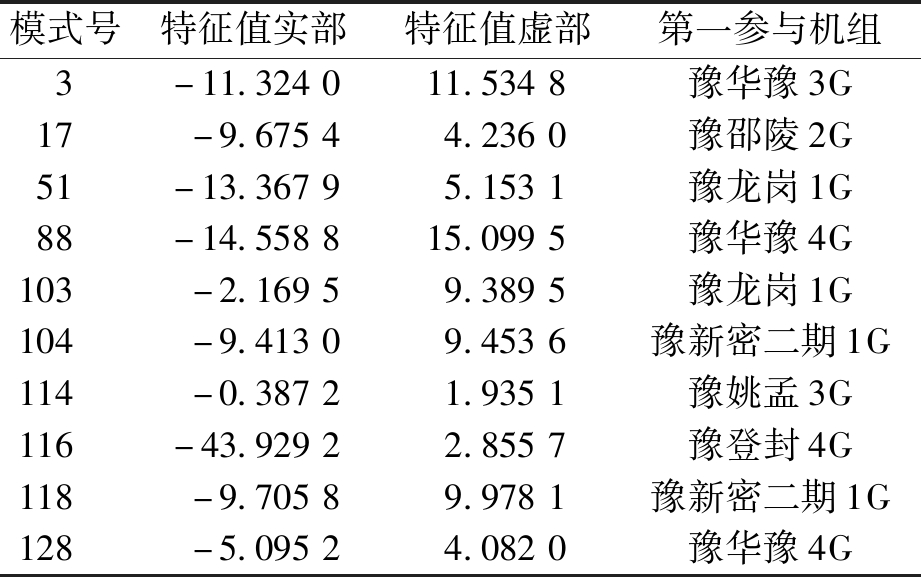
表3 峰运行方式下Kqv=67时调相机相关电压模式
Table 3 Voltage oscillation modes relevant to condensers under the peak-operation mode with Kqv=67
模式号特征值实部特征值虚部第一参与机组3-11.324011.5348豫华豫3G17-9.67544.2360豫邵陵2G51-13.36795.1531豫龙岗1G88-14.558815.0995豫华豫4G103-2.16959.3895豫龙岗1G104-9.41309.4536豫新密二期1G114-0.38721.9351豫姚孟3G116-43.92922.8557豫登封4G118-9.70589.9781豫新密二期1G128-5.09524.0820豫华豫4G
峰运行方式下,Kqv应不大于67。该值大于平运行方式下的24,可能是由于全网发电机的增多,调相机的影响相对变小。
(3)谷运行方式下的Kqv上限。谷运行方式下,电网有64台发电机,1 220个特征值。当Kqv从0逐渐增大到19.4时,相关电压振荡模式稳定,列于表4;Kqv达到19.5时,不稳定。
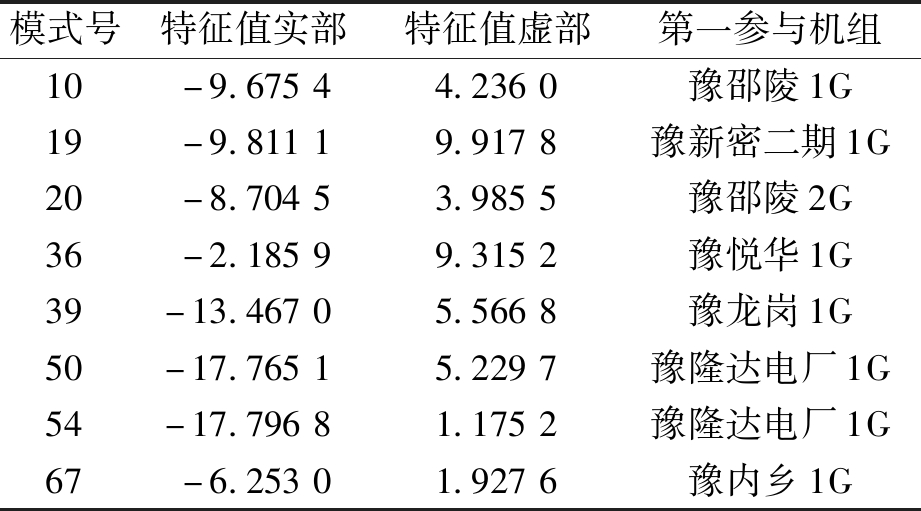
表4 谷运行方式下Kqv=19.4时调相机相关电压模式
Table 4 Voltage oscillation modes relevant to condensers under the valley-operation mode with Kqv=19.4
模式号特征值实部特征值虚部第一参与机组10-9.67544.2360豫邵陵1G19-9.81119.9178豫新密二期1G20-8.70453.9855豫邵陵2G36-2.18599.3152豫悦华1G39-13.46705.5668豫龙岗1G50-17.76515.2297豫隆达电厂1G54-17.79681.1752豫隆达电厂1G67-6.25301.9276豫内乡1G
谷运行方式下,Kqv应不大于19.4。该值小于其他两种运行方式下的值,可能是由于全网发电机的减少,调相机的影响相对变大。
4.4 Kqv变化对功角振荡模式的影响
平运行方式下,两台调相机无功出力均为1 p.u.。PSVR的时间常数采用4.1节确定的值,增益系数Kqv分别取0、10、20、50、100,与调相机相关的功角振荡模式列于表5。
表5 不同Kqv取值下的调相机相关功角振荡模式
Table 5 Power angle oscillation modes relevant to condensers under different Kqv values
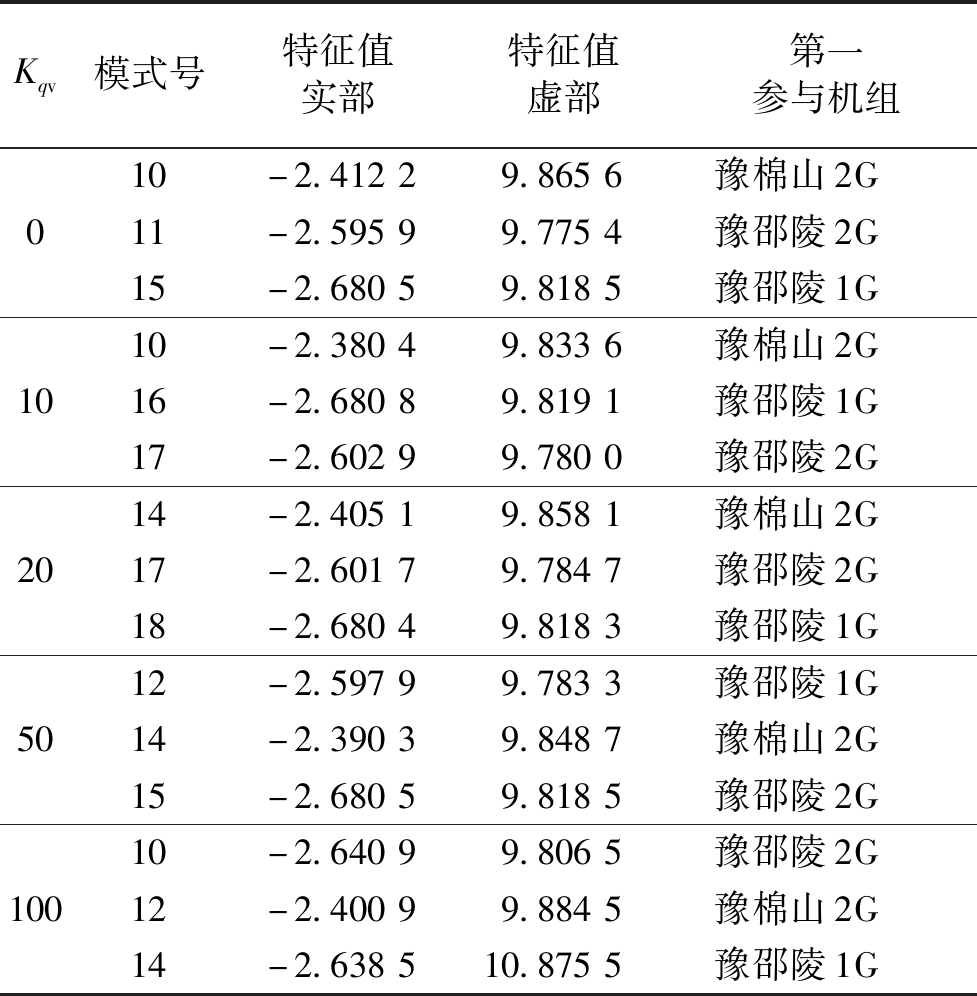
Kqv模式号特征值实部特征值虚部第一参与机组010205010010-2.41229.8656豫棉山2G11-2.59599.7754豫邵陵2G15-2.68059.8185豫邵陵1G10-2.38049.8336豫棉山2G16-2.68089.8191豫邵陵1G17-2.60299.7800豫邵陵2G14-2.40519.8581豫棉山2G17-2.60179.7847豫邵陵2G18-2.68049.8183豫邵陵1G12-2.59799.7833豫邵陵1G14-2.39039.8487豫棉山2G15-2.68059.8185豫邵陵2G10-2.64099.8065豫邵陵2G12-2.40099.8845豫棉山2G14-2.638510.8755豫邵陵1G
由表5可知,PSVR增益系数变化对调相机功角振荡模式有影响,但不大。
4.5 调相机无功出力变化对功角振荡模式的影响
不计PSVR,两台调相机无功出力相等,分别取值0、1、3 p.u.,计算系统特征值,与调相机相关的功角振荡模式列于表6。其中,无功出力为1、3 p.u.时,调相机参与了其他更多的振荡模式,未在表6中列出。
表6 调相机不同无功出力下的功角振荡模式
Table 6 Power angle oscillation modes under different reactive power outputs of condensers
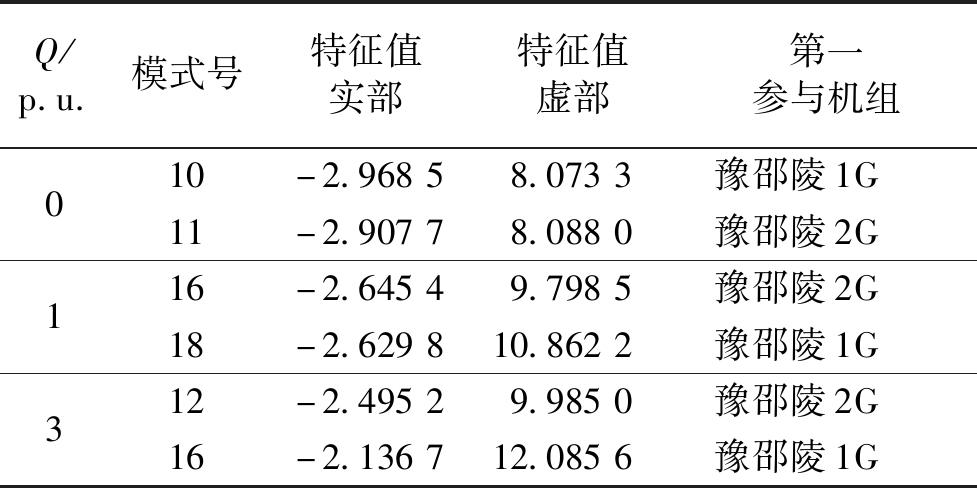
Q/p.u.模式号特征值实部特征值虚部第一参与机组01310-2.96858.0733豫邵陵1G11-2.90778.0880豫邵陵2G16-2.64549.7985豫邵陵2G18-2.629810.8622豫邵陵1G12-2.49529.9850豫邵陵2G16-2.136712.0856豫邵陵1G
因此,无功出力变化对特征值实部有一定影响,随无功出力增加,阻尼有所下降;但对虚部影响较大,例如,由空载时的8.073 3到满载时的12.085 6。
4.6 分析
(1)单机无穷大模型下,调相机无功出力变化对转子转矩的影响几乎可略去;但在多机系统下,该影响不可略去,需在调整PSVR参数时考虑。
(2)合理调整PSVR移相环节的时间常数值,可降低PSVR对功角振荡模式的影响。
(3)过大的PSVR增益系数,会导致调相机更大程度地参与其他振荡模式,以及调相机电压振荡模式的不稳定。
(4)确定PSVR增益系数上限值时,需考虑多种系统运行方式。
(5)河南电网邵陵站调相机的PSVR增益系数值不宜超过19.4。
5 结论
以河南电网新增的大容量同步调相机为例,从调相机动态特性和小干扰稳定性角度提出调相机PSVR参数调整方法。与发电机相比,调相机的无功电压对功角的影响要小得多,但仍需校核;通过调整PSVR移相环节时间常数,降低PSVR对调相机功角特性的影响;计算多系统系统运行方式下的电压振荡模式,结合功角振荡模式,确定PSVR增益系数调整范围。
[1] 王雅婷,张一驰,周勤勇,等.新一代大容量调相机在电网中的应用研究[J].电网技术,2017,41(1):22-28.
[2] 崔挺,沈阳武,张斌,等.300 Mvar级同步调相机对湖南电网稳定的影响研究[J].湖南电力,2016,36(3):1-4,8.
[3] 赵一琰,华文,邓晖,等.调相机接入对浙江电网的影响研究[J].浙江电力,2018,37(1):8-12.
[4] 蔡晖,张文嘉,祁万春,等.调相机接入江苏电网后的适应性研究[J].电力电容器与无功补偿,2017,38(2):23-27.
[5] 陈新琪,俞鸿飞,卢嘉华,等.电力系统电压调节器原理及试验分析[J].电力系统自动化,2012,36(3):92-96.
[6] 周晓渊,邱家驹,陈新琪.高压侧电压控制对单机-无穷大系统稳定性的影响[J].中国电机工程学报,2003,23(1):60-63.
[7] 陈新琪,秦刚华,杨敏,等.基于PSCAD的电力系统电压调节器仿真分析[J].中国电力,2019,52(3):81-86,139.
[8] NOGUCHI S,SHIMOMURA M,PASERBA J.Improvement to an advanced high side voltage control[J].IEEE transactions on power systems,2006,21(2):683-692.
[9] DONG Y P,XIE X R,ZHOU B R,et al.An integrated high side var-voltage control strategy to improve short-term voltage stability of receiving-end power systems[J].IEEE transations on power systems,2015,31(3):1-11.
[10] 石祥建,牟伟,韩焦,等.大型同步调相机控制策略研究[J].中国电力,2017,50(12):44-50.
[11] 陈新琪,陈皓,竺士章.电力系统电压调节器参数整定[J].中国电力,2004,37(7):12-15.
[12] 张振,刘艳红.基于特征值的单机无穷大电力系统随机稳定性分析[J].郑州大学学报(工学版),2018,39(4):58-63.
[13] 罗丹,王克文,王君亮.小干扰稳定分析中状态矩阵的快速形成[J].电测与仪表,2015,52(10):56-60,91.
[14] 康礼彦,王克文,王君亮.电网电力系统稳定器的交互影响分析[J].自动化仪表,2013,34(8):5-8.