0 引言
汽车声品质体现了人对噪声的主观感受,关于声品质的研究主要采用主观评价试验,它能直接反映出声品质,但是评价过程比较复杂,费时费力。于是,很多学者基于心理声学客观参数建立了预测模型,但汽车噪声多属于非稳态信号,只研究时域或频域特征不能准确提取非稳态信号特征。此时,应该从时频联合域上研究并提取信号特征,然而基于时频信号处理方法(如小波分解、EMD等)建立的声品质预测模型并没有得到广泛应用[1]。
针对非稳态排气噪声声品质预测问题,笔者引入CEEMD方法对非稳态信号进行分解,计算IMF分量样本熵值,并使用PCA方法进行降维处理,得到新参量矩阵,建立了基于SQP-CSP新参量的GA-BP预测模型。为了对比此模型,建立了基于Zwicker时变算法[2]计算非稳态信号的心理声学客观参量的GA-BP预测模型。结果表明,新参量建立的模型预测精度较好。
1 排气噪声采集及主客观评价分析
1.1 排气噪声样本采集
根据GB/T 14365—2017《声学 机动车辆定置噪声声压级测量方法》,采用LMS测试并采集了10款某国产车1档急加速(1G WOT)和2档急加速(2G WOT)排气噪声信号,布置如图1所示。采集数据时参数设置如下:采样频率为44 100 Hz,分辨率为1 Hz,采样时间为15 s。

图1 试验示意图
Figure 1 Sketch map of the vehicle test
1.2 排气噪声的主观评价及客观参数
本次主观试验截取加速工况下的特征信号10 s进行成对比较法评价。样本两两配对比较,听音者认为效果好的样本记1分,差的不计分,最终每个样本都会有一个确定的数值用于评价其声品质,并用于后期模型的建立。
参与主观评价的人员共有40名[3],分别来自某大学车辆相关专业的在读研究生、研究院的相关工作者以及普通人员。其中男性有22名,女性有18名,年龄在24~46岁。对样本重合度[4]和一致性系数[5]进行计算,剔除了4名评价人员的数据,最终得到样本的平均重合度为0.779,平均一致性系数为0.916。其中一致性系数采用Kendall法[6]计算。
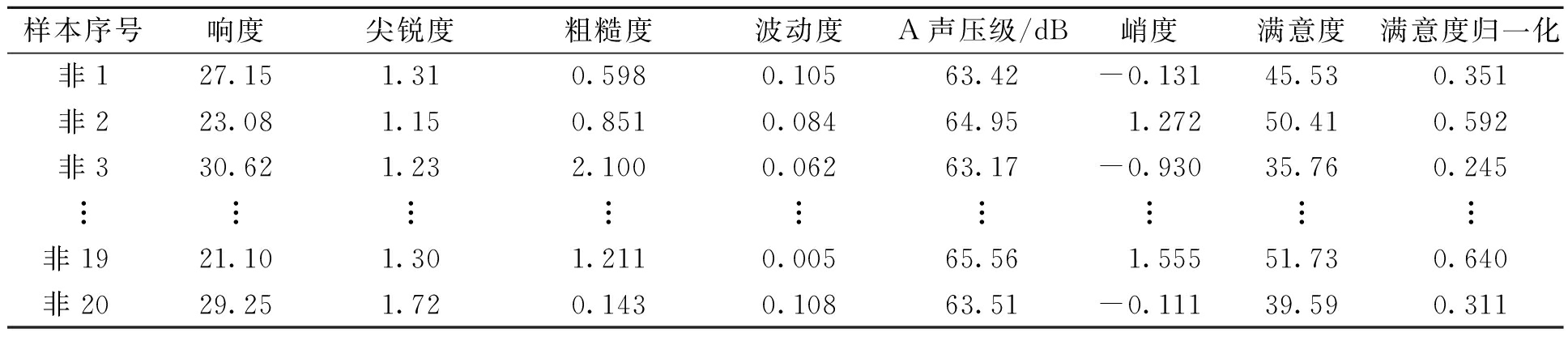
心理声学参数能较好地反映人的主观感受,所以基于Zwicker时变算法在ArtermiS中计算非稳态信号的心理声学客观参量。根据研究经验[7-8],心理声学客观参量采用Zwicker响度、尖锐度、粗糙度、波动度、峭度及A计权声压级。样本的心理声学客观参量及主观试验得到的统计结果如表1所示,其中满意度归一化公式为:
(1)
表1 心理声学客观参量值及满意度值
Table 1 Psychoacoustic objective parameter value and satisfaction value
样本序号响度尖锐度粗糙度波动度A声压级/dB峭度满意度满意度归一化非127.151.310.5980.10563.42-0.13145.530.351非223.081.150.8510.08464.951.27250.410.592非330.621.232.1000.06263.17-0.93035.760.245︙︙︙︙︙︙︙︙︙非1921.101.301.2110.00565.561.55551.730.640非2029.251.720.1430.10863.51-0.11139.590.311
1.3 相关性分析
为了分析主观满意度与心理声学客观参量之间的联系,对主观评价试验满意度得分和心理声学客观参量采用SPSS软件进行相关分析,并采用spearman秩相关双尾进行相关分析来消除声品质客观参量中存在的极端值,spearman秩相关计算公式为:
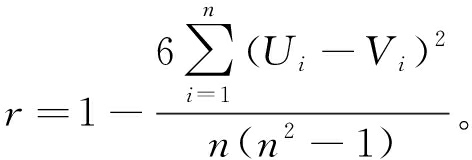
(2)
式中:Ui和Vi为两变量的秩,主要是为了将定距型变量变为非定距型,从而减小极端值对结果的影响;n为样本数;r为spearman秩相关系数。
相关性分析的结果如表2所示。从表2中可以看出,主观评价满意度与响度的相关性系数大于0.7,相关显著性小于0.01,可见主观满意度与响度具有一定的线性关系;与尖锐度的相关系数为0.571,线性相关性较弱;粗糙度、波动度、峭度与主观评价满意度相关系数都较低,说明相关性较差。同时也可以看出,响度、尖锐度、波动度与主观满意度成负相关,粗糙度、峭度与主观满意度成正相关。因此,考虑到非稳态排气噪声声品质与主观评价之间关系的复杂性,引入具有较强的非线性映射能力的神经网络对声品质进行预测研究。
表2 主观评价与心理声学客观参量的相关系数
Table 2 Correlation coefficient between subjective
evaluation and objective parameters of psychoacoustics

心理声学参数相关系数响度-0.791**尖锐度-0.571*粗糙度0.227*波动度-0.145*峭度0.264*
注:**为双侧置信度为0.01时,显著相关;*为双侧置信度为0.05时,显著相关。
2 基于样本熵计算CEEMD的特征提取
2.1 CEEMD
CEEMD是在EEMD(ensemble empirical mode decomposition)基础上进行改进后得出的一种处理非平稳信号的方法。其原理是根据信号本身的时间尺度进行分解,然后得到一系列不同特征尺度的数据序列IMF分量[9]。本征模态函数描述的是单分量物理意义的振动信号。Yeh等[10]在EEMD的基础上提出了CEEMD方法,将白噪声以正负成对的形式添加到原始信号当中,从而降低平均次数,计算效率得到明显提高,也有效解决了模态混叠问题,CEEMD分解步骤如下。
步骤1 将n组白噪声以正负成对的形式添加到原始信号当中,形成两组集合:
(3)
式中:s(t)为原始信号;n(t)为白噪声;m1、m2分别为添加了正负成对白噪声的合成信号。
步骤2 对2n组集合信号进行EEMD分解,设置集合平均次数,由此每一个信号都能得到一系列的IMF分量,记imfij(t)为第i个信号的第j个分量。
步骤3 求解线性平均值:
(4)
式中:imfj(t)为2n组信号在分解后第j个分量的线性平均值。
经过CEEMD分解后,原始信号可以用各层分量和残差之和来表示:
(5)
式中:m为IMF分量的个数;s(t)为原始信号;rm(t)为残余分量。
2.2 样本熵
样本熵(sample entropy,SE)的物理意义是通过度量信号中产生新模式的概率来判断时间序列的复杂性,并且样本熵对数据的长度没有要求,也具备更好的一致性,因此适合对非稳态信号的特征进行计算。
假设一个由N个数据组成时间序列{x(n)}={x(1),x(2),…,x(N)},样本熵的计算方法具体如下。
步骤1 按序号形成一组m维的向量组Xm(1),…,Xm(N-m+1),其中Xm(i)={x(i),x(i+1),…,x(i+m-1)},1≤i≤N-m+1。
步骤2 定义两个向量Xm(i)和Xm(j)之间的距离d[Xm(i),Xm(j)]为向量组中对应元素差值的绝对值中的最大值。即:
d[Xm(i),Xm(j)]=
(6)
步骤3 对于给定的Xm(i),计算Xm(i)和Xm(j)之间的距离小于等于r的数目,记为Bi(即模板匹配数),并计算Bi和距离总数N-m+1的比值,记为:
(7)
步骤4 定义Bm(r)为:
(8)
步骤5 将维数m增加1至(m+1)维,对(m+1)维向量重复步骤1~4,得B(m+1)(r)。
步骤6 该信号序列的样本熵值为:
(9)
式中:m为重构维数;r为相似容限;N为数据长度。m一般选择1或2,实际使用中学者都优先选择m=2,r选择原始数据标准偏差的0.1~0.25倍。
2.3 主成分分析
主成分分析(PCA)方法是一种数学方法,其主要思想是将一组相关的向量转换成另一组不相关的向量,从而达到降维的目的,新的向量按方差进行降序排列,将具有最大方差的向量称为第一主成分,第二大方差称为第二主成分,第K个向量称为第K个主成分。PCA计算步骤如下。
步骤1 假设数据矩阵为X=(Xij)m×n,其中,i=1,2,…,m,其中m是样本数量;j=1,2,…,n,其中n是特征维数;Xij是第i个样本的第j个特征。

(10)
通过Z-score方法对矩阵X进行标准化处理,从而得到标准化矩阵Z:
(11)
式中: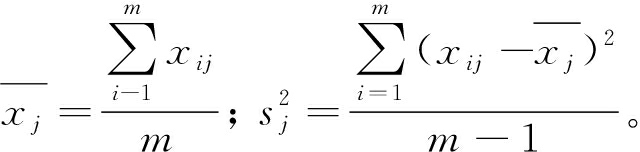
步骤2 计算标准化矩阵Z的相关系数矩阵R。
(12)
式中:j=1,2,…,n;k=1,2,…,n。
步骤3 求解相关系数矩阵R的特征值λ=(λ1,λ2,…,λn)和特征向量αk=(αk1,αk2,…,αkn),k=1,2,…,n,并通过累计贡献率法确定前p个主成分,累计贡献率法公式为:
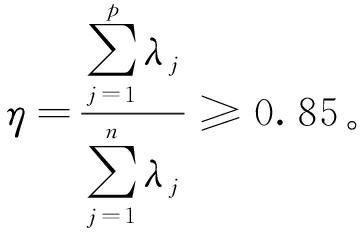
(13)
步骤4 确定主成分得分,第l个主成分(l=1,2,…,p)计算如下:
Fl=αk1Z1+αk2Z2+…+αknZn。
(14)
2.4 非稳态排气噪声信号特征构造
图2所示为样本7的原始信号和处理后样本的频谱图,从图7中可以看出,非稳态排气噪声能量集中分布在500 Hz以下的低频区域,然而基于Zwicker计算的尖锐度强调中高频区域的能量,即中高频成分在整体信号中的占比,也验证了表2中尖锐度与满意度的弱相关性,粗糙度和波动度反映人耳对声音调制频率和调制幅度的感受,峭度则反映信号的平坦程度,然而它们与满意度的相关性较差,对非稳态信号特征表现不足。基于上述分析,引入CEEMD分解及PCA处理样本熵的方法对非稳态排气噪声信号进行特征构造,主要步骤如下。
步骤1 滤波。首先对采集的20组非稳态排气噪声样本进行巴特沃斯高通滤波,滤除20 Hz以下的次声波。
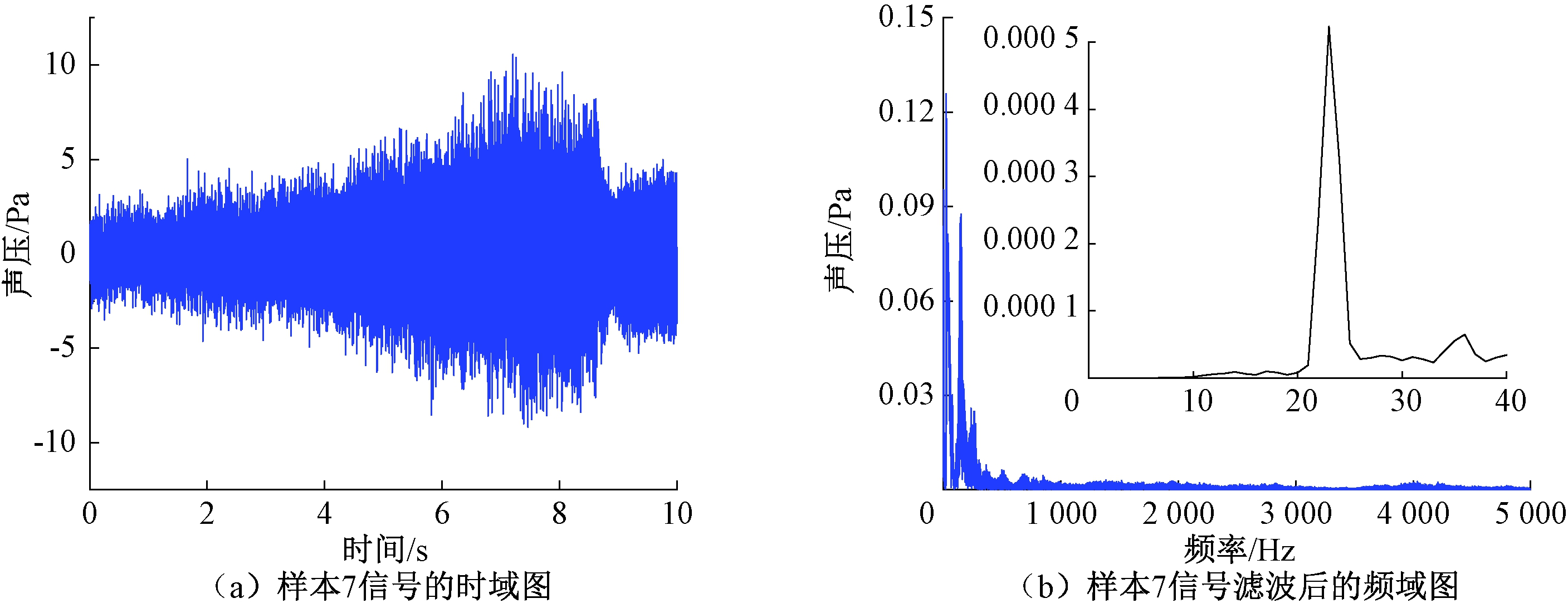
图2 非稳态样本7的信号
Figure 2 Unsteady signal of sample 7
步骤2 CEEMD分解。将高通滤波后的信号进行CEEMD分解,并将n组白噪声以正负成对的形式添加到原始信号当中,由于目前对添加白噪声幅值系数的选取没有固定规则,故参考以往学者的研究经验[11],幅值系数选择为0.4倍原噪声信号的标准偏差,由此计算得到16个分量,分别是15个IMF分量和1个残余分量。分解结果如图3所示,可以看到原始信号经过CEEMD分解为15个IMF分量和一个残余分量res。通过CEEMD分解,对原始信号进行多尺度分解,每进行一次分解,去除高频信号,使得15个IMF分量的频率由高频向低频排列。
步骤3 特征构造。通过图3可以看出第16阶分量属于分解趋势项,对信号特征的提取没有明显意义,所以对前15阶分量进行样本熵计算。根据参考文献[12]中计算样本熵时参数的选择结果显示,当m取2,r取原始数据标准偏差的0.25倍时,样本熵的计算结果更具有合理性。最终得到非稳态信号的各样本各阶分量的样本熵值如表3所示。
步骤4 降维处理。首先对计算得到的样本熵矩阵进行标准化处理,得到标准化矩阵Z,再计算矩阵Z的相关系数矩阵R。在MATLAB中求解相关系数矩阵R的特征值和特征向量,提取累计贡献率超过84%的主成分,各主成分特征值及其贡献率如表4所示。显然前2个主成分累计贡献率已经超过84%,但是为了更好地表现特征,故选取3个主成分进行分析,按式(14)计算各个样本的SQP-CSP值如表5所示。从第一主成分的特征值和特征向量分析发现IMF2、IMF3分量对非稳态信号的特征表现更加明显。
表3 各样本各阶分量的样本熵值
Table 3 Sample entropy of each order component for
each sample
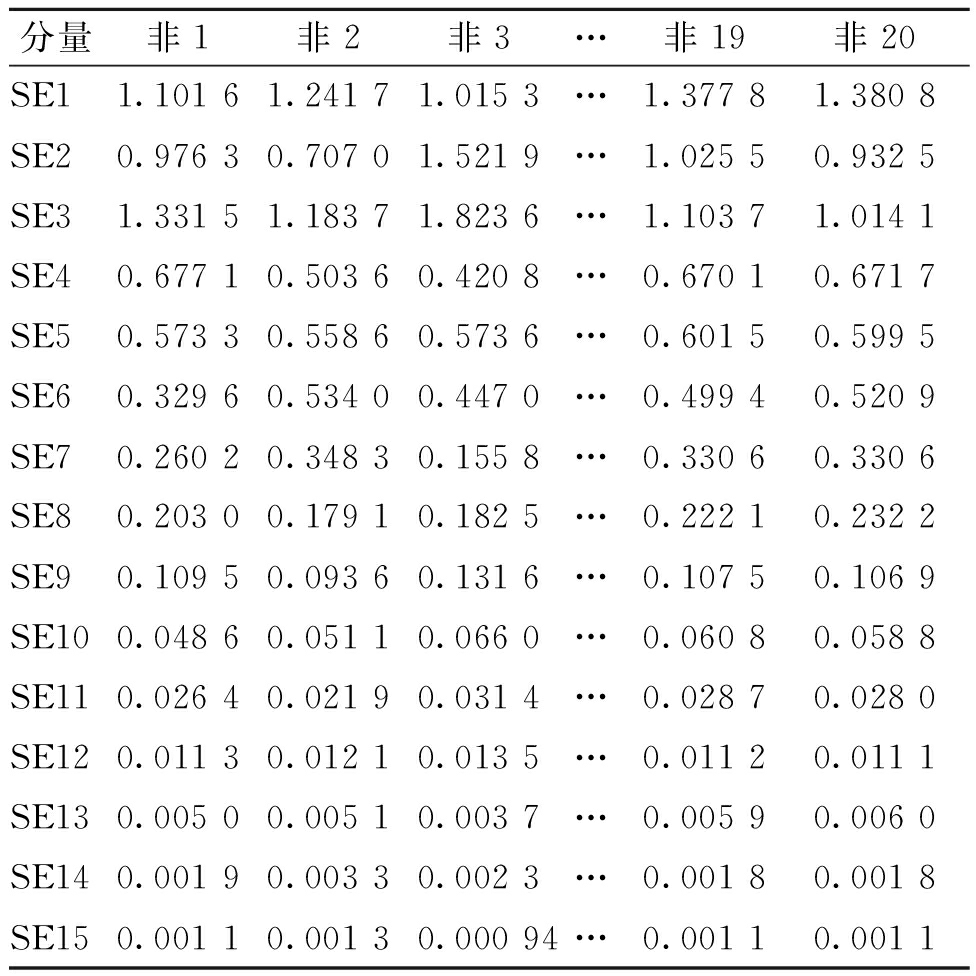
分量非1非2非3…非19非20SE11.101 61.241 71.015 3…1.377 81.380 8SE20.976 30.707 01.521 9…1.025 50.932 5SE31.331 51.183 71.823 6…1.103 71.014 1SE40.677 10.503 60.420 8…0.670 10.671 7SE50.573 30.558 60.573 6…0.601 50.599 5SE60.329 60.534 00.447 0…0.499 40.520 9SE70.260 20.348 30.155 8…0.330 60.330 6SE80.203 00.179 10.182 5…0.222 10.232 2SE90.109 50.093 60.131 6…0.107 50.106 9SE100.048 60.051 10.066 0…0.060 80.058 8SE110.026 40.021 90.031 4…0.028 70.028 0SE120.011 30.012 10.013 5…0.011 20.011 1SE130.005 00.005 10.003 7…0.005 90.006 0SE140.001 90.003 30.002 3…0.001 80.001 8SE150.001 10.001 30.000 94…0.001 10.001 1
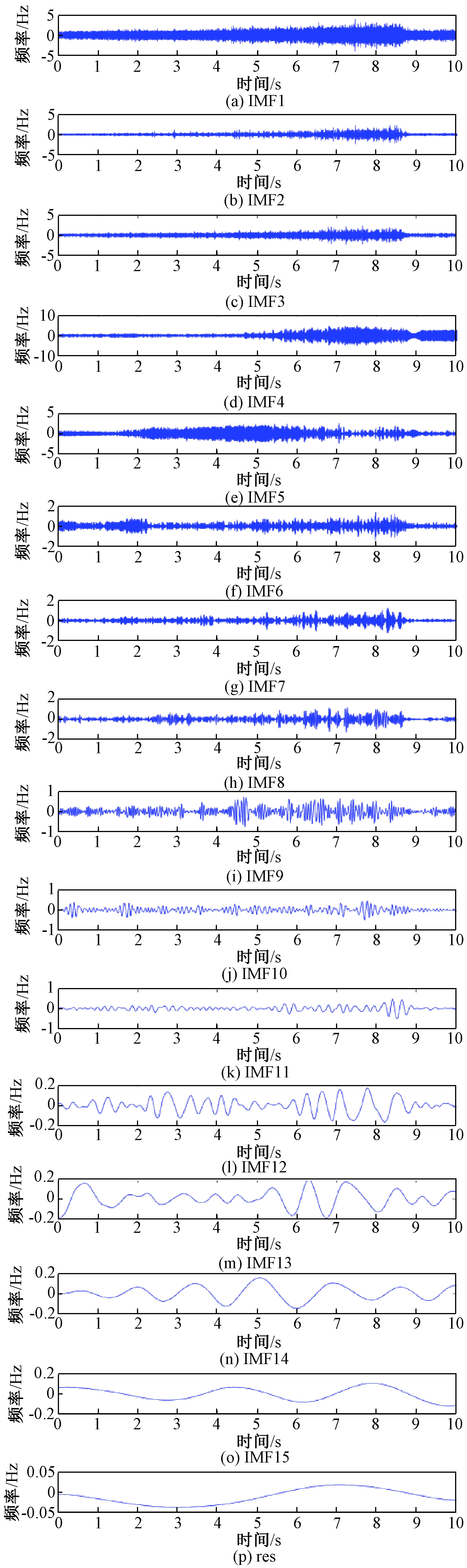
图3 样本7信号CEEMD分解结果
Figure 3 CEEMD decomposition result of sample 7
表4 各主成分特征值及其贡献率
Table 4 Principal component eigenvalues and
contribution rates
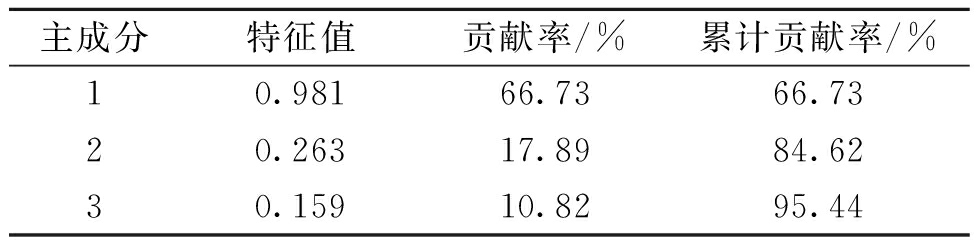
主成分特征值贡献率/%累计贡献率/%10.98166.7366.7320.26317.8984.6230.15910.8295.44
表5 非稳态样本信号的SQP-CSP值S
Table 5 SQP-CSP value of the unsteady sample signal

SQP-CSP值S非1非2非3…非19非20S10.9571.3340.845…0.7630.836S2-0.221-0.559-0.893…-0.758-0.136S31.1091.5141.269…1.6321.709
3 排气噪声声品质预测对比分析
3.1 基于客观参数的声品质预测
利用反向传播特性的BP神经网络对前面处理好的数据进行训练,并采用遗传算法[13]优化神经网络的权值和阈值,避免BP神经网络模型计算时陷入局部极小值,也提高了计算速度和准确度,所建立模型如图4所示。隐含层节点数根据公式![]() 计算后并根据训练结果选取7结点,其中,n1和n2分别为输入和输出层节点数,a为一个0~9之间的整数。选取18个非稳态样本作为模型的训练集,剩下2个样本作为模型准确性的验证集。
计算后并根据训练结果选取7结点,其中,n1和n2分别为输入和输出层节点数,a为一个0~9之间的整数。选取18个非稳态样本作为模型的训练集,剩下2个样本作为模型准确性的验证集。
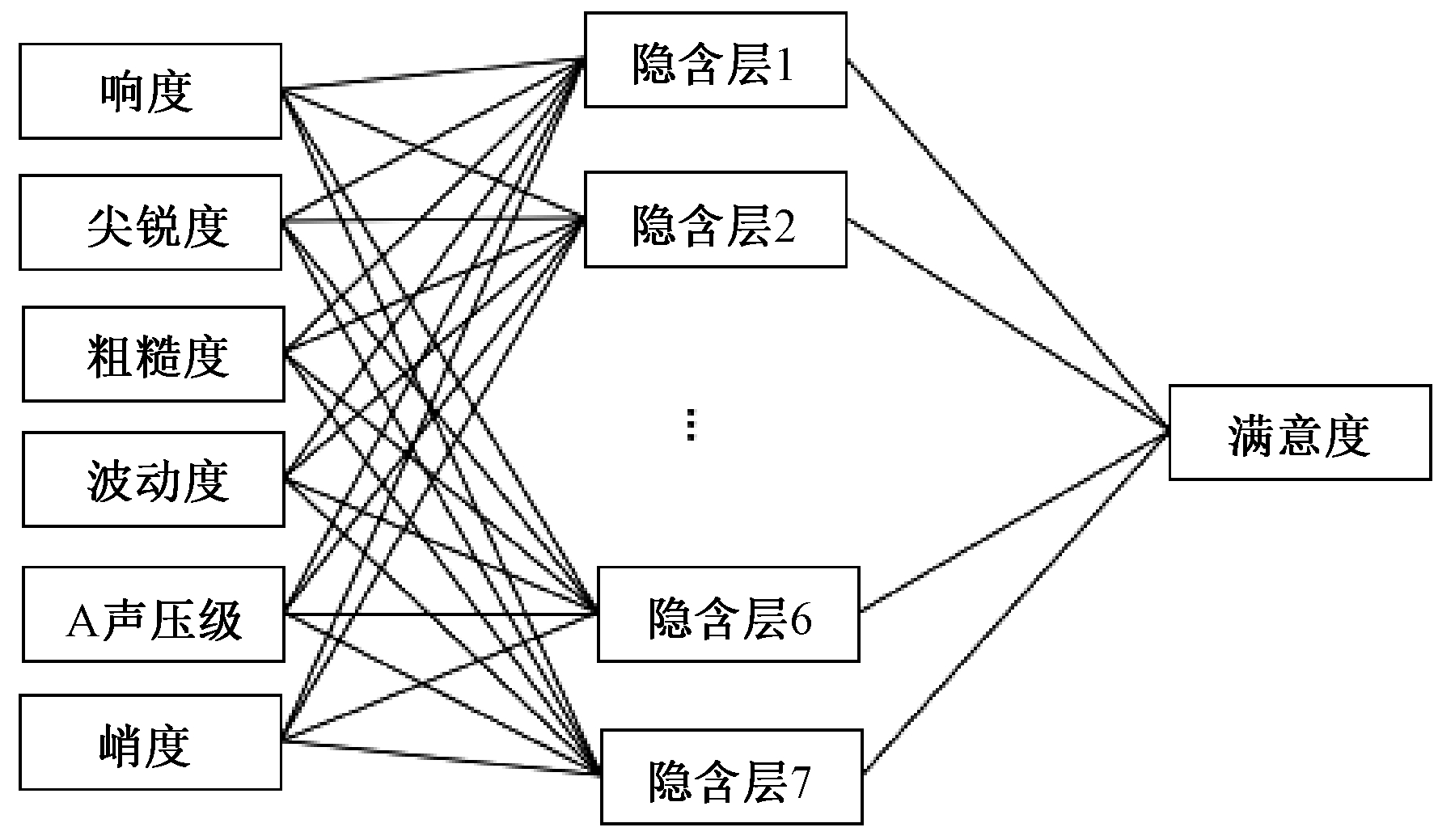
图4 GA-BP神经网络拓扑结构
Figure 4 Neural network topology structure of GA-BP
模型将tansig和purelin函数分别作为隐含层和输出层的传递函数,选取梯度下降算法为网络学习算法,学习效率为0.1,动量系数设为0.9,训练目标均方误差设为0.001。遗传算法参数如表6所示。
模型的训练过程如图5所示,由训练结果可以看到,随着遗传算法迭代次数的增加,种群均值对应的目标值不断减小,即适应度不断增大,大约在第50次迭代时趋于稳定。遗传算法优化后,网络训练的目标函数值随着训练次数的不断增加而越来越小,在100次迭代后模型目标值趋于稳定,误差达到设定目标。训练结果拟合校验值R2为0.923,样本期望值和训练值误差较小。
表6 遗传算法主要参数
Table 6 Genetic algorithm main parameter

最大遗传代数种群规模遗传代沟交叉概率变异概率200400.850.70.01
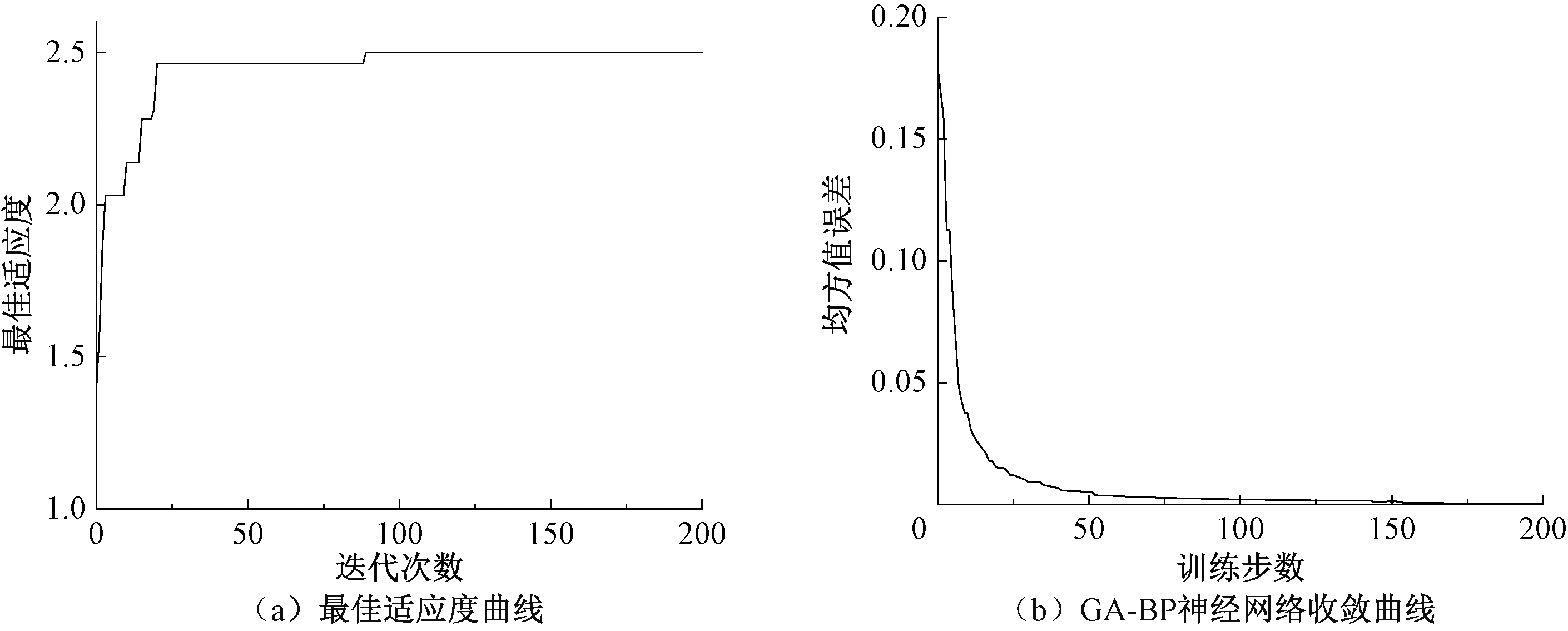
图5 最佳适应度曲线和GA-BP神经网络收敛曲线
Figure 5 Best-fitness curve and GA-BP neural network convergence curve
训练完成后,将剩余的两个非稳态排气噪声信号的心理声学客观参量值作为训练GA-BP模型的输入,两种样本预测的结果对比如图6所示,验证误差分别为12.19%、9.00%,平均验证误差为10.595%。
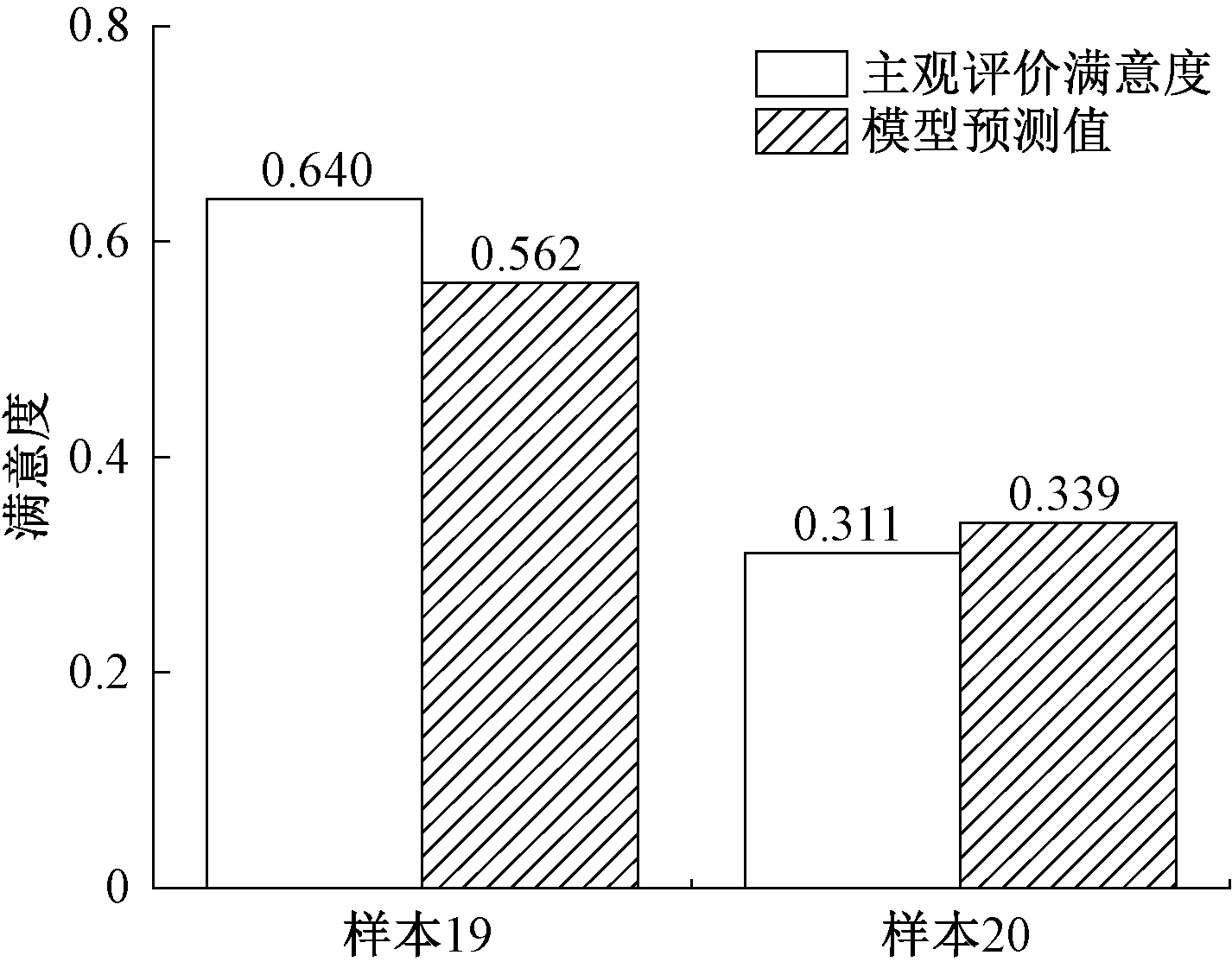
图6 两种样本预测结果
Figure 6 Two prediction results of the model
3.2 基于SQP-CSP的声品质预测
将计算得到的SQP-CSP值S1、S2、S3归一化后作为GA-BP模型的输入,根据隐含层节点数的选取规则,建立一个3-5-1的声品质模型,遗传算法的主要参数及目标函数与前文训练心理声学客观参量模型保持一致。将前18组样本的SQP-CSP值作为模型的输入,主观评价满意度值作为模型输出。训练后预测值与目标值的均方根误差为0.759,预测结果的相关系数R2为0.976,效果均优于将心理声学客观参量作为输入的预测。
将样本19和20的SQP-CSP值S代入已训练好的模型中,得到预测结果。表7是两种模型的预测结果对比。由此可以发现,IMF分量和样本熵构造出的声信号特征再经PCA降维后,较心理声学客观参量更适合用作非稳态排气噪声声品质预测。
表7 两种模型预测结果对比
Table 7 Comparison of prediction results of two models
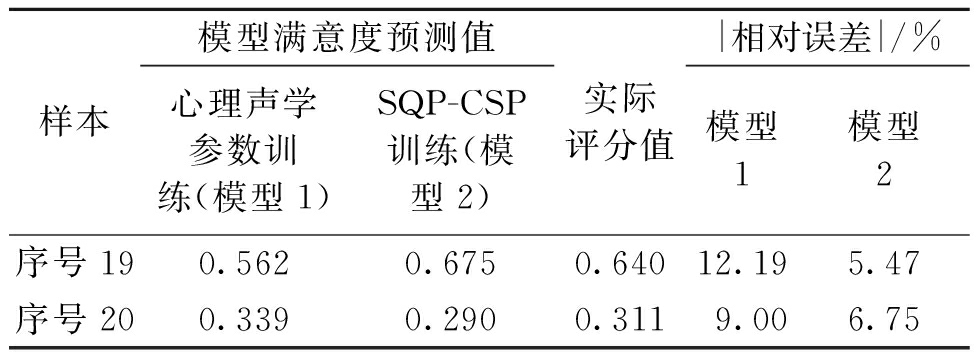
样本模型满意度预测值心理声学参数训练(模型1)SQP-CSP训练(模型2)实际评分值|相对误差|/%模型1模型2序号190.5620.6750.64012.195.47序号200.3390.2900.3119.006.75
4 结论
(1)基于Zwicker计算了非稳态排气噪声的心理声学客观参量,进行了定性分析,结果表明主观满意度与响度与具有一定的线性关系,与尖锐度的线性相关性较弱,粗糙度、波动度、峭度与主观评价满意度的相关性较差。同时,建立了GA-BP声品质预测模型,对非稳态排气噪声进行预测。
(2)利用CEEMD分解,获得相应的IMF分量,计算各阶分量对应的样本熵值并得到新的特征向量,并通过PCA对数据进行降维处理,得到新参量SQP-CSP值S与心理声学客观参量进行对比分析,验证所构造特征的可行性,预测结果表明新参量能够有效提取信号特征,可以用于非稳态信号的研究。
[1] CHANDRIKA U K,KIM J H.Development of an algorithm for automatic detection and rating of squeak and rattle events[J].Journal of sound and vibration, 2010,329(21):4567-4577.
[2] 刘程,贺岩松,于海兴,等.汽车制动工况下车内时变噪声响度特征[J].汽车工程学报,2013,3(1):40-46.
[3] 沈哲,左言言,宋乃华,等.影响车辆声品质听审实验的相关因素研究[J].噪声与振动控制,2008,28(6):97-100.
[4] 鲍海鹏.车辆排气噪声声品质评价的方法研究[D].太原:太原理工大学,2016.
[5] 陈娟娟,王生昌,刘丹,等.乘用车转向性能主观评价与客观评价的相关性[J].公路交通科技,2018,35(1):137-141.
[6] HUSSAIN M,GÖLLES J,RONACHER A,et al.Statistical evaluation of an annoyance index for engine noise recordings[C]//SAE Technical Paper Series,400 Commonwealth Drive. New York: SAE International, 1991: 1-9.
[7] LIU H,ZHANG J H,GUO P,et al.Sound quality prediction for engine-radiated noise[J].Mechanical systems and signal processing, 2015,55-57:277-287.
[8] 毕凤荣,李琳,张剑,等.基于EEMD-HT与LSSVM的柴油机辐射噪声品质预测技术[J].天津大学学报(自然科学与工程技术版),2017,50(1):28-34.
[9] 蔡艳平,李艾华,王涛,等.基于EMD-Wigner-Ville的内燃机振动时频分析[J].振动工程学报,2010,23(4):430-437.
[10] YEH J R,SHIEH J S,HUANG N E.Complementary ensemble empirical mode decomposition:a novel noise enhanced data analysis method[J].Advances in adaptive data analysis, 2010,2(2):135-156.
[11] WU Z H,HUANG N E.A study of the characteristics of white noise using the empirical mode decomposition method[J].Proceedings of the royal society of london series A:mathematical,physical and engineering sciences, 2004,460(2046):1597-1611.
[12] 赵晓华,许士丽,荣建,等.基于ROC曲线的驾驶疲劳脑电样本熵判定阈值研究[J].西南交通大学学报,2013,48(1):178-183.
[13] 穆瑞杰. 基于遗传算法的地铁车站引导标识布点探析[J].郑州大学学报(工学版), 2018, 39(1):73-77,89.