0 引言
在实际工程应用中,有许多目标函数为2~3个的优化问题[1-3],且目标函数间具有彼此冲突的特点,此类问题一般被认为NP-Hard问题。传统的方法,如线性规划、梯度下降等,由于对问题特征具有较为严格的要求,导致解决此类问题时要付出极为昂贵的时间代价,甚至在有限时间内无法获得满意解。进化算法的出现为此类问题提供了新思路。典型算法如NSGA-II[4]、SPEAII(improved strength pareto evolutionary algorithm)[5],以及NNIA(multi-objective immune algorithm with non- dominated neighbor-based selection)[6]等在此类问题上均表现突出。其中,NSGA-II作为多目标优化算法的典型代表,受到很多研究者的广泛关注。根据研究角度不同,可将近些年研究成果作如下分类。
就应用角度而言,NSGA-II及其改进方法已经被应用到许多实际优化问题中。为解决服装调度生产中最大完成时间和最小延期交货时间的问题,陆金芳[7]提出改进排序适应度和按需分层策略,极大提高了服装调度的效率。黄敏镁等[8]为了最大化供应链环境下协商Agent自身效用和合作企业建议相似度,采用了正整数和小数混合的实数编码方式,并在遗传操作中增加了约束限制,以剔除算法运行中产生不可行个体。在应急物流系统设计中,需要综合考虑系统总成本、总耗时以及道路安全性等问题。陈刚等[9]针对此问题特点提出了改进个体交叉和变异方式,并进一步将精英策略融入NSGA-II。在将NSGA-II应用于水污染修复管理模型时,NSGA-II不能有效地收敛到真实Pareto 前沿。为提升NSGA-II收敛性,宋健[10]提出将HCS(hill climber with step)融入NSGA-II,极大地提升了算法收敛能力。
在理论研究方面,NSGA-II也得到了极大的改进。为解决NSGA-II拥挤度距离机制无法有效区分多样性个体的缺陷,崔志华等[1]提出了基于平均距离聚类的多样性评价指标,并进一步提出了基于平均距离聚类的NSGA-II。受无免费午餐定理启发,陈辅斌等[11]提出将免疫平衡原理引入NSGA-II选择策略。为解决NSGA-II中拥挤度距离机制无法衡量个体周围个体密度的缺陷,王祥[12]提出将密度聚类思想融入到个体拥挤度评价机制,并进一步提出了个体邻域的构建方法。汪文文等[13]将禁忌搜索的思想融入精英保留策略,有效地平衡了全局搜索和局部搜索。为了拓展NSGA-II在高纬多目标优化问题上的性能,Yang等[14]提出利用基于网格支配的方法区分个体,并进一步利用网格支配产生后代。同样针对此类问题,Zhang等[15]提出将分解的思想引入到多目标优化问题中,可有效避免Pareto支配失效的问题。
虽然NSGA-II在理论和应用方面已经取得了很大的进步,但是采用的锦标赛策略会导致重复父代个体的产生,并由此导致后代多样性受到影响。为解决此问题,笔者从以下两方面进行改进,第一,引入Lévy分布,增加发现父代个体周围潜在较优个体的能力;第二,提出三交叉父代策略,进一步降低重复父代个体对后代多样性的影响。最后提出基于混合策略的NSGA-II(fast non-dominated sorting genetic algorithm II based on hybrid strategies,HSNSGA-II)。
1 基本概念以及锦标赛选择策略
1.1 基本概念
一个典型多目标优化问题可形式化表示如下[1]:
min F(X)=[f1(X),f2(X),…,fM(X)],
(1)
s.t.X∈Ω,
式中:X=(x1,x2,x3,…,xD)是一个D维决策向量;Ω⊆Rn为决策空间;M为目标函数数量。由于多目标优化问题中不同目标间具有相互冲突的特点,导致不存在最优个体,而是最优解集。以下为多目标优化问题中的主要概念。
定义1:若变量X目标函数f(X)=(f1(X),f2(X),…,fM(X))T,变量X′目标函数f(X′)=(f1(X′),f2(X′),…,fM(X′))T,当且仅当对于∀i∈{1,2,…,M},fi(X)≤fi(X′)成立,且存在k∈{1,2,…,M},使得fk(X)<fk(X′)严格成立,则称X支配X′,记作:X X′。
X′。
定义2:决策空间上所有Pareto最优解构成的集合称为Pareto最优解集。
定义3:Pareto最优解集在目标空间上对应解集合称Pareto前沿面。
1.2 基本NSGA-II框架以及缺陷分析
作为多目标优化领域里的典型代表算法,NSGA-II有两个核心策略,非支配排序和拥挤度距离。非支配排序用于强化种群个体间的选择压力,拥挤度距离用于评价个体的多样性,通过上述两种策略达到种群个体不断进化。种群更新主要过程可简述如下。
设P和Q分别为具有N个个体的父代种群和对应的子代种群。首先,将两种种群合并为C=P∪Q。为从合并的种群C中选择出N个后代个体,利用非支配排序策略对种群C进行操作,可得到多个Pareto前沿面。然后,从第1层前沿面开始,累积计算个体数量,直到第l层个体数量首次超过N。为从第l层选择出较优个体,利用拥挤度距离计算第l层个体中每个个体的拥挤度,选择拥挤度距离大的个体作为下一代个体。
NSGA-II中交叉操作和变异操作为常见操作,在此不再赘述。需要指出的是,NSGA-II中选择操作所用策略为锦标赛策略,描述如下:
(1) 确定每次选择个体数量,在此为2个。
(2) 从种群中随机选择个体,选择适应度值较优个体作为后代个体。
(3) 重复上述步骤(2),直到达到预定个体数量。
从上述步骤可以看出,若个体I为第1层Pareto前沿面上个体,且具有较优多样性指标,则其在下次被选中的概率依然很大。
图1展示了采用锦标赛策略选择父代个体重复个体数量统计数据。采用测试函数为ZDT2,种群数量为50,关于测试函数详细信息在后续实验部分详细阐述。从上述统计数据中可以看出,每代都有平均15个个体的重复量,最高甚至达到32个重复个体。这些重复个体虽然携带了较优的基因,可以为后代个体提供较好的搜索方向,但是也造成了后代多样性较差的缺陷。
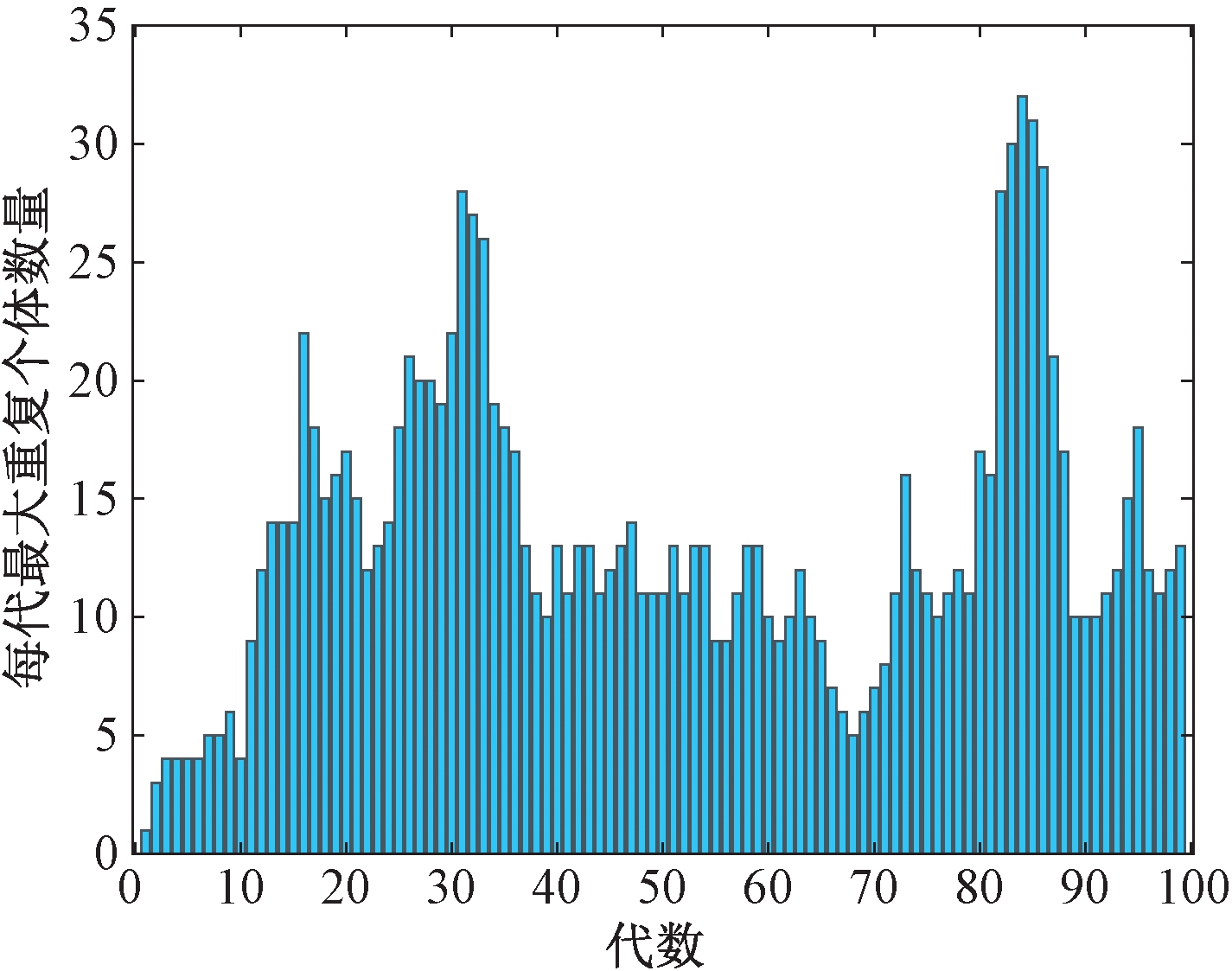
图1 重复个体数量统计
Figure 1 Statistics of repeated individuals
2 基于混合策略的NSGA-II
针对NSGA-II上述缺陷,笔者提出引入Lévy分布策略和三交叉父代策略。下面简要介绍Lévy 分布策略,然后详细介绍本文改进算法。
Lévy分布概率密度函数可形式化表示如下:
L(δ)~u=t-1-δ, 0<δ<2,
(2)
其简化形式可表示如下:
L(δ)~φ·u/|v|1/δ,
(3)
其中,u和v是符合高斯分布的随机数,δ设置为1.5[13],φ定义如下:
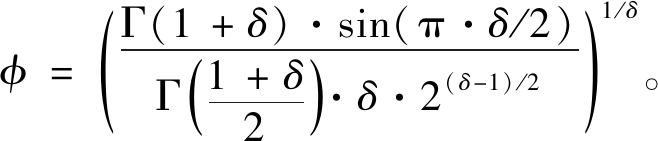
(4)
图2展示了Lévy分布所生成的100个采样点取值。统计一下Lévy分布取值范围,可发现,93%的取值落在[-1.8,1.8]内。从图2可以看出,Lévy分布不仅可以使算法搜索聚焦于个体局部区域,也可使搜索跳出局部范围,增加后代多样性,避免陷入局部最优。
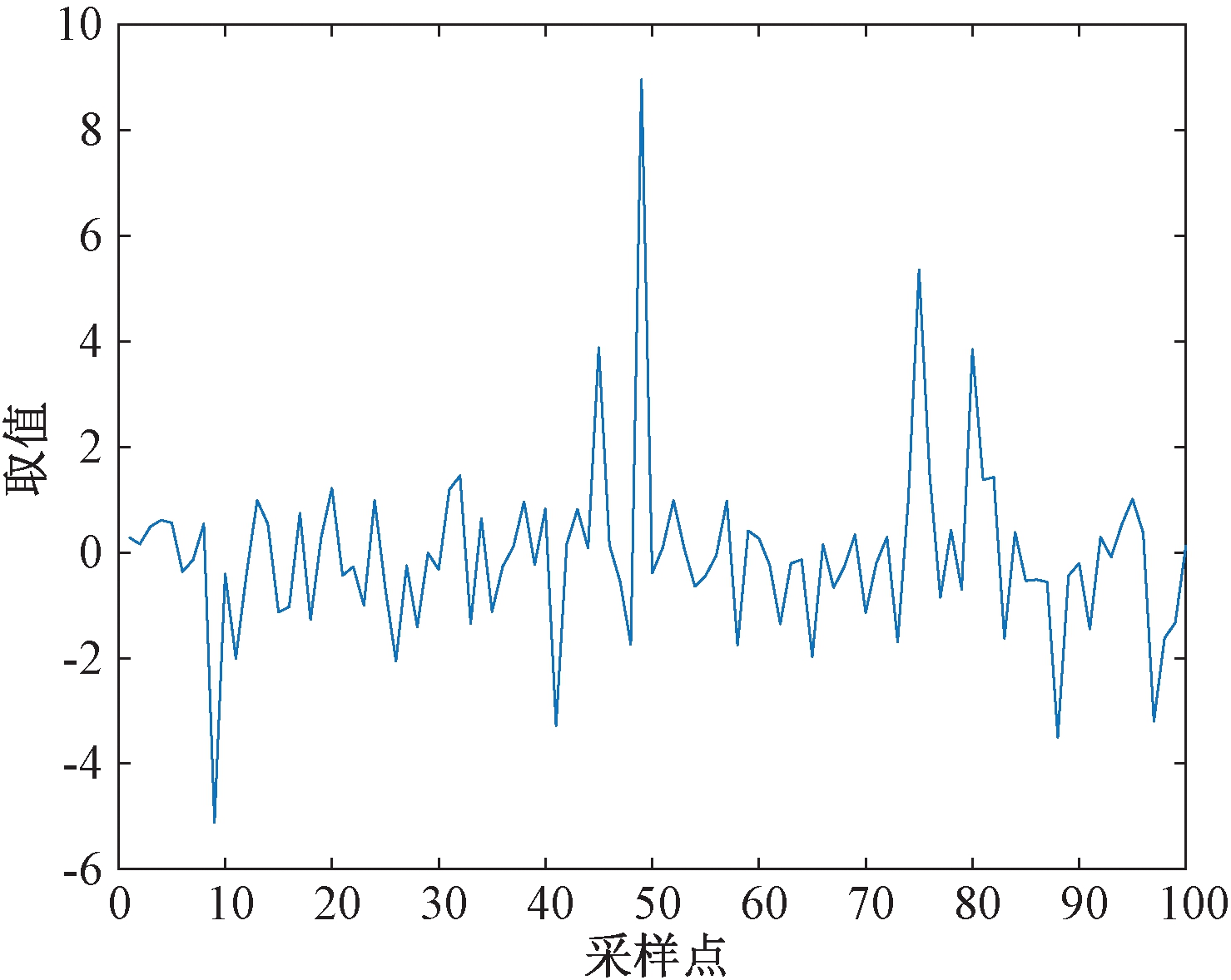
图2 Lévy分布采样点
Figure 2 Sampling points with Lévy distribution
设P1、P2、P3分别为锦标赛选择策略所选出父代个体。原交叉算子可定义如下:
(5)
其中,beta是NSGA-II中定义参数,请参考文献[4]。
改进后交叉算子可表示如下:
(6)
式中:L即为上文所述L分布函数。从上式可以看出,Lévy起到扰动作用,可以极大增加发现父代个体周围潜在较优个体的概率,同时引入P3则可进一步减小父代个体为同一个个体的概率。
基于混合策略的NSGA-II伪代码如下。
1:初始化种群以及相关参数
2: While (是否满足结束条件) do
3: 快速非支配排序
4: 采用锦标赛策略,从种群中选择较优个体
5: 采用式(6)对父代个体执行交叉操作
6: 对个体执行变异操作
7: 环境选择,更新种群
8: End while
9:输出种群
3 实验结果及分析
3.1 参数设置
为综合测试笔者所提算法性能,将HSNSGA-II传统算法SPEA2[5]、PEASII[16]、NNIA[6]以及最近提出的算法MOEAIGDNS(multi-objective evolutionary algo-rithm based on enhanced IGD)[17]和ADCNSGA-II(NSGA-II with average distance clustering)[1]进行对比。注意,所有参数设置均按照原始参考文献设置,有兴趣读者请参阅文献[5-6,16-17]。实验所用计算机为Inter Core i 5-2400 3.10 GHz CPU,6.00 GB内存,Windows7操作系统,运行环境为MATLAB7.9。每个算法独立运行20次,对ZDT测试函数集最大迭代100次;对DTLZ1函数最大迭代700次;对DTLZ2、DTLZ4和DTLZ5函数迭代250次;对DTLZ3函数迭代1 000次;种群个体为50。
采用ZDT测试函数集[18],这些函数具有凸、凹、连续、非连续和具有多重局部最优等特点;评价指标采用IGD[19]。IGD是一个综合指标,可同时评价算法收敛性和多样性,其值越小表示算法性能越优,定义为:
(7)
式中:P*为目标空间真实Pareto前沿面上均匀分布点的集合;P为算法所求解集;dist(v,P)为点v和集合P中点的最小欧几里得距离。
3.2 算法对比及分析
表1列出了笔者所提算法和对比算法在测试函数上的实验结果,每个结果为算法运行20次的IGD的均值与方差,最优结果用黑体显示。从上述实验结果可以看出,与传统算法相比,HSNSGA-II在ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ2、DTLZ5上表现均较为突出,仅在DTLZ1、DTLZ3、DTLZ4上表现较差。相比于最近提出的算法MOEAIGDNS 和ADCNSGA-II,可以看出HSNSGA-II仍然具有较大的优势。因此,综合上述实验结果,可以看出笔者所提策略明显地提高了NSGA-II的性能。
表1 实验结果对比
Table 1 Comparison of experimental results

函数类别HSNSGA-IINSGA-IINNIAPESA-IISPEA2MOEAIGDNSADCNSGA-IIZDT1ZDT2ZDT3ZDT4ZDT6DTLZ1DTLZ2DTLZ3DTLZ4DTLZ5均值1.7457e-17.1005e-16.1746e+01.0370e+01.9952e+01.7102e+01.9853e-1方差1.13e-15.10e-13.49e+06.90e-11.11e+06.59e-13.41e-1均值6.0143e-11.0503e+01.2746e+19.5321e-11.6424e+01.6780e+06.0475e-1方差5.97e-22.50e-15.05e+09.14e-27.13e-15.52e-16.21e-2均值1.9925e-15.0955e-16.6365e+01.0715e+07.2531e-11.0587e+01.9928e-1方差1.12e-11.41e-13.02e+04.24e-13.27e-13.76e-12.18e-1均值2.2760e-14.8095e-11.0260e+08.9952e-17.8586e-18.8590e-12.8411e-1方差1.42e-11.60e-16.80e-12.58e-13.99e-13.85e-11.04e-1均值6.9959e-22.1840e-13.9427e-11.2281e-11.8376e-16.3911e-17.1242e-1方差8.16e-24.65e-21.26e-11.35e-21.32e-11.21e-15.17e-2均值2.0775e-14.5335e-34.7201e-39.3093e-33.9146e-33.9731e-33.8641e-3方差1.86e-13.20e-51.40e-41.83e-32.01e-43.41e-41.94e-1均值5.2011e-31.0218e-21.0694e-21.8827e-28.5682e-38.1707e-34.8642e-3方差2.84e-43.97e-48.68e-44.30e-31.61e-41.12e-45.21e-4均值8.6863e+01.1435e-21.2595e-22.1854e-29.0320e-31.1936e-28.1472e-1方差5.00e+01.08e-33.71e-49.84e-43.47e-41.12e-44.14e-1均值1.5245e-11.1590e-21.0394e-23.8030e-13.7537e-17.4209e-11.0724e-2方差3.30e-12.05e-49.05e-65.12e-15.19e-16.89e-83.01e-1均值5.0716e-31.1179e-21.0980e-21.7238e-28.4375e-38.1512e-35.2846e-3方差1.90e-41.02e-35.34e-48.56e-48.32e-61.19e-52.01e-4
图3展示了HSNSGA-II和NSGA-II在ZDT3测试函数上的实验结果对比。从图3可以看出,HSNSGA-II可以搜索到右下角区域,而标准NSGA-II却无法有效搜索到该区域,说明所提混合策略可以提高后代个体的多样性并达到了预期,进一步验证了笔者所提策略的有效性。
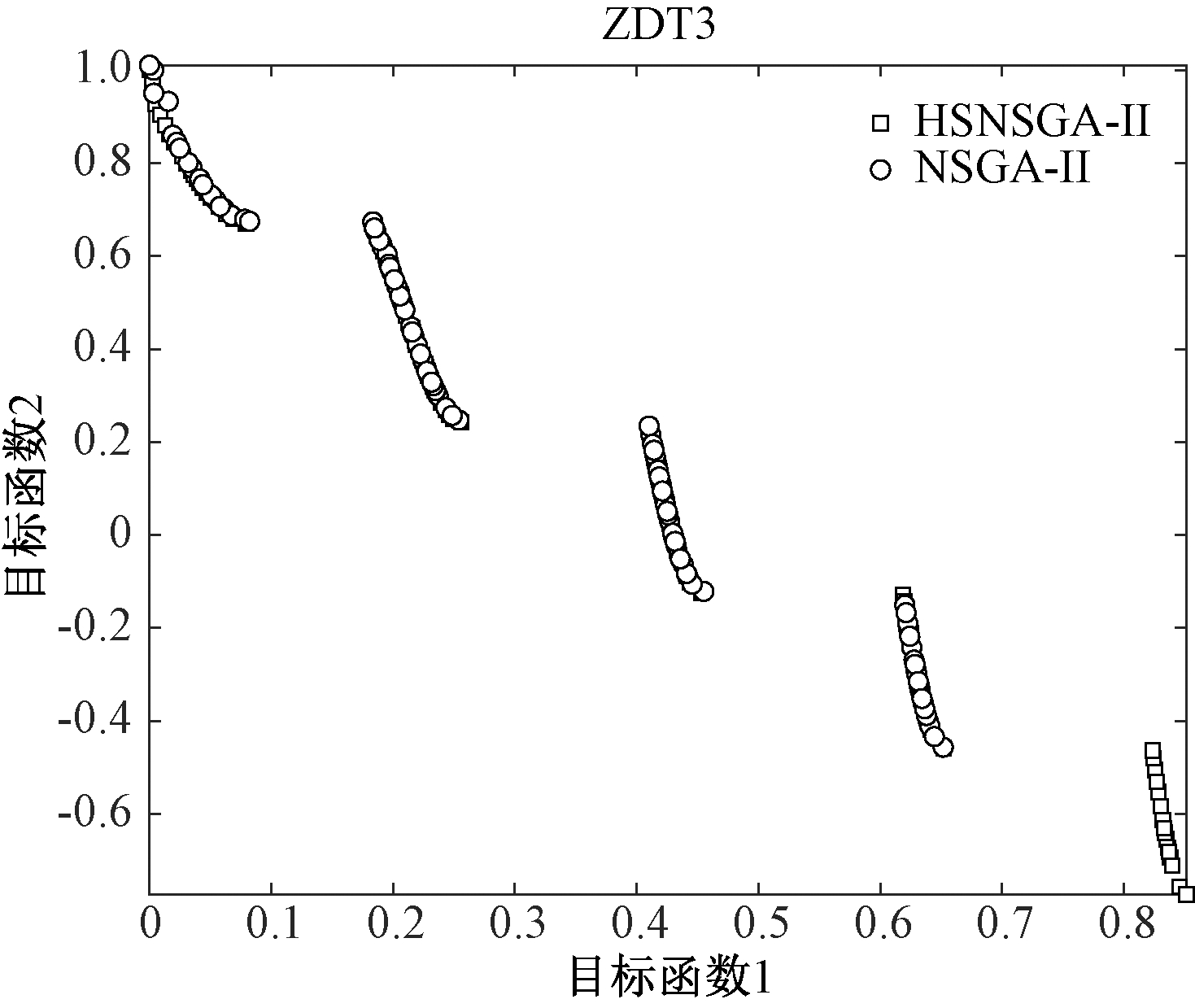
图3 在ZDT3函数上实验结果对比
Figure 3 Comparison of experimental results on ZDT3
4 结论
NSGA-II是多目标优化领域较为经典算法,然而其采用的锦标赛选择策略可导致重复选择父代个体,进而导致后代多样性受到影响。为解决此问题,笔者提出融合Lévy分布和三交叉父代的策略,第一个策略可有效强化搜索父代周围潜在个体的能力,第二个策略可进一步降低所选父代为同一个个体的现象。通过实验对比,验证了笔者所提算法在多个测试集上的有效性。
[1] 崔志华,张茂清,常宇,等.基于平均距离聚类的NSGA-II[J/OL].自动化学报:1-12(2019-04-11)[2019-12-20].https://doi.org/10.16383/j.aas.c180540.
[2] 蒋佩华,华冰,黄宇,等.基于遗传算法的变质量航天器姿态控制方法[J].郑州大学学报(工学版),2019,40(4):1-7.
[3] 龙志伟,肖松毅,王晖,等.基于粒子群算法的水资源需求预测[J].郑州大学学报(工学版),2019,40(4):32-35,47.
[4] DEB K,PRATAP A,AGARWAL S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE transactions on evolutionary computation,2002,6(2):182-197.
[5] ZITZLER E,LAUMANNS M,THIELE L.SPEA2:improving the strength pareto evolutionary algorithm[C]//Proceedings of Conferencs on Evolutionary Methods for Design Optimization and Control with Applications to Industrial Problems.Barcelona:CIMNE,2001:5-10.
[6] GONG M G,JIAO L C,DU H F,et al.Multiobjective immune algorithm with nondominated neighbor-based selection[J].Evolutionary computation,2008,16(2):225-255.
[7] 陆金芳.改进的NSGAII算法在服装企业生产调度中的应用研究[D].广州:暨南大学,2018.
[8] 黄敏镁,袁际军,曹亮.基于NSGAII的协同产品开发项目自动协商决策[J].运筹与管理,2017,26(3):86-91,99.
[9] 陈刚,付江月.基于NSGAII的应急物流多目标LRP研究[J].软科学,2016,30(4):135-139.
[10] 宋健.多目标遗传算法的改进及其在地下水污染修复管理中的应用[D].南京:南京大学,2017.
[11] 陈辅斌,李忠学,杨喜娟.基于改进NSGA2算法的多目标柔性作业车间调度[J].工业工程,2018,21(2):55-61.
[12] 王祥.基于改进NSGA-Ⅱ算法的应急物资模块化调度问题建模与求解[D].合肥:合肥工业大学,2018.
[13] 汪文文,方玺,何朗,等.NSGA-Ⅱ算法的改进及其在应急管理中的应用[J].计算机工程与应用,2018,54(16):241-247.
[14] YANG S X,LI M Q,LIU X H,et al.A grid-based evolutionary algorithm for many-objective optimization[J].IEEE transactions on evolutionary computation,2013,17(5):721-736.
[15] ZHANG Q F,LI H.MOEA/D:a multiobjective evolutionary algorithm based on decomposition[J].IEEE transactions on evolutionary computation,2007,11(6):712-731.
[16] CORNE D,JERRAM N,KNOWLES J,et al.PESA-II:region-based selection in evolutionary multiobjective optimization[C]//Proceedings of the Genetic and Evolutionary Computation Conference (GECCO′2001).San Francisco:Morgan Kanfmar,2001:283-290.
[17] TIAN Y,ZHANG X Y,CHENG R,et al.A multi-objective evolutionary algorithm based on an enhanced inverted generational distance metric[C]//2016 IEEE Congress on Evolutionary Computation (CEC).Vancouver:IEEE,2016:24-29.
[18] ZITZLER E,DEB K,THIELE L.Comparison of multiobjective evolutionary algorithms:empirical results[J].Evolutionary computation,2000,8(2):173-195.
[19] COELLO C A C,CORTES N C.Solving multiobjective optimization problems using an artificial immune system[J].Genetic programming and evolvable machines,2005,6(2):163-190.