0 引言
车辆路径问题[1](vehicle routing problem,VRP)是指使用一组车辆从配送中心出发给已知客户进行配送服务,在满足一定约束条件下,求解最短路径的线路。带时间窗的车辆路径问题(vehicle routing problem with time window,VRPTW)是VRP的拓展,它在VRP的基础上增加了服务时间的限制,即每个客户都有接受服务的时间范围,称为时间窗,车辆必须在时间窗内对客户进行服务。良好的路径规划不仅可以节省运输成本,提高配送效率,还可以提升服务质量,带来巨大的经济效益。
由于VRPTW是一个非确定性多项式难题(NP-Hard),精确算法无法在有效时间内完成求解,使用启发式算法求解大规模客户VRPTW问题受到专家学者的广泛关注,比如遗传算法[2-3]、差分进化算法[4]、粒子群优化算法[5]、布谷鸟搜索算法[6]等。
蚁群算法[7]在解决VRPTW问题上取得了众多成果,如Yu等[8]提出了蚁群算法和禁忌搜索混合的算法,该算法先使用蚁群算法得到一个局部最优解,然后使用一次禁忌搜索算法来跳出局部最优;Ding等[9]对蚁群系统作了进一步改进,在计算转移概率时考虑了节点之间的节约值,同时采用λ-interchange作为局部优化方法,提升了算法的收敛速度;朱杰等[10]将模拟退火算法和蚁群算法结合,改进了蚁群算法中状态转移公式和信息素更新策略,提高算法搜索能力;刘云等[11]将单亲遗传算法和蚁群算法相结合,提升了传统蚁群算法的计算效率和收敛速度,并通过实际算例说明算法的实用性;柴获等[12]采用一种混合蚁群算法来解决双目标带时间窗车辆路径问题,提出了一种新的搜索空间构建方法,并改进了蚁群算法的状态转移公式;孙小军等[13]提出一种动态混合蚁群优化算法,该算法将蚁群算法和遗传算法进行融合,自适应控制蚁群算法参数;葛斌等[14]提出了一种动态混合改进蚁群算法,该算法在对客户分区的基础上,引入了交通拥堵因子来改进传统算法中的状态转移公式,并将挥发因子设置为随机变量,使算法更稳定地收敛到全局最优解。
上述文献通过对传统蚁群算法的改进,促进了蚁群算法在VRPTW问题上的应用及发展,但仍存在不足。如Yu等[8-10]提出的算法均是以最短路径为目标,但是在实际问题中还要考虑车辆数等多个目标,单目标优化无法满足实际需求。刘云等[11-12]提出了解决实际问题的多目标改进蚁群算法,但所解决问题中节点数较少,在解决大规模节点问题上存在搜索能力不足、收敛速度慢等缺点。针对这些问题,笔者提出一种用于解决大规模双目标VRPTW的改进混合蚁群算法。
1 VRPTW数学模型
记G=(V,E)为赋权图,V为顶点集,V=V0∪Vc,其中V0={0}表示配送中心,Vc={1,2,…,n}表示配送节点;E为边集,E={(i,j)|i,j∈V,i≠j}表示节点i和j之间的有向线段。设dij表示节点i、j之间的距离,tij表示车辆从i到j的时间。节点i的需求量为di,接受服务的时间窗为[ETi,LTi],服务时长为STi。K={1,2,…,m}表示车辆编号,每辆车载重恒定为D,车辆k到达节点i的时间Tik,若车辆k在时间窗开始之前到达,则需等待一段时间wik,wik=max(0,ETi-Tik)。定义变量:

本文中VRPTW的双目标数学模型可表述为:
(1)
(2)
s.t:
(3)
(4)
(5)
(6)
(7)
Tik<LTi,∀i∈V,
(8)
Tik+wik+STi+tij<LTj,∀i,j∈V,∀k∈K。
(9)
其中,式(1)、(2)为目标函数,表示以路径的最短距离和最小车辆数为目标;约束条件(3)表示每条线路上的客户需求量不能超过车辆容量限制;约束条件(4)表示每个客户只能被访问一次;约束条件(5)表示车辆在服务节点j之前只服务了一个节点i;约束条件(6)表示车辆在服务节点i后只服务了一个节点j,避免线路内部产生回路;约束条件(7)表示每辆车的起点和终点都必须是配送中心;式(8)~(9)为时间窗约束。
2 基本混合蚁群算法求解VRPTW
2.1 可行解的构建
使用基本蚁群算法求解VRPTW时,首先令每只蚂蚁从配货中心出发,根据状态转移概率随机地从候选节点集合中选择下一节点来构建可行线路,若线路上无可行节点添加时,该蚂蚁返回配货中心,完成一条可行线路的构建。接着重复上述过程,继续从剩余节点中构建可行线路,直到所有节点都被访问,完成一个可行解的构建。
假设当前节点为i,下一个节点的候选集合为W0,蚂蚁从节点i转移至节点j的转移概率为:
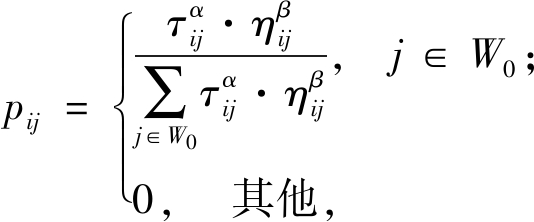
(10)
式中:pij表示蚂蚁从节点i转移到节点j的概率;τij为i、j两点的信息素浓度;![]() 为能见度;α、β为启发因子。
为能见度;α、β为启发因子。
当所有蚂蚁完成可行解的构建后,按照下式进行全局信息素更新。
(11)
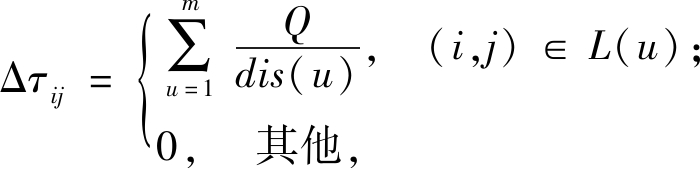
(12)
式中:ρ(0<ρ<1)为常数,表示信息素的挥发速率;Δτij为信息素累计量;m为蚂蚁数量;L(u)为第u只蚂蚁的路径,dis(u)表示第u只蚂蚁的总距离;Q为常数,表示每只蚂蚁释放信息素的总量。
2.2 局部优化算法
车辆路径问题中常用的局部优化算法有2-interchange和or-interchange。2-interchange用于两条路径间的邻域搜索,该算法从两条路径分别选取a和b个节点进行交换来产生邻域解(a,b∈{0,1,2}且a和b不同时为0)。图1表示了a=1、b=1时的一个样例:将路径l中的1个节点x与路径k中的1个节点y进行交换产生邻域解。
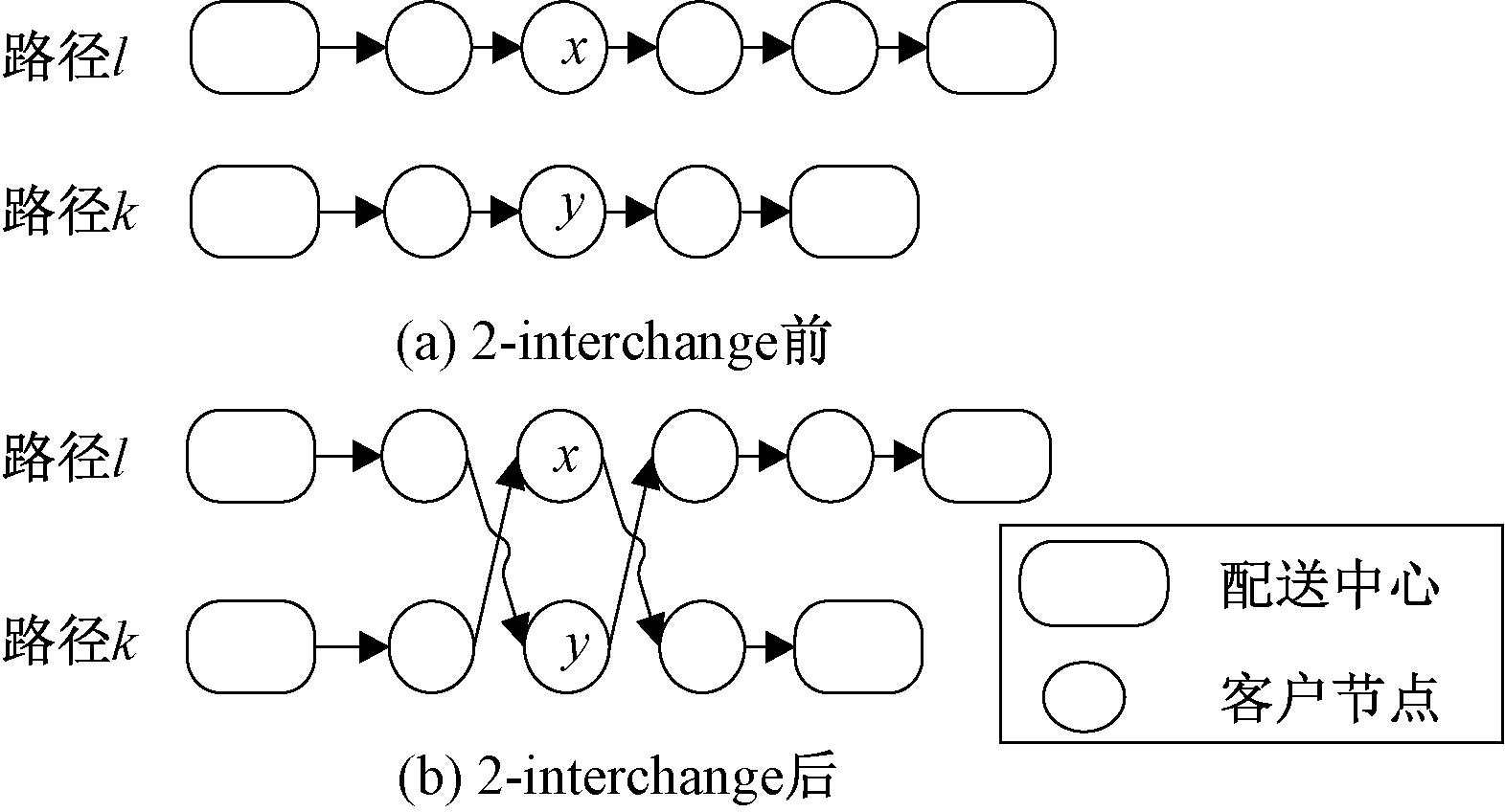
图1 a=1、b=1时2-inerchange变换
Figure 1 2-inerchange transformation when a=1,b=1
or-interchange用于单条线路的邻域搜索,将线路内部两个节点交换位置来产生邻域解。图2表示将路径l中x、z两个节点交换产生邻域解。
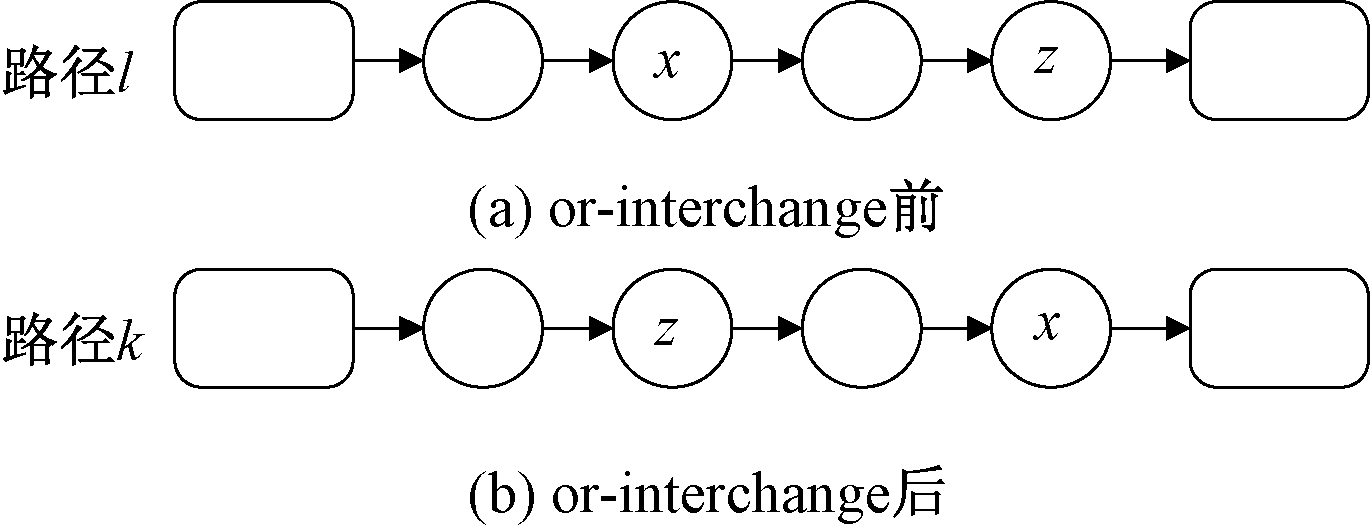
图2 or-interchange变换过程
Figure 2 or-interchange transform process
3 改进的混合蚁群算法
在面对大规模VRPTW时,由于较多的节点数量和复杂的约束,上述基本混合蚁群算法收敛速度慢,搜索效率低,并且无法满足多目标的需求。笔者从候选节点的选择、转移概率和信息素叠加机制等方面对基本蚁群算法进行改进,并提出了一种新的局部优化方法来提升算法的搜索能力。
3.1 候选节点集合的改进
(1)周边搜索策略。在解决大规模节点问题时,基本蚁群算法产生的候选节点集合中节点数量较多,算法难以搜索到最优解。笔者结合VRPTW的问题特点,采用周边搜索策略来缩小候选节点搜索范围。该策略是从下一个可行节点的集合中,选择距离当前节点最近的若干节点作为候选节点集合W,如图3所示。
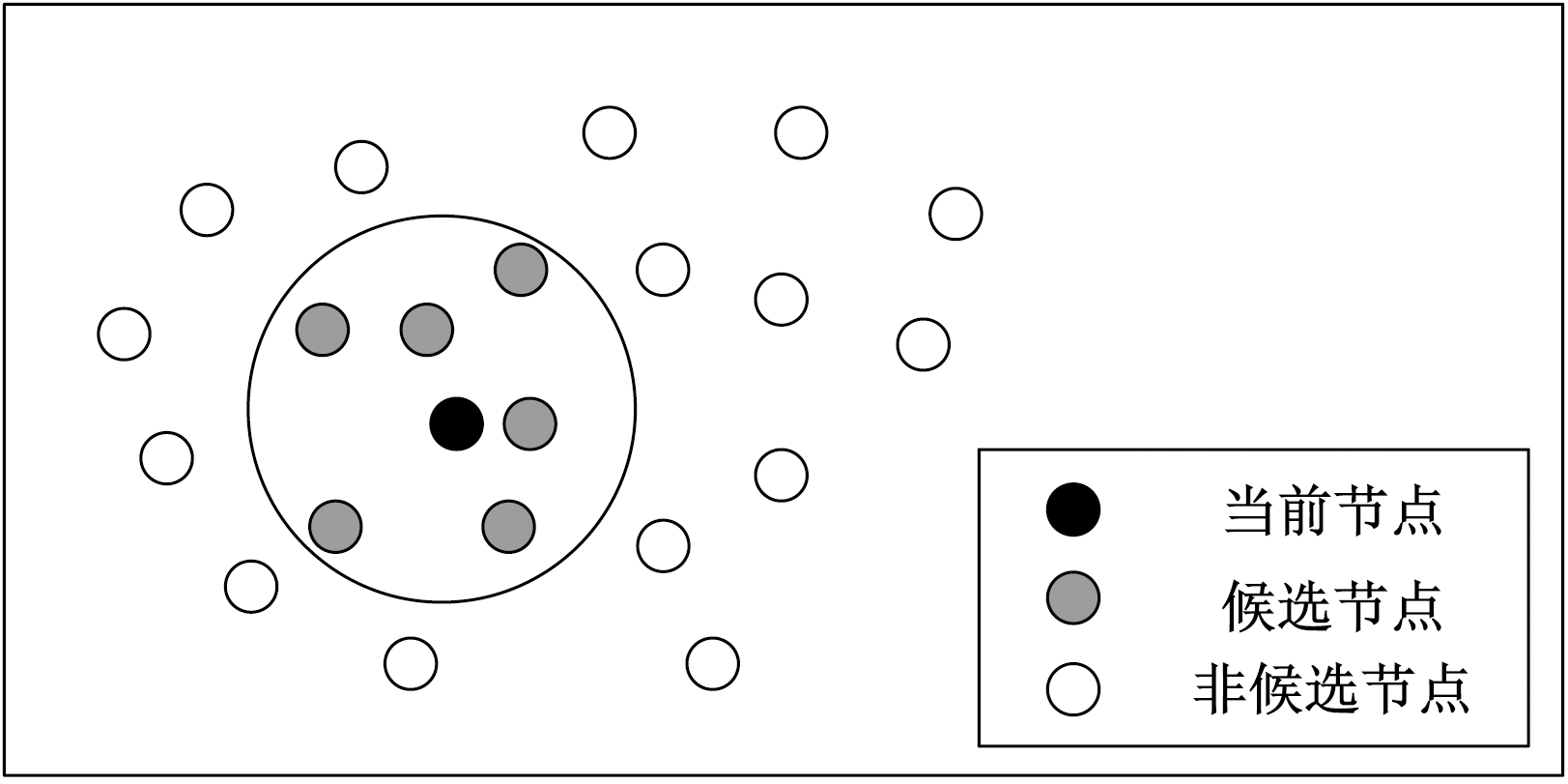
图3 周边选择策略
Figure 3 Peripheral selection strategy
(2)首节点的选择。在可行线路的构建过程中,线路上首节点的选择将会影响接下来整条路径的节点选择,对全局规划来说非常重要。面对大规模客户的VRPTW问题,线路上的首个节点相对于其他节点来说约束较少,可行节点的数量远多于路径中的节点,为了能够从众多可行节点中选择最合适的节点,笔者提出一种首节点选择策略来提升算法的收敛性。该策略可表述为:迭代初期,每条可行线路上的首个节点按概率从候选节点中随机选取,当迭代进度达到一定条件时,首节点为候选节点中转移概率最大的节点。线路的首节点用i1表示,其选取规则如下:
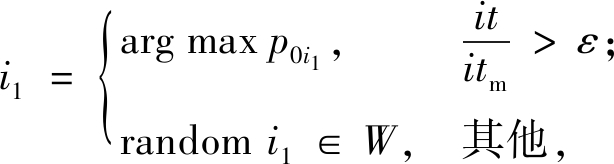
(13)
式中:p0i1表示配货中心到i1的转移概率;it表示当前迭代次数;itm表示最大迭代次数;ε表示迭代的进行程度的参数;W为候选节点集合。
3.2 转移概率公式改进
在解决大规模复杂约束的车辆路径问题时,基本蚁群算法的转移概率公式中包含节点的特征信息较少,导致算法搜索能力不足,收敛速度慢。为了提升算法的收敛性,将节约算法[15]加入转移概率公式。节约算法首先将两个节点i、j分别分配到一条空余的线路上,再计算将两个节点合并到一条线路上后可节省的节约值Sij。式(14)为节约值计算公式。
Sij=d0i+d0j-dij,
(14)
式中:d0i、d0j和dij分别表示配货中心到i、j节点的距离和i、j两节点的距离。改进后的状态转移公式如下:

(15)
3.3 信息素叠加公式的改进
基本蚁群算法在叠加信息素时仅考虑路径的总距离,未对车辆数进行优化。为了在优化距离的同时降低车辆数,本文算法对基本蚁群算法的信息素叠加公式进行了改进,如式(16)所示,使其能够完成双目标的优化。
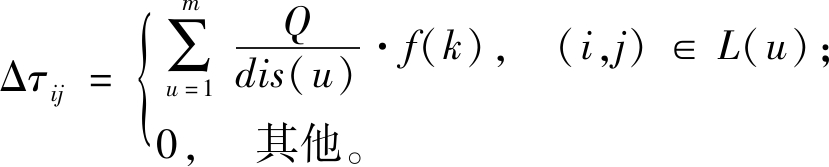
(16)
和式(12)相比,式(16)中增加了和车辆数相关的函数f(k)。f(k)如式(17)所示。
(17)
式中:V(k)为第k只蚂蚁求得可行解的车辆数;Vglobalbest为当前迭代种群中的最小车辆数;Vlocalbest为全局最小车辆数。f(k)可以根据当前解的车辆数对它的信息素浓度进行奖励或惩罚:若当前迭代种群中的最小车辆数大于全局最小车辆数,则对V(k)>Vlocalbest的解进行惩罚;若当前迭代种群中最小车辆数小于全局最小车辆数,那么对V(k)>Vglobalbest的解进行惩罚,对V(k)<Vglobalbest的解进行奖励。
由于蚁群算法中信息素叠加是一个正反馈过程,为了避免搜索停滞,笔者采用最大最小蚁群算法将信息素浓度限定于[τmax,τmin],如式(18)所示
(18)
式中:τinitial表示信息素的初始值。
3.4 改进的局部优化算法
笔者通过实验研究发现,在处理大规模节点和复杂约束的VRPTW问题时,基本蚁群算法构建的可行解中会产生客户数量比较少的线路,这将极大降低车辆的利用率,传统的局部优化算法对此类问题考虑不够。因此笔者提出了一种新的局部优化方法,将插入算法和2-interchange结合,在优化距离同时降低车辆数,提高车辆的利用效率。算法步骤如下。
Step 1 将当前解分为节点数量不小于3的线路集合RM和节点数量小于3的线路集合RN,如图4所示。
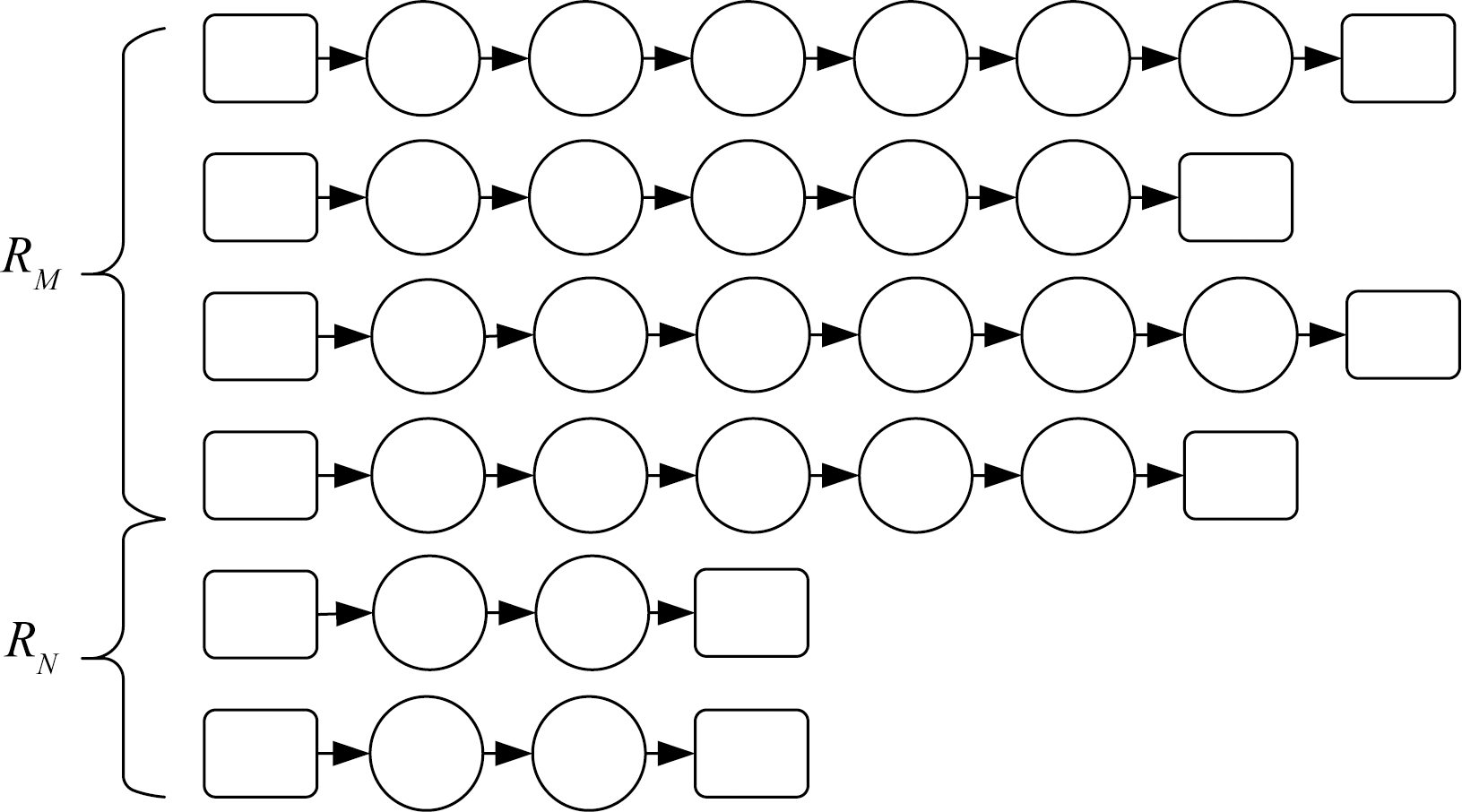
图4 路线分类示意图
Figure 4 Schematic diagram of route classification
Step 2 使用2-interchange和or-interchange对RM进行局部优化z次。迭代初期z取较大值可以加速解的收敛,随着迭代进行,算法产生更优邻域解的难度逐渐加大,通过z取值逐渐减小来提升算法效率。在本文算法中,z初始值为6,每经过10次迭代减小1。
Step 3 设l(i)为RN中第l条线路上的第i个节点,初始化l=1,i=1。
Step 4 将l(i)插入到RM中的所有节点之间。若l(i)插入RM中第k条线路的第j个节点后产生了可行解,根据式(19)计算插入后的ΔCostlikj。式(19)中,cost为线路的总距离;l、k为插入前的线路;lnew、knew为插入后的线路。直到遍历RM中所有线路上的所有节点,计算所有可行解的ΔCostlikj,跳转Step 6。若l(i)插入RM的所有节点之间均无法产生可行解,则转到Step 5。
ΔCostlikj=cost(l)+cost(k)-cost(lnew)-
cost(knew)。
(19)
Step 5 将l(i)与RM中随机一个节点进行交换,要求交换后不改变解的可行性。然后重复Step 4。值得注意的是,每个节点优化时本步骤仅执行一次,若仍无可行解产生,则跳转至Step 7。
Step 6 将l(i)插入到ΔCostlikj最大的位置。更新插入后的线路。
Step 7 令i=i+1,返回至Step 4,继续对下一个节点进行优化,直到线路l上所有节点完成优化。
Step 8 令l=l+1,转至Step 2,继续对下一条线路进行优化,直到RN中所有线路完成优化。
Step 9 将RN中剩余节点使用2-interchange方法优化。
3.5 改进算法整体过程
改进算法整体流程图如图5所示。
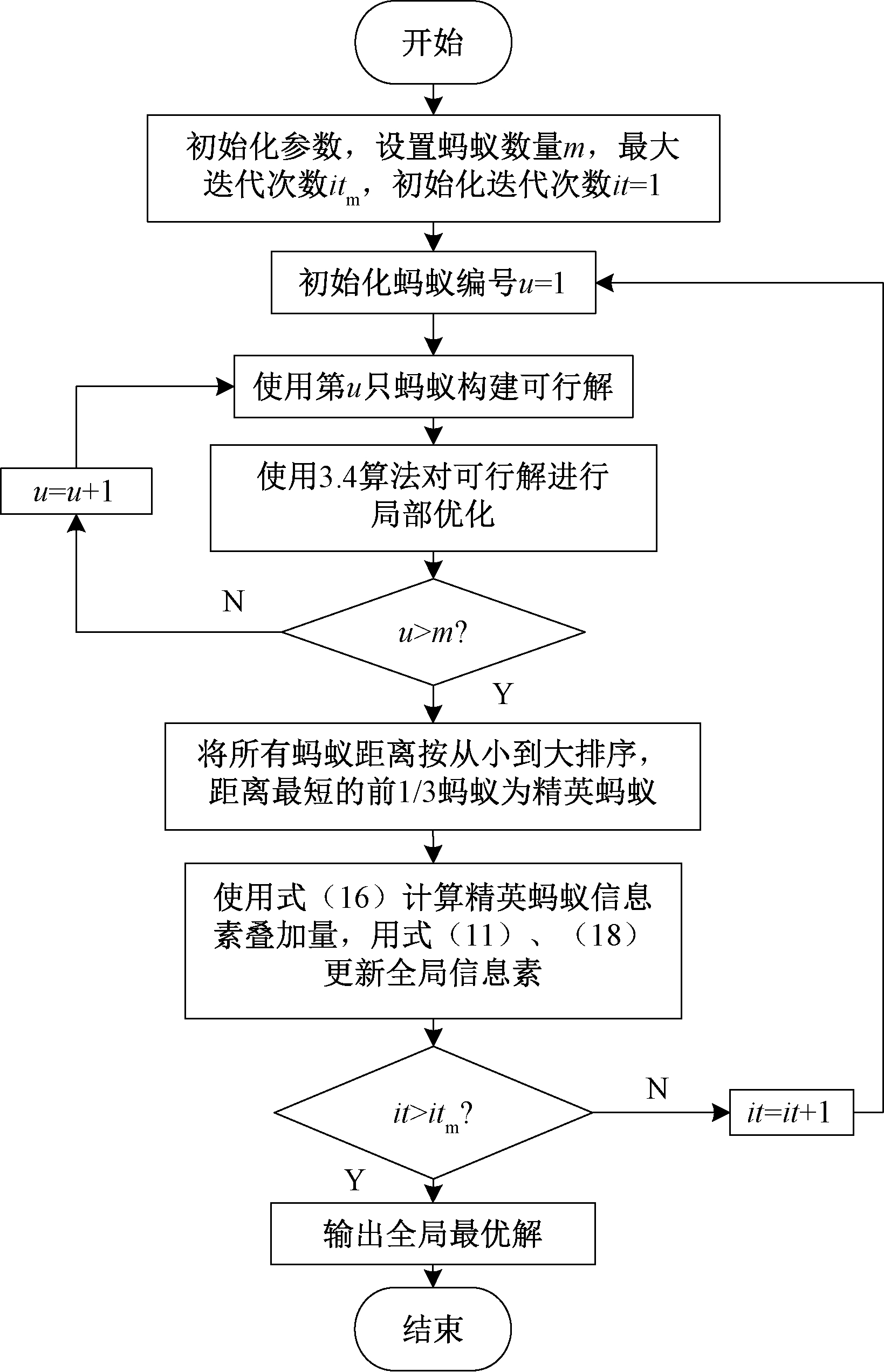
图5 改进算法整体流程图
Figure 5 The overall flow chart of the improved algorithm
4 实验与分析
笔者将改进的蚁群算法在Solomon[16]标准数据集上进行实验。Solomon标准数据集有R1、R2、C1、C2、RC1、RC2共6类问题。这6类问题按节点分布方式可分为随机分布(R)、聚集分布(C)和混合分布(RC)。其中R1、C1、RC1问题中节点的时间窗较窄,车辆载重较小;R2、C2、RC2问题中节点的时间窗较宽,车辆载重较大。Solomon数据集场景多样具有代表性,因此其常被文献用于算法评估。
4.1 参数设置
笔者提出的改进混合蚁群算法中主要参数有式(15)中启发因子α、β和式(16)中每只蚂蚁信息素总量Q。为了分析这些参数对算法的影响,笔者在C101测试问题上进行实验。每组实验均进行5次,取结果的平均值。实验最大迭代次数itm=60,信息素挥发速率ρ =0.08。α、β与结果的关系如图6所示。每只蚂蚁释放信息素总量Q与结果的关系如图7所示。
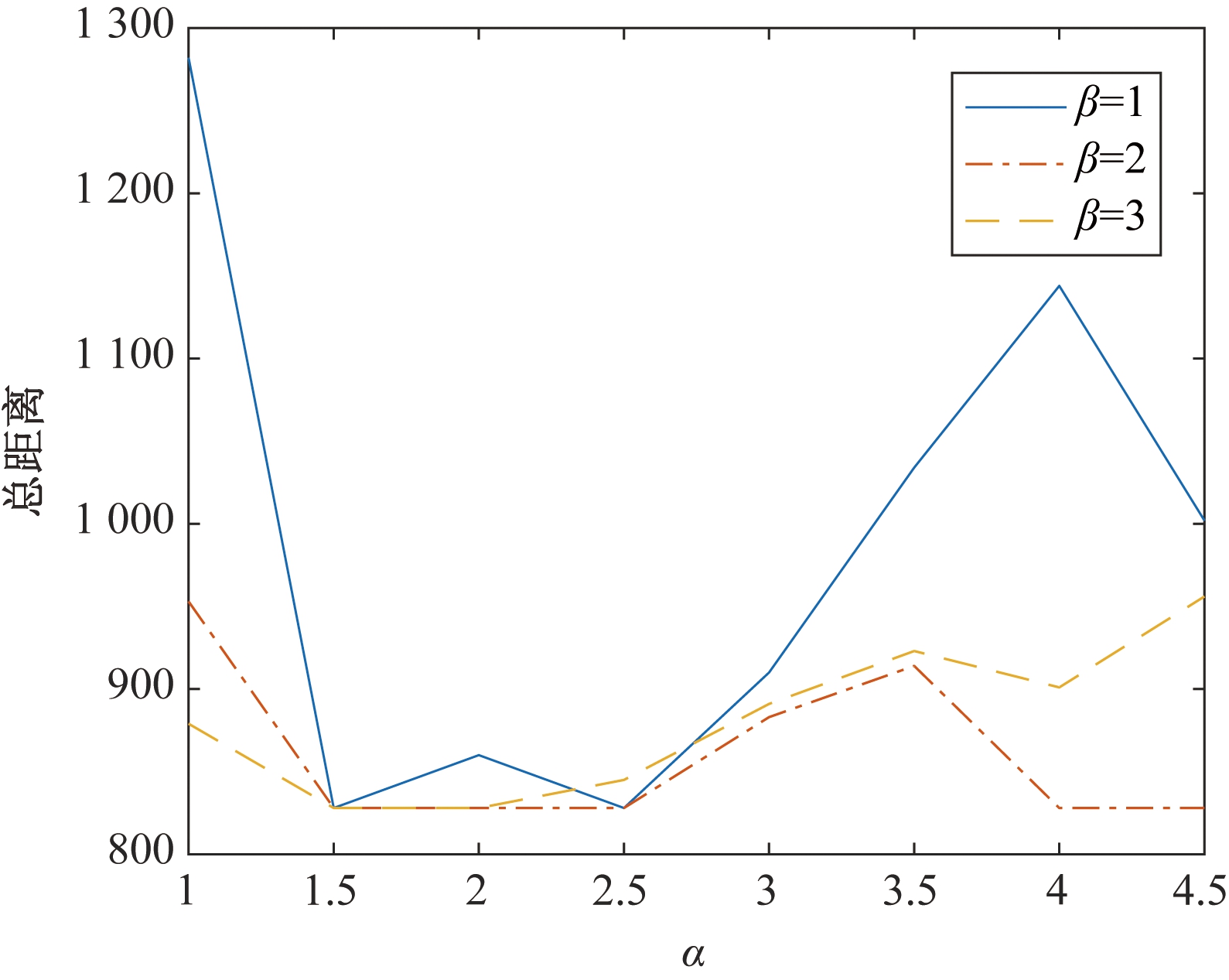
图6 α、β取值与总距离的关系
Figure 6 The relationship between the values of α,β and the total distance
从图6可以看出,当1.5<α<2.5、β=2时,算法取得较好结果。从图7可以看出,60<Q<100时,算法可以取得较好结果。
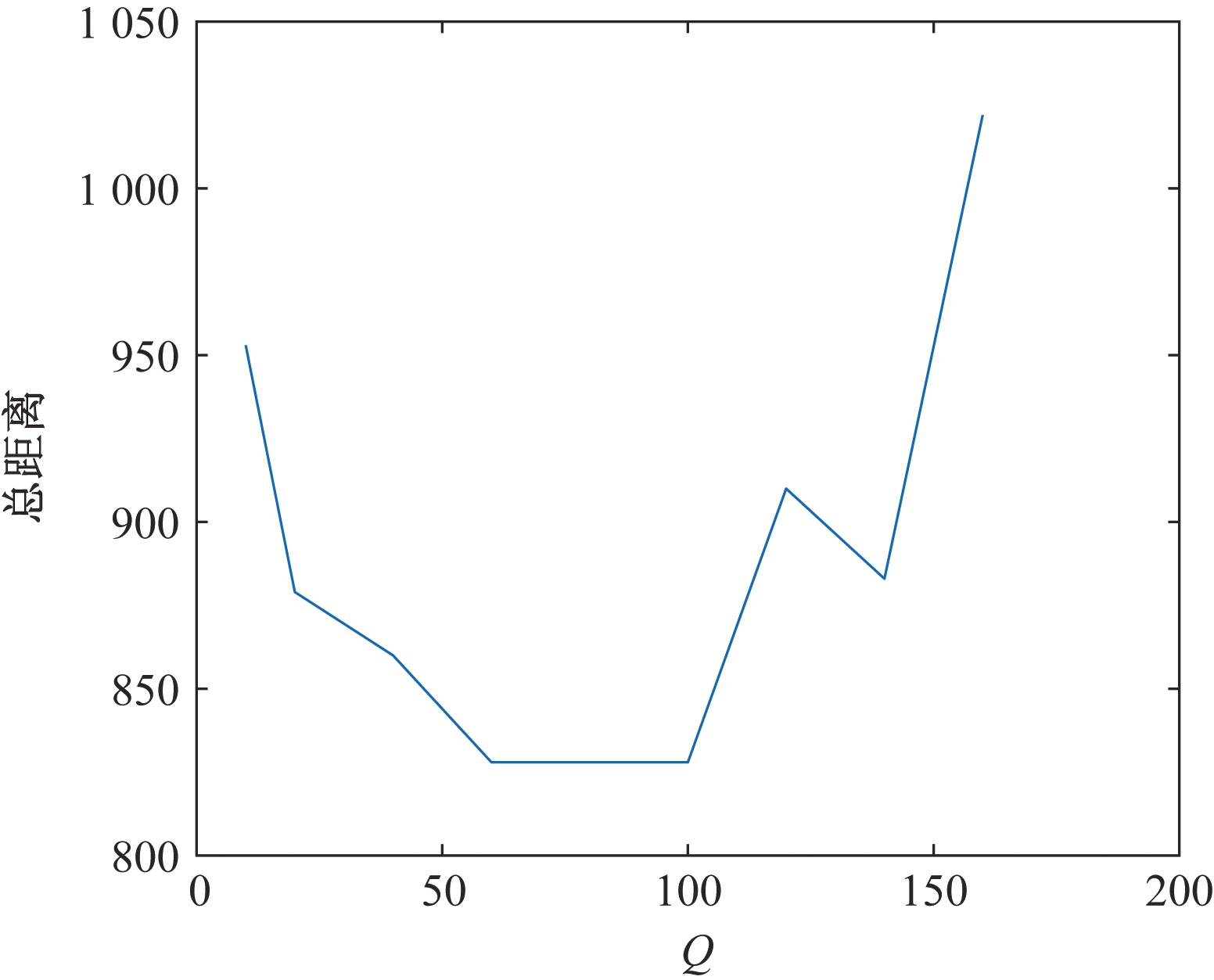
图7 Q取值与总距离的关系
Figure 7 The relationship between Q and total distance
4.2 首节点选择策略的有效性
为了验证首节点选择策略的有效性,在标准数据集中C101测试问题上进行了相关实验。
首先对式(13)中参数ε的取值进行相关实验。若ε过小,算法会过早收敛,陷入局部最优;若ε较大,算法收敛速度慢,不能收敛于最优解。本实验中对每个ε取值都进行5次实验,结果取平均值。实验结果如图8所示。
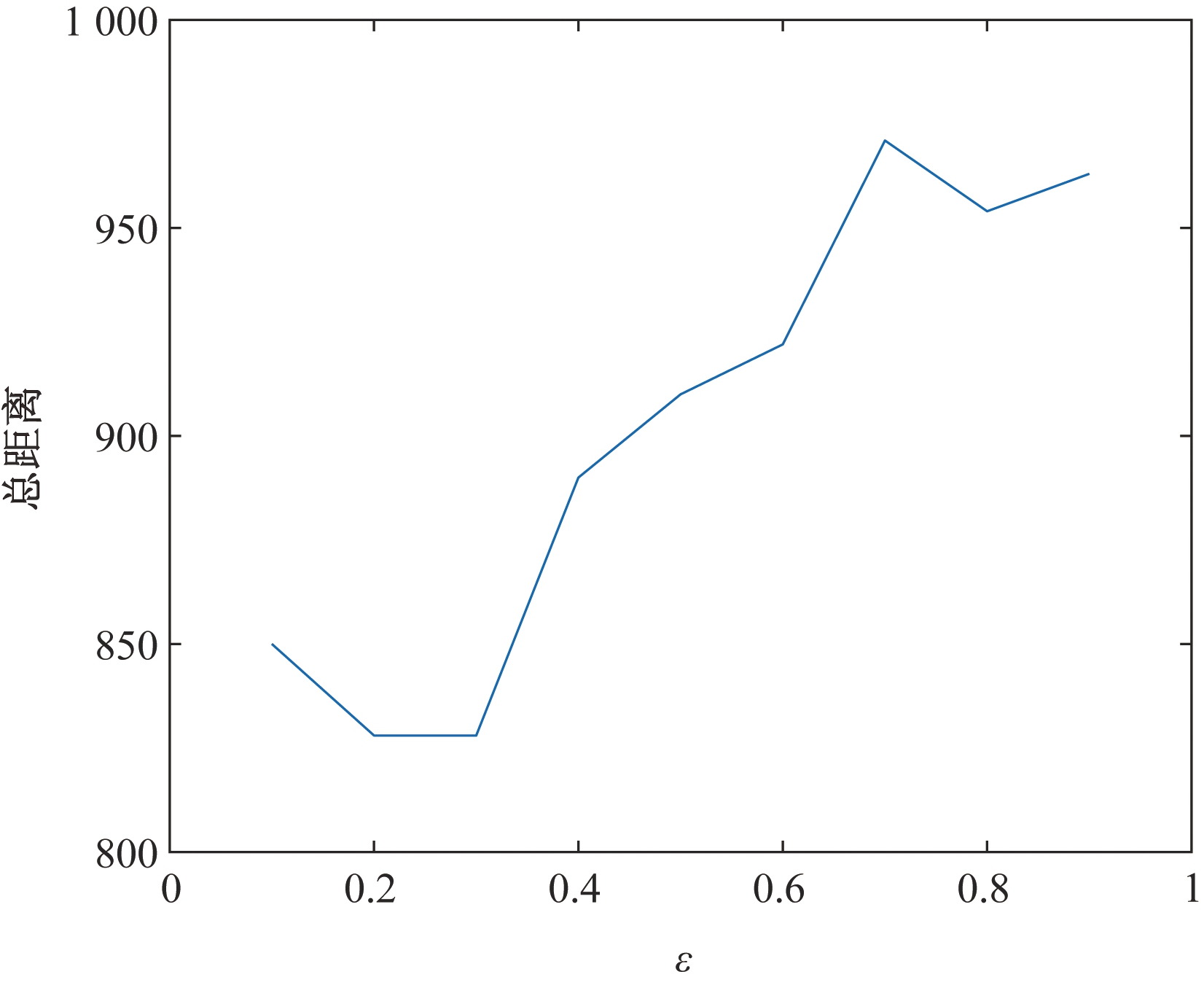
图8 ε取值与总距离关系
Figure 8 The relationship between ε and total distance
从图8中可以看出,当0.2<ε<0.3时算法取得较好结果。
在相同条件下将无首节点选择策略的算法和加入首节点选择策略的算法进行对照试验。两者都运行5次,结果取平均值,实验结果如图9所示。
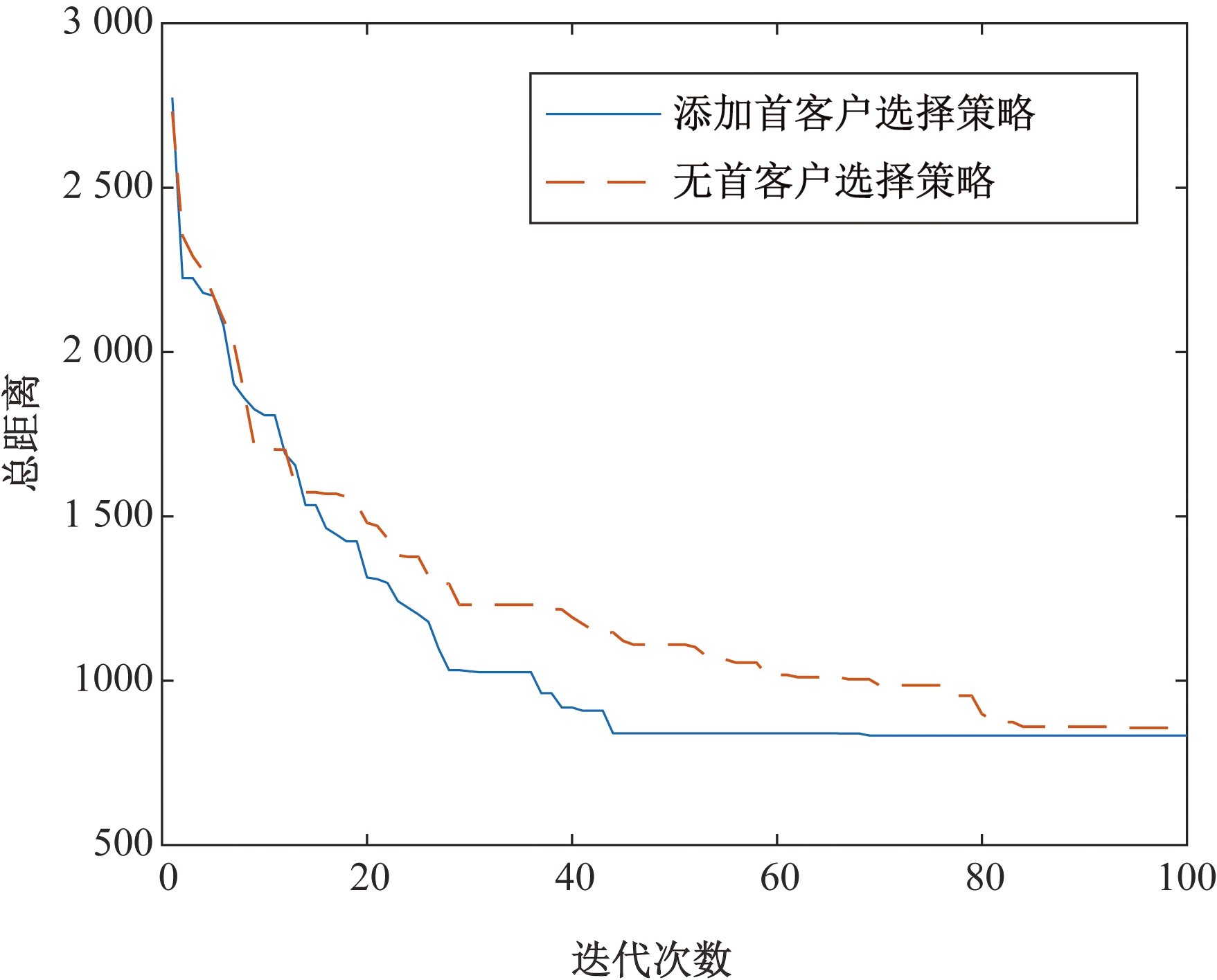
图9 添加首节点选择策略和无首节点选择策略的比较
Figure 9 Comparisons of adding first node selection policy and no-first node selection policy
从图9中可以看出,虽然两者算法都收敛于最优解,但是加入首节点选择策略后算法的收敛速度明显变快,这也证明笔者提出的首节点选择策略可以提高算法的收敛速度。
4.3 标准数据集测试
为了说明本文算法具有适应性和有效性,笔者从标准数据集的每类问题中选取一个进行实验,将实验结果与基本蚁群算法和Teymourian等[6]提出的混合蚁群算法、Ghoseiri等[17]提出的混合遗传算法进行比较。实验用MATLAB 2016a进行编程,在Intel Core i5-5200 CPU,4 GB内存,windows8.1操作系统的计算机上运行。实验参数蚂蚁数量m=15,最大迭代次数itm=60,ρ=0.08,根据参数设置的实验结果取α=2、β=2、Q=80。本文算法在所选问题上运行3次取最优结果,实验结果如表1所示。其中总距离为TD,车辆数为VN。为了便于比较算法平均值之间的差异,设res表示本文结果的平均值,res′表示其他算法结果的平均值,Δ表示结果之间的差距百分比,按式(20)计算。
(20)
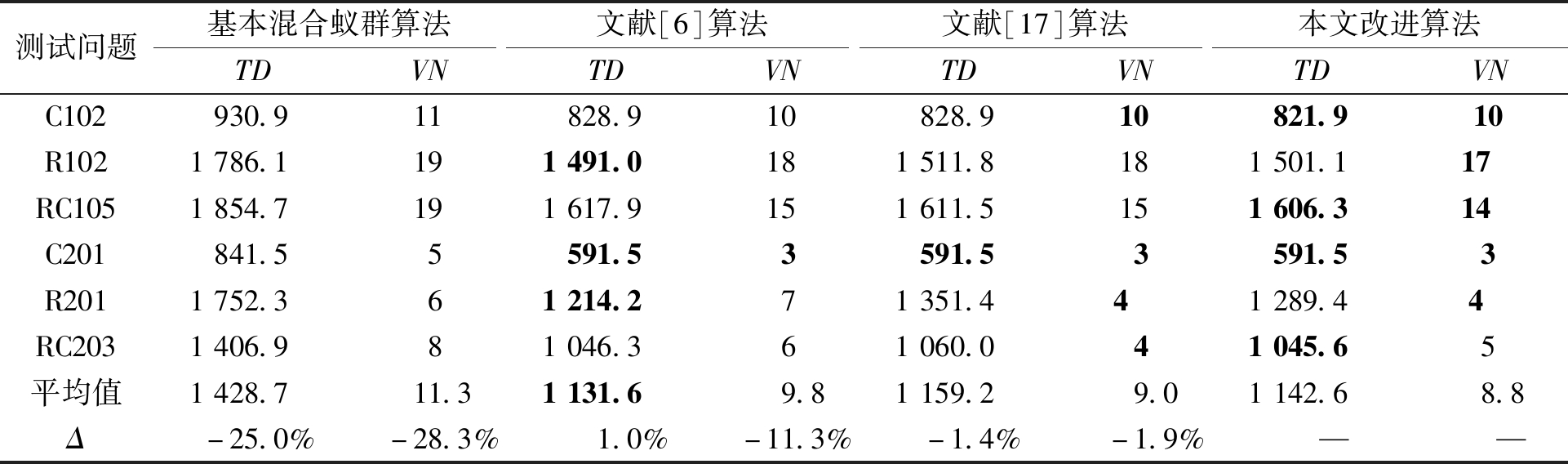
从表1中可以看出,在得出的12个结果中,笔者提出的改进算法在总距离和车辆数上都明显优于基本混合蚁群算法;和文献中算法相比,本文算法75%的结果取得了最优解,文献[6]算法41.6%的结果取得最优解,文献[17]算法41.6%的结果取得最优解。从所有结果的平均值来看,与基本混合蚁群算法相比,本文算法在总距离上领先了25.0%,在车辆数上领先了28.3%;与文献[6]算法相比,本文算法在总距离上落后了1.0%,但是在车辆数上领先了11.3%;与文献[17]算法相比,本文算法在总距离上领先了1.4%,在车辆数上领先了1.9%。此外本文算法在不同类型测试问题上均采用相同参数进行实验,这也说明了本文算法具有较强的适应能力。
表1 Solomon数据集测试结果
Table 1 Solomon data set test results
测试问题基本混合蚁群算法文献[6]算法文献[17]算法本文改进算法TDVNTDVNTDVNTDVNC102930.911828.910828.910821.910R1021786.1191491.0181511.8181501.117RC1051854.7191617.9151611.5151606.314C201841.55591.53591.53591.53R2011752.361214.271351.441289.44RC2031406.981046.361060.041045.65平均值1428.711.31131.69.81159.29.01142.68.8Δ-25.0%-28.3%1.0%-11.3%-1.4%-1.9%——
5 结论
笔者通过分析传统混合蚁群算法在求解大规模带时间窗路径规划问题(VRPTW)中存在的不足,提出了一种改进的双目标混合蚁群算法。该算法有针对性地采用了首节点选择策略和改进状态转移公式来加速收敛过程;考虑到路径距离与车辆数量两个优化目标,在信息素叠加过程增加了车辆数惩罚,同时改进了全局信息素更新策略。本文改进算法有效地提高了车辆利用率,扩大了搜索空间,能够在双目标下给出较优解。通过在Solomon标准数据集上的实验,验证了笔者所提算法的有效性。
[1] DANTZIG G B,RAMSER J H.The truck dispatching problem[J].Management science,1959,6(1):80-91.
[2] MOHAMMED M A,GANI M K A,HAMED R I,et al.Solving vehicle routing problem by using improved genetic algorithm for optimal solution[J].Journal of computational science,2017,21:255-262.
[3] DE OLIVEIRA DA COSTA P R,MAUCERI S,CARROLL P,et al.A genetic algorithm for a green vehicle routing problem[J].Electronic notes in discrete mathematics,2018,64:65-74.
[4] 汪慎文,杨锋,徐亮,等.离散差分进化算法求解共享单车调度问题[J].郑州大学学报(工学版),2019,40(4):48-53.
[5] 崔岩,张子祥,时新,等.考虑顾客时间紧迫度的生鲜电商配送路径优化问题[J].郑州大学学报(工学版),2017,38(6):59-63.
[6] TEYMOURIAN E,KAYVANFAR V,KOMAKI G M,et al.Enhanced intelligent water drops and cuckoo search algorithms for solving the capacitated vehicle routing problem[J].Information sciences,2016,334:354-378.
[7] DORIGO M,MANIEZZO V,COLORNI A.Ant system:optimization by a colony of cooperating agents[J].IEEE transactions on systems,man and cybernetics,part B (cybernetics),1996,26(1):29-41.
[8] YU B,YANG Z Z,YAO B Z.A hybrid algorithm for vehicle routing problem with time windows[J].Expert systems with applications,2011,38(1):435-441.
[9] DING Q L,HU X P,SUN L J,et al.An improved ant colony optimization and its application to vehicle routing problem with time windows[J].Neurocomputing,2012,98:101-107.
[10] 朱杰,张培斯,张询影,等.基于改进蚁群算法的多时间窗车辆路径问题[J].计算机技术与发展,2019,29(1):102-105.
[11] 刘云,张惠珍.多目标带时间窗的车辆路径问题的单亲遗传混合蚁群算法[J].公路交通科技,2016,33(6):95-100,106.
[12] 柴获,何瑞春,苏江省,等.求解双目标带时间窗车辆路径问题的蚁群算法[J].交通运输系统工程与信息,2018,18(4):156-162.
[13] 孙小军,介科伟.求解带时间窗动态车辆路径问题的改进蚁群算法[J].大连理工大学学报,2018,58(5):539-546.
[14] 葛斌,韩江洪,魏臻,等.求解带时间窗车辆路径问题的动态混合蚁群优化算法[J].模式识别与人工智能,2015,28(7):641-650.
[15] CLARKE G,WRIGHT J W.Scheduling of vehicles from a central depot to a number of delivery points[J].Operations research,1964,12(4):568-581.
[16] SOLOMON M M.Algorithms for the vehicle routing and scheduling problems with time window constraints[J].Operations research,1987,35(2):254-265.
[17] GHOSEIRI K,GHANNADPOUR S F.Multi-objective vehicle routing problem with time windows using goal programming and genetic algorithm[J].Applied soft computing,2010,10(4):1096-1107.