0 引言
电网重构是一种通过改变配电系统线路的分段开关和联络开关，甚至调节微源以及负荷的功率，进而调整系统网架结构和潮流分布的手段。在组建电网准则和系统安全运行的条件下，通过重构使某些指标最优。所以，微电网重构具有改善供电电能质量[1]、平衡负荷[2]、提高系统的经济性、支援大电网恢复等的能力。
目前，电力系统重构的相关研究已有不少成果，其中对重构方法的研究较多。Shariatzadeh等[3]采用遗传算法(genetic algorithm,GA)解决微电网故障重构问题，验证了实时重构的可行性。 Chen等[4]为解决灾后微电网由局部到整体的重构问题，采用多代理系统的重构策略，通过自主通信实现恢复供电。 Zhao等[5]提出了基于拉格朗日技术和动态规划的重构策略，解决了主网非计划故障时微电网孤岛重构问题。李咸善等[6]提出了分级优化的重构方法，将不涉及潮流计算的寻优过程作为第一级先行处理，将涉及潮流计算的寻优过程作为第二级后续优化处理，提高了计算效率。 Gazijahani等[7]为解决微电网中的不确定性提出了鲁棒框架法，并采用灰狼优化算法(grey wolf optimization,GWO)解决重构优化问题。
电网重构多采用群体智能优化算法，如GA、粒子群算法(particle swarm optimization,PSO)或GWO。其中，GWO比GA原理简单，比PSO求解精度高、稳定性好，但是具有种群多样性差和易陷入局部最优的缺点[8]。另外，在电网重构中群体智能算法的解分为环路解、含孤立支路的解和辐射状解，其中辐射状解是可行解，环路解和含孤立支路的解是无效解。这些无效解既不符合微电网开环运行的特点，也不便于系统网络的潮流计算。一般会筛掉无效解[9]，而直接筛掉无效解会缩小搜索空间范围，影响求解效果。
针对以上问题，提出一种深度优先搜索(deep first search,DFS)和GWO相结合的重构方法，以GWO为框架，每次迭代后用DFS处理解集，将其中的无效解转化为可行解。GWO与DFS结合后，既可解决无效解造成的求解问题，又可增加GWO的种群多样性。
1 微电网重构模型
微电网是中低压自治配电系统，典型设备有分布式电源、储能装置、负荷和配电线路等。以IEEE33节点测试系统作为微电网测试系统[10]，见图1。图1中网架结构主要由节点和支路构成，其中节点由母线、变电站、配电柜、负荷等效而成，支路由配电线路及其上的分段开关和联络开关等效而成。该系统网架结构共有33个节点，32个分段开关，5个联络开关和5个环路。
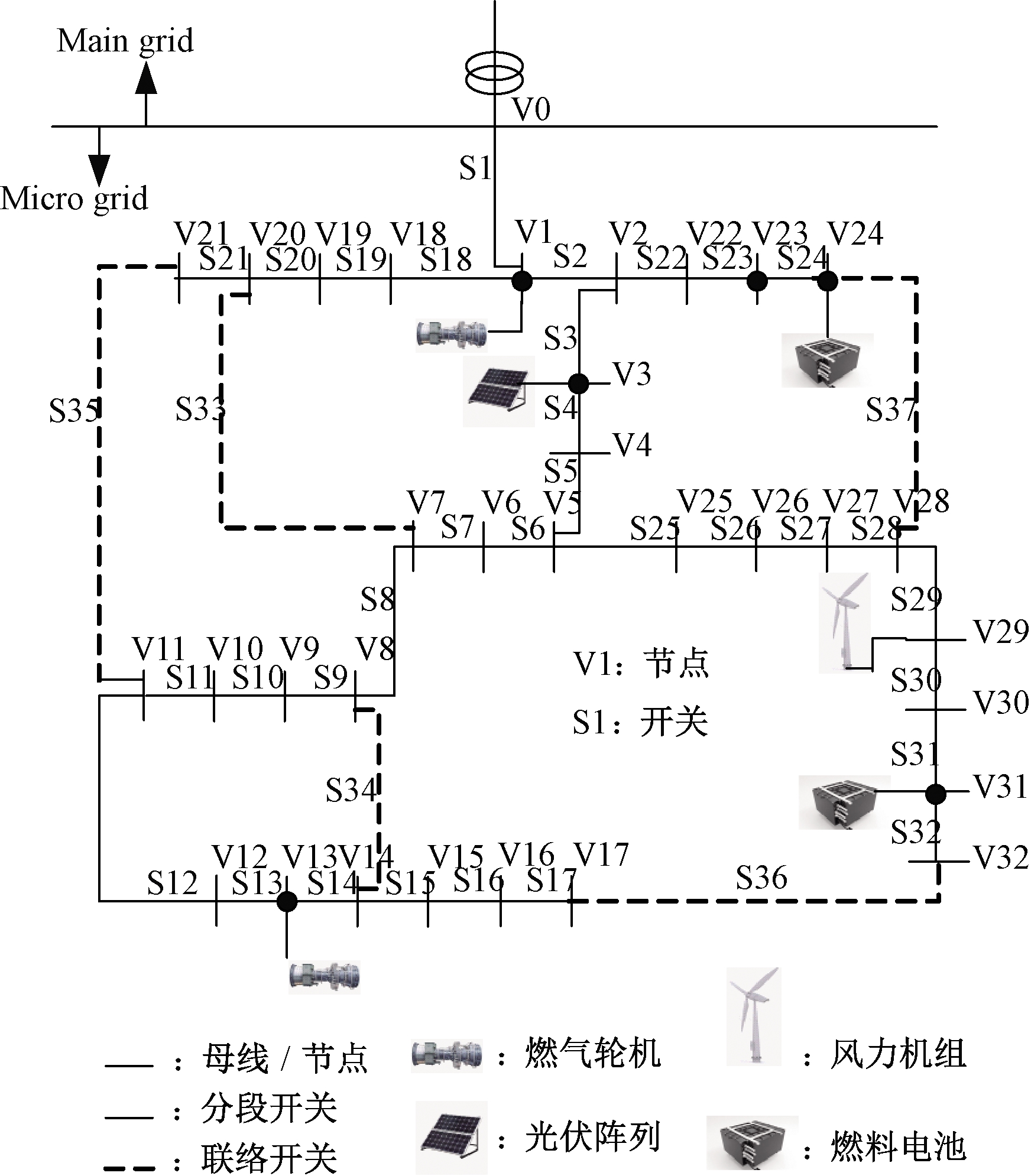
图1 IEEE33节点微电网测试系统
Figure 1 33 nodes IEEE Test System of Microgrid
为保证重构方案正常运行所需的电气约束条件和组网准则，建立的微电网重构模型有重构目标、发用电设备模型和配电系统网络模型3部分。电网优化问题往往离不开功率调节[11]，所以重构模型中的控制变量包括开关和可调功率。
1.1 重构目标
以保留供电负荷最大和电压偏移最小为重构指标，则重构目标表示为
(1)
式中:ω1、ω2为两个指标的权重系数；
分别为系统的基准电压和基准功率；m为节点m；Um为节点m的电压；
为节点m的电压额定值；
为节点m上的负荷。
1.2 发用电设备模型
将储能装置和分布式电源作为微源，包括燃气轮机、光伏阵列、风力机组、燃料电池。微电网孤岛重构时，燃气轮机作为支撑型微源，稳定系统电压和支撑系统频率；风力机组作为不可调微源，因为其功率不能及时响应负荷变化；非支撑型燃气轮机、光伏阵列和燃料电池作为可调微源。负荷可以分为可调负荷和不可调负荷。如果给定功率因数，则这些设备的无功功率由其有功功率决定。 因此将这些设备的有功功率作为控制变量中的可调功率变量。
微源可调功率约束条件:
(2)
(3)
式中：
为节点m上微源的工作状态，其值是0或1， 0表示不工作，1表示正常工作；
分别表示节点m上微源的有功功率及其上下限与无功功率及其上下限。储能装置充电时，其输出功率取为负值，仍受式(2)、(3)约束。
负荷可调功率约束条件：
(4)
(5)
式中:
为节点m上负荷的工作状态，其值是0或
和
分别表示节点m上负荷的有功功率及其上下限与无功功率及其上下限。其中不可调负荷的功率由日负荷预测曲线得到。
1.3 配电网络模型
网架结构主要由节点和支路构成，相关的状态变量有节点注入电流、节点电压、支路电流和损耗功率、网架结构等，故配电网络模型[10]如下：
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
r∈ΩRadia，
(16)
式中：
分别为节点m上的注入有功功率和无功功率；
为节点m上注入电流相量的复数共轭；Um为节点m的电压相量；k为节点m下游邻节点；Cm为节点m的所有下游邻节点构成的集合；rlm、xlm分别为支路lm的电阻和电抗；
为流过支路lm的电流相量；
为流过支路lm的电流幅值及其上限；
为支路lm损耗的有功功率和无功功率；
分别表示节点m上的电压幅值及其上下限；r为一种网架结构；ΩRadia为所有辐射状网架结构构成的集合。
2 模型处理
2.1 适应度函数
根据式(6)～(9)、(11)、(12)，采用前推回代法[12]，计算出网架结构的潮流。根据式(2)～(5)，检查功率变量是否越界，如果越界，则限制在邻近的边界上。根据重构模型的式(10)、(13)～(15)，将系统功率平衡状况和状态变量是否超过安全域表示如下:
(17)
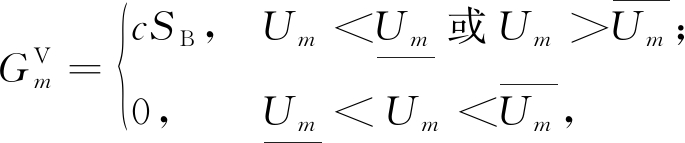
(18)
(19)
(20)
式中：c为一个比较大的常数，以保证当系统运行状态超出安全域时
和
的值非常大。
根据式(1)、(17)～(20)，得到综合适应度函数如下：
(21)
式中：ω1+ω2+ω3+ω4 +ω5=1，显然，适应度值越小重构方案越优秀，其单位为VA。
2.2 DFS
重构模型的解由开关状态的组合序列和可调功率构成，其中不同的开关组合表示不同的网架结构，如公式(16)可由DFS程序进行处理。DFS的功能为：1)识别网架结构中开关的状态，是打开还是闭合；2)判断网架结构的类型，是环路解、含孤立支路解，还是辐射状解；3)保留辐射状解，打开环路解中的环路，新产生随机辐射状解取代含孤立支路的解。
3 重构方法
3.1 GWO
假设灰狼群体数量为N，由适应度大小将群体分为4个小狼群，最优α狼群、次优β狼群、第3最优δ狼群和普通ω狼群。第t代狼群的位置向量为Xt，第t+1代灰狼群的更新位置向量Xt+1，那么由第t代到第t+1代的灰狼数学模型[13]如下:
(22)
A=2a·r1-a；
(23)
C=2r2；
(24)
(25)
(26)
(27)
式中：a为迭代因子；A为灰狼对猎物的包围圈；C为灰狼围绕猎物的扰动因子；t为迭代次数；tmax为最大迭代次数；a随着t由2线性减小到0；r1、r2为[0,1]的随机数；显然，A的范围为
分别是在第t次迭代中各等级灰狼的最佳位置。
第t次迭代，经各等级小灰狼群指导后，狼群更新的位置向量，表示为
(28)
(29)
(30)
综合式(28)、(29)、(30)，最终获得第t+1代全体灰狼的位置向量，表示为
(31)
3.2 与DFS结合的GWO重构算法步骤
(1)初始化程序中微电网的基本信息。
(2)获取微电网运行的实时信息。
(3)设置算法的参数。
(4)初始化个体信息，主要是包含网架结构和可调功率的控制变量。
(5)采用DFS对个体的网架结构进行识别、分析和处理，保证所有个体的网架结构均为辐射状结构。
(6)计算个体网架结构的节点注入功率，用前推回代法计算各个体网架结构的节点电压分布。
(7)根据式(21)，计算个体的适应度，根据适应度的大小将群体分为α、β、δ、ω 4个等级，并在不同等级最优个体的指导下，用公式(22)～(31)对个体的控制变量进行更新，获得新一代个体。
(8)判断是否达到最大迭代次数。没有达到，返回步骤(5);否则，输出最佳重构方案。
4 仿真分析
IEEE33节点微电网测试系统的电压等级为12.66 kV，正常运行时电压范围为11.39～12.66 kV。初始网架结构为5个联络开关处于断开状态，其他分段开关处于闭合状态。某一时刻的系统网架信息和各节点注入功率数据见文献[14]。离网重构时节点1处的燃气轮机组作为平衡微源，微源和可调负荷的参数见表1和表2。计算时，额定电压为12.03 kV，功率基准值为1 000 kVA，电压基准值为12.66 kV,编程软件为MATLAB2014a。
表1 微源参数
Table 1 Characteristic of generating equipments in microgrid
参数燃气轮机组燃气轮机组光伏阵列风力机组燃料电池燃料电池有功功率/MW1.000～3.0000.600～1.0000.000～2.0000.000～1.5000.050～0.2000.050～0.200功率因数—0.851.000.801.001.00节点1133292431
表2 可调负荷参数
Table 2 Characteristic of adjustable loads in microgrid
参数负荷1负荷2负荷3负荷4负荷5负荷6负荷7有功功率/MW0.000～0.2000.000～0.2000.200～0.4200.200～0.4200.000～0.2000.000～0.1500.100～0.210功率因数0.900.900.900.901.000.900.90节点672324293031
4.1 控制变量对系统运行状态的影响
当仅以开关状态为控制变量时，节点13、24、29、31处的微源和可调负荷均以最大功率运行。分别以开关状态、可调功率、开关状态与可调功率的组合为控制变量，随机生成500组数据。对这3种情况，利用前推回代法分别计算系统的节点电压，结果见图2～图4。
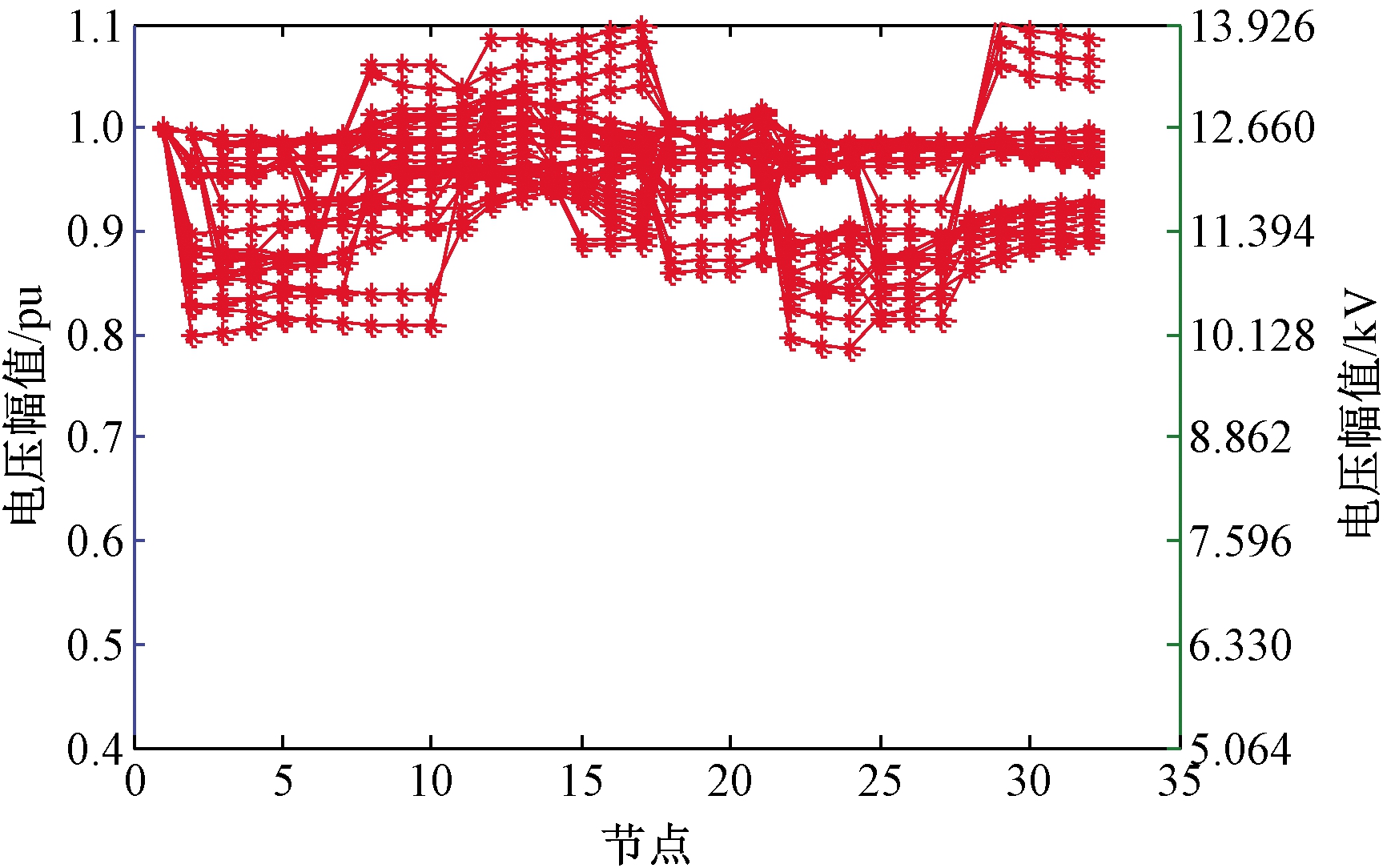
图2 以开关状态为控制变量时电压分布曲线
Figure 2 Voltage distribution curve with switch as control variable
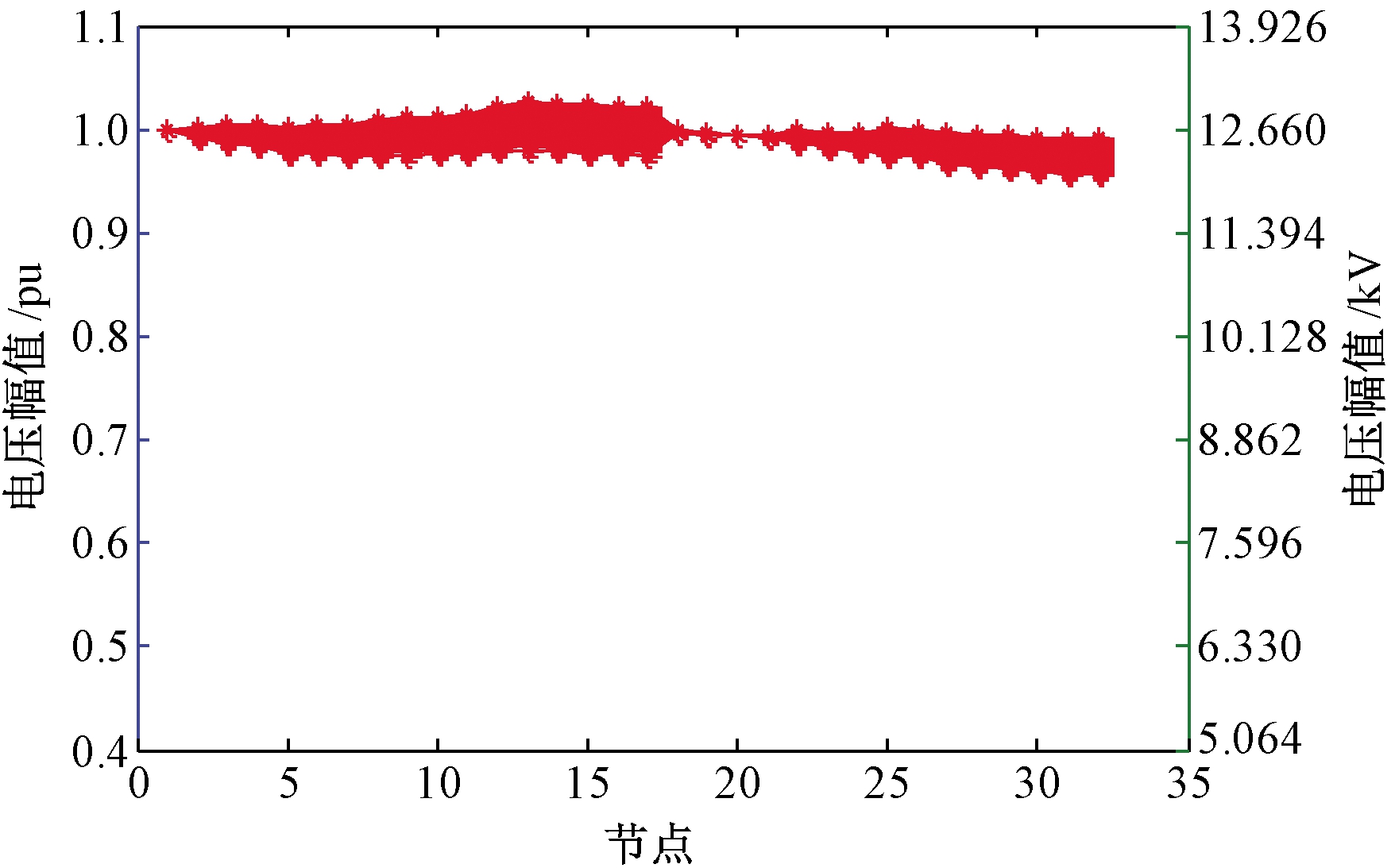
图3 以功率为控制变量时电压分布曲线
Figure 3 Voltage distribution curve with power as control variable
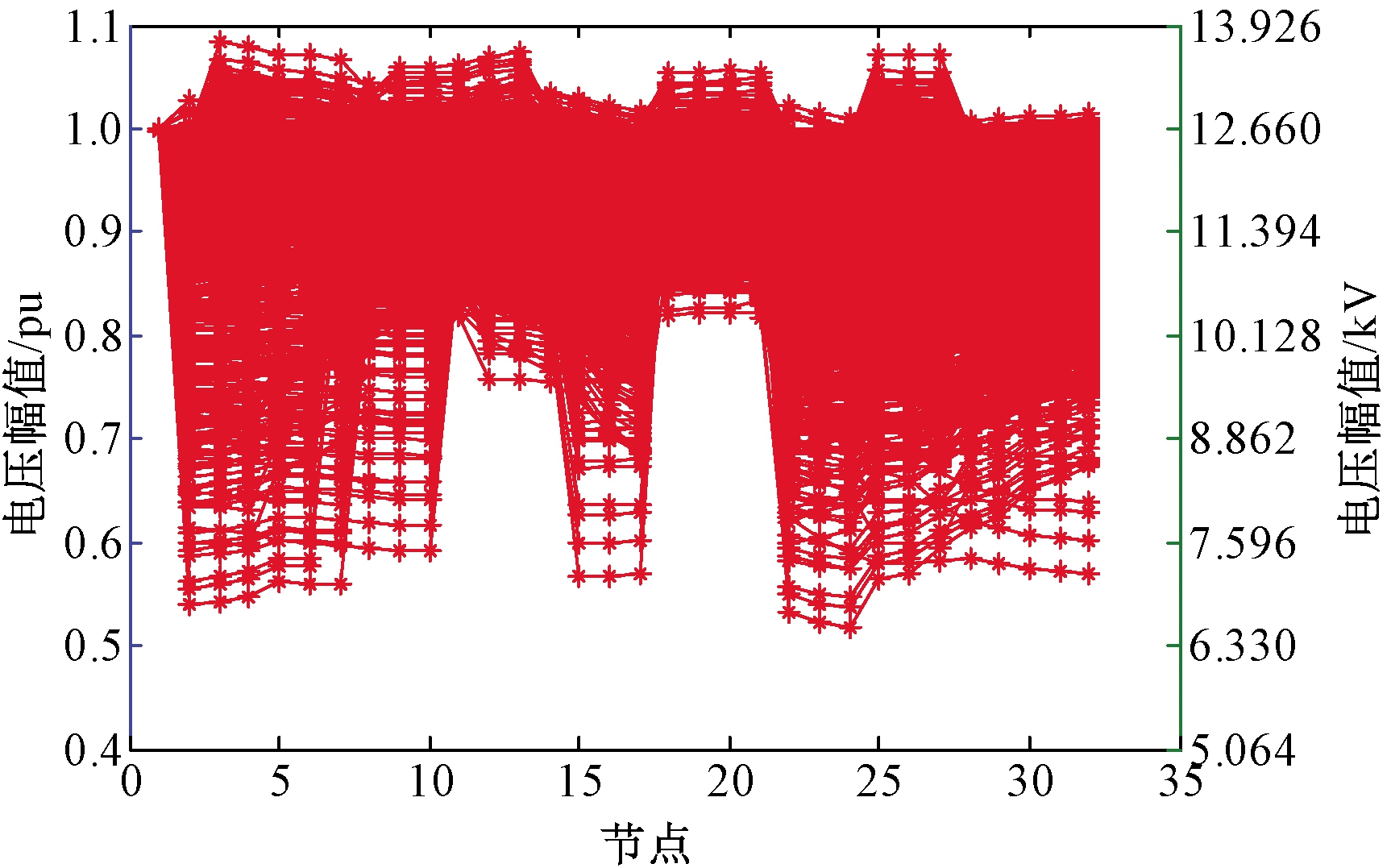
图4 以开关状态和功率为控制变量时电压分布曲线
Figure 4 Voltage distribution curve with switch and power as control variable
由图2可知，当仅以开关状态为控制变量时，系统电压幅值的调整范围比较大，甚至部分方案的调整范围超出了±5%，并且曲线之间存在较大的调整盲区，不能做到电压幅值的平滑调节。由图3可知，当仅以可调功率为控制变量时，系统电压幅值调整的特点与仅以开关状态为控制变量时相反，电压幅值调整能够做到平滑调节，并且调整范围比较小。由图4可知，当以开关状态和可调功率的组合作为控制变量时，具有明显优势，系统电压幅值既能平滑调整，调整范围又更大。
4.2 应用结合DFS的GWO算法进行重构
假设光伏阵列功率可以达到最大值、风力机组功率的预测值为800 kW和燃料电池均放电。适应度函数的系数c=1 000，权重系数ω1=0.469 5，ω2=0.046 9，ω3=0.469 5，ω4=0.009 4，ω5=0.004 7。重构算法的每代个体数为50个，最大迭代次数为100代。
由结合DFS的GWO算法得到最佳重构方案，操作的开关组合为闭合S35、S36和S37,打开S3、S11和S18，微源最佳输出功率和可调负荷最佳保留功率分别见表3和表4，而节点电压分布曲线见图5。
表3 最佳重构方案中微源输出功率
Table 3 Output power of generating enuipments in the optimal reconfiguration scheme
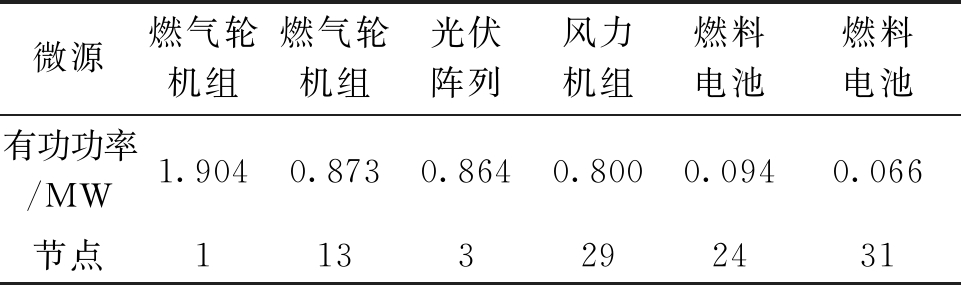
微源燃气轮机组燃气轮机组光伏阵列风力机组燃料电池燃料电池有功功率/MW1.9040.8730.8640.8000.0940.066节点1133292431
表4 最佳重构方案中可调负荷保留功率
Table 4 Reserve power of adjustable loads in the optimal reconfiguration scheme
参数负荷1负荷2负荷3负荷4负荷5负荷6负荷7有功功率/MW0.2000.2000.4200.4200.2000.1500.210节点672324293031
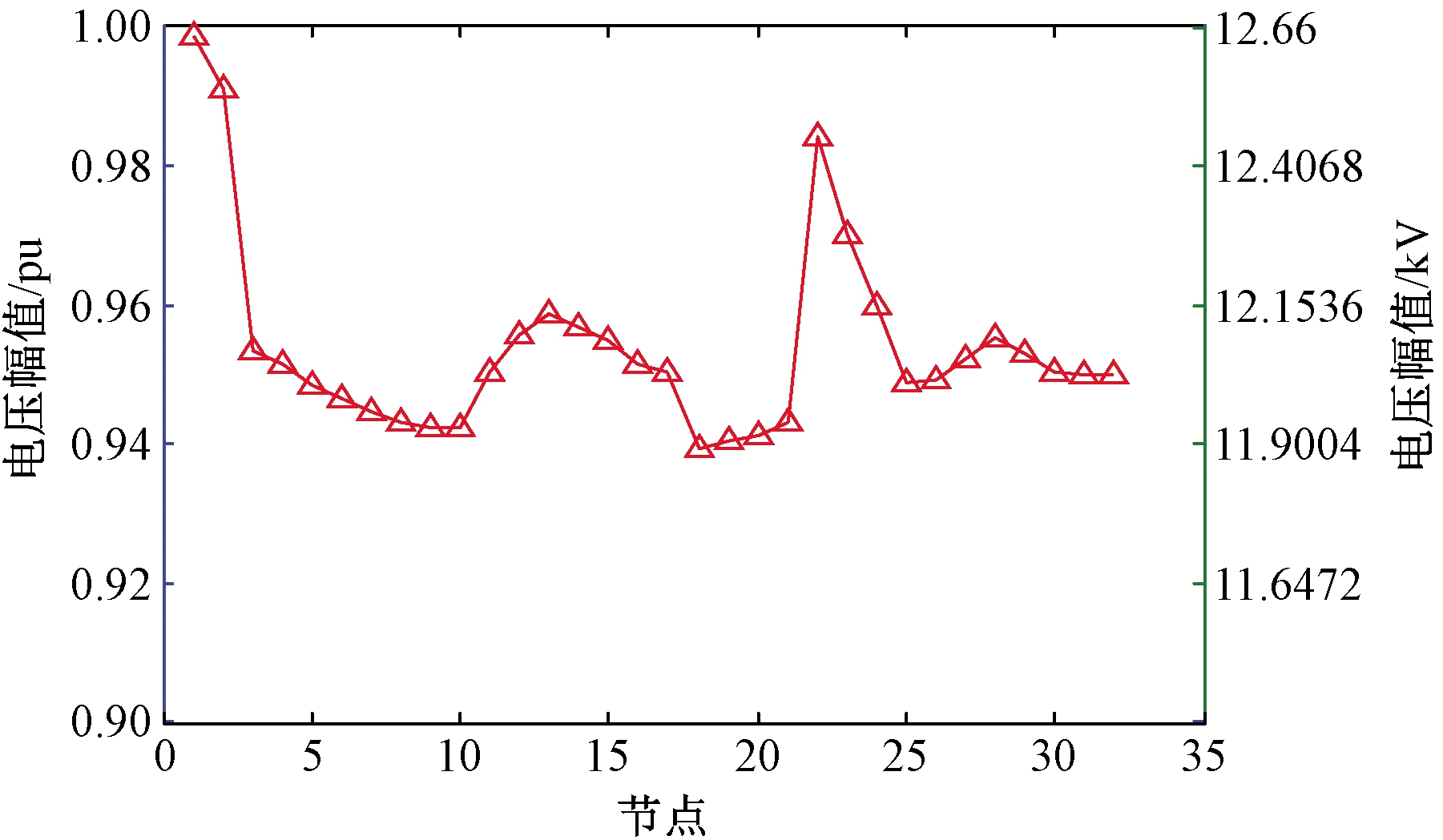
图5 最佳重构方案的节点电压分布曲线
Figure 5 Voltage distribution curve of the optimal reconfiguration scheme
在图1中按照重构方案对开关进行操作后，供电网络形似一个Y结构，4个主要微源分别位于Y结构的中心和3条供电路径中部，两处燃气轮机组和光伏阵列分布在Y结构的3条供电路径中部，风力机组在Y结构的中心，形成比较均衡的供电结构。
从图5可知，12.03 kV额定电压下，节点为1和节点为18的电压偏差是最大的，并且所有节点的电压偏移范围在-1.13%～4.86%。因此，各节点电压幅值均在正常范围内。
从表3可知，微电网中出力的主要微源是支撑型燃气轮机组，次要微源是非支撑型燃气轮机组、风力机组和光伏阵列，其中非支撑型燃气轮机组和光伏阵列输出功率并未达到最大值。2个燃料电池还有足够的可调功率裕度。从表4可知，所有可调负荷都能得到最大程度地供电。
整体上，重构方案比较理想，具有可行性。
4.3 比较3种重构方法
结合DFS的PSO、普通GWO、结合DFS的GWO 3种重构方法中，微电网系统信息相同，综合适应度函数的参数设置相同。结合DFS的PSO的参数：两个学习因子分别为1.2、2.2，惯性权重为0.6。普通GWO采用邻接矩阵的性质判断网架结构类型。分别采用3种重构方法，各执行重构20次，获得20组最佳重构结果，比较其适应度和优化时间。为方便重构方法之间的横向对比，将每种重构方法的20组最佳重构结果的适应度和优化时间分别按降序和升序排序，并绘制如图6和图7所示。在普通GWO求解过程中，记录每代解中无效解的比重，见图8。
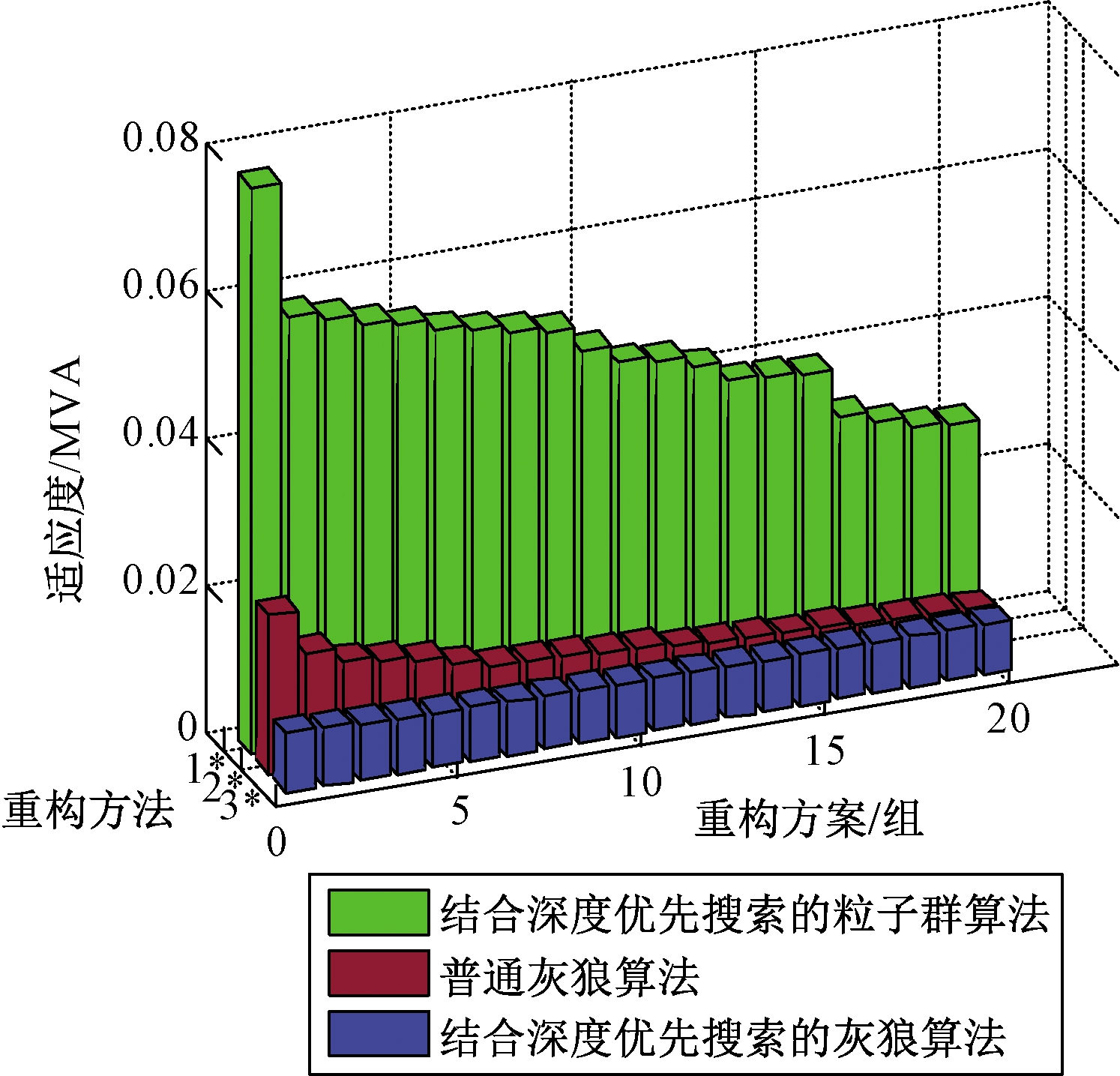
图6 3种重构方法的适应度
Figure 6 Fitness of three reconstruction methods
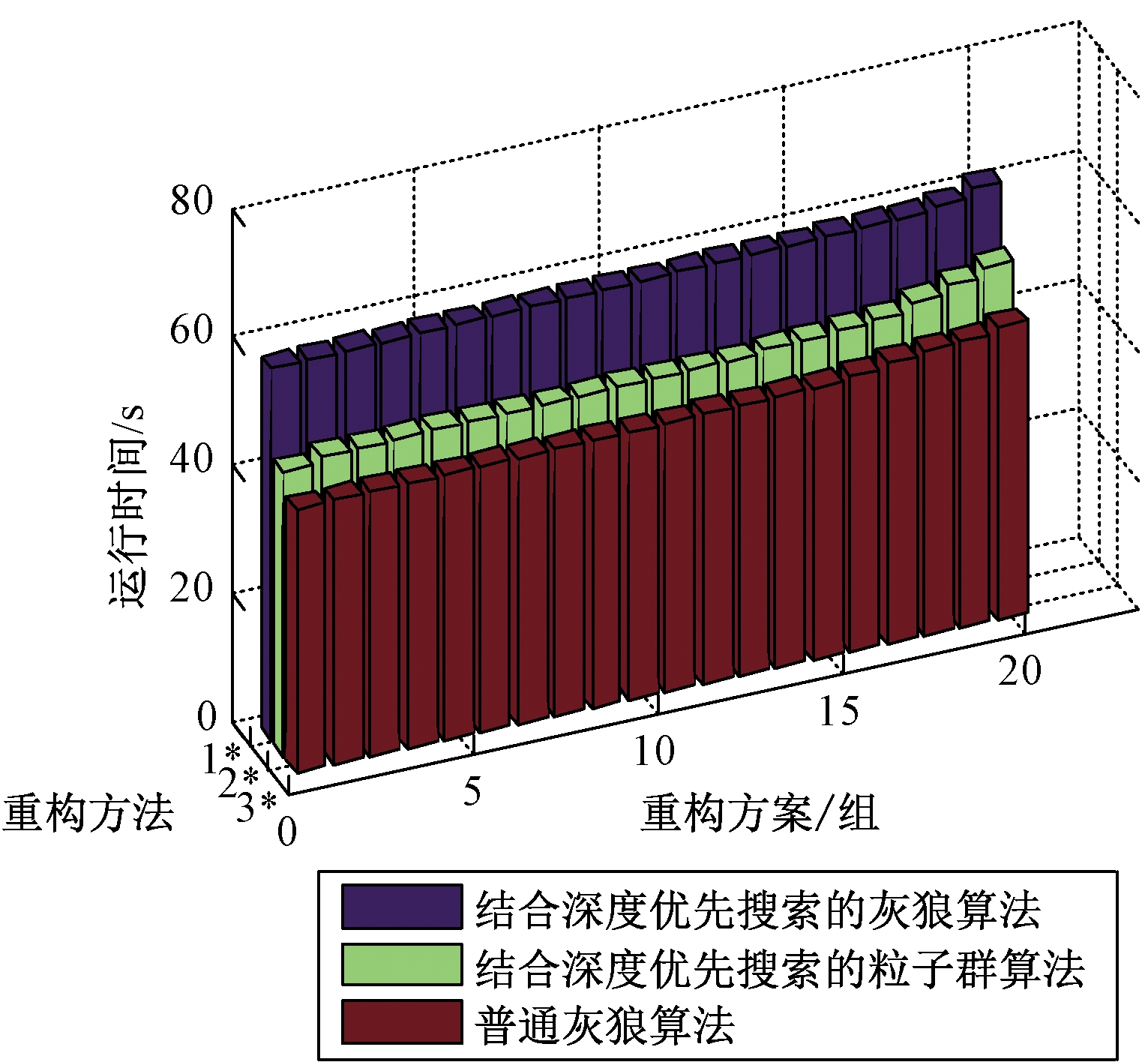
图7 3种重构方法的运行时间
Figure 7 Runtime of three reconfiguration methods
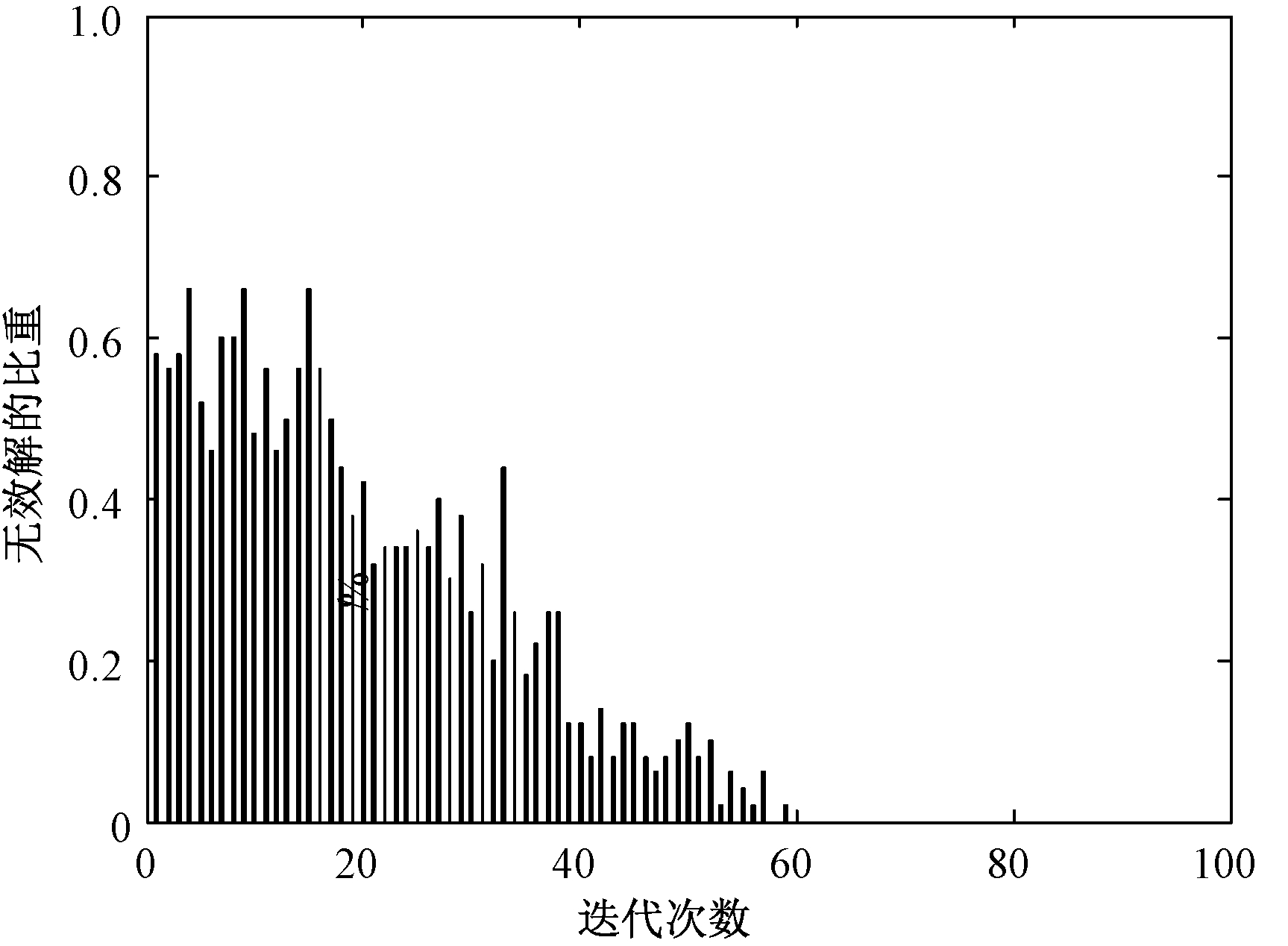
图8 普通GWO每代解中无效解比重
Figure 8 Proportion of invalid solutions in solution set of each iteration by ordinary GWO
由图6可知，与DFS结合的PSO、普通GWO都比与DFS结合的GWO的适应度值小。因为适应度越小说明重构方案越优秀，所以图6验证了与DFS结合的GWO的求解精度更高。
由图7可知，从运行时间看，普通GWO最快，结合DFS的PSO次之，结合DFS的GWO最慢。但是从优化运行角度，结合DFS的GWO的运行时间仍可以接受。
图8表示在普通GWO的前期和中期，每代解集中无效解的占比。这些无效解不仅影响搜索范围，还不能为更新和产生下一代解贡献作用。与DFS结合的GWO解决了无效解的问题，提高了算法的搜索范围，所以与DFS结合的GWO在全局搜索能力和求解精度方面存在优势。
5 结论
(1)建立了微电网重构模型，并分成3部分进行处理，即拓扑识别、潮流计算和优化算法的适应度函数，提出了结合DFS的GWO重构方法。
(2)研究了控制变量对微电网系统运行状态的影响，控制变量兼有网络开关状态和可调功率，能够扩大电压幅值的调整范围以及达到电压幅值平滑调整的效果。
[1] 瞿合祚,李晓明,杨玲君,等.考虑负荷和分布式电源时变性的配电网多目标动态重构和DG调度[J].高电压技术,2019,45(3):873-881.
[2] 陈新岗, 余兵, 陈小青, 等. 基于PAM时段划分的配电网动态重构[J]. 电力系统保护与控制, 2019, 47(7): 99-105.
[3] SHARIATZADEH F, VELLAITHURAI C B, BISWAS S S, et al. Real-time implementation of intelligent reconfiguration algorithm for microgrid[J]. IEEE transactions on sustainable energy, 2014, 5(2): 598-607.
[4] CHEN C, WANG J H, QIU F, et al. Resilient distribution system by microgrids formation after natural disasters[J].IEEE transactions on smart grid, 2016, 7(2):958-966.
[5] ZHAO B Y, DONG X D, BORNEMANN J. Service restoration for a renewable-powered microgrid in unscheduled island mode[J]. IEEE transactions on smart grid, 2015, 6(3): 1128-1136.
[6] 李咸善,徐浩,邹芳, 等. 微电网分级优化故障重构[J]. 中国电机工程学报, 2015,35(24): 6378-6386.
[7] GAZIJAHANI F S, SALEHI J. Robust design of microgrids with reconfigurable topology under severe uncertainty[J]. IEEE transactions on sustainable energy, 2018, 9(2): 559-569.
[8] 张晓凤,王秀英. 灰狼优化算法研究综述[J]. 计算机科学, 2019, 46(3): 30-38.
[9] 辛文成,向铁元,詹昕, 等. 邻接矩阵和粒子群优化算法应用于微电网重构[J]. 电力系统及其自动化学报, 2014, 26(11): 37-41.
[10] KAVOUSI-FARD A, ZARE A, KHODAEI A. Effective dynamic scheduling of reconfigurable microgrids[J].IEEE transactions on power systems, 2018, 33(5): 5519-5530.
[11] 王克文,刘凯,刘艳红.计及功率预测误差的主动配电网运行方式优化[J].郑州大学学报(工学版), 2020,41(1):75-82.
[12] 王佳佳, 吕林, 刘俊勇, 等. 基于改进分层前推回代法的含分布发电单元的配电网重构[J]. 电网技术, 2010, 34(9): 60-64.
[13] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in engineering software, 2014, 69: 46-61.
[14] 黄训诚,张秀阁,任晔. 智能配电网调度建模理论与分析[M]. 北京:中国电力出版社, 2014: 111-114.