0 引言
作为新型可设计性非均匀复合材料结构,功能梯度材料圆柱壳(以下简称FG圆柱壳)在船舶和海洋工程中有着广泛的应用,其力学行为已经成为复合材料力学的重要研究方向[1]。由于功能梯度材料性质在厚度方向的连续性变化导致功能梯度材料结构表现出与均匀材料结构不同的特性[2-3], 在壳体几何参数、载荷工况以及边界条件等相同的情况下,FG圆柱壳的振动、屈曲等宏观力学行为的分析要比相应各向同性圆柱壳更为复杂。
近年来,虽然已经有研究涉及水下圆柱壳这一领域,但是这些研究主要关注水下各向同性圆柱壳的宏观力学行为[4-9],讨论各向同性圆柱壳的振动特性和稳定性,分析各向同性圆柱壳固有频率和屈曲临界载荷的影响因素[4-6],以及针对各向同性圆柱壳进行临界载荷预测[7-9]。关于非均匀材料圆柱壳方面的研究则主要集中在FG圆柱壳的振动特性和稳定性[1,10]以及对传统复合材料和夹芯复合材料圆柱壳的振动特性以及屈曲研究上[11-12],主要讨论非均匀材料的特殊性质、壳体几何尺寸、载荷工况、边界条件等对非均匀材料圆柱壳力学行为的影响,而针对水下FG圆柱壳的振动频率和屈曲临界载荷预测方法的研究还十分有限。
为此,笔者基于水下FG圆柱壳固有频率和静水压力之间的关系,提出了一种适用于水下FG圆柱壳的屈曲临界载荷和固有频率预测方法。预测时,最少需3组固有频率数据便可在保证精确度的基础上快速建立静水压力下FG圆柱壳固有频率趋势线方程,进而得到水下FG圆柱壳屈曲临界载荷和固有频率的预测值。通过多组算例对比分析,验证了预测方法的可行性和准确性。
1 FG圆柱壳的力学模型
假定FG圆柱壳力学模型如图1所示,壳体外表面材料为金属、内表面材料为陶瓷,平均半径为R,长度为L,壁厚为h。将正交坐标系(x,θ,z)建立在壳体中面上,其中x、θ和z分别表示壳体的轴向、周向和径向;u、v和w表示壳体中面轴向、周向和径向位移。
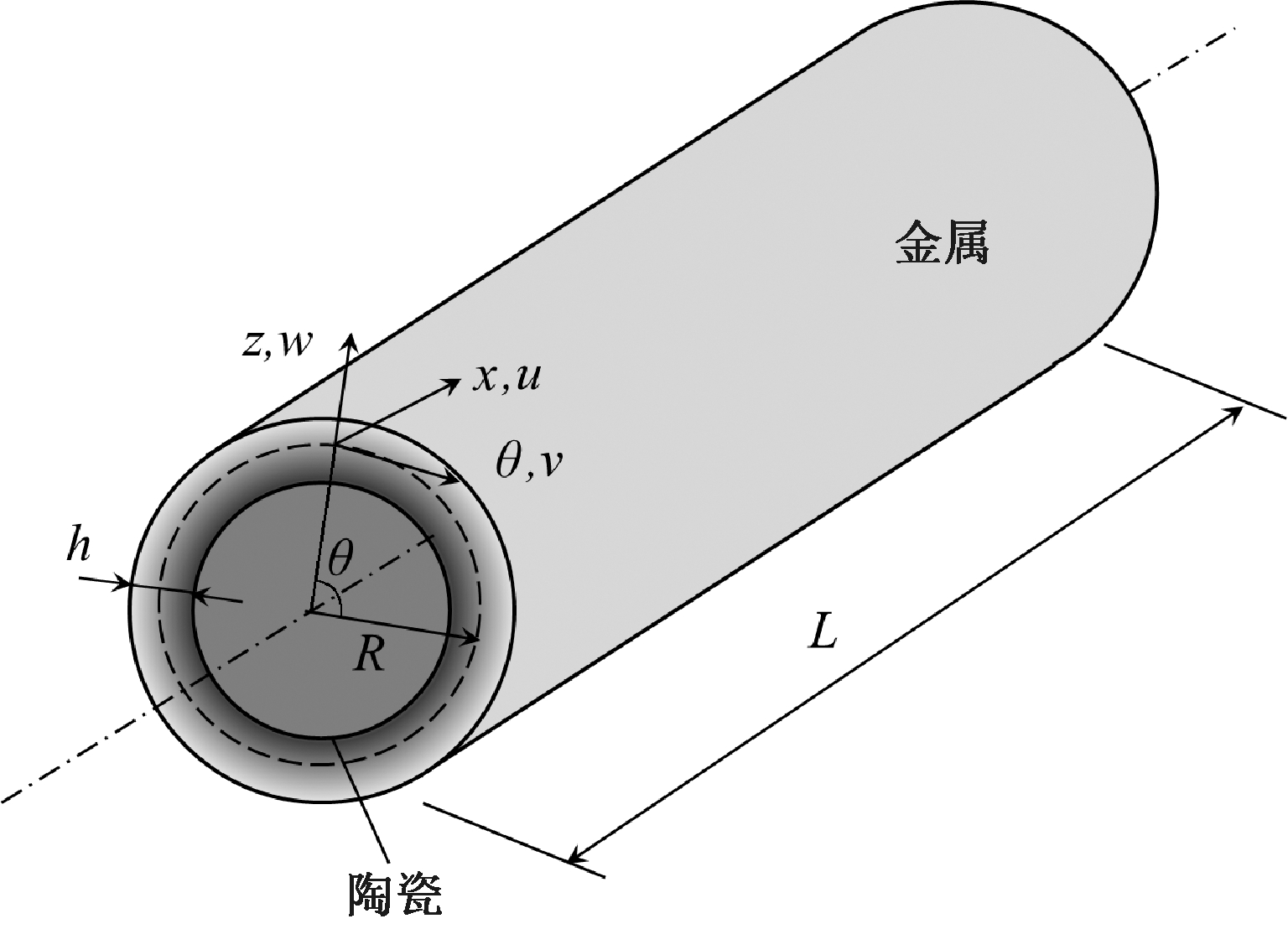
图1 FG圆柱壳模型
Figure 1 Geometry of a FG cylindrical shell
由于功能梯度材料的结构和组成沿厚度方向呈梯度连续变化,其材料的力学性能由组分材料的体积分数比所控制。对于具有均匀厚度h的功能梯度圆柱壳,其体积比可表示为[3]:
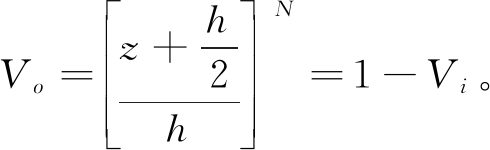
(1)
式中:Vi和Vo分别为功能梯度材料内外表面材料的体积百分比;N为非负实数幂指数(0≤N<+∞),当N=0时,功能梯度材料退化为各向同性材料。
本文中,FG圆柱壳内外表面材料参数分别为弹性模量Ei、Eo,泊松比μi、μo,质量密度ρi、 ρo,则FG圆柱壳沿壳体厚度方向等效的弹性模量E、泊松比μ和质量密度ρ如下所示:
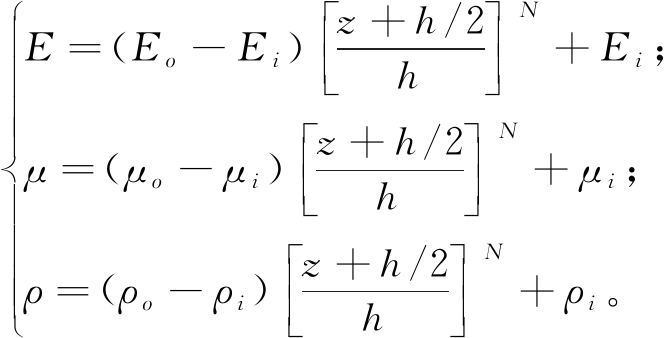
(2)
2 理论推导
根据Flügge[13]理论,静水压力下圆柱壳的运动方程可以写成如下形式:
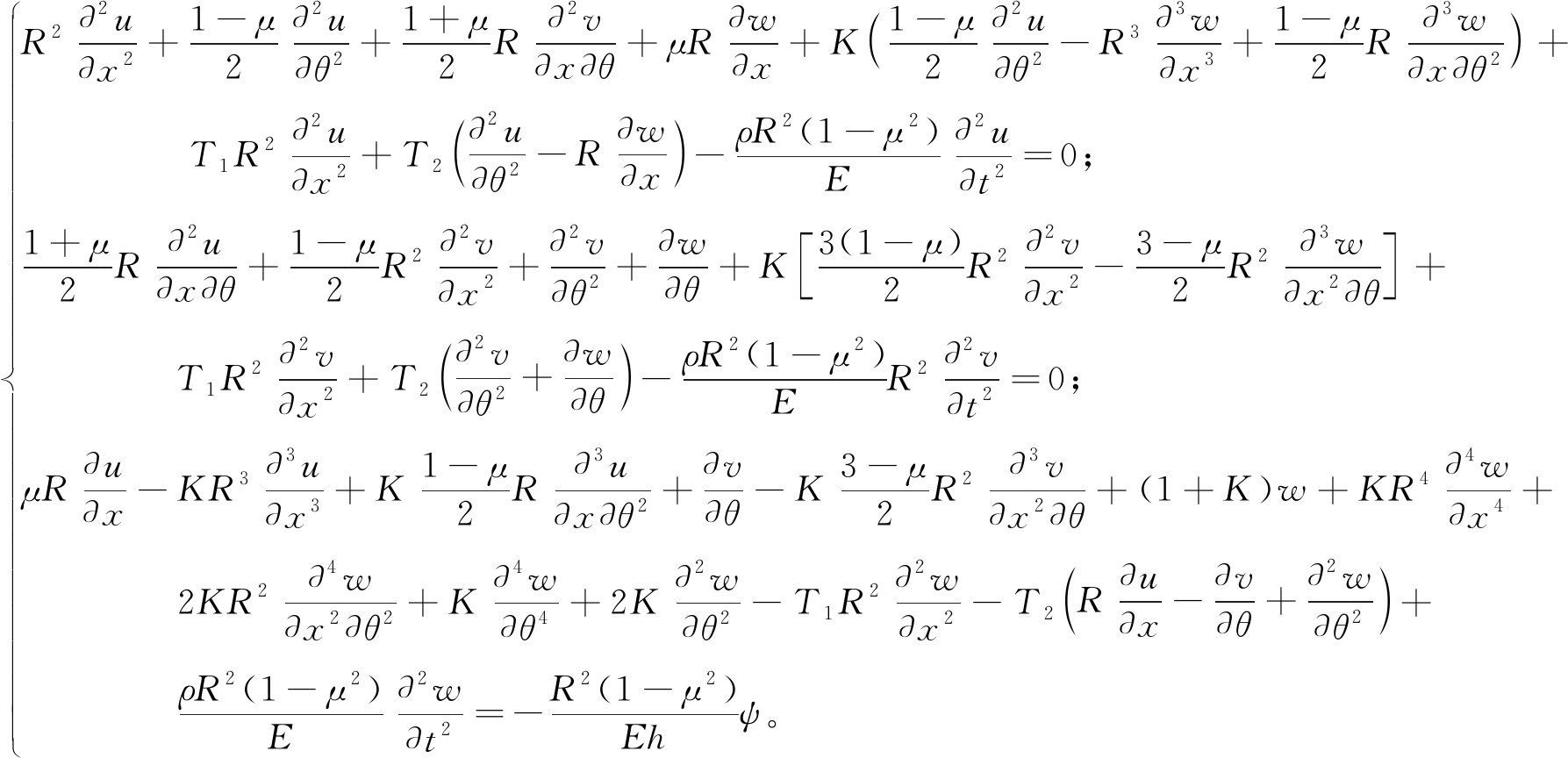
(3)
式中:ψ为声压;T1和T2分别为静水压力对壳体轴向和环向的影响因子,T1=R(1-μ2)Po/(2Eh),T2=R(1-μ2)Po/(Eh);Po为静水压力;K=h2/(12R2)。
假设流体介质为理想流体,则圆柱壳外部声场满足柱坐标系(x,θ,r)下的Helmholtz方程[14]:
(4)
式中:t为时间;CF为流体声速;x和θ与壳体对应坐标一致;r坐标沿壳体z轴方向选取。
在壳体外壁与流体的接触面上,流体径向位移与壳体径向位移必须相等。该耦合条件表达式为:
(5)
由式(4)、(5)可得到由于流体声场作用产生的流体载荷项:
(6)
式中:ρf为流体密度;kr为径向波数;![]() 为第二类n阶Hankel函数,
为第二类n阶Hankel函数,![]() 表示对变量krR的导数;径向波数kr和轴向波数km之间满足关系式(krR)2=Ω2(CL/CF)2-(kmR)2,Ω和CL分别为无量纲频率参数以及圆柱壳声速。
表示对变量krR的导数;径向波数kr和轴向波数km之间满足关系式(krR)2=Ω2(CL/CF)2-(kmR)2,Ω和CL分别为无量纲频率参数以及圆柱壳声速。
圆柱壳方程的位移形态可以用含有轴向波数km(与边界条件有关[15])和环向波数n的波传播形式表示:
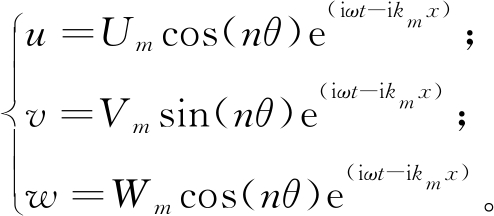
(7)
式中:Um、Vm、Wm分别表示x、θ和r方向的波幅;ω为固有角频率。
将式(7)代入式(3),结合方程(6)得到水下FG圆柱壳矩阵形式耦合系统的运动方程:
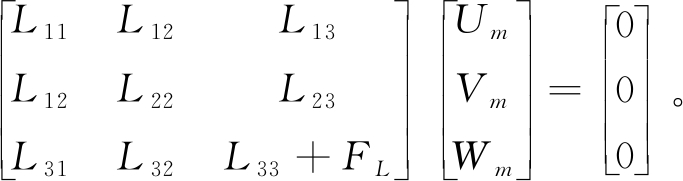
(8)
求解方程(8),可以得到:
P1(ω)-P2(ω)FL=0。
(9)
式中,P1(ω)和P2(ω)分别为关于未知数ω的多项式,固有频率f=ω/2π,通过使用牛顿迭代法即可得到给定静水压力下FG圆柱壳的固有频率值。当FL=0、Po=0时,即可还原为真空中FG圆柱壳的固有频率计算。
静水压力不变情况下,固有频率随模态改变而发生变化,固有频率最小值即为基频。当静水压力下FG圆柱壳的基频为0时,可认为此时的静水压力值即为圆柱壳屈曲临界载荷值[8]。但是,由于水下FG圆柱壳固有频率计算过程较为复杂,合理有效且便于实际应用的屈曲临界载荷和固有频率预测方法现在还很有限。为此,笔者基于水下FG圆柱壳固有频率的平方和静水压力之间的线性关系,提出了一种简便实用的水下FG圆柱壳屈曲临界载荷和固有频率预测方法。
3 算例与讨论
3.1 计算方法的正确性和有效性验证
表1计算了真空中FG圆柱壳的固有频率;表2则以水下各向同性圆柱壳作为研究对象,计算了不同边界条件下壳体的屈曲临界载荷值。通过与Loy等[3]和Zhu等[9]的分析结果进行对比,验证了本文关于静水压力下FG圆柱壳固有频率以及屈曲临界载荷计算方法的正确性和有效性。
3.2 屈曲临界载荷预测
本文算例中,FG圆柱壳外表面材料为金属,内表面材料为陶瓷,材料参数(室温)见表3[16-17]。
为了能够对水下FG圆柱壳进行屈曲临界载荷预测,首先考察了水下FG圆柱壳基频与静水压力之间的关系,讨论了材料组分、壳体几何尺寸以及边界条件等对这两者关系的影响(见图2~6)。计算结果显示,FG圆柱壳基频与静水压力呈非线性关系,且越接近临界值(f=0)下降幅度越大,而基频的平方与静水压力却呈线性关系。通过进一步计算发现,任意模态固有频率的平方与静水压力均呈线性关系,验证了水下FG圆柱壳与相应均匀材料圆柱壳[7-9]的基频变化规律之间呈现很强的相似性这一研究设想。以上结果说明,水下FG圆柱壳屈曲临界载荷的预测值可以通过线性拟合方法求得。因此,图2(b)、图3(b)、图4(b)、图5(b)、图6(b)分别给出了采用该方法得到的不同情况下屈曲临界载荷的预测结果。
表1 真空中Ⅰ型FG圆柱壳固有频率对比分析
Table 1 Comparison of natural frequencies for type Ⅰ FG cylindrical shell in vacuum Hz
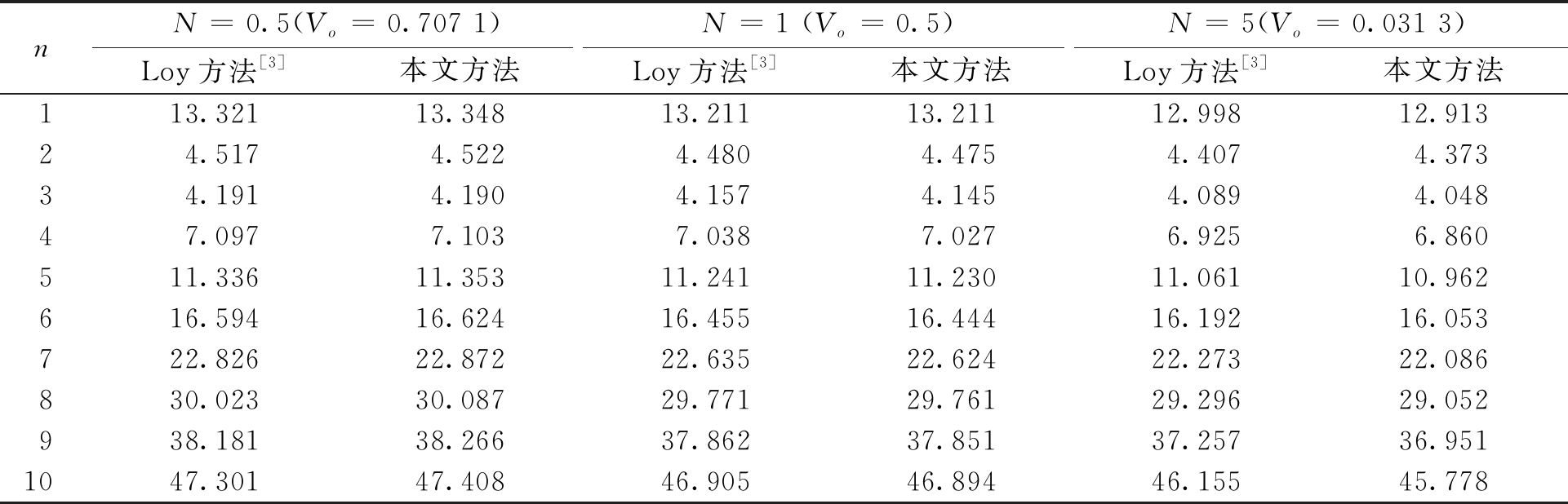
nN=0.5(Vo=0.707 1)N=1 (Vo=0.5)N=5(Vo=0.031 3)Loy方法[3]本文方法Loy方法[3]本文方法Loy方法[3]本文方法113.32113.34813.21113.21112.99812.91324.5174.5224.4804.4754.4074.37334.1914.1904.1574.1454.0894.04847.0977.1037.0387.0276.9256.860511.33611.35311.24111.23011.06110.962616.59416.62416.45516.44416.19216.053722.82622.87222.63522.62422.27322.086830.02330.08729.77129.76129.29629.052938.18138.26637.86237.85137.25736.9511047.30147.40846.90546.89446.15545.778
表2 不同边界时水下各向同性圆柱壳屈曲临界载荷
Table 2 The critical buckling pressures for a submerged cylindrical shell with different boundary conditions MPa

方法SS-SSC-CC-FC-SSZhu方法[9]0.0840.1880.0610.121本文方法0.0840.1880.0590.121
注:本文中,SS-SS为两端简支边界;C-C为两端固定边界;C-F为一端固定一端自由边界;C-SS为一端固定一端简支边界。
表3 材料参数表
Table 3 Properties of materials
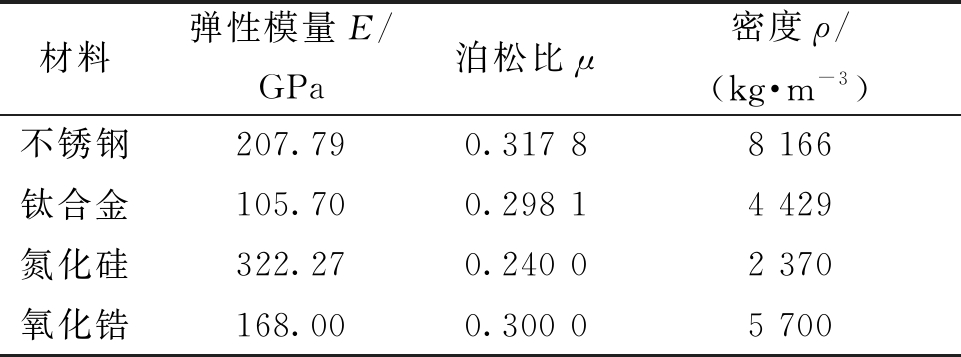
材料弹性模量E/GPa泊松比μ密度ρ/(kg·m-3)不锈钢207.790.317 88 166钛合金105.700.298 14 429氮化硅 322.270.240 02 370氧化锆168.000.300 05 700
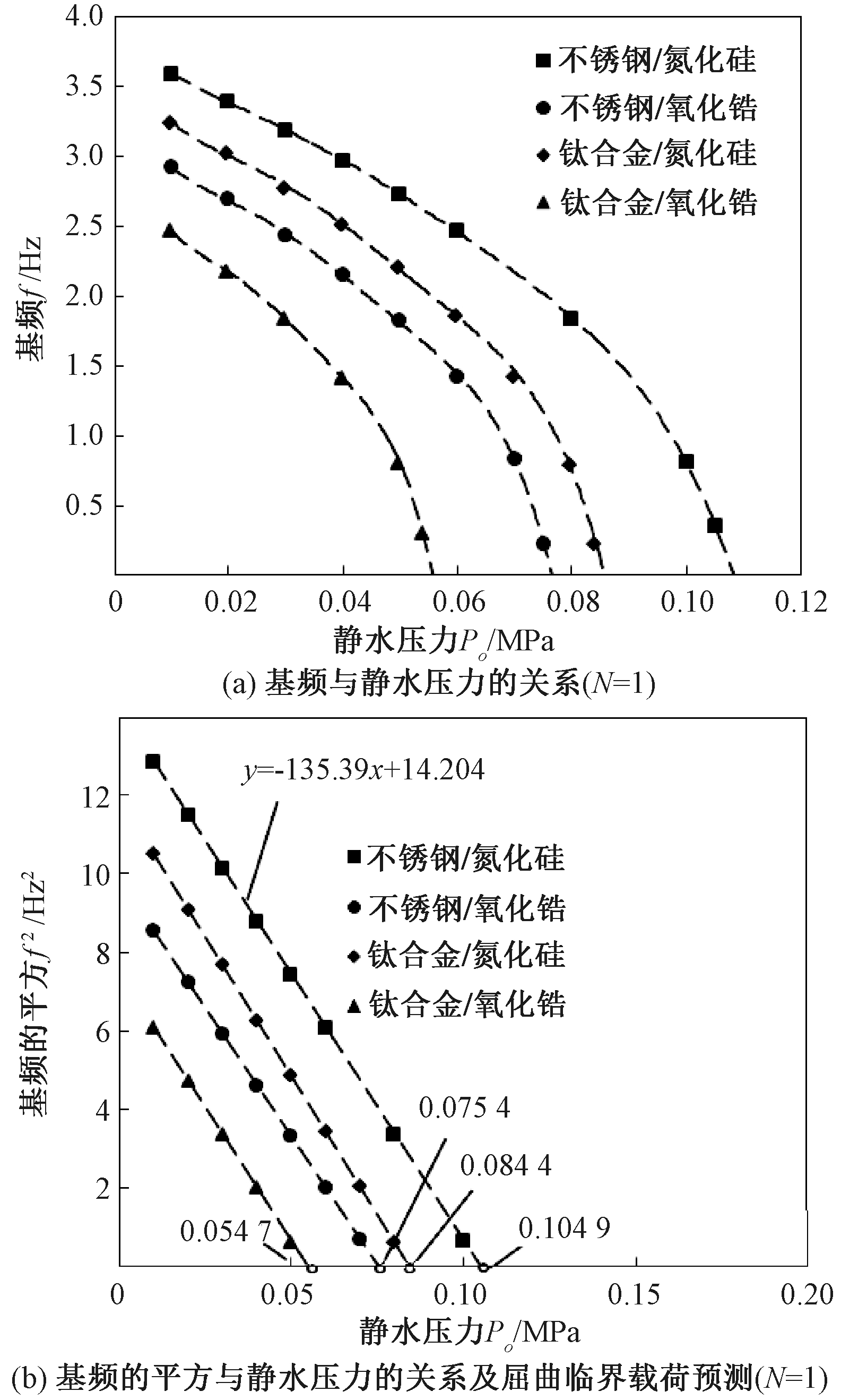
图2 不同材料组分时FG圆柱壳屈曲临界载荷预测
Figure 2 The prediction of the critical pressure of FG cylindrical shell with different material components
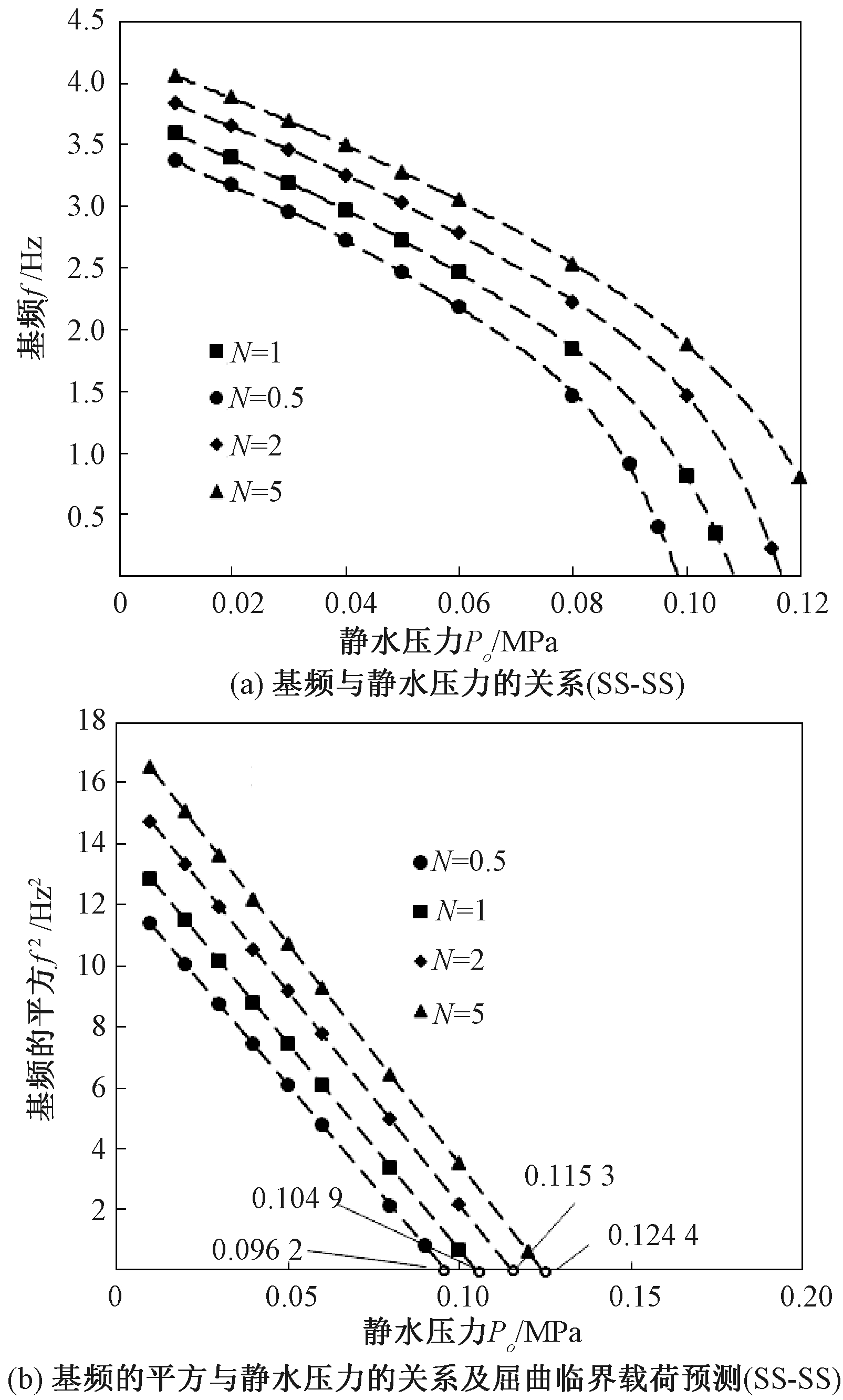
图3 不同幂指数N时FG圆柱壳屈曲临界载荷预测
Figure 3 The prediction of the critical pressure of FG cylindrical shell with different power law index N
首先以两端简支FG圆柱壳为例,给出了不同材料组分时FG圆柱壳的屈曲临界载荷预测值(见图2(b))。图2~4中,壳体几何参数为:h/R=0.01,L/R=20。
以由不锈钢/氮化硅复合的FG圆柱壳为例,使用Excel软件拟合后得到的线性趋势线方程式为y=-135.39x+14.204。令y=0,则x=0.104 9,即可得到临界载荷预测值Pcr=0.104 9 MPa。且拟合时采用的最大静水压力不论是0.03 MPa还是0.07 MPa,得到的临界载荷数值均相同。通过进一步计算发现,最少需3组数据便可以在保证精确度的基础上进行预测。例如,仅使用Po=0.01、0.02、0.03 MPa时的基频进行预测,同样可得到y=-135.39x+14.204,Pcr=0.104 9 MPa。
功能梯度材料的力学性能由组分材料的体积分数控制。图3~6中,FG圆柱壳材料组合形式为不锈钢/氮化硅。如图3所示,FG圆柱壳的基频数值与体积分数的幂指数N有关。当N发生变化,而壳体其余参数不变,通过使用图2所示拟合方法,可得到不同N时FG圆柱壳的屈曲临界载荷预测值(见图3(b))。同理,可得到简支(SS)边界、固定(C)边界、自由(F)边界下FG圆柱壳的屈曲临界载荷预测值(见图4)。
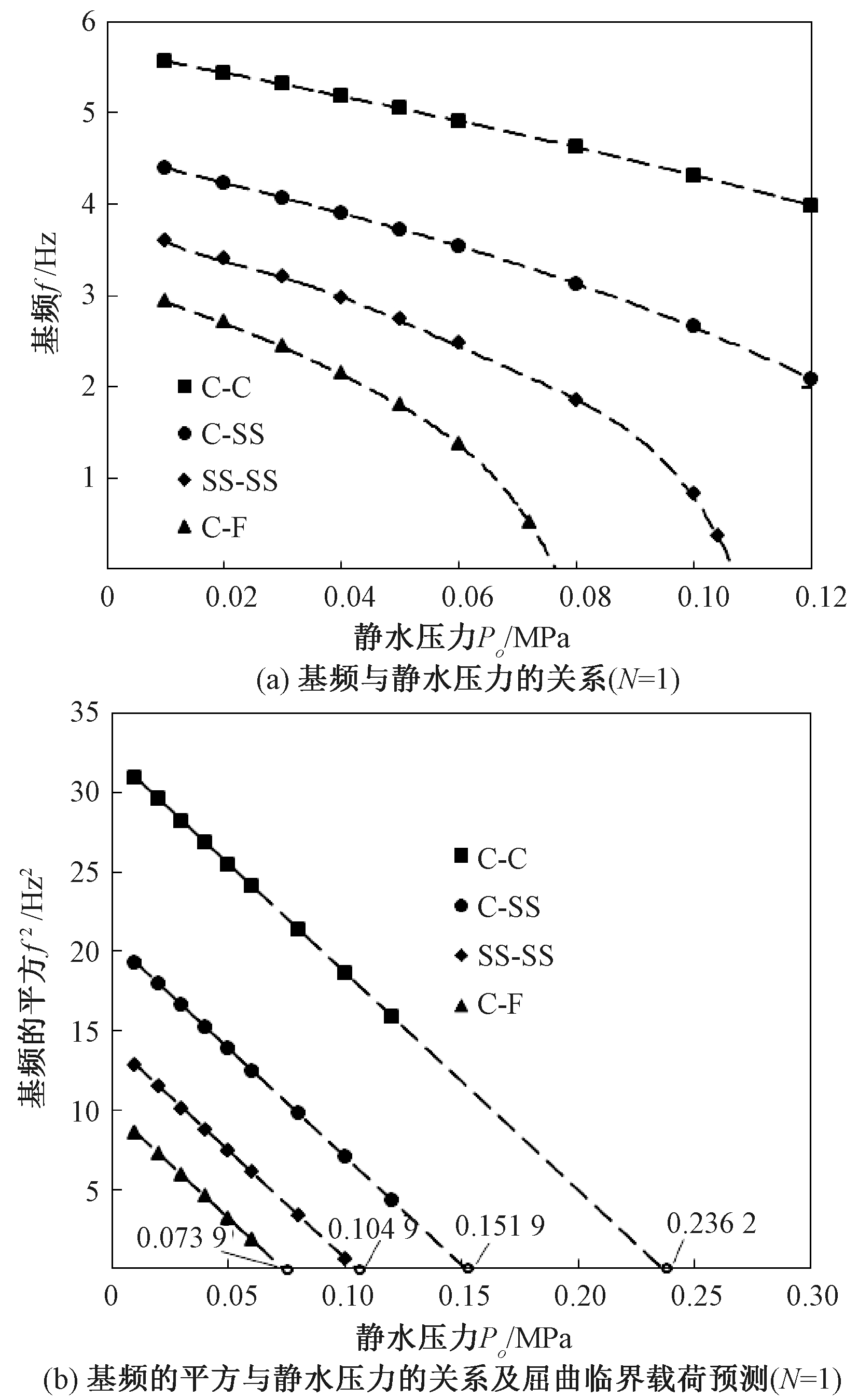
图4 不同边界条件下FG圆柱壳屈曲临界载荷预测
Figure 4 The prediction of the critical pressure of FG cylindrical shell with different boundary conditions
当FG圆柱壳壁厚半径比(h/R)和长度半径比(L/R)发生改变,而其余壳体参数不变时,同样可以由本文方法得到FG圆柱壳的屈曲临界载荷预测值(见图5、图6)。壳体参数为:N=1,SS-SS。由于静水压力可能改变结构的基频模态[18],当静水压力增大到一定程度时,L/R=5和L/R=10时的基频模态分别由(1, 2)和(1,3)变为(1, 3)和(1,4),因此图5中这两种情况仅分别给出(1,3)和(1,4)时的数据结果。
将线性拟合方法预测得到的屈曲临界载荷和由式(9)计算得到的屈曲临界载荷进行对比,发现预测结果和式(9)计算结果之间相对误差均小于0.03%。以上结果表明,本文方法适用于水下FG圆柱壳的屈曲临界载荷预测,且预测精确高、计算量小。
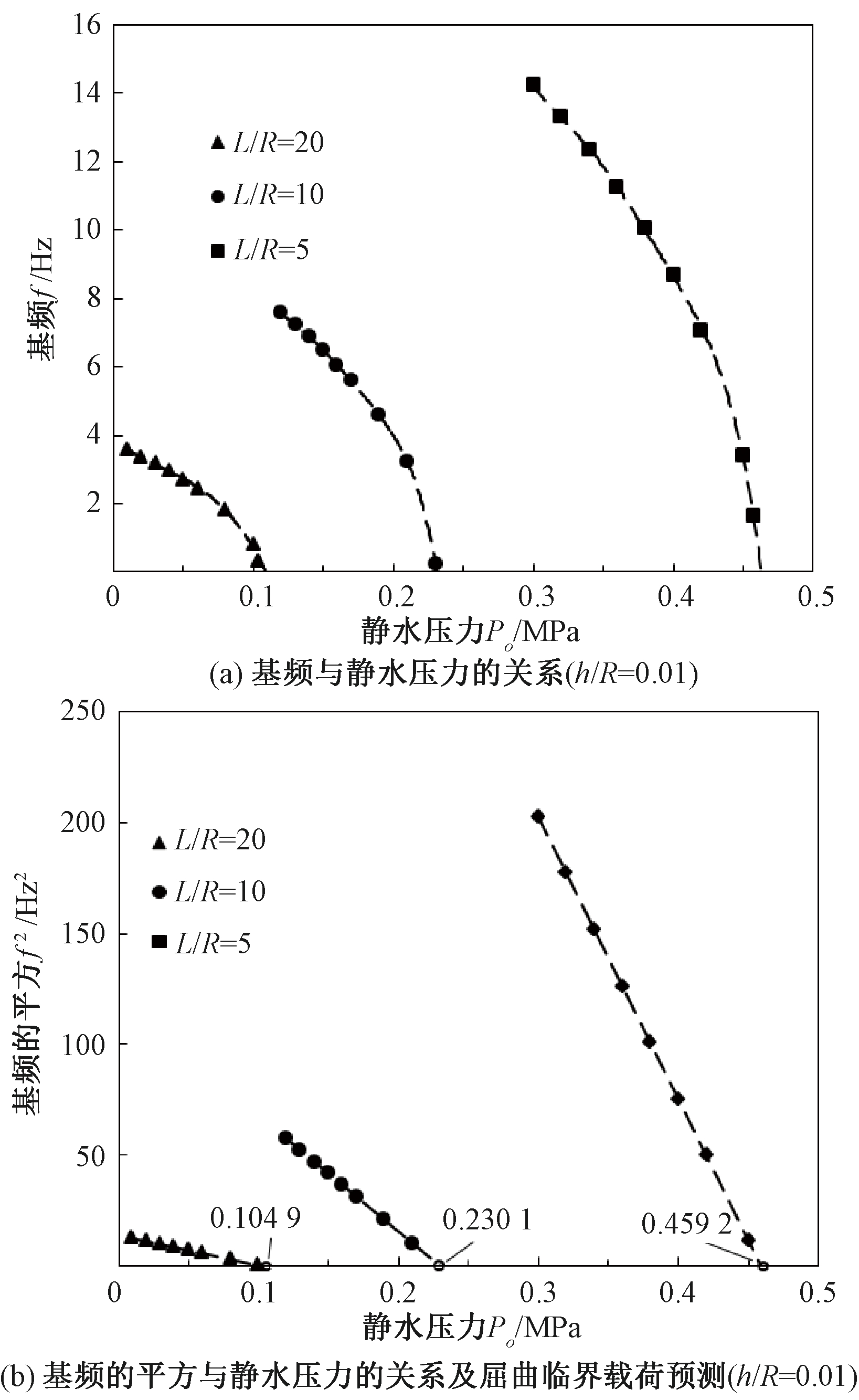
图5 不同L/R时FG圆柱壳屈曲临界载荷预测
Figure 5 The prediction of the critical pressure of FG cylindrical shell with different L/R ratios
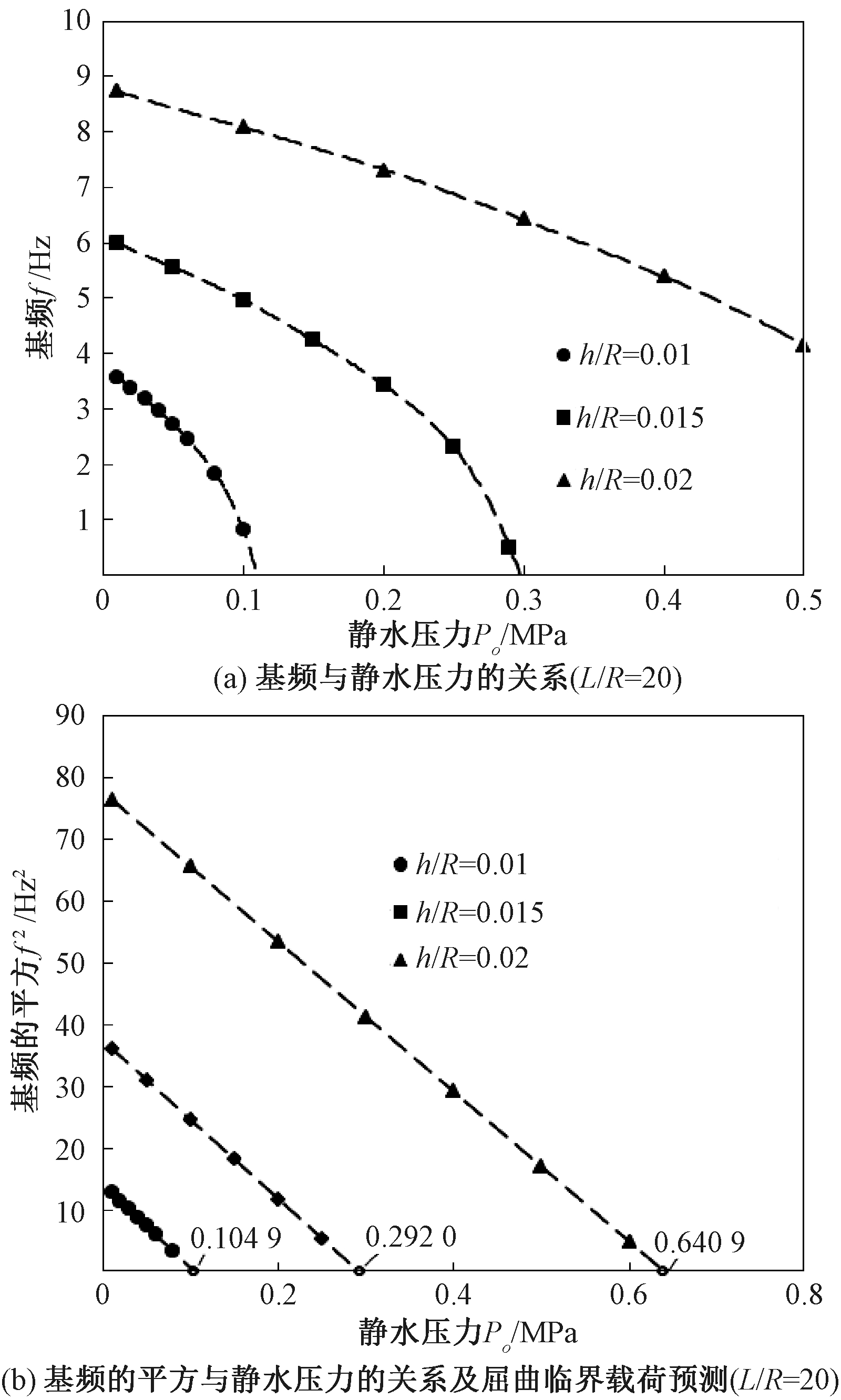
图6 不同h/R时FG圆柱壳屈曲临界载荷预测
Figure 6 The prediction of the critical pressure of FG cylindrical shell with different h/R ratios
3.3 固有频率预测
本文方法不仅可以预测屈曲临界载荷,还可预测任意模态的固有频率。作为算例,表4和表5分别给出了4种FG圆柱壳和刘佩等[18]对圆柱壳的固有频率预测结果。表4中,选取Po=0.01、0.02、0.03、0.04、0.05、0.06、0.07、0.08 MPa时的固有频率进行预测。壳体几何参数为:h/R=0.01,L/R=20,m=1,n=2,SS-SS。表5中选取相对深度(水深/半径)为5、20、50、100、150、300、500时的固有频率进行预测。壳体参数为:L=1.284 m,R=0.180 m,h=0.003 m,E=206 GPa,ρ=7 850 kg/m3,μ=0.3。结果显示,表4中的固有频率预测误差均控制在0.1%以内;表5中的预测误差基本控制在3%以内,仅模态(1,3),相对深度=300、500时预测误差略大,误差原因与本文预测方法是基于理论分析方法,而刘佩等[18]采用有限元分析方法有关,预测时将FG圆柱壳退化为各向同性圆柱壳也可能导致些许预测误差。
表4 FG圆柱壳固有频率预测
Table 4 Prediction of natural frequency of FG cylindrical shell Hz
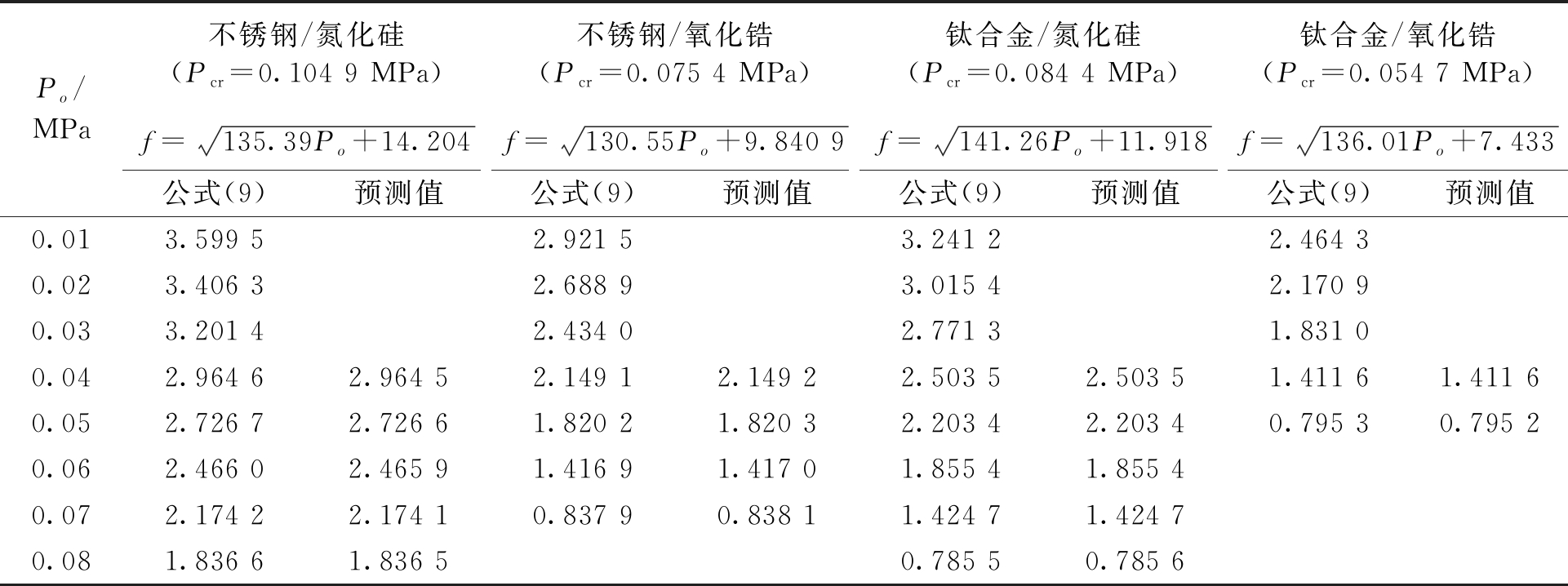
Po/MPa不锈钢/氮化硅(Pcr=0.104 9 MPa)不锈钢/氧化锆(Pcr=0.075 4 MPa)钛合金/氮化硅(Pcr=0.084 4 MPa)钛合金/氧化锆(Pcr=0.054 7 MPa)f=135.39Po+14.204 f=130.55Po+9.840 9f=141.26Po+11.918 f=136.01Po+7.433 公式(9)预测值公式(9) 预测值公式(9) 预测值公式(9) 预测值0.013.599 52.921 53.241 22.464 30.023.406 32.688 93.015 42.170 90.033.201 42.434 02.771 31.831 00.042.964 62.964 52.149 12.149 22.503 52.503 51.411 61.411 60.052.726 72.726 61.820 21.820 32.203 42.203 40.795 30.795 20.062.466 02.465 91.416 91.417 01.855 41.855 40.072.174 22.174 10.837 90.838 11.424 71.424 70.081.836 61.836 50.785 50.785 6
表5 各向同性圆柱壳固有频率预测
Table 5 Prediction of natural frequency of isotropic cylindrical shell Hz
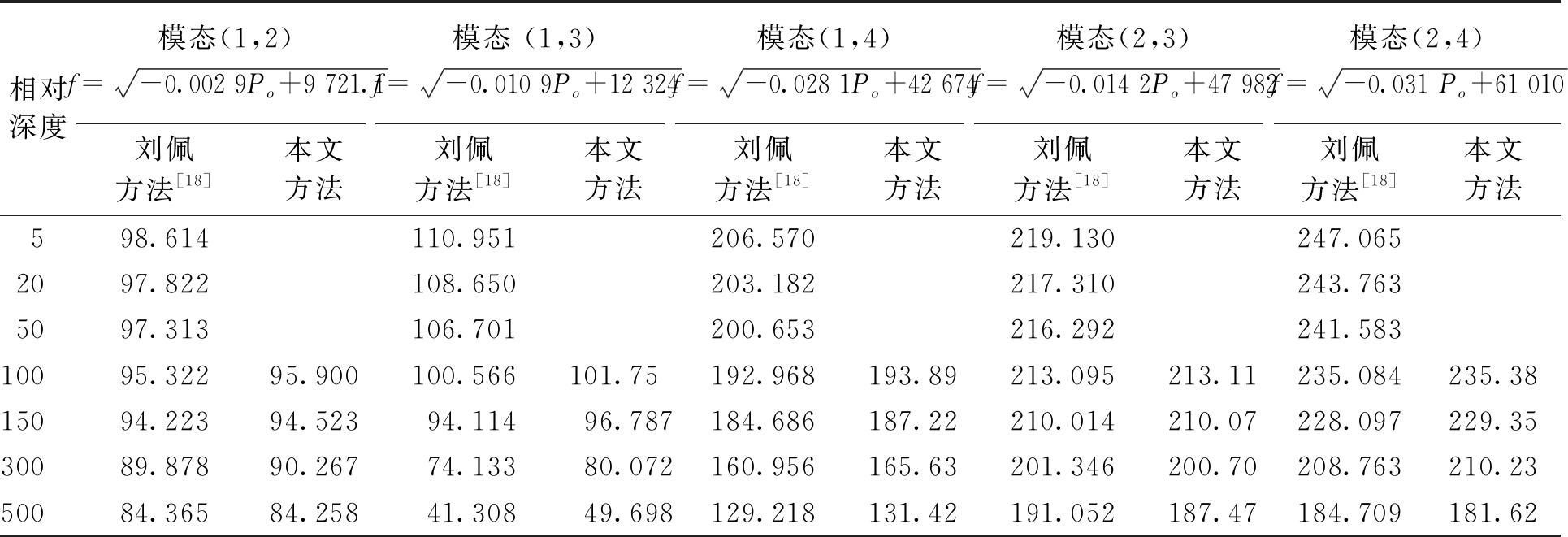
相对深度模态(1,2)f=-0.002 9Po+9 721.1模态 (1,3)f=-0.010 9Po+12 324模态(1,4)f=-0.028 1Po+42 674模态(2,3)f=-0.014 2Po+47 982模态(2,4)f=-0.031 Po+61 010刘佩方法[18]本文方法刘佩方法[18]本文方法刘佩方法[18]本文方法刘佩方法[18]本文方法刘佩方法[18]本文方法598.614110.951206.570219.130247.0652097.822108.650203.182217.310243.7635097.313106.701200.653216.292241.58310095.32295.900100.566101.75192.968193.89213.095213.11235.084235.3815094.22394.52394.11496.787184.686187.22210.014210.07228.097229.3530089.87890.26774.13380.072160.956165.63201.346200.70208.763210.2350084.36584.25841.30849.698129.218131.42191.052187.47184.709181.62
与传统临界载荷计算方法相比,本文预测方法计算量小,预测精度高,可以在数据有限的情况下快速获得屈曲临界载荷以及固有频率预测值。本文预测方法不仅适用于振动数值分析预测,还可用于振动试验预测,但是振动试验预测研究结果还很有限,后续将对此进行深入研究。
4 结论
基于水下FG圆柱壳固有频率的平方和静水压力之间呈线性关系这一重要结论,提出了一种适用于水下FG圆柱壳的屈曲临界载荷和频率预测方法。该方法能够在保证精确度的基础上快速得到水下FG圆柱壳屈曲临界载荷预测值以及任意静水压力下固有频率预测值,计算量小,且可以在数据有限的情况下进行预测。将预测结果与数值分析及数值模拟结果进行对比,表明本文预测方法精确度高,便于实际应用。
[1] BRISCHETTO S, TORNABENE F, FANTUZZI N, et al. 3D exact and 2D generalized differential quadrature models for free vibration analysis of functionally graded plates and cylinders[J]. Meccanica, 2016, 51(9): 2059-2098.
[2] LI X, DU C C, LI Y H. Parametric instability of a functionally graded cylindrical thin shell subjected to both axial disturbance and thermal environment[J]. Thin-walled structures, 2018, 123: 25-35.
[3] LOY C T, LAM K Y, REDDY J N. Vibration of functionally graded cylindrical shells[J]. International journal of mechanical sciences, 1999, 41(3): 309-324.
[4] 王鹏, 李天匀, 朱翔, 等. 近水面状态有限长圆柱壳振动特性分析[J]. 振动工程学报, 2016, 29(5): 772-778.
[5] ZHANG X M. Frequency analysis of submerged cylindrical shells with the wave propagation approach [J]. International journal of mechanical sciences, 2002, 44(7): 1259-1273.
[6] ABRAMOVICH H, SINGER J, WELLER T. Repeated buckling and its influence on the geometrical imperfections of stiffened cylindrical shells under combined loading[J]. International journal of non-linear mechanics, 2002, 37(4/5): 577-588.
[7] 陈忱, 李天匀, 朱翔, 等. 基于波传播法的水下圆柱壳临界载荷-频率特性分析[J]. 中 国 造 船, 2012,53(1):130-136.
[8] PLAUT R H, VIRGIN L N. Use of frequency data to predict buckling [J]. Journal of engineering mechanics, 1990, 116 (10): 2330-2335.
[9] ZHU X, YE W B, LI T Y, et al. The elastic critical pressure prediction of submerged cylindrical shell using wave propagation method[J]. Ocean engineering, 2013, 58: 22-26.
[10] 梁斌, 陈金晓, 李戎, 等. 水下环肋功能梯度材料圆柱壳稳定性研究[J]. 振动与冲击, 2017, 36(13): 80-85, 121.
[11] 孟豪, 韩志军, 路国运. 复合材料圆柱壳非轴对称动力屈曲[J]. 振动与冲击, 2017, 36(11): 27-30, 78.
[12] 仝博, 朱锡, 任春雨, 等. 复合材料夹芯圆柱壳自由振动研究[J]. 海军工程大学学报, 2017, 29(5): 97-102.
[13] FLÜGGE W. Stresses in shells[M]. Berlin: Springer-verlag, 1960.
[14] MORSE P M, INGARD K U. Theoretical acoustics[M]. New York: McGraw-Hill Book Company, 1968.
[15] ZHANG X M, LIU G R, LAM K Y. Coupled vibration analysis of fluid-filled cylindrical shells using the wave propagation approach[J]. Applied acoustics, 2001, 62(3):229-243.
[16] KIM Y W. Temperature dependent vibration analysis of functionally graded rectangular plates[J]. Journal of sound and vibration, 2005, 284(3/4/5): 531-549.
[17] KWAK M K, KOO J R, BAE C H. Free vibration analysis of a hung clamped-free cylindrical shell partially submerged in fluid[J]. Journal of fluids and structures, 2011, 27(2): 283-296.
[18] 刘佩, 刘书文, 黎胜. 潜深对水下圆柱壳振动声辐射特性的影响[J]. 舰船科学技术, 2014, 36(5): 36-41, 48.