0 引言
滚动轴承作为旋转机械等工业生产设备的重要组成元件,其工作环境复杂多变,是最容易受损的零部件之一[1]。一旦轴承发生故障,将会对机械设备的稳定性和使用寿命造成一定的影响,因此对轴承的运行状态进行识别具有很重要的研究意义。
近年来,随着机器学习的不断发展,智能故障诊断算法为故障诊断领域注入了新的活力,传统的智能故障诊断算法通常包括信号采集、特征提取和选择、故障识别3个模块[2]。深度学习作为机器学习中的热门研究领域,已经广泛应用于人脸识别、图像处理、语音识别、无人驾驶等领域,但是深度学习在故障诊断领域的研究还处于起步阶段[3]。郭亮等[4]提出了一种基于稀疏自编码器的深度学习方法,通过提取信号的时域、频域、时频域特征构成特征集作为网络的输入,最终准确率达到90.86%。Janssens等[5]利用卷积神经网络对齿轮箱建立了故障诊断模型,其网络隐层只有一个卷积层和全连接层组成,将信号的频域信息作为网络输入,对轴承和齿轮进行状态识别。Chen等[6]提出一种深度卷积神经网络的故障诊断模型,网络将振动信号的时域统计特征和频域特征作为输入,实现对故障模式的诊断。袁建虎等[7]通过对轴承故障信号构建时频信息的方式,将信号的时频图作为卷积神经网络的输入对轴承进行模式识别。
1 全矢谱技术
传统的振动信息分析方法在进行信号处理时,通常会以单一方向的信号为基础对设备进行状态识别,由于信息的不完全,易产生错判和漏判。全矢谱理论根据转子的涡动轨迹是各谐波组合作用下产生的一系列椭圆,将椭圆的长轴定义为主振矢,短轴定义为副振矢,并作为振动剧烈程度的指标及故障诊断的依据之一[8]。
设x、y方向上的振动信号序列为{xi}和{yi},将其构成复序列zi=xi+jyi(i=1,2,…,N/2-1),j为虚数,对{zi}进行傅里叶变换得到{Zk},由傅里叶变换的共轭性可得:
(1)
(2)
式中:k=0,1,2,…,N-1。
由傅里叶变换的性质得到:
(3)
(4)
式中:k=0,1,2,…,N/2-1;RLk为主振矢;RSk为副振矢,具体数学推导过程可参考文献[9]。
2 深度卷积神经网络
2.1 卷积神经网络
卷积神经网络属于典型的前馈型神经网络,一般的卷积神经网络包括:输入层、卷积层、池化层、全连接层、输出层[10]。本文采用的网络结构如图1所示,网络通过多组卷积层和池化层对输入的数据进行特征提取,网络层数越多,提取的特征就越抽象,输出层前一层则采用全连接型神经网络。其训练过程包括前向传播和反向传播,前向传播是将信号输入到模型中得到输出结果;反向传播过程首先计算网络输出与真实结果之间的误差,将得到的差值反向传播,得到各层的误差,利用梯度下降等算法调整网络的参数,直至达到预期目标或终止条件[11]。
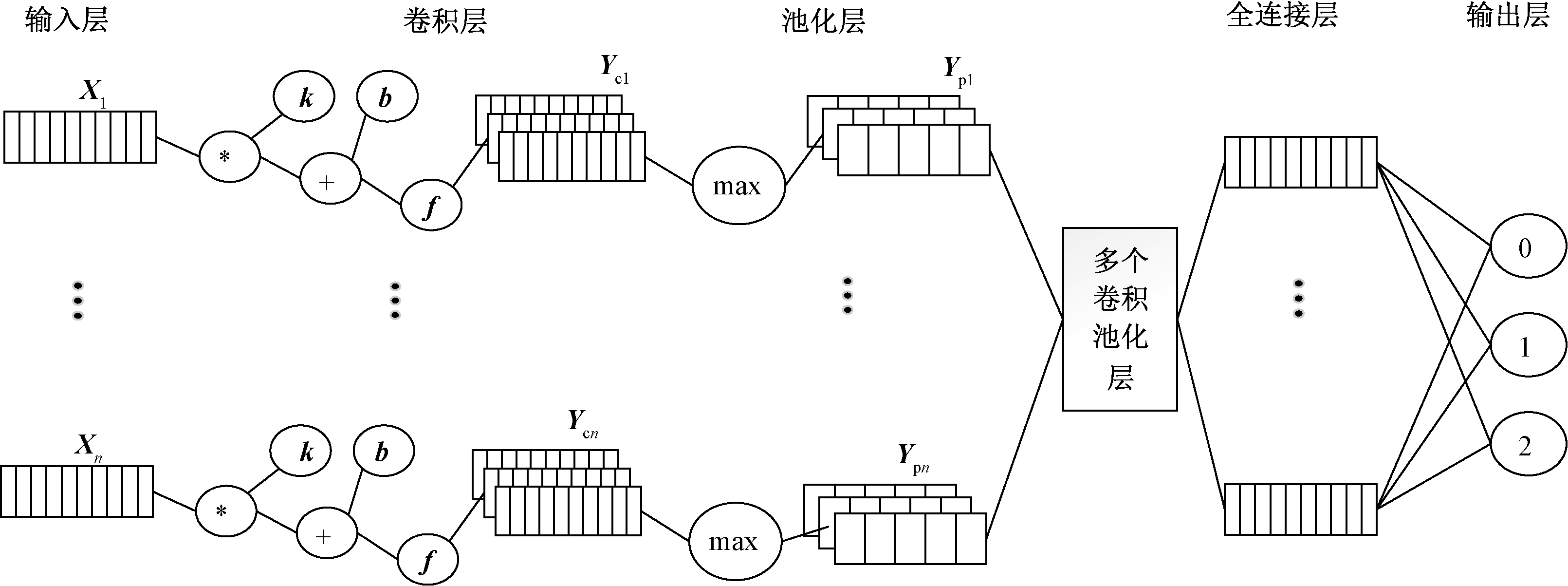
图1 卷积神经网络结构
Figure 1 Convolutional neural network structure
卷积层通过卷积核对输入信号进行卷积运算,其产生的结果就是提取的特征。图1中Yc1为卷积层输出的结果。卷积层最重要的特点就是权值共享和局部感知,一个卷积核会通过特定的步长将输入数据进行一次卷积操作。权值共享可以减少网络参数,有效抑制过拟合现象。卷积层的数学模型如下所示:
(5)
式中:![]() 代表第l层卷积输出的第i个特征信号;Mi表示输入当前层信号的集合;
代表第l层卷积输出的第i个特征信号;Mi表示输入当前层信号的集合;![]() 表示卷积核的权值矩阵中的元素;
表示卷积核的权值矩阵中的元素;![]() 为卷积层的偏置。
为卷积层的偏置。
池化层主要是对上一层的输出进行降采样操作,能够减少神经网络的参数,对数据进行降维和特征提取。图1中Yp1是池化层的输出结果,池化包含平均池化和最大池化。平均池化是求数据的均值,综合数据中不同的特征信息;最大池化则保留数据中最明显的特征,除去微弱的信号。卷积网络模型采用最大池化,在图1中表示为max。
输出层表示网络的分类结果,输出层与池化层之间有一个全连接层。全连接层与上一层的节点完全连接。将提取的特征综合在一起,由于全连接的特性,其参数是所有层结构中最多的。
2.2 故障诊断建模的一般步骤
时域信号是最原始的信号,它包含的信息量大,波形具有直观、便于理解的特点。但是由于故障的发生及后续的发展往往造成频域上的变化,为了准确分析故障的状态,通常需要频域信息,频域分析也是故障诊断上广泛使用的方法之一。通过建立卷积神经网络模型和传统BP神经网络模型来对比分析,模型故障诊断的流程图如图2所示。
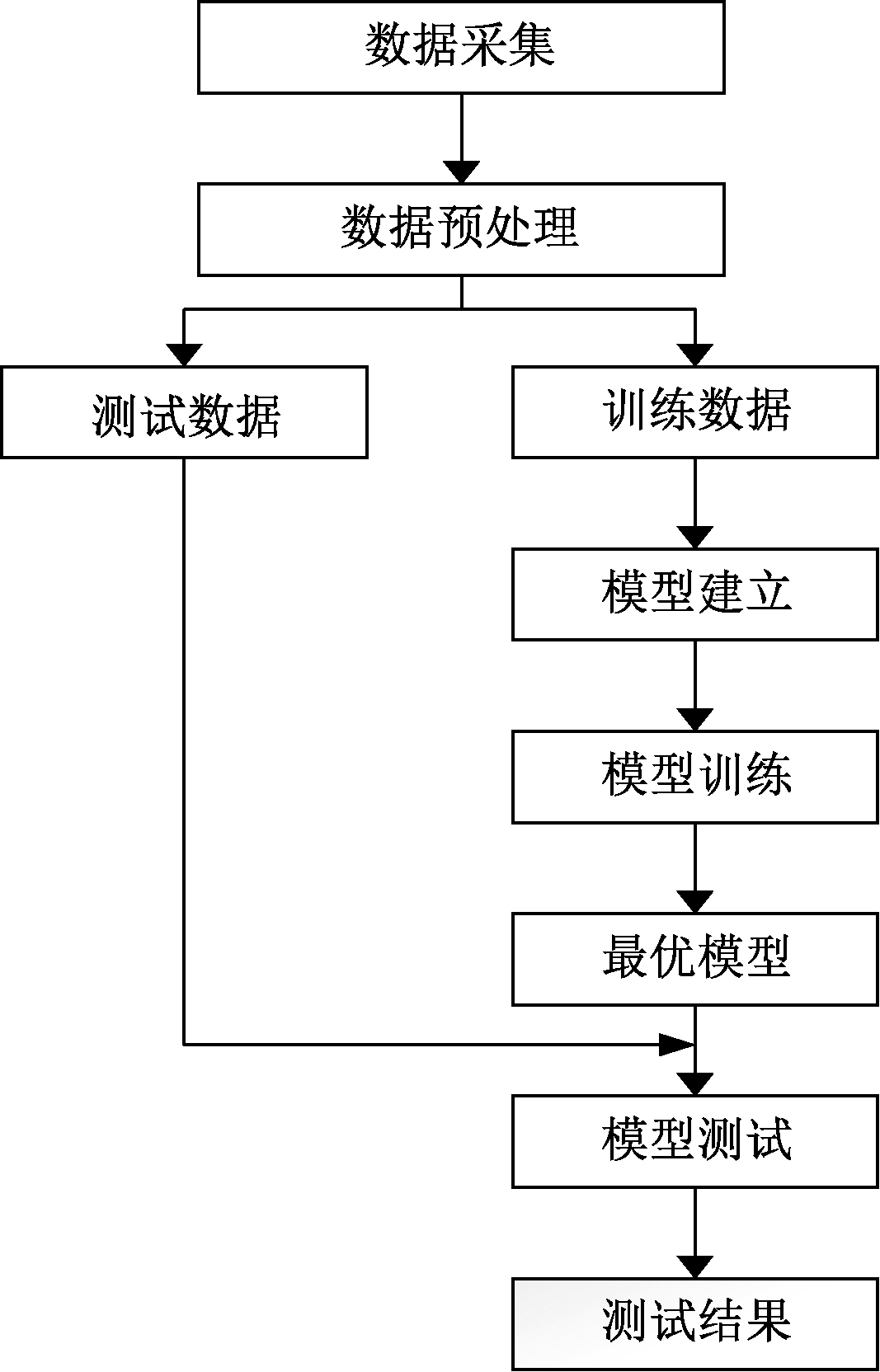
图2 故障诊断流程图
Figure 2 Fault diagnosis flow chart
3 试验分析
数据采用美国辛辛那提大学智能维护中心提供的滚动轴承数据。设备简图如图3所示,主轴安装有4个滚动轴承,传动轴由直流电机驱动,电机转速为2 000 r/min,施加6 000磅的径向载荷,轴承润滑良好,每个轴承都安装了两个PCB公司353B33型号的加速度传感器,传感器相互垂直布置,采集的信号属于同源双通道信号,满足全矢谱融合条件。信号的采样频率为20 000 Hz,每组数据有20 480个数据点。测点布置如图3所示。
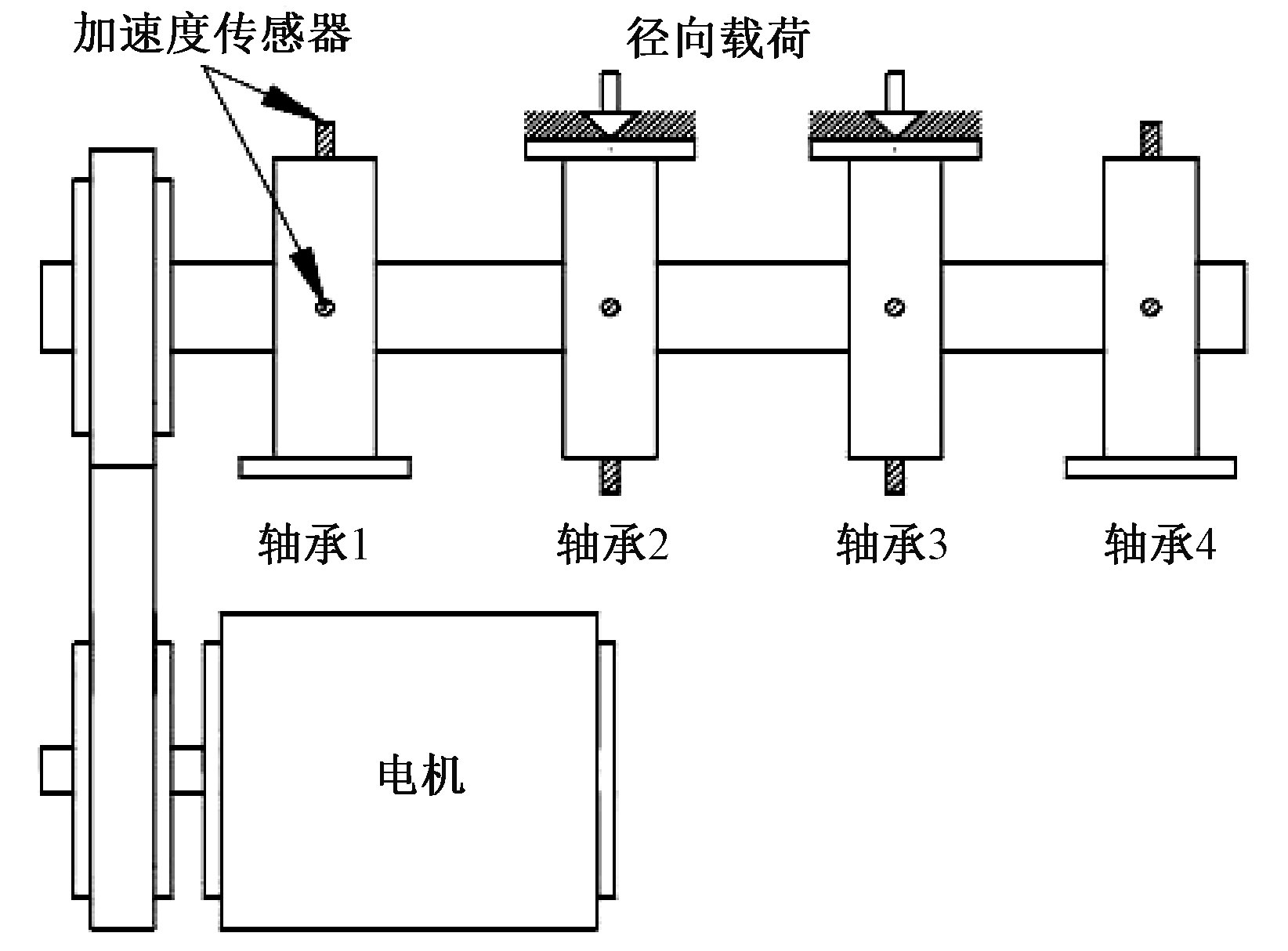
图3 轴承测点分布图
Figure 3 Distribution of measuring point bearing
数据处理:为扩充实验样本,将实验数据进行无重叠的样本分割,每组信号有2 048个数据点,总计3 000组实验样本,将样本分割为训练集和测试集,比例为7∶3。样本包含正常状态、内圈故障、滚动体故障3种状态标签。
卷积网络模型有2个卷积层,2个池化层,1个全连接层,神经元个数为32,卷积结构参数如表1所示。
表1 卷积模型参数表
Table 1 Convolution parameter table

参数卷积核层数步长paddingConv17*181*1samePool12*182*1sameConv23*1321*1samePool22*1322*1same
BP神经网络模型有3个隐层,其神经元个数为128、64、32。模型训练次数为200次,训练数据分割为batch的形式对网络进行训练。训练参数如表2所示。
表2 模型训练参数
Table 2 Parameter table of model

输入数据优化函数迭代次数学习率分类器[1 024,1]AdamOptimizer2005×10-4Softmax
4种模型在200次的迭代学习中测试集上的准确率如图4所示,其中全矢CNN(CNN_FV)模型的效果最好,模型准确率在99.80%±0.05%。单通道CNN模型的收敛速度比全矢CNN模型慢,但两者的准确率相差不大,模型准确率在99.30%±0.05%。单通道BP模型和全矢BP(BP_FV)模型的收敛速度和准确率均低于全矢CNN和单通道CNN模型,其准确率分别在94.00%±0.10%和97.00%±0.10%。
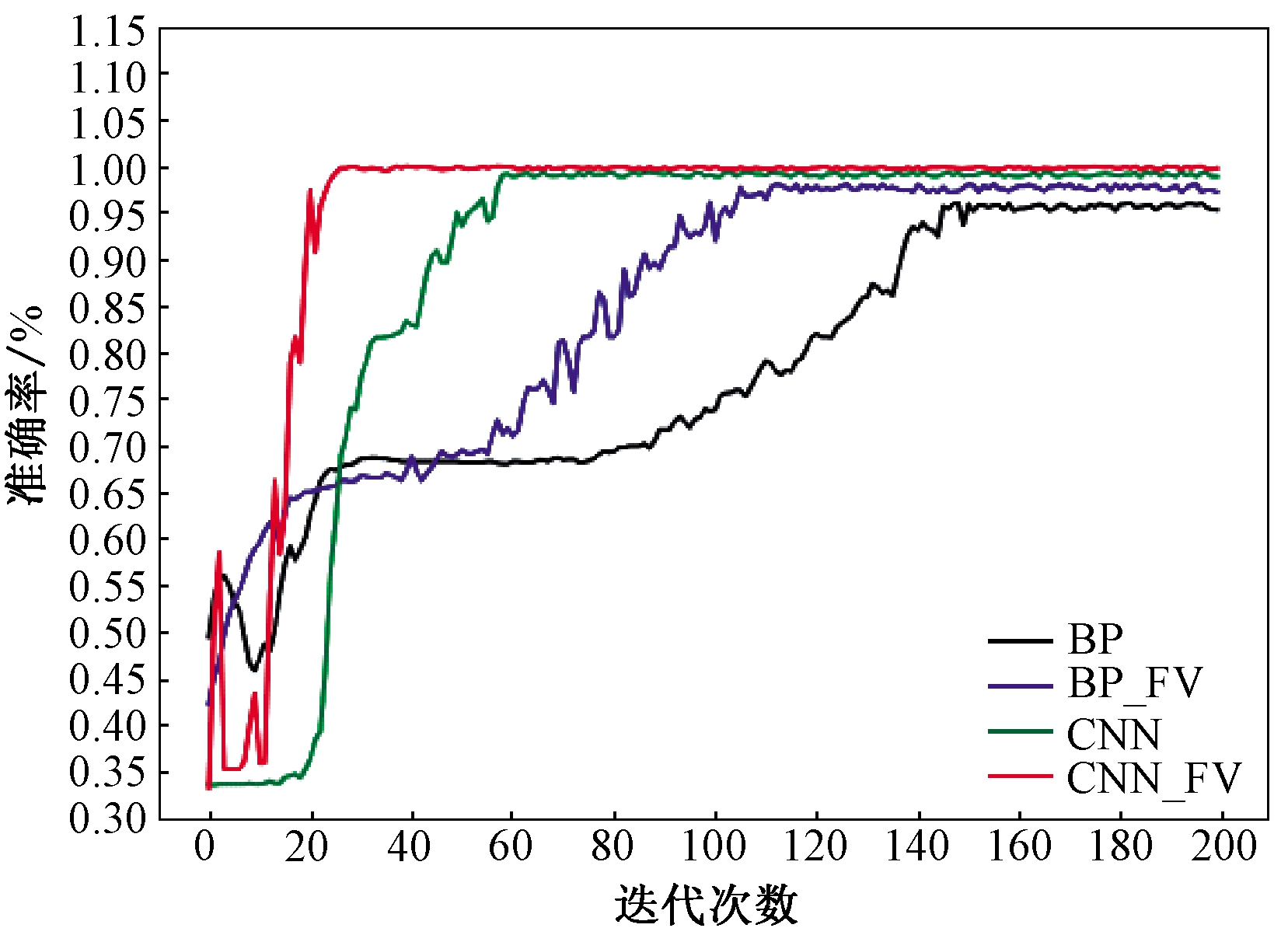
图4 测试集准确率
Figure 4 Test set accuracy
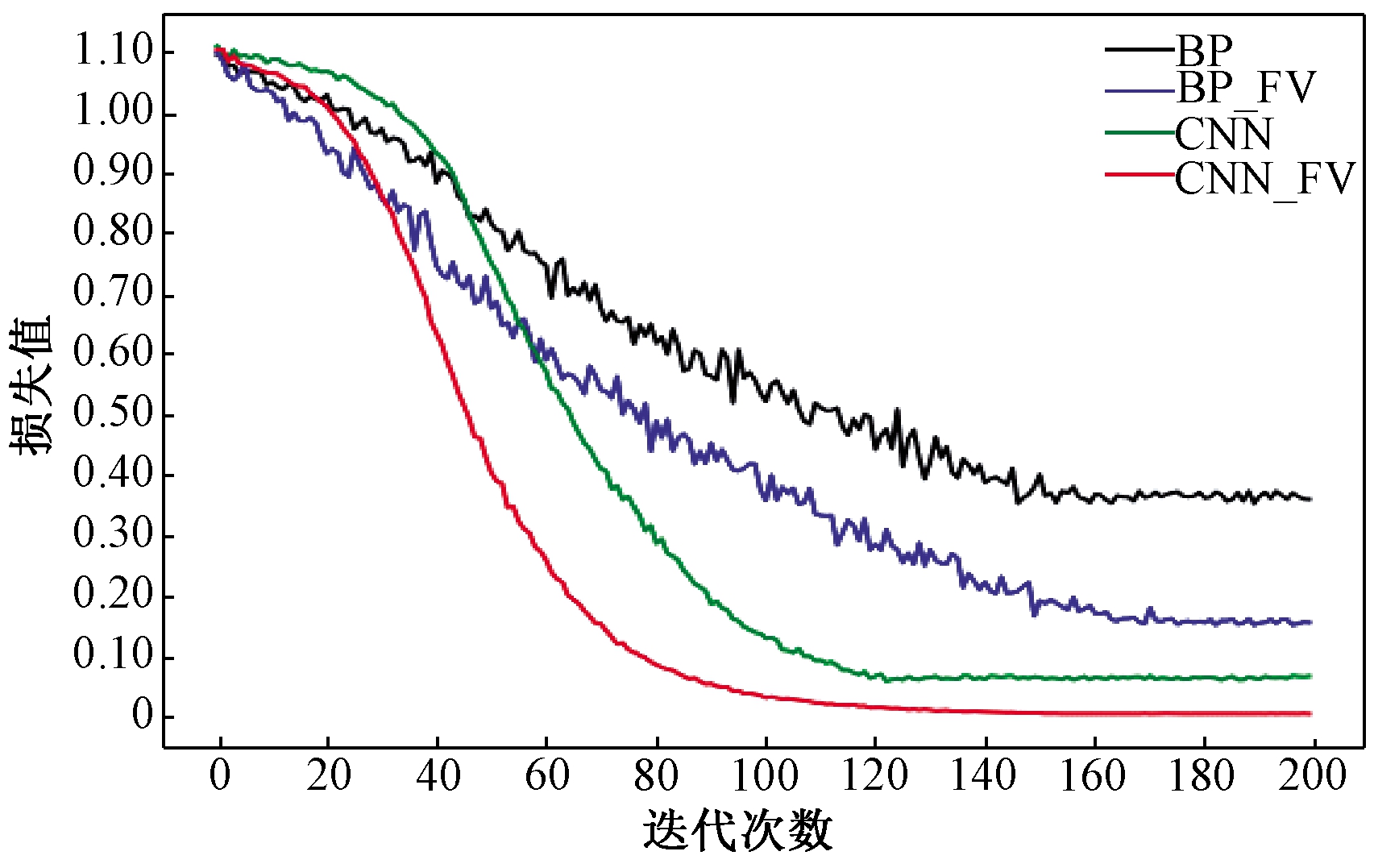
图5 4种模型的损失值
Figure 5 Loss values for the four models
如图5所示,4种模型的损失值都随着训练次数的增加而减小,在前30次训练中BP模型的收敛速度比CNN模型的收敛速度都要快,30次以后CNN模型的收敛速度要优于BP模型。4种模型中单通道CNN和全矢CNN的损失值分别在epoch达到120次和100次左右开始趋于稳定,而单通道BP和全矢BP分别在150次和160次趋于稳定。从图中可以看出通过全矢谱技术构建的网络模型比单通道模型的损失值小,损失值越小代表网络的鲁棒性越好。
提取模型对轴承数据进行特征聚类的结果,利用PCA进行降维,提取前两维主成分分量用于可视化,如图6所示。
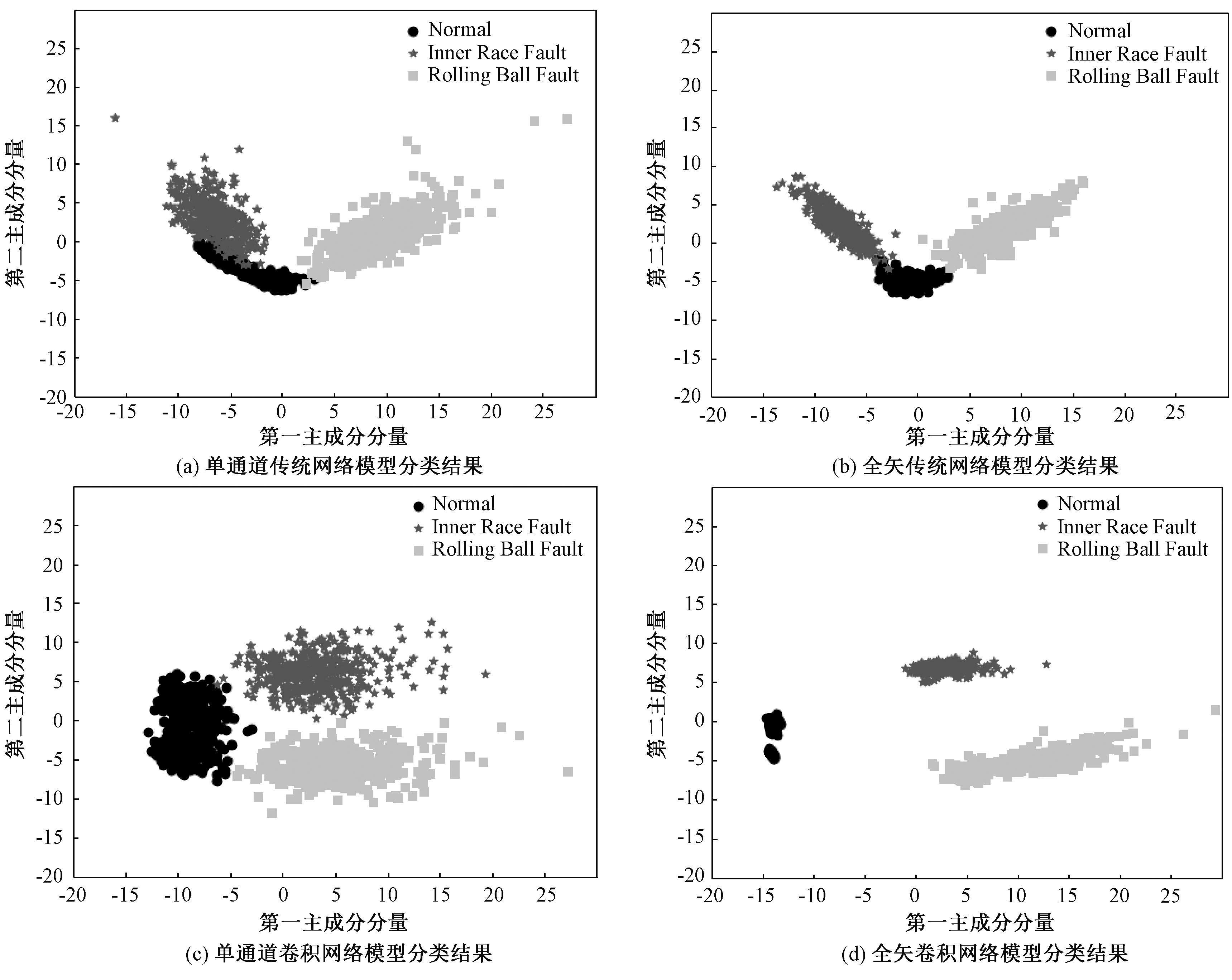
图6 4种模型分类结果
Figure 6 Classification results of four models
图中3种不同类型点分别代表滚动轴承的3种状态:正常状态(Normal)、内圈故障(Inner Race Fault)、滚动体故障(Rolling Ball Fault)。从图中可以看出,4种模型都能够识别轴承的故障状态,但都存在一定的缺陷。单通道BP、全矢BP模型和单通道CNN模型在识别3类故障时都存在一定的误判,全矢CNN模型能够将3类状态准确地识别,但是从识别的结果来看4种模型都存在一定的发散情况。
4 结论
本文构建了一种全矢谱技术与卷积神经网络的滚动轴承故障识别模型,将双通道信号进行全矢数据融合得到主振矢数据集,将其作为卷积神经网络的训练样本,能够弥补单通道信号信息遗漏的问题。从实验结果来看,构建的全矢模型相比单通道模型有更高的准确率和更小的损失值;CNN模型相比传统的BP神经网络模型具有更高的准确率和更快的收敛速度。
[1] LEI Y G, LIN J, HE Z J, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical systems and signal processing, 2013, 35(1/2): 108-126.
[2] 雷文平,吴小龙,陈超宇,等.基于自动编码器和SVM的轴承故障诊断方法[J].郑州大学学报(工学版),2018,39(5):68-72.
[3] 雷亚国,贾峰,周昕,等.基于深度学习理论的机械装备大数据健康监测方法[J].机械工程学报,2015,51(21):49-56.
[4] 郭亮, 高宏力, 张一文, 等. 基于深度学习理论的轴承状态识别研究[J]. 振动与冲击, 2016, 35(12): 166-170, 195.
[5] JANSSENS O, SLAVKOVIKJ V, VERVISCH B, et al. Convolutional neural network based fault detection for rotating machinery[J]. Journal of sound and vibration, 2016, 377: 331-345.
[6] CHEN Z Q,LI C,SANCHEZ R V. Gearbox fault identification and classification with convolutional neural networks[J]. Shock and vibration,2015(2):1-10.
[7] 袁建虎,韩涛,唐建,等.基于小波时频图和CNN的滚动轴承智能故障诊断方法[J].机械设计与研究,2017,33(2):93-97.
[8] 管腾飞. 全矢高阶统计量及其在故障诊断中的应用研究[D]. 郑州:郑州大学,2015.
[9] 韩捷,石来德.全矢谱技术及工程应用[M].北京:机械工业出版社,2008:65-70.
[10] 张伟. 基于卷积神经网络的轴承故障诊断算法研究[D]. 哈尔滨:哈尔滨工业大学,2017.
[11] GOODFELLOW I, BENGIO Y, COURVILLE A. Deep learning[M/OL]. Cambridge, MA:MIT Press, 2016[2019-05-07]. http://www.deeplearningbook.org.