0 引言
在长期的研究工作中，人们逐渐认识到材料的性能以及一些关键构件的疲劳失效及断裂不仅与材料的化学成分有关，还在很大程度上取决于材料的微结构。Huang等[1]通过表面轧制处理，在AISI 316 L不锈钢中生成了梯度纳米层结构，在对其疲劳性能的研究中发现，疲劳裂纹在表面下500 μm深处萌生，并向表面和内部扩展，最终导致试样瞬间断裂。大多数金属材料通常是晶体的集合体，即多晶体，在宏观上表现为各向同性；而在微观上，晶粒的形状、大小、晶体取向都不相同，表现为各向异性。可见建立具有微观组织结构的多晶体模型对于模拟材料性能和疲劳性能也变得越来越重要。
将晶体塑性有限元方法与随机的晶粒结构、晶体取向等结合起来，是目前在晶粒尺寸水平上研究微结构局部变形、应力变化的主要手段。微结构有限元模型的建立通常采用Voronoi图原理的方法，或者采用EBSD技术进行微结构的重构。获取单晶体的材料参数最直接的方法就是通过制备单晶试样进行各种材料试验来确定[2-3]。考虑到这种方法既耗时耗力，成本又太高，因此大多数采用Materials Studio模拟软件[4]，通过建立晶体原子结构模型计算得出。晶体塑性本构模型的塑性参数通常通过拟合试样的应力-应变曲线来获得。
通过晶体塑性有限元方法来模拟多晶体有限元模型的应力-应变曲线[5]，通过误差函数确定与实验得到的拉伸曲线吻合最好的应力-应变曲线，最终确定了18CrNiMo7-6合金钢晶体本构模型的最优塑性参数，为后续的有限元模拟提供材料参数。
1 力学性能试验与有限元模型
1.1 18CrNiMo7-6合金钢的拉伸实验
研究的材料为18CrNiMo7-6合金钢，为出厂状态(锻造处理)，材料成分如表1所示。为了确定18CrNiMo7-6合金钢晶体本构模型的塑性参数，首先需要对该材料进行拉伸实验，获得应力-应变曲线。拉伸试样采用圆棒试样，试样规格采用国家标准GB 228—2002标准规定的尺寸，如图1所示。拉伸实验在MTS(370.25)试验机上进行，按照应变加载的方式进行加载，加载应变率为0.001/s，拉伸过程中采用引伸计对应变进行测量，试样的应力-应变曲线如图2所示。
表1 18CrNiMo7-6合金钢的化学成分的质量分数
Table 1 The mass fraction of chemical composition of 18CrNiMo7-6 alloy %
CSiMnPSCrMoNi0.15～0.210.400.50～0.900.025≤0.0351.50～1.800.25～0.351.40～1.70
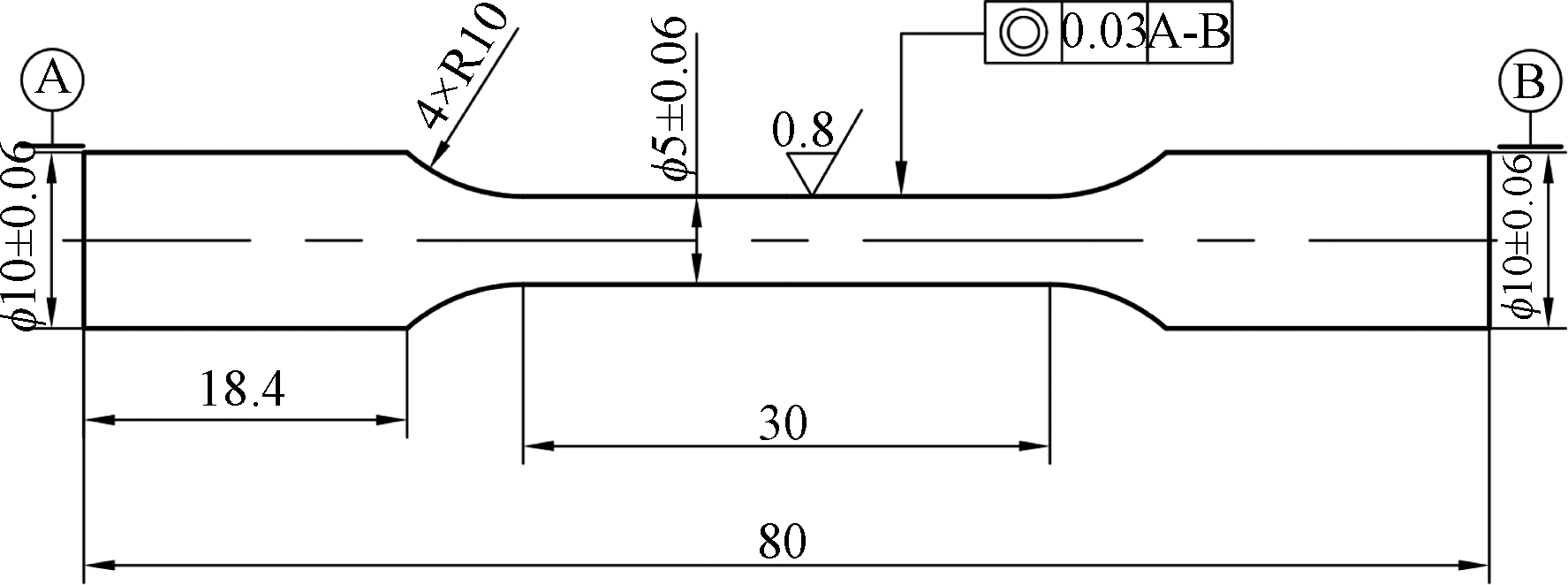
图1 拉伸试样的尺寸图
Figure 1 Dimensions of the tensile specimen
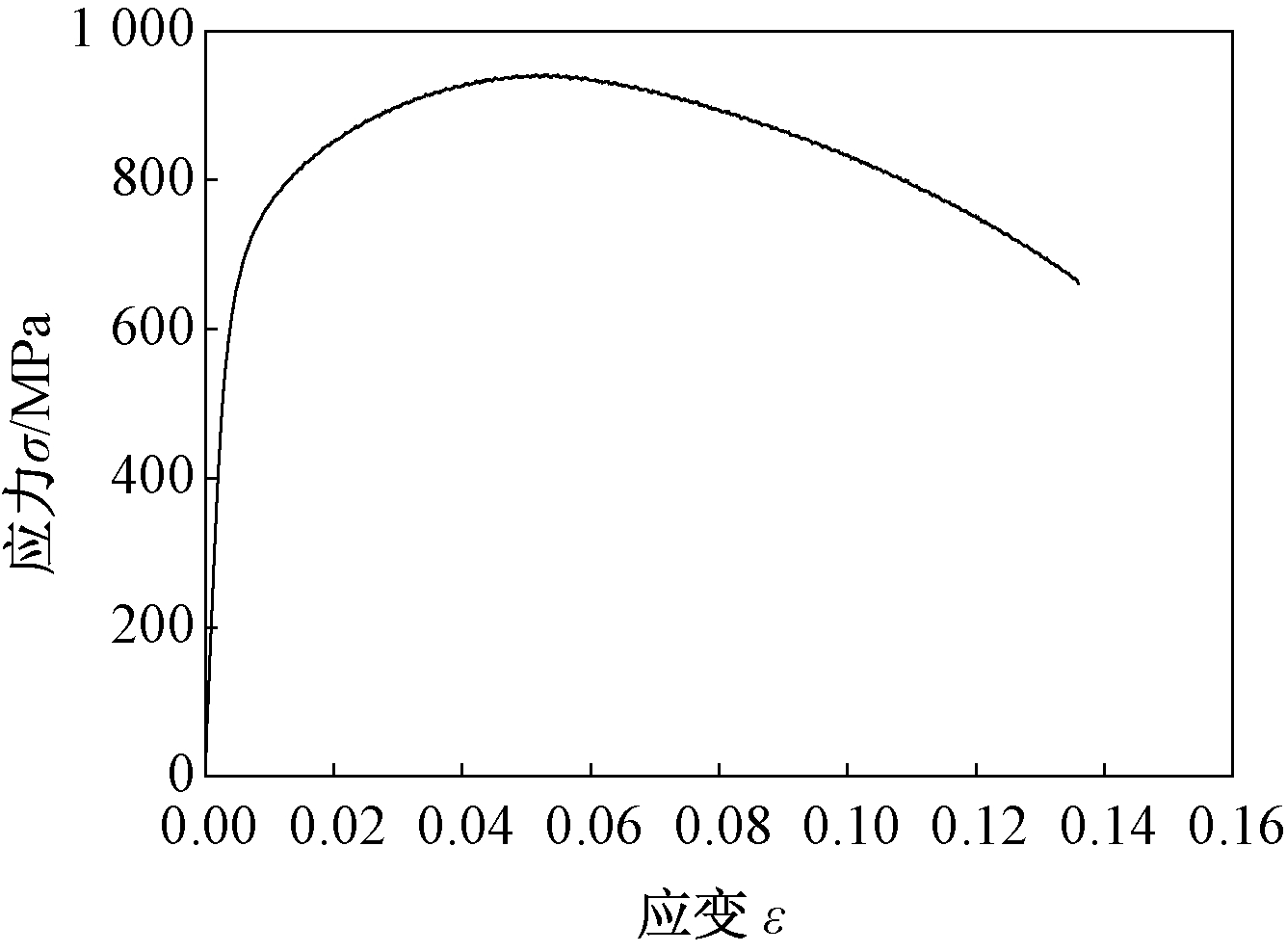
图2 18CrNiMo7-6合金钢试样的应力-应变曲线
Figure 2 Stress-strain curve of 18CrNiMo7-6 alloy specimen
对应力-应变曲线进行数据拟合等一系列处理之后，得到18CrNiMo7-6合金钢原材料的材料参数，如表2所示。
表2 18CrNiMo7-6合金钢的材料参数
Table 2 Material parameters of 18CrNiMo7-6 alloy
试样材料弹性模量/GPa屈服强度/MPa抗拉强度/MPa18CrNiMo7-6201.36670941
1.2 多晶体有限元模型
多晶体的几何模型采用Voronoi图的原理生成，Voronoi图原理是由俄国数学家Georgy Fedosievych Voronoy于1908年定义并命名的[6]，其是由一组连接两邻点直线的垂直平分线构成的连续多边形组成(如图3所示)。其实质是按照临近原则对空间的一种剖分形式，由剖分后所形成的多边形(体)集合构成[7]。Voronoi图原理被广泛运用于生物细胞结构、城市规划、地理学、气象学、结晶学、图像处理和微结构模拟等复杂问题中[8]。
利用MATLAB自带的Voronoi函数，在一定的范围内随机撒种子点，生成多晶体二维几何模型，并提取几何模型的顶点信息，按一定的顺序存放在记事本文件中。采用Python语言脚本在ABAQUS中调用记事本文件中的顶点数据，经过处理后在Part模块中生成多晶体的微结构模型。考虑计算效率问题，本文中所建立的晶粒尺寸模型要比实际的晶体尺寸略大，因此本文内容建立了一个包含16个晶粒的多晶体微结构模型，如图4所示。
图4 带有16个晶粒的微结构模型
Figure 4 Microstructure model with 16 grains
1.3 边界条件和网格划分
建立的几何模型长和宽为1 mm，由16个随机大小和形状的晶粒组成，每个晶粒的晶体取向随机分布。网格划分采用全局种子点控制，网格尺寸0.01 mm，网格单元数量为10 647个，单元类型为平面应力四节点完全积分单元。模型左端固定，采用位移边界条件，约束U1和U2方向(即U1=0, U2=0)。在模型右端外部的中间位置建立一个参考点，该参考点与模型右端耦合，通过参考点施加位移边界条件进行拉伸模拟，如图5所示。在分析中，模型被嵌入到一个更大的主体中。为了便于与试验对比，拉伸位移设置为0.05 mm。提取参考点的支反力及位移与拉伸试验的前半段进行拟合。
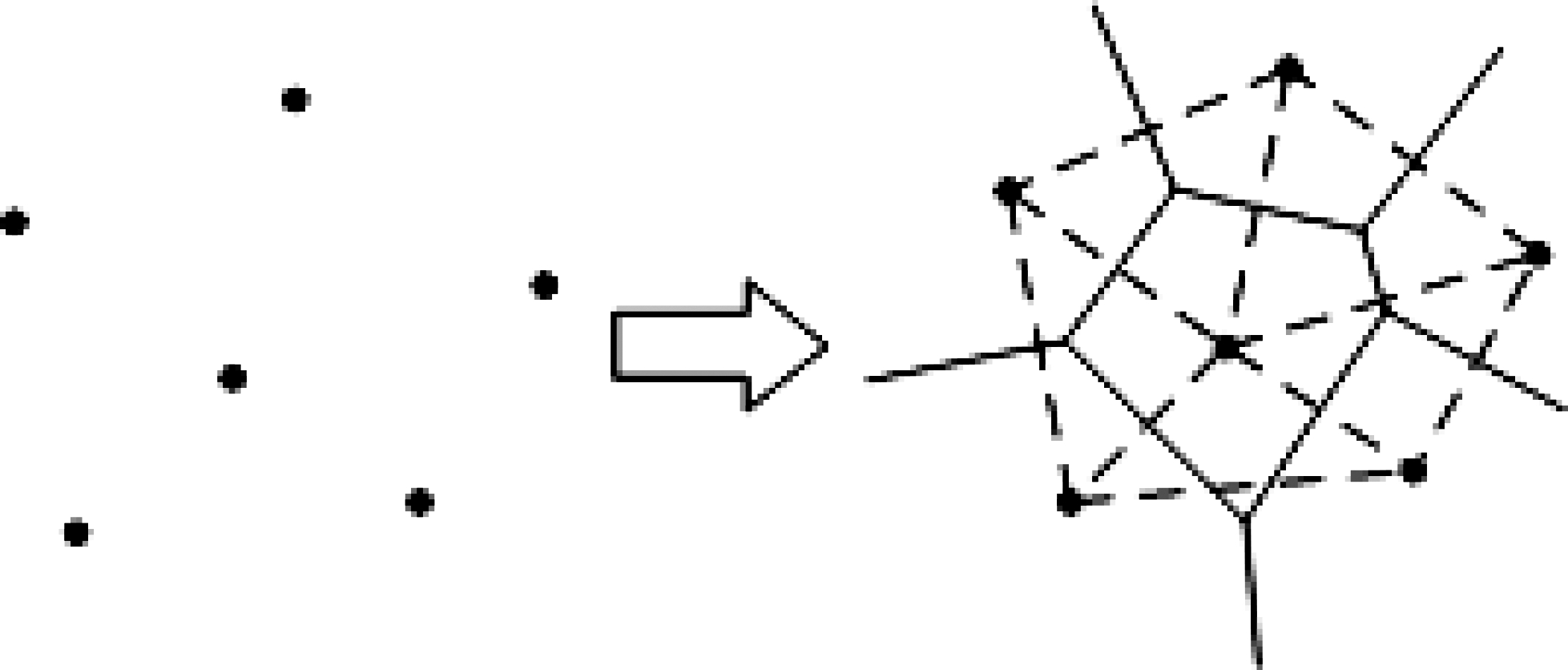
图3 二维voronoi图生成原理
Figure 3 Formation principle of 2D voronoi diagram
图5 有限元模型的边界条件和网格划分
Figure 5 Boundary conditions and meshing of the finite element model
1.4 率相关晶体硬化模型
基于施密特定律，在对单晶硬化率相关黏塑性理论研究的基础之上，Perice等[9]认为率相关晶体的第α个滑移系上的滑移率
可以由其相应的分解剪切应力τ(α)来确定：
(1)
式中：常数
是第α个滑移系上的参考应变率；g(α)是描述第α个滑移系上当前强度的一个变量；无量纲函数f(α)是一个描述应变率对应力依赖关系的通用函数。
Hutchinson[10]用一个简单的幂分布形式来描述多晶体的蠕变：
f(α)(x)=x|x|n-1，
(2)
式中：n是率敏感指数，当n趋向于无穷时，这个幂分布形式接近于一个率无关材料。
应变硬化通过增量关系强度g(α)的演化来描述：
(3)
式中：hαβ是滑移硬化模量，该式表示对所有激活的滑移系统进行求和； hαα(no sum)称为自硬化模量； hαβ (α≠β)称为潜硬化模量。Perice等[11]和Asaro[12-13]用一个简单的形式来描述自硬化模量：
(4)
式中:h0是初始硬化模量；τ0是初始屈服应力，它等于当前强度g(α)(0)时的初始值；τs是阶段I的应力或者说是大塑性流动开始时的突破应力；γ是所有滑移系统上的泰勒累积剪切应变。
(5)
潜硬化模量用下式来表示:
hαβ=qh(γ)， α≠β,
(6)
式中:q是一个常数。这些硬化模量的表达式忽略了晶体中的包辛格效应。
笔者采用Huang[14]单晶体模型的UMAT，由于该种率相关硬化模型只需要确定晶体的3个塑性参数，即初始屈服应力τ0、阶段I的应力τs、初始硬化模量h0，其他参数从文献中获得。
2 本构模型参数的确定及讨论
2.1 弹性参数
根据文献[15]可知，少量的合金元素并不会显著地改变晶粒的弹性刚度，所以用体心立方晶体α-Fe的弹性常数作为18CrNiMo7-6合金的单晶材料常数[16]，即C11=230 GPa，C12=135 GPa，C44=117 GPa，齐纳(Zener)[17]各向异性系数
(7)
符合各向异性。
2.2 塑性参数
进行拉伸模拟的材料参数参考文献[5]中相似的材料，初步设置为初始屈服应力τ0=200 MPa，第Ⅰ阶段的应力τs=30 MPa，初始硬化模量h0=100 MPa，体心立方晶体的3个滑移系包括一个主滑移系{1 1 0}<1 1 1>，两个次滑移系{1 1 2}<1 1 1>和{1 2 3}<1 1 1>。由于体心立方晶体滑移系的启动比较复杂，在低温条件下，{1 1 0}<1 1 1>滑移系往往会开动，在室温或高温时，{1 1 2}<1 1 1>和{1 2 3}<1 1 1>滑移系有可能会开动[18]。Kothari和Anand等[19]采用基于位错滑移的晶体塑性本构模型对BCC晶体钽的变形行为进行了模拟，发现在常温下BCC晶体塑性变形中滑移系开动的个数为24个。利用有限元模拟，依次设置只有1、2、3组滑移系开动，结果如图6所示。应变率敏感指数n=50，参考剪切应变率
硬化因子q=1等从文献[20]中获得。
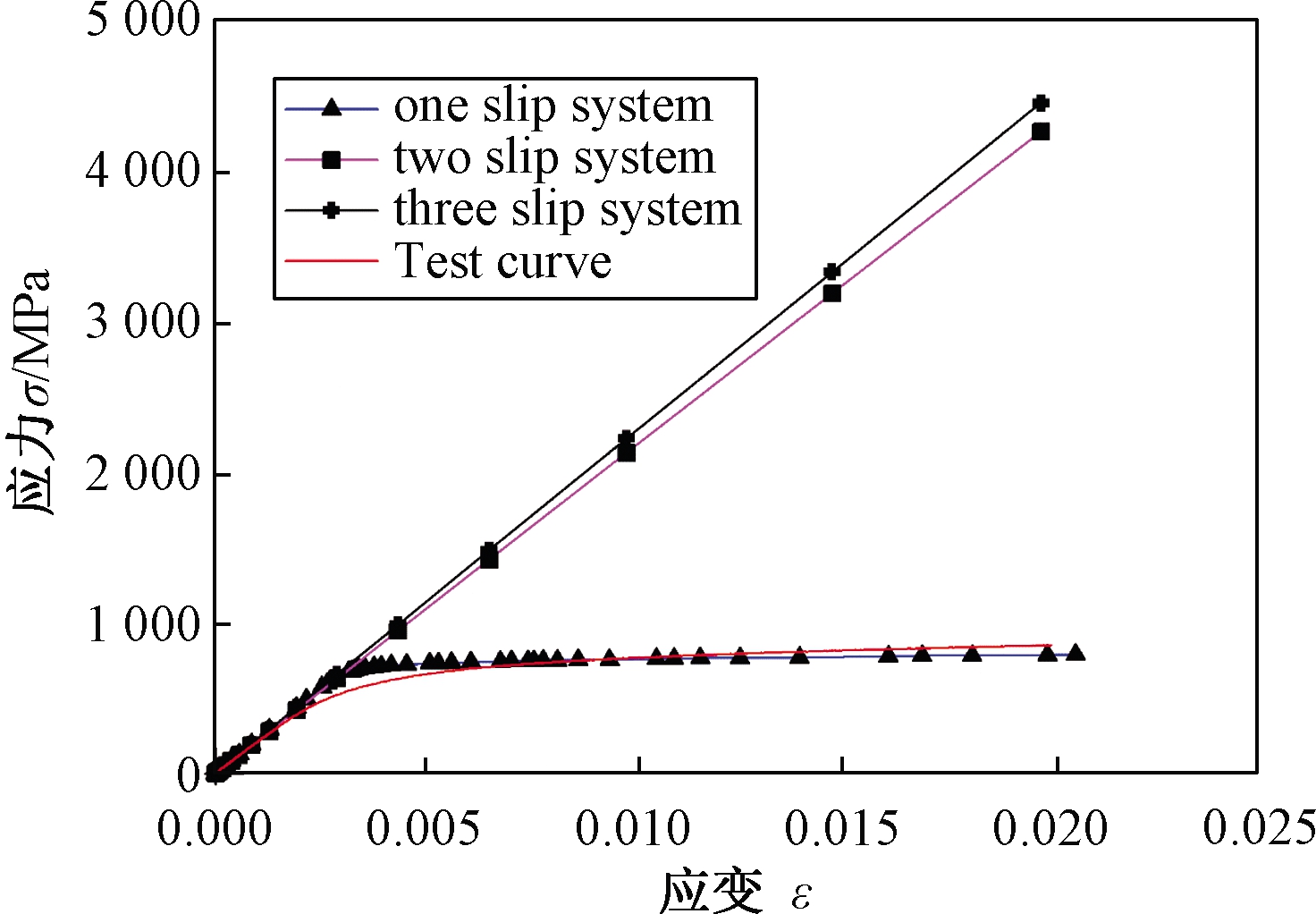
图6 不同滑移系组数对应的应力-应变曲线与试验曲线的对比图
Figure 6 Comparison of stress-strain curve corresponding to the number of different slip system groups and the test curve
从图6可以看出，当只有一个滑移系开动时，即主滑移系{110}<111>开动，多晶体的宏观应力-应变曲线有明显的拐点，即进入屈服阶段，与试验曲线比较吻合。当有2组或者3组滑移系开动时，多晶体的宏观应力-应变曲线只有弹性变形，与试验曲线相差较大。因此采用晶体塑性有限元方法的仿真均只采用一个主滑移系开动。下面对晶体的3个塑性参数进行研究，评价这些参数对多晶体宏观应力-应变曲线的敏感性影响。
固定晶体塑性中第Ⅰ阶段的应力τs和初始硬化模量h0两个参数，只改变初始屈服应力τ0。通过ABAQUS进行有限元仿真，将结果与试验曲线进行对比分析表明，参数初始屈服应力τ0的改变对多晶体的屈服点产生了影响，多晶体的屈服应力随着τ0的增大而逐渐增大，如图7所示。
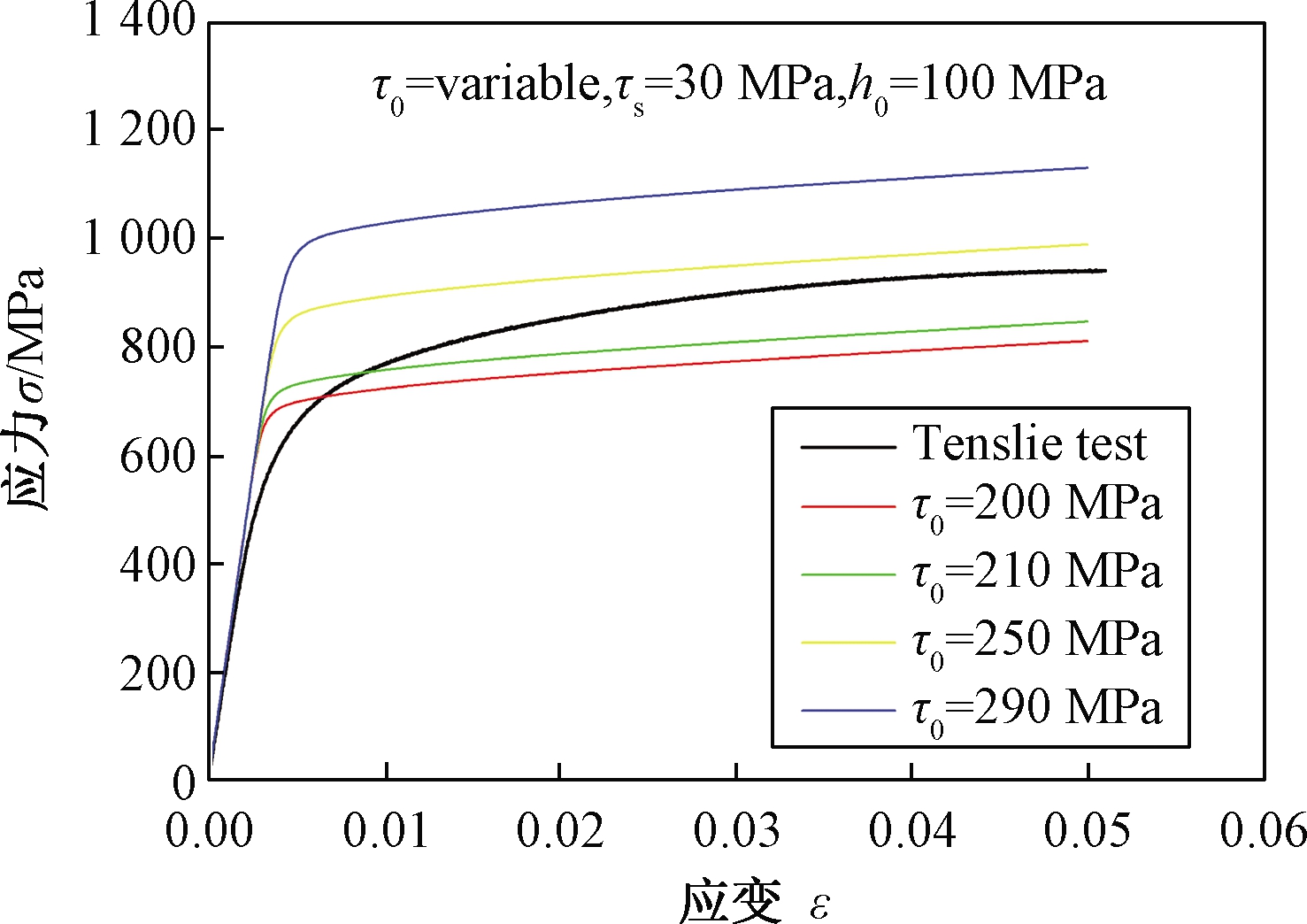
图7 初始屈服应力τ0对宏观应力-应变曲线的影响
Figure 7 Influence of initial yield stress τ0 on macroscopic stress-strain curve
固定晶体塑性中的初始屈服应力τ0和初始硬化模量h0两个参数，只改变第Ⅰ阶段的应力τs这个参数，通过ABAQUS进行有限元仿真，将结果与试验曲线进行对比，见图8。可见参数第Ⅰ阶段的应力τs的变化对屈服点几乎没有影响，但对屈服点以后的应力-应变曲线产生了影响，当接近τ0时几乎与x轴平行。随着τs的增加后半段的斜率也逐渐增加，当增大到一定程度后几乎不再变化。参数τs不能等于τ0，否则它将在方程(4)中产生奇异性。
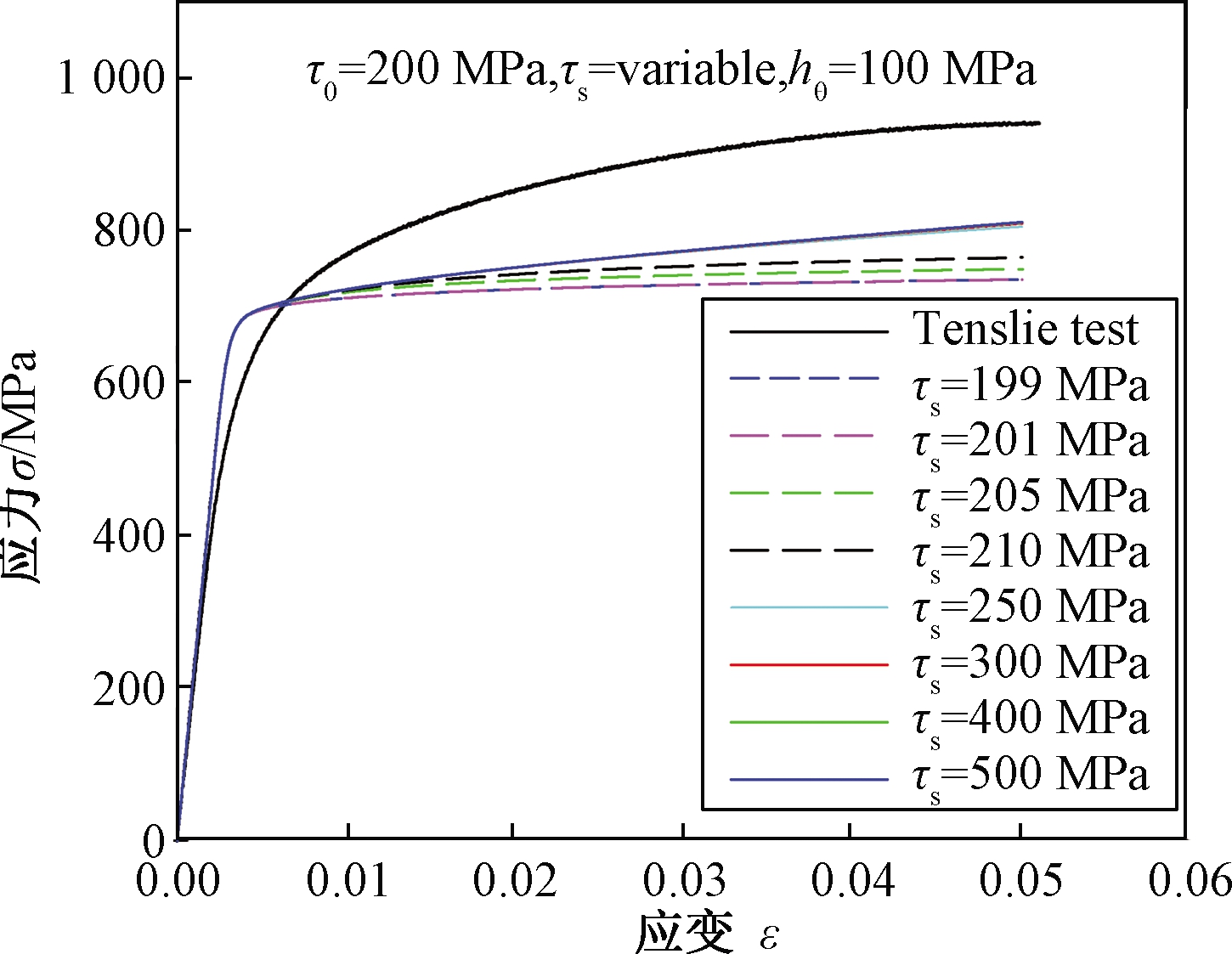
图8 第Ⅰ阶段应力τs对宏观应力-应变曲线的影响
Figure 8 Influence of stage I stress τs on macroscopic stress-strain curve
固定晶体塑性中的初始屈服应力τ0和第Ⅰ阶段的应力τs两个参数，只改变初始硬化模量h0这个参数，通过ABAQUS进行有限元仿真，将结果与试验曲线进行对比分析，见图9。可见参数初始硬化模量h0的变化对屈服点也几乎没有影响，但对屈服点附近的曲线斜率产生了较大的影响，斜率随着h0的增大而逐渐增大。
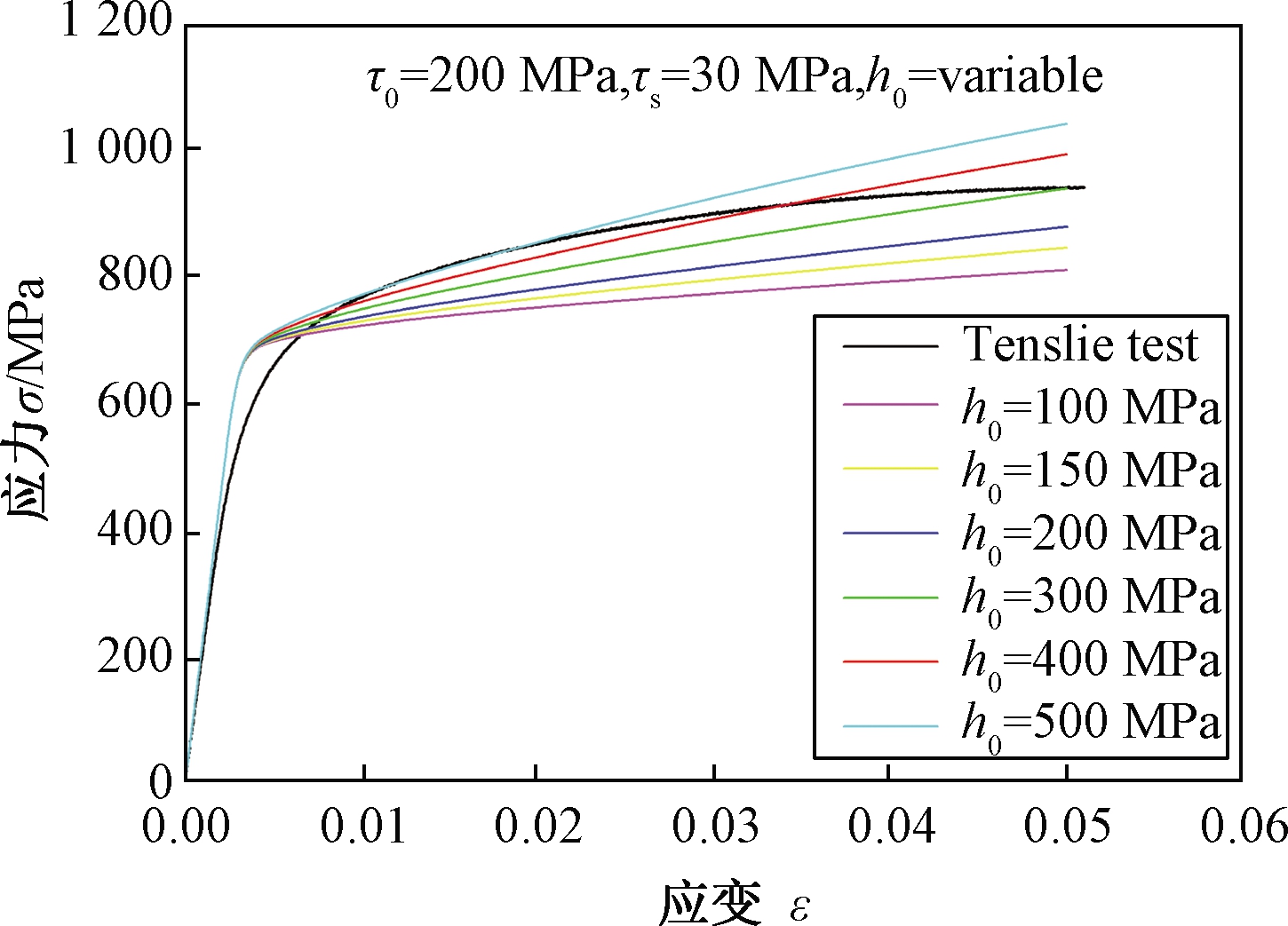
图9 初始硬化模量h0对宏观应力-应变曲线的影响
Figure 9 Influence of initial hardening modulus h0 on macroscopic stress-strain curve
通过考察晶体的3个塑性参数(初始屈服应力τ0、第Ⅰ阶段的应力τs、初始硬化模量h0)对多晶体宏观上应力-应变曲线的敏感性分析，初步确定了它们的变化趋势和大致的变化范围，据此初步估算有限元的计算次数，估计计算所需要的时间成本。τ0在180～240 MPa范围内变化，每次变化10 MPa；τ0=200 MPa时，τs在200～300 MPa范围内变化，每次变化10 MPa；h0在50～600 MPa范围内变化，每次变化50 MPa。由于第I阶段的应力τs大于初始屈服应力τ0且不相等，而初始屈服应力不受影响，所以τ0每增加一次计算，τs的计算次数便减少一次。为了提高计算的准确度，τs初始值比τ0大1 MPa，之后τs取整数，则计算次数如表3所示。
表3 有限元模拟所需的计算次数
Table 3 Number of calculations required for finite element simulation
塑性参数τ0=180～240 MPaτs=200～300 MPah0=50～600 MPa计算次数7、8、9、10、11、12、1312计算总次数840
参考 Moussa等[21]给出的代价函数来判断参数拟合的优劣程度。代价函数的值越小，说明模型拟合的程度越好，此时对应的塑性参数即为所求的最优结果。选择在线性回归中最常用的代价函数形式中的均方误差模型，其形式如下：
(8)
式中：m=εmax/ε,εmax是最大应变，在本文中εmax=0.05,ε是选取的应变小区间；m则是应变点的总数；i是第i个应变点
是拉伸实验中第i个应变点处对应的应力值；
有限元仿真中第i个应力点处对应的应力值。
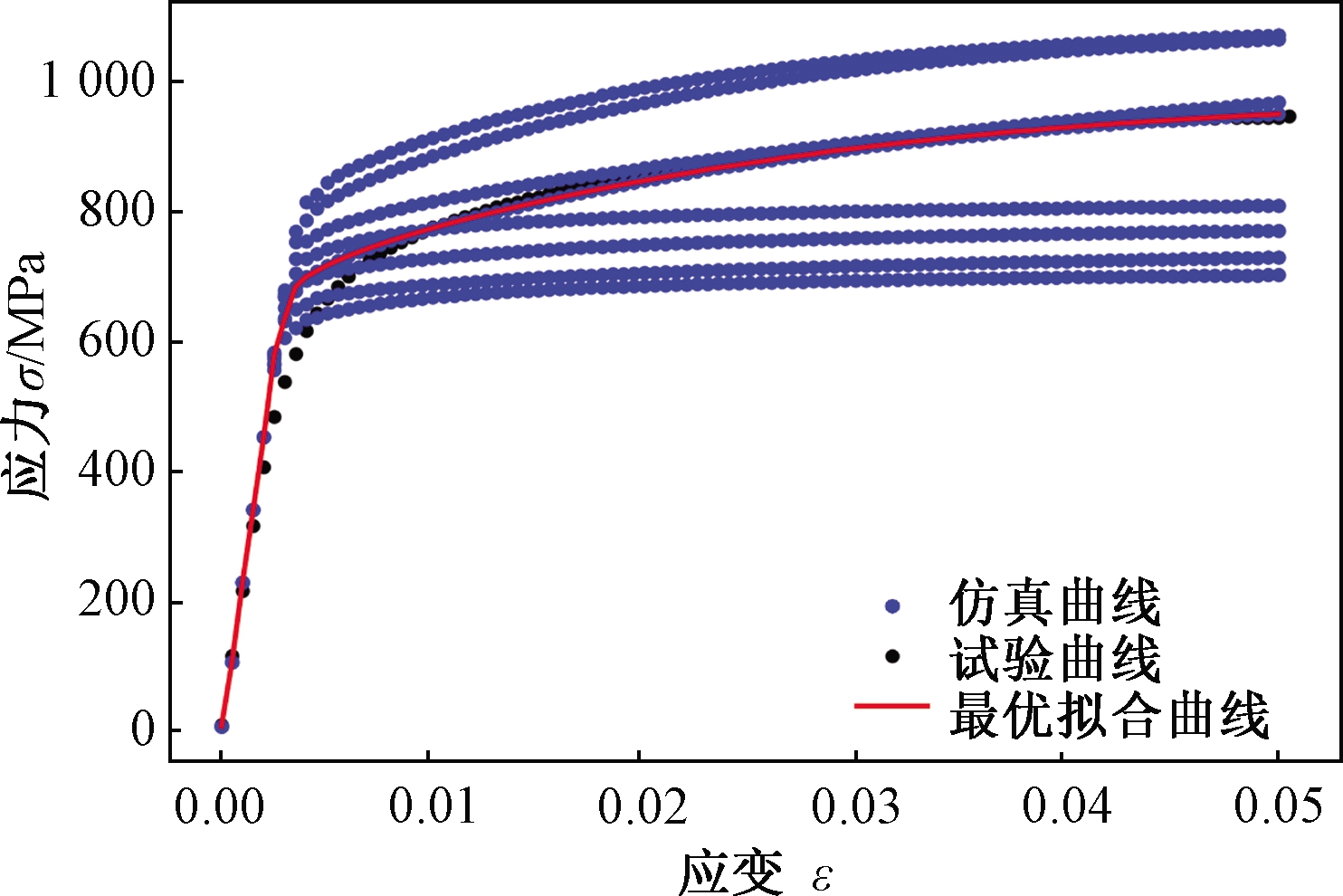
图10 840组拟合曲线与试验曲线的对比示意图
Figure 10 Comparison of the 840 sets of fitted curves and test curves(Schematic diagram)
对840组仿真结果中提取出的数据进行Python编程处理，并与试验得到的应力-应变曲线进行对比分析，通过代价函数比对选择，选出了一条最优的拟合曲线(如图10所示，其中只给出了具有代表性的几组拟合曲线)。输出该曲线的参数组合，最终得到的最优晶体塑性参数组合如表4所示。最优的参数组合为τ0=200 MPa，τs=270 MPa，h0=500 MPa。得出的最优拟合曲线与实验曲线如图11所示，从中可以清楚地看出两条曲线吻合较好，其相对误差范围在0～10.4%。
表4 有限元拟合的最优材料参数
Table 4 Optimal material parameters for finite element fitting
初始屈服应力τ0/MPa第Ⅰ阶段的应力τs/MPa初始硬化模量h0/MPa200270500
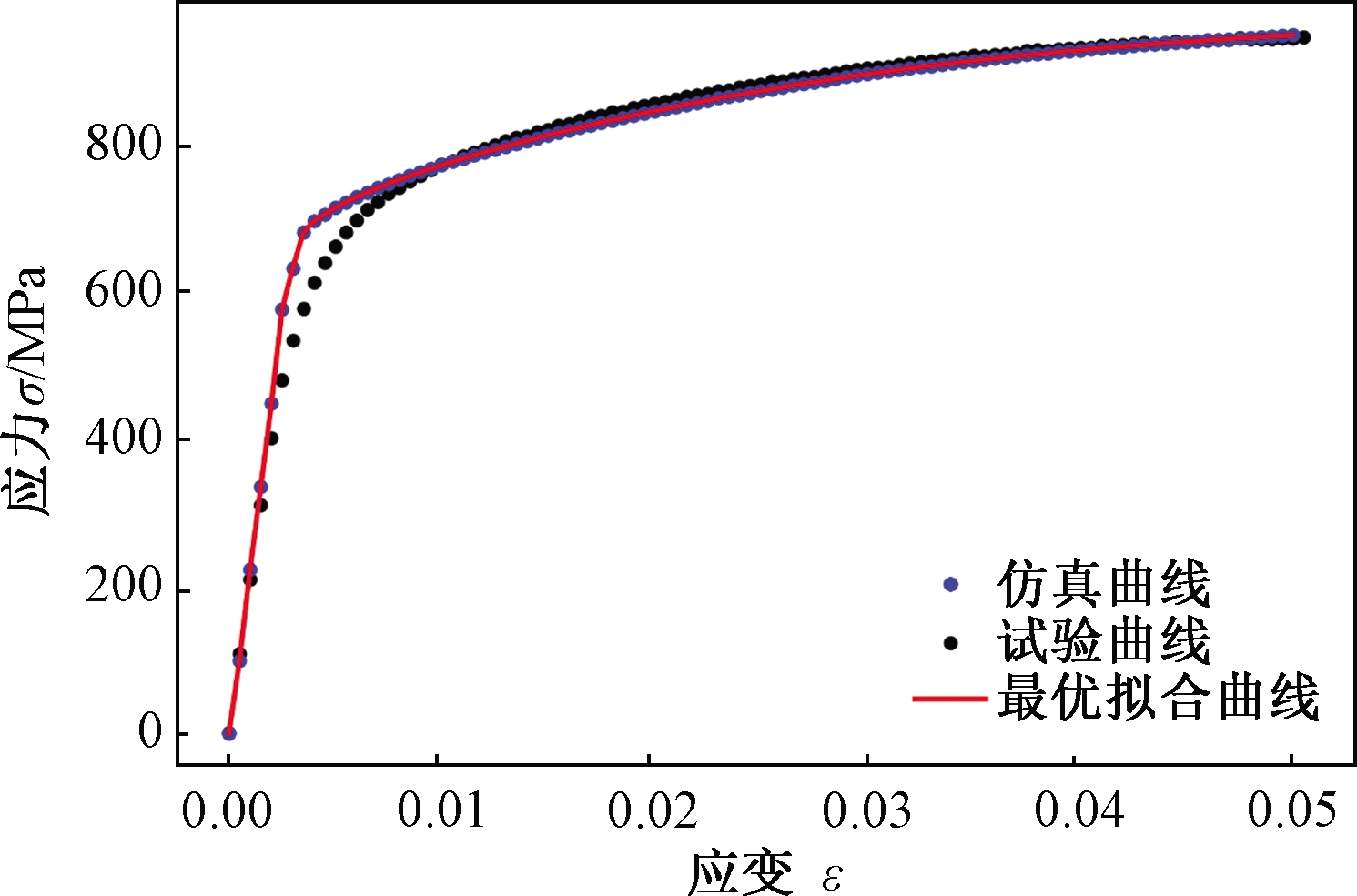
图11 最优拟合曲线与试验曲线
Figure 11 Best fit curve and test curve
3 结论
笔者采用晶体塑性有限元的方法，通过建立有限元模型模拟了应力-应变曲线，并与实验得到的应力-应变曲线进行了比较。利用建立的误差函数进行分析，有限元分析的结果和实验获得的应力-应变曲线吻合较好。最终确定了18CrNiMo7-6合金钢的3个主要单晶塑性参数为τ0=200 MPa，τs=270 MPa，h0=500 MPa。
[1] HUANG H W, WANG Z B, LU J, et al. Fatigue behaviors of AISI 316L stainless steel with a gradient nanostructured surface layer[J]. Acta materialia, 2015(87):150-160.
[2] 郭运强, 张克实, 耿小亮, 等. 晶体塑性模型在单晶铜低周疲劳行为中的应用[J]. 机械强度, 2009, 31(2): 276-281.
[3] 张克实, 耿小亮, 李金山, 等. 铜单晶试样在滑移变形机制下的拉伸颈缩[J]. 中国科学E辑, 2007, 37(7):866-874.
[4] 李东营. 基于晶体塑性理论的超薄带材轧制数值模拟[D]. 秦皇岛: 燕山大学, 2017.
[5] SIMONOVSKI I, NILSSON K F, CIZELJ L. Material properties calibration for 316 L steel using polycrystalline model [C]//Abstracts of the 13th International Conference on Nuclear Engineering. Beijing, China: CNS, 2005:111.
[6] AURENHAMMER F. Voronoi diagrams: a survey of a fundamental geometric data structure[J]. ACM computing surveys, 1991, 23(3): 345-405.
[7] 方伟, 梅希薇. 基于Voronoi盲区的三维无线传感器网络覆盖优化算法[J]. 郑州大学学报(工学版), 2017, 38(4):73-78.
[8] 司良英, 邓关宇, 吕程, 等. 基于Voronoi图的晶体塑性有限元多晶几何建模[J]. 材料与冶金学报, 2009, 8(3):193-197.
[9] PEIRCE D, ASARO R J, NEEDLEMAN A. Material rate dependence and localized deformation in crystalline solids[J]. Acta metallurgica, 1983, 31(12): 1951-1976.
[10] HUTCHINSON J W. Bounds and self-consistent estimates for creep of polycrystalline materials[J]. Proceedings of the royal society A: mathematical, physical and engineering sciences, 1976, 348(1652): 101-127.
[11] PEIRCE D, ASARO R J, NEEDLEMAN A. An analysis of nonuniform and localized deformation in ductile single crystals[J]. Acta metallurgica, 1982, 30(6): 1087-1119.
[12] ASARO R J. Crystal plasticity[J]. Journal of applied mechanics, 1983, 50(4b): 921-934.
[13] ASARO R J. Micromechanics of crystals and polycrystals[J]. Advances in applied mechanics, 1983, 23(8):1-115.
[14] HUANG Y. A user-material subroutine incorporating single crystal plasticity in the ABAQUS finite element program, MECH-178[R]. Cambridge, MA：Harvard University,1991.
[15] ATKINS A G. Deformation-mechanism maps (the plasti-city and creep of metals and ceramics)[J]. Journal of mechanical working technology, 1984, 9(2): 224-225.
[16] GRIMVALL G. Thermophysical properties of materials[M]. Amsterdam：North-Holland, 1999.
[17] ZENER C. Elasticity and anelasticity of metals[M]. Chicago: The University of Chicago Press, 1948.
[18] 杨梅. 基于晶体塑性理论的板材塑性及损伤行为研究[D]. 上海: 上海交通大学, 2009.
[19] KOTHARI M, ANAND L. Elasto-viscoplastic constitutive equations for polycrystalline metals: Application to tantalum[J]. Journal of the mechanics and physics of solids, 1998, 46(1): 51-83.
M, CIZELJ L. Modeling elasto-plastic behavior of polycrystalline grain structure of steels at mesoscopic level[J]. Nuclear engineering and design, 2005, 235(17/18/19): 1939-1950.
[21] MOUSSA C, BARTIER O, MAUVOISIN G, et al. Characterization of homogenous and plastically graded materials with spherical indentation and inverse analysis[J]. Journal of materials research, 2012, 27(1): 20-27.