0 引言
在工业4.0技术和智能制造引领制造业的背景下,随着计算机数值计算方法的引入和快速发展,热处理的数值模拟大大地提高了人们对热处理过程的控制能力和理解水平[1-2]。国内外陆续开发出能够进行热处理模拟的有限元软件,比如专用热处理模拟软件DEFORM-HT[3]、COSMAP、SYSWELD-HT等;另外通过在大型通用有限元软件ABAQUS[4]、ANSYS、MARC等添加用户自定义程序,实现热处理过程的理论数学模型,也成为了重要的热处理模拟方法。渗碳工艺是现代工业生产中普遍运用的一种表面硬化工艺,例如轴类零件和齿轮等工件的硬化[5]。笔者采用DEFORM软件对18CrNiMo7-6的渗碳工艺进行数值模拟。
扩散系数和传递系数是控制渗碳过程的两大关键因素,其数学模型的选择直接决定着渗碳工艺数值模拟的精确度。多数学者对传递系数大多采用与温度有关的函数模型,并给出了不同的经验公式[6-7]。扩散系数反映物体内部碳原子扩散速度的快慢,其影响因素有温度、晶体结构、碳浓度、合金元素等,学者们基于不同影响因素提出了各自的数学模型。最早的经典理论认为扩散系数是温度的函数D(T),A.G.Guy和J.J.Hren[8]在“物理冶金学原理”中给出了模型中的扩散激活能等参数。但经典的扩散理论是建立在稀“溶液”的基础上的,而实际的渗碳过程中,碳的质量分数是达到甚至超过饱和值的,所以在第二届国际热处理大会上,C.Borgianni[9]对扩散理论进行了修正,提出了与温度和碳含量均有关的扩散系数模型D(T,C),并指出碳的扩散系数随含碳量的增大而增大。随着研究的深入,多数学者提出了基于此模型的经验公式。王顺兴[10]设计了一组渗碳工艺,根据一维气体渗碳数学模型,由误差最小原则对比实验碳梯度和模拟值结果,计算和确定了扩散系数和传递系数模型的参数。张星[11]以界限含碳量为判断标准,比较了两种扩散数学模型D(T)和D(T,C)对一种渗碳工艺的模拟精度,得出后者的吻合度更高。然而在严格意义上,与温度和含碳量有关的扩散系数模型只适用于碳钢,因为合金元素会影响碳原子的传递和扩散过程[12]。Rowan等[13]研究了4种不同化学成分的合金钢在相同的渗碳工艺下的碳梯度,发现碳化物元素Cr、Mo等会降低碳的扩散系数,增大环境碳势与工件表面的传递速度,而使奥氏体稳定的元素Mn、Ni等会增大扩散系数,降低传递系数。Lee等[14-15]将前人的扩散模型进行了总结对比,采用一个判断实验数据与经验公式结果吻合程度的评判参数,提出了考虑微量元素M的扩散模型D(T,M,C)。
笔者采用2种扩散系数模型D(T,C)和D(T,M,C)对3种不同渗碳工艺(渗层深度分别为1、2、4 mm)进行数值模拟。重点考虑合金元素对渗碳过程中扩散系数以及渗层中碳浓度分布的影响。采用机械剥层法测得分别经过3种渗碳工艺的试样据表面不同深度的碳含量分布,并与仿真结果对比以进行试验验证。
1 试验材料与方法
1.1 试验材料
试验材料为18CrNiMo7-6钢是一种常用的渗碳齿轮钢。经DF-100型光电直读光谱仪测得其化学成分如表1所示,化学成分符合标准。材料的原始组织为调质态,经调质预处理的材料具有良好的综合力学性能,且组织均匀稳定。
表1 18CrNiMo7-6的化学成分的质量分数
Table 1 Chemical composition of 18CrNiMo7-6 steel %
CSiMnSAlCrNiMoFe0.210.340.720.0040.041.581.40.26Bal.
1.2 渗碳工艺的基本理论
渗碳工艺是一个随时间变化的过程,常选用菲克第二定律作为其扩散方程:
(1)
式中:C为含碳量,%;t为扩散时间,s;x为沿扩散方向的距离,mm;D为碳原子在奥氏体中的扩散系数,mm2/s。
初始条件:
C|t=0=C0,
(2)
式中:C0为初始时刻工件的碳浓度分布,%。本研究中18CrNiMo7-6的初始碳含量为0.21%。
外边界条件:
(3)
式中:C∞为环境碳势,%;Cs为工件表面的含碳量,%;β 为碳从气相流入固相的传递系数,mm/s,反映为工件表面碳原子的传递速度,常选为与温度有关的函数:
(4)
式中:β0为常值;E为激活能,kJ/mol;T为温度,K。根据文献[7],分别取β0=0.003 47 mm/s、E=34 kJ/mol;R为8.314 J/(mol·K)。
1.3 渗碳扩散系数的数学模型
模型1 考虑温度和碳原子的扩散系数模型D(T,C)[16-17]:
(5)
式中: Q为碳原子的扩散激活能,Q=141 kJ/mol;D0.4为碳的质量分数为0.4%时的扩散常数,决定了渗碳层碳浓度的大小和分布,D0.4=25.5 mm2/s;Bc为反映碳原子对碳浓度分布规律影响大小的常数,主要对含碳量沿深度分布的斜率产生影响,Bc=0.8。
模型2 考虑温度、碳原子和合金元素的扩散系数模型D(T,M,C)[14]:
D(T,M,C)=
(0.146 -0.036 C(1-1.075 Cr)+∑k1M)·
(6)
式中:M为合金元素的质量分数,%;k1、k2为合金元素的合金参数,其取值如表2所示。
表2 扩散系数模型的合金元素和及其合金参数
Table 2 Alloying parameters for the diffusivity coefficient and the activation energy of carbon in austenite

合金参数MnSiNiCrMoAlk1-0.031 50.050 9-0.008 50.0*0.303 1-0.052 0k2-4.366 34.050 7-1.240 77.726 012.126 6-6.788 6
*在前面的指数部分已考虑。
与模型1相比,模型2增加了合金元素对碳原子扩散的影响。假定渗碳温度为915 ℃,两个模型在不同碳含量处的扩散系数分布如图1所示。可以看出,相同碳含量下,模型2明显低于模型1的扩散系数。
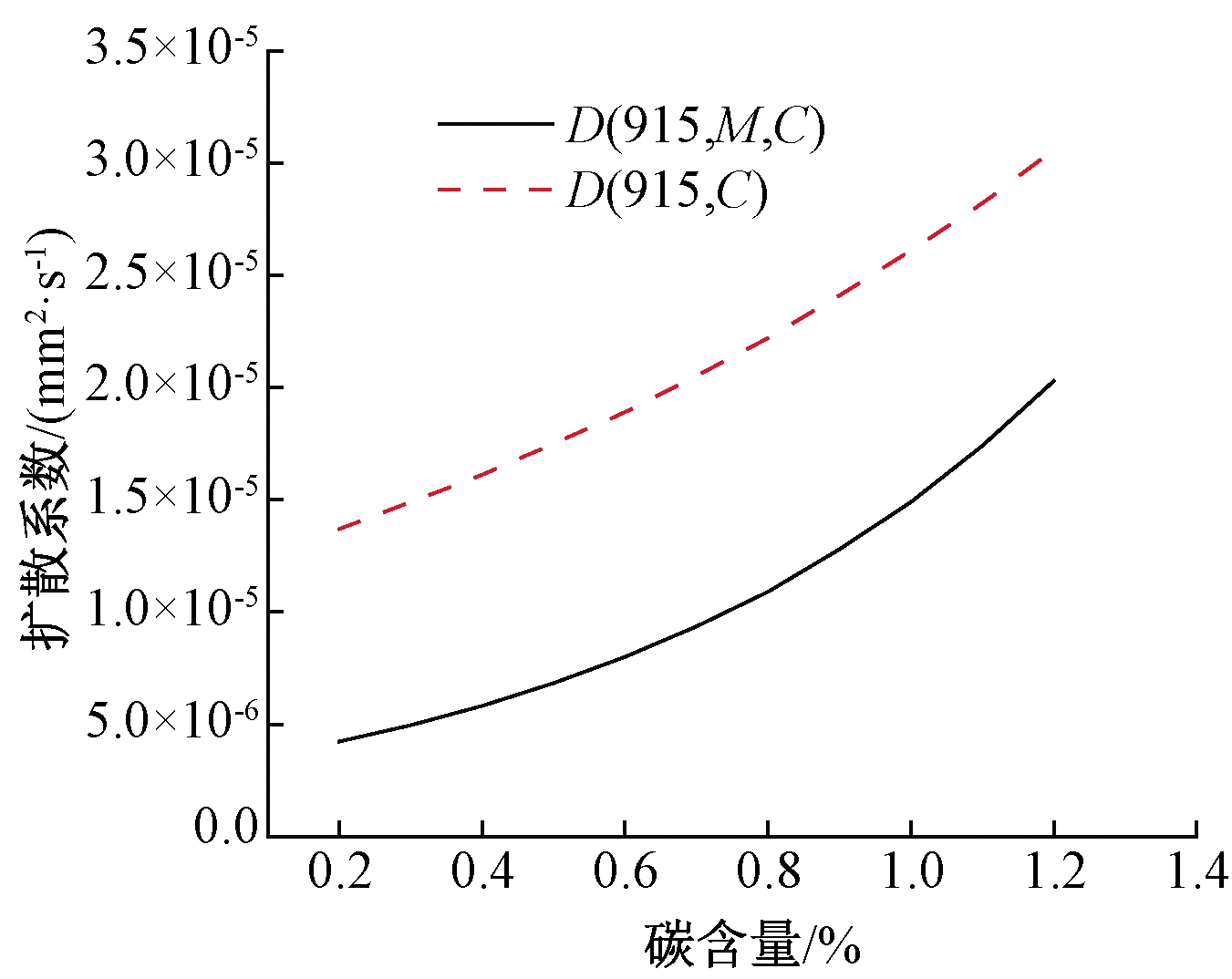
图1 两种扩散模型的扩散系数对比
Figure 1 Comparison of diffusion coefficients between the two diffusion models

图2 圆棒试样的几何模型
Figure 2 Finite element model of cylindrical specimen
2 仿真分析
2.1 仿真模型的建立
采用DEFORM-HT软件模拟圆棒试样的渗碳工艺。圆棒为轴对称几何图形,因此建立二维模型,如图2所示。以AB为对称轴,建立半径为8.36 mm、长为2 mm的二维无限长的几何模型。采用均匀的四边形网格,网格数为7 000(已达收敛性要求),在CD边施加温度和渗碳碳势的边界条件,在AB边施加x方向的力边界条件,AC和BD边施加y方向的力边界条件(灰色三角形)。
2.2 仿真的工艺参数
笔者使用气体渗碳法对试样进行渗碳处理。采用氮-甲醇气氛,在AlCHELlN(爱协林)4/1型箱式多用炉生产线进行渗碳。富化气为丙烷,渗碳过程由电脑程序全自动控制,控制系统为可视化多功操作系统TP-1200,碳势测量和控制系统采用程序化的MTK-1000,控温精度≤1 ℃,碳势均匀度≤±0.05%,碳势控制精度±0.05%。
为了研究合金元素对扩散系数以及碳浓度梯度的影响规律,对渗碳层深度L=1、2、4 mm的渗碳工艺进行数值模拟和试验验证,且分别称为工艺1、工艺2和工艺3。渗碳试样在工厂中随炉渗碳处理,其渗碳工艺参数如表3所示。
表3 3种渗层深度的渗碳工艺
Table 3 Carburizing process of three kinds of carburized layers
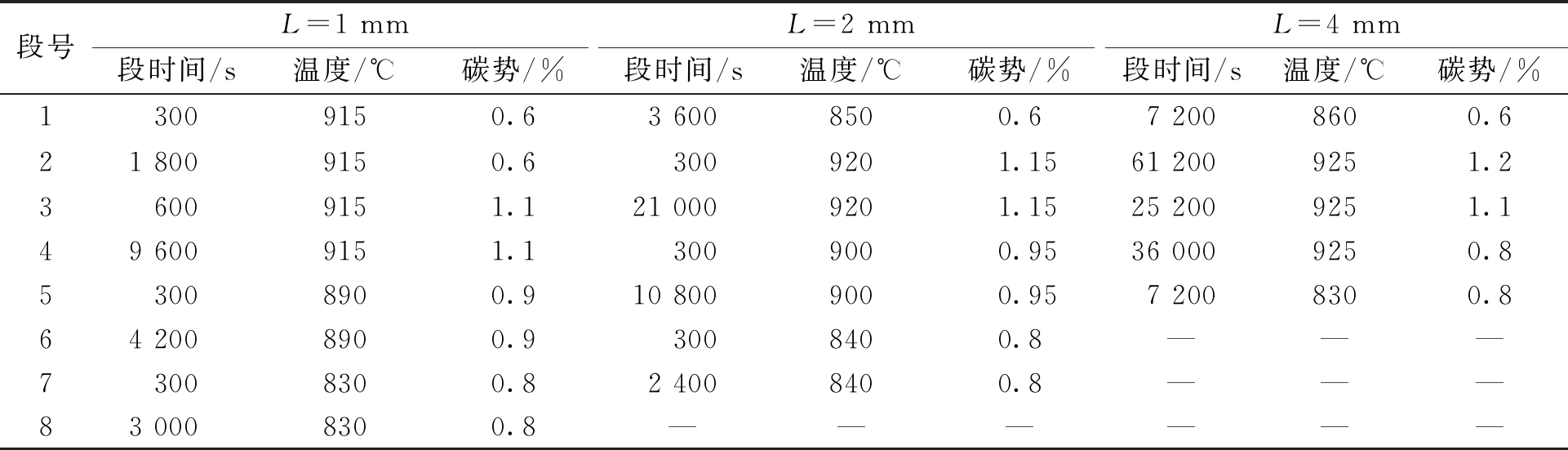
段号L=1 mmL=2 mmL=4 mm段时间/s温度/℃碳势/%段时间/s温度/℃碳势/%段时间/s温度/℃碳势/%13009150.63 6008500.67 2008600.621 8009150.63009201.1561 2009251.236009151.121 0009201.1525 2009251.149 6009151.13009000.9536 0009250.853008900.910 8009000.957 2008300.864 2008900.93008400.8———73008300.82 4008400.8———83 0008300.8——————
3 实验与仿真结果及其分析
3.1 实验结果
为了测量碳含量沿深度的分布,用NJFY-CS100 A碳硫分析仪测量渗碳试样距表面不同深度的含碳量。每个参数测量3次取平均值,3种渗碳工艺的测量结果如图3所示。碳硫分析仪是以化学燃烧法为原理,要求试样的质量在0.1 g至0.4 g之间,取3次测量结果的平均值作为不同深度的碳含量。由于渗碳油淬处理后的试样硬度较高,为了降低硬度,改善切削加工性,故对试样进行完全退火处理。采用机械剥层方法制备不同深度处的材料。用车床使用0.1 mm的进给量切削并收集铁屑,由于去除的铁屑质量较小,为了便于收集,可把磁铁放置在车刀附近,进而把切削下来的铁屑吸附在磁铁上。
如图3中的实验结果所示,18CrNiMo7-6圆棒试样在经过3种渗碳工艺后,均在圆棒表层一段距离内形成渗碳层,碳含量从表面的最高值逐渐降低,直至心部的基体碳含量;经过工艺1以及工艺2后,圆棒的最高碳含量达到0.8%,渗碳层深度分别为1 mm和2 mm;而经过工艺3处理后的圆棒,渗碳层深度达到4 mm,表层最高碳含量达到1.0%,明显高于工艺1与工艺2。
3.2 仿真与实验结果的对比与分析
对上述3种渗碳工艺分别采用上文1.3中的模型1和模型2进行仿真,将其结果与实验结果对比,如图3所示。可以看出,对于3种渗碳工艺而言,模型2的仿真结果与实验结果的吻合度明显比模型1高;特别对于渗碳工艺1以及工艺2,碳梯度的仿真结果与实测结果近乎完全吻合。距表面相同距离处,采用模型1模拟的含碳量均显著高于模型2的仿真结果。这说明合金元素会影响碳原子的扩散过程。碳原子在扩散过程中,一部分以原子状态进入固溶体中,另一部分则与碳化物元素Cr、M等形成置换式合金渗碳体,如(Fe,Cr,)2C6、(Fe,Cr,Mo)3C和(Fe,Cr)7C3等,进而阻碍碳原子的扩散[18]。另外,对于非碳化物形成元素Co、Ni等,一般以原子状态存在于奥氏体从而造成晶格畸变,反而会提高碳原子在奥氏体中的扩散速度[19]。因此,对于扩散系数的数学模型的选择,钢中的合金元素必须作为影响因素考虑进去[20]。
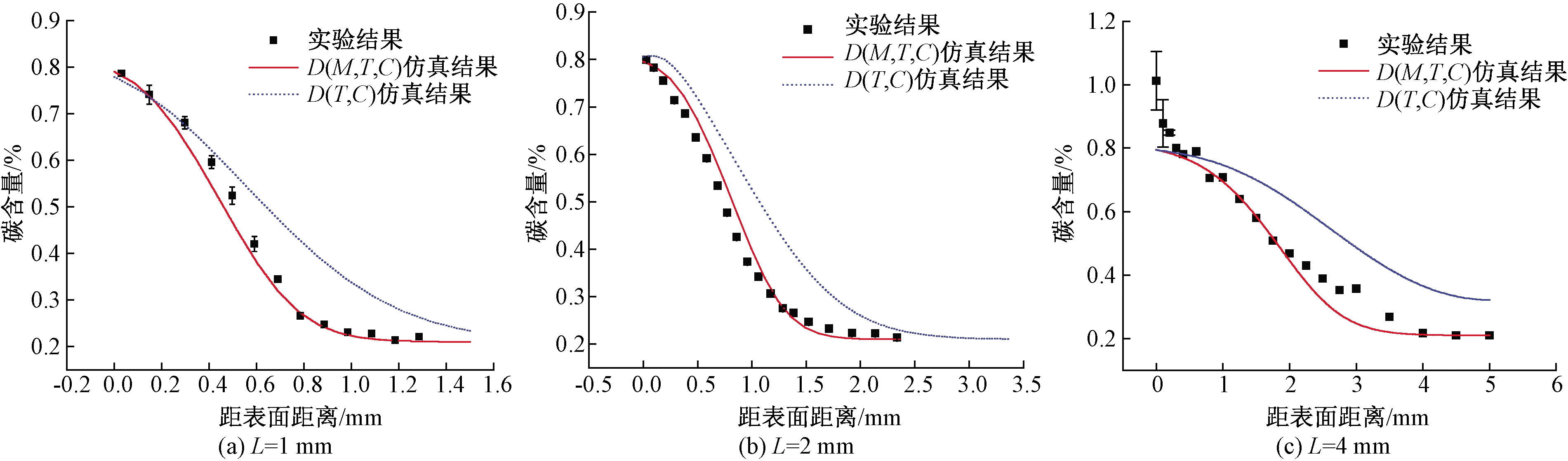
图3 3种渗层深度的碳含量实验和模拟结果对比
Figure 3 Comparison between experimental and simulated results of carbon content of three kinds of carburized layers
如图3(c)所示,采用模型2时,深度大于0.7 mm部分的碳含量仿真结果与实验测量值较吻合,而渗层深度小于0.7 mm部分相差较远。采用模型2的仿真结果显示,碳含量最高点位于样品表层处且碳浓度为0.8%,远小于实验值1.0%。这是由于DEFORM-HT软件无法识别并形成碳化物,而4 mm渗碳工艺的最后一段环境碳势为0.8%,直接导致模拟过程中碳原子从表层一直向内扩散而不形成碳化物。但通过样品的SEM研究发现,表层高碳含量处生成了大量碳化物,如(Fe,Cr)7C3、(Fe,Cr)3C甚至Fe 3C等,如图4所示。因为4 mm渗层的渗碳工艺的前两段环境碳势分别达到了1.2%、1.1%,时长分别为17 h、7 h,这远远高于工艺1及工艺2中的渗碳时间,长时间的高碳势渗碳使材料表面的碳含量超过了18CrNiMo7-6钢在该温度下的饱和碳浓度。并且由于碳化物元素Cr、Mo等合金元素的存在,在渗碳过程中阻碍了碳原子的扩散,使试样表层形成大量的碳化物,造成了样品表层碳浓度的实验结果显著高于仿真结果。而对于工艺1与工艺2,由于渗碳时间不够长,大大减少了样品表层形成的碳化物,使实验结果与仿真结果较吻合。
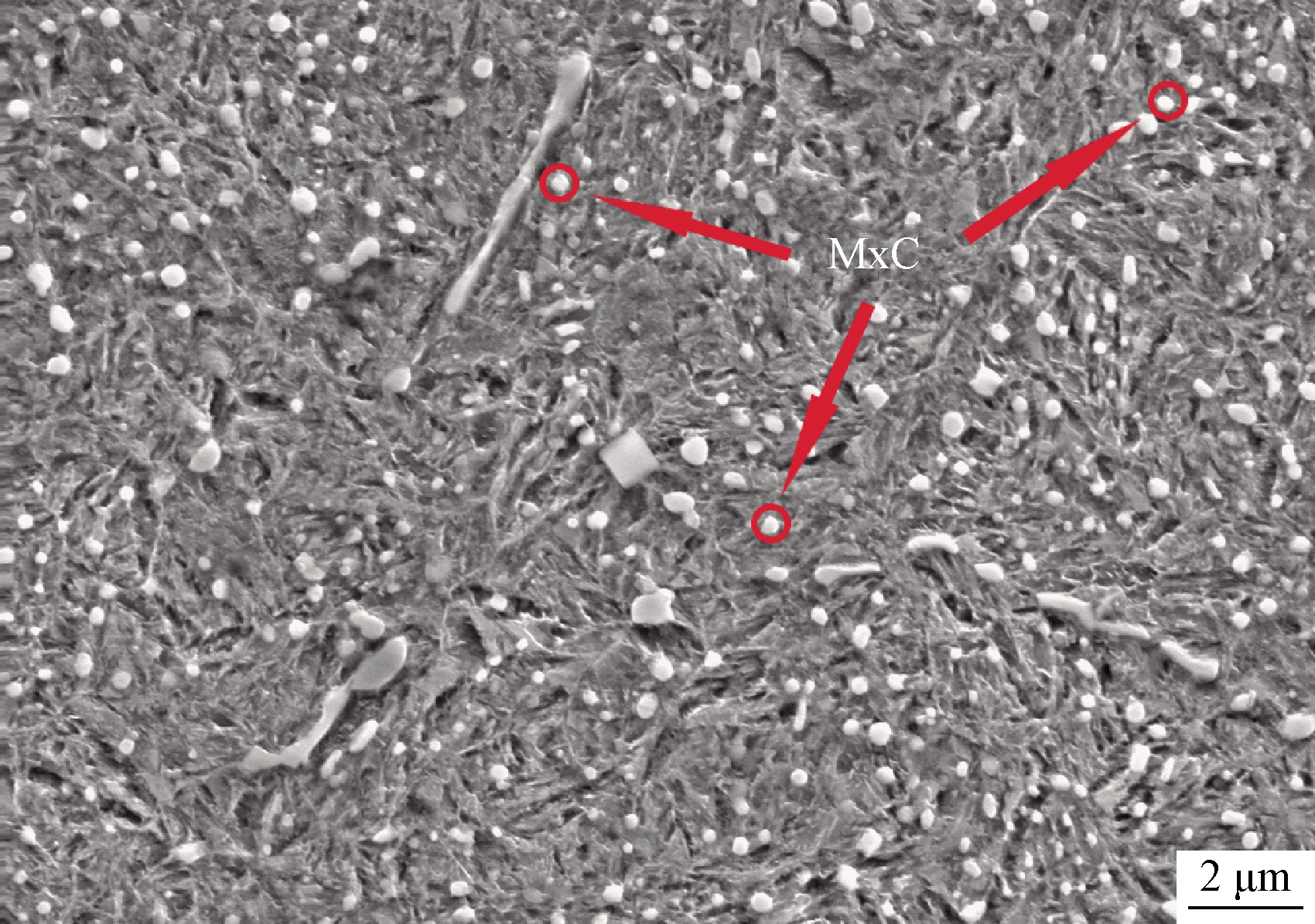
图4 4 mm渗层的表层碳化物分布
Figure 4 The surface carbide distribution of 4 mm carburized layer
可以发现采用模型1得到的碳浓度梯度均高于实测值,如图3所示。这说明在不考虑合金元素对碳扩散影响的情况下,碳原子扩散得更快,从而使位于渗层相同深度处的碳浓度显著升高。但实际上,合金元素会对渗碳过程中碳原子的扩散产生影响,这种影响既包含了Cr、Mo等元素对碳原子扩散的阻碍作用,又有Mn、Ni等对碳原子扩散的促进作用,而合金元素的阻碍作用是高于促进作用的,这正好符合上文1.3中D(T,M,C)扩散系数模型中合金参数的正负取值,如表2所示。可见,相较于模型1,模型2更加适合18CrNiMo7-6合金钢的渗碳过程仿真。当渗碳工艺达到一定条件时,如高碳势且长时间渗碳(如工艺3)时,合金元素对碳原子的阻碍作用将更加明显,即大量的碳化物在渗碳层表面形成。由于碳化物的含碳量远高于0.8%,使得渗层表面的碳含量明显上升,如图3(c)所示。可见,对于综合考虑了合金元素、碳含量、温度等影响因素的扩散系数模型D(T,M,C),其并非适用于合金钢的所有渗碳工艺仿真,在实际工程使用时仍要注意。
4 结论
(1)与碳钢不同,对合金钢渗碳工艺的仿真必须考虑合金元素对碳原子扩散的影响。相比于模型D(T,C),采用考虑合金元素的扩散系数模型D(T,M,C),使渗碳仿真结果与实验结果吻合度较高。但模型D(T,M,C)并非适用于合金钢的所有渗碳工艺仿真,其使用仍有一定的局限性。
(2)对于在高碳势下的长时间渗碳工艺而言,碳化物元素与碳原子形成稳定存在的碳化物,一方面阻碍碳原子的扩散,另一方面造成样品表层碳含量的升高。
[1] 赵振业.中国热处理与表层改性技术路线图[J].金属热处理, 2014,39(4):156-160.
[2] 赵振业.发展热处理和表面改性技术,提升国家核心竞争力[J].金属热处理,2013,38(1):1-3.
[3] 王栋,张晓晴.基于虚拟现实技术的十字轴锻造过程仿真[J].郑州大学学报(工学版),2016,37(3):74-77.
[4] 李斌,方宏远,王复明.脱空排水管道高聚物修复前后力学特性分析[J].郑州大学学报(工学版),2019,40(1):62-66.
[5] 王栋,刘昱范,陈鑫.18CrNiMo7-6高速磨削条件下表面质量的试验研究[J].郑州大学学报(工学版),2017,38(3):78-81.
[6] 刘博勋,张幸,顾剑锋.基于钢箔渗碳的碳传递系数的精确测定[J].金属热处理, 2016,41(1):211-216.
[7] 陈卫,刘勇,王顺兴.碳的扩散系数和传递系数的一种计算方法[J].河南科技大学学报(自然科学版), 2003,24(3):11-13.
[8] GUY A G, HREIV J J. 物理冶金学原理[M]. 徐纪楠,译. 北京: 机械工业出版社, 1981.
[9] BORGIANNI.渗碳过程动力学及数学模型的研究[C]//中国机械工程学会热处理学会.第二届国际材料热处理大会论文集.北京:中国机械工程学会热处理学会编,1983:316-323.
[10] 王顺兴, 刘勇. 实用热处理模拟技术[M]. 北京: 机械工业出版社, 2002.
[11] 张星,唐进元.17CrNiMo6钢内齿圈渗碳仿真关键技术研究[J]. 金属热处理, 2015,40(3):185-189.
[12] BABU S S, BHADESHIA H K. Diffusion of carbon in substitutionally alloyed austenite[J]. Journal of materials science letters, 1995, 14(5): 314-316.
[13] ROWAN O K, SISSON R D. Effect of alloy composition on carburizing performance of steel[J]. Journal of phase equilibria and diffusion, 2009, 30(3): 235-241.
[14] LEE S J, MATLOCK D K, VANTYNE C J. An empirical model for carbon diffusion in austenite incorporating alloying element effects[J]. ISIJ International, 2011, 51(11): 1903-1911.
[15] LEE S, MATLOCK D K. Carbon diffusivity multi-component austenite[J]. Scripta materialia, 2011, 64(9):805-808.
[16] 王顺兴,刘勇,魏世忠.气体渗碳数学模型及物理参数的计算[J].金属热处理, 2002(1):36-39.
[17] ZHANG X, TANG J. An optimized hardness model for carburizing-quenching of low carbon alloy steel[J]. Journal of central south university, 2017, 24(1):9-16.
[18] 胡赓祥, 蔡珣. 材料科学基础[M]. 上海: 上海交通大学出版社, 2000.
[19] 叶健松, 邱春城, 戚正风. 高合金钢固体渗碳及渗层扩散的计算机模拟[J]. 金属热处理, 2001, 26(7): 22-24.
[20] KIM D W, CHO Y G, CHO H H, et al. A numerical model for vacuum carburization of an automotive gear ring[J]. Metals and materials international, 2011, 17(6): 885-890.