0 引言
21世纪以来,随着机器人在搜索救援、医疗援助、侦察和行星探测等领域的广泛应用[1],路径规划逐渐进入研究人员的视野,并成为当今机器人领域的一项重要研究课题。通常,路径规划分为环境建模、路径搜索、路径优化这3个重要环节。针对第一层环境建模,常用的方法有C空间法[2]、栅格法[3]、自由空间法[4]、voronoi图法[5]及三角形法[6];针对第二、三层的路径搜索和优化,过去常用的方法有人工势场法[7]、模拟退火算法[8-9]、蚁群算法[10-11]等,现在常用的方法有神经网络算法[12]、遗传算法[13]和粒子群优化算法[14-15]。其中,遗传算法是由美国的Holland[16]于1975年首先提出一类借鉴生物界的进化规律演化而来的随机搜索方法。遗传算法具有良好的全局搜索能力,但遗传算法对初始种群有较强的依赖性且搜索效率低。粒子群优化算法是近年来由Eberhart等[14]开发的一种模拟鸟群觅食新的优化算法,它通过追随当前搜索到的最优值来寻找全局最优。同遗传算法比较,粒子群优化算法也属于迭代算法,其优势在于操作简单且搜索效率更高但易陷入局部最优。
然而,上述单独任何一种路径规划算法在耗时较少并且复杂的环境下不能得到最优或次优路径。于是,研究人员考虑在机器人工作过程中利用层次结构结合各算法优点进行路径规划。Zuo等[17]提出了一种用于复杂环境下移动机器人导航的层次路径规划方法。他们在第一层中利用基于网格的A算法快速查找初始几何路径,然后在第二层利用最小二乘策略迭代生成平滑的路径。Yang等[18]提出了一种针对动态环境的基于模糊逻辑的分层目标运动规划策略。首先,他们在第一层中利用全局目标信息和远程感知信息生成中间路径节点(即子目标),然后在第二层中利用近程感知信息引导移动机器人避开障碍物的同时到达子目标。Mac等[19]提出了一种基于混沌环境的移动机器人层次全局路径规划方法。他们在第一层中采用三角型法进行环境建模,在第二层应用Dijkstra算法寻找初始几何路径,最后提出了一种新的粒子群优化方法——约束多目标粒子群优化方法来优化路径。
考虑单独的路径规划算法存在着缺陷,笔者提出了基于混合遗传粒子群优化算法的层次路径规划方法。该方法的主要创新点:一是采用以时间为序的层次结构在路径规划过程中结合了三角形法、改进遗传算法和粒子群优化算法,实现复杂环境下的移动机器人路径规划;二是利用人工势场法的方向性改进了遗传算法,提高了遗传算法的搜索效率。
1 相关工作
1.1 路径规划
快速有效的路径规划是移动机器人正常完成其作业的重要保证。根据移动机器人对环境信息的掌握程度可以将路径规划分为基于先验信息的全局路径规划和基于传感器信息的局部路径规划。层次路径规划,是指把路径规划分为环境建模、路径搜索和路径优化3个基本环节,然后按时间顺序操作每个环节逐步实现路径规划。在操作每个环节的过程中,可以使用同一算法或不同算法。
1.2 遗传算法
遗传算法是一种基于“适者生存、优胜劣汰”原则的随机搜索的优化算法。遗传算法模拟了达尔文自然选择、物竞天择、适者生存的进化论,通过多代的选择、交叉、变异等操作进化出问题的最优解。基本遗传算法包含3种遗传算子:选择算子,交叉算子,变异算子。
1.2.1 选择算子
从种群中选择优秀个体,淘汰劣质个体的操作叫选择。选择的目的是把已优化的个体通过交叉产生新的个体遗传到下一代或直接复制到下一代。选择操作是建立在种群中个体的适应度评估基础上的。目前常用的选择方法有以下几种:适应度比例方法、随机遍历抽样法、局部选择法,其中适应度比例法是最简单也是最常用的方法。个体li被选择的概率:
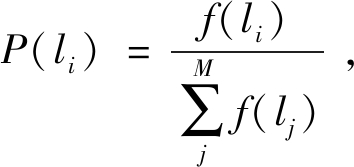
(1)
式中:M为种群规模;i、j为个体序号;f为个体的适应度。
1.2.2 交叉算子
交叉操作是指在上一代的染色体中寻找两条染色体作为父代个体l1、l2,然后将这两条染色体的某一个位置切断,然后拼接在一起,从而生成两条新的染色体,即子代个体![]() 交叉的方法有很多,比如单点交叉、多点交叉等,其中单点交叉是比较常用的交叉方法。单点交叉是指将两父代个体的共有节点(不包括起始点和目标点)作为切断位置,然后进行拼接。单点交叉具体示例如下:
交叉的方法有很多,比如单点交叉、多点交叉等,其中单点交叉是比较常用的交叉方法。单点交叉是指将两父代个体的共有节点(不包括起始点和目标点)作为切断位置,然后进行拼接。单点交叉具体示例如下:
父代个体l1[24,64,10,13,4,15,26];
父代个体l2[24,39,23,3,13,10,6,26]。
可以看出,两父代个体的共有节点为10、13,随机选择其中一个节点作为切断位置。假如选择的是13,交叉后的子代个体如下:
子代个体![]()
子代个体![]()
1.2.3 变异算子
变异操作是指对种群中的个体的某些基因座上的基因值作变动。一般来说,变异算子操作的基本步骤如下:
Step 1 对种群中所有个体以事先设定的变异概率判断其是否进行变异。
Step 2 对要进行变异的个体随机选择变异位置进行变异。
1.3 粒子群优化算法
粒子群优化算法是一种模拟鸟群觅食的优化算法,它通过追随当前搜索到的最优值来寻找全局最优。在粒子群优化算法中,每个优化问题的解都是搜索空间中的一只鸟,称之为“粒子”,以符号p表示。所有的粒子都有一个由被优化的函数决定的适应值,还有一个速度决定它们飞翔的方向和距离。在每一次迭代中,粒子通过跟踪两个“极值”来更新自己的速度及位置。第一个极值是粒子本身所找到的最优解,这个解叫作个体极值。另一个极值是整个粒子群当前找到的最优解,这个解叫作全局极值。
粒子速度、位置更新公式如下:
v(k+1)=c1·rand·(pBest(k)-p(k))+
c2·rand·(gBest(k)-p(k))+
w·v(k);
(2)
p(k+1)=p(k)+v(k+1),
(3)
式中:w为惯性权重;v(k)为k时刻粒子的速度;p(k)为k时刻粒子的位置;pBest(k)为k时刻粒子本身所找到的最好位置;gBest(k)为k时刻整个粒子群目前找到的最优位置;rand为介于0~1之间的随机因子;c1、c2是学习因子。
2 以时为序的多算法融合层次路径规划方法的设计
2.1 环境建模
环境建模是路径规划的基础环节,其目的是建立一个便于计算机进行路径规划所使用的环境模型,即将实际的物理空间抽象成算法能够处理的抽象空间,实现相互间的映射。尽管栅格法在路径规划环境建模中有广泛的应用,但考虑其把现实物理空间过于理想化,笔者使用更加接近真实环境的三角形法对移动机器人的自由活动空间进行建模。三角形法是基于可视图法创建的一种新的二维地图构建方法,其作用是把除障碍物外的自由空间划分为若干个邻域相通三角形。具体实现步骤如下:
Step 1 将多边形障碍物的顶点及运动空间的4个顶点进行相互连接。
Step 2 将顶点与顶点之间的线段两两进行比较。判断两线段是否相交,若相交,去除比较长的线段。
Step 3 判断线段的两顶点是否属于同一多边形障碍物,若是,删除对应的线段。
Step 4 计算剩下所有线段的中点,并按其对应线段的长短由短到长进行标号排序。
至此,移动机器人的自由活动空间已被划分为由若干个相互连通的三角形组成的环境模型,如图1所示。
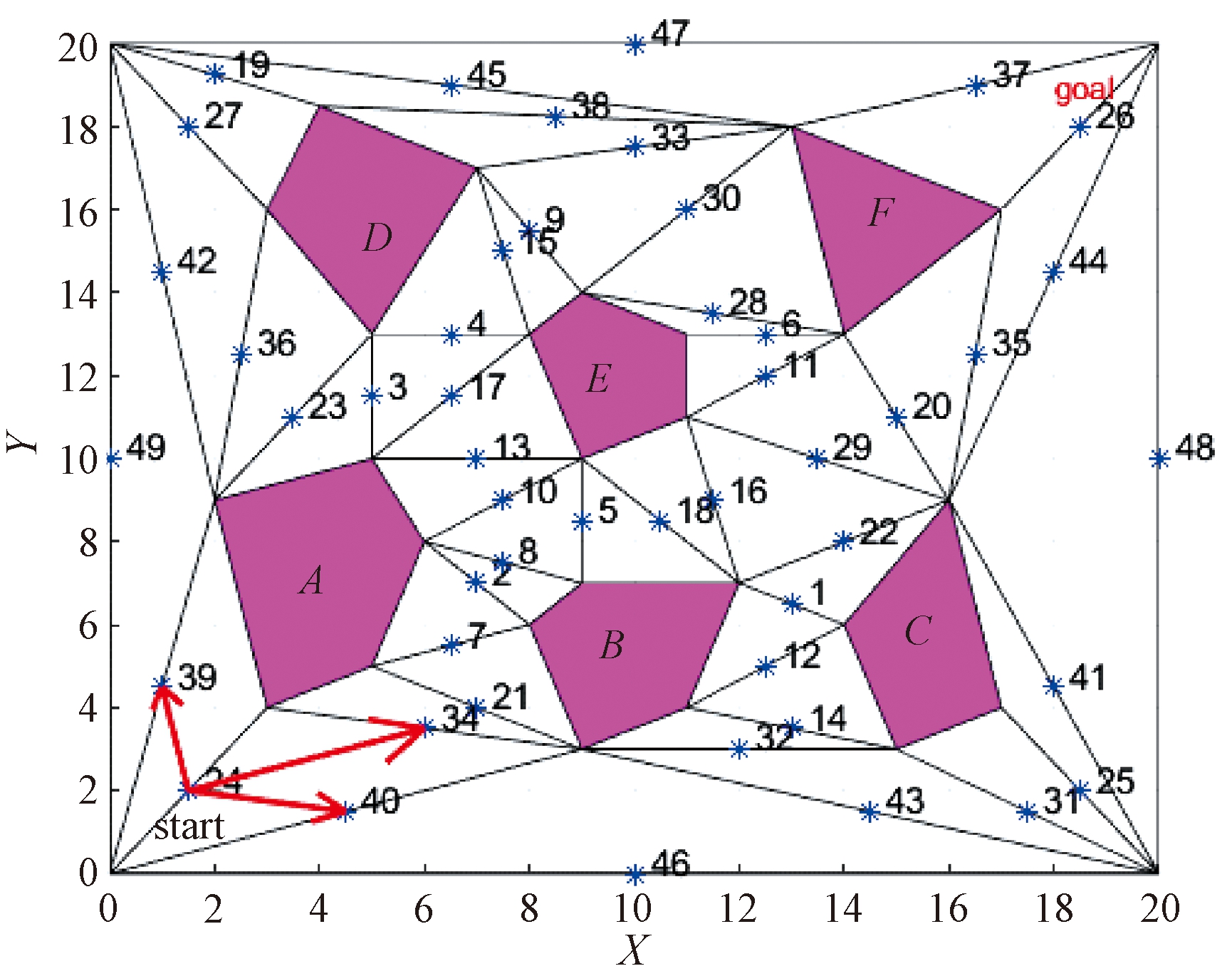
图1 环境模型
Figure 1 Environment model
2.2 改进遗传算法的设计及初次路径规划
2.2.1 路径编码
路径编码是实现遗传算法的重要环节,笔者以移动机器人从起点到终点所经过的所有中点序号的集合表示一个个体,每个个体代表一条路径,所有个体的集合代表一个种群。例如,图1中,[24 40 43 31 25 41 44 26]可以表示由start(24)到goal(26)的某条路径编码。
2.2.2 种群初始化
种群初始化是遗传算法必要的步骤,初始种群的质量严重影响遗传算法路径搜索的结果。一般来说,遗传算法中的初始种群是随机产生的。尽管这种随机产生种群的方式很简单,但是由于产生的个体质量通常不高,会导致遗传算法收敛速度慢,最终影响路径规划的效率。因此,提高初始种群的质量,对提高遗传算法的性能有重大的意义。
人工势场法基本思想是将机器人在周围环境中的运动设计成一种抽象的人造引力场中的运动,目标点对移动机器人产生“引力”,障碍物对移动机器人产生“斥力”,最后通过求合力来控制移动机器人的运动。笔者采用人工势场法的“引力”思想来改进传统遗传算法的种群初始化过程,移动机器人的引力势函数可以表示为:
(4)
式中:katt代表引力比例因子,设为1;i为移动机器人当前点的中点序号;g为目标点序号;x为序号对应的实际坐标位置;Uatt为引力势函数。
引力F通常取引力势函数的负梯度:
F(i,g)=-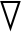 Uatt(i,g)=-katt|xi-xg|。
Uatt(i,g)=-katt|xi-xg|。
(5)
利用人工势场法初始化种群的具体步骤如下:
Step 1 初始化相关参数,包括移动机器人的起始点s、目标点g、种群规模M等。
Step 2 寻找移动机器人下一步的可选点集合V,即寻找与移动机器人相邻的点。这里相邻的点,是指以移动机器人当前点所在的边构成的两个连通三角形对应边上的点,如图1所示,start(24)相邻的点为34、39和40。
Step 3 计算移动机器人下一步可选点集合V中所有点可选的概率pij,其公式如下:
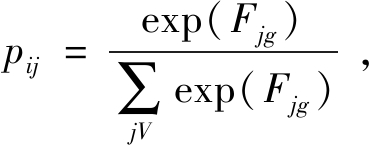
(6)
式中:i表示移动机器人当前点的序号;j表示下一步可选点的序号;g为目标点序号;Fjg表示目标点g对j点的引力。
Step 4 判断移动机器人是否经过目标点g,若是,则成功生成一个个体;若否,则回到Step 2。
Step 5 判断种群规模是否达到M,若是,停止种群初始化;若否,移动机器人回到起始点s,继续产生个体。
2.2.3 优化种群
(1)删除冗余。在初始化种群的过程中,为了确保遗传算法的全局性,常需要随机搜索产生个体。然而,随机搜索意味着产生的个体存在重复路径,这会影响遗传算法的效率,因此需要删除冗余。假设生成的初始路径个体l为[22,35,67,34,45,67,24,67,44],删除冗余的具体步骤如下:
Step 1 判断路径个体l是否存在相同元素,若是,继续下一步;若否,退出。
Step 2 查找相同元素所在数组中对应的位置,将位置相差最大的两相同元素之间的元素全部删除,包括两相同元素的其中一个。如路径个体l中,相同元素为67,所在数组中的位置分别为3、6和8,因此应将位置3和8之间的元素全部删除,包括位置8的元素。删除后的路径个体l为[22,35,67,44]。
Step 3 继续判断路径个体l是否存在相同元素,若是,返回step 2;若否,退出。图2是路径个体删除冗余的示意图。
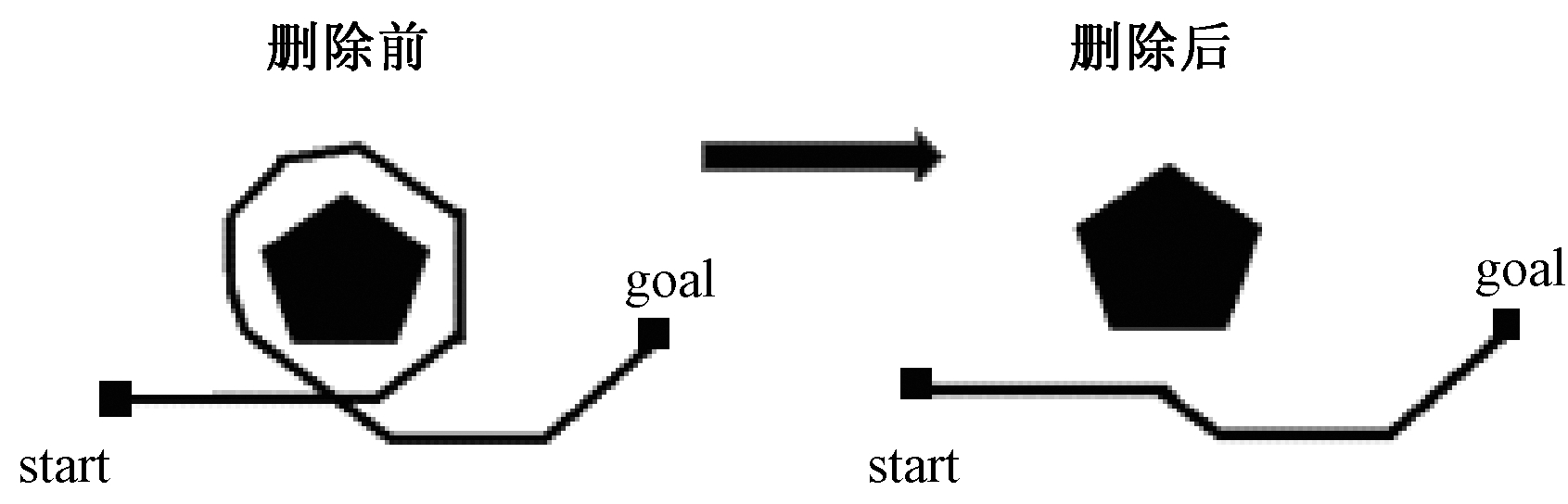
图2 删除冗余示意图
Figure 2 The schematic of removing the redundace
(2)判断三角形。在初始种群的过程中,生成的路径个体可能存在一些不必要的路径点,导致遗传算法的搜索效率降低。判断路径个体相邻的3个路径点对应的边是否可以组成1个三角形来删除这些不必要的点。图3是判断三角形前后的路径个体对比图。
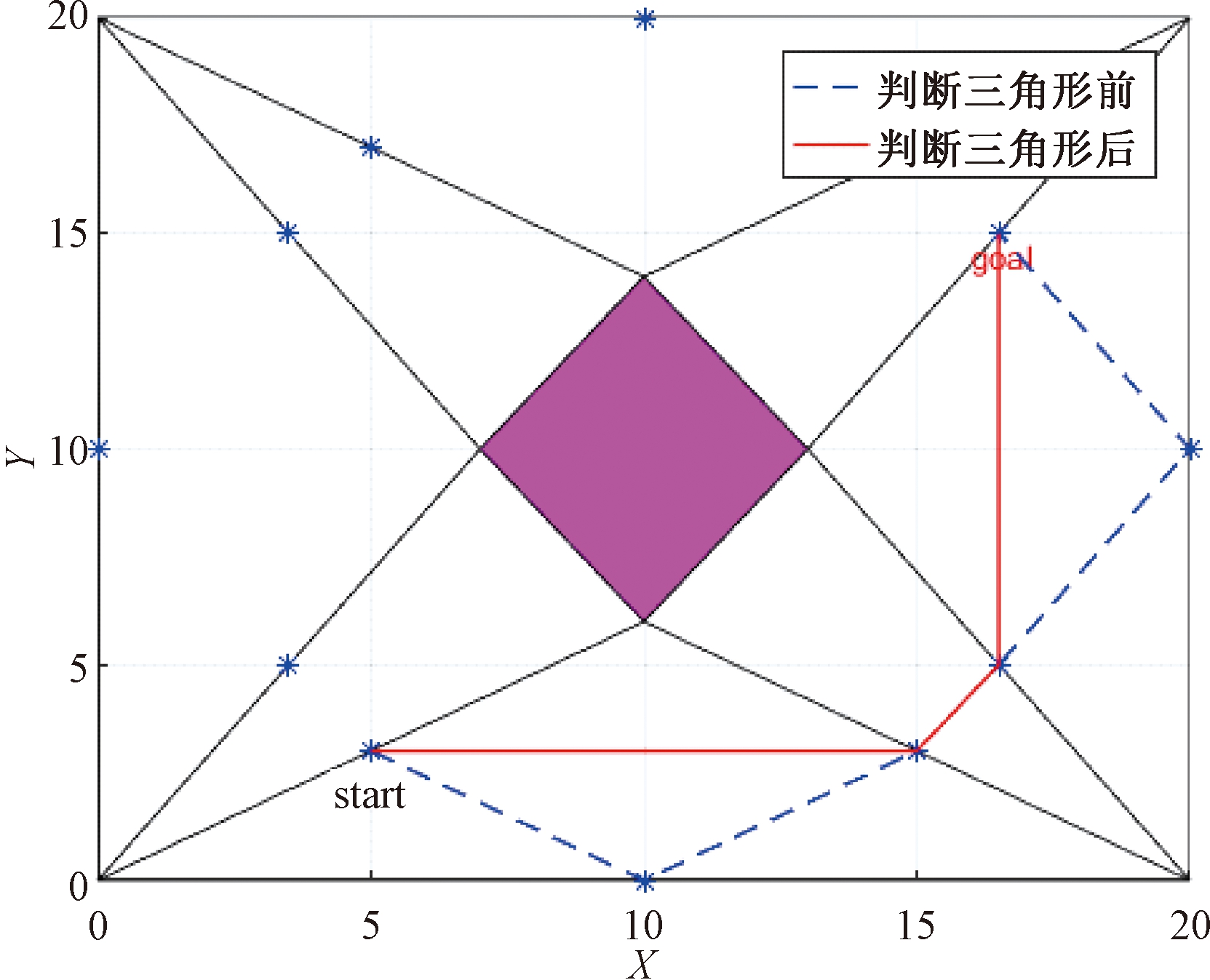
图3 判断三角形
Figure 3 Judging triangle
2.2.4 交叉、变异操作
为了保证路径的连续性,本文的交叉操作采用1.2.2所述的单点交叉方式,交叉操作的步骤如下:
Step 1 对种群中个体以事先设定的交叉概率判断其是否进行交叉。
Step 2 从种群中随机抽取另外一个个体,判断其与需要交叉的个体是否存在相同的路径点,若是,进行单点交叉;若否,继续下一步。
Step 3 是否遍历种群所有个体,若是,结束;若否,返回Step 1。
由于产生的初始种群均为连续路径,若采用随机变异操作将使间断路径导致种群退化。为解决这个问题,笔者首先随机选取需变异个体两个路径点,然后将两个路径点间所有路径点删除,然后用种群初始化办法修补间断路径,修补后的路径个体为已经变异的个体。
2.3 基于粒子群算法的路径优化
2.3.1 粒子群初始化
粒子群初始化是实现粒子群优化算法的基本步骤。在已获得初始全局最优路径的情况下,笔者将初始全局最优路径作为粒子群算法的初始粒子产生的母体,这里称之为粒子母体。初始的全部粒子均由粒子母体随机扩展产生,如图4所示。粒子群初始化的步骤具体如下:
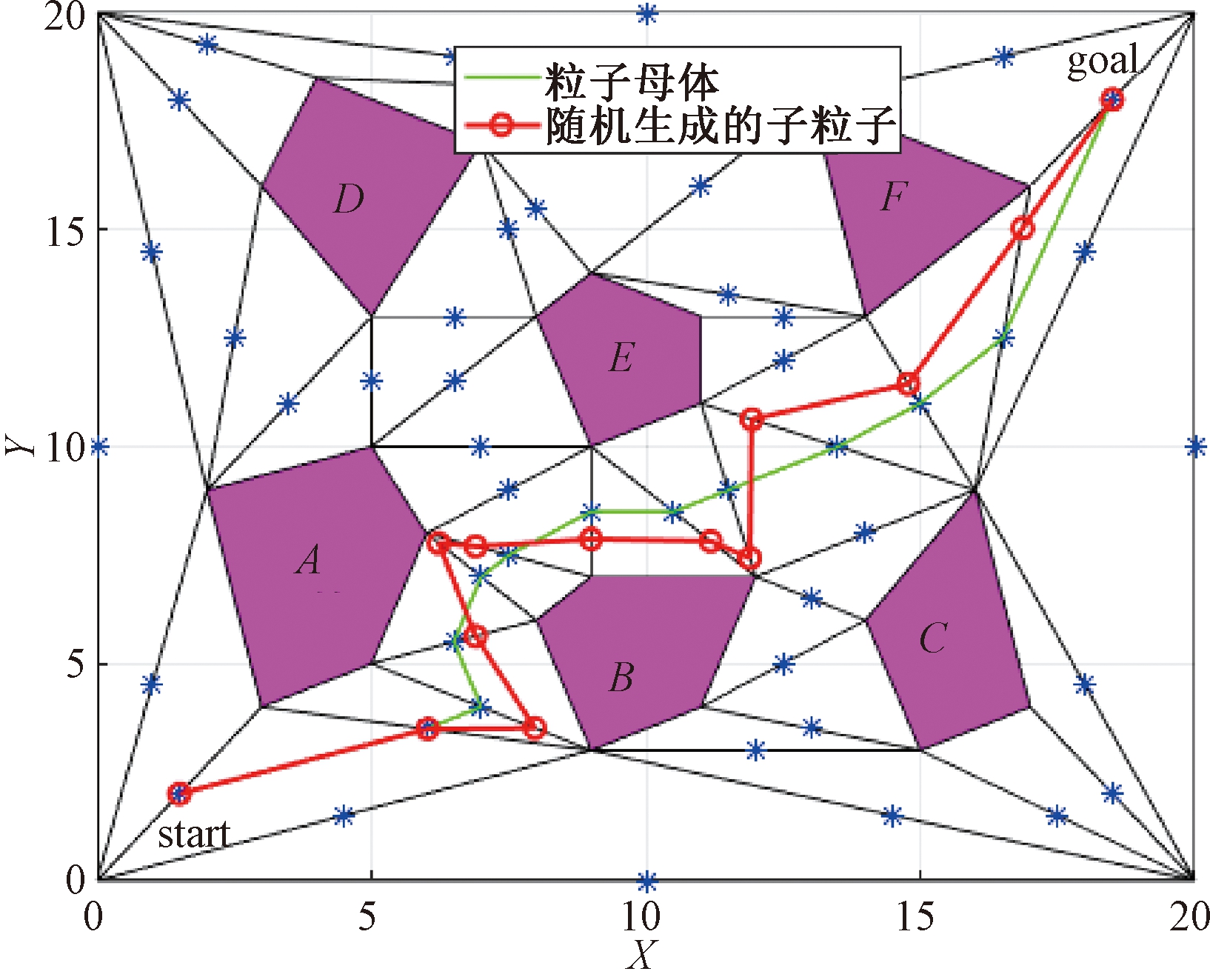
图4 粒子群初始化
Figure 4 The initialization of particle swarm
Step 1 初始化相关参数,包括粒子群规模M等。
Step 2 在粒子母体每个路径点对应的线段上随机生成一个子路径点,所有的子路径点的集合p表示为一个 随机生成的子粒子,这里的每个粒子和遗传算法中的个体含义一样,也代表一条路径。
Step 3 判断是否达到粒子群规模M,若是,结束;反之,回到Step 2。
2.3.2 适应度函数
在粒子群迭代寻找最优路径的过程中,需要一个目标函数来约束粒子群的运动,以达到优化路径的期望,笔者以路径最短作为迭代过程中粒子的约束条件。粒子的适应度计算公式如下:
(7)
f(p)=D(p),
(8)
式中:xi为第i个路径点的位置;xi+1为第i+1个路径点的位置;p为粒子;n为该粒子含有路径点的总数;D为粒子长度;f为粒子的适应度,在粒子群迭代的过程中,笔者期望其最小化。
2.4 全局层次路径规划的实现
图5是全局层次路径规划的实现流程。笔者将移动机器人的路径规划按时间顺序分为3个层次。第1层是采用三角形法进行环境建模;第2层是采用笔者所设计的改进遗传算法进行初次路径规划以寻找初始全局最优路径;第3层是在获取初始全局最优路径的情况下,运用粒子群优化算法对初始最优路径进一步优化以获得全局最优路径。

图5 全局层次路径规划的实现流程
Figure 5 The process of global hierarchical path planning
需要注意的是,在第2层遗传迭代搜索初始全局路径的过程中,种群中的个体的约束函数和第3层的粒子约束函数一样,即式(8)。
3 仿真实验结果与分析
为了验证基于混合遗传粒子群优化算法的层次路径规划方法的有效性和可行性,笔者对该方法进行了仿真,图6是层次路径规划的结果。该实验中,设置了3个目标点,其中绿色实线是程序执行完第2层获得初始全局最优路径,红色虚线是执行完第3层程序的优化结果。实验结果表明,笔者设计的全局层次路径规划方法是有效的。
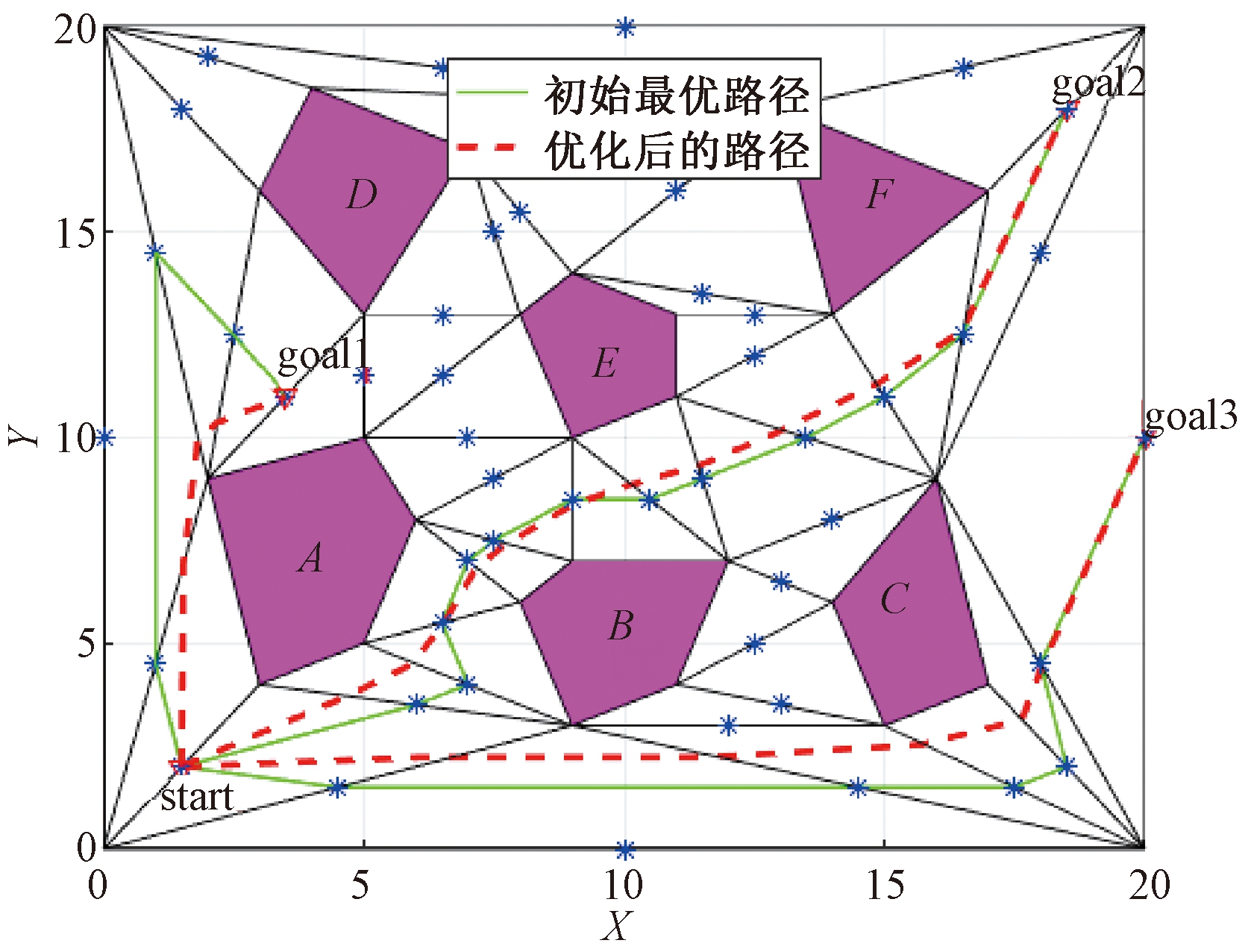
图6 全局层次路径规划
Figure 6 Global hierarchical path planning
图6实验的参数设置:针对第2层改进遗传算法,初始种群规模M=10,最大迭代次数n1=15,交叉概率pc=0.5,变异概率pm=0.5;针对第3层粒子群优化算法,初始粒子群规模M=100,最大迭代次数n2=50,学习因子c1=0.2,c2=0.1,惯性权重w=0.15。
为了更清楚观察全局层次路径规划方法各层次的工作效率,设定移动机器人从start运动到goal2,在路径长度几乎一致的情况下,做了3次独立实验,并分别统计每次实验各层所花费的时间。表1是移动机器人在各层所损失时间的仿真结果(表中第2层的时间分别为采用传统遗传算法和笔者设计的改进遗传算法所消耗的时间,括号内是改进后的时间)。
表1实验结果表明,主要影响全局层次路径规划方法的工作效率是第2层搜索初始全局最优路径的过程,而笔者提出的改进遗传算法在搜索初始全局最优路径的过程中所耗费的时间远比传统遗传算法少,能够提高全局层次路径规划方法的整体效率。
表1 层次路径规划各层的时间损失
Table 1 Time loss of layers in hierarchical path planning s

算法第1层第2层第3层10.6595.892(1.592)0.44620.7596.224(1.326)0.50730.7985.467(1.453)0.515
为了观察所设计的层次路径规划方法时移动机器人路径长度随时间的变化,设定移动机器人从start运动到goal2,图7是路径长度随时间的变化结果。图7中,横坐标表示层次路径规划方法的整体迭代次数,包括第2层的遗传迭代次数和第3层的粒子群迭代次数。绿色虚线左半部分,表示程序正在执行第2层搜索初始全局最优路径的操作,15为改进遗传算法设置的迭代次数。绿色虚线右半部分表示程序正在执行第3层优化路径操作,此时粒子群的迭代次数设置为50。图7结果表明,针对第2层改进遗传算法,其最佳迭代次数为12左右;针对第3层粒子群优化算法,其最佳迭代次数为25左右。
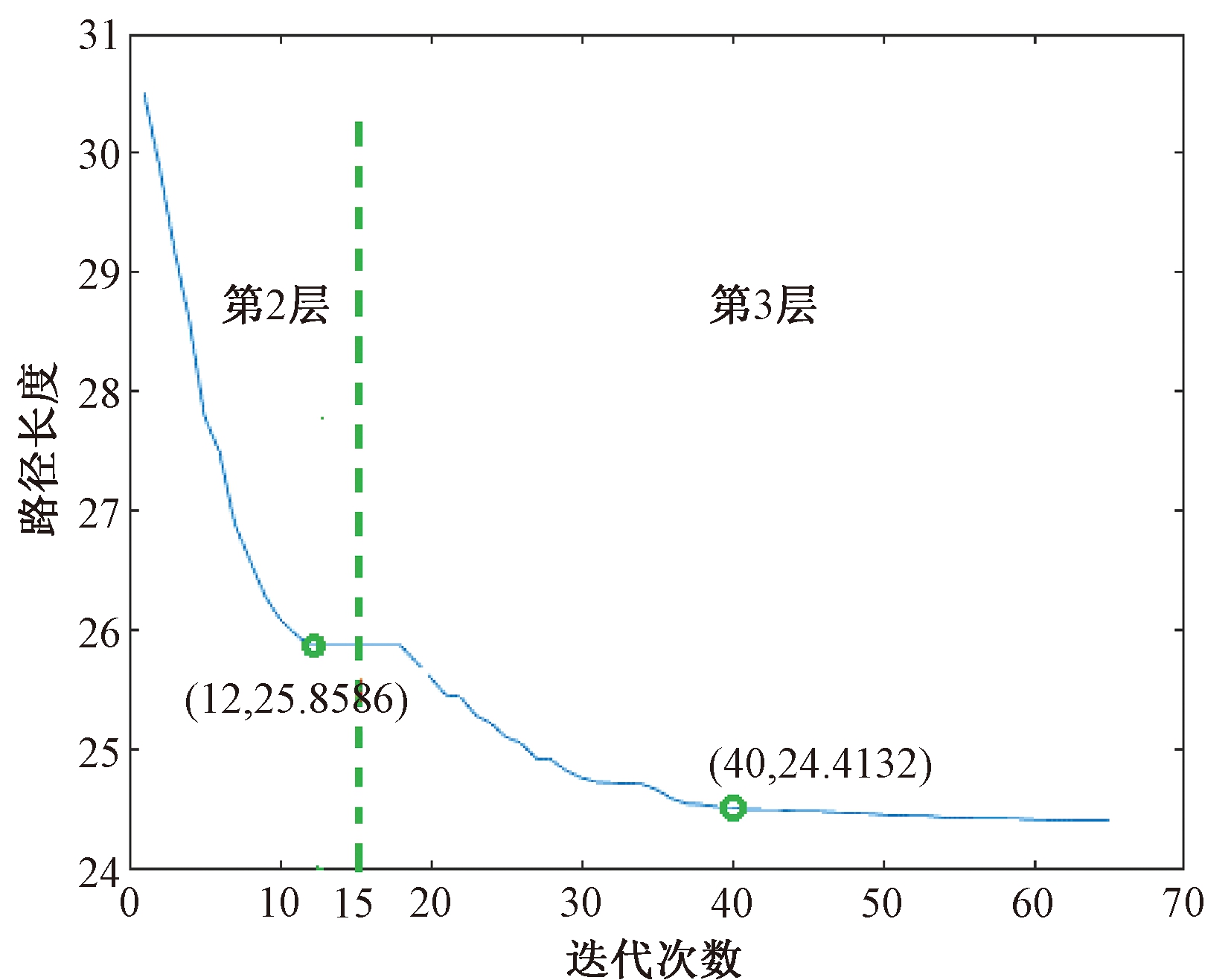
图7 路径长度变化
Figure 7 Change of path length
为了进一步比较所设计的层次路径规划方法和当今主流算法性能的差异,在设定移动机器人从start运动到goal2的情况下,图8和表2分别是采用笔者提出的层次路径规划算法和采用文献[20]中的改进差分进化算法进行路径规划实际效果图和数值比较表。
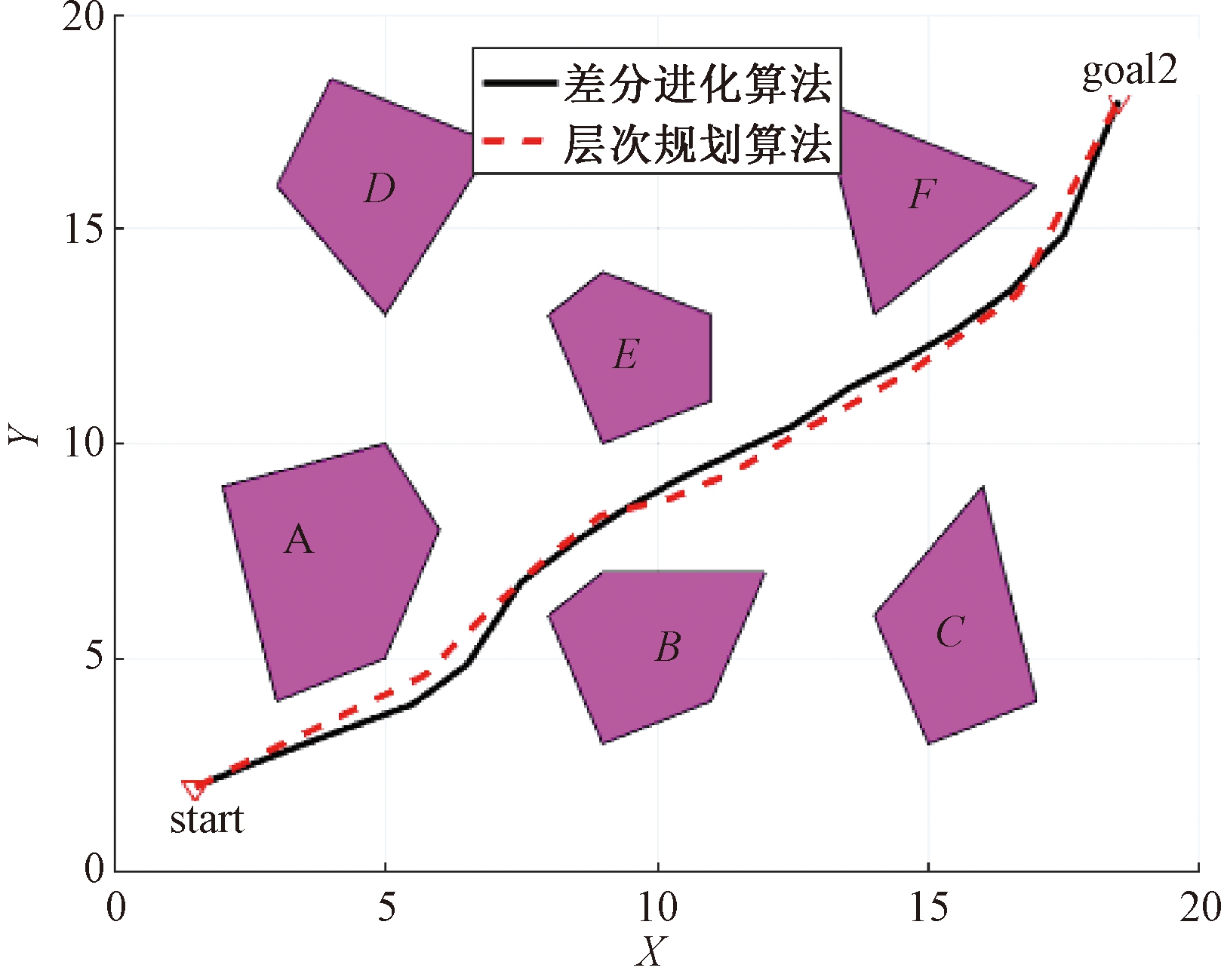
图8 层次规划法和差分进化法对比
Figure 8 Comparison between hierarchical planning and differential evolution
表2 数值比较
Table 2 Numerical comparison s
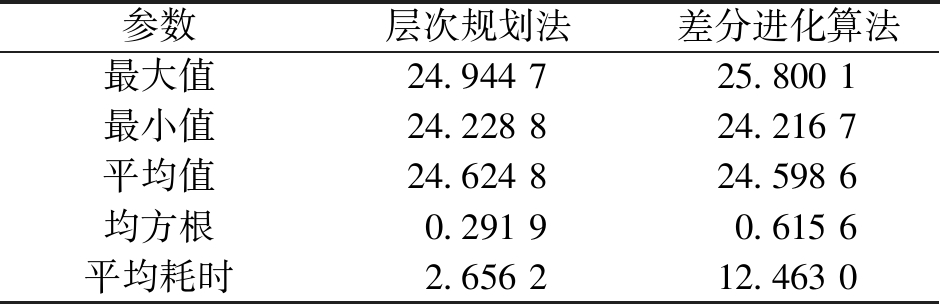
参数层次规划法差分进化算法最大值24.944725.8001最小值24.228824.2167平均值24.624824.5986均方根0.29190.6156平均耗时2.656212.4630
图8中,采用文献[19]中的改进差分进化方法进行路径规划时需要先用外接圆将多边形障碍物覆盖起来,外接圆内均为不可运动空间。针对表2,分别为6次实验中移动机器人从start运动到goal2的最短距离的最大值、最小值、平均值、均方根和平均耗时。其结果表明,在相同的环境和目标要求下,笔者提出层次路径规划算法和文献[20]中改进差分进化算法均能获得较好的结果,层次路径规划方法的稳定性和搜索效率优于改进差分进化算法。
4 结论
仿真结果表明,笔者提出的基于混合遗传粒子群优化算法的全局层次路径规划方法能够在复杂的环境中快速有效地寻找到无碰撞、最优的路径。同时,提高了遗传算法的搜索效率,使得层次路径规划方法整体上的搜索效率高于现阶段一些主要的算法。
[1] 海星朔,徐炳辉,任羿,等.基于改进鸽群优化的机器人自抗扰控制方法[J].郑州大学学报(工学版),2019,40(4):20-24,31.
[2] NEUS M,MAOUCHE S.Motion planning using the modified visibility graph[C]//Proceedings of 1999 IEEE International Conference on Systems,Man,and Cybernetics.Tokyo,IEEE:1999:651-655.
[3] PANOV A I,YAKOVLEV K S,SUVOROV R.Grid path planning with deep reinforcement learning:preliminary results[J].Procedia computer science,2018,123:347-353.
[4] GHITA N,KLOETZER M.Trajectory planning for a car-like robot by environment abstraction[J].Robotics and autonomous systems,2012,60(4):609-619.
[5] MO H W,XU L F.Research of biogeography particle swarm optimization for robot path planning[J].Neurocomputing,2015,148:91-99.
[6] 郗安民,王琦,孙学彬.一种有效的地图创建方法和机器人的路径规划[J].机械设计,2010,27(1):35-37.
[7] HOU P Q,PAN H,GUO C.Simulation research for mobile robot path planning based on improved artificial potential field method recommended by the AsiaSim[J].International journal of modeling,simulation,and scientific computing,2017,8(2):1-14.
[8] PAN Q Y,WANG X Y.Independent travel recommendation algorithm based on analytical hierarchy process and simulated annealing for professional tourist[J].Applied intelligence,2018,48(6):1565-1581.
[9] 陶重犇,雷祝兵,李春光,等.基于改进模拟退火算法的搬运机器人路径规划[J].计算机测量与控制,2018,26(7):182-185.
[10] JIAO Z Q,MA K,RONG Y L,et al.A path planning method using adaptive polymorphic ant colony algorithm for smart wheelchairs[J].Journal of computational science,2018,25:50-57.
[11] HUANG L P,ZHANG B,YUAN X,et al.A novel Bi-Ant colony optimization algorithm for solving multi-objective service selection problem[J].Journal of intelligent and fuzzy systems,2016,31(2):873-884.
[12] XU D P,SHAO H M,ZHANG H S.A new adaptive momentum algorithm for split-complex recurrent neural networks[J].Neurocomputing,2012,93:133-136.
[13] 王雷,李明.改进自适应遗传算法在移动机器人路径规划中的应用[J].南京理工大学学报,2017,41(5):627-633.
[14] EBERHART R C,KENNEDY J.Particle swarm intelligence[C]//Proceedings of the IEEE International Conference on Neural Networks.Perth:IEEE,1995:1942-1948.
[15] LI G S,CHOU W S.Path planning for mobile robot using self-adaptive learning particle swarm optimization[J].Science china information sciences,2018,61:1-18.
[16] HOLLAND J H.Adaptation in natural and artificial systems[M].Ann Arbor:University of Michigan Press,1975.
[17] ZUO L,GUO Q,XU X,et al.A hierarchical path planning approach based on A* and least-squares policy iteration for mobile robots[J].Neurocomputing,2015,170(25):257-266.
[18] YANG X,MOALLEM M,PATEL R V.A layered goal-oriented fuzzy motion planning strategy for mobile robot navigation[J].IEEE transactions on systems,man,and cybernetics,part B (cybernetics),2005,35(6):1214-1224.
[19] MAC T T,COPOT C,TRAN D T,et al.A hierarchical global path planning approach for mobile robots based on multi-objective particle swarm optimization[J].Applied soft computing,2017,59:68-76.
[20] 范柄尧,张春美.移动机器人路径规划的混合差分进化算法[J].太原科技大学学报,2019,40(1):6-12.