0 引言
随着经济社会快速发展,中国许多地区大量开采深层承压水造成承压水位不断下降、水质恶化、含水层疏干、地面沉降等一系列环境地质问题,严重危及国家和地区的饮水安全。针对突出的地下水超采问题,2012年《国务院关于实行最严格水资源管理制度的意见》中进一步强调了严格地下水管理和保护、实行地下水取用水总量控制和水位控制管理的必要性。近年来,许多学者就地下水管理控制水位划定方法展开研究。袁长极[1]提出了地下水临界深度及确定方法。方樟等[2]提出了地下水控制性管理水位及阈值的概念,并利用地下水流数值模拟方法确定了示范区不同季度不同水平年在不同降水保证率下的控制性管理水位及阈值,将地下水控制性管理水位定量化。于璐等[3]在对海水入侵区地下水管理控制水位概念界定的基础上,提出了地下水管理控制水位红线-黄线-蓝线分级模式。总体来看,中国在地下水资源管理方面进行的研究工作主要是关于浅层地下水管理方面的研究,对深层承压水管理的相关研究工作相对滞后。本文重点从承压水管理中存在的实际问题出发,以西平县新建深层承压水水源地为研究区,通过对承压水水源地不同开采情景下未来水位变化情况进行预测,得出一套服务于当前最严格水资源管理制度建设的城市水源地承压水合理开采水位的划定方法。
1 研究方法
1.1 承压水合理开采水位的界定
结合城市水源地开采地下水的特点,本文提出了承压水合理开采水位的概念。承压水合理开采水位是从水资源管理者的角度出发,根据城市水源地深层承压水的开采现状、未来经济发展用水需求、地下水系统的涵养保护需要以及深层承压水控制指标标准而划定的具有强制性效果的承压水水位阈值区间。
承压水合理开采水位的划定思路为:收集研究区地下水水位变化资料、水文地质资料以及钻孔资料等,建立水文地质概念模型和地下水数值模型,得到研究区范围内不同开采强度下承压水水位的变化情况;通过地面沉降经验公式法计算出研究区范围内不同开采强度下年均沉降速率的大小,绘制出年均沉降速率等值线图;结合已划定的水源地保护区边界,将地下水开采所引发的地面沉降控制在某一合理阈值区间以内(例如对保护区以外的地面建筑物不造成显著影响),此时所对应的承压水位区间即为承压水合理开采水位。
因此承压水合理开采水位是位于正常开采水位和禁止开采水位之间且由一组水位所构成的调控阈值区间。同时,为使承压水合理开采水位具有操作性,引入禁止开采水位、限制开采水位和正常开采水位的概念及划定方法。禁止开采水位是指地下水开发利用时不能突破的临界限值。承压水位在该水位或低于该水位状态下,应该减少水源地的开采规模,防止出现严重的环境地质问题。限制开采水位位于禁止开采水位和正常开采水位之间,用于警示管理者控制地下水开采规模。当承压水位低于该水位状态时,应控制承压水的开采规模。正常开采水位是承压水开发利用相对安全值。当承压水位处于正常开采水位和限制开采水位之间时,承压水开发利用可以正常进行。承压水合理开采水位概念示意图如图1所示,图中黑色曲线表示承压水水位随着开采强度增加不断下降,反映了水源地承压水水位和开采强度的关系。
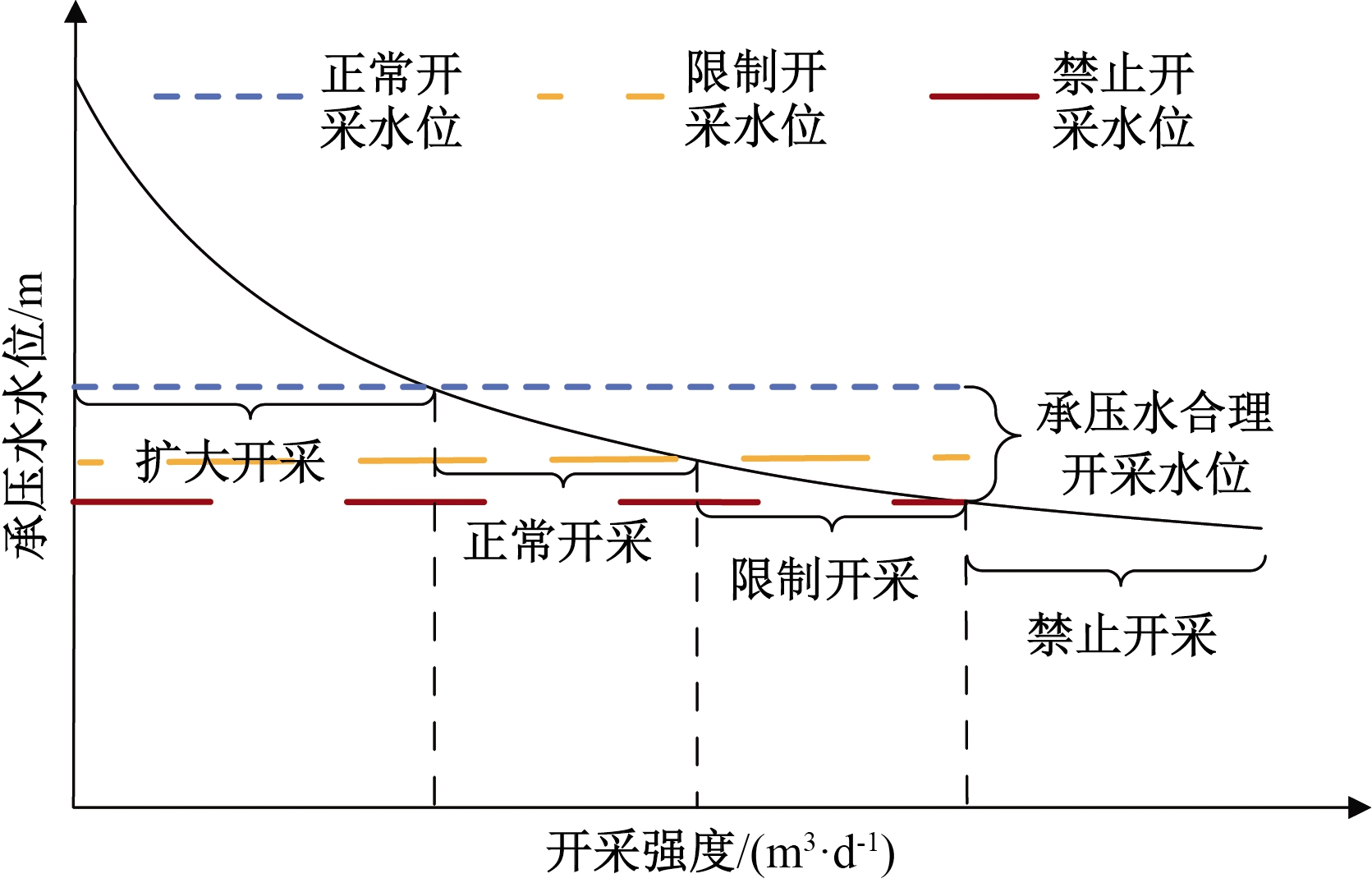
图1 承压水合理开采水位概念示意图
Figure 1 Schematic diagram of rational water level concept of confined water
1.2 承压水合理开采水位的控制指标
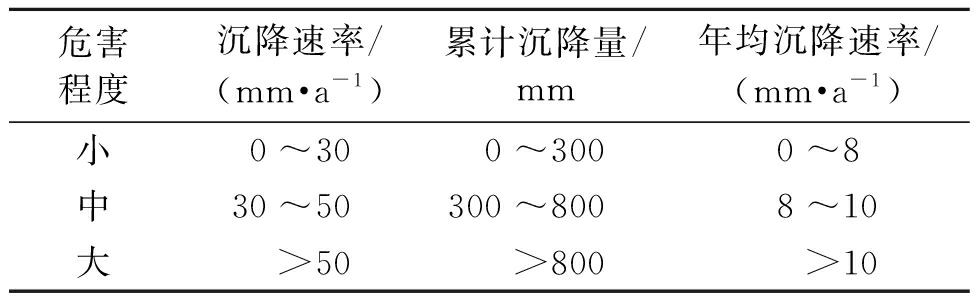
城市承压水水源地集中开采承压水,由于开采量巨大,极易形成承压水位降落漏斗,进而引起区域地面沉降。研究表明,地面沉降量大小与地下水位变化高度相关,但是地面沉降过程相对滞后于地下水位的变化[4]。因此,选取年均沉降速率作为量化城市水源地承压水合理开采水位的依据。目前,中国并没有统一的地面沉降危害性程度划分标准。如表1所示,天津市目前多用沉降速率来划分地面沉降危害性程度,浙江省采用累积沉降量作为分级标准,研究区采用年均沉降速率作为地面沉降危害性程度划分依据。
表1 地面沉降危害性分级表
Table 1 Hazardous classification of land subsidence
危害程度沉降速率/(mm·a-1)累计沉降量/mm年均沉降速率/(mm·a-1)小0~300~3000~8中30~50300~8008~10大>50>800>10
针对承压水水源地的特点,依据国家HJ 338—2018《饮用水水源地保护区划分技术规范》中地下水饮用水源保护区的划分要求,将地下水饮用水源地保护区划分为一级保护区和二级保护区。研究区水源地一级保护区半径为500 m,水源地二级保护区半径为2 000 m。
1.3 地下水数值模型
近年来,地下水流数值模拟得到了长足的发展,在各个领域得到了广泛应用[5]。地下水数学模型是以水文地质概念模型为基础建立起来的,研究区地下水流动系统的数值模型可以概化为非均质各向异性三维非稳定流系统[6],建立孔隙含水层的地下水数学模型见式(1):
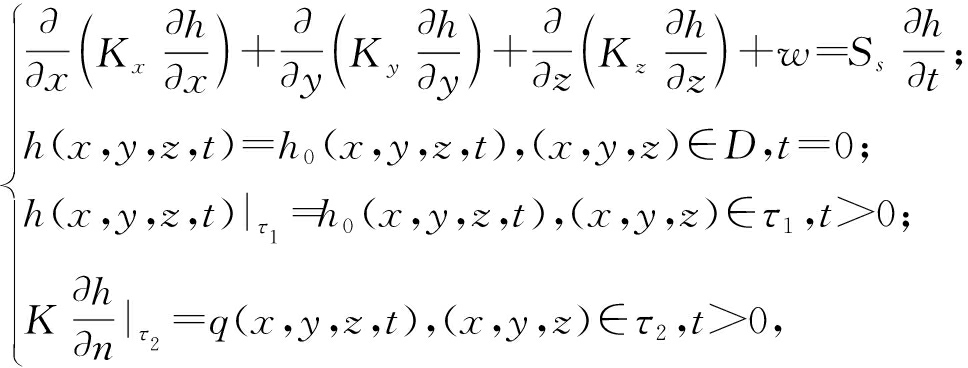
(1)
式中:D为渗流区域;Kx、Ky、Kz分别为含水层和弱透水层x、y、z方向上渗透系数,m·d-1;w为含水层的源汇项,d-1;Ss为储水系数,m-1;h为水位,m;h0(x, y, z, t)为某一已知函数,m;q(x, y, z, t)为二类边界上定流量边界,m3/d;τ1和τ2分别为第一类边界和第二类边界;n为边界内法线。
1.4 地面沉降计算方法
地下水开发利用引起的地面沉降问题一直备受关注,尤其是城市水源地集中大量开采深层承压水引起地下水位持续下降,进而形成区域地面沉降[7]。选取年均沉降速率作为量化新建城市承压水源地深层承压水合理开采水位依据。由于研究区缺乏相应的地面沉降监测数据,故采用经验公式法计算研究区的年均沉降速率。经验公式法是基于太沙基一维固结理论,根据含水层和弱透水层的沉降机理不同,分层计算地面沉降量[8]。侯伟等[9]运用经验公式法,对北京市东部区域抽取地下水引起的地面沉降进行计算。
经验公式法为典型的渗流和地面沉降两步计算模型[10]:第一步,计算研究区范围内地下水开采引起的水位降深;第二步,根据水位降深求出研究区范围内各点的地面沉降量,进而求出年均沉降速率,计算公式见式(2):
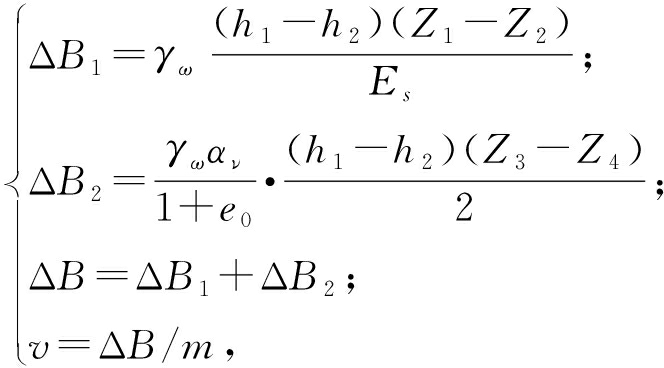
(2)
式中:ΔB1为含水层的沉降量,mm;ΔB2为弱透水层的沉降量,mm;ΔB为总沉降量,mm;m为沉降时间,a;v为年均沉降速率,mm/a;γω为水的重度,取9 800 N/m3;αν为弱透水层压缩系数,MPa-1;Es为含水层的压缩模量,MPa;e0为初始孔隙比;压缩系数、压缩模量以及初始孔隙比为土力学参数,通过土力学实验获得参数取值;h1和h2分别为地下水数值模型的初始水位和模拟结果水位,m;Z1、Z2、Z3和Z4分别为含水层的顶板标高和底板标高以及弱透水层的顶板标高和底板标高,m。
2 实例分析
2.1 研究区概况
研究区位于西平县中部地区洪河冲积平原区,北部和东南部局部为冲积缓倾斜平原。区内农业灌溉、部分乡镇居民生活用水以开采浅层地下水为主,浅层地下水水位埋深为1~6 m,井深一般在50 m以内;承压水水位埋深为5~30 m,开采层位为120~200 m,研究区范围内承压水开采量基本不变,承压水水位埋深相对稳定。原承压水水源地开采井14眼,设计开采能力为20 000 m3/d,新建承压水水源地开采井15眼,设计开采能力为30 000 m3/d。研究区井位分布及目标含水层初始水位见图2。
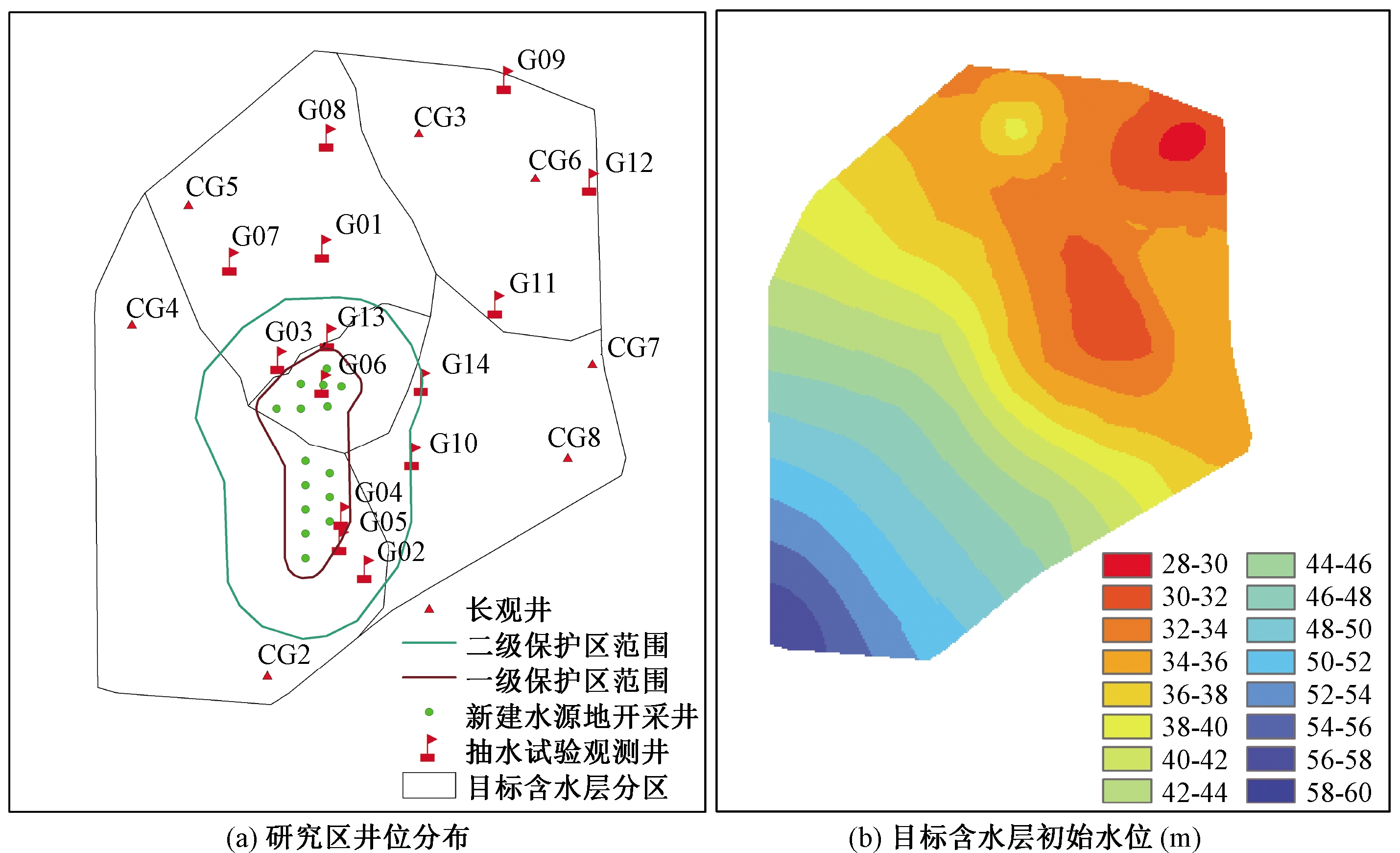
图2 研究区井位分布及目标含水层初始水位
Figure 2 Well location in the study area and initial water level of target aquifer
2.2 地下水数值模型的建立
本次地下水数值模拟采用了当前国际上运用较广的GMS软件,建立了研究区水文地质概念模型。
2.2.1 水文地质结构模型
根据所收集的研究区内22个钻孔资料、4幅水文地质剖面图以及其他相关资料,通过系统分析与研究,明确研究区的水文地质条件,概化为3个含水层组,分别为潜水含水层、第I承压含水层和第II承压含水层,其中第II承压含水层为目标层。研究区范围内地层比较简单,地层厚度变化不大,垂向上可以概化为6层。
2.2.2 水文地质参数初始值
根据地下水富水性特征,将目标含水层(即第II承压含水层)划分为5个区域,其他含水层和隔水层概化成1个区域,如图2(a)所示。水文地质参数主要包括贮水系数(Ss)和渗透系数(K),水文地质参数初始值见表2。水文地质参数初始值参考了前人开展的抽水试验和数值模型识别结果。
表2 目标含水层水文地质参数的初始值和识别值
Table 2 Initial value and identification value of hydrogeological parameters of target aquifer m·d-1
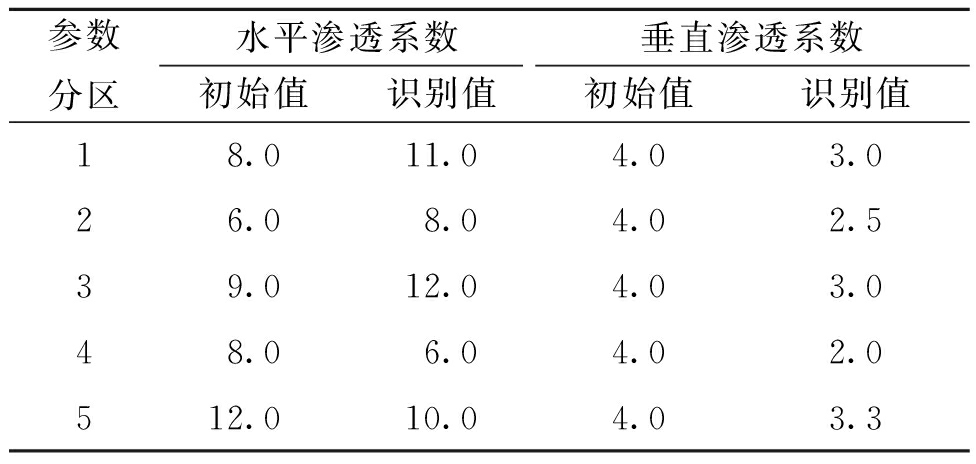
参数分区水平渗透系数垂直渗透系数初始值识别值初始值识别值18.011.04.03.026.08.04.02.539.012.04.03.048.06.04.02.0512.010.04.03.3
2.2.3 计算条件确定
研究区面积157.1 km2,使用MODFLOW模块对计算区域进行自动剖分,在平面上将研究区剖分为100行和100列,共10 000个网格单元,其中有效单元格7 766个。研究区目标含水层系统边界上多个观测井均具有长时间的观测资料,含水层连续且分布面积较大,故研究区边界定义为已知水头边界。模型目标含水层补给项仅考虑侧向径流补给和越流补给。排泄项主要包括人工开采和侧向径流。
2.2.4 模型的识别和验证
本次模拟采用2016年1月21日到2017年1月21日一个完整水文年的观测数据对模型参数进行识别,采用2017年6月9日22时至2017年6月21日22时群孔抽水试验获得的观测数据对模型参数进行验证。东观测井实测水位与计算水位拟合曲线见图3,目标含水层水文地质参数的识别值见表2。可以看出,该数值模型具有相当高的模拟能力和计算精度,能反映出示范区第四系承压水含水系统的实际特征,可以用于对不同开采情景下水源地地下水位变化的预测。
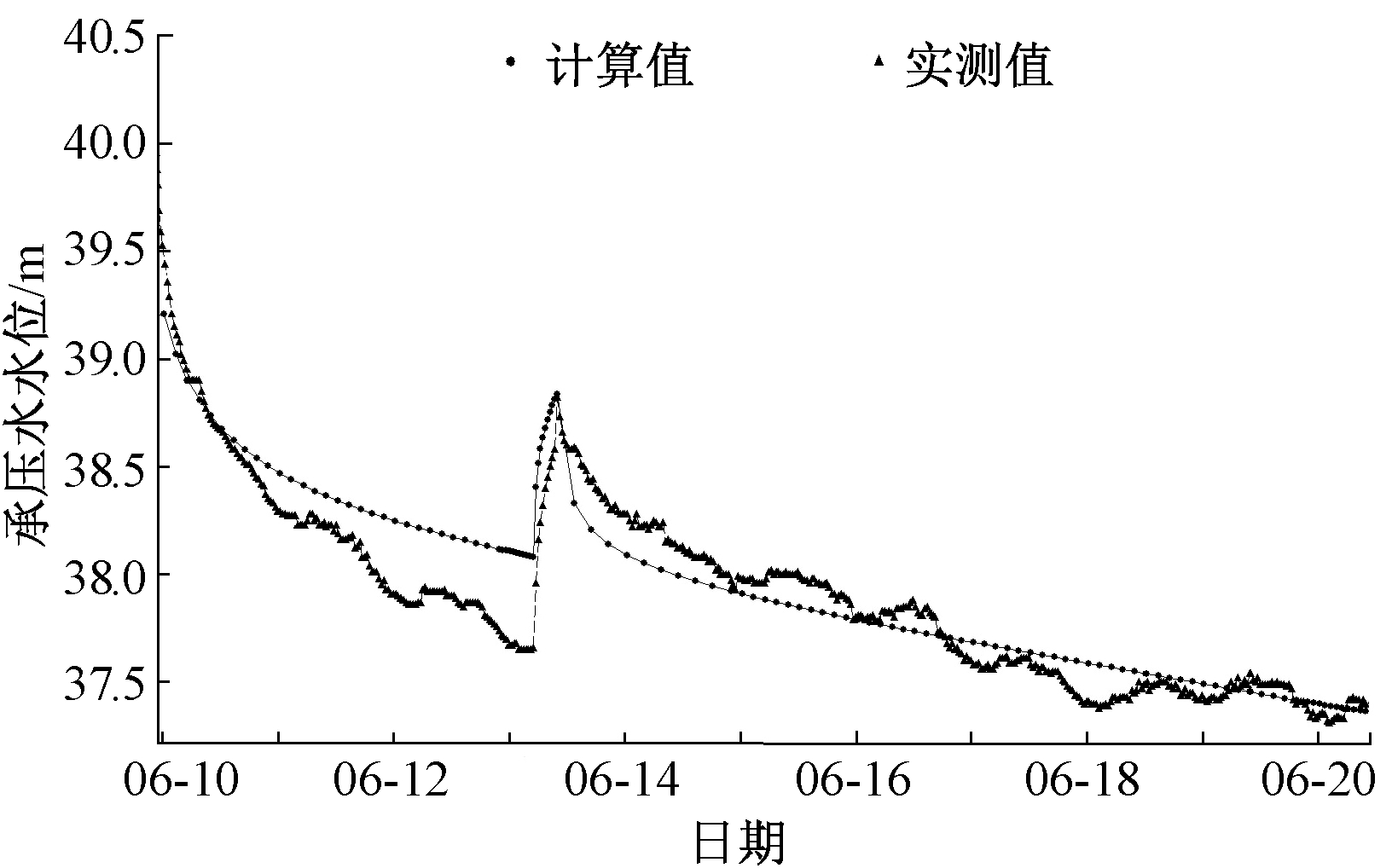
图3 东观测井拟合曲线图
Figure 3 The fitting curve of east observation well
2.3 不同开采强度下地面沉降量预测
2.3.1 开采情景设计
保持现有开采量不变,根据新建水源地地下水开采量的不同,确定不同的地下水开采情景。新建水源地共设定了6种不同的情景(S1,…,S6),开采量分别为15 000 m3/d(S1)、20 000 m3/d(S2)、25 000 m3/d(S3)、30 000 m3/d(S4)、40 000 m3/d(S5)、45 000 m3/d(S6),以不同开采强度开采20 a,不同开采情景下的计算结果如表3所示。
2.3.2 S1~S6情景下地下水位的变化
结果表明,新建水源地不同开采强度下承压水位的响应情况差别很大。当研究区范围内承压水位处于稳定时,开采强度越大,新建水源地降落漏斗面积越大且漏斗中心承压水位越小。S1~S6情景下的漏斗中心水位计算结果见表3。
2.3.3 S1~S6情景下的地面沉降量比较
不同情景下地面沉降的结果表明,新建水源地开采强度越大,降落漏斗中心水位越低,最大年均沉降速率越大,年均沉降速率大于10 mm/a的面积越大,典型观测井地下水位越小。S1~S6情景下的地面沉降量的计算结果见表3。
表3 S1~S6情景下地面沉降量的计算结果
Table 3 Calculation results of land subsidence under S1~S6 scenarios
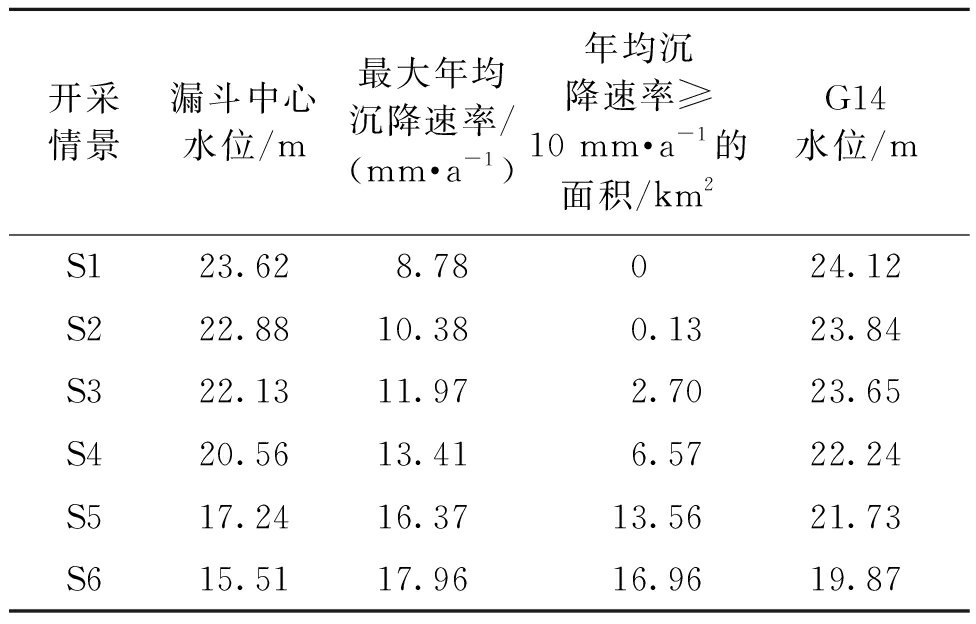
开采情景漏斗中心水位/m最大年均沉降速率/(mm·a-1)年均沉降速率≥10 mm·a-1的面积/km2G14水位/mS123.628.78024.12S222.8810.380.1323.84S322.1311.972.7023.65S420.5613.416.5722.24S517.2416.3713.5621.73S615.5117.9616.9619.87
在S1情景下,研究区年均沉降速率均小于10 mm/a,最大年均沉降速率为8.78 mm/a,且年均沉降速率大于8 mm/a的区域均位于水源地一级保护区范围内;在S3情景下,年均沉降速率大于10 mm/a的面积扩大为2.70 km2,研究区最大年均沉降速率为11.97 mm/a,均位于水源地一级保护区范围内,年均沉降速率大于8 mm/a的区域仍位于水源地二级保护区范围内;在S5和S6情景下,研究区最大年均沉降速率分别为16.37 mm/a和17.96 mm/a,年均沉降速率大于10 mm/a的面积为13.56 km2和16.96 km2,已远远超出一级保护区的范围。S1~S6开采情景下年均沉降速率等值线图见图4。

图4 S1~S6情景下年均沉降速率等值线图
Figure 4 Contour map of annual average land subsidence under S1~S6 scenarios
2.4 承压水合理开采水位的确定
2.4.1 承压水合理开采水位划定原则
禁止开采水位的划定原则为年均沉降速率大于或等于8 mm/a的区域均位于水源地二级保护区范围内时所对应的临界水位;限制开采水位划定原则为年均沉降速率大于或等于10 mm/a的区域均位于研究区一级保护区范围内,或年均沉降速率大于或等于8 mm/a的区域均位于研究区二级保护区范围内时所对应的临界水位;正常开采水位的划定原则是研究区范围内年均沉降速率均小于10 mm/a,且年均沉降速率大于或等于8 mm/a的区域均位于研究区一级保护区范围内时所对应的临界水位。
2.4.2 承压水合理开采水位划定
依据承压水合理开采水位的划定原则,通过调整新建水源地地下水开采强度,分别求出正常开采水位、限制开采水位和禁止开采水位划定原则所对应的临界开采强度。正常开采水位对应的临界开采强度为18 200 m3/d,限制开采水位对应的临界开采强度为28 600 m3/d,禁止开采水位对应的临界开采强度为33 400 m3/d。通过地下水数值模型,得到相应开采强度下承压水位的响应情况,即为相应的承压水合理开采水位。典型观测井的承压水合理开采水位如表4所示。
表4 承压水合理开采水位
Table 4 Rational water level of confined water
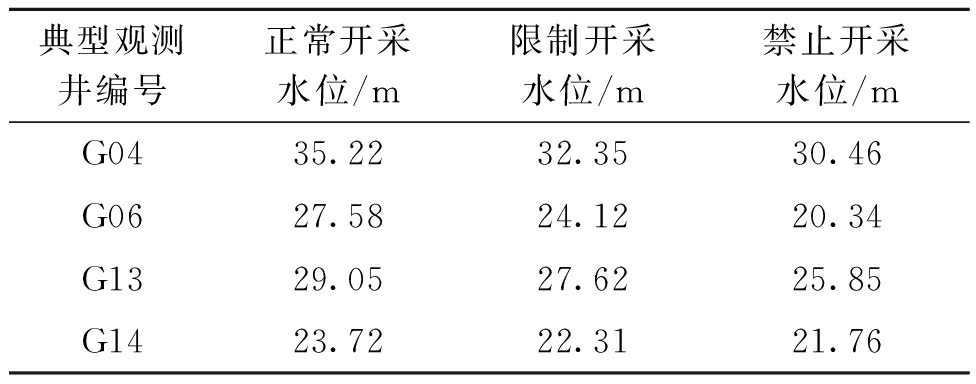
典型观测井编号正常开采水位/m限制开采水位/m禁止开采水位/mG0435.2232.3530.46G0627.5824.1220.34G1329.0527.6225.85G1423.7222.3121.76
3 结论
以河南省西平县城市水源地为研究区,构建了一套城市水源地承压水合理开采水位的划定方法。通过对该区水文地质条件、地下水实际开发利用情况分析,建立地下水模型,通过不同开采方案下地下水流场的预测和地面沉降量的计算,以地面沉降为约束条件,划定研究区承压水合理开采水位,为城市水源地承压水的有效控制管理提供了参考。但由于缺乏研究区地面沉降数据,无法对计算结果进行验证,故可能存在一定的计算误差。
[1] 袁长极.地下水临界深度的确定[J].水利学报, 1964,25(3):50-53.
[2] 方樟,谢新民,马喆,等.河南省安阳市平原区地下水控制性管理水位研究[J].水利学报, 2014, 45(10):1205-1213.
[3] 于璐,窦明,赵辉,等.海水入侵区地下水管理控制水位划定方法研究[J].水电能源科学, 2015, 33(12):143-147.
[4] 陈远洪.某高速铁路车站路基沉降处治[J].郑州大学学报(工学版), 2015, 36(2):67-70.
[5] 王浩,陆垂裕,秦大庸,等.地下水数值计算与应用研究进展综述[J].地学前缘, 2010, 17(6):1-12.
[6] 窦明,张彦,米庆彬,等.地温空调井布局方式对地下水流场和温度场的影响分析[J].郑州大学学报(工学版), 2014, 35(5):124-128.
[7] 薛禹群,张云,叶淑君,等.中国地面沉降及其需要解决的几个问题[J].第四纪研究, 2003, 23(6):585-593.
[8] 耿冬青,贾振宇,韩建聪.关于降水引起地面沉降问题的探讨[J].施工技术, 2005,34(增刊1):55-56.
[9] 侯伟,罗文林,韩煊.抽取地下水引起地面沉降的实用计算方法研究[J].工业建筑, 2015, 45(2):90-94,84.
[10] 骆勇,祝晓彬,郭飞,等.不同方法求解疏排水引起的地面沉降对比研究[J].水文地质工程地质, 2018, 45(5):150-157.