0 引言
水是大自然重要的组成物质,是生命的起源,是人类生产生活和社会发展不可缺少的重要资源,也是生态系统中最活跃的要素,是维持生态平衡的基础.随着社会经济的发展、人口的增加、人类对水资源需求质量的提高以及水资源的日益短缺等问题越来越严重,导致水资源供需矛盾更加突出.因此,对水资源进行需求预测是每个国家、每个地区在对水资源进行分配过程中都必不可少的一个关键步骤.早期的城市工业化水资源需求预测研究,如今海绵城市的研究,水资源需求预测都是至关重要的一步.但是由于水的随机性行为,以及受到经济、人口、环境等等诸多动态因素的影响,水资源需求预测一直以来都是一个十分困难的问题.
目前,常见的水资源需求预测方法有:回归分析方法[1]和组合神经网络法[2].回归分析方法需要大量的原始资料才能保证模型的准确性,原始资料的获取是比较困难的,连续完整的资料很难获得.组合神经网络法要求水资源数据有一定的精度,但是数据往往会有噪声影响,从而对结果造成干扰.粒子群算法(particle swarm optimization, PSO)是一种基于群智能的全局优化算法[3],其原理简单,操作方便,且收敛速度快,具有较好的寻优能力,已被广泛地应用于各种优化问题的求解[4-6].
针对南昌市未来水资源需求预测问题,提出了一种基于粒子群算法的水资源需求预测方法.以南昌市历史用水分布和经济结构为基础,分析了影响水资源需求的影响因素,并构造了不同的预测模型.仿真实验结果表明,笔者提出的方法能获得较好的预测精度.
1 粒子群算法
群智能算法是一类模拟生物群体的智能优化算法,它对问题的连续性和可微性没有要求,通用性较好,更易于求解复杂的优化问题[7-10].粒子群算法是一种流行的群智能算法,该方法通过随机初始化一个种群(称为初始种群),群体中个体(称为粒子)按照某种规则在搜索空间中不断地寻找新的解,以达到寻优的目的.在粒子群算法中,每个粒子包含两个分量:速度和位置.假设种群有N个粒子,第i个粒子表示为(Vi, Xi),其中Vi={vi1,vi2,…,viD}和Xi={xi1,xi2,…,xiD},D为问题的维数.在搜索过程中,每个粒子向其历史最好粒子pbest和全局最好粒子gbest移动.通过移动,粒子不断地更新自己的位置,以寻找更好的潜在解.在粒子群算法中,粒子按照如下公式进行更新[11]:
Vi(t+1)=w·Vi(t)+c1r1(pbesti-Xi(t))+
c2r2(gbest(t)-Xi(t));
(1)
Xi(t+1)=Xi(t)+Vi(t+1),
(2)
式中:i=1,2,…,N;r1和r2是0到1之间均匀分布的随机数;w是惯性权值参数;c1和c2是学习因子参数.
粒子群算法步骤如下:
(1)随机初始化N个粒子的速度和位置组成初始种群P(t), t=0.计算每个粒子的适应值f(Xi(t)),更新每个粒子的pbesti和种群中的gbest.
(2)对于种群中的每个粒子,按照式(1)和(2)更新粒子的速度Vi(t+1)和位置项Xi(t+1),并计算更新后粒子的适应值f(Xi(t+1)).如果更新后的粒子的适应值优于其pbest,则将更新后的粒子赋值给pbest,即保持pbest的更新.
(3)对于种群中每个粒子的pbest,如果其优于gbest,则将该pbest赋值给gbest,即保持gbest的更新.
(4)令t=t+1,如果算法还未达到停机条件,则跳转到步骤(2);否则停止算法运行,输出结果.
2 基于粒子群算法的水资源需求预测
2.1 影响因子分析
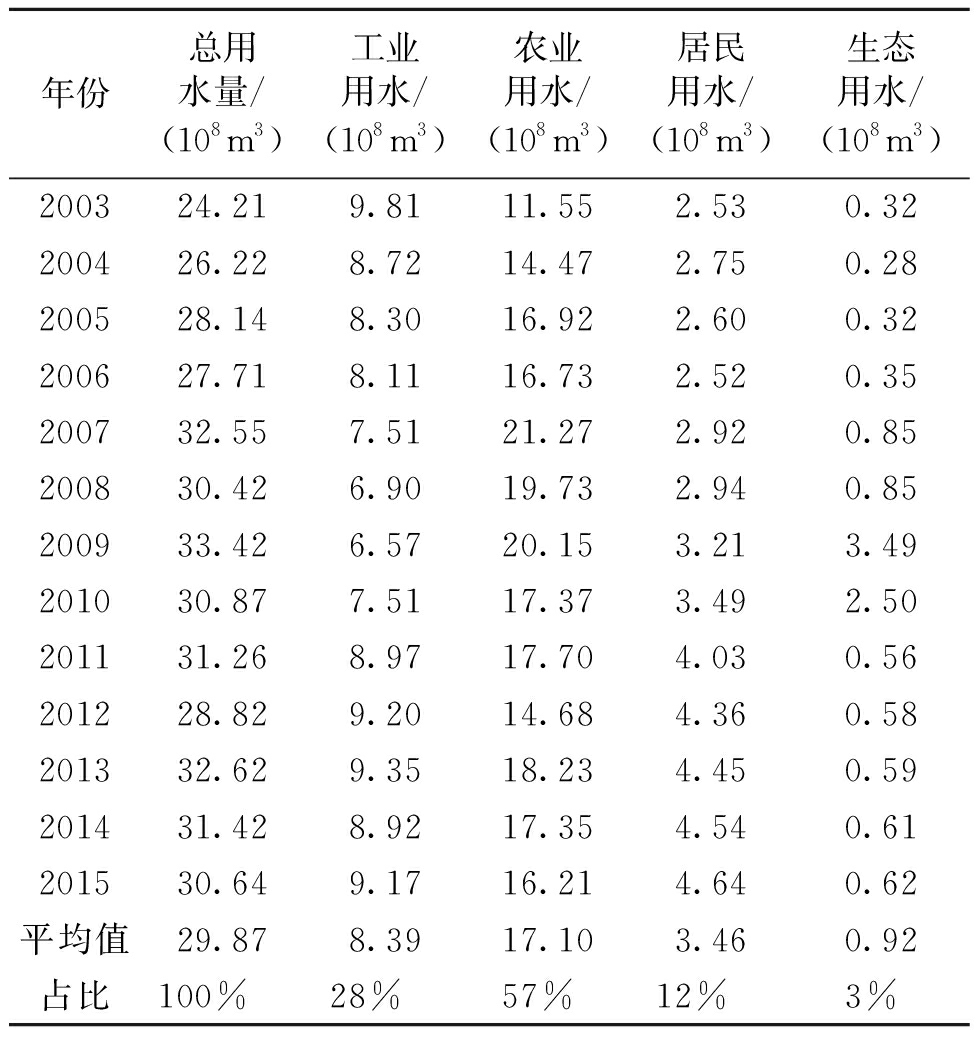
影响城市水资源需求的因素有很多,如地理位置、经济发达程度、人口密集情况、耕地面积、河流流域面积、植被覆盖率、气候、水价以及供水基础设施建设等情况.表1给出了南昌市2003~2015年的历史用水数据[12],从表中可以看出,实际用水包含了4个部分:工业用水、农业用水、居民用水和生态用水.随着时间的发展,南昌市的总用水量逐渐递增,然后在该值附近波动.从各部分的平均用水占比来看,农业用水占比达到57%,工业和居民用水占比也较高,分别为28%和12%,而生态用水仅占3%.图1清晰地阐述了各部分用水分布情况.为了简化影响南昌市水资源需求量的因素,笔者仅考虑工业、农业和居民3个部分用水的影响,而忽略生态用水[13-14].
2.2 水资源需求预测模型
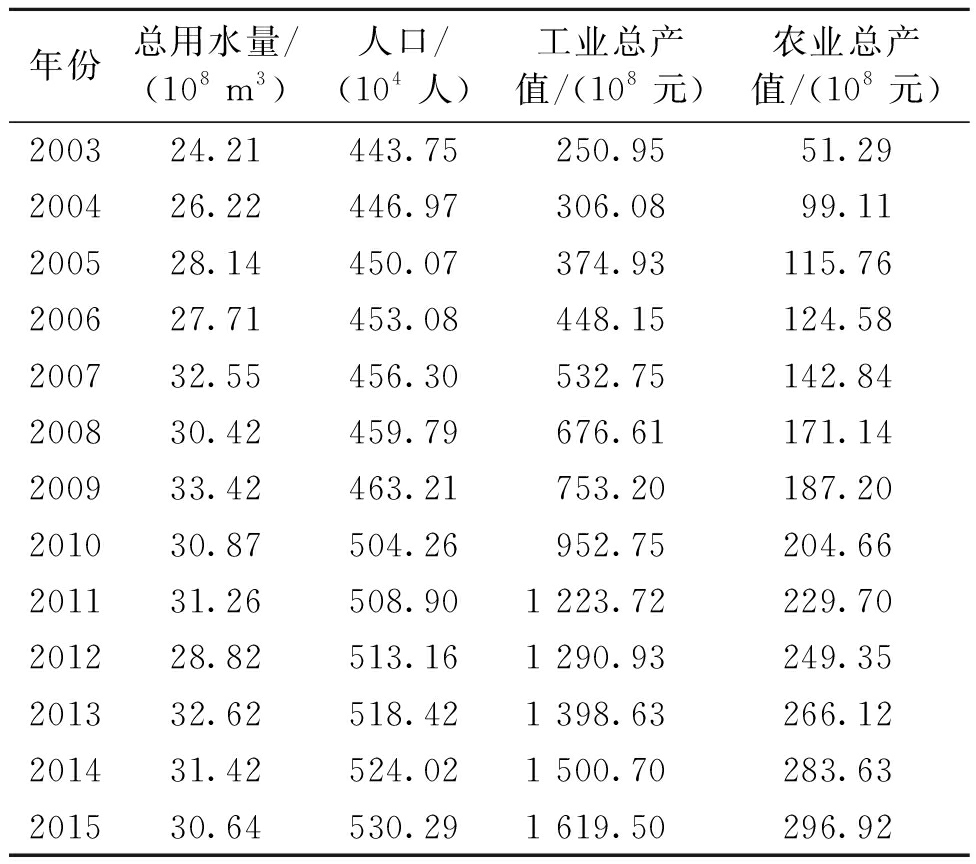
基于上面的分析,在构造南昌市水资源需求预测模型时,笔者仅考虑工业、农业和居民3个部分用水所关联的因子.考虑到工业用水和农业用水受到经济发展程度、科学技术和国家政策的影响很大,而工业和农业用水主要是用于工业和农业生产,因此,使用工业生产总值代表工业用水,农业生产总值代表农业用水.居民用水主要受人口数量的影响,城市常住人口多,用水就多,反之就少,因而使用人口数量关联居民用水量.表2列出了2003~2015年南昌市的总用水量、人口、工业总产值和农业总产值.
表1 南昌市2003~2015年实际用水数据
Tab.1 Actual water use data of Nanchang between 2003 and 2015
年份总用水量/(108m3)工业用水/(108m3)农业用水/(108m3)居民用水/(108m3)生态用水/(108m3)200324.219.8111.552.530.32200426.228.7214.472.750.28200528.148.3016.922.600.32200627.718.1116.732.520.35200732.557.5121.272.920.85200830.426.9019.732.940.85200933.426.5720.153.213.49201030.877.5117.373.492.50201131.268.9717.704.030.56201228.829.2014.684.360.58201332.629.3518.234.450.59201431.428.9217.354.540.61201530.649.1716.214.640.62平均值29.878.3917.103.460.92占比100%28%57%12%3%
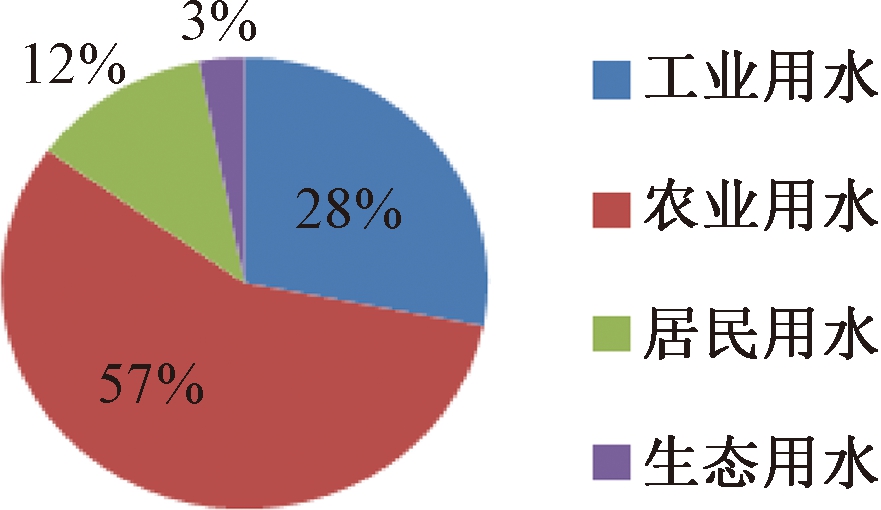
图1 南昌市历史用水分布图
Fig.1 Distribution of historical water use in Nanchang
假设某年的人口数量为S1,工业总产值为S2,农业总产值为S3,该年的总需水量为Y.根据上述因子,笔者提出了3种水资源需求预测模型:线性(Yx)、指数(Yz)和混合模型(Yh).
线性模型:
Yx=x1·S1+x2·S2+x3·S3+x4;
(3)
指数模型:
(4)
混合模型:
Yh=x0·Yx+(1-x0)·Yz,
(5)
式中:xi是模型的权重因子.将Yx和Yz带入式(5)后,混合模型可写为:
表2 南昌市2003~2015年历史总用水量、人口、工业总产值和农业总产值
Tab.2 Historical total water use, population, gross industrial production, gross agricultural production in Nanchang between 2003 and 2015
年份总用水量/(108 m3)人口/(104人)工业总产值/(108元)农业总产值/(108元)200324.21443.75250.9551.29200426.22446.97306.0899.11200528.14450.07374.93115.76200627.71453.08448.15124.58200732.55456.30532.75142.84200830.42459.79676.61171.14200933.42463.21753.20187.20201030.87504.26952.75204.66201131.26508.901 223.72229.70201228.82513.161 290.93249.35201332.62518.421 398.63266.12201431.42524.021 500.70283.63201530.64530.291 619.50296.92
Yh=x0·(x1·S1+x2·S2+x3·S3+x4)+![]()
(6)
2.3 数据处理
利用表2中列出的2003~2015年的历史数据,对水资源需求预测模型进行求解和检验.由于不同的变量因子单位和量纲都不同,因此要对变量进行标准化处理,以消除不同量纲的影响.标准化处理采用的是min-max标准化方法,也被称为离差标准化[13].需要找到样本数据的最大值和最小值,最大值标准化后的值为1,最小值标准化后的值为0,其余值处于0~1.
(7)
式中:S*为归一化后的值;S是要进行归一化的值;Smin和Smax分别是相应变量的最小值和最大值.
2.4 适应值函数
将南昌市2003~2012年的历史需水数据作为训练样本,利用粒子群算法对3种预测模型的权重因子进行优化.将2013~2015年的用水数据作为测试样本来检验预测模型的性能.为了评估预测模型,笔者采用误差平方和法来构造评价函数[7].
(8)
式中:Ypre和Yact分别为预测的需水量和实际需水量;m是训练样本大小.
3 仿真实验
3.1 模型求解
在实验中,将粒子群算法应用于水资源需求预测模型权值参数的优化.将表2中2003~2012年的数据作为训练样本来优化预测模型,然后使用2013~2015年的数据作为测试样本来验证模型.仿真实验中的算法参数如下:N=30、w=0.73、c1=c2=1.496.算法停止条件为最大适应值评估次数,当适应值评估次数达到1.0E+05时,算法停止运行并输出结果.对于每种模型,算法运行10次.
表3~5分别给出了线性预测模型、指数预测模型和混合预测模型的最好计算结果.最好结果是指基于训练样本,算法运行10次后挑选出的最好模型,然后根据该模型基于测试样本计算得到的预测误差值.从表3可以看出,基于线性预测模型得到的平均误差值为4.49%,预测精度达到95.51%.在2013年的预测结果上,误差仅为1.72%,但是2015年的误差较高.
表3 线性预测模型的最好计算结果
Tab.3 Best results achieved by the linear prediction model

年份实际值/(108 m3)预测值/(108 m3)误差/%201332.6232.061.72201431.4232.633.85201530.6433.067.90
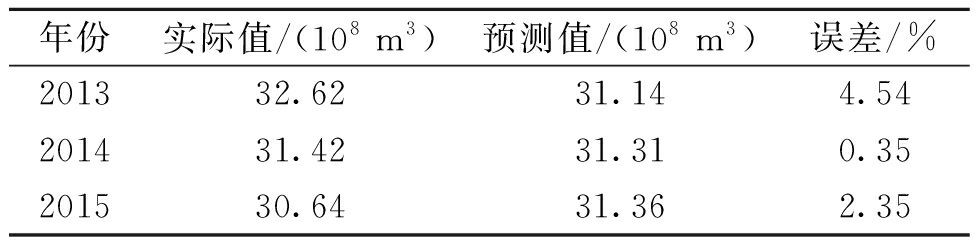
表4 指数预测模型的最好计算结果
Tab.4 Best results achieved by the exponential prediction model
年份实际值/(108 m3)预测值/(108 m3)误差/%201332.6231.144.54201431.4231.310.35201530.6431.362.35
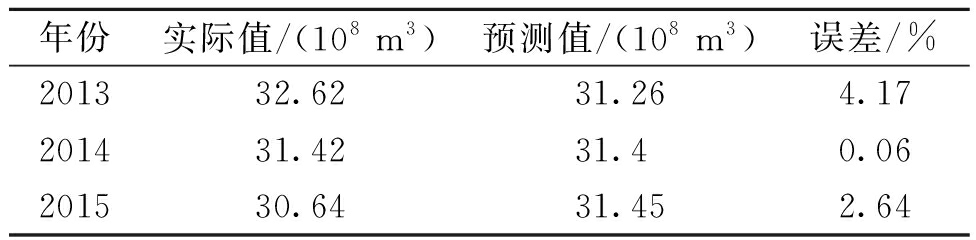
表5 混合预测模型的最好计算结果
Tab.5 Best results achieved by the hybrid prediction model
年份实际值/(108 m3)预测值/(108 m3)误差/%201332.6231.264.17201431.4231.40.06201530.6431.452.64
从表4的结果来看,基于指数预测模型得到的平均误差为2.41%,预测精度达到97.59%.在某一年度的预测结果上,最小误差仅为0.35%,最大误差为4.54%.与线性预测模型相比,指数预测模型较大地提升了预测精度.
从表5的结果可以看出,基于混合预测模型得到平均误差要小于指数预测模型,预测精度达到97.71%.在某一年度的预测结果上,最小误差仅为0.06%,最大误差为4.17%,均优于线性预测模型和指数预测模型.
从3种预测模型的计算结果来看,最后得到的预测精度介于95.51%~97.71%,获得了较好的预测效果.指数预测模型优于线性预测模型,而混合预测模型是3种模型中最好的.
3.2 南昌市未来水资源需求预测
要对未来某年水资源需求总量进行预测,只需要求得对应年份的3个变量因子的值,然后通过得到的预测模型进行计算,就能得到该年度的水资源需求预测值.笔者以2017年数据为基础,采用近三年的平均增长率来估算南昌市2018~2020年的人口数量、工业总产值和农业总产值.根据南昌市统计资料,2018~2020年人口数量的增长率为0.682%,工业总产值的增长率为9.30%,农业总产值的增长率为4.00%.
由于混合预测模型的性能优于线性预测模型和指数预测模型,因此本部分只给出基于混合预测模型计算得到的未来水资源需求预测结果.2018年预测总需水量为30.85×108 m3,2019年为31.14×108 m3;2020年为31.45×108 m3.由于经济和科学技术水平的飞速发展,工业总产值和农业总产值是呈上升的趋势,但是人口数量和地形地貌等一些因素每年变化不大,导致未来南昌市水资源需求总量还是呈递增的趋势.
4 结论
针对南昌市水资源需求预测问题,笔者提出基于粒子群算法的水资源需求预测方法.基于南昌市历史用水数据和经济结构,构建了线性、指数和混合3种预测模型.基于误差平方和适应值函数,利用粒子群算法优化预测模型的权重因子,得到合理的预测模型.仿真实验结果显示,基于3种预测模型计算得到的预测精度介于95.51%~97.71%,获得了较好的预测效果.最后,对南昌市2018~2020年的水资源需求进行了预测.结果表明,未来南昌市水资源需求总量是呈递增的趋势.由于模型的限制,预测未来水资源需求总量、农业用水、工业用水、居民用水需求量不能分别求出.除此之外,模型只考虑人口、工业总产值和农业总产值的影响,忽略了生态用水、气候、水价等因素,模型还有待进一步改进.
[1] 田乐蒙. 回归分析在水资源短缺预测中的应用[J]. 统计与决策, 2012(14): 84-86.
[2] 王坚. 基于改进组合神经网络的水资源预测研究[J]. 计算机科学, 2016, 43(6A): 516-517.
[3] KENNEDY J, EBERHART R. Particle swarm optimization[C]// Proceedings of ICNN′95 International Conference on Neural Networks. Perth,WA: IEEE, 1995: 1942-1948.
[4] 毛晓波,张群,梁静,等. 基于PSO-RBF神经网络的雾霾车牌识别算法研究[J]. 郑州大学学报(工学版), 2017, 38(4):46-50.
[5] 夏星宇,高浩,王创业. 均衡策略粒子群算法在图像分割中的应用[J]. 郑州大学学报(工学版), 2018, 39(1):59-66.
[6] 李婕,白志宏,于瑞云,等.基于PSO优化的移动位置隐私保护算法[J]. 计算机学报, 2018, 41(5):1037-1051.
[7] 孙辉,谢海华,赵嘉. 正弦选择概率模型的全局最优引导人工蜂群算法[J]. 南昌工程学院学报, 2018, 37(6): 84-90.
[8] 梁静,宋慧,瞿博阳,等.基于改进粒子群算法的路径优化问题研究[J]. 郑州大学学报(工学版), 2014, 35(1):34-38.
[9] 肖辉辉,万常选,段艳明,等. 基于引力搜索机制的花朵授粉算法[J]. 自动化学报,2017, 43(4): 576-594.
[10] CAI X, WANG H, CUI Z H, et al. Bat algorithm with triangle-flipping strategy for numerical optimization[J]. International journal of machine learning and cybernetics, 2018, 9(2): 199-215.
[11] SHI Y, EBERHART R. A modified particle swarm optimizer[C]// 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence. Anchorage, AK: IEEE, 1998: 69-73.
[12] 江西省统计局. 江西统计年鉴[M]. 北京:中国统计出版社, 2013-2015.
[13] WANG H, CUI Z H, WANG W J, et al. Firefly algorithm for demand estimation of water resources[C]//Proceedings of the 24th International Conference on Neural Information Processing (ICONIP 2017). Guangzhou: Springer, 2017:11-20.
[14] WANG H, WANG W J, CUI Z H, et al. A new dynamic firefly algorithm for demand estimation of water resources[J]. Information sciences, 2018, 438: 95-106.