0 引言
约束阻尼结构具有结构简单、布置方便、占用空间少和在宽频带范围内具有很好减振降噪效果等特点[1]，在工程的减振降噪领域得到了广泛应用。对约束阻尼材料的布局进行优化，获得约束阻尼材料的优化构型，使约束阻尼材料粘贴在最佳的位置是严格控制附加质量、提高约束阻尼材料使用效率有效的方法。
当前，很多学者以模态损耗因子最大化为优化目标对约束阻尼材料的布局进行优化，使优化的构型能够提高结构的模态损耗因子，有效抑制结构的振动响应[2-5]。此外，以约束阻尼薄壁件的声辐射最小化为优化目标对阻尼材料的布局优化，优化结果对声辐射有很好的抑制效果[6-7]。
基于频率响应的拓扑优化能够直接反映结构的动力学响应，具有良好的工程应用性和设计针对性[8-12]。结构往往经受复杂的振动激励，特别是随机激励，会引起设备适应性与人员舒适性以及结构振动疲劳等问题[13]。约束阻尼结构具有非比例阻尼特性， 结构随机响应的灵敏度计算成本很高，因此，提出高效的灵敏度分析方法是随机激励下约束阻尼结构布局优化亟待解决的问题。
采用拓扑优化方法对平稳随机激励下约束阻尼结构的布局进行优化。以平稳随机激励下约束阻尼结构位移响应的均方根值为优化目标建立拓扑优化模型。提出复模态叠加法和伴随法相结合的灵敏度分析方法，有效提高灵敏度计算效率。采用移动渐近线法(MMA)对建立的拓扑优化模型求解，得到优化的约束阻尼结构布局，提高约束阻尼结构的减振降噪特性。
1 平稳随机激励下约束阻尼结构振动响应分析
采用复模量对黏弹性阻尼材料进行表征，建立平稳随机激励下约束阻尼结构的动力学方程为：
(1)
式中：M为结构的质量矩阵；KR和KI分别为结构刚度矩阵的实部和虚部；
和x分别为结构节点的加速度向量和位移向量；
激励力f为平稳随机过程，其功率谱密度矩阵为Sff。
当前，对随机激励下结构振动响应分析常用的方法有完全二次法(CQC)、平方和开平方法(SRSS)以及虚拟激励法(PEM)[14]。虚拟激励法将平稳随机振动分析转变为简谐振动分析，在保持计算精度的前提下，可有效提高计算效率。构造虚拟激励和其对应的响应为：
(2)
式中：l为激励力分布向量；
和
分别为位移响应幅值的实部和虚部。
将式(2)代入式(1)可得：
(3)
式中：
采用复模态叠加法对式(3)求解可得：
(4)
式中：φr为第r阶复模态振型向量；ωr为第r阶复圆频率。
平稳随机激励下约束阻尼结构第i个自由度位移响应的功率谱密度Sxixi和均方根值νxixi为：
(5)
(6)
式中：[ωα,ωβ]为随机激励的频率区间。
2 平稳随机激励下约束阻尼结构的拓扑优化
2.1 拓扑优化模型
平稳随机激励下，以约束阻尼结构位移响应均方根值最小化为优化目标和约束阻尼材料体积为约束条件，建立其拓扑优化模型为：
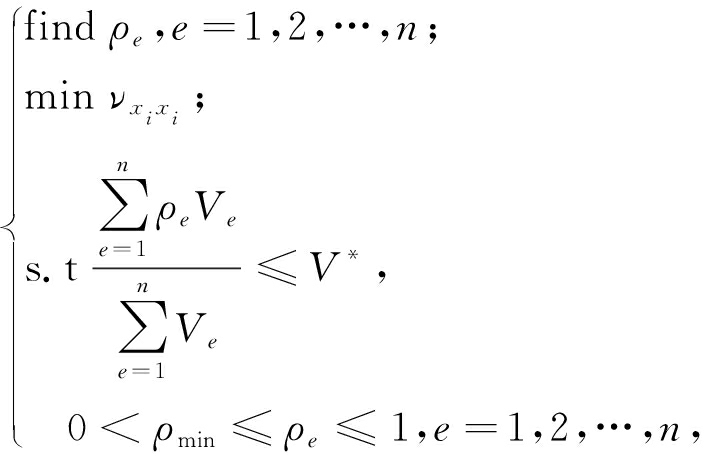
(7)
式中:ρe为设计变量e的密度值，取值为(0,1]；ρmin为设计变量密度值的最小值，本文取值为0.000 1；n为设计变量总数；Ve为设计变量密度值ρe=1时的约束阻尼材料的体积；V*为约束阻尼材料的体积分数。
2.2 灵敏度分析
优化目标关于设计变量e的灵敏度为：
(8)
式(5)两边关于设计变量密度值的偏导为：
(9)
从式(8) 和式(9)可以看出，要得到优化目标的灵敏度须先计算
和
由于激励力与结构无关，因而式(3)两边关于设计变量密度值ρe的偏导为：
(10)
对式(10)进行静力学分析就可以得到
此方法称为直接法。直接法具有高的计算精度，但是对于优化目标自由度少且设计变量多的优化设计，它的计算效率很低。为了提高计算效率，提出复模态叠加法和伴随法相结合的方法。
引入向量：
αi=[0,0,…,1,0,…,0]T,
(11)
式中除了优化目标自由度i所对应的第i个元素的值为1，其他元素值均为0。则
(12)
引入复伴随向量：
Λ=ΛR+jΛI。
(13)
将式(10)两边左乘于ΛT并加上式(12)，可得
(14)
使复伴随向量满足以下方程：
αi-ΛT(KR+jKI-Mω2)=0。
(15)
式(15)即为伴随方程，采用复模态叠加法对式(15)求解即可得到伴随向量，则
(16)
根据SIMP的插值模型，约束阻尼结构的质量矩阵和刚度矩阵可表示为：
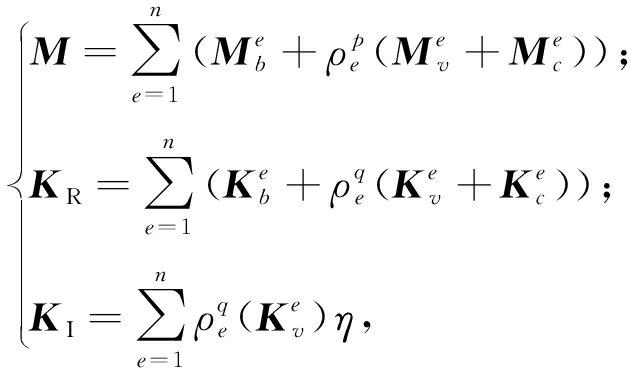
(17)
式中：p和q为惩罚因子，本文取值分别为1和
和
分别为单元e的基层、黏弹性阻尼层和约束层的质量矩阵；
和
分别为单元e的基层、黏弹性阻尼层和约束层的刚度矩阵；η为黏弹性阻尼材料的损耗因子。
约束阻尼结构的质量矩阵和刚度矩阵关于设计变量的灵敏度为：
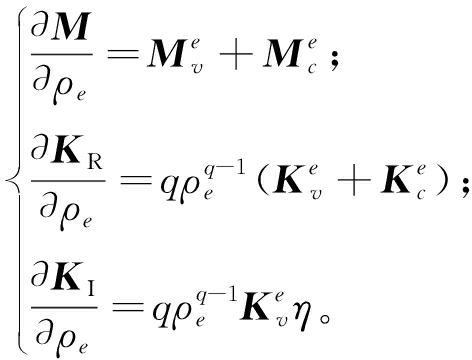
(18)
2.3 优化流程
采用MMA对设计变量更新，最终获得约束阻尼结构的优化构型，优化流程如图1所示。
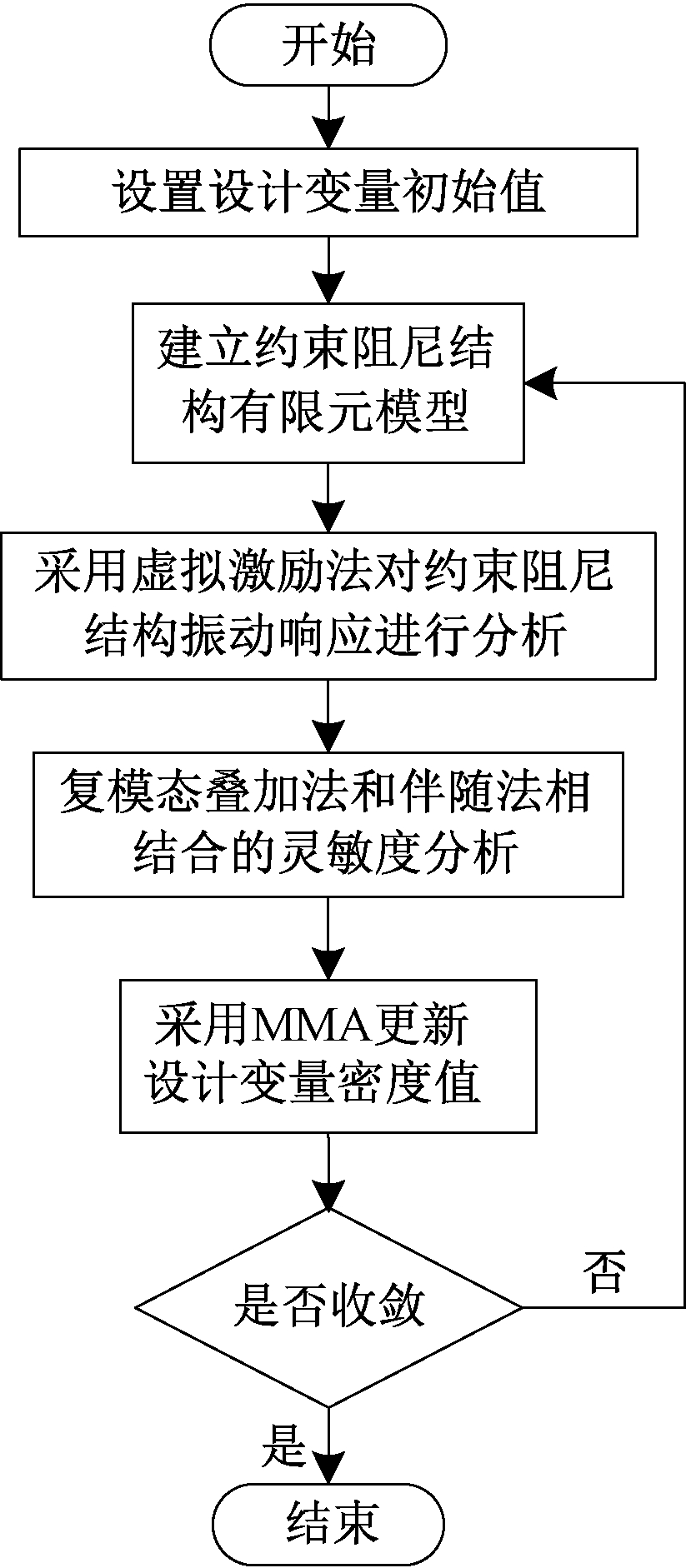
图1 优化流程
Figure 1 Block diagram of the optimization procedure
3 算例分析
3.1 悬臂的约束阻尼板
悬臂的矩形约束阻尼板的尺寸为：200 mm×100 mm，黏弹性阻尼层的弹性模量、密度、泊松比和损耗因子分别为：12 MPa、1 200 kg/m3、0.495和0.5，厚度为0.1 mm。基层和约束层均为铝，其弹性模量、密度和泊松比分别为：70 GPa、2 700 kg/m3和0.3，其厚度分别为2 mm和0.2 mm。约束阻尼板的左边约束，右边自由，如图2所示。
图2 悬臂的约束阻尼板
Figure 2 The cantilever plate/CLD system
平稳随机激励作用于自由端中间，其功率谱密度矩阵为Sff=1 N2/Hz。以激励点处的垂向位移响应的均方根值最小为优化目标。约束阻尼材料的体积分数为0.5。对约束阻尼结构优化的两个随机激励的频率区间分别为：f1=[0,100] Hz和f2=[100, 1 000] Hz。
首先对提出的灵敏度计算方法和直接法的计算效率进行对比分析，频率区间为f1=[0,100] Hz时，笔者提出的灵敏度计算方法对优化目标的灵敏度计算时间为27.56 s，而直接法的计算时间为124.25 s。可以看出，笔者提出的灵敏度计算方法的计算效率远高于直接法。
优化的约束阻尼材料的布局分别如图3和图4所示，图中黑色部分为约束阻尼材料的布置区域，从图中可以看出当优化的频率区间不同时，约束阻尼材料的优化布局不同。优化前后目标值的对比如表1所示。图5和图6分别为优化前后各优化频段内优化目标位置处位移响应的功率谱密度，从图5、6中可以看出，在各个优化频段内结构的振动得到了有效抑制。
图3 优化构型(f1=[0,100] Hz)
Figure 3 The optimal layouts of CLD treatment
(f1=[0,100] Hz)
图4 优化构型(f2=[100,1 000] Hz)
Figure 4 The optimal layouts of CLD treatment (f2=[100,1 000] Hz)
表1 优化前后优化目标值对比
Table 1 The comparison of the values of objective function before and after optimization
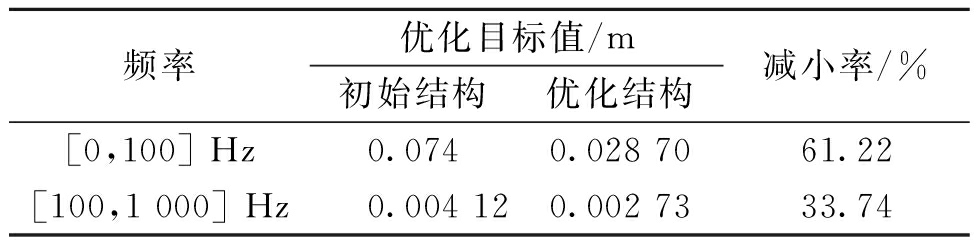
频率优化目标值/m初始结构优化结构减小率/%[0,100] Hz0.0740.028 7061.22[100,1 000] Hz 0.004 120.002 7333.74
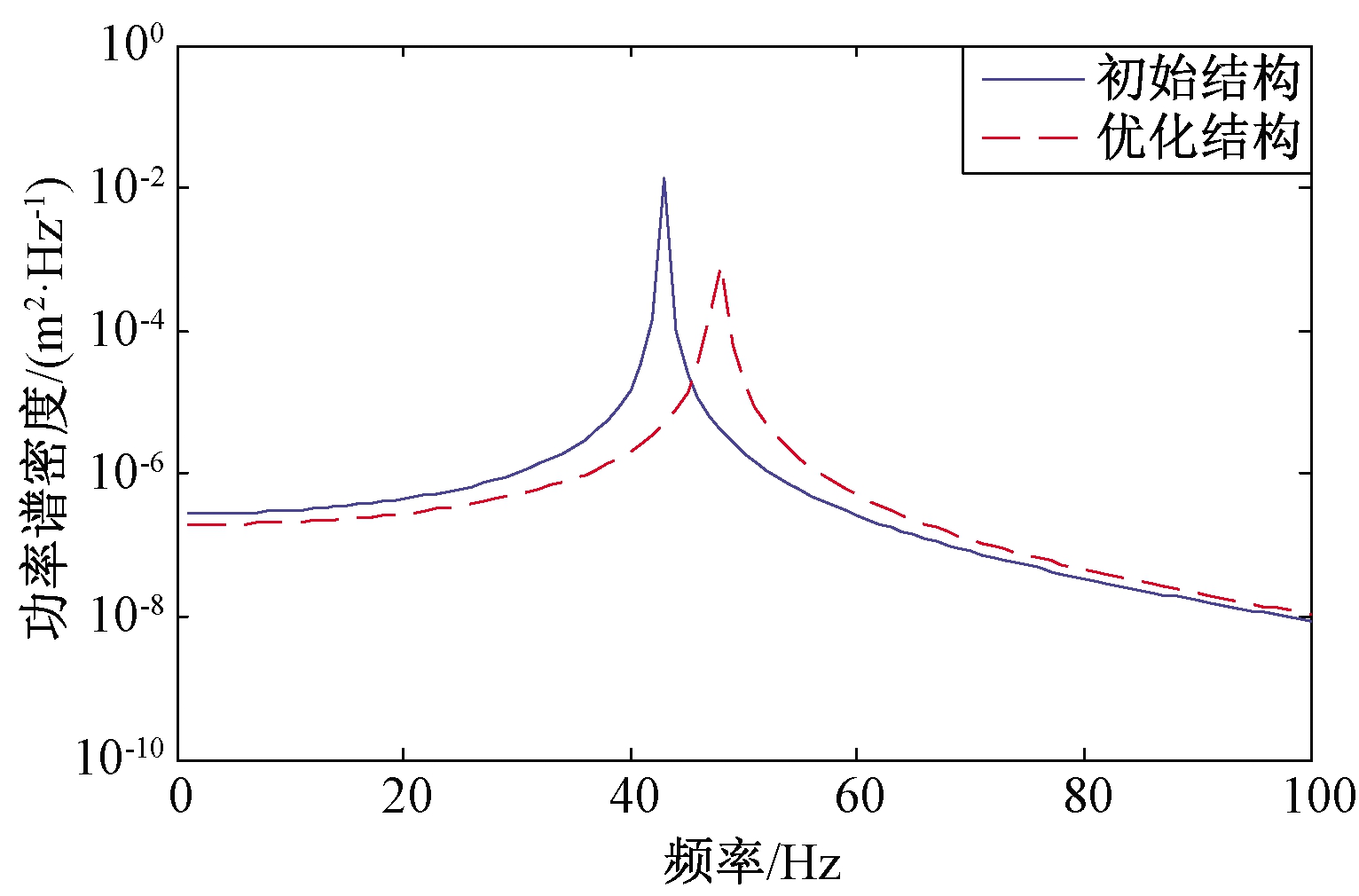
图5 优化前后功率谱密度对比图(f1=[0,100] Hz)
Figure 5 PSD curves of the initial and optimal design of CLD treatment (f1=[0,100] Hz)
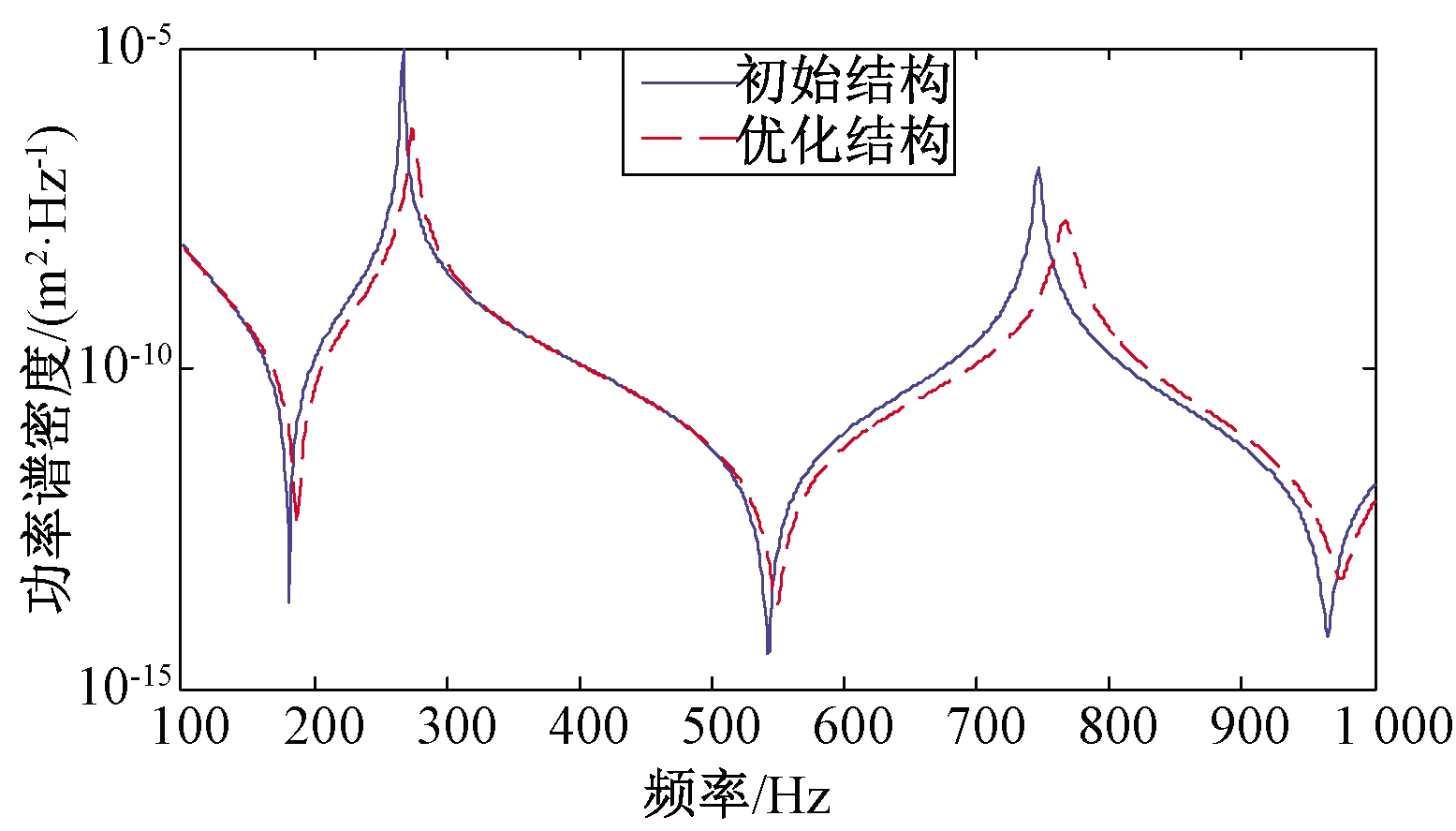
图6 优化前后功率谱密度对比图(f2=[100,1 000] Hz)
Figure 6 PSD curves of the initial and optimal design of CLD treatment (f2=[100,1 000] Hz)
3.2 两短边固定的约束阻尼板
约束阻尼矩形板的尺寸为：400 mm×200 mm，其他尺寸和物理参数与算例1相同，两短边固定，两长边自由。平稳随机激励作用于约束阻尼板的中心，其功率谱密度矩阵为Sff=1 N2/Hz。仍然以激励点处的垂向位移响应的均方根值最小为优化目标。约束阻尼材料的体积分数分别为0.5和0.75。对约束阻尼结构优化的随机激励的频率区间为：f=[0,1 000] Hz。
优化的约束阻尼材料的布局分别如图7和图8，计算结果表明：体积分数分别为0.5和0.75的优化结构的优化目标比初始结构的优化目标分别减小了32.26%和40.78%。图9为优化前后目标位置处位移响应的功率谱密度，从图中可以看出，两个体积分数的优化结构在优化目标位置处的位移响应功率谱密度都比初始结构有明显减小。
图7 优化构型 (V*=0.5)
Figure 7 The optimal layouts of CLD treatment (V*=0.5)
图8 优化构型 (V*=0.75)
Figure 8 The optimal layouts of CLD treatment (V*=0.75)
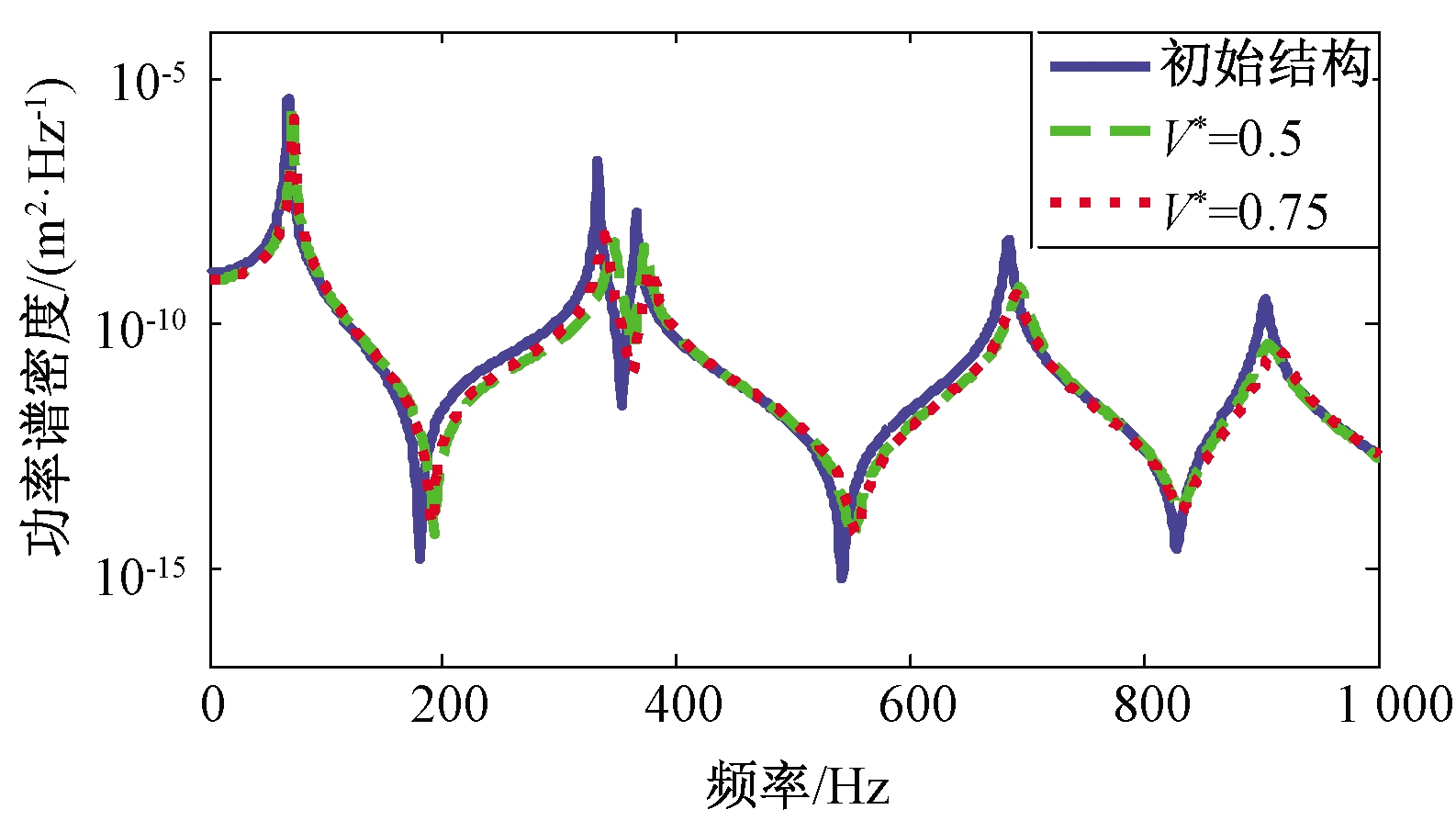
图9 优化前后功率谱密度对比图
Figure 9 PSD curves of the initial and optimal design of CLD treatment
4 结论
(1) 以约束阻尼结构位移响应均方根值最小化为优化目标，约束阻尼材料体积为约束条件，约束阻尼单元为设计变量，建立平稳随机激励下约束阻尼结构的拓扑优化模型。
(2) 针对拓扑优化属于优化目标少、设计变量多的情况，提出了复模态叠加法和伴随法相结合的灵敏度分析方法，有效提高灵敏度计算效率。
(3) 采用MMA算法对建立的约束阻尼结构优化模型进行求解，对平稳随机激励下的约束阻尼结构进行优化，得到优化的约束阻尼结构比初始结构的振动响应明显减小，验证了笔者提出的优化算法的正确性和有效性。
[1] 伍先俊.约束阻尼结构阻尼效果的有限元预测方法研究 [J].噪声与振动控制，2019，39(1)：205-209，234.
[2] 窦松然，桂洪斌，李承豪，等.圆柱壳振动控制中的约束阻尼拓扑优化研究 [J]. 振动与冲击，2015，34(22)：149-153.
[3] ALFOUNEH M，TONG L Y. Maximizing modal damping in layered structures via multi-objective topology optimization [J]. Engineering structures，2017，132：637-647.
[4] 贺红林，陶结.约束阻尼板增材式拓扑渐进法减振动力学优化 [J].机械科学与技术，2017，36(6)：972-977.
[5] LIU Q M，RUAN D，HUANG X D. Topology optimization of viscoelastic materials on damping and frequency of macrostructures [J]. Computer methods in applied mechanics and engineering，2018，337：305-323.
[6] 徐伟，张志飞，庾鲁思，等.附加自由阻尼板阻尼材料降噪拓扑优化 [J].振动与冲击，2017，36(11)：192-198，223.
[7] 张宇，杨家友，韦正.基于阻尼层拓扑优化的车内噪声控制 [J].噪声与振动控制，2018，38(6)：101-104.
[8] FANG Z P，ZHENG L. Topology optimization for minimizing the resonant response of plates with constrained layer damping treatment [J].Journal of vibroengineering，2015，17(6)：2763-2780.
[9] TAKEZAWA A，DAIFUKU M，NAKANO Y，et al. Topology optimization of damping material for reducing resonance response based on complex dynamic compliance [J].Journal of sound and vibration，2016，365：230-243.
[10] SHI J X，HIRANO R，SHIMODA M. Design optimization of damping material-inlaid plates for vibration control [J].Composite structures，2016，148：50-58.
[11] YUN K S，YOUN S K. Multi-material topology optimization of viscoelastically damped structures under time-dependent loading [J].Finite elements in analysis and design，2017，123：9-18.
[12] 侯俊剑，房占鹏，何文斌.基于位移响应最小化的约束阻尼结构优化设计 [J].郑州大学学报(工学版)，2017，38(3)：87-91.
[13] ZHANG W H，LIU H，GAO T. Topology optimization of large-scale structures subjected to stationary random excitation：an efficient optimization procedure integrating pseudo excitation method and mode acceleration method [J]. Composite & structures，2015，158：61-70.
[14] LIN J H，ZHAO Y，ZHANG Y H. Accurate and highly efficient algorithms for structural stationary/non-stationary random responses [J].Computer methods in applied mechanics and engineering，2001，191(1/2)：103-111.