0 引言
风电机组的有功出力受自然风影响,具有较高的间歇性和波动性。当大规模风电并网运行时,传统电力系统的平衡能力受到破坏,给电力部门的调控策略带来极大的挑战[1]。要想在提高风力发电在电力系统中比重的同时,确保电力系统安全稳定运行,使用较高精度的短期风电功率预测技术是有效措施之一。
目前,短期风电功率预测技术主要分为物理方法和统计方法[2]。物理方法通过对风电场的地理位置进行物理建模,将高精度的数值天气预报(numerical weather prediction,NWP)结果和风电场的地理信息转换为风机轮毂高度处的风速、风向等信息,再结合功率曲线推算出风机的有功出力[3];统计方法需要准确的风电场历史观测数据去训练模型,由于组合预测方法和先进的参数寻优算法能明显提高其预测精度,使得统计方法成为目前较为常用的短期风电功率预测方法[4]。
然而,统计方法的训练样本多数为风电场全年的历史观测数据,一方面,过多的训练样本存在冗余信息,会导致过拟合现象;另一方面,这种整体性地选择训练样本难以适应复杂多样的天气状况,预测精度也往往达不到理想效果。近年来,一些学者借鉴电力负荷预测中“相似日”的原理选取训练样本,并取得了不错的预测效果。文献[5-7]选取风速、风向、温度、气压和相对湿度等气象信息的均值或最值构成天气模式向量,通过关联系数和夹角余弦等作为相似性判据,对历史日进行搜索,构成训练样本集。文献[8-11]采用聚类方式,根据相似的天气模式向量将训练样本归类,建立自适应天气变化的预测模型。以上结果表明,与没有对样本进行筛选和分类的其他模型相比,其预测精度得到明显提高。
由于天气状况比较复杂,实践中很难将其定性为特定的类别,即使在相似的天气状况下,风速变化曲线也会相差较大。而风速作为影响风机出力的主要因素,由于风机桨叶的惯性作用,风速的波动对风电机组的有功出力会有较大影响[12-13]。因此,在选择相似日时应充分考虑风速变化趋势的相似性。基于此,通过离散Fréchet距离作为风速、风向、温度、气压、相对湿度等时间序列的相似性判据来匹配相似日。此外,这些气象要素之间存在复杂的非线性关系,使用核熵成分分析(kernel entropy component analysis, KECA)在高维特征空间提取非线性主元作为支持向量机(SVM)的输入。实验结果表明,该方法能够较好地从历史数据中选取相似日和非线性主元,且预测精度较高。
1 数据和方法
1.1 数据
以云南某风电场为例,实验数据为13台型号相同的风机运行数据和测风塔采集的气象数据,采样时段为2016年7月至8月,采样间隔为15 min,风机信息如表1所示。
表1 风机基本信息
Table 1 Basic information of wind turbines

切入风速/(m·s-1)额定风速/(m·s-1)切出风速/(m·s-1)额定功率/MW风轮直径/m扫风面积/m2311251.5936 805
1.2 离散 Fréchet 距离
Fréchet距离是法国数学家Fréchet基于空间路径相似度的方法提出的,能够度量两曲线间整体走势的相似情况,其定义[14]如下:
定义 设f,g:[0,1]→R2是给定两条连续曲线,α,β:[0,1]→[0,1]为连续非减的实函数,且满足α(0)=β(0)=0,α(1)=β(1)=1,则两曲线间的Fréchet距离为:
![]()
(1)
可见,Fréchet距离的实质是寻找一对实函数α(t)、β(t)最小化曲线f与g之间连通的最大距离。为解决实际问题,Eiter和Mannila在此基础上,通过离散化和求极限的思想提出了离散Fréchet距离的概念。
设给定两条离散有序序列P=<u1,…,up>和Q=<v1,…,vq>,L为P、Q间各序列点组成的序列点对:
L={(ua1,vb1),(ua2,vb2),…,(uak,vbk)},
其中,a1=b1=1,ak=p,bk=q且对于i=1,…,k,满足ai+1=ai或ai+1=ai+1,bi+1=bi或bi+1=bi+1,即序列点对L同时服从P、Q中各序列点的对应次序关系。
定义‖L‖为序列点对L中最长连接的长度,表示如下:
(2)
则两曲线间的离散Fréchet距离的定义[15]为:
d(P,Q)=min{‖L‖}。
(3)
d(P,Q)可根据以下公式递归求解:
d(P,Q)=
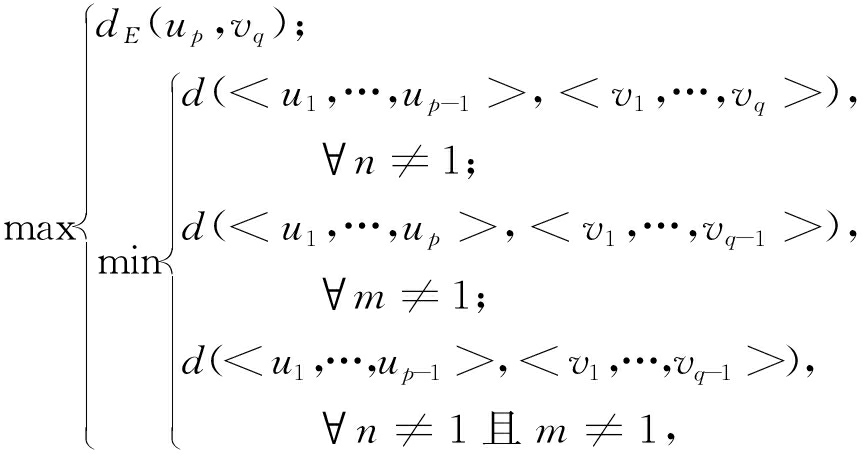
(4)
式中:dE(up,vq)是两点up和vq间的欧式距离。
1.3 核熵成分分析(KECA)原理
核熵成分分析(kernel entropy component analysis, KECA)是数据转换与维度变换的一种新方法。该方法以二次Renyi熵值作为信息量的度量,在高维特征空间提取非线性主元,能够很好地表征原始特征数据关于熵的内在结构[16]。
设某一概率系统中,有概率密度函数为p(x)的数据集X=[x1,x2,…,xN],xi∈RD,X对应的二次Renyi熵表示如下:
(5)
令![]() 为求H(p)的值,需对V(p)进行核密度估计,核密度估计函数为:
为求H(p)的值,需对V(p)进行核密度估计,核密度估计函数为:
(6)
式中:kσ(x,xi)为核函数;σ为宽度参数。
根据高斯函数卷积定理,化简可得
(7)
式中:K为N×N核矩阵;I为各元素均为N×1的矩阵。将K特征值分解为:K=EDET,其中D为特征值λ1,λ2,…,λN构成的对角矩阵,E为对应的特征向量e1,e2,…,eN构成的特征矩阵,则式(7)可表示为:
(8)
KECA根据每个![]() 对二次Renyi熵的估计,将核矩阵的特征值和相应的特征向量按估计值大小对其降序排列,由此产生的KECA映射Φeca为:
对二次Renyi熵的估计,将核矩阵的特征值和相应的特征向量按估计值大小对其降序排列,由此产生的KECA映射Φeca为:
(9)
式中:Dd为对特征值λ1,λ2,…,λN降序排列后选取的前d个特征值所构成的对角矩阵;Ed则是由相应的特征向量构成。
对于一个新的测试样本xnew在特征空间上的投影可表示为:
(10)
由上述可知,核相关矩阵的维数等于训练样本的个数。因此,KECA方法最多能够从高维特征空间提取N个非线性主元作为训练模型的输入。
1.4 SVM理论
支持向量机(support vector machine, SVM)是建立在VC维理论(Vapnik-Chervonenkis dimen-sion)和结构风险最小化准则的基础上的,相较神经网络等学习方法而言具有严格的理论基础[17]。此外,SVM能够很好地解决小样本、非线性和高维度等问题。在案例中,使用了著名的开源软件包LibSVM[18],选取的SVM核函数为径向基函数。
2 基于相似日和特征提取的SVM建模
2.1 相似日的匹配
影响风机出力的主要因素有风速、风向、温度、气压、相对湿度等5个气象要素,以这些气象要素的采样点序列匹配相似日,具体步骤如下。
(1)假设有N个历史日,首先分别将N个历史日和预测日各气象要素的采样点序列表示成{(i,ci)}i=1,…,k形式,其中i是按采样时间顺序排列的序列号,ci是采集数据的瞬时值,每隔15 min采样一次,则k=96。
(2)分别将风速、风向、温度、气压、相对湿度的采样点序列按式(11)归一化处理:
(11)
根据式(4)分别计算各历史日与预测日对应气象要素采样点序列的离散Fréchet距离di,j,获得的距离矩阵D如下:
D=[di,j],
(12)
式中:i=1,…,5为第i个气象要素;j=1,…,N为第j个历史日。
(3)根据距离矩阵D计算各历史日与预测日的整体相似度,为表征影响风机出力的关键因素在相似日判定中的主导作用,采用连乘的方式定义整体相似度公式,整体相似度公式如下:
(13)
(4)选取N个历史日中相似度最高的m日作为预测日的相似日样本。
2.2 特征提取
风机发电功率与各影响因素之间存在着复杂的非线性关系。KECA方法通过核函数把输入的数据映射到高维特征空间,进行非线性主元的提取,最大化保留了原始数据中的信息熵。
数据集X=[x1,x2,…,xm×96]为选取出来的m个相似日数据,xi表示为同时刻风速、风向、温度、气压、相对湿度构成的向量,则基于KECA方法的特征提取的具体步骤分为以下3步。
(1)选取径向基函数作为式(6)的核函数,并构造相应的核相关矩阵K,径向基函数表示为:
(14)
(2)对核矩阵K进行特征值分解,并根据式(8)对二次Renyi熵的估计,将核矩阵的特征值和相应的特征向量按估计值大小降序排列。
(3)确定非线性主元个数d,即将数据映射到由降序排列后的前d个特征值和特征向量所张成特征子空间中。根据式(9)求取产生的非线性映射。
2.3 预测模型建立
结合相似日的外推效果,KECA方法能够表征数据关于熵的内在结构及SVM处理小样本、高维度的优点,提出了基于相似日和特征提取的SVM短期风电功率预测模型,如图1所示。
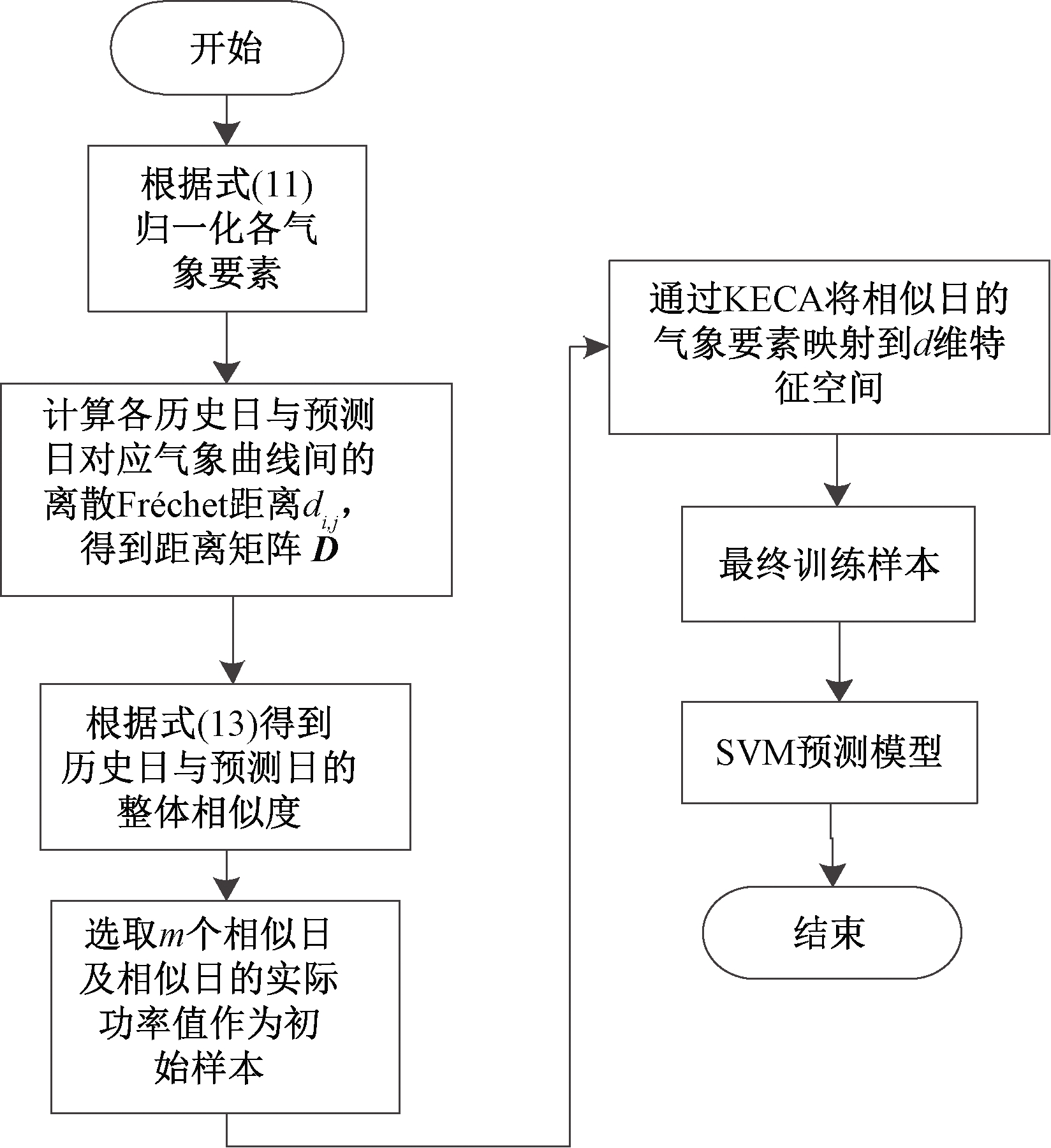
图1 预测流程图
Figure 1 Forecasting flow chart
将m个相似日的风速、风向、温度、气压、相对湿度及相应时刻的功率作为初始样本集,通过KECA方法对这5个气象要素的初始样本进行分析,提取出的非线性主元作为SVM模型的输入,输出为对应时刻的实际功率值,完成SVM预测模型的训练。预测时,需要根据式(10)将预测日的气象数据即风速、风向、温度、压力、相对湿度映射到KECA产生的特征子空间中,并将其作为预测时的输入。
3 算例分析
以8月27日为预测日,其余为历史日,利用所提出的匹配相似日的方法,可找出历史日中与预测日相似度最高的前m天。为确定m值,将m取值为1~15,分别使用相似日-KECA-SVM方法对预测日的功率进行预测。实验中,通过网格法求取径向基核函数的参数和非线性主元的个数。图2为预测结果的相对均方根误差(rRMSE)对比图。从图2可以看出,较少的相似日数量,无法代表样本空间的特征;当相似日选取较多时,存在冗余信息,不仅降低模型的预测性能,而且需要过多的训练时间。当m=7时,模型预测的效果相对较好,对应的径向基参数σ为4.5,非线性主元d为25。因此相似日为7 d,表2为这7个相似日与预测日的整体相似度计算结果。
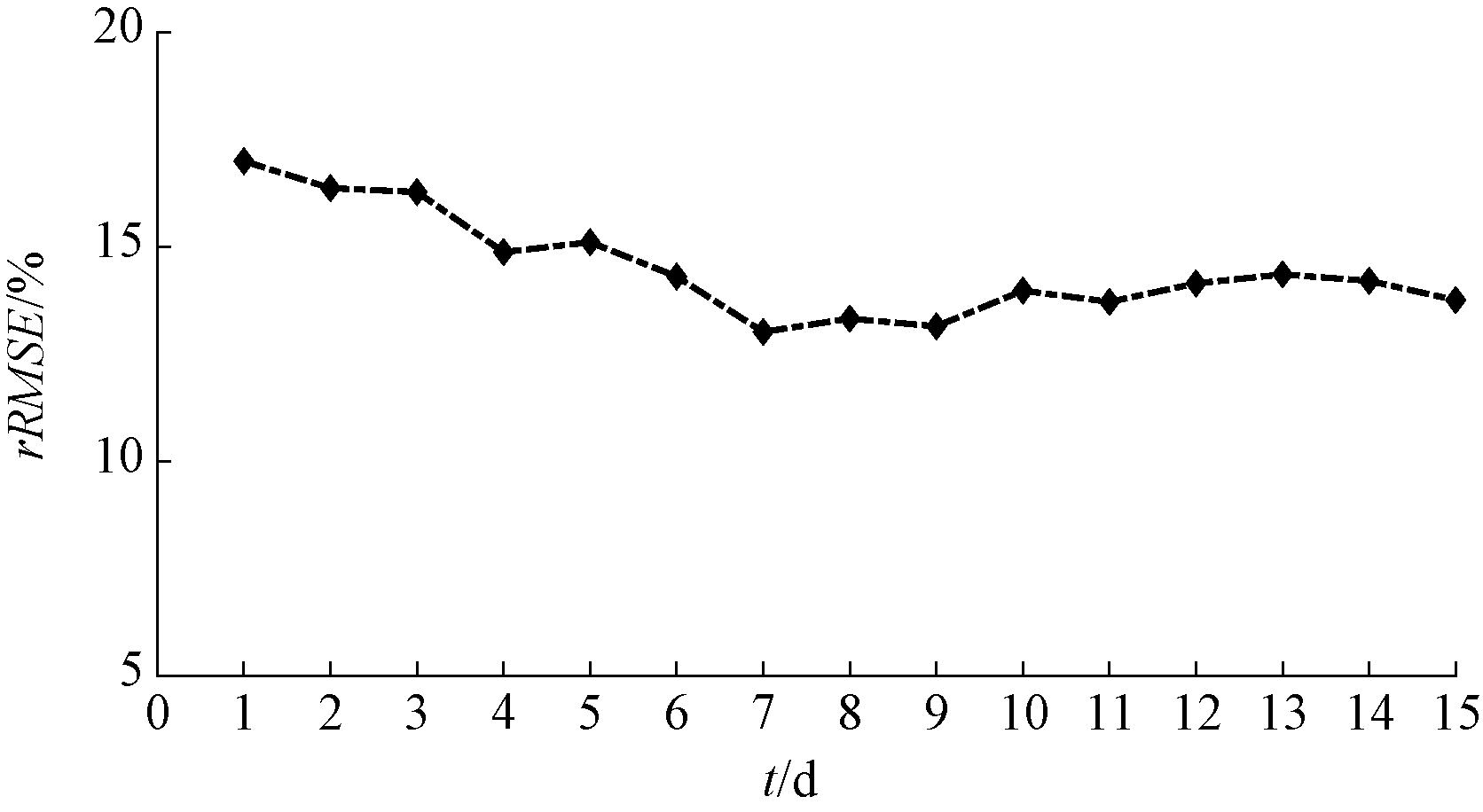
图2 不同数量的相似日预测误差对比
Figure 2 Comparison of prediction errors for different quantities of similar days
表2 整体相似度计算结果
Table 2 Calculation results of similarity degree
相似日07-0207-0307-0407-1908-0508-1108-18相似度0.1660.1840.1560.2050.1860.1620.180
图3为用离散Fréchet距离作为相似性判据提取出的相似日的风速曲线。图中每个采样点为每15 min采样一次。为了能清楚直观地比较,图中给出了较为相似的一条风速曲线。可以看出,提取出的相似日的风速曲线不仅在幅值上与预测日的风速曲线比较接近,而且整体的变化趋势上也大致相同。说明整体相似度的定义能够很好地表征风速的主导作用,而离散Fréchet距离作为曲线相似性的判据,能够充分考虑到风速整体走势的相似情况。选取相似日后,相似日和预测日的风速有了相似的变化趋势,天气状况也较为接近。
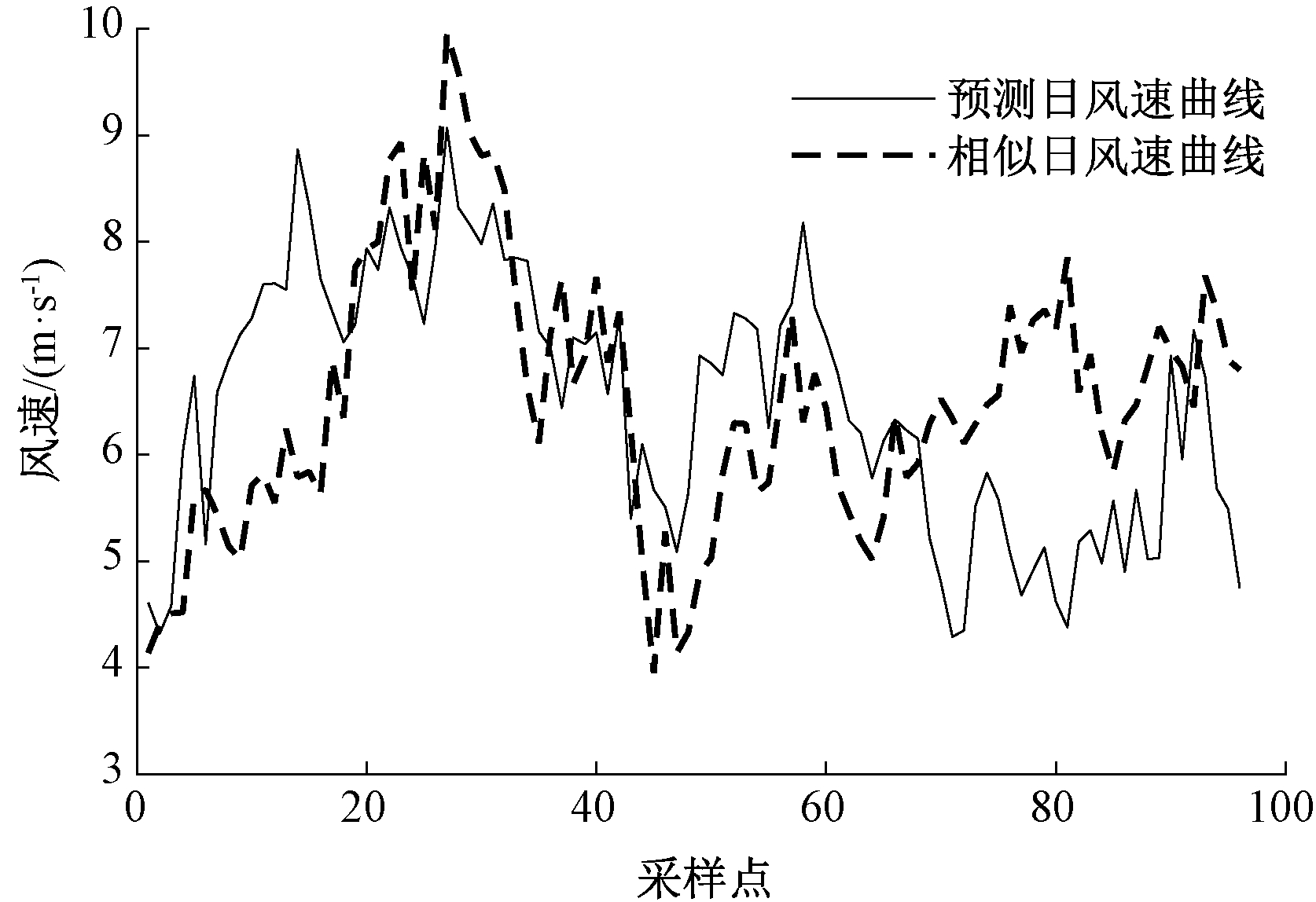
图3 相似日的风速曲线
Figure 3 Wind speed curve on similar days
为了验证相似日匹配和核熵成分分析方法的合理性和有效性,将以下3种预测方法进行对比。
方法1:SVM预测方法,即直接使用原始样本训练SVM模型,由于原始样本数据量大,模型的训练需要花费大量的时间。
方法2:相似日-SVM预测方法,即采用上述的相似日匹配的方法,从原始样本中提取相似日,将相似日的风速、风向、温度、气压、相对湿度和对应时刻的实际功率作为SVM的训练样本。
方法3:相似日-KECA-SVM预测方法,即在方法2的基础上将7个相似日的风速、风向、温度、气压、相对湿度及对应时刻的实际功率作为初始样本,并采用KECA方法提取相似日各气象要素的非线性主元,最后将d个主元作为SVM的输入节点和实际功率作为输出,完成SVM模型的训练。
上述3种方法的预测结果如图4所示。图中每个采样点为每15 min采样一次。结合图3可以看出,使用原始样本做预测时,单纯的SVM预测结果较差,大多数的预测值与实际值相比明显偏低。相似日-SVM预测方法过滤了原始样本中的冗余信息,使得相似日和预测日的气象信息较为接近,而且风速变化的整体趋势也较为吻合。预测的结果表明,在风速变化较大的时间段预测值更加接近实际观测值。相似日-KECA-SVM预测方法不仅在风速变化较大的时间段的预测精度得到提高,而且在风速变化幅度较小的时间段(即采样点为70~90)预测精度也有一定的提高。

图4 各方法风电功率预测值对比
Figure 4 Comparison of predicted values of different methods
图5为3种方法预测的绝对误差,图中每个采样点为每15 min采样一次。从中可以看出单纯地使用支持向量机作预测,其绝对误差的波动范围较大,出现较大误差的次数较多。经过相似日方法处理后,误差波动范围变小,尤其在风速波动较大的时间段,出现较大误差的次数也较少。而经过相似日匹配和核熵成分分析后,预测效果最好。
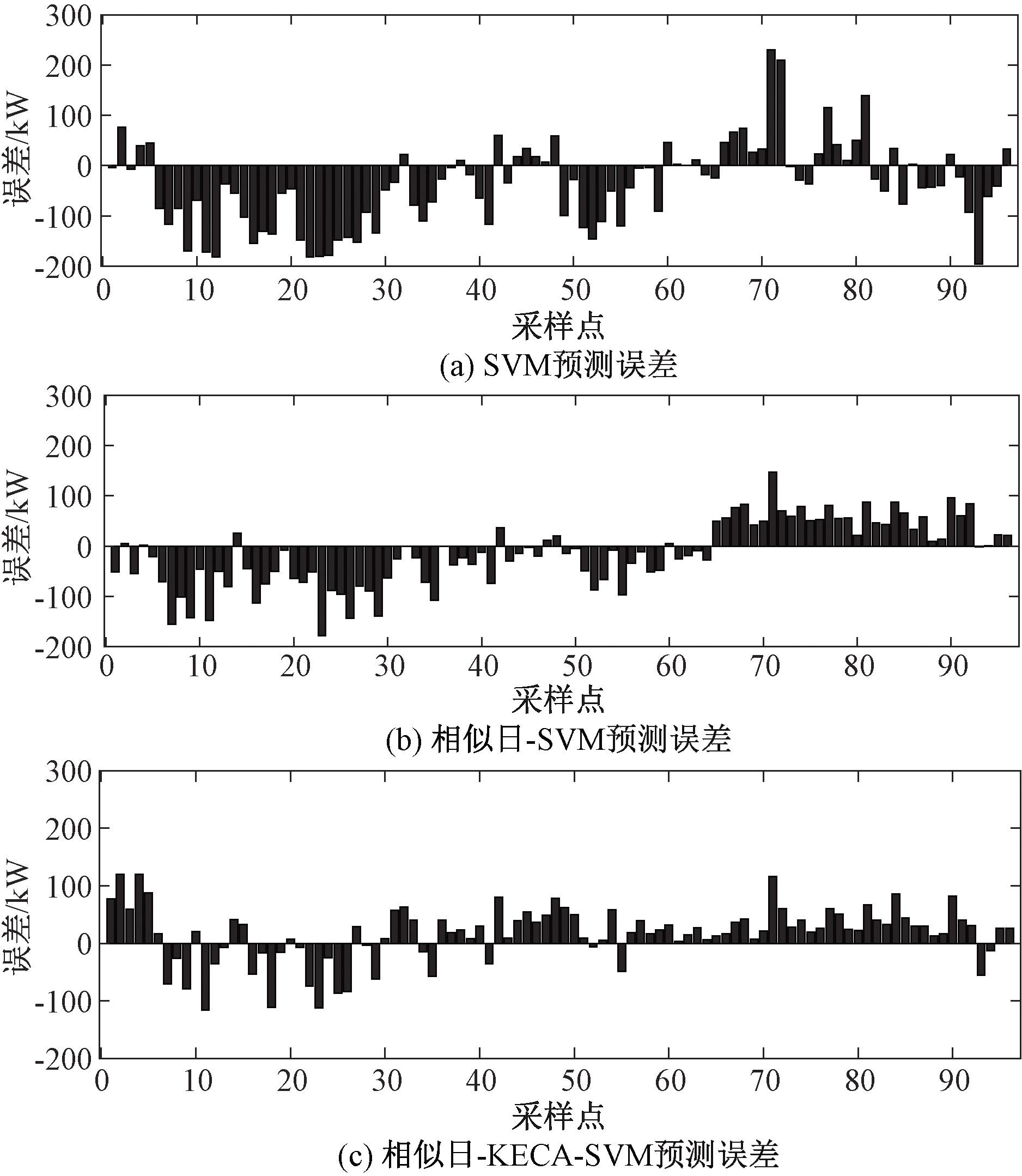
图5 各种方法预测的绝对误差
Figure 5 Prediction absolute error of various methods
分别采用相对平均绝对误差(rMAE)、相对均方根误差(rRMSE)和均方根误差(RMSE)作为评价各方法预测效果的指标,各误差计算结果如表3所示。
表3 各方法预测误差比较
Table 3 Comparison of prediction errors
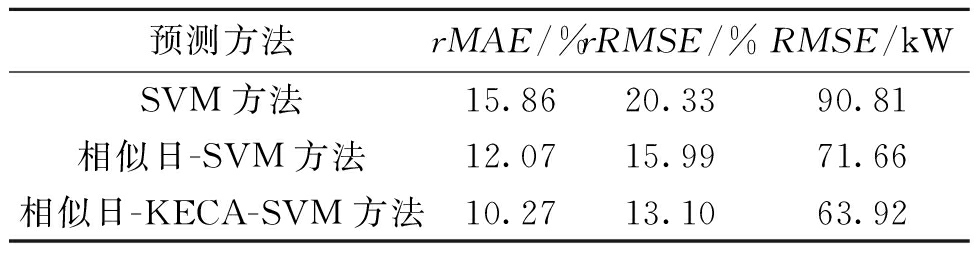
预测方法rMAE/%rRMSE/%RMSE/kWSVM方法15.8620.3390.81相似日-SVM方法12.0715.9971.66相似日-KECA-SVM方法10.2713.1063.92
从表3可以看出,经过相似日的匹配和核熵成分分析后,各个误差指标都有不同程度的降低。相比于使用全部样本,相似日-KECA-SVM预测效果更好,说明所提出的相似日匹配方法和核熵成分分析方法能够有效提高建模数据的相似性,从而降低误差。
4 结论
结合相似日原理和核熵成分分析方法对中国云南某风电场的采集数据进行预处理,主要优点如下:
(1)风速是影响风机出力的关键因素,其变化趋势在相似日判定中至关重要,通过离散Fréchet距离判别曲线相似性的方法来匹配相似日,有效兼顾了风速的变化趋势。相似日的选取增强了数据的相关性,提高了模型的预测精度。
(2)风机出力和各影响因素之间存在着复杂的非线性关系,经过核熵成分分析后在高维特征空间能更好地呈现数据集的特点,有利于预测精度的提高。
(3)针对风力发电的周期性不太明显、相似日出现的频率较低的情况,结合SVM具有支持小样本建模和较强的非线性学习等特点,建立的短期风电功率预测模型具有较好的泛化能力。
[1] 王健, 严干贵, 宋薇,等. 风电功率预测技术综述[J]. 东北电力大学学报, 2011, 31(3):20-24.
[2] 李军, 卓泽赢. 基于经验小波变换和多核学习的风电功率短期预测[J]. 信息与控制, 2018, 47(4):437-447.
[3] 孙晓燕, 时良振, 徐瑞东,等. 基于区间样本和回声状态网络的风电功率不确定性预测[J]. 郑州大学学报(工学版), 2017, 38(1):56-62.
[4] 阎洁, 许成志, 刘永前,等. 基于风速云模型相似日的短期风电功率预测方法[J]. 电力系统自动化, 2018, 42(6):53-59.
[5] 孟洋洋, 卢继平, 孙华利,等. 基于相似日和人工神经网络的风电功率短期预测[J]. 电网技术, 2010, 34(12):163-167.
[6] 倪鹏, 孙富荣. 基于相似日和风速连续性的风电场短期功率预测[J]. 山东电力技术, 2016, 43(11):39-43.
[7] 张宜阳, 严欢. 基于分段分层相似日搜索和自适应脊波神经网络的风电功率多步预测[J]. 电网与清洁能源, 2015, 31(4):124-131.
[8] YESILBUDAK M. Clustering analysis of multidimensional wind speed data using K-means approach[C]//2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA).Birmingham, United Kingdom: IEEE, 2016: 961-965.
[9] 丁志勇, 杨苹, 杨曦,等. 基于连续时间段聚类的支持向量机风电功率预测方法[J]. 电力系统自动化, 2012, 36(14):131-135.
[10] 郑婷婷, 王海霞, 吕泉,等. 基于相似日选取样本的短期风电功率混沌预测[J]. 电网与清洁能源, 2013, 29(3):74-79.
[11] 郁琛, 薛禹胜, 文福拴,等. 按时序特征优化模型后在线选配的超短期风电预测[J]. 电力系统自动化, 2015, 39(8):5-11.
[12] GANGER D, ZHANG J S, VITTAL V. Statistical characterization of wind power ramps via extreme value analysis[J]. IEEE transactions on power systems, 2014, 29(6):3118-3119.
[13] 叶小岭, 陈浩, 郭晓杰,等. 基于风速升降特征的短期风电功率预测[J]. 电力系统保护与控制, 2016, 44(19):56-62.
[14] ALT H, GODAU M. Computing the Fréchet distance between two polygonal curves[J]. International journal of computational geometry & applications, 1995, 5(1/2):75-91.
[15] EITER T, MANNILA H. Computing discrete fréchet distance[R]. Viena: Information System Department, Technical University of Vienna, 1994.
[16] 李思同, 庄强, 金琳,等. 基于时频特征核熵成分分析的局部放电模式识别方法[J]. 高压电器, 2018,54(6):125-131.
[17] 彭怀午, 杨晓峰, 刘方锐. 基于SVM方法的风电场短期风速预测[J]. 电网与清洁能源, 2009, 25(7):48-52.
[18] CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J]. ACM transactions on intelligent systems and technology, 2011, 2(3): 27.