0 引言
多目标优化问题是指目标函数数量为2～3个的优化问题[1-3]。一般情况下，多目标优化问题不同目标之间具有相互冲突的特点，即一个目标性能增加会导致另外一个目标性能降低。为求解此类优化问题，许多学者提出了有效的求解算法，如NSGA-II[4]、SPEA2[5]、PEASII[6]以及最近提出的MOEAIGDNS[7]等。NSGA-II[4]是Deb等于2002年提出的算法。由于其在多目标优化问题上较优的求解性能引起了广大研究者关注，并被应用到许多实际工程优化问题中。根据不同研究角度，可将近些年对NSGA-II的研究做如下分类。
优化NSGA-II中支配关系，进一步拓展算法求解问题范围。针对实际工程领域中复杂非线性多目标优化问题，赖文星等[8]发现NSGA-II无法有效识别伪非支配解。为解决此类问题，赖文星等[8]采用快速支配强度排序法构造非支配集,引入基于方差的拥挤距离公式,并通过自适应精英保留策略动态调整精英保留规模。为在理论上解决NSGA-II中Pareto支配在高维多目标优化问题上无法区分有效解的问题，Yang等[9]提出利用基于网格的支配方法来区分不同个体，并利用网格产生待交叉父代个体。同样为解决此类问题，Zhang等[10]则提出基于分解的进化算法，即将多目标优化问题分解为多个单目标优化问题，有效避免了多目标优化问题中支配关系，提升了算法的收敛性能。
针对实际工程应用问题特点，改善算法适用性，郝志宽等[11]针对车辆悬架系统中多目标优化问题特点，提出引入精英保持策略,去除重复个体,减少变量重复性,有效提高了算法的效率。面向特定区域部署的临近空间通信网络需要兼顾考虑资源分配、覆盖率及载荷功率等多个因素，为了针对性优化此类复杂问题，唐树祝等[12]将动态反向学习机制和差分局部变异算子引入NSGA-II，为网络实际部署提供了参考。为应对跨区域突发事件过程中受灾点服务差异化需求问题,宋艳等[13]通过设计分段染色体编码方式改进NSGA-Ⅱ算法，提升运算效率，并且有效地解决了多目标选址决策问题。
虽然NSGA-II在理论以及应用方面[14]已有广泛研究，但其采用的锦标赛选择策略(tournament selection)会产生大量重复个体，从而导致后代种群多样性受到影响。针对此类问题，笔者设计具有维度扰动策略的NSGA-II(non-dominated sorting genetic algorithm II based on dimensionality perturbation, DPNSGA-II)，该算法通过采用对部分维度进行扰动的方法消除重复个体，从而有效地提高了算法的整体性能。
1 基本概念以及锦标赛选择策略
1.1 基本概念
笔者考虑如下多目标优化问题[15]：
(1)
式中：
表示第i个目标函数
为决策变量空间。
定义1：若变量
目标函数为
变量
目标函数为
当且仅当对于
成立，且存在k∈{1,2,…,M}，使得
严格成立，则称
支配
记作：
定义2：决策空间上所有pareto最优解构成的集合称为pareto最优解集(pareto set)。
定义3：pareto最优解集在目标空间上对应点集称pareto前沿面(pareto front)。
1.2 锦标赛选择策略以及分析
NSGA-II[4]是多目标优化算法中经典的算法,其涉及快速非支配排序、锦标赛选择策略(tournament selection)、交叉算子、变异算子以及拥挤度距离等多种策略。NSGA-II中种群个体间进化压力以及多样性保持策略主要依赖快速非支配排序以及拥挤度距离的方法。锦标赛选择策略是NSGA-II算法中用于选择待交叉父代个体的主要方法，如图1所示。首先从种群中以等概率选择个体，然后从所选个体中选择最优个体作为父代个体，按照上述方法多次选择即可产生多个交叉父代。从上述过程可看出，若个体Ii为种群中第一层非支配个体，则其有很大概率在多次选择较优个体时被再次选中，从而导致出现多个重复个体现象。
图1 锦标赛选择策略说明
Figue 1 Illustration of tournament selection
图2为运行NSGA-II 算法时，运用锦标赛选择策略单个个体每代最大重复次数统计，图3为算法运行到70代时运用锦标赛选择策略所产生重复个体数量统计，其中运行条件为种群个体数量为100，算法运行80代，测试函数为ZDT1(请见实验部分)。从图2可以看出，算法NSGA-II计算过程中每代都会出现每个个体5次的重复次数，最大出现10次重复。从图3可看出，就某一代重复个体而言，较优个体出现4次，甚至最高出现10次重复次数。若每个个体均按照上述数量重复，则可导致后代个体多样性变差以及算法整体性能降低。
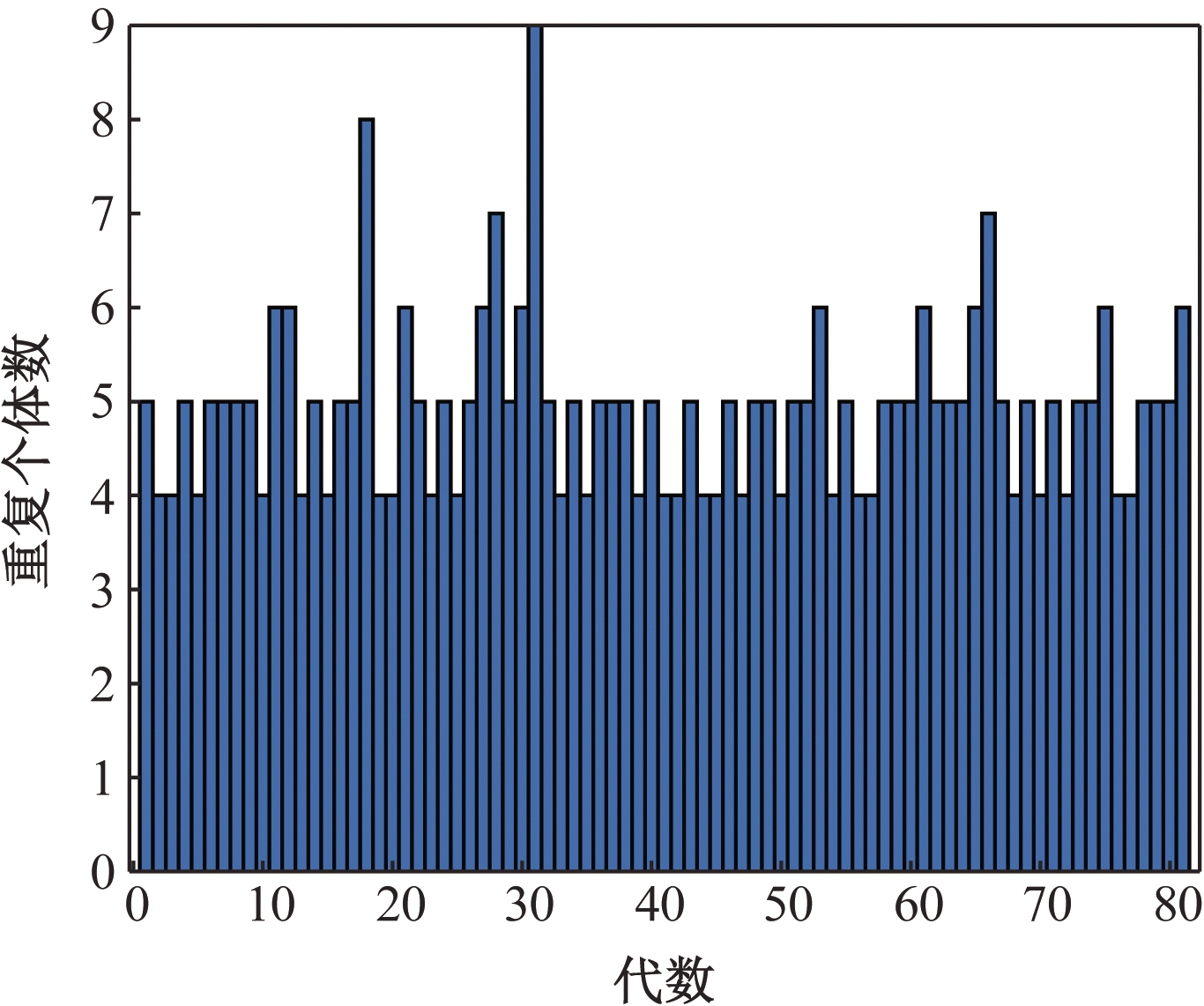
图2 每代重复个体统计
Figue 2 Statistics of repeated individual per generation
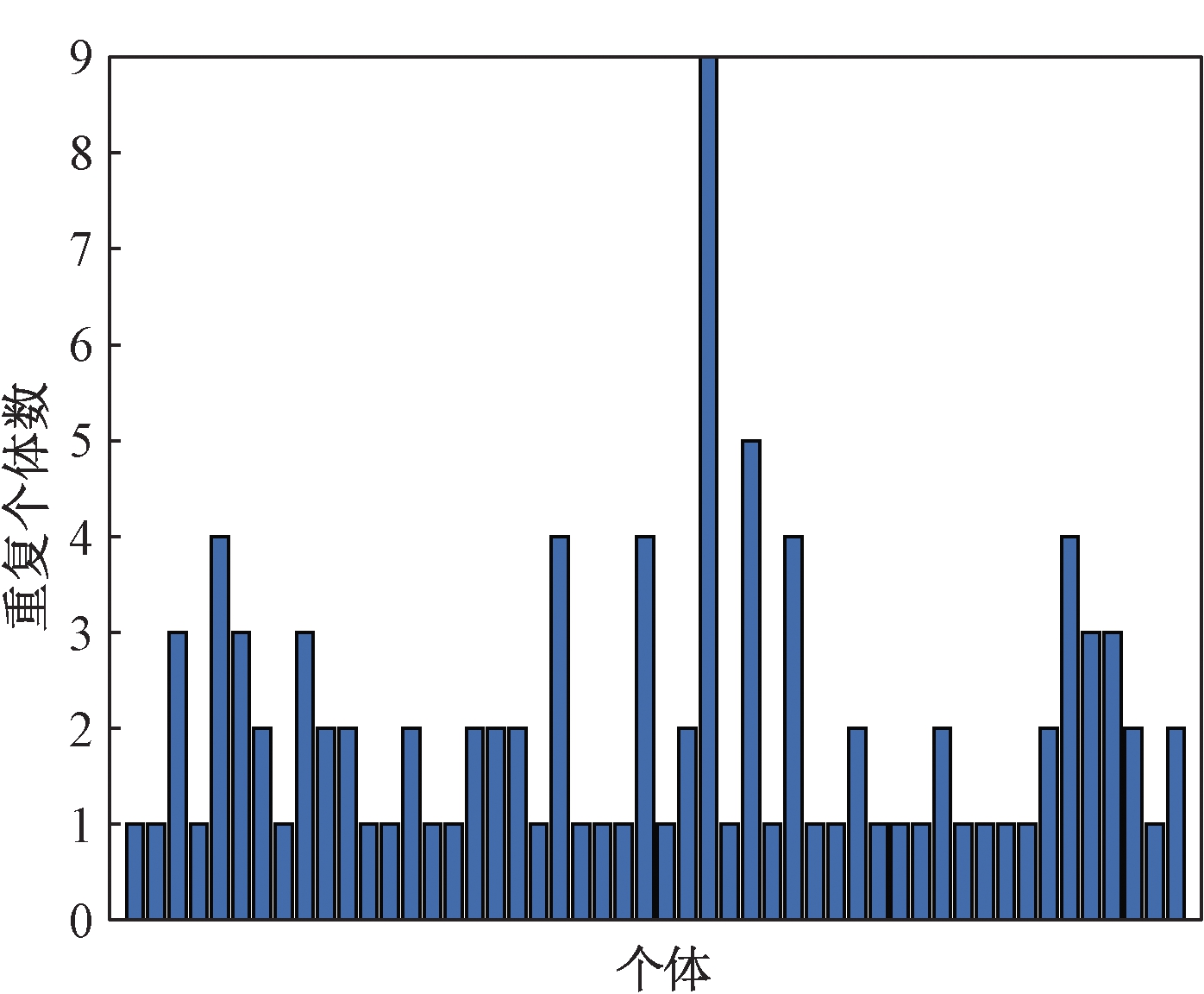
图3 第70代重复个体数量统计
Figue 3 Statistics of repeated individuals at 70th generation
2 维度扰动策略
为解决个体重复问题，笔者提出基于维度扰动策略的NSGA-II。设Ii和Ij为锦标赛选择算法挑选出的待交叉父代，⊗为父代个体间的交叉操作。则Ii=(x1,x2,…,xD)(D为个体变量维度)按照如下方式产生扰动个体
第i维度：
(2)
式中：normrnd(·)表示以xi为均值，
为方差的正态分布函数；ri为随机产生0或1随机数；λ为参数，可取值1.0E-02、1.0E-03、1.0E-04、1.0E-05，后续实验将详细验证；xupper、xlower分别为xi取值上界和下界；N为种群个体。则个体
可表示为：
(3)
同理，可得出个体
则产生的后代个体可表示为：
(4)
如图4所示为个体Ii第i维度xi扰动示意图。从图4可以看出，局部扰动可产生以xi为期望，riλ为方差的正态分布随机数
当ri为0时，表示个体Ii第i维度xi保持不变；当ri为1时，表示个体Ii第i维度xi按照上述方式产生扰动值与标准锦标赛选择策略相比，基于维度扰动策略可以有效减少重复个体数量，同时可以扩大后代搜索范围，增加了后代多样性。
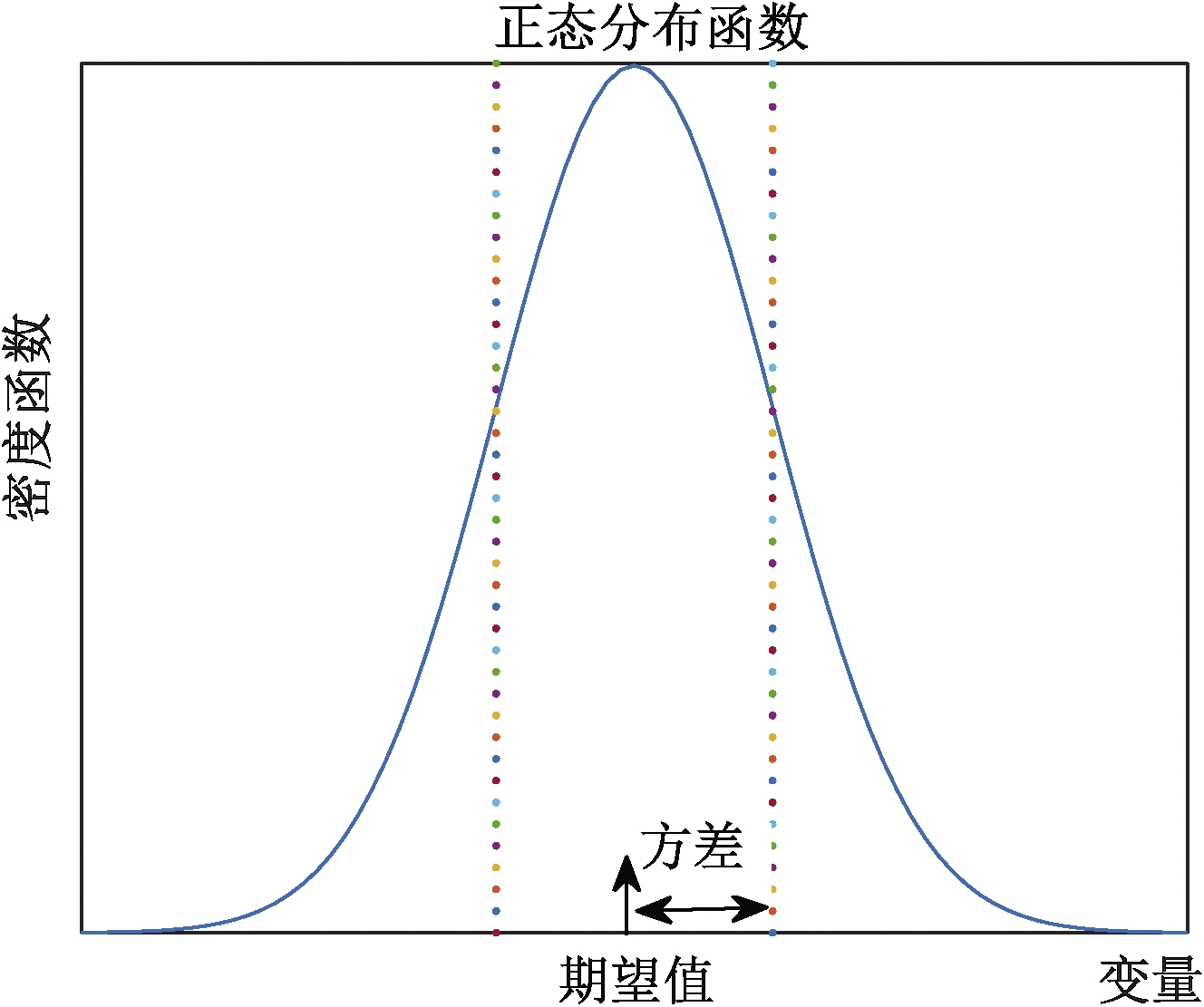
图4 维度扰动示意图
Figue 4 Illustration of dimensionality perturbation
3 实验结果及分析
为验证笔者所提算法性能，本部分实验为两小部分：
(1)第一部分验证笔者所提算法参数λ取1.0E-02、1.0E-03、1.0E-04、1.0E-05对算法性能的影响；
(2)第二部分将笔者所提基于维度扰动的NSGA-II与传统算法SPEA2[5]、PEASII[6]以及最近提出的算法MOEAIGDNS[7]做对比。表1列出了上述不同算法运行所需参数。其中pc为交叉概率；pm表示变异概率；D为测试函数变量维度。div为每个目标分量个数。注意，所有参数设置均按照原始参考文献设置，有兴趣读者请参阅文献[5-7]。
表1 算法参数说明
Table 1 Illustration of Parameters of different algorithms
算法参数设置NSGA-IIpc=1,pm=1/DDPNSGA-IIpc=1,pm=1/DSPEA2pc=1,pm=1/DMOEAIGDNSpc=1,pm=1/DPEASIIdiv=10
(3)展示种群多样性指标与个体进化代数之间的关系图，并进一步分析验证本文前述维度扰动策略所起作用。
为了综合测试算法性能，笔者采用ZDT测试函数集[16]，如表2所示。ZDT测试函数集由Zitzler和Deb在2000年提出，这些函数具有凸、凹、连续、非连续和具有多重局部最优等特点，评价指标采用IGD[17]。
实验所用计算机为Inter Core i 5-2400 3.10 GHz CPU, 6.00 GB内存，Windows7操作系统，运行环境为Matlab7.9。每个算法独立运行20次，算法最大迭代100次，种群个体为50。
3.1 参数.对算法影响
表2所示为不同λ取值对本文算法的影响，其中每个取值为算法独立运行20次IGD均值。最后一行为Friedman检验结果ranking值(排序值)，值越小表示算法性能越优，Friedman检验是对每个算法运行20次的IGD均值计算得出的，最优值用黑体显示。对比算法的方式为首先通过比较不同算法在各个测试函数集上的IGD均值以及在整个测试函数上占优的总数，然后进一步比较Friedman检验结果，综合以上方法得出最优算法。
表2 实验算法所求平均IGD对比
Table 2 Comparison of average IGD obtained by experimental algorithms
函数集λ=1.0E-05λ=1.0E-04λ=1.0E-03λ=1.0E-02ZDT18.59E-017.48E-019.24E-019.26E-01ZDT21.20E+001.44E+001.03E+001.20E+00ZDT39.13E-016.51E-017.26E-011.03E+00ZDT47.09E-017.77E-017.93E-018.60E-01ZDT65.00E-014.79E-014.89E-013.52E-01ranking值3.202.603.003.60
从表2可看出，λ=1.0E-04时分别在ZDT1、ZDT2、ZDT4表现较优，在ZDT2和ZDT6表现略差。从Friedman检验结果来看，λ=1.0E-04时具有最小检验值。因此，综合而言，当λ=1.0E-04时本文算法具有较优性能。下面实验将采用λ=1.0E-04作为算法DPNSGA-II参数。
3.2 与现有算法对比
表3列出了笔者所提算法与NSGA-II、PEASII、SPEA2、MOEAIGDNS对比结果，其中“均值”表示算法运行20次的IGD平均值，“方差”表示算法20次求解IGD结果“方差”。最后一行为Friedman检验结果ranking值，其由在每个测试函数上对每个算法运行20次的IGD均值计算得出。
从表3可以看出，与NSGA-II相比，笔者所提算法在ZDT1、ZDT2、ZDT3、ZDT4上均表现较优，说明笔者所提基于维度扰动的策略有效地改善了算法性能。与其他算法相比，笔者所提算法在ZDT3上超过SPEA2性能。就Friedman测试结果而言，笔者所提算法具有较小ranking值，说明本文算法整体性能较优。
图5展示算法DPNSGA-II、NSGA-II以及真实前沿面在不同测试函数上的对比效果。从图5可以看出，在收敛性方面，算法DPNSGA-II与NSGA-II在ZDT1测试函数上有明显差距；在ZDT2上，算法NSGA-II所求结果均匀性稍差于DPNSGA-II。在ZDT3和ZDT6测试函数上可明显看出，NSGA-II算法在某些点上存在明显偏离真实pareto前沿面(true pareto front)的个体。在ZDT4上的两个算法性能表现可以充分说明改进算法DPNSGA-II有效地改善了NSGA-II 收敛性，提高了算法的整体性能。
表3 不同算法获得的IGD值
Table 3 IGD results of Different algorithms
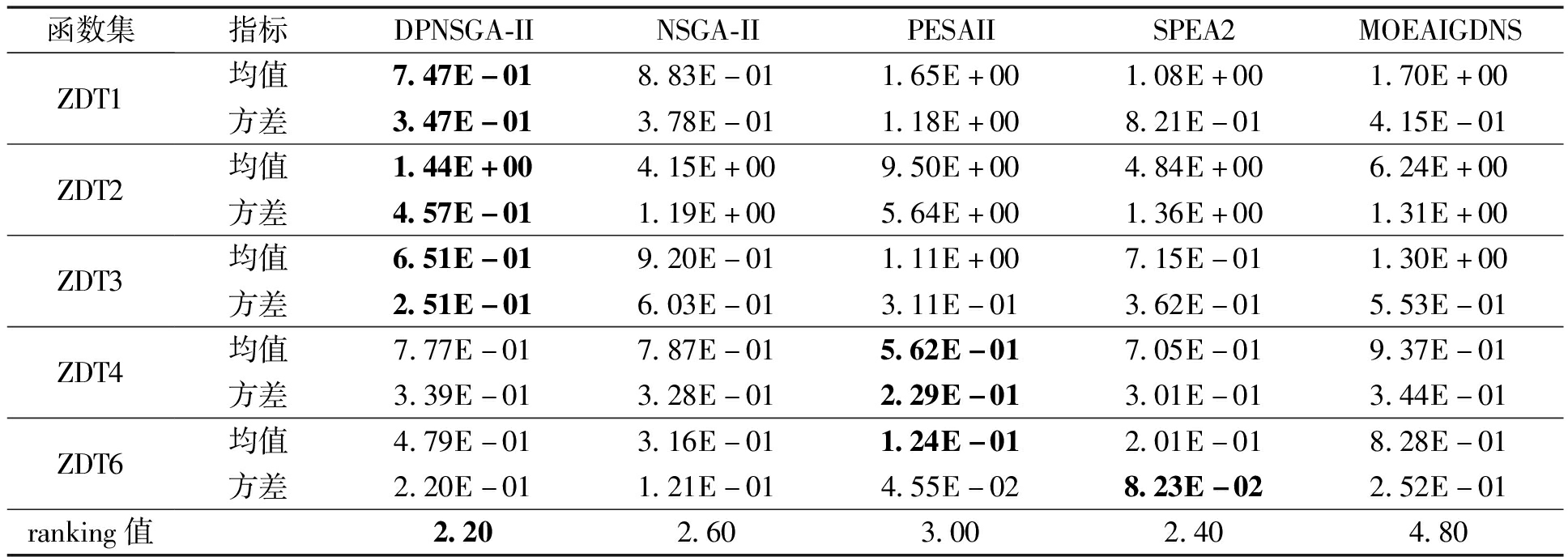
函数集指标DPNSGA-IINSGA-IIPESAIISPEA2MOEAIGDNSZDT1ZDT2ZDT3ZDT4ZDT6ranking值均值7.47E-018.83E-011.65E+001.08E+001.70E+00方差3.47E-013.78E-011.18E+008.21E-014.15E-01均值1.44E+004.15E+009.50E+004.84E+006.24E+00方差4.57E-011.19E+005.64E+001.36E+001.31E+00均值6.51E-019.20E-011.11E+007.15E-011.30E+00方差2.51E-016.03E-013.11E-013.62E-015.53E-01均值7.77E-017.87E-015.62E-017.05E-019.37E-01方差3.39E-013.28E-012.29E-013.01E-013.44E-01均值4.79E-013.16E-011.24E-012.01E-018.28E-01方差2.20E-011.21E-014.55E-028.23E-022.52E-012.202.603.002.404.80
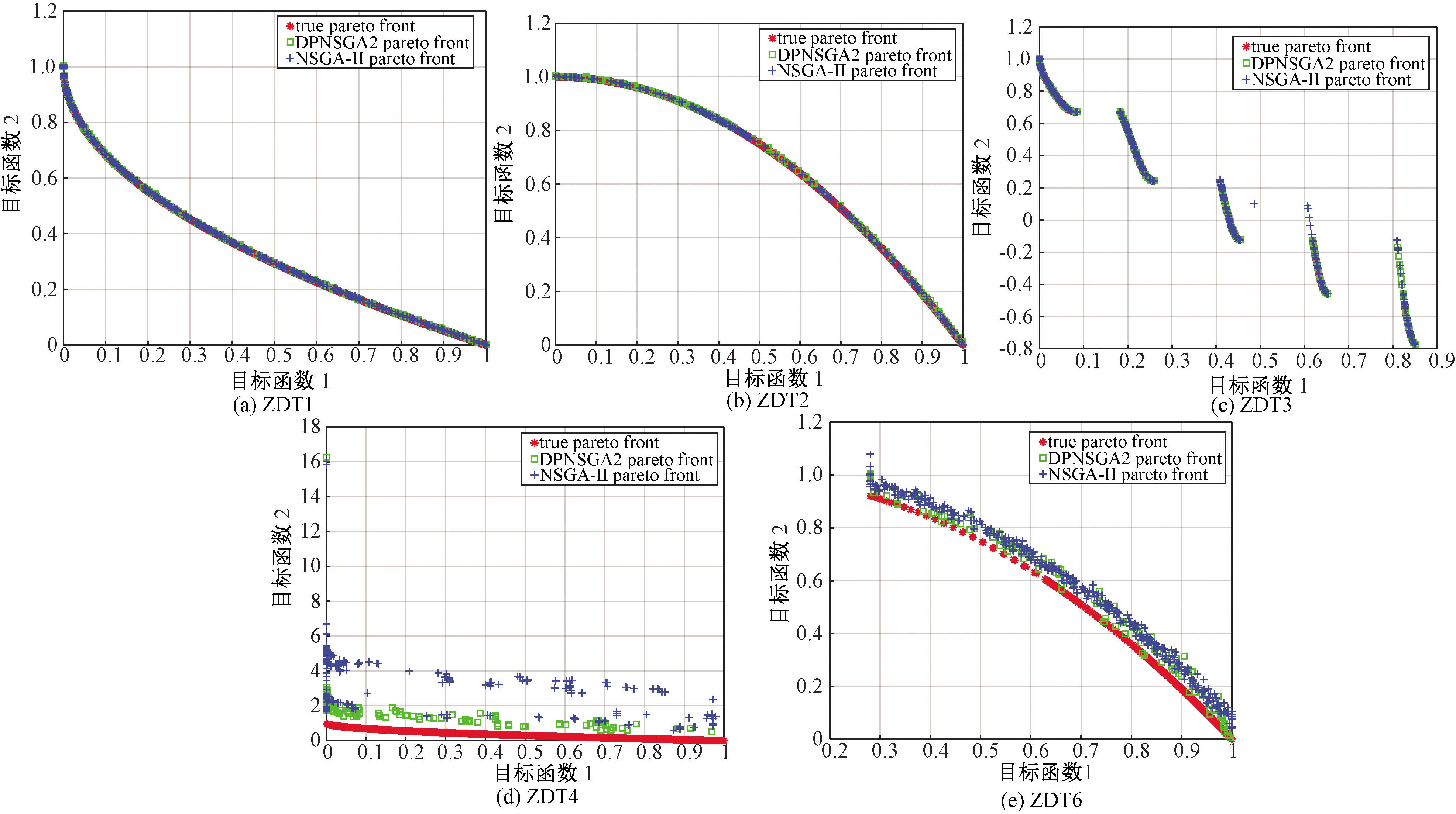
图5 不同算法pareto前沿面对比
Figue 5 Comparison of different Pareto fronts
3.3 种群多样性指标分析
图6展示了DPNSGA-II和NSGA-II算法在运行过程中种群多样性变化趋势，其中横坐标表示算法评价次数(即种群个体与算法运行代数的乘积，此方式相比于以代数更加精细反应种群多样性的变化)，纵坐标表示多样性指标，所用测试函数为ZDT1。
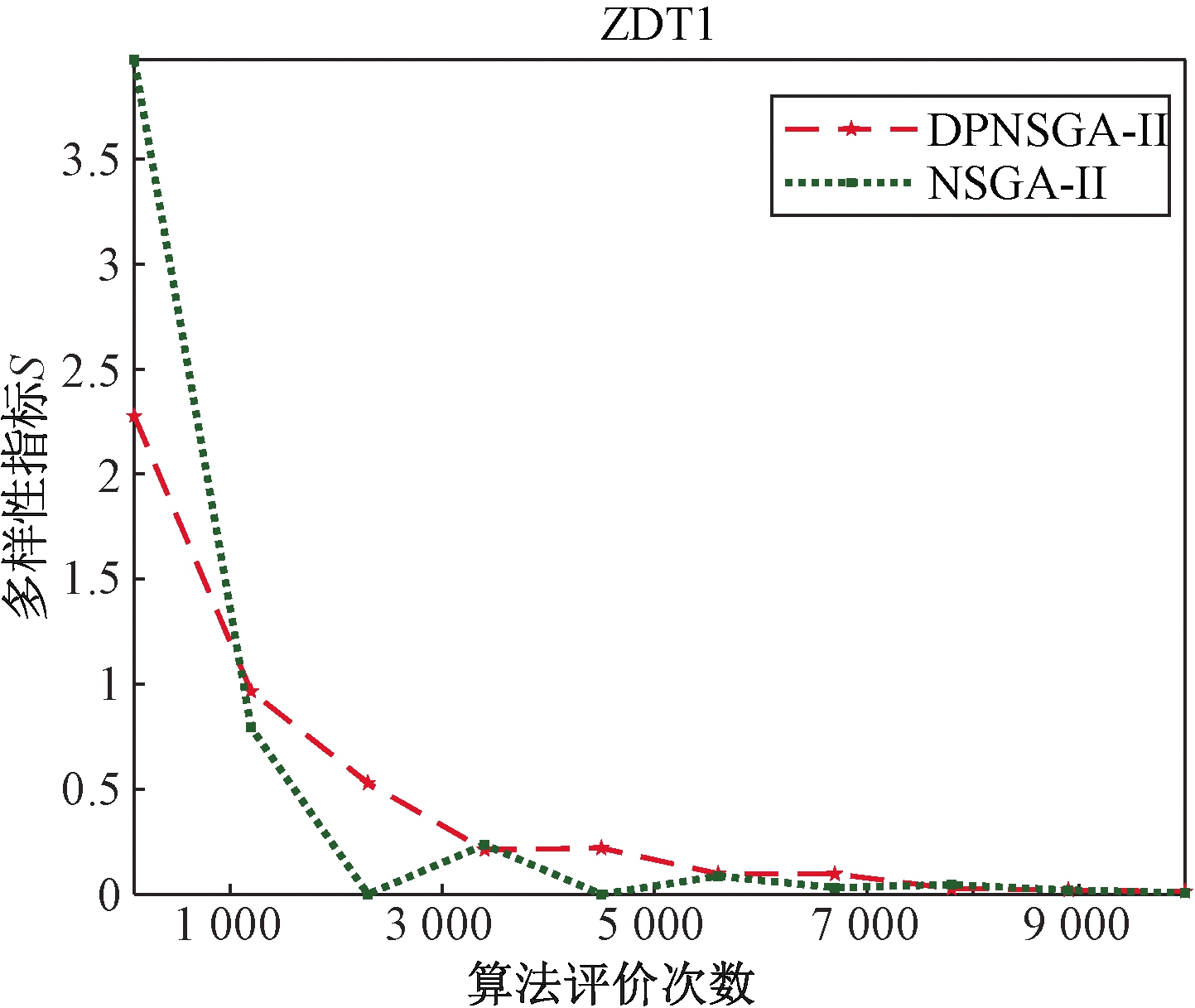
图6 种群多样性随代数变化趋势说明
Figue 6 Illustration of the diversity of population with evolution of generation
根据第二部分介绍的扰动策略，该方法可以有效减少重复个体数量。从图6种群多样性变化趋势对比可以看出，笔者提出的DPNSGA-II 算法在运行初期相对于NSGA-II多样性较差，其原因是在初始化种群时，种群个体间本身具有较大距离，且分布相对均匀，此时笔者所提维度扰动策略只能在个体附近产生扰动，并未产生明显效果。随着种群个体不断进化，在算法运行到1 000次评价时，DPNSGA-II对应种群多样性明显优于NSGA-II对应种群性能，并一直保持到算法运行结束。在1 000次评价之后，个体不断逼近真实pareto前沿面，同时，个体间距离不断缩小，此时维度扰动策略产生作用，使得种群多样性保持在一定程度，有利于种群向更优的方向进化。
基于以上讨论，综合比较而言，笔者所提算法DPNSGA-II通过降低算法重复个体的方式，有效改进了算法整体性能，证明笔者所提改进策略的有效性。
4 结论
锦标赛选择策略是NSGA-II用于选择产生后代的策略，由于其固有缺陷导致产生大量重复个体。为了解决此问题，笔者提出了基于维度扰动的策略，即通过以当前父代位置为期望，融入方差参数的正态分布函数进行扰动，以此消除重复个体现象。通过实验数据可以说明，提出的基于维度扰动的策略可以有效地提升算法性能，达到了预期的效果。后期研究工作将专注于NSGA-II算法性能的进一步提升。
[1] ZHANG M Q, WANG H, CUI Z H, et al.Hybrid multi-objective cuckoo search with dynamical local search[J].Memetic computing, 2018, 10(2):199-208
[2] CHENG R, JIN Y C, OLHOFER M, et al.A reference vector guided evolutionary algorithm for many-objective optimization[J].IEEE transactions on evolutionary computation, 2016, 20(5):773-791.
[3] ZHANG M Q, ZHU Z H, CUI Z.H, et al.NSGA-II with local perturbation[C]// 29th Chinese Control and Decision Conference.Chongqing:IEEE, 2017:208-213.
[4] DEB K, PRATAP A, AGARWAL S, et al.A fast and elitist multi-objective genetic algorithm: NSGA-II[J].IEEE transactions on evolutionary computation, 2002, 6(2): 182-197.
[5] ECKART Z, MARCO L, LOTHAR T.SPEA2: improving the strength pareto evolutionary algorithm[J].TIK-report,2001,103:95-100.
[6] CORNE D W, JERRAM N R, KNOWLES J D,et al.PESA-II: region-based selection in evolutionary multi-objective optimization[C]// Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation.San Francisco: Morgan Kaufmann, 2001:283-290.
[7] TIAN Y, ZHANG X Y, CHENG R, et al.A multi-objective evolutionary algorithm based on an enhanced inverted generational distance metric[C]// IEEE Congress on Evolutionary Computation.Vancouver:IEEE, 2016:5222-5229.
[8] 赖文星,邓忠民.基于支配强度的NSGA2改进算法[J].计算机科学, 2018,45(6):187-192.
[9] YANG S X, LI M Q, LIU X H, et al.A grid-based evolutionary algorithm for many-objective optimization[J].IEEE transactions on evolutionary computation, 2013, 17(5): 721-736.
[10] ZHANG Q F, LI H.MOEA/D: a multi-objective evolutionary algorithm based on decomposition[J].IEEE transactions on evolutionary computation, 2007, 11(6): 712-731.
[11] 郝志宽.基于灵敏度分析及改进遗传算法的悬架优化和整车操纵稳定性分析[D].重庆:重庆理工大学, 2018.
[12] 唐树祝, 游鹏, 闫大伟, 等.基于改进NSGA2的临近空间通信网络优化设计[J].计算机工程与应用, 2018, 54(14): 203-210.
[13] 宋艳,滕辰妹,姜金贵.基于改进NSGA-Ⅱ算法的多级服务设施备用覆盖选址决策模型[J].运筹与管理,2019, 28(1):71-78.
[14] 李章晓,宋微,田野.基于深度学习和进化计算的外汇预测与投资组合优化[J].郑州大学学报(工学版), 2019, 40(1):92-96.
[15] YANG X S.Bat algorithm for multi-objective optimization[J].Bio-inspired computation, 2012, 3(5): 267-274.
[16] ZITZLER E, DEB K, THIELE L.Comparison of multiobjective evolutionary algorithms: empirical results[J].Evolutionary computation, 2000, 8(2):173-195.
[17] LI M Q, ZHENG J H.Spread assessment for evolutionary multi-objective optimization[C]//Proceedings of 5th International Conference on Evolutionary Multi-Criterion Optimization.Nantes:Springer,2009:216-230.