0 引言
与交叉口的交通运行不同,出入口是城市道路路段上的重要接入点,其数量及间距是城市道路路段通行能力的重要影响因素之一。为此,GB/T 36670—2018《城市道路交通组织设计规范》[1]规定,出入口数量不宜过多,并应保持适当间距,且应根据实际采取让行、右进右出等交通组织方式。GB/T 51328—2018《城市综合交通体系规划标准》[2]提出,车辆通过固定的接入点进入沿线用地时,接入点密度为2~3个/km。但这些规定均为定性描述或者建议,从而导致在工程实践中,由于交通影响分析时缺少定量化的评价方法,使得经常存在路段出入口数量过多、间距偏小亦或位置不尽合理的情况,严重影响道路交通的运行,导致通行能力降低,道路功能实现程度低。
国内外关于路段通行能力折减的问题研究较多,然而均未考虑出入口数量的影响。Chen等[3]研究了混合车流对左转机动车道通行能力的影响;邓社军等[4-5]研究了单个路外停车出入口的车辆从最右侧车道右转驶离主路进入停车场的过程对于上游运行车辆的影响区长度,以及路外停车驶入对主路路段交通流的影响模型;唐伯明等[6]研究了车辆进出不同方式及不同规模停车场时对路段通行能力的影响;Cao等[7]研究了路边停车对路段通行能力的影响;秦丽辉等[8-9]提出了城市干路路段实际通行能力计算与服务水平评价的平行式公交停靠数量修正系数与阈值建议,并采用回归分析的方法计算了城市干路路段实际通行能力的路侧自行车数量修正系数。亦有研究侧重于交通组织的优化设计,以期提高道路路段的通行能力。蔡建荣等[10]基于通行能力的折减程度建立了可变车道的优化方法,以解决潮汐现象所引起的交通拥堵及道路资源闲置问题。Tang等[11]建立了考虑道路通行能力的宏观交通流模型。
基于此,笔者构建了出入口影响下的路段通行能力的计算模型,并将其应用于出入口位置优化中,以期为出入口位置的设置提供技术支持。
1 考虑出入口干扰的路段通行能力
在城市道路的路段上设置出入口,出入口车道与路段邻近车道(简称为最外侧车道)形成交叉,使该车道的设计连续交通流变为间断交通流,导致基本通行能力的折减,且在同一路段上出入口设置越多,基本通行能力折减愈大。将该影响采用最外侧车道出入口物理修正系数进行表征。
在交通运行阶段,当某出入口有车辆驶入和驶出时,将导致最外侧车道上的车辆发生减速跟驰、变换车道等行为,干扰交通流的正常运行,并将进而影响其临近车道,且依次往内,乃至影响靠近中央分隔带的最内侧车道。该影响程度依次递减,且随出入口的增加而加强。将其采用横向折减系数进行表征。
1.1 最外侧车道出入口物理修正系数
当路段上设置有接入点时,其最外侧车道将在纵向被物理划分为两个或多个串联子车道。即假设某路段上有n个车道,由内至最外侧分别记为车道1、车道 2、…、车道n。该路段设置有m个出入口,则其最外侧车道n被分隔为m+1个串联子车道单元,则可根据串联单元逻辑关系,计算该最外侧车道考虑接入点设置影响的通行能力物理折减系数为:
(1)
式中:L为路段长度;lk为外车道第k子车道的长度,l1+l2+…+lk+…+lm+1=L。
1.2 车道通行能力综合修正系数
将路段上第i车道的横向折减系数记为αi,计算公式为:
(2)
式中:qi为车道i上受到某出入口处驶入和驶出车辆影响而发生减速跟驰、变换车道等行为的车辆总数;Qi为车道i上的交通量。
可采用无人机或者摄像机进行实地调查,录制出入口附近及上、下游车辆运行状况的视频,通过车辆行为采集系统分析软件从视频中提取速度、加/减速度、行驶轨迹等车辆行为参数。通过参数分析判识受到出入口驶入驶出交通流影响的车道i上的车辆行为,包括减速跟驰、减速通过、停车等待、变换车道等,从而统计得到qi。Qi则可直接通过统计车道i上的交通量得到。已有研究[5]发现,出入口上游40~70 m处车辆速度波动较大。故可取出入口上、下游70 m内的车辆运行状况作为实地调查范围。
路段上设置m个出入口,根据各车道所受到的物理影响和横向影响,可求得路段上第i车道的通行能力综合修正系数为:
(3)
1.3 修正后的路段通行能力
考虑出入口干扰影响下的车道i的实际通行能力![]() 为:
为:
(4)
式中:Ci为车道i在没有出入口干扰影响下的基本通行能力。
单条车道基本通行能力的计算可采用停车线法[12],即:
(5)
式中:hi为饱和车头时距。
路段通行能力C为:
(6)
2 道路出入口位置优化模型
2.1 目标函数
城市道路分为快速路、主干路、次干路、支路4个等级。其中,快速路全部控制出入,不设住宅、商业设施、单位等出入口。出入口一般沿主干路、次干路、支路设置。受CJJ 152—2010《城市道路交叉口设计规程》[13]约束,交叉口附近禁止设置出入口,其禁止设置区域长度与城市道路路段等级相关。
如图1所示,选取某居住区、商业设施或单位及其周围道路作为研究对象。变量为出入口的数量与设置位置,即假设在路段1、路段2、路段3、路段4上选择设置g(g≥1)个出入口。各路段上出入口的数量分别为g1、g2、g3、g4,即g=g1+g2+g3+g4。图1中的虚线为禁止设置出入口的区域。目标函数为在设置g(g≥1)个出入口的情况下,周围道路的通行能力之和Z最大,即:
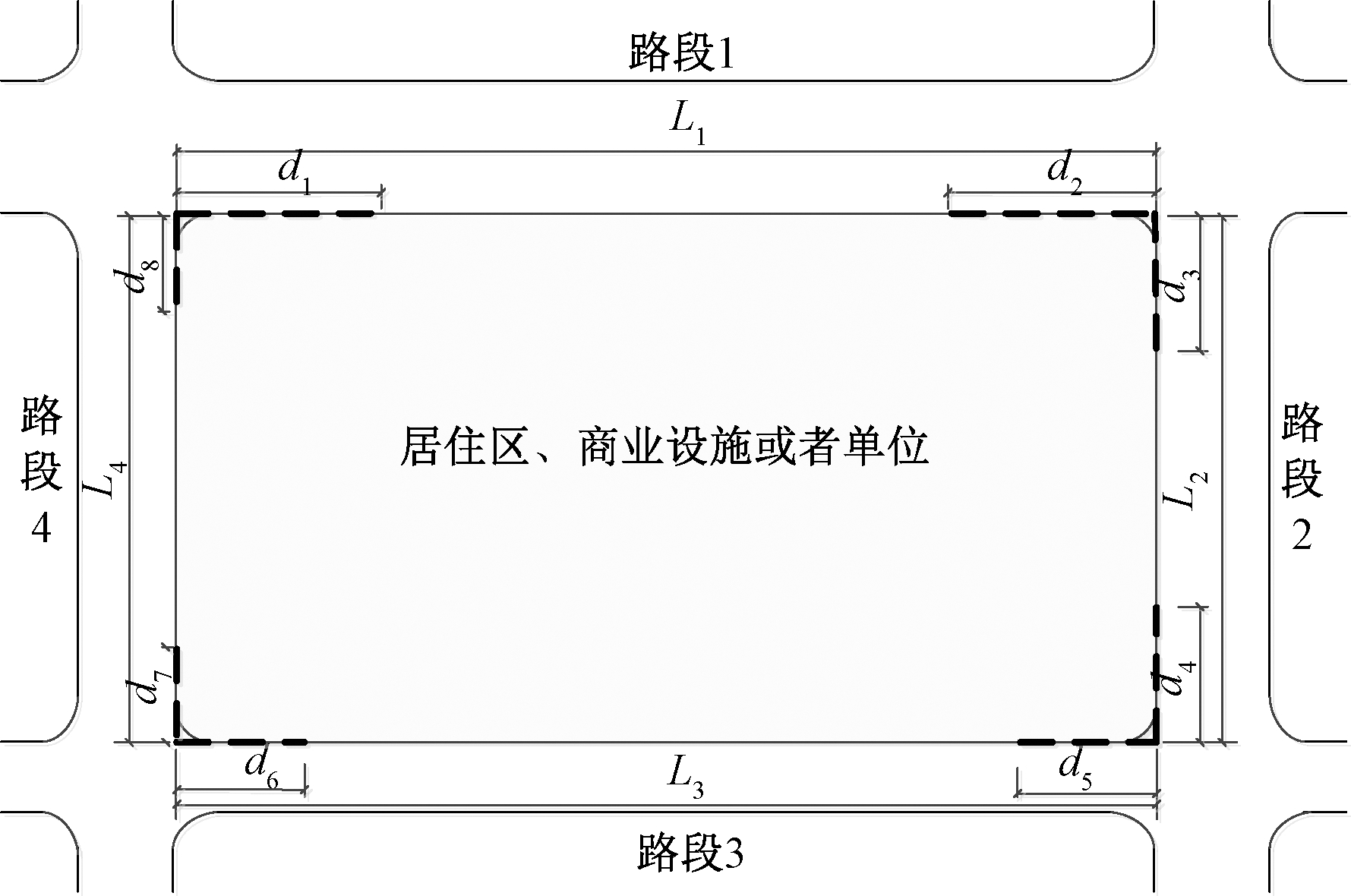
图1 居住区、商业设施或单位及其周围道路
Figure 1 Residential area,commercial facilities or units and their surrounding urban roads
(7)
式中:Cs为路段s(s=1、2、3、4)受到出入口干扰影响后的修正通行能力,采用式(6)进行计算。
2.2 约束条件
(1)出入口与城市道路交叉口停止线的距离。CJJ 152—2010《城市道路交叉口设计规程》第4.2.17条规定了交叉口附近地块或建筑物出入口的设置要求:①主干路上,距平面交叉口停止线不应小于100 m,且应右进右出;②次干路上,距平面交叉口停止线不应小于80 m,且应右进右出;③支路上,距离与干路相交的平面交叉口停止线不应小于50 m,距离同支路相交的平面交叉口不应小于30 m。即出入口的位置应满足:
d≥D,
(8)
式中:d为出入口距离平面交叉口停止线的长度。当出入口位于主干路路段时,D=100 m;当出入口位于次干路路段时,D=80 m;当出入口位于支路路段且该支路与干路相交时,D=50 m;当出入口位于支路路段且该支路与支路相交时,D=30 m。
(2)出入口间距要求。GB/T 51328—2018《城市综合交通体系规划标准》[2]规定,主干路、次干路为沿线用地服务时,接入点密度为2~3个/km。故主干路、次干路上出入口间距不宜小于500 m,而支路以服务功能为主,直接为沿线用地服务,其接入点密度可适当提高。则出入口间距应满足:
de≥500 m,
(9)
式中:de为主干路或次干路路段上相邻出入口之间的距离。
3 实例分析
选取郑州市某居住区作为分析对象,如图2所示。周围4条道路分别为长椿路(主干路)、翠竹街(主干路)、石楠路(次干路)、金菊街(支路)。各条道路的断面形式、车道数等基本参数如表1所示。基本通行能力通过实地调查获得的饱和车头时距计算得到。各路段的起、终点距离交叉口停止线的距离,可通过测距仪进行实地测量得到,如表2所示。
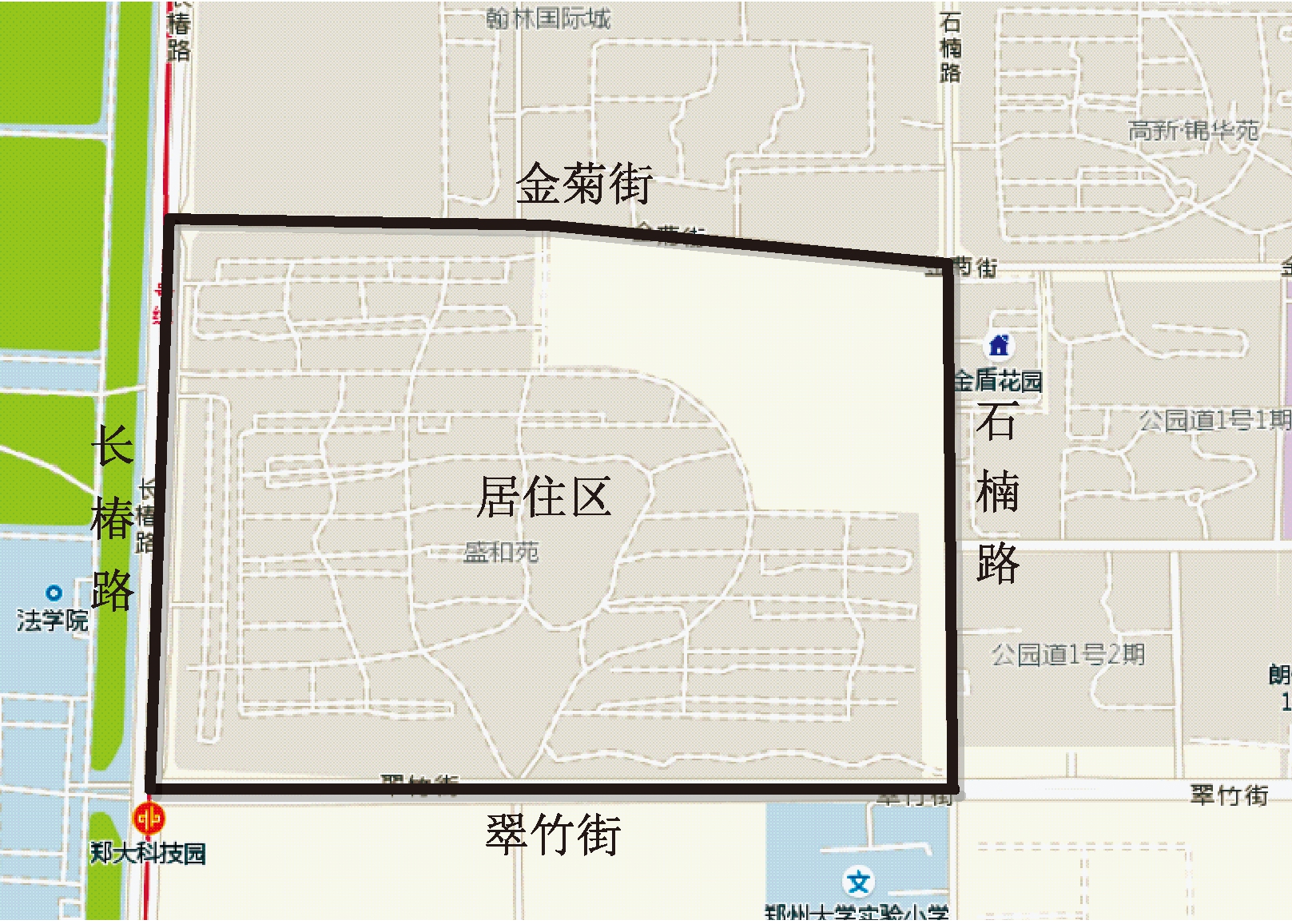
图2 居住区位置
Figure 2 Location of the studied residential area
表1 居住区周围城市道路基本参数
Table 1 Basic parameters of urban roads surrounding the studied residential area
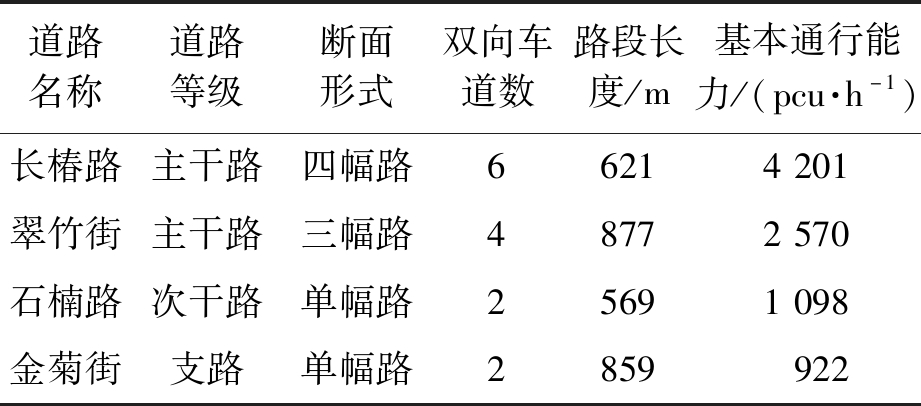
道路名称道路等级断面形式双向车道数路段长度/m基本通行能力/(pcu·h-1)长椿路主干路四幅路66214201翠竹街主干路三幅路48772570石楠路次干路单幅路25691098金菊街支路单幅路2859922
表2 道路出入口位置的距离约束
Table 2 Distance constraints of road access points m
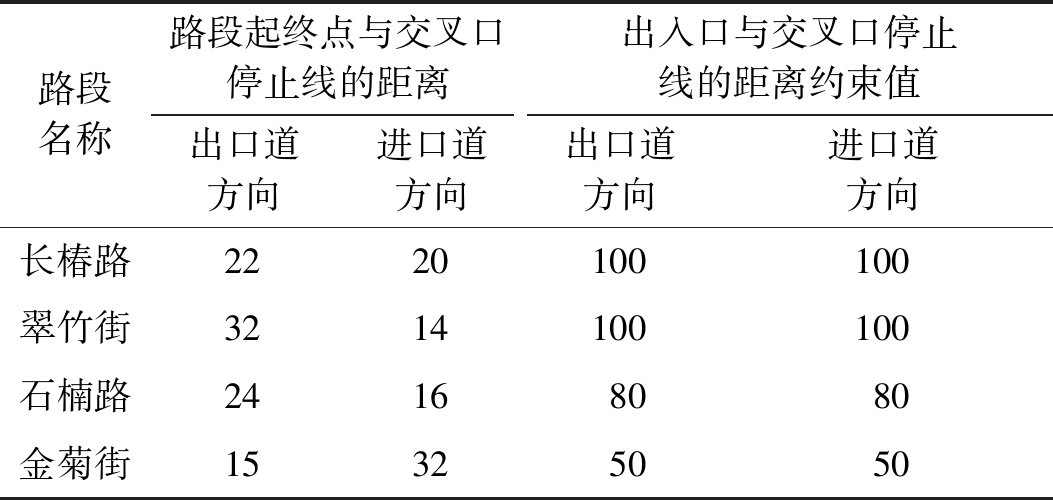
路段名称路段起终点与交叉口停止线的距离出入口与交叉口停止线的距离约束值出口道方向进口道方向出口道方向进口道方向长椿路2220100100翠竹街3214100100石楠路24168080金菊街15325050
道路出入口与城市道路交叉口停止线的距离约束值参考规范要求,主干路、次干路、支路分别为100 m、80 m和50 m。采用无人机在高空录制视频,拍摄各出入口处驶入、驶出车辆对主路交通流运行的干扰情况,计算得到不同车道位置的平均横向折减系数见表3。
表3 横向折减系数
Table 3 Average transverse reduction coefficient

车道位置长椿路翠竹街石楠路金菊街内侧车道0.0100.064——中间车道0.064———最外侧车道0.1100.1100.1100.110
基于式(1)~(7),以及出入口与城市道路交叉口停止线的距离、出入口间距约束条件,以长椿路与翠竹街的交叉口为坐标原点(0,0),以5 m为单位步长,构建坐标体系。出入口的位置点均只能在周围4条道路上选取,采用Python语言编写程序,计算出入口数量g=1、g=2、g=3、g=4时,各出入口的最优设置位置。
当g=1,即居住区设置1个出入口时,可接入道路有4条。计算结果表明,当出入口设置于金菊街(支路)的中点位置处时,居住区周边路网的通行能力之和最大,通行能力降低比例仅为7.86%。将其与设置于其他3条道路中点位置的方案进行对比,如表4所示,发现当设置于长椿路(主干路)的中点位置时,降低比例达到20%以上。与CJJ 37—2012《城市道路工程设计规范》[14]中的“主干路两侧不宜设置吸引大量车流、人流的公共建筑物的出入口”一致,表明方法可行。
表4 设置1个出入口时的不同方案对比
Table 4 Comparison of different scenarios when one access is set up
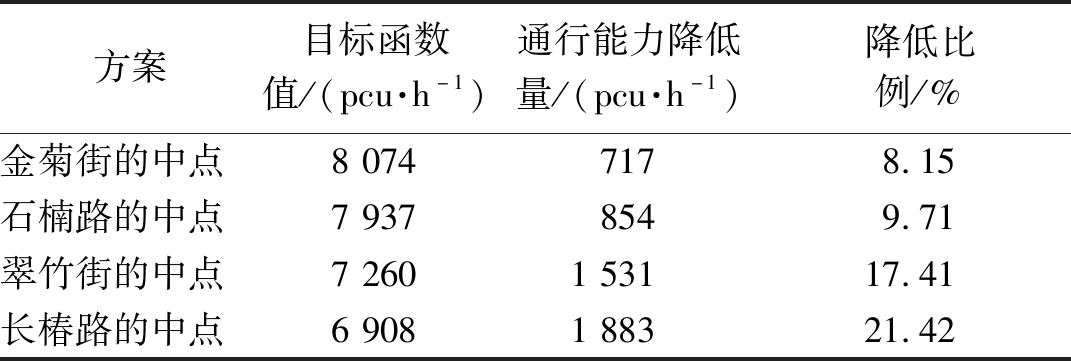
方案目标函数值/(pcu·h-1)通行能力降低量/(pcu·h-1)降低比例/%金菊街的中点80747178.15石楠路的中点79378549.71翠竹街的中点7260153117.41长椿路的中点6908188321.42
当居住区拟设置2个出入口时,计算结果为将其分别设置于金菊街(支路)的3等分点处,此时通行能力之和降低比例为9.45%,如表5所示。如若要求将2个出入口设置在不同道路路段上,则宜选择1个位于金菊街(支路)的中点,1个位于石楠路(次干路)的中点。
表5 设置2个出入口时的不同方案对比
Table 5 Comparison of different scenarios when two accesses are set up
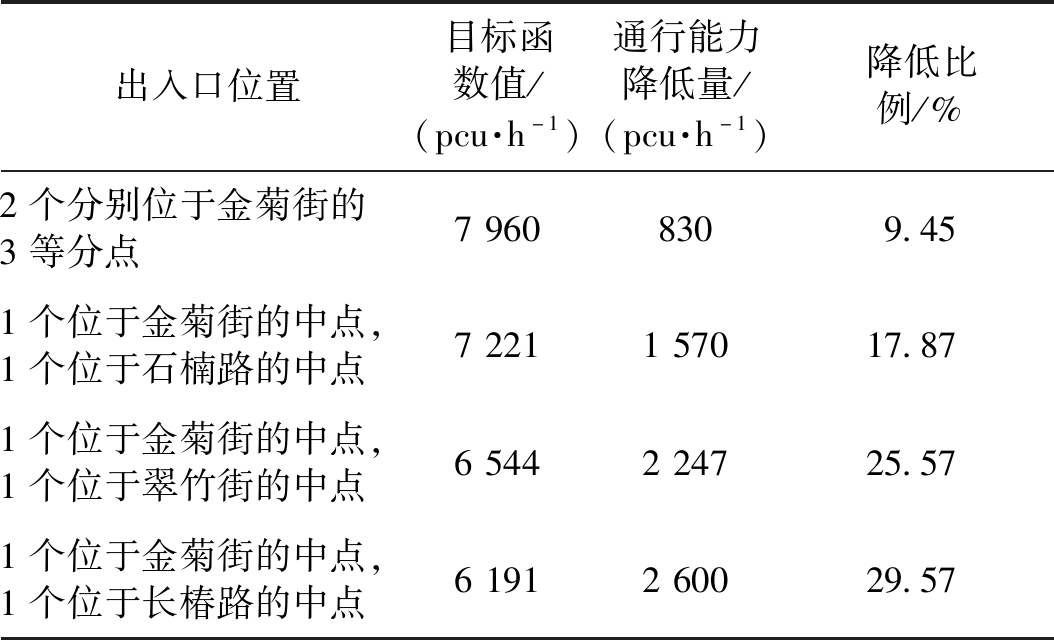
出入口位置目标函数值/(pcu·h-1)通行能力降低量/(pcu·h-1)降低比例/%2个分别位于金菊街的3等分点79608309.451个位于金菊街的中点,1个位于石楠路的中点7221157017.871个位于金菊街的中点,1个位于翠竹街的中点6544224725.571个位于金菊街的中点,1个位于长椿路的中点6191260029.57
当居住区设置3个出入口时,最优方案:将2个出入口设置于金菊街(支路)的3等分点处,1个出入口设置于石楠路(次干路)的中点处。此时,居住区周边道路的通行能力之和最大,通行能力降低19.16%。
当居住区设置4个出入口时,最优方案为在3个出入口时最优方案的基础上,在翠竹街(主干路)的中点设置第4个出入口,此时通行能力降低36.57%。
不同出入口数量情况下的最优出入口设置位置如图3所示。
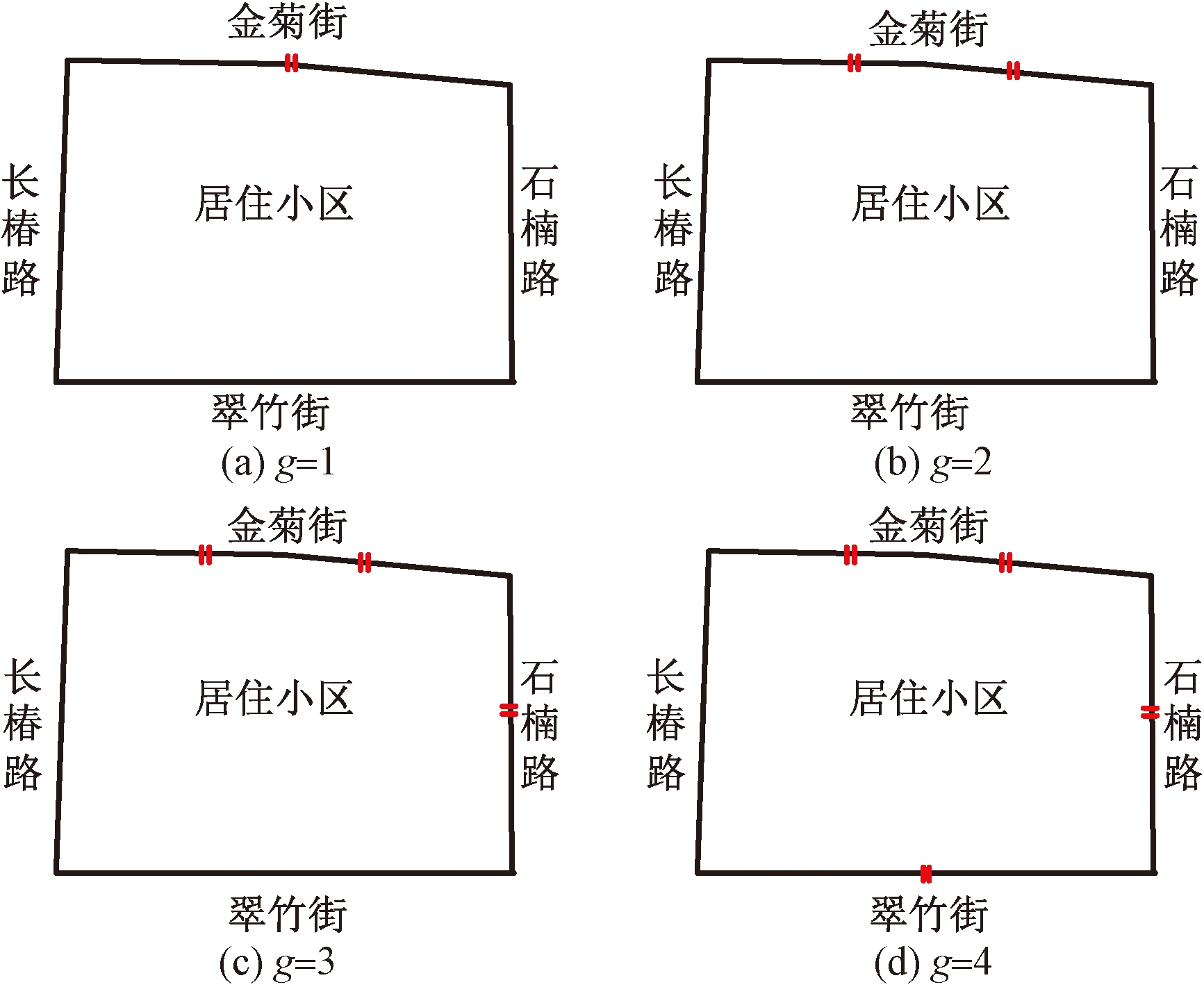
图3 不同数量出入口情况下的最优接入位置
Figure 3 Optimum location of different number of accesses
4 结论
分析了道路出入口处车辆的驶入和驶出对主路路段通行能力的影响机理,采用半解析的方式构建了考虑出入口干扰的路段通行能力模型。进而考虑出入口与交叉口的距离、出入口的间距等约束条件,提出了基于通行能力修正的出入口位置优化方法。主要研究结论如下:
(1)为使居住区周边道路的通行能力之和最大,出入口应优先设置于等级较低的路段中点处。
(2)随着出入口设置数量的增加,出入口的位置宜由低等级道路向高等级道路依次布设。
(3)当城市道路等级相同时,宜优先选择在车道数较少的道路路段设置出入口。
后续拟构建受出入口影响的车辆数与出入口路段上流量、出入口处进出交通量之间相关关系的数学模型,并将其与统计分析值进行对比,以进一步梳理不同流向交通流之间的影响特征。此外,未来可采用VISSIM模拟手段,构建不同出入口设置位置情况下的路段交通流微观仿真模型,结合通行能力指标,对笔者所提出的优化方法进行多方位验证。
[1] 中国国家标准化管理委员会.城市道路交通组织设计规范:GB/T 36670—2018 [S].北京:中国标准出版社,2018.
[2] 中国城市规划设计研究院.城市综合交通体系规划标准:GB/T 51328—2018[S].北京:中国标准出版社,2018.
[3] CHEN J X,WANG W,LI Z B,et al.Dispersion effect in left-turning bicycle traffic and its influence on capa-city of left-turning vehicles at signalized intersections[J].Transportation research board,2014,2468(1):38-46.
[4] 邓社军,叶晓飞,陈峻.路外停车右转驶入对主路上游车流影响的动态长度模型[J].公路交通科技,2014,31(3):125-132.
[5] 邓社军,叶晓飞,陈峻.路外停车驶入对出入口交通流影响模型[J].哈尔滨工业大学学报,2016,48(3):101-107.
[6] 唐伯明,王卫军,刘唐志,等.停车场建设规模对道路通行能力影响的分析[J].重庆交通大学学报(自然科学版),2016,35(2):100-104.
[7] CAO Y,YANG Z Z,ZUO Z Y.The effect of curb parking on road capacity and traffic safety[J].European transport research review,2017,9(1):4.
[8] 秦丽辉,裴玉龙,汪恩良.公交停靠影响下的城市干路通行能力与服务水平[J].哈尔滨工业大学学报,2017,49(9):90-96.
[9] 秦丽辉,裴玉龙,白崇喜.自行车干扰下的城市干路路段通行能力与服务水平[J].哈尔滨工业大学学报,2018,50(9):61-67.
[10] 蔡建荣,黄汝晴,黄中祥.考虑通行能力折减的可变车道优化[J].中南大学学报(自然科学版),2018,49(7):1838-1844.
[11] TANG T Q,SHI W F,YANG X B,et al.A macro traffic flow model accounting for road capacity and reliability analysis[J].Physica A:statistical mechanics and its applications,2013,392(24):6300-6306.
[12] 徐吉谦,陈学武.交通工程总论[M].3版.北京:人民交通出版社,2008.
[13] 中华人民共和国住房和城乡建设部.城市道路交叉口设计规程:CJJ 152—2010[S].北京:中国建筑工业出版社,2010.
[14] 中华人民共和国住房和城乡建设部.城市道路工程设计规范:CJJ 37—2012 [S].2016年版.北京:中国建筑工业出版社,2016.