0 引言
超分辨率重构技术[1]能够把低分辨率的图像重构出与真实图像相近的超分辨率图像,这样可从软件角度解决成像的硬件设备问题。超分辨率重构技术作为目前计算机视觉领域的主要研究热点之一,在遥感成像[2]、医学影像分析[3]、工业成像等领域具有广泛的应用前景。目前,超分辨率重构技术主要分为3类:插值、重构和学习的超分辨率重构算法。
基于插值算法[4-5]就是利用低分辨率图像中已知像素点对未知像素点进行估计,虽然其计算复杂度较低,但易放大边缘,造成细节模糊和锯齿边界。基于重构的超分辨率算法是利用数字图像处理技术求解成像模型的逆过程,从而进一步实现超分辨重构,常用的模型有全变分正则化模型[6-7]、梯度轮廓先验[8]等。其尽管引入了先验知识,但对具有较为丰富结构信息类型的图像来说,该方法仍难以获得边界清晰的视觉效果。
Freeman等[9-10]首先提出了基于学习思想的图像超分辨重构,主要分为2个阶段:训练阶段和重构阶段。该方法训练所需样本数量大,重构速度慢。随后,Sun等[11]在文献[9-10]的算法基础上提出了样本学习法,因为从原始图像空间中学习到维度较小的图像基元空间,所以可以用少数基元表示原始图像,从而改善高低分辨率之间的映射关系,提高重构精度。
Chang等[12]借鉴流形学习的思想,引入局部线性嵌入,提出了基于邻域嵌入方法的图像超分辨率复原算法。Yang等[13-14]提出了基于稀疏表示(sparse coding super resolution,SCSR)的图像超分辨率重构算法,该方法通过训练学习高、低分辨率图像的映射关系,用优化方法求得低分辨图像的稀疏系数矩阵,最后通过稀疏系数矩阵重构高分辨率图像。Zeyde等[15]对文献[13-14]的方法进行了改进,并采用K-奇异值分解(K-singular value decomposition,K-SVD)算法[16]和最优方向法(method of optimal direction,MOD)[17]分别学习高、低分辨率的字典,大大提升了学习效率。以上各方法虽然可小幅提升超分辨率重构质量,但高、低分辨率字典稀疏系数矩阵不具有不变性的缺陷,制约了重构图像质量的提升。王杰等[18]采用自适应交替方向乘子方法对图像进行去模糊,在保证计算速度的同时自适应地复原出最佳图像。针对上述不足,Wang等[19]提出半耦合字典学习(semi-coupled dictionary learning,SCDL)算法,该方法从样本图像中学习到的高、低分辨率字典稀疏系数矩阵具有不变性,提高了算法的重构效果。杨爱萍等[20]利用分类稀疏编码、非局部相似性改进SCDL算法,进一步提高了重构精度。尽管SCDL框架和改进的方法增强了学习高、低分辨率图像块之间映射关系的能力,提升了重构精度,但由于忽略了较为重要的细节信息,比如边界,而这些细节信息对于重构后的图像影响较大,从而限制了算法的重构精度。
笔者针对半耦合字典学习算法的不足,提出了基于细节约束因子和半耦合字典学习的图像超分辨重构方法:以半耦合字典学习算法为框架,引入双向梯度的边界差异,构建边界保持约束项,重构出接近真实而丰富边界;引入边界保持约束项,考虑边界差异的拉普拉斯分布,提出了自适应边界约束系数求解方法,使其能够在半耦合字典学习算法整体框架下实现超分辨率重构,进一步提升超分辨率重构质量。
1 相关工作
低分辨率图像的获取过程被认为是高质量图像退化过程,假设给定低分辨率图像y,则图像的获取过程可描述为
y=BHx+n。
(1)
式中:x为高质量图像;B为采样因子;H为模糊操作;n为噪声。
通过上述过程可以看出,超分辨率重构过程实际上是图像退化过程的逆向实现过程。然而从低分辨率图像中重构出高分辨率图像y,是一种病态问题。为了解决这个问题,稀疏表示[9-13]被提出来实现超分辨重构。将稀疏表示的相关理论引入到图像超分辨过程,主要包括2个阶段:字典训练阶段和重构阶段。
假定来自低分辨率图像y的块yi可用字典Dy来表示,即yi=Dyαi。可通过优化如下目标函数来求得稀疏系数αi:
(2)
于是,重构的块![]() 可表示为
可表示为![]() 由于提取的块是重叠的,因此,通过平均所有重构的图块形成重构图像x。
由于提取的块是重叠的,因此,通过平均所有重构的图块形成重构图像x。
2 重构模型的实现
2.1 半耦合字典学习训练阶段
假设给定高、低分辨率图像块数据X=[x1,x2,…,xn]和Y=[y1,y2,…,yn],其中{xi,yi}是相应的高、低分辨率对应的图像块,Dx、Dy分别表示高、低分辨率对应字典,αx、αy分别表示高、低分辨率图像块对应的稀疏表示系数。半耦合字典学习的基本思想是首先建立对应的高低分辨率图像块,然后假设图像块在相应字典下的稀疏表示系数不再是相同的,而是通过一个稀疏域的映射矩阵相关联。SCDL 算法框架放宽了约束条件,加强了高、低分辨率图像块之间映射关系的学习能力,提高了重构质量,其在训练阶段可一并得到半耦合的高、低分辨率字典以及稀疏域映射矩阵W:
αx=Wαy。
(3)
SCDL算法基于l1范数正则化的稀疏表示模型,引入了映射误差惩罚项,改进高、低分辨率稀疏表示问题,从而获得半耦合字典学习模型,即
(4)
在SCDL算法中,半耦合字典学习最优化问题转化为3个子问题交替求解,采用以LARS算法为基础的SPARS工具箱解决l1范数正则化的稀疏表示子问题。笔者这里采用交替启发式学习框架进行稀疏求解。首先初始化映射矩阵W和字典对Dx和Dy,稀疏系数可通过下面子问题进行求解:
min{αx}![]()
(5)
min{αy}![]()
(6)
式(5)、(6)是一个多任务LASSO问题,笔者采用LARS进行求解。然后,根据已求的αx和αy,同样采用交替迭代学习策略求解Dx和Dy:
min{Dx,Dy}![]()
(7)
固定Dx、Dy、αx和αy,求解映射矩阵W:
min{W}![]()
(8)
训练阶段的伪代码描述如下。
输入:低分辨率图像 X,高分辨率图像Y,Dx、 随机初始化字典矩阵Dy,初始化映射矩阵W,参数λx、λy、λW、 γ。
for每次迭代until收敛
for每个聚类中心
Step 1 根据式(5)和(6)计算稀疏系数αx和αy;
Step 2 根据式(7)更新字典Dx、Dy;
Step 3 根据式(8)更新映射函数W
输出:Dx、Dy、Wx、Wy。
2.2 超分辨率重构阶段
笔者所提出的算法框架的训练过程如图1所示。
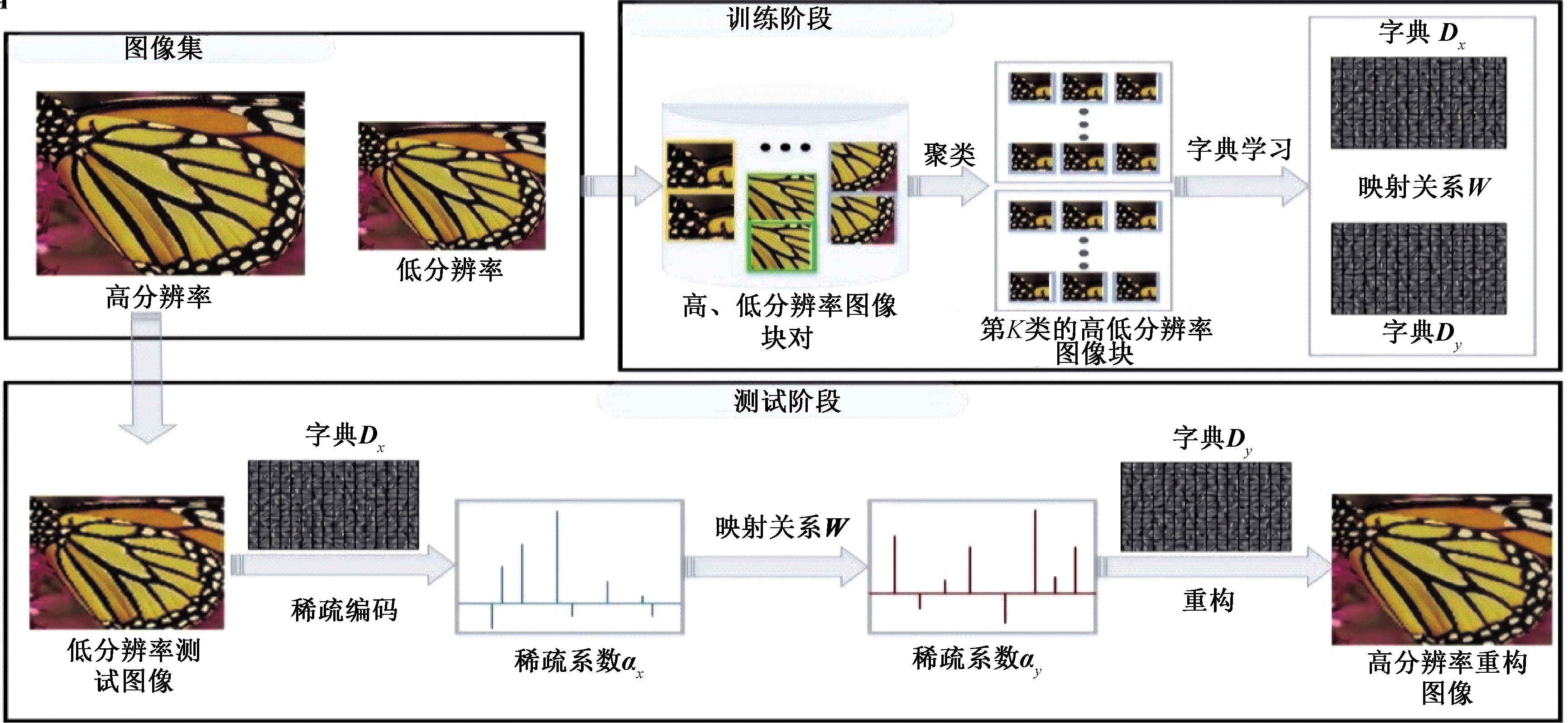
图1 所提算法的流程图
Figure 1 Flow chart of the proposed algorithm
2.2.1 细节约束因子
细节信息的重构对于后续图像分析非常有价值。然而,在超分辨率图像重构过程中,往往会丢失重要的细节信息。因此,笔者试图利用一维图像处理,充分考虑各个方向上的纹理梯度信息。对于图像x而言,纹理梯度信息定义为
(9)
式中:xh和xv分别表示水平方向和垂直方向的纹理信息。假设已获得重构图像![]() 重构图像与真实超分辨率图像的纹理差异为
重构图像与真实超分辨率图像的纹理差异为
(10)
实际上,真实超分辨率图像x是未知变量。为了衡量纹理差异,将其转化为低分辨率图像y与超分辨率重构图像的退化图像的纹理差异:
(11)
利用稀疏表示,式(11)重新写为
GD=G(y)-G(BHDα)。
(12)
2.2.2 测试阶段
通过半耦合字典学习交替进行的学习策略,能够学到对应的稀疏系数和字典矩阵。为了保证重构图像的细节,在测试阶段引入细节保持因子。给定低分辨率图像x,字典矩阵Dx和Dy,通过构造以下目标函数重构高分辨率图像y:
![]()
![]()
![]()
(13)
式中:xi和yi分别表示低分辨率和重构图像的图像块。笔者采用one-by-one求解策略来更新稀疏系数。固定稀疏系数αyi,稀疏系数αxi可以通过下面表达式进行优化:
min{αxi}![]()
(14)
然后通过式(15)求解稀疏系数αyi:
min{αyi}![]()
(15)
其中,μ为正则项参数,用来约束纹理细节项的贡献。为了更好描述约束项的贡献,笔者采用一种权重自适应优化方法:
(16)
式中:σn为噪声标准差;σi为第i块的差异标准差。
通过式(17)可求得高分辨率图像的稀疏系数αyi,根据稀疏字典表示方法重构高分辨率图像:
yi=Dyαyi。
(17)
3 实验及结果分析
为了验证笔者所提算法的有效性,先将纹理细节保持约束引入到半耦合字典学习框架中,再采用交替学习与重构策略,最后通过构建参数自适应学习,保证约束项的贡献度。对改进的半耦合字典学习方法的时间复杂度进行分析,假设训练图像的尺寸为N×N,提取N2个大小为![]() 的训练图像块,则时间复杂度为O(N4)。通过对Kodak Photo CD database数据集的24幅图像进行训练,然后对5幅图像(butterfly、fence、girl、Parthenon、starfish)进行纵向对比实验。在实验过程中,统一条件和参数如下:图像块的大小为5×5,聚类的数目为32,正则项参数λx、λy、λW、γ分别为0.01、0.01、0.1、0.1。主要评价指标为峰值信噪比(PSNR)和结构相似性(SSIM[21])。PSNR计算方法为
的训练图像块,则时间复杂度为O(N4)。通过对Kodak Photo CD database数据集的24幅图像进行训练,然后对5幅图像(butterfly、fence、girl、Parthenon、starfish)进行纵向对比实验。在实验过程中,统一条件和参数如下:图像块的大小为5×5,聚类的数目为32,正则项参数λx、λy、λW、γ分别为0.01、0.01、0.1、0.1。主要评价指标为峰值信噪比(PSNR)和结构相似性(SSIM[21])。PSNR计算方法为
(18)
(19)
为了评价笔者所提算法性能,将其与现有的单幅图像超分辨率重构算法进行对比分析,选取近年来相对较为先进的超分辨率重构算法,主要包括Bicubic插值、SRCNN算法[22]、SCDL算法[19]。为了使对比更为客观,采用相同的训练集和测试集。
笔者采用的实验方案如下:①受篇幅限制,对超分辨率图像只进行2倍下采样获得低分辨率图像,评价算法的重构性能;②对超分辨图像进行加噪声,然后进行2倍下采样获得含有噪声的低分辨率图像,评价算法的重构性能。
实验1:未加噪声实验分析。以butterfly为例,评价图像在2倍下采样各算法的超分辨率重构结果如图2所示。由实验看出,利用Bicubic插值算法重构的图像存在锯齿边界,而且边界模糊。而采用深度学习方法SRCNN效果好于Bicubic插值算法,消除了锯齿状边界,但大边界仍存在模糊现象。SCDL算法重构的图像虽具有更强的边界表达能力,然而在局部区域会出现一定的噪声和边界模糊。笔者提出的算法在重构纹理细节、消除噪声及重构细节结构方面具有很好的效果,重构图像更能接近原始高分辨率图像,表1给出了上述各超分辨率算法重构图像的PSNR值和SSIM值。

图2 在2倍下采样各算法超分辨率重构结果
Figure 2 Super resolution reconstruction results of each algorithm for 2 times down sampling
实验2:加噪声实验分析。以Parthenon为例,在无噪声图像上加噪声水平nsignal=10的噪声,评价图像在2倍下采样各算法的超分辨率重构结果如图3所示。对于有噪声图像而言,Bicubic插值对噪声敏感,放大了噪声水平。SRCNN算法对噪声具有一定的克服能力,但在边界上仍有噪声存在,从而导致重构图像的边界细节重构能力明显不足。SCDL算法虽然有一定的克服能力,但在重构过程中,边界细节重构方面的能力仍然不足。笔者提出的算法对噪声具有一定的鲁棒性,在有效去除噪声的同时能够很好地重构出细节信息。表1给出了在噪声条件下,各算法的重构图像的PSNR值和SSIM值。
表1 不同策略下重构图像的PSNR值和SSIM值
Table 1 PSNR values and SSIM values of reconstructed images under different strategies
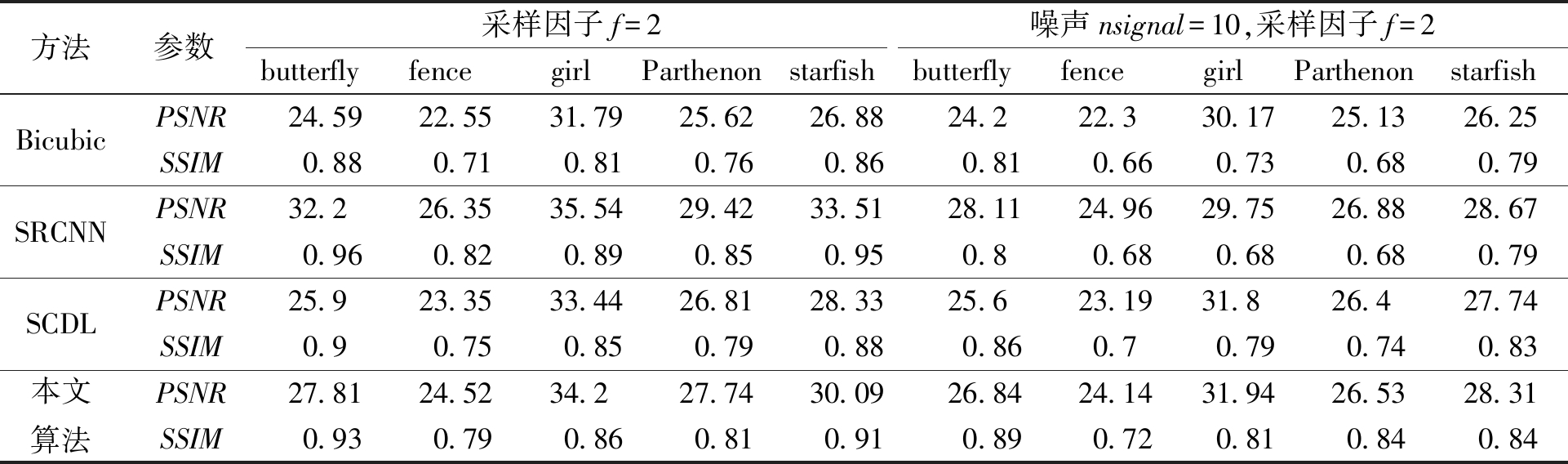
方法参数采样因子f=2噪声nsignal=10,采样因子f=2butterflyfencegirlParthenonstarfishbutterflyfencegirlParthenonstarfishBicubic SRCNN SCDL本文算法PSNR24.5922.5531.7925.6226.8824.222.330.1725.1326.25SSIM0.880.710.810.760.860.810.660.730.680.79PSNR32.226.3535.5429.4233.5128.1124.9629.7526.8828.67SSIM0.960.820.890.850.950.80.680.680.680.79PSNR25.923.3533.4426.8128.3325.623.1931.826.427.74SSIM0.90.750.850.790.880.860.70.790.740.83PSNR27.8124.5234.227.7430.0926.8424.1431.9426.5328.31SSIM0.930.790.860.810.910.890.720.810.840.84

图3 在2倍下采样各算法超分辨率重构结果(nsignal=10)
Figure 3 Super resolution reconstruction results of each algorithm for 2 times down sampling(nsignal=10)
4 结论
针对单幅图像的超分辨率细节弱重构的问题,笔者采用将细节约束因子引入到半耦合字典学习框架中的方法,捕获图像的结构信息,重构出更多的图像细节信息;根据边界差异的分布实现参数自适应选择。另外,笔者又采用了利用交替学习策略进行模型的优化。实验结果表明,笔者提出的引入细节约束因子的半耦合字典学习超分辨重构算法构造的模型能够较好地重构出图像细节结构。
[1] BAKER S,KANADE T.Limits on super-resolution and how to break them[J].IEEE transactions on pattern analysis and machine intelligence,2002,24(9):1167-1183.
[2] 王雪,隋立春,杨振胤,等.最优方向耦合字典学习的遥感影像超分辨率重建[J].计算机工程与应用,2018,54(7):201-205.
[3] TRINH D H,LUONG M,DIBOS F,et al.Novel example-based method for super-resolution and denoising of medical images[J].IEEE transactions on image processing,2014,23(4):1882-1895.
[4] MICHAELI T,ELDAR Y C.A hybrid vector Wiener filter approach to translational super-resolution[J]. IEEE transactions on image processing,2010,1:1-18.
[5] 毛晓波,张志超.基于二维经验模态分解的单幅图像超分辨率重建[J].郑州大学学报(工学版),2014,35(5):15-18.
[6] MARQUINA A,OSHER S J.Image super-resolution by TV-regularization and bregman iteration[J].Journal of scientific computing,2008,37(3):367-382.
[7] 徐志刚,李文文,朱红蕾,等.一种基于L1/2正则约束的超分辨率重建算法[J].华中科技大学学报(自然科学版),2017,45(6):38-42.
[8] SUN J,XU Z B,SHUM H Y.Image super-resolution using gradient profile prior[C]//2008 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE,2008:1-8.
[9] FREEMAN W T, PASZTOR E C, CARMICHAEL O T. Learning low-level vision[J]. International journal of computer vision, 2000, 40(1):25-47.
[10] FREEMAN W T,JONES T R,PASZTOR E C.Example-based super-resolution[J].IEEE computer graphics and applications,2002,22(2):56-65.
[11] SUN J,ZHENG N N,TAO H,et al.Image hallucination with primal sketch priors[C]//2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2003 Proceedings.Piscataway:IEEE,2003:729-736.
[12] CHANG H,YEUNG D Y,XIONG Y M.Super-resolution through neighbor embedding[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2004. Piscataway:IEEE,2004:1-8.
[13] YANG J C,WRIGHT J,HUANG T,et al.Image super-resolution as sparse representation of raw image patches[C]//2008 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE,2008:1-8.
[14] YANG J C,WRIGHT J,HUANG T S,et al.Image super-resolution via sparse representation[J].IEEE transactions on image processing,2010,19(11):2861-2873.
[15] ZEYDE R,ELAD M,PROTTER M.On single image scale-up using sparse-representations[C]//7th International Conference on Curves and Surfaces, Curves and Surfaces 2010.Cham:Springer,2012:711-730.
[16] AHARON M,ELAD M,BRUCKSTEIN A.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE transactions on signal processing,2006,54(11):4311-4322.
[17] ENGAN K,AASE S O,HAKON HUSOY J.Method of optimal directions for frame design[C]//1999 IEEE International Conference on Acoustics,Speech,and Signal Processing.Proceedings.Piscataway:IEEE,1999:2443-2446.
[18] 王杰,李胜光,宋一帆,等.图像去模糊的自适应交替方向乘子重叠组稀疏方法[J].郑州大学学报(工学版),2018,39(5):52-57,78.
[19] WANG S L,ZHANG L,LIANG Y,et al.Semi-coupled dictionary learning with applications to image super-resolution and photo-sketch synthesis[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition.Piscataway:IEEE,2012:2216-2223.
[20] 杨爱萍,钟腾飞,何宇清.基于非局部相似性和分类半耦合字典学习的超分辨率重建[J].天津大学学报(自然科学与工程技术版),2015,48(1):87-94.
[21] WANG Z,BOVIK A C,SHEIKH H R,et al.Image quality assessment:from error visibility to structural similarity[J].IEEE transactions on image processing,2004,13(4):600-612.
[22] DONG C,LOY C C,HE K M,et al.Learning a deep convolutional network for image super-resolution[C]// European Conference on Computer Vision, Computer vision-ECCV 2014. Cham:Springer,2014:184-199.