0 引言
动力电池是电动汽车三大核心部件之一,有锂离子电池、氢燃料电池、超级电容和铝空气电池,以及适于特殊车辆的复合电源[1]等,其中锂离子电池运用最为广泛。众所周知,锂离子电池充放电过程中会大量发热,其电池特性与环境温度紧密相关[2],因此,基于车辆行驶形成自然风的冷却结构构型就成为了电池箱设计的关键。刘振军等[3]对锂离子电池组箱体前后端面增设前大后小的进出风口,增大进风量以降低箱内温度和单体电池温差。吴宏等[4]利用狭缝空腔中自然对流换热原理,优化出了一种正面通风口加装风挡板的结构,使冷却空气在电池缝隙的流动更加均匀化。对于电池箱内部模块排列,眭艳辉等[5]依据通道面积与风速成反比的关系,采用梯形排列样式平衡了进出口区域电池模块的散热效果,但其形状会明显导致装车空间利用率低下的问题。因此笔者拟采用矩形错位排列与凹凸箱体壁相结合的结构,研究流道参数与电池模块散热的内在关系,探寻电池箱紧凑化设计方法,为高比能量电池箱开发提供理论支持。
1 动力电池系统温度场理论
动力电池系统的能量传递采用电化学-热耦合模型,电池内部只考虑导热,并将其简化为一个等效固体,在直角坐标系中方型电池热模型表达为式(1)[6-8]:
(1)
式中:ρ为电池密度;CP为电池比热容;T为电池温度;Q为电池产生的热量;λx、λy、λz分别为电池在x、y、z方向上的导热系数。
在流动传热过程中,系统除满足质量守恒定律、动量守恒定律和能量守恒定律外,还需满足如下湍流方程(k-ε模型):
(2)
(3)
式中:ηt=cμρk2/ε;k为流体传热系数;ε为耗散率,其系数取值如表1所示[9-10]。
表1 k-ε 模型的系数取值
Table 1 Values of coefficients in k-ε
cμ c1c2σkσεσT0.091.441.921.01.30.9~1.0
在电池表面与流体对流换热时,表面能量传递满足关系式(4):
Q=hA(T1-T0),
(4)
式中:Q为对流换热能量,W;h为对流换热系数,W/(m2·K);A为换热面积,m2;T0、T1为边界两侧温度,K。
2 仿真模型与实验设计
2.1 热模型
图1为电池箱内部模块排列布置结构,初始行距、列距和边距均设为50 mm,设计的电池箱最大轮廓尺寸1 070 mm×1 370 mm×150 mm,采用圆形出入风口(入口直径Di,出口直径DO),其中电池模块采用错位排列方式,编号格式为x(行)y(列),自左向右和自下向上排列,列距PL、行距PT和边距LW构成冷却空气流道。
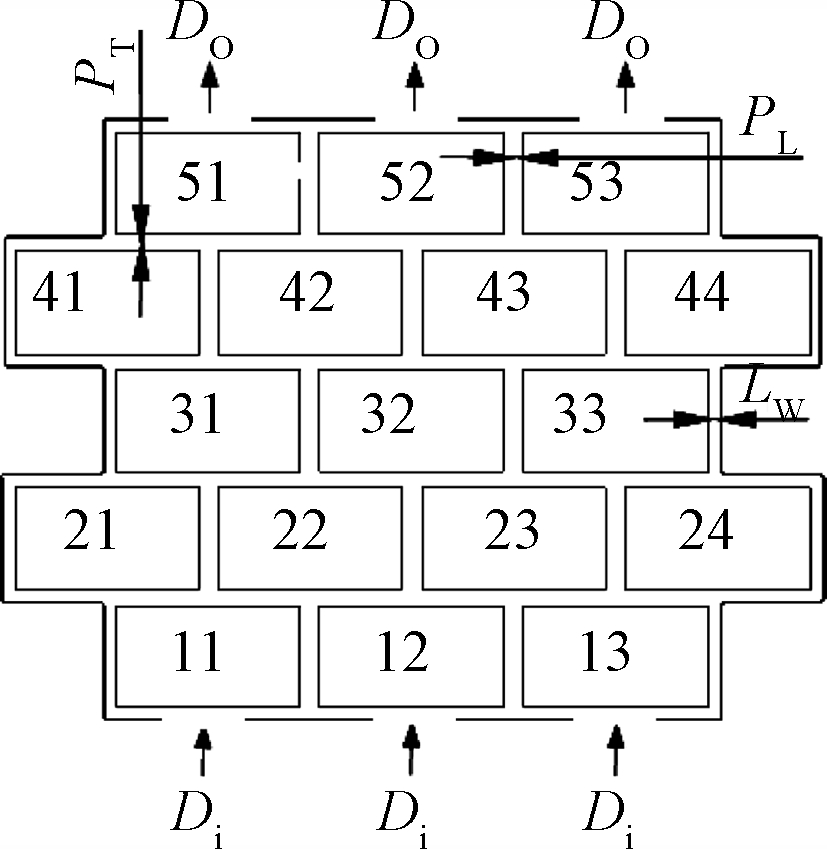
图1 电池模块阵列方案
Figure 1 Battery module array scheme
假设空气为理想不可压缩流体,流体的边界压力为零,且不考虑其惯性力;单体电池选择磷酸铁锂动力电池,规格为20 mm×100 mm×140 mm,型号3.2 V 22 Ah,质量0.59 kg;其生热为体热源,且生热速率不受温度影响,不考虑电池组热变形[11-13]。
仿真条件设置:入口为自然风,风速2.5 m/s;电池模块和外部环境初始温度均设为25 ℃;自然对流边界设置为5 W/(m2·K);电池表面与空气接触边界设置为耦合边界;电池采用1C10A充电,生热速率为2 592.86 W/m3。
2.2 热仿真正交试验
仿真采用5因素4水平的16组正交实验仿真方法,如表2所示,其中PL、PT、LW均取20、25、30、35 mm;Di、DO均取90、95、100、105 mm。在此基础上,后续LW增加取值15 mm,Di增取110、120、130 mm。
表2 5因素4水平正交实验参数
Table 2 L16(45) orthogonal experimental parameters mm
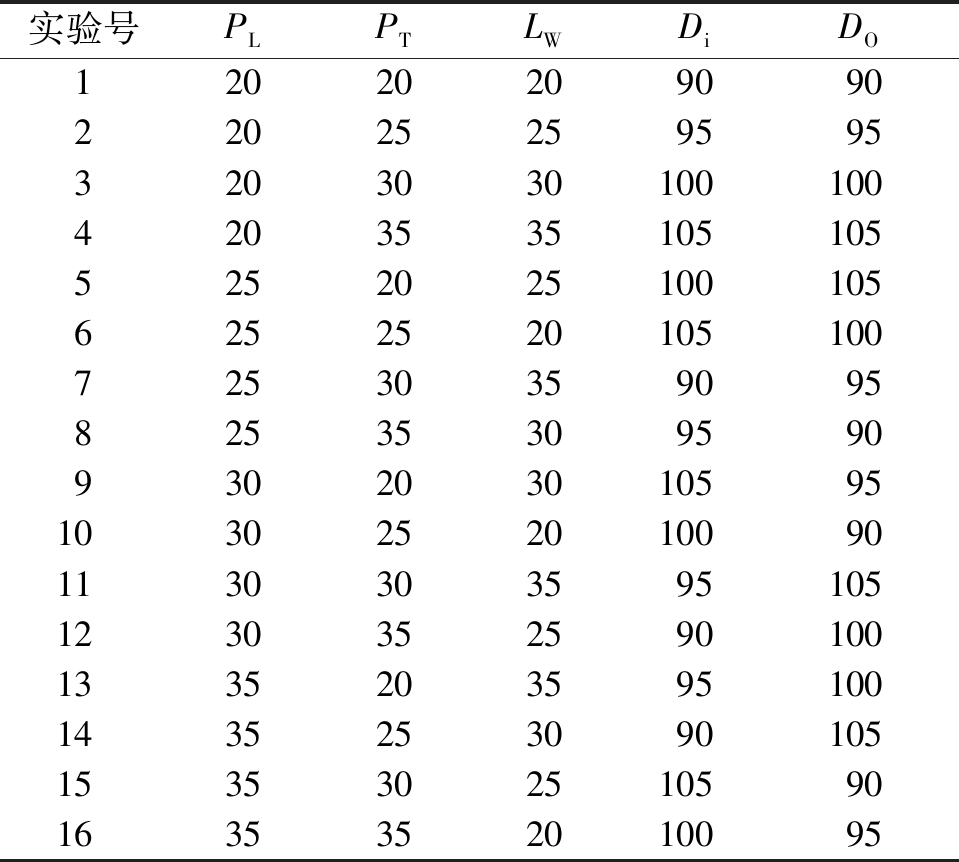
实验号PLPTLWDiDO1202020909022025259595320303010010042035351051055252025100105625252010510072530359095825353095909302030105951030252010090113030359510512303525901001335203595100143525309010515353025105901635352010095
3 仿真结果与分析
3.1 仿真结果
限于篇幅,仅列举第1、7组实验结果,温度云图结果如图2所示。从图2可知,位于冷却风出口端的第4、第5两行中间电池模块有高温分布存在。正交试验仿真结果分析见表3。由表3可知,设计参数按影响散热效果重要性依次递减为:入口直径、列距、边距、行距、出口直径,行距和出口直径对最高温度的影响较小。
表3 仿真结果与极差分析
Table 3 Simulation results and their range analysis ℃
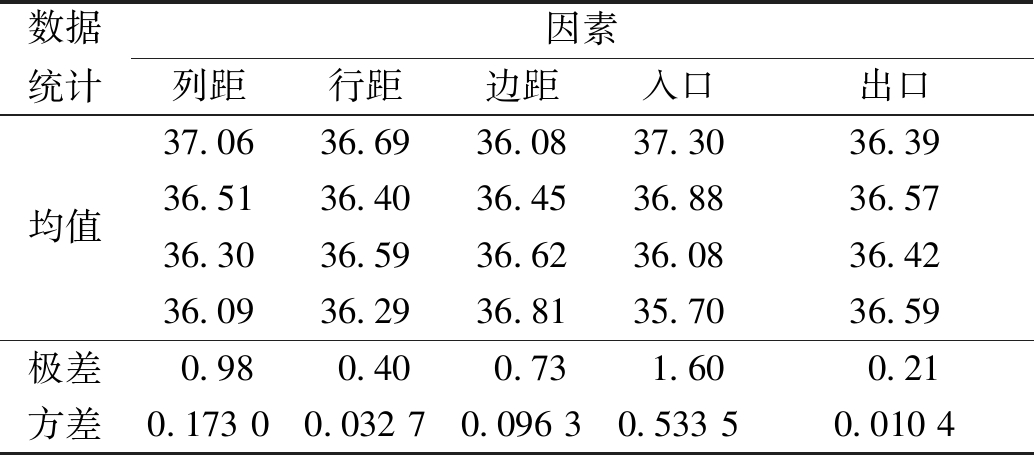
数据统计因素列距行距边距入口出口均值极差方差37.0636.6936.0837.3036.3936.5136.4036.4536.8836.5736.3036.5936.6236.0836.4236.0936.2936.8135.7036.590.980.400.731.600.210.173 00.032 70.096 30.533 50.010 4
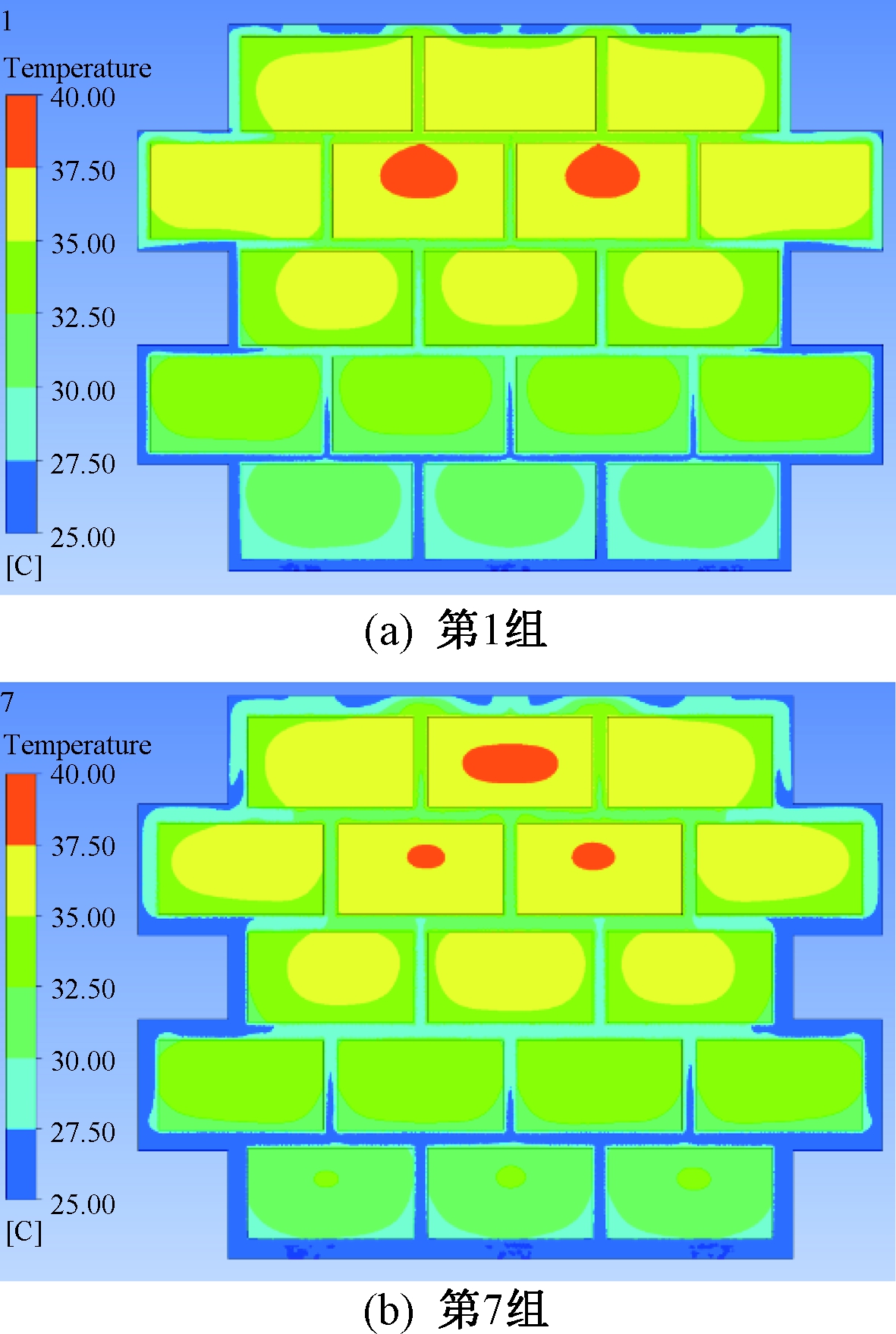
图2 第1组和第7组仿真实验温度场云图
Figure 2 Cloud map of temperature field simulation about group 1 and group 7
图3为入口直径-最高温度关系图。可以看出,随入口直径增大,最高温度呈不断下降趋势。显然,入口直径越大,进入电池箱流道的空气量越多,故越利于使电池模块保持较低温升。
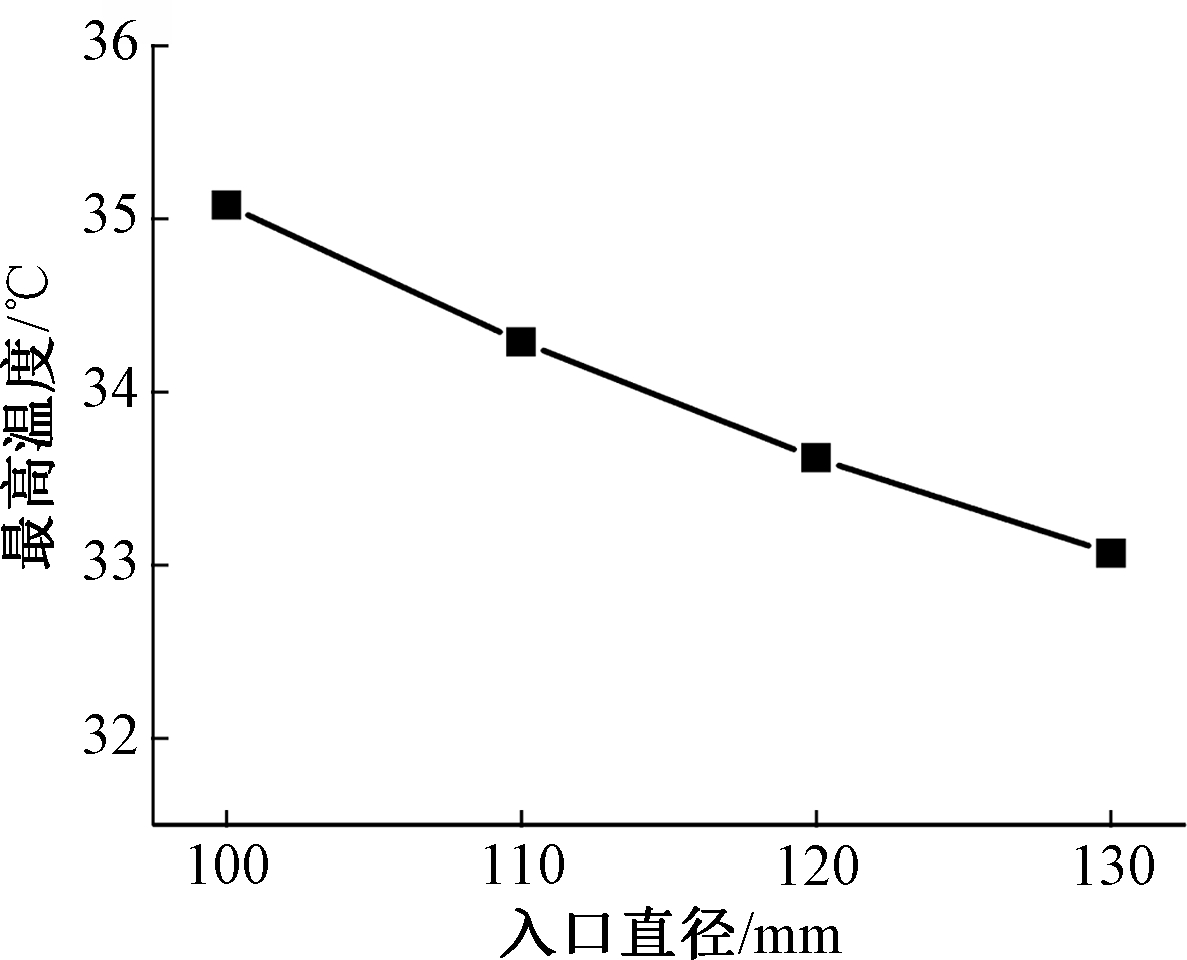
图3 入口直径与最高温度关系
Figure 3 Relationship between inlet diameter and maximum temperature
图4为列距、边距与最高温度关系图。可以看出,随列距增大,最高温度呈现出明显下降趋势,但列距超过30 mm后基本趋于平稳变化;而随边距增大,最高温度呈先减小后增大趋势。得出初步的结构参数优化组合为:边距20 mm,列距30 mm,入口直径120 mm,行距25 mm,出口直径90 mm。
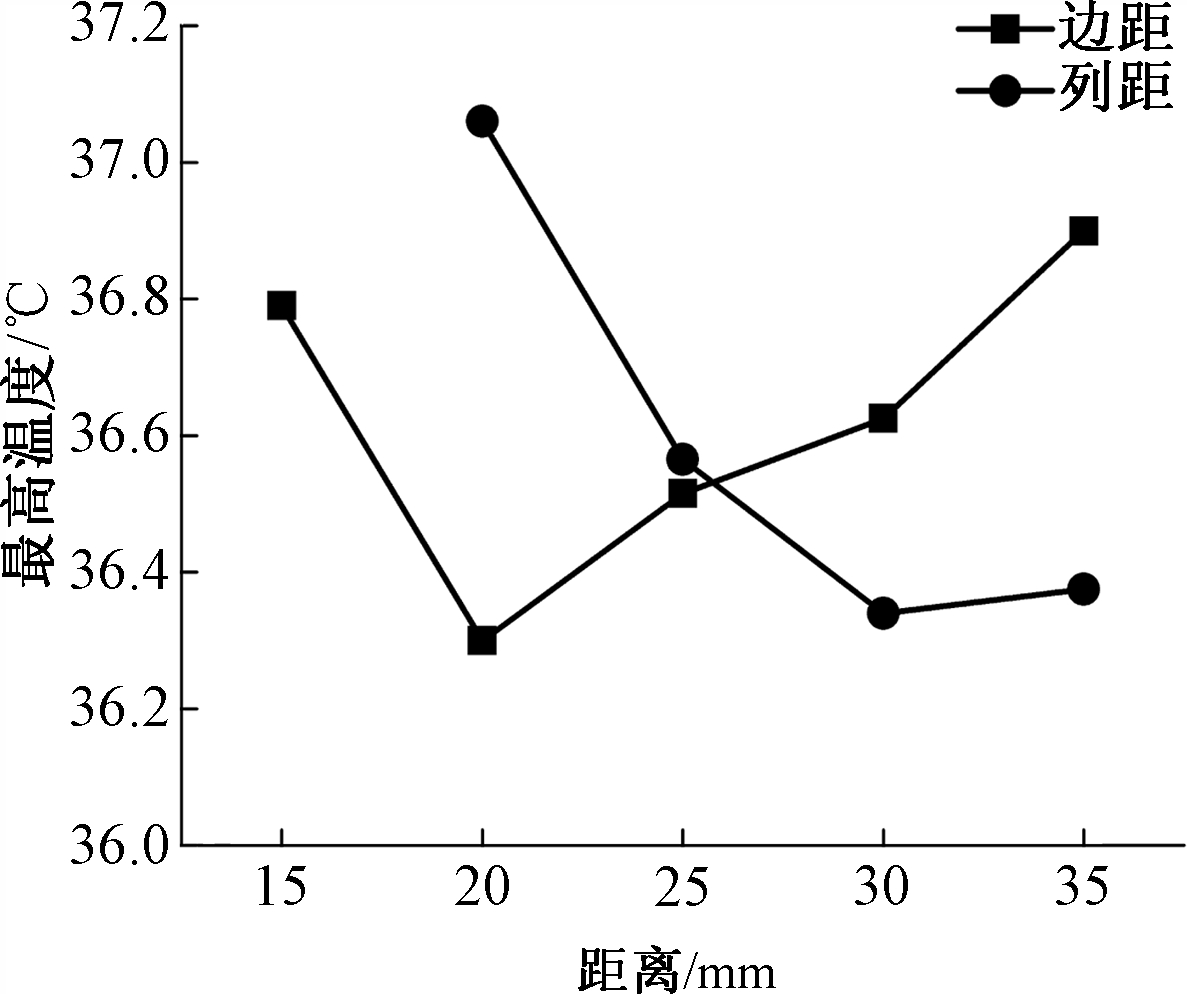
图4 列距、边距与最高温度关系
Figure 4 Relationship between column or side distance and maximum temperature
3.2 仿真结果拟合
通过相关性分析,参考相关文献[14],采用类比法,并反复调教函数形式,拟合得到基于最高温度要求的设计式(高温式):
(5)
图5为高温式计算仿真结果与应用拟合公式计算结果的比较,其最大误差小于5%。
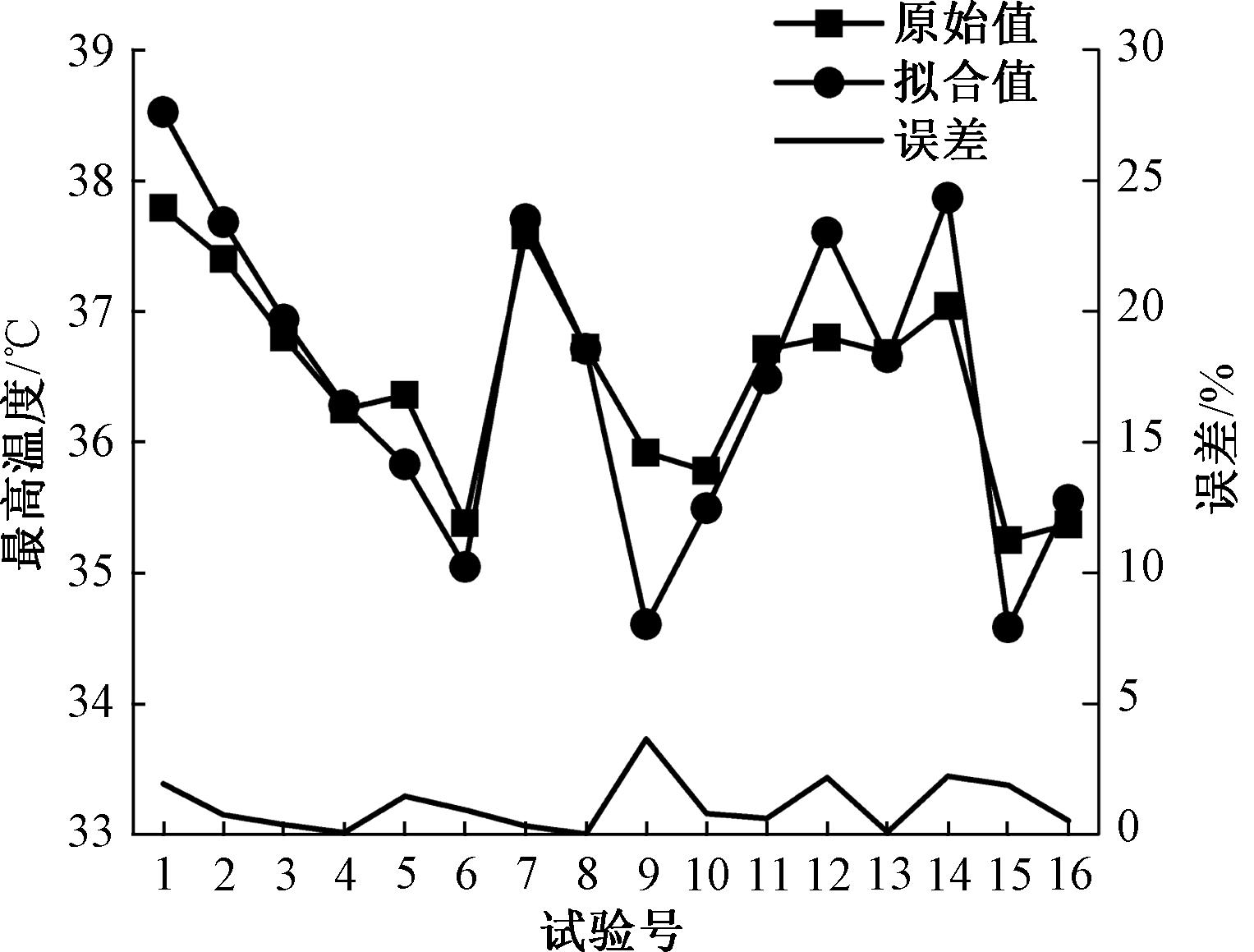
图5 高温式计算与仿真结果比较
Figure 5 Result errors comparison between high temperature formula calculation and simulation
同理,可得基于最大温差的设计式(温差式):
(6)
图6为温差式计算仿真结果与应用拟合公式计算结果的比较,其最大误差也小于5%。
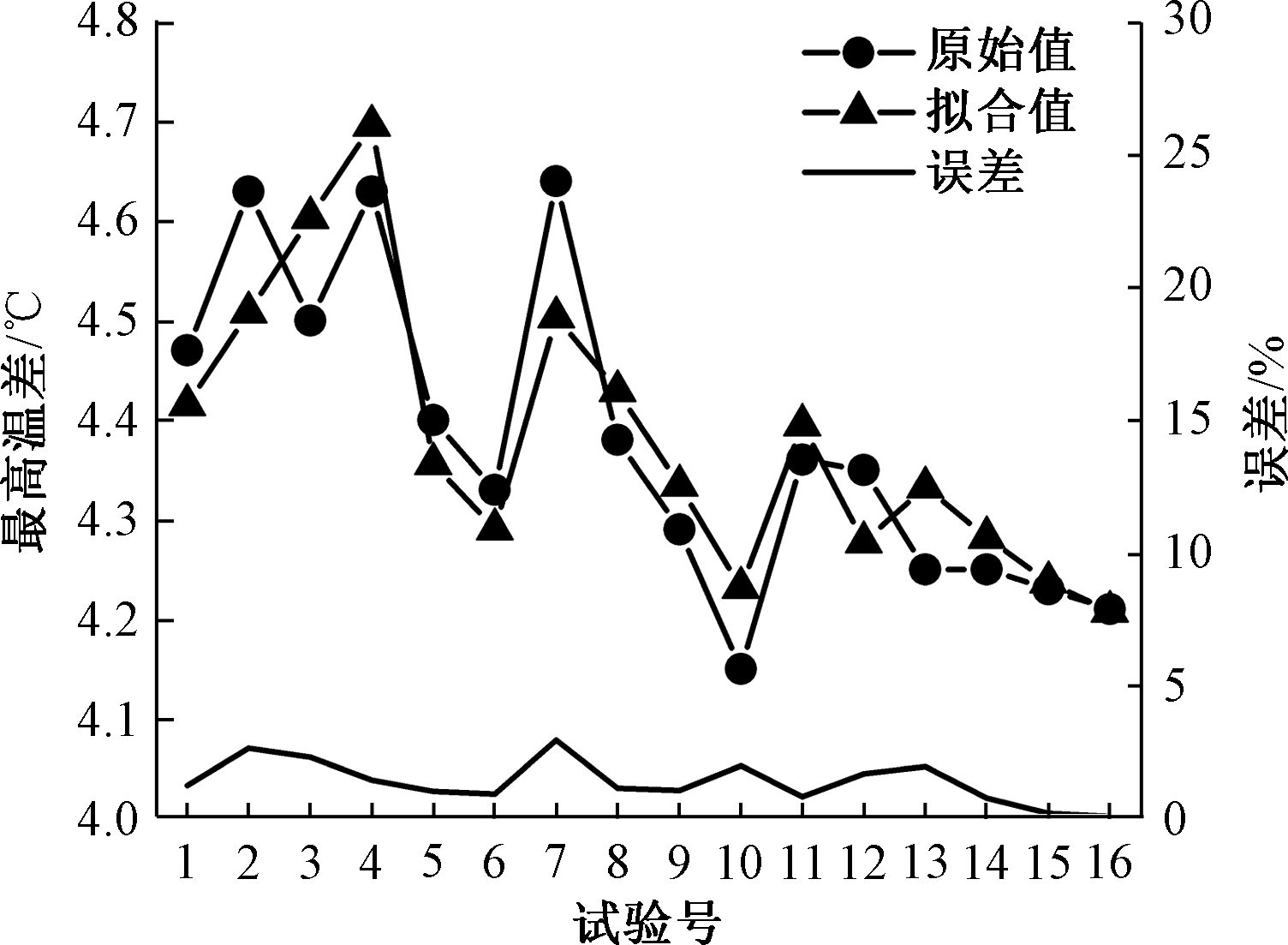
图6 温差式计算与仿真结果比较
Figure 6 Result errors comparison between temperature difference formula calculation and simulation
3.3 拟合公式验证
为求解电池箱内部空气流道特征尺寸的最优组合,需优化问题可概括为:
min(k1Tmax+k2ΔT),
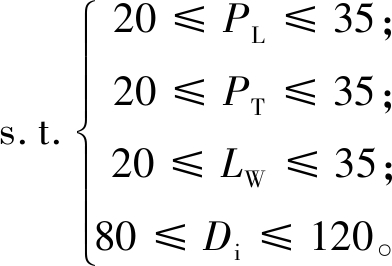
(7)
当权重k1、k2不同时(k1+k2=1),求解结果基本一致,主要结构参数圆整结果和初步的结构参数优化组合模型一致,结果如表4所示。
表4 不同权重系数下的计算结果
Table 4 Calculation results under different weight coefficients
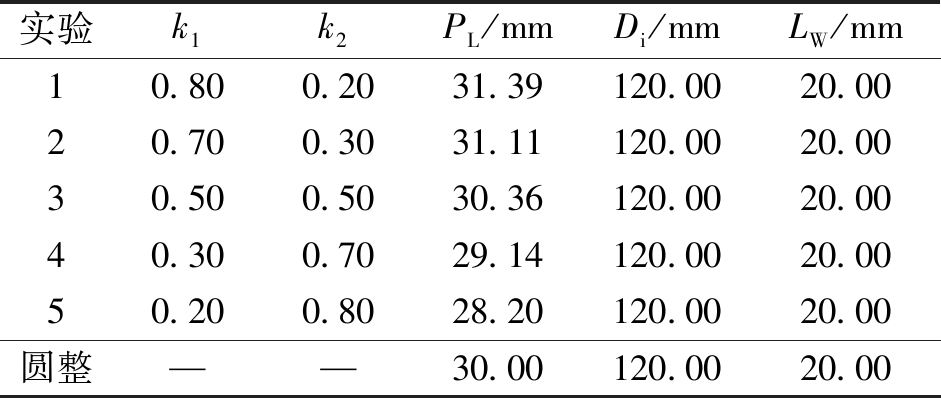
实验k1k2PL/mmDi/mmLW/mm10.800.2031.39120.0020.0020.700.3031.11120.0020.0030.500.5030.36120.0020.0040.300.7029.14120.0020.0050.200.8028.20120.0020.00圆整——30.00120.0020.00
建立对应的动力电池箱模型,采用Fluent仿真得到温度分布云图如图7所示(PT=20 mm,DO=90 mm)。
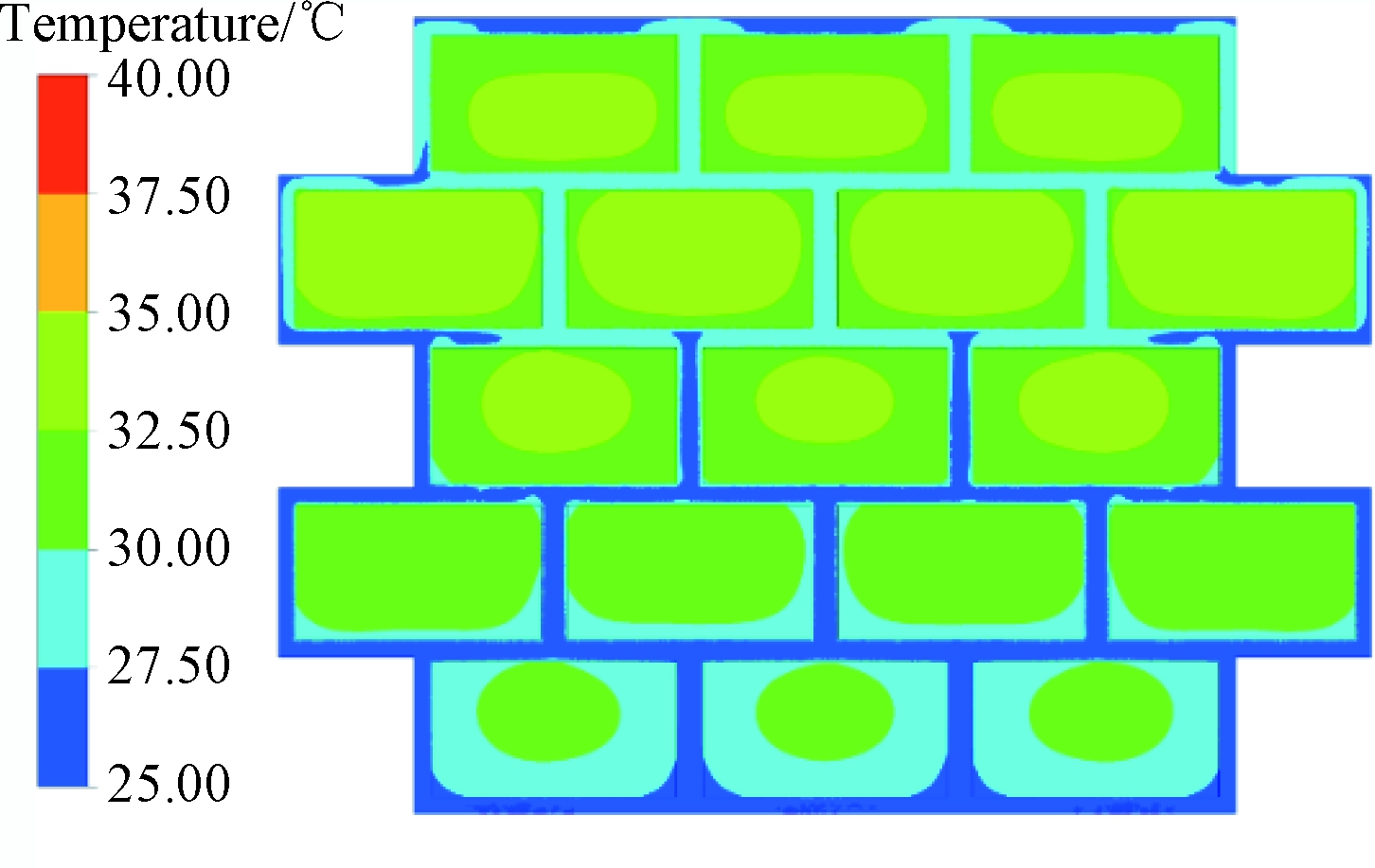
图7 圆整模型温度场仿真云图
Figure 7 Simulation cloud map of temperature field on the modification model
4 局部尺寸优化
在以上仿真中发现,电池箱内温度较高处主要集中在第4、5两排,尤其是第4排(Row4)。对Row4单独改变边距,电池箱最高温度变化如图8所示。
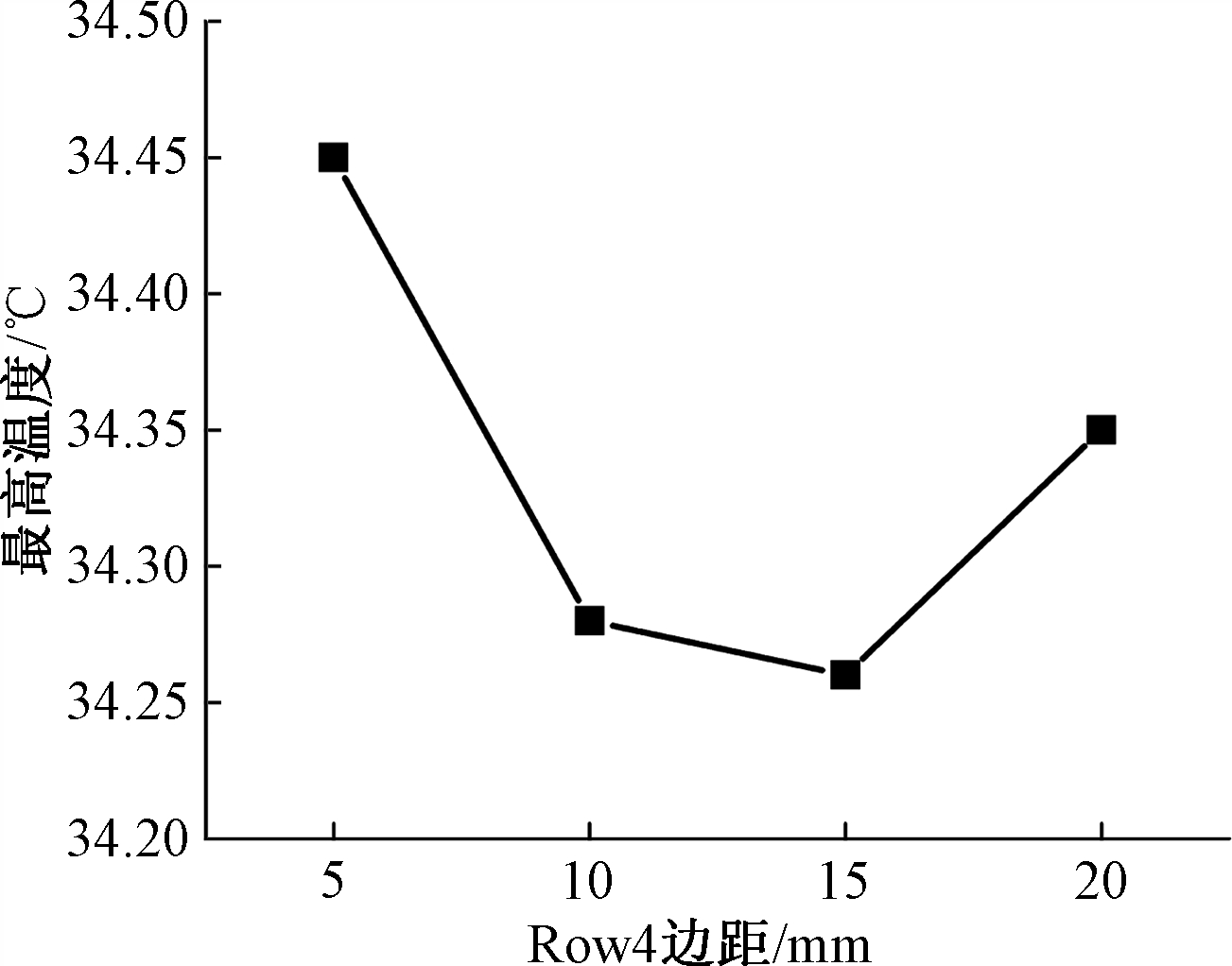
图8 最高温度与Row4边距变化关系
Figure 8 Relationship between maximum temperature and Row 4 sides distance
由图8可见,边距LW=15 mm时,最高温度为34.26 ℃,极差为0.2 ℃,对最高温度的影响不大,但是高温区面积ST35首次降为0,ST32.5降为23.988 dm2,ST30降为63.750 dm2,温度场均匀性得到较大改善。
位于电池箱左右两侧的箱体圆角半径、数目对最高温度和高温区面积的影响关系结果见图9。
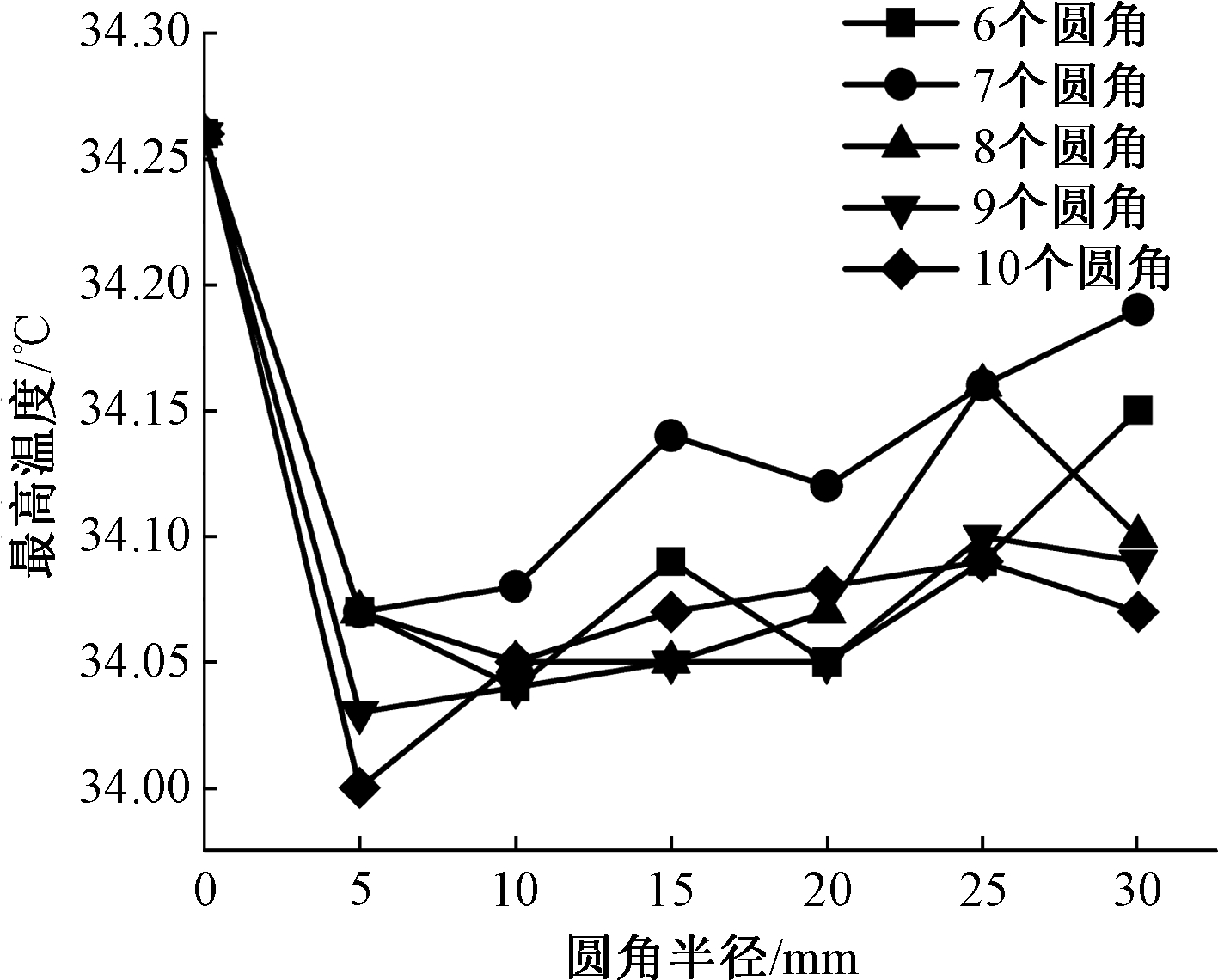
图9 不同圆角半径、数目与最高温度关系图
Figure 9 Relationship between different fillet radii, number and maximum temperature
由图9可见,当电池箱每侧采用10个半径5 mm圆角时,最高温度为34 ℃,Fluent计算结果显示高温区面积ST35为0,ST32.5降为22.737 dm2,ST30为63.806 dm2。电池最高温度满足工作范围0~40 ℃,最大温差小于5 ℃的要求[5]。将Di=120 mm模型的各优化历程结果对比见图10。
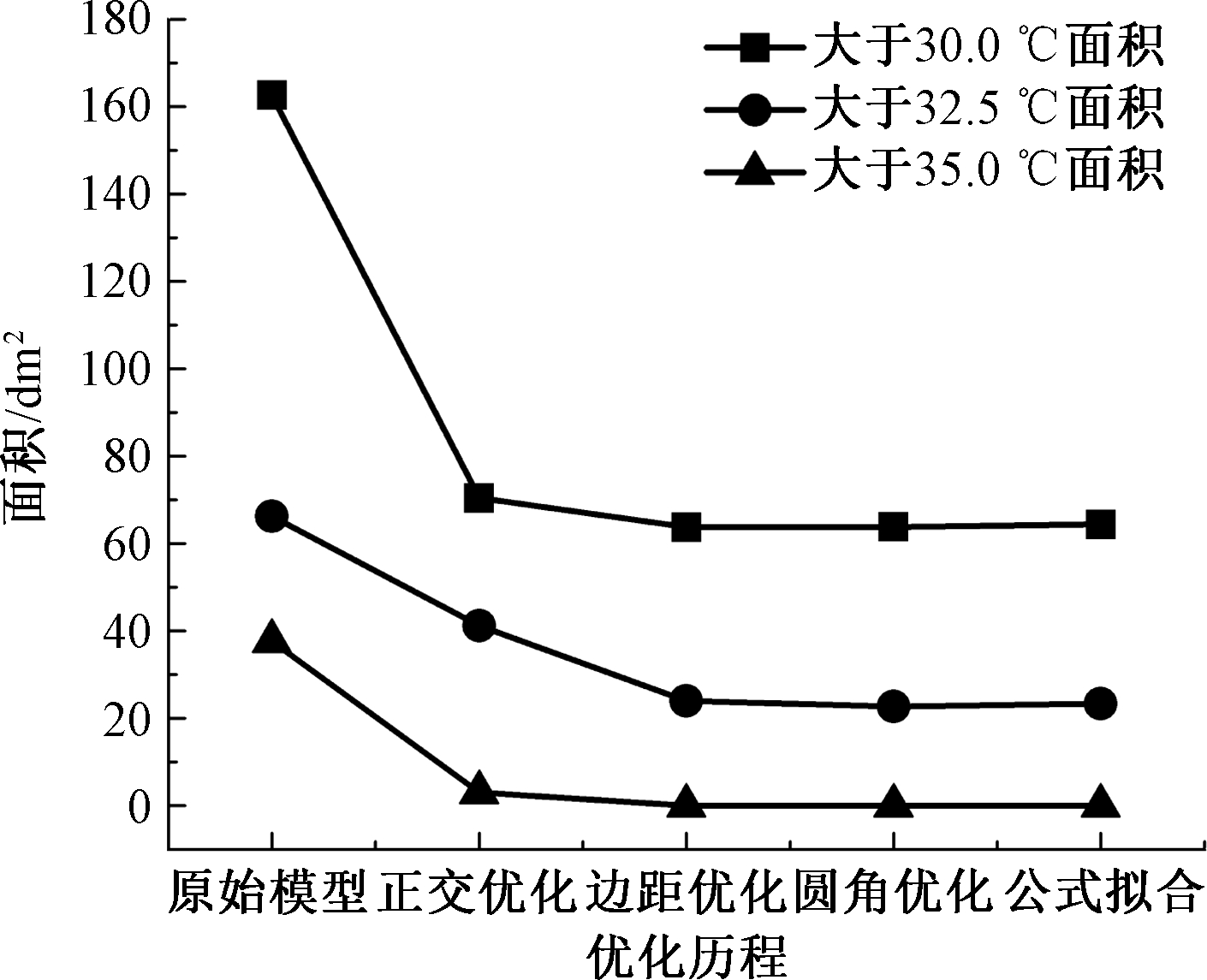
图10 高温区面积优化历程对比
Figure 10 Comparison of high temperature area in optimization process
此时,电池箱内电池模块的最高温度由37.27 ℃下降为34 ℃,下降8.77%;最大温差由4.48 ℃下降为4.31 ℃,下降3.79%;高温区面积ST32.5由66.243 dm2下降为22.737 dm2,下降65.68%;ST30由162.657 dm2下降为63.806 dm2,下降60.77%。与最初设计模型相比,散热效果得到改善的同时,行距由50 mm降为25 mm,下降50%;列距由50 mm下降为30 mm,下降40%;边距由50 mm下降为20 mm,下降60%,Row 4边距下降70%。
综上优化结果得到紧凑化电池箱结构参数如表5所示,可知最终入口直径为120 mm。
表5 紧凑化电池箱结构参数
Table 5 Structural parameters of compact battery box mm
PLPTLWDiDORow4边距圆角R30252012090155
5 结论
(1)提出电池模块矩形错位阵列布置复合凹凸箱体壁的紧凑化构型,并经行距、列矩和边距等参数,以及箱体内部直角的圆角半径优化,最高温度降为34 ℃,最大温差降为4.31 ℃,优于电池工作温度控制在0~40 ℃和模块间温差在5 ℃以下的目标。
(2)运用正交实验法仿真确认了入口直径、列距和边距等几何特征参数是影响电池箱平衡散热效果的主要因素,采用类比调教方法建立的紧凑化设计式计算结果与仿真结果的相对误差小于5%,可为高比能量电池箱结构设计计算提供参考。
[1] 贺伊琳, 许世维, 刘瑞,等. 纯电动赛车复合电源动力系统控制研究[J]. 郑州大学学报 (工学版) 2016,37(1):40-44.
[2] 李哲,韩雪冰,卢兰光,等.动力型磷酸铁锂电池的温度特性[J].机械工程学报, 2011, 47(18):115-120.
[3] 刘振军,林国发,秦大同,等.电动汽车锂电池组温度场研究及其结构优化[J].汽车工程,2012,34(1):80-84.
[4] 吴宏,李育隆,杨凯.电动汽车电池箱通风冷却结构的研究[J].汽车工程,2012,34(6):556-560,565.
[5] 眭艳辉,王文,夏保佳,等.混合动力汽车镍氢电池组通风结构优化分析[J].汽车工程, 2010, 32 (3):203-208.
[6] FAN L W, KHODADADI J M, PESARAN A A. A para-metric study on thermal management of an air-cooled lithium-ion battery module for plug-in hybrid electric vehicles [J]. Journal of power sources, 2013, 238: 301-312.
[7] SANTOS I M C, GOWREESUNKER B L, TASSOU S A, et al. Investigations into air and refrigerant side heat transfer coefficients of finned-tube CO2 gas coolers[J]. International journal of heat and mass transfer,2017,107:168-180.
[8] 张新强.风冷式动力电池热管理系统技术数值研究[D]. 广州:华南理工大学,2016.
[9] WAGNER M. 热分析应用基础[M]. 陆立明,译. 上海:东华大学出版社, 2011.
[10] FLUENT Inc. FLUENT 6.1.22 user′s guide[M]. Lebanon, NH: FLUENT Incorporated, 2003.
[11] 安治国,李升东,张栋省,等.动力锂离子电池放电热模拟分析[J].电源技术,2018,42(2):188-190.
[12] 李秋芬.车用动力电池包的散热仿真分析[D]. 广州:华南理工大学,2016.
[13] 罗宗鸿.电动汽车电池热特性及电池组风冷散热研究[D]. 南昌:南昌航空大学,2018.
[14] 英克鲁佩勒, 德维特,伯格曼,等.传热和传质基本原理[M]. 葛新石,叶宏,译. 北京:化学工业出版社, 2007.